| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321231 | |
| Published online | 11 July 2013 | |
Rotational non-LTE in HCN in the thermosphere of Titan: Implications for the radiative cooling
1 Max Planck Institute for Solar System Research, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
e-mail: rezac@mps.mpg.de
2 The Catholic University of America, 620 Michigan Ave., Washington DC 20064, USA
3 NASA Goddard Space Flight Center, Mailcode 674, Greenbelt Rd., Greenbelt, MD 20771, USA
4 Laboratoire d’Astrophysique, UMR 5571 CNRS, Université Joseph-Fourier, BP 53, 38041 Grenoble Cedex 9, France
5 Centre National de la Recherche Scientifique/École Polytechnique, Laboratoire de Météorologie Dynamique, 91128 Palaiseau-Cedex, France
Received: 4 February 2013
Accepted: 6 June 2013
Context. The thermal structure of Titan’s thermosphere is determined by the balance between several heating and cooling processes. These processes must be accurately modeled to correctly interpret the available measurements and enhance our understanding of the formation and evolution of this atmosphere. One of the most important thermospheric cooling process for Titan is emission in the HCN rotational band.
Aims. We aim to determine the validity of local thermodynamic equilibrium (LTE) for the HCN rotational distribution in the thermosphere of Titan and the impact of its breakdown on the HCN radiative cooling rate in the thermosphere.
Methods. A general non-LTE radiative transfer code for rotational lines based on the accelerated lambda iteration (ALI) was used to calculate the excitation of HCN rotational levels in Titan’s atmosphere. These level populations were then used to calculate the associated cooling rate.
Results. We show that the common assumption in the models of Titan’s thermospheric energy balance, namely the LTE distribution of rotational lines of HCN, is generally not valid above about 1100 km, or ~0.025 nbar, which will affect the derived thermospheric cooling rates. The effect of non-LTE is to reduce the cooling rate to 15% of the LTE value at around the exobase altitudes depending on the given density of HCN and collisional partners (N2, CH4, H2, and electrons). Since collision state-to-state quenching rates of HCN rotational levels are poorly known, a sensitivity analysis of our results to these rates is also presented.
Key words: radiation mechanisms: non-thermal / line: formation / planets and satellites: atmospheres
© ESO, 2013
1. Introduction
Titan, the second-largest moon in the solar system, is the only satellite with a dense atmosphere composed primarily of N2 (98%), CH4 (1.4%), H2, and other species resulting mainly from photochemistry of the primary constituents (Vinatier et al. 2009; Krasnopolsky 2010). The atmospheric surface pressure, p0, is about 1.5 bar, and the exosphere is at about 1500 km (De La Haye et al. 2007, 2008). Several clues (such as the D/H and 15N/14N ratios) obtained by recent measurements indicate the atmosphere of Titan may have been subject to a significant atmospheric loss (Marten et al. 2002; Niemann et al. 2005), which provides hints on the evolution of the atmosphere. One of the important factors determining the atmospheric escape is the thermospheric/exospheric thermal profile, which also impacts the chemistry and dynamics of the region. The current understanding of Titan’s upper atmospheric (~600–1500 km) energy budget is still under development (De La Haye et al. 2007, 2008; Bell et al. 2010), including the escape rate mechanism (Yelle et al. 2008; Strobel 2009; Schaufelberger et al. 2012) and chemistry (Hörst et al. 2008; Lavvas et al. 2008; Krasnopolsky 2009, 2012, and references therein).
The estimates on the upper atmospheric heat budget and interpretation of the thermal profile have been initiated by the Voyager data and modeling efforts of Friedson & Yung (1984), which were later corrected by the model of Lellouch et al. (1990). The result was an empirical temperature profile with a cold region around 800 km due to cooling from the ro-vibrational bands of C2H2. The subsequent work of Yelle (1991) included a more sophisticated approach that accounted for non-LTE in the ro-vibrational bands of CH4, C2H2, and C2H6, identifying all important radiative processes, which provided more accurate cooling/heating rates for these molecules. That work then predicted even a lower altitude of the mesospheric temperature minimum (~600 km) due to the additional CH4 cooling (shown to be the dominant process). Furthermore, Yelle (1991) was the first to identify that emission from HCN rotational transitions is the dominant cooling process, balancing the solar EUV heating, and is therefore responsible for the thermal structure of the thermosphere. Nevertheless, Yelle (1991) assumed that the HCN rotational lines probably are in LTE throughout the thermosphere and argued that they are optically thin. The LTE assumption has since propagated into all subsequent models that deal with Titan’s energetic and heat transport (e.g. Müller-Wodarg et al. 2000; De La Haye et al. 2008; Strobel 2009; Bell et al. 2010). Krasnopolsky (2010) has re-examined this assumption and estimated that it may have a limited validity even below the exobase for a typical thermospheric molecular density. The goal of this paper is to investigate the departure of the HCN rotational distribution from LTE in the thermosphere of Titan and how it affects the cooling rate by using fully detailed non-LTE calculations that account for radiative transfer within the lines and collisional excitation. The state-to-state collision rates of HCN with the most abundant molecules are poorly known, and therefore a discussion on the estimated collision rates and sensitivity study is also presented.
2. HCN rotational cooling with non-LTE
Formally, the radiative cooling/heating rate, h, is given by the radiative flux divergence, and can be obtained from integrating the radiative transfer equation over frequency and solid angle (for non-overlapping lines): ![\begin{equation} h = -\sum_{\rm lines} \int_{\nu} \int_{\Omega} \mu\dfrac{{\rm d}I(z,\nu,\Omega)}{{\rm d}z} {\rm d}\Omega {\rm d}\nu, \quad \left[{\rm Wm}^{-3}\right]. \label{eq:1} \end{equation}](/articles/aa/full_html/2013/07/aa21231-13/aa21231-13-eq9.png) (1)Ω and ν are the solid angle and frequency, I(z,ν,Ω) is the radiation intensity at a given height, z, and μ is the cosine of zenith angle. The sum is over all rotational lines of the HCN vibrational ground state.
(1)Ω and ν are the solid angle and frequency, I(z,ν,Ω) is the radiation intensity at a given height, z, and μ is the cosine of zenith angle. The sum is over all rotational lines of the HCN vibrational ground state.
In LTE, the distribution of molecular levels from which the emissions originate are given by the Boltzmann distribution (function of only Tkin) and the cooling-rate calculations are straight-forward. On the other hand, if the molecular collisions are not frequent enough to maintain the level population in the Boltzmann distribution, a detailed modeling of the microscopic processes is necessary to obtain the level populations.
We calculated the HCN rotational populations with a general non-LTE code based on the ALI approach (Rybicki & Hummer 1991) that is applied in the code ALI-ARMS for molecular bands (Kutepov et al. 1998; Gusev 2003). We considered only the radiative transitions of the rotational substructure of the ground-vibrational level from which the cooling originates. The processes that affect the populations of HCN rotational levels in the thermosphere of Titan are collisions with the main constituents of the atmosphere (N2, CH4, H2), electrons, and radiative transfer among the atmospheric layers. Once the populations at each level are known, the radiative cooling rate can be calculated using Eq. (1) expressed in another convenient form as ![\begin{equation} h = \sum_{lines} h\nu_{ji} \left[n_{i}B_{ij}\bar{J} - n_{j}(A_{ji} + B_{ji}\bar{J})\right]. \end{equation}](/articles/aa/full_html/2013/07/aa21231-13/aa21231-13-eq16.png) (2)nj and ni are the number densities of the upper and lower levels, Aji, Bij, and Bji are the Einstein coefficients, and
(2)nj and ni are the number densities of the upper and lower levels, Aji, Bij, and Bji are the Einstein coefficients, and 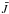 is the frequency-integrated mean intensity weighted with the line profile function for the transition. Because we are concerned here only with the upper atmosphere (>700 km), the line profiles are purely Doppler broadened. The assumption of complete frequency redistribution within the line is also used in these calculations so that the line emission and absorption profiles are the same.
is the frequency-integrated mean intensity weighted with the line profile function for the transition. Because we are concerned here only with the upper atmosphere (>700 km), the line profiles are purely Doppler broadened. The assumption of complete frequency redistribution within the line is also used in these calculations so that the line emission and absorption profiles are the same.
3. Inputs and the HCN non-LTE model
In this section, we present details of the input parameters and describe the available HCN collision rates needed for the calculations of the rotational populations. Because the aim is to evaluate the importance of non-LTE effects on the HCN cooling, only a model atmosphere of Titan is used. The temperature profile, HCN, N2, CH4, and H2 number densities are taken from the photochemical model of Krasnopolsky (2012). The electron density profile is adopted from the Cassini measurements (Kliore et al. 2011) (the higher value is considered ~1500 cm-3). The electron temperature, Te, profile is taken from Galand et al. (2006).
The non-LTE populations are calculated including 25 radiative transition among the first 26 rotational sublevels (up to ΔE = 1380 K) of the HCN ground-vibrational level ignoring the hyper-fine splitting (blended lines). The molecular parameters are taken from the LAMDA1 database (Schöier et al. 2005).
Even though the HCN rotational spectra are routinely analyzed under non-LTE conditions for galactic objects and cometary comas (e.g. Salter et al. 2011; Bockelée-Morvan et al. 1994; Paganini et al. 2010; de Val-Borro et al. 2012), the state-to-state collision rates are not well known, particularly for the higher-lying transitions. This is especially true for the most abundant collision partners in the thermosphere of Titan, the N2 and CH4. In this study the N2 collision rates were estimated by scaling the HCN-He rates from Dumouchel et al. (2010) with a factor 3.1 derived from the collisional broadening measurement of the HCN lines by N2 and He as presented in Rohart et al. (2007). The information on the HCN-CH4 collision quenching rates is virtually non-existent. In this case the collision rate was simply estimated as, k[cm3 s-1 molec-1] = 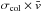 , where
, where 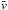 , [cm/s], is the average velocity of the Maxwell distribution, and σcol = 4.6 × 10-15 is the collisional cross-section for CH4 in [cm2] (Atkins & de Paula 2009). The recent work of Dumouchel et al. (2010) provides collision rates with He, which are normally used for a reasonable indirect estimate of the rate coefficients with H2. Nevertheless, explicitly calculated rate coefficients at T ≤ 100 K with para-H2 (j = 0) differ by typically a factor of 3 from the He values (Abdallah et al. 2012). Because of the relatively low abundance of H2 in the thermosphere of Titan, the H2 collisional quenching is negligible (as discussed below). On the other hand, the detailed theoretical calculations on the HCN-electrons collisional quenching (Faure et al. 2007) indicate the necessity to account for this process in the non-LTE model. The collision rates for ΔJ = 1 are up to 1 × 106 times higher than the HCN-He rates. Table 1 summarizes the information on the collision rates in this work and the range of uncertainty (as scaling factors) used in the sensitivity study.
, [cm/s], is the average velocity of the Maxwell distribution, and σcol = 4.6 × 10-15 is the collisional cross-section for CH4 in [cm2] (Atkins & de Paula 2009). The recent work of Dumouchel et al. (2010) provides collision rates with He, which are normally used for a reasonable indirect estimate of the rate coefficients with H2. Nevertheless, explicitly calculated rate coefficients at T ≤ 100 K with para-H2 (j = 0) differ by typically a factor of 3 from the He values (Abdallah et al. 2012). Because of the relatively low abundance of H2 in the thermosphere of Titan, the H2 collisional quenching is negligible (as discussed below). On the other hand, the detailed theoretical calculations on the HCN-electrons collisional quenching (Faure et al. 2007) indicate the necessity to account for this process in the non-LTE model. The collision rates for ΔJ = 1 are up to 1 × 106 times higher than the HCN-He rates. Table 1 summarizes the information on the collision rates in this work and the range of uncertainty (as scaling factors) used in the sensitivity study.
Collisional processes for the HCN rotational levels.
The excitation of vibrational levels by solar radiation with subsequent cascading down to the lower level(s) through ro-vibrational transitions may ultimately contribute to the excitation of rotational levels in the vibrational ground-state of HCN. The significance of this mechanism can be estimated from knowing the degree of vibrational excitation due to solar absorption, i.e. the vibrational temperatures, Tv. The number of molecules in the upper vibrational level, v, spontaneously decay approximately at a rate exp( − ΔE/kTv) × Av0. If exp( − ΔE/kTv) × Av0 ≪ Cjj′(v = 0), where Cjj′ = kjj′nN2 is the collisional de-excitation rate of rotational levels in the vibrational ground-state, this process will not influence the ground state rotational populations. For the two most important vibrational bands at 7 and 3 μm, (the 14 μ band is subthermal), Tv~ = 190 and 300 K, respectively (Adriani et al. 2011). Considering the collision rate with N2, kjj′ ~ 1 × 10-11, exp( − ΔE/kTv) × Av0/kjj′ implies that the N2 density must be lower than 1 × 106 cm-3 for this mechanism to start to be significant. Provided that the N2 density at the exobase is >5 × 106 cm-3, and that we omit other collisional quenchers, it is reasonable to neglect this process in our non-LTE consideration.
4. Results
Figure 1 shows profiles of several calculated HCN cooling rates from published works (see the figure caption). All profiles assume LTE conditions and the plane-parallel approximation including our calculations, which are shown for comparison. Because of the LTE assumption, the different profiles vary depending on the exact temperature as well as on the HCN number density used in the calculations.
 |
Fig. 1 Different HCN rotational cooling-rate profiles extending to the exobase, calculations assume LTE conditions. The red full and dashed lines are taken from De La Haye et al. (2008) and present night and day conditions for one of the Cassini flybys (T5), respectively, and the blue full and dashed lines are the same for the second flyby (Ta). The dark green curve is taken from Bell et al. (2010). Results of this work under LTE are shown as the black curve with squares. |
The cooling-rate calculations taking into account non-LTE are presented in Fig. 2 as the non-LTE to LTE ratio. In panel A), the different curves illustrate the relative contribution of different collisional partners where the blue curve incorporates non-LTE calculations including all relevant collisional process (see figure caption for details). These baseline results for the adopted nominal values of collision rate coefficients demonstrate that non-LTE effects start to be important above about 1100 km. Near the exobase, at 1500 km, the non-LTE cooling rate is reduced by approx. 85% with respect to the LTE value. Figure 2 (panel A) furthermore demonstrates that of all rotation-translation processes the HCN-N2 process is dominant (~95%), followed by the HCN-electron collisions with ~4% and the HCN-H2, HCN-CH4 processes with only about 1% combined contribution. Because the electron temperature in the thermosphere is more than 500 K higher than the neutral kinetic temperature, the collisional process with electrons is more closely related with electron cooling, and therefore has only an indirect role in establishing the neutral kinetic temperature profile.
How the uncertainty in the collision rates influences the results is depicted as shaded regions in Fig. 2 panel B). For the sensitivity calculations, we adopted the scaling factors for the respective collision rates as presented in Table 1. Because of the high density of N2, the corresponding collision rates are crucial in determining the height of deviations from LTE populations, and hence the cooling rates. For HCN-N2 rates higher by a factor of 5, the non-LTE cooling rate calculations begin to deviate from the LTE at the higher altitude of ~1200 km, but retain quite strong deviations from LTE at the exobase (by about 65%). For an N2 quenching rate lower by a factor of 5, the altitude of non-LTE/LTE cooling rate differences of 10% occur at around 1000 km. The uncertainty in collision rates of HCN-electrons is less important because it has a quite asymmetrical response on the non-LTE cooling rate. Decreasing the rate by a factor of 5 has an effect of only 3% decrease in the non-LTE cooling rate, in contrast to the 18% increase when we consider the rate to be five times higher (applies at the exobase altitudes). The uncertainties in the H2 and CH4 rates also produce an asymmetric response, but the combined effect is about 1/3 of the HCN-electrons effects. We point out that scaling the respective collision rates can also be interpreted as a test of the importance of non-LTE effects with scaling the number density of colliders when the collision-rate coefficients are considered fixed.
 |
Fig. 2 Panel A) shows profiles of non-LTE to LTE cooling-rate ratios. The four curves show how the ratio changes by successively including more collisional processes. The black curve includes only the collisions with N2, for the red curve the collision partner CH4 was included in addition, and adding H2 is shown as green. Because of the relatively small contribution, the red and green curves are nearly identical and overlap the black one in the plot. The blue curve gives the ratio for all processes along with collisions with free electrons. Panel B) shows four shaded regions that illustrate how the ratio varies with the uncertainty in the collision rates (see Table 1) with N2 (black region), electrons (red region), H2 (dark green), and CH4 (blue). Again, the colors for H2 and CH4 nearly exactly overlap and only the blue region is visible. |
Figure 3 shows the non-LTE distribution of rotational levels of HCN compared with the LTE at altitudes of 1200, 1300, and 1450 km. The calculations were performed for the nominal values of collision-rate coefficients and our model atmosphere as described in Sect. 3.
 |
Fig. 3 NLTE/LTE populations of rotational levels of HCN as calculated from our model versus the rotational quantum number, J. The different line styles correspond to distributions at the different altitudes as shown in the label. |
5. Summary
The aim of this paper was to investigate whether the rotational populations of HCN depart from LTE in the thermosphere of Titan and the corresponding impact on the associated cooling-rate. Using a general non-LTE line-transfer code taking into account collisional and radiative processes, we found that the HCN populations deviate appreciably from LTE values above 1100 km. The HCN rotational non-LTE in the thermosphere of Titan is established by a relatively fast spontaneous emission from HCN rotational levels that compete with much slower collisional excitation and absorption of upwelling radiation.
Because of its large abundance in the atmosphere of Titan, the N2 molecule is the most important collisional partner for rotationally excited HCN molecules. The HCN-electron collisions are second in importance, but contribute only a small fraction (~4%) of the excitation relative to the N2 process. The H2 and CH4 collisional processes both show only a negligible impact on the rotational level populations of HCN in the thermosphere. It should be kept in mind that Te ≫ Tneutral so that HCN-electrons really reflect the cooling of hot electrons, but this process must still taken into account in calculations of the rotational levels population.
In general, the state-to-state collision rates are poorly known, therefore, large but realistic uncertainty estimates were used to test the robustness of our calculations. Increasing the HCN-N2 collision rate by a factor of 5 (see Table 1) still indicates that rotational populations are in non-LTE above 1200 km, resulting in cooling rates of only 35% of the LTE value at the exobase. The sensitivity to the electron collision rates reaches about 20% at the exobase for an increase of a factor of 5. We also tested the sensitivity to electron temperatures, but found them to be very weak (<1%) within the range of Te ± 200 K. Only a relatively small error in the non-LTE calculations comes from CH4 and H2 collision rate uncertainties for the nominal values adopted in this study. A set of calculations was performed, adopting the neutral temperature profile as given in Yelle et al. (2008) and Adriani et al. (2011), which confirmed that the non-LTE/LTE cooling-rate ratio is only very weakly temperature dependent. This is in part due to the nearly isothermal thermospheric profile and the moderate temperature variation in the thermosphere of Titan. Nevertheless, the absolute values of the non-LTE cooling rate depends on the adopted temperature profile.
Relying on the currently available collision rate coefficient data, this study demonstrated that a breakdown of LTE for the HCN rotational levels occurs in the thermosphere of Titan (as first hypothesized by Krasnopolsky 2010). The deviations from LTE are rather strong leading to a reduction in the cooling rate by more than 50% above 1300 km and by 85% near the exobase
for the nominal collision rate coefficients. This fact should be taken into account in the current energetics models of Titan’s thermosphere and re-evaluate our current understanding how the thermal profile is established and maintained.
Future improvements on this study can be accomplished by obtaining more accurate collisional coefficients, especially with the main collisional partner, N2. Second, the non-LTE/LTE ratio in Fig. 2 already provides a relatively easy and simple way to use the results of this study in the energetics and global circulation models of Titan’s upper atmosphere, but more sophisticated parametrization may be developed in the future that allows for the variable number density of quenchers and different rate coefficients.
Acknowledgments
This work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number HA 3261/7-1.
References
- Abdallah, D. B., Najar, F., Jaidane, N., Dumouchel, F., & Lique, F. 2012, MNRAS, 419, 2441 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, A., Dinelli, B. M., López-Puertas, M., et al. 2011, Icarus, 214, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Atkins, P., & de Paula, J. 2009, Elements of Physical Chemistry (Oxford University Press), 28 [Google Scholar]
- Bell, J. M., Bougher, S. W., Waite, Jr., J. H., et al. 2010, J. Geophys. Res., 115, E12002 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Padman, R., Davies, J. K., & Crovisier, J. 1994, Planet. Space Sci., 42, 655 [NASA ADS] [CrossRef] [Google Scholar]
- De La Haye, V. R. E., Johnson, J. H. W., Yelle, R. V., et al. 2007, J. Geophys. Res., 112, A07309 [NASA ADS] [CrossRef] [Google Scholar]
- De La Haye, V. R. E., Waite, Jr., J. H., Cravens, T. E., et al. 2008, J. Geophys. Res., 113, A11314 [Google Scholar]
- de Val-Borro, M., Hartogh, P., Jarchow, C., et al. 2012, A&A, 545, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumouchel, F., Faure, A., & Lique, F. 2010, MNRAS, 406, 2488 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Varambhia, H. N., Stoecklin, T., & Tennyson, J. 2007, MNRAS, 382, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Friedson, A. J., & Yung, L. Y. 1984, J. Geophys. Res., 89, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Galand, M., Yelle, R. V., Coates, A. J., Backes, H., & Wahlund, J. 2006, Geophys. Res. Lett., 33, L21101 [NASA ADS] [CrossRef] [Google Scholar]
- Gusev, O. 2003, Ph.D. Thesis, Ludwig-Maximilians-Universität München [Google Scholar]
- Hörst, S. M., Vuitton, V., & Yelle, R. V. 2008, J. Geophys. Res., 113, 10006 [Google Scholar]
- Kliore, A. J., Nagy, A. F., Cravens, T. E., Richard, M. S., & Rymer, A. M. 2011, J. Geophys. Res., 116, A11318 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A. 2009, Icarus, 201, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A. 2010, Planet. Space Sci., 58, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, V. A. 2012, Planet. Space Sci., 73, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Kutepov, A. A., Gusev, O. A., & Ogibalov, V. P. 1998, J. Quant. Spectr. Rad. Transf., 60, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Lavvas, P. P., Coustenis, A., & Vardavas, I. M. 2008, Planet. Space Sci., 56, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Hunten, D. M., Kockarts, G., & Coustenis, A. A. 1990, Icarus, 83, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Marten, A., Hidayat, T., Biraud, Y., & Moreno, R. 2002, Icarus, 158, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Wodarg, I. C. F., Yelle, R. V., Mendillo, M., Young, L. A., & Aylward, A. D. 2000, J. Geophys. Res., 105, 20833 [NASA ADS] [CrossRef] [Google Scholar]
- Niemann, H. B., Atreya, S. K., Bauer, S. J., et al. 2005, Nature, 438, 779 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Paganini, L., Villanueva, G. L., Lara, L. M., et al. 2010, ApJ, 715, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Rohart, F., Nguyen, L., Buldyreva, J., Colmont, J., & Wlodarczak, G. 2007, J. Mol. Spectr., 246, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Salter, D. M., Hogerheijde, M. R., van der Burg, R. F. J., Kristensen, L. E., & Brinch, C. 2011, A&A, 536, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaufelberger, A., Wurz, P., Lammer, H., & Kulikov, Y. N. 2012, Planet. Space Sci., 61, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strobel, D. F. 2009, Icarus, 202, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Vinatier, S., Bézard, B., Nixon, C. A., et al. 2009, Icarus, 205, 559 [Google Scholar]
- Yelle, R. V. 1991, ApJ, 383, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. V., Cui, J., & Muller-Wodarg, I. C. F. 2008, J. Geophys. Res., 113, 10003 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Different HCN rotational cooling-rate profiles extending to the exobase, calculations assume LTE conditions. The red full and dashed lines are taken from De La Haye et al. (2008) and present night and day conditions for one of the Cassini flybys (T5), respectively, and the blue full and dashed lines are the same for the second flyby (Ta). The dark green curve is taken from Bell et al. (2010). Results of this work under LTE are shown as the black curve with squares. |
| In the text | |
 |
Fig. 2 Panel A) shows profiles of non-LTE to LTE cooling-rate ratios. The four curves show how the ratio changes by successively including more collisional processes. The black curve includes only the collisions with N2, for the red curve the collision partner CH4 was included in addition, and adding H2 is shown as green. Because of the relatively small contribution, the red and green curves are nearly identical and overlap the black one in the plot. The blue curve gives the ratio for all processes along with collisions with free electrons. Panel B) shows four shaded regions that illustrate how the ratio varies with the uncertainty in the collision rates (see Table 1) with N2 (black region), electrons (red region), H2 (dark green), and CH4 (blue). Again, the colors for H2 and CH4 nearly exactly overlap and only the blue region is visible. |
| In the text | |
 |
Fig. 3 NLTE/LTE populations of rotational levels of HCN as calculated from our model versus the rotational quantum number, J. The different line styles correspond to distributions at the different altitudes as shown in the label. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


