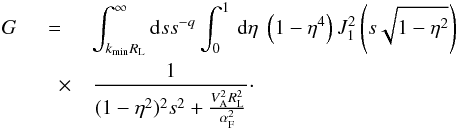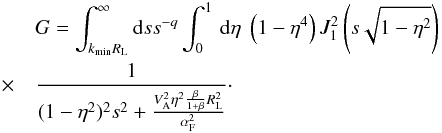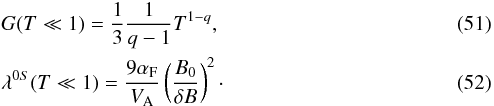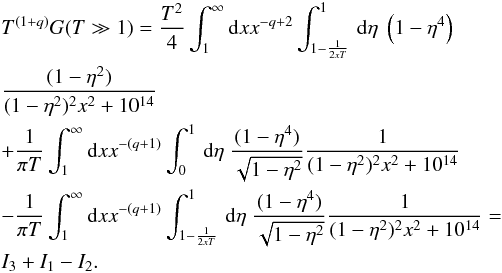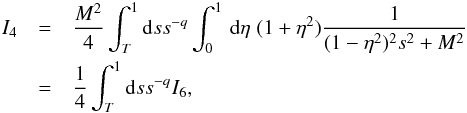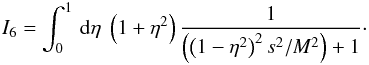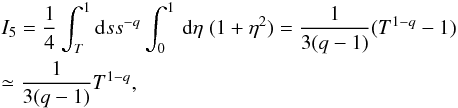| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321191 | |
| Published online | 10 July 2013 | |
The scattering mean free path of cosmic ray particles in isotropic damped plasma wave turbulence
1 Institut für Theoretische Physik, Lehrstuhl IV: Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
e-mail: vuk.mira@gmail.com
2 University of Defence, Military Academy, Pavla Jurisica Sturma 33, 11000 Belgrade, Serbia
Received: 30 January 2013
Accepted: 3 May 2013
An analytical expression for the mean free path of single-charged cosmic ray particles, especially for positrons, is derived in isotropic plasma wave turbulence, where the crucial scattering of cosmic ray particles with small pitch-angle cosines is caused by resonant cyclotron interactions with oblique magnetosonic waves. In this calculation, viscous damping effects are included, which results in broadening of the resonance function. It is demonstrated that including resonance function broadening ensures a finite mean free path for cosmic ray energies, for which previously reported types of turbulence predicted an infinitely large mean free path.
Key words: scattering
© ESO, 2013
1. Introduction
A Galactic bulge-to-disk ratio of the luminosity of diffuse 511 keV positron annihilation radiation is, as measured by INTEGRAL, four times larger than a stellar bulge to disk ratio of the Galactic supernovae (SNe). SNe are thought to be the principal source of the annihilating positrons. This large discrepancy has started a search for new sources. It has been shown that the measured 511 keV luminosity ratio can be understood well in the context of a Galactic SN origin when the differential propagation of these MeV positrons in the various phases of the interstellar medium is taken into consideration (Higdon et al. 2009), since these relativistic positrons must first slow down to energies less than 10 eV before they can annihilate.
A large number of potential sources have been proposed over the years: cosmic ray interaction with the interstellar medium (Ramaty et al. 1970), pulsars (Sturrock 1971), radioactive nuclei produced in SN (Clayton 1973), compact objects (Ramaty & Lingelfelter 1979), dark matter (Boehm 2004), and microquasars (Guessoum et al. 2006). Some of these theories either are problematic or have a wide range of uncertainties. For example, the predicted distributions of positrons from radionuclei synthesized in SN are only marginally compatible with observations (Milne et al. 2002). However, the recent mapping of the Galaxy at 511 KeV (Knödlseder et al. 2005) has placed severe constraints on the possible positron sources.
On the other hand, the positron excess in Galactic cosmic ray positrons above 10 GeV has been confirmed by PAMELA (Adriani et al. 2009). The most recent confirmation of the PAMELA result on positrons in the Galaxy cosmic ray spectrum has just been published (Aguilar et al. 2013). There are several astrophysical explanations for possible sources of these positrons, such as dark matter annihilation (Hooper et al. 2009) or decay (Arvanitaki et al. 2009). According to a recent investigation (Pohl & Eichler 2009), Fermi measurements of the high-latitude γ-ray background (Abdo et al. 2009) constrain a decaying-dark-matter origin for the GeV Galactic positron anomaly measured by PAMELA.
To quantify scattering mean free paths for MeV interstellar positrons, an analytic approximation has been used (Teufel & Schlickeiser 2002) for slab-like dynamical turbulence, which predict that is a mean free path in MeV energies proportional to r1/3, where r is defined as particle rigidity. This model for GeV particles predicts an infinitely large mean free path. The other slab plasma-wave turbulence model (Schlickeiser et al. 2010), which is more plausible when compared to the dynamical one, predicts an infinite positron scattering mean free path at MeV energies, while it has finite values proportional to r1/3 for GeV energies.
Here, we propose a damped plasma wave turbulence model, which can assure a finite mean free path for MeV and GeV positrons, and compare our result with results of previously mentioned models.
A key parameter for the cosmic ray transport is the parallel spatial diffusion coeffcient κ = vλ/3, which is conventionally expressed in terms of the mean free path λ along the background magnetic field and the particle speed v. In many studies, the parallel mean free path also controls the perpendicular spatial diffusion coefficient κ⊥ = ακ∥, which is assumed to be proportional to κ∥ due to the lack of a rigorous theory of perpendicular diffusion. When discussing the ratio of perpendicular and parallel mean free path, it has been published from proton observations that 0.02 < λ⊥/λ∥ < 0.083 over the rigidity range of 0.5MV < R < 5GV (Palmer 1982), which assures parallel mean free path values to be high enough that we can neglect the perpendicular component. Hereafter, we only consider parallel mean free path.
The scattering mean free path is the result of resonant particle-wave interactions of cosmic ray particles with the turbulent component of cosmic magnetic fields, and thus depends on the nature and geometry of cosmic turbulent magnetic fields (Schlickeiser 2002). Many observations of plasma turbulence in the solar wind indicate that the turbulent magnetic field is a mixture of slab (i.e., parallel to the ordered background magnetic field) waves, a dominating 2D component (Bieber et al. 1996) with a negligible contribution to particle scattering (Shalchi & Schlickeiser 2004), and obliquely propagating magnetosonic waves that reveal through electron density fluctuations because of their compressive nature. In the static magnetosonic limit, the scattering rate from the 2D component vanishes (Shalchi & Schlickeiser 2004).
For small amplitude waves, an appreciable interaction between a wave and a particle arises only when the particle is moving at nearly the parallel wave phase speed. The interaction is resonant and the subsequent physics is close to that of Fermi acceleration: particles with v∥ slightly greater than ω/k∥ suffer a trailing collision with a wave compression and slow down, while particles with v∥ slightly less than ω/k∥ are stuck by a compression and speed up. This process could be called resonant Fermi acceleration, but the usual term is transit-time acceleration or transit-time damping (TTD). The name is given because the resonance condition can be rewritten as λ∥/v∥ ≈ t, where t is the wave period and λ∥ = 2π/kη is the parallel wavelength. That means a wave and a particle will interact strongly when the particle transit time across the wave compression is approximately equal to the period.
Schlickeiser & Miller (1998) and Schlickeiser & Vainio (1999) have investigated the quasilinear interactions of charged particles with Alfven and magnetosonic plasma modes. A cosmic ray particle of given velocity v, Lorentz factor γ = (1 − (v2/c2))− 1/2, pitch angle cosine μ = v∥/v, mass m, the speed of light c, charge qi = e | Zi | Q with Q = sgn(Zi), and gyrofrequency Ωc = QΩ with Ω = qiB0/(mcγ) interacts with waves whose wavenumber k, cosine of propagation angle η = k∥/k, and real frequency f obey the resonance condition f(k) = vμkη + nΩc for entire n ∈ [ − ∞,∞]. For slab(η = 1) Alfven waves, only gyroresonant interactions with n = 1 are possible. In contrast, the n = 0 resonance for obliquely propagating fast magnetosonic waves, which do not include gyroresonance interactions (n ≠ 1), is possible due to their compressive magnetic field component. The n = 0 interactions are referred to as transit-time damping (TTD). Using n = 0 the resonance condition requires the parallel cosmic ray velocity vμ = f/(kη)f/k ≃ VA to be greater than the finite phase velocity of magnetosonic waves, which is given by the Alfven speed. TTD interactions therefore only occur for cosmic ray particles with pitch-angle cosines μ > | VA/v | = ϵ. At these pitch angle cosines, TTD interactions provide most of the particle scattering.
Thus, the crucial scattering in small μ is provided for energetic particles by only gyroresonances with slab plasma waves and oblique magnetosonic waves (Schlickeiser et al. 2010): ![\begin{eqnarray} \label{mfp1} \lambda\!=\!\frac{3v}{8}\int_{-\epsilon}^{\epsilon}{\rm d}\mu\frac{\left(1-\mu^{2}\right)}{D_{\mu\mu}^{\rm slab}(\mu)+D_{\mu\mu}^{\rm g-ms}(\mu)}\simeq\frac{3V_{\rm A}}{4[D_{\mu\mu}^{\rm slab}(0)+D_{\mu\mu}^{\rm g-ms}(0)]}\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq37.png) (1)According to Schlickeiser & Miller (1998), the magnetosonic contribution
(1)According to Schlickeiser & Miller (1998), the magnetosonic contribution 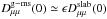 for energetic particles (ϵ ≪ 1) is much smaller than the slab contribution for similar turbulence power spectra of slab and magnetosonic waves. However, this latter reduction is not justied for cosmic ray positrons with Lorentz factors γ < mp/me = 1836. These positrons no LH polarized slab waves to find resonantly interact with, so that
for energetic particles (ϵ ≪ 1) is much smaller than the slab contribution for similar turbulence power spectra of slab and magnetosonic waves. However, this latter reduction is not justied for cosmic ray positrons with Lorentz factors γ < mp/me = 1836. These positrons no LH polarized slab waves to find resonantly interact with, so that 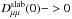 . In this case, the contribution from gyroresonant interactions with magnetosonic waves provides small but finite scattering (Schlickeiser et al. 2010).
. In this case, the contribution from gyroresonant interactions with magnetosonic waves provides small but finite scattering (Schlickeiser et al. 2010).
It is the purpose of this work to involve oblique magenetosonic waves and quantitatively investigate the influence of wave damping on the quasilinear scattering mean free paths of cosmic rays, especially for positrons with Lorentz factors γ < mp/me = 1836. In a plasma in rough equipartition of kinetic and magnetic pressure, oblique magnetosonic waves are expected to be overdamped by Landau absorption (Fedorenko 1992). Thus, the second-order Fermi acceleration using oblique fast magnetosonic waves cannot work in a plasma in rough equipartiton (Achterberg 1979). It is possible to overcome this difficulty either by considering that this mechanism works, in the interstellar medium with small β (relatively cold medium) or by including the finite wave cascading that exists in the interstellar medium. Due to the large amplitude of interstellar turbulence, there is no doubt that wave cascading exists and will then transfer this spectral energy to higher wavenumbers. One property of the diffusion equation for isotropic turbulence (Eq. (11.3.6), Schlickeiser 2002) is that it yields finite positive wave spectral energy densities at all wavenumbers k, even if the net damping rate is negative in some wavenumber intervals.
We show then that the inclusion of resonance broadening caused by wave damping in the resonance function guarantees that the transit-time damping contribution holds at small pitch angle cosines μ ≤ | Va/v |, unlike the case of neglible wave damping (Vukcevic & Schlickeiser 2007). We expect that TTD makes an overwhelming contribution to particle scattering because the cosmic ray particle interacts with the whole wave spectrum in this interaction. This contrasts gyroresonances that single out individual resonant wave numbers (Schlickeiser 2003). However, quantitative analysis of gyroresonance contribution in damped plasma wave turbulence will be studied in a separate, forthcoming investigation. Therefore we only consider the TTD-contribution to particle scattering in the following and assume n = 0 both in the resonance function and in the calculation of the Fokker-Planck coefficients.
In Sect. 2, we present the general plasma wave turbulence and relevant magnetohydrodynamic plasma modes. In Sect. 3, we calculate the Fokker-Planck coefficient for fast mode waves and discuss relevant domains for application to cosmic ray positrons. In Sect. 4, we derived the Fokker-Planck coefficient for slow mode waves. The analytical expressions of a mean free path for fast and slow plasma waves and the comparison with different previously reported turbulence models are given in Sect. 5. The summary and conclusion are presented in the last section.
2. Plasma wave turbulence
According to our discussion in the paragraph above and in the two paragraphs after Eq. (1), the relevant mean free path for the positrons with Lorentz factor γ < mp/me = 1836 in small pitch-angle cosine becomes 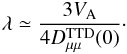 (2)Hereafter, we omit TTD notation and keep only notation for relevant magnetosonic waves. The Fokker-Planck coefficient Dμμ is computed by employing the Kubo formula (Kubo 1957),
(2)Hereafter, we omit TTD notation and keep only notation for relevant magnetosonic waves. The Fokker-Planck coefficient Dμμ is computed by employing the Kubo formula (Kubo 1957), 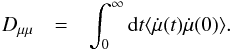 (3)The pitch-angle variation
(3)The pitch-angle variation 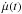 is obtained from the Newton-Lorentz equation:
is obtained from the Newton-Lorentz equation: ![\begin{eqnarray} \label{ mi} \dot{\mu} &=& \frac{\Omega \sqrt{1-\mu^{2}}}{B_{0}} \left[\frac{c}{v}\sqrt{1-\mu^{2}} \delta E_{||} + \frac{{\rm i}}{\sqrt{2}} \left[ {\rm e}^{{\rm i}\phi} \left(\delta B_{r}+ {\rm i} \mu \frac{c}{v}\delta E_{r}\right)\right. \right.\nonumber\\ &\quad -&\left. \left. {\rm e}^{-{\rm i} \phi} \left(\delta B_{l}-{\rm i} \mu \frac{c}{v} \delta E_{l}\right)\right]\right]. \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq49.png) (4)
(4)
In these equations, we use pitch-angle cosine μ, the particle speed v, the gyrophase φ, the cosmic ray particle gyrofrequency in the background field B0 and the turbulent fields δBl,r and δEl,r, which are related to the left-handed and right-handed polarized field components. The term δE| | is parallel component relative to the background magnetic field.
The simplest method to calculate Dμμ is the application of perturbation theory (Jokipii 1966). In this case, we have applied a quasilinear approximation for a fluctuating electric and magnetic field, a quasistationary turbulence condition, and the existence of a finite correlation time tc. The last two assumptions guarantee a diffusive behavior of transport (Shalchi & Schlickeiser 2004). The assumption of homogeneous turbulence will imply that the turbulence fields at different wavevectors are uncorrelated.
Next, we define the properties of the plasma turbulence that will be considered. We follow the approach for the electromagnetic turbulence that represents the Fourier transforms of the magnetic and electric field fluctuations as a superposition of N individual weakly damped plasma modes of frequencies: 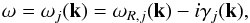 (5)where j = 1,...N, which can have both the real and imaginary parts with | γj | ≪ | ωR,j |, so that
(5)where j = 1,...N, which can have both the real and imaginary parts with | γj | ≪ | ωR,j |, so that ![\begin{eqnarray} \label{k9} \left[\textbf{B}({\vec k},t), \textbf{E}({\vec k},t)\right]= \sum_{j=1}^{N}\left[\textbf{B}^{j}({\vec k}), \textbf{E}^{j}({\vec k})\right]{\rm e}^{-{\rm i}\omega_{j}t}. \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq60.png) (6)Damping of the waves is counted with a positive γj > 0.
(6)Damping of the waves is counted with a positive γj > 0.
In the case we consider here, the time integration of the Fokker-Planck coefficient Dμμ yields the Lorentzian resonance function: ![\begin{eqnarray} \label{k12} {\cal R}_j(\gamma _j)&=&\int_0^\infty {\rm d}u\; {\rm e}^{-{\rm i}(k_{\parallel}v_{\parallel}+\omega _{R,j}+n\Omega)u-\gamma _ju} \nonumber\\ &= &{\gamma _j({\vec k})\over \gamma ^2_j({\vec k})+[k_{\parallel}v_{\parallel}+\omega _{R,j}({\vec k})+n\Omega)]^2}\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq62.png) (7)The detailed derivation of the Fokker-Planck coefficient for this case (vanishing magnetic helicity and isotropic turbulence) is performed in the PhD Thesis of Vukcevic (2007), which contrasts the case of negligible damping γ − > 0 (Schlickeiser 2001) in which the use of the δ-function representation
(7)The detailed derivation of the Fokker-Planck coefficient for this case (vanishing magnetic helicity and isotropic turbulence) is performed in the PhD Thesis of Vukcevic (2007), which contrasts the case of negligible damping γ − > 0 (Schlickeiser 2001) in which the use of the δ-function representation 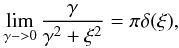 (8)reduces the resonance function (7) to sharp δ-functions,
(8)reduces the resonance function (7) to sharp δ-functions, 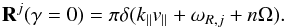 (9)Next, it is necessary to specify the geometry of the plasma wave turbulence itself through the correlation tensors, which will be adopted throughout this work in the form (Mattheus & Smith 1981) of
(9)Next, it is necessary to specify the geometry of the plasma wave turbulence itself through the correlation tensors, which will be adopted throughout this work in the form (Mattheus & Smith 1981) of ![\begin{eqnarray} \label{k14} P_{\alpha\beta}^{j}({\vec k})= \frac{g_{i}^{j}({\vec k})}{{\vec k}^{2}}\left[\delta _{\alpha\beta}- \frac{{\vec k}_{\alpha} k_{\beta}}{k^{2}} +{\rm i} \sigma({\vec k})\epsilon_{\alpha\beta\lambda}\frac{k_{\lambda}}{k}\right], \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq67.png) (10)where σ(k) is the magnetic helicity and the function g(k) determines different turbulence geometries. This was to illustrate the result, although this model is not in accord with the known polarization properties of fast-mode waves at oblique angles.
(10)where σ(k) is the magnetic helicity and the function g(k) determines different turbulence geometries. This was to illustrate the result, although this model is not in accord with the known polarization properties of fast-mode waves at oblique angles.
2.1. Relevant magnetohydrodynamic plasma modes
It has been already emphasized that there is no TTD for shear Alfven waves (Teufel et al. 2003) in the case of negligible damping, and the gyroresonant interactions provided by shear Alfven waves is small compared to the same contribution provided by fast magnetosonic waves (Vukcevic & Schlickeiser 2007). As a consequence, we consider only fast and slow magnetosonic waves.
2.1.1. Fast magnetosonic plasma modes
For the fast plasma modes, we use a simplified dispersion relation, 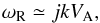 (11)which is relevant at wavenumbers kc ≪ k ≪ ξkc, where kc = ωp,i/c is the inverse ion skin length, and
(11)which is relevant at wavenumbers kc ≪ k ≪ ξkc, where kc = ωp,i/c is the inverse ion skin length, and 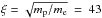 .
.
In the dispersion equation, forward (j = 1) and backward (j = − 1) moving fast mode waves are described. The associated electric field and magnetic field polarizations are (Dogan et al. 2006) 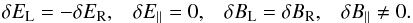 (12)
(12)
2.1.2. Slow magnetosonic plasma modes
The dispersion relation for slow magnetosonic waves in low-β plasma reads (Dogan et al. 2006) 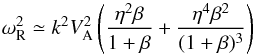 (13)with η = cosθ and β as the ratio of thermal and magnetic pressure. In the last equation, we neglect the second term in brackets in the first approximation, since it is one order smaller than the first term. The associated electric field and magnetic field polarizations are
(13)with η = cosθ and β as the ratio of thermal and magnetic pressure. In the last equation, we neglect the second term in brackets in the first approximation, since it is one order smaller than the first term. The associated electric field and magnetic field polarizations are 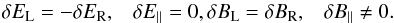 (14)Consideration of the dispersion relation in high frequencies could change the result, since we expect nondispersive effects in that range. The polarization of the waves in that domain could also affect the transport coefficients through the correlation tensors. However, a detailed inspection of the dispersion relation in the high-frequency domain is needed to draw a quantitative conclusion, and it will be discussed in a separate investigation.
(14)Consideration of the dispersion relation in high frequencies could change the result, since we expect nondispersive effects in that range. The polarization of the waves in that domain could also affect the transport coefficients through the correlation tensors. However, a detailed inspection of the dispersion relation in the high-frequency domain is needed to draw a quantitative conclusion, and it will be discussed in a separate investigation.
2.2. Damping rate
The damping of magnetosonic waves is caused by both collisionless Landau damping and collisional viscous damping and by Joule damping and ion-neutral friction. The dominant contribution is provided by viscous damping with the rate calculated for plasma parameters of the diffuse intercloud medium (Spanier & Schlickeiser 2005) ![\begin{eqnarray} \gamma _{\rm F} &=&{1 \over 12} \beta V_{\rm A}^2 \tau _ik^2 \left[\sin ^2\theta + 5 \times 10^{-9} \cos ^2 \theta \right]\nonumber\\ &=& 2.9 \times 10^5 \beta V_{\rm A}^2k^2 \left[ \sin ^2\theta +5 \times 10^{-9}\cos ^2\theta \right] \label{f5} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq80.png) (15)in terms of the ion-ion collisional time τi = 3.5 × 106 s. Except at very small propagation angles, the second term in Eq. (15) is negligible, and we infer
(15)in terms of the ion-ion collisional time τi = 3.5 × 106 s. Except at very small propagation angles, the second term in Eq. (15) is negligible, and we infer 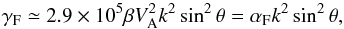 (16)where
(16)where 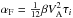 .
.
3. Fast mode waves
With Eqs. (11) and (16), the resonance function (7) for forward and backward moving fast mode waves becomes ![\begin{eqnarray} \label{d1} {\cal R}^j_{\rm F}(n)={\alpha_{\rm F}k^2\sin ^2\theta \over (\alpha_{\rm F}k^2\sin ^2\theta )^2+[kv\mu \cos \theta +jV_{\rm A} k + n\Omega)]^2}, \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq84.png) (17)which describes both gyroresonant (n ≠ 0) and transit-time damping (n = 0) wave-particle interactions.
(17)which describes both gyroresonant (n ≠ 0) and transit-time damping (n = 0) wave-particle interactions.
The non-vanishing parallel magnetic field component B∥ ≠ 0 (see Eq. (12)) of fast mode waves allows TTD interactions with n = 0, so that we procede with n = 0. The resonance function (17) becomes ![\begin{eqnarray} \label{d2} {\cal R}^j_{\rm F} (0)&=&{\alpha_{\rm F}k^2\sin ^2\theta \over (\alpha_{\rm F}k^2\sin ^2\theta )^2+[kv \mu \cos \theta +j V_{\rm A}k]^2}\nonumber\\ &=&{\alpha_{\rm F}(1-\eta ^2) \over (\alpha_{\rm F}k(1-\eta ^2))^2+[v\mu \eta +jV_{\rm A}]^2}\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq87.png) (18)Throughout this work, we consider isotropic turbulence gj(k) = gj(k). Modifications due to different turbulence geometries are possible and will be the subject of further analysis (in particular anisotropic turbulence).
(18)Throughout this work, we consider isotropic turbulence gj(k) = gj(k). Modifications due to different turbulence geometries are possible and will be the subject of further analysis (in particular anisotropic turbulence).
For energetic cosmic ray particles with v ≫ VA, the pitch-angle Fokker-Planck coefficient then simplifies as 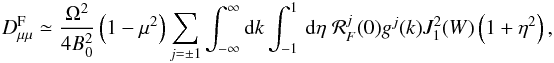 (19)where J1(W) is a Bessel function with the argument
(19)where J1(W) is a Bessel function with the argument 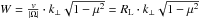 that involves the cosmic ray Larmor radius RL = v/ | Ω |.
that involves the cosmic ray Larmor radius RL = v/ | Ω |.
We further simplify Eq. (19) by assuming equal intensity of forward and backward waves (a vanishing cross helicity of each plasma mode): 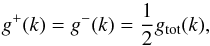 (20)which reads as
(20)which reads as 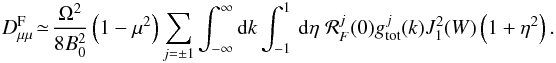 (21)To illustrate our results, we adopt a Kolmogorov-type power law dependence on gj(k) above and below some minimum and maximum wavenumber kmin and kmax, respectively
(21)To illustrate our results, we adopt a Kolmogorov-type power law dependence on gj(k) above and below some minimum and maximum wavenumber kmin and kmax, respectively 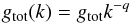 (22)for kmin < k < kmax.
(22)for kmin < k < kmax.
The magnetic energy density in wave component j is given by 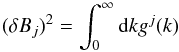 (23)which implies
(23)which implies 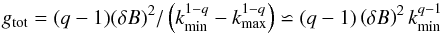 (24)for kmax ≫ kmin.
(24)for kmax ≫ kmin.
With Eqs. (22), (23), (24) the pitch-angle Fokker-Planck coefficient 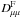 reads as
reads as 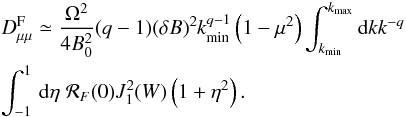 (25)
(25)
Now, we must approximate the resonance function (Eq. (18)). In doing this, we consider two cases:
-
a) η < ηc;
-
b) η > ηc,
where ϵ = VA/v and ηc = ϵ/μ. The parameter ηc divides the integration domain with respect to η, in which either VA, vμη or both values are relevant. By using 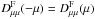 and the substitution
and the substitution 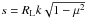 and RL = v/ | Ω |, we derive
and RL = v/ | Ω |, we derive
3.1. High values of μ > ϵ
For large pitch-angles μ > ϵ we obtain
3.2. Small values μ < ϵ
This case is important when treating damped waves. For the small pitch-angles μ < ϵ, we obtain
We have already discussed that inclusion of resonance broadening due to wave damping in the resonance function guarantees dominance of transit-time damping. The main contribution of wave damping comes exactly in the region | μ | < ϵ that is relevant for deriving the spatial diffusion coefficient and related mean free path, both of which are given by the average over μ of the inverse of Dμμ. Therefore, we can further consider only the case Dμμ(μ = 0), which simplifies the analysis enormously and reads as
In the last equation, s = kRL, and each term under integration is dimensionless.
4. Slow mode waves
With Eqs. (13) and (16), the resonance function (7) for slow mode waves becomes ![\begin{eqnarray} \label{res1} {\cal R}^j_{\rm S}(n) = {2.9\!\times\! 10^5\beta V_{\rm A}^2k^2\sin ^2\!\theta \!\over \left(2.9\!\times \!10^5\beta V_{\rm A}^2\!k^2 \!\sin ^2\theta\right)^2\! + \! \left[kv \mu \cos \theta \!+\!jV_{\rm A} k \eta\sqrt{\frac{\beta}{1\!+\!\beta}}\!+\!n\Omega) \right]^2}\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq130.png) (30)The non-vanishing parallel magnetic field component B∥ ≠ 0 (see Eq. (14)) of slow mode waves allows TTD interactions with n = 0, so that we procede with n = 0. The resonance function (30) becomes
(30)The non-vanishing parallel magnetic field component B∥ ≠ 0 (see Eq. (14)) of slow mode waves allows TTD interactions with n = 0, so that we procede with n = 0. The resonance function (30) becomes ![\begin{eqnarray} \label{res2} {\cal R}^j_S(0)&=&{2.9\times 10^5\beta V_{\rm A}^2k^2\sin ^2\theta \over \left(2.9\times 10^5 \beta V_{\rm A}^2k^2\sin ^2\theta \right)^2+ \left[kv\mu \cos \theta +jV_{\rm A}k \eta \sqrt{\frac{\beta}{1+\beta}}\right]^2} \nonumber\\ &=&{\alpha_{\rm F}\sin ^2\theta \over \left(\alpha_{\rm F}k\sin ^2\theta \right)^2+\left[v\mu \cos \theta +jV_{\rm A}\eta\sqrt{\frac{\beta}{1+\beta}}\right]^2}, \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq132.png) (31)where αF is the same as in the fast mode case.
(31)where αF is the same as in the fast mode case.
Following the same procedure for fast mode waves in Sect. 3, we assume (20), (22), (23), and imply (24). We derive
which can be simplified if we consider the energetic cosmic ray particles v ≫ VA, or namely, the last two terms, to be small (order of ϵ and ϵ2) and neglected. Then, we obtain the same expression as in the case for fast mode waves:
Next, we have to approximate the resonance function for slow mode waves. As in the fast mode case, there are two cases:
-
a)
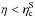 ;
; -
b)
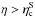 ,
,
where 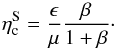 (34)Note that
(34)Note that 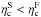 . Using
. Using 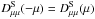 and the substitution
and the substitution 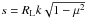 , we derive
, we derive
where ϵ = VA/v.
4.1. High values of μ > ϵ
For large pitch-angles μ > ϵ we obtain
4.2. Low values of μ < ϵ
This case is important for treating damped waves for the same reason as discussed for fast mode waves (Sect. 3). For the small pitch-angles μ < ϵ, we obtain
or for μ = 0, we read
In the last equation, s = kRL.
5. Cosmic ray mean free path
5.1. Fast mode waves
In this section, we calculate the mean free path, which is connected with the spatial diffusion coefficient through 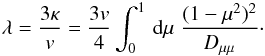 (39)For the case in which we are interested, we can write
(39)For the case in which we are interested, we can write 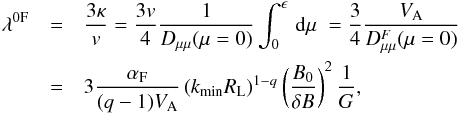 (40)where
(40)where
Now, we consider two limits: kminRL ≪ 1, and kminRL ≫ 1, where kminRL = T = E and is normalized with respect to 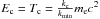 . Expressing kmin = Lmax/2π in the terms of the longest wavelength of isotropic fast mode waves, kc = Ω0,e/vA = ωp,e/c and for following plasma conditions (
. Expressing kmin = Lmax/2π in the terms of the longest wavelength of isotropic fast mode waves, kc = Ω0,e/vA = ωp,e/c and for following plasma conditions (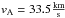 ,
, 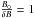 , Beck 2007),
, Beck 2007), 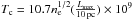 MV). For these values, the particle mean free path is measured by
MV). For these values, the particle mean free path is measured by 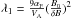 . We have used interplanetary plasma conditions that have been used in both models (Schlickeiser et al. 2010; Teufel & Schlickeiser 2002) for comparison. We note that for interstellar medium plasma conditions, λ1 is one or two orders of magnitude larger than for interplanetary conditions, which is also a reasonable value.
. We have used interplanetary plasma conditions that have been used in both models (Schlickeiser et al. 2010; Teufel & Schlickeiser 2002) for comparison. We note that for interstellar medium plasma conditions, λ1 is one or two orders of magnitude larger than for interplanetary conditions, which is also a reasonable value.
For kminRL ≫ 1:
This case is treated in detail in Appendix A, where we derive 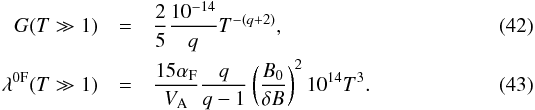 At relativistic rigidities, we find that λ0 ~ T3. As we consider certain positron energies 1–100 GeV, this case is not relevant. For kminRL ≪ 1:
At relativistic rigidities, we find that λ0 ~ T3. As we consider certain positron energies 1–100 GeV, this case is not relevant. For kminRL ≪ 1:
This case is treated in detail in Appendix A, where we derive 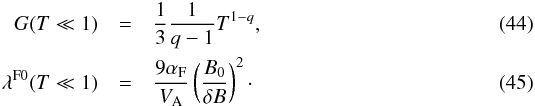 In this energy limit, the mean free path is constant with respect to T, which is relevant for considered positron energies.
In this energy limit, the mean free path is constant with respect to T, which is relevant for considered positron energies.
5.2. Slow mode waves
In this subsection, we calculate the mean free path which is connected with the spatial diffusion coefficient through 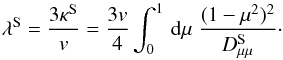 (46)For the case for which we are interested, we can write
(46)For the case for which we are interested, we can write 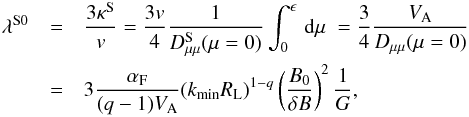 (47)where
(47)where
We consider two limits: kminRL ≪ 1, and kminRL ≫ 1, where kminRL = T = E and is normalized with respect to Ec.
For kminRL ≫ 1:
This case is treated in detail in Appendix B, where we derive 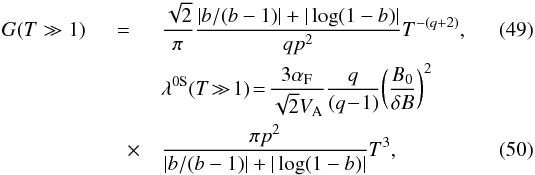 where T = kminRL and b ≪ 1.
where T = kminRL and b ≪ 1.
At relativistic rigidities, we find that λ0S ~ T3.
For kminRL ≪ 1:
This case is treated in detail in Appendix B, where we derive
In this energy domain, the mean free path is constant with respect to T, which is important for cosmic ray positrons with Lorentz factor γ < mp/me = 1836. Although the mean free path for slow magnetosonic waves has the same expression as in the case for fast waves for energies less than Tc, the low energy limit here is caused by plasma-β (Appendix B). However, it is always less than Tc and does not violate previous conditions.
The turbulence model considered in this paper ensures that all energy particles below the Tc value are scattered by the proposed resonant interaction.
Considering dynamical magnetic slab turbulence and random sweeping slab turbulence (Teufel & Schlickeiser 2002), there is a sharp cutoff of the turbulence power spectrum at kmin. The consequence is that the mean free path for all particles with energies higher than 1010 eV with typical parameters rapidly grows and becomes larger than the size of ambient interstellar medium. For the slab plasma waves model (Schlickeiser et al. 2010) at rigidities less than 2 × 108 eV, the positron mean free path becomes infinitely large. It is because these positrons find no LH polarized slab waves with which to resonantly interact. In the turbulence model proposed in this paper, the positron mean free path does not depend on energy, in domain from 105 eV to 1012 eV.
The comparison of our result with previously reported turbulence models are given in Fig. 1, where the mean free path is in units of λ1 = 0.2β AU (AU = 1.5 × 1013 cm). To interpret the MeV positrons propagation and explain their diffusion, the model of the dynamical turbulence can be applied. However, this model fails to explain transport mechanisms for energetic positrons with energies of 100 GeV. In contrast, the slab gyroresonat plasma wave turbulence model is able to hold on energetic GeV positrons but fails in explaining the transport properties of MeV positrons. The isotropic damped magnetosonic plasma wave turbulence model, which is proposed in this paper, seems to be more plausible, since it covers energies in both domains. This model could be used in modeling turbulence that scatters positrons, resolving the problems stated by the results of either the INTEGRAL or PAMELA experiments.
The inclusion of viscous damping implies either steep turbulence spectra (q > 2.4) for isotropic turbulence with fixed values of kmax and kmin, or the existence of high wavenumber cutoff for isotropic turbulence with a spectral index q = 5/3 (Spanier & Schlickeiser 2005). To justify the use of kmax and kmin in our model, it is necessary to assume turbulence with a spectral index that is not less than 2.4. This value is higher than the Kolmogorov value of 5/3 (Kolmogorov 1941) or Kraichan-Iroshnikov value of 3/2 (Kraichnan 1965), but both theories consider an inertial range, where damping effects have been neglected. Interstellar medium has strong damping features, which does not mean that there is no inertial range. It could be that there is an intermediate regime between the inertial and dissipation range. Thus, the request for steep turbulence spectra is not in contradiction to neither Kolmogorov theory, or our calculation, in which there is only a restriction on q to be greater than 1.
The broadening of the resonance function could also be insured by nonlinear treatment of the specific turbulence model. Nonlinear theory (second order theory of Shalchi 2005) applied to the magnetostatic slab model (Shalchi et al. 2009) would lead to a broadened resonance function that is similar to the one obtained for the random sweeping model, which is linear (Teufel & Schlickeiser 2002). We have already mentioned that this linear model could be used to explain MeV positrons but fails for GeV positrons. Thus, we expect, at least mathematically, that inclusion of nonlinear effects to the slab model would have the cutoff at the same wavenumbers as in the random sweeping linear model. However, it would be useful to compare timescales of nonlinear effects and damping effects within the same turbulence model, in order to make a general conclusion on the importance of each of them.
 |
Fig. 1 The positron mean free path. The black line represents the mean free path obtained using the slab turbulence model and gyroresonant interactions, which exhibit a cutoff at particle energies less than 2 × 108 eV. The red line is the mean free path obtained using the dynamical magnetic slab turbulence, or the random sweeping slab turbulence model, which exhibit a sharp cutoff at particle energies of 1010 eV. The blue line is the mean free path obtained using isotropic magnetosonic damped plasma wave turbulence, which remains constant for particle energies from 105 eV to 1012 eV. All mean free paths are normalized with respect to the λ1 value. |
6. Summary and conclusion
We have investigated the implications of isotropically distributed interstellar damped plasma waves on the scattering mean free path on the cosmic ray positrons with a Lorentz factor γ < mp/me = 1836. We show that inclusion of resonance broadening due to wave damping in the resonance function guarantees that dominance of transit-time damping also holds for cosmic ray particles at small pitch angle cosines μ ≤ | Va/v |, unlike the case of negligible wave damping.
For small rigidities, or consequently low energies T < Tc, the mean free path is constant with respect to energy. The mean free path at high energies T > Tc approaches a much steeper dependence, namely λ ~ T3 for both fast and slow waves.
It is difficult to draw any general conclusion on the ratio of fast and slow modes mean free path, since there is an integral dependence on the pitch angle and the plasma-beta parameter are mixed in the latter case. For cold plasma, the mean free path of slow mode merges to the mean free path of the fast one, as expected. However, this turbulence model is able to ensure scattering of the cosmic ray positrons with Lorentz factor γ < mp/me = 1836 via resonant interaction.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Phys. Rew. Lett. 102, 1101 [Google Scholar]
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical functions 1966 [Google Scholar]
- Achterberg, A. 1979, A&A, 76, 276 [NASA ADS] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2009, Nature, 458, 607 [CrossRef] [PubMed] [Google Scholar]
- Agular, M., et al. 2013, Phys. Rew. Lett., 110, 141102 [CrossRef] [Google Scholar]
- Arvanitaki, A., Dimopoulos, S., Dubovsky, S., et al. 2009, Phys. Rew. D, 80, 55011 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2007, EAS Pub. Ser., 23, 19 [Google Scholar]
- Bieber, J. W., Wanner, W., & Matthaeus, W. M. 1996, J. Geophys. Res., 101, 2511 [Google Scholar]
- Boehm, C., Hooper, D., Silk, J., et al. 2004, Phys. Rev. Lett., 92, 1301 [Google Scholar]
- Clayton, D. D. 1973, Nature Phys. Sci., 244, 137 [NASA ADS] [Google Scholar]
- Dogan, A., Spanier, F., Vainio, R., & Schlickeiser, R. 2006, J. Plasma Phys., 72, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Fedorenko, V. N. 1992, Sov. Sci. Rev. E, 8, 4 [Google Scholar]
- Guessoum, N., Jean, P., & Prantzos, N. 2006, A&A, 457, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Higdon, J. C., Lingenfelter, R. E., & Rothschild, R. E. 2009, ApJ, 698, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., Stebbins, A., & Zurek, K. N. 2009, PRD, 79, 103513 [NASA ADS] [CrossRef] [Google Scholar]
- Jokippi, J. R. 1966, ApJ 146, 480 [Google Scholar]
- Knödlseder, J., Jean, P., Lonjou, V., et al. 2005, A&A, 441, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolmogorov, A. N. 1941, Dokl. Akad. Nauk. SSSR, 30, 301 [NASA ADS] [Google Scholar]
- Kraichnan, R. 1965, Phys. Fluids, 8, 1835 [Google Scholar]
- Kubo, R. 1957, J. Phys. Soc. Jpn. 12, 570 [Google Scholar]
- Matthaeus, W. H., & Smith, C. W. 1981, Phys. Rev. A 24, 2135 [Google Scholar]
- Milne, P. A., Kurfess, J. D., Kinzer, R. L., & Leising, M. D. 2002, New Astron. Rev., 46, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, I. D. 1982, Rew. Geophys. Space Phys., 20, 335 [Google Scholar]
- Pohl, M., & Eichler, D. 2010, ApJ, 712, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., & Lingenfelter, R. E. 1979, Nature, 278, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., Stecker, F. W., & Misra, D. 1970, J. Geophys. Res., 75, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [Google Scholar]
- Schlickeiser, R. 2003, Lect. Not. Phys., 612, 230 [Google Scholar]
- Schlickeiser, R., & Miller, J. A. 1998, ApJ 492, 352 [Google Scholar]
- Schlickeiser, R., & Vainio, R. 1999, Astrophys. Space Sci., 264, 457 [Google Scholar]
- Schlickeiser, R., Lazar, M., & Vukcevic, M. 2010, ApJ, 719, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2005, Phys. Plasmas, 12, 052905 [Google Scholar]
- Shalchi, A., & Schlickeiser, R. 2004, A&A, 420, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shalchi, A., Škoda, T., Tautz, R. C., & Schlickeiser, R. 2009, Phys. Rev. D, 80, 023012 [Google Scholar]
- Spanier, F., & Schlickeiser, R. 2005, A&A, 436, 1 [Google Scholar]
- Sturrock, P. A. 1971, ApJ, 164, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Teufel, A., & Schlickeiser, R. 2002, A&A, 393, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teufel, A., Lerche, I., & Schlickeiser, R. 2003, A&A 397, 776 [Google Scholar]
- Vukcevic, M., & Schlickeiser, R. 2007, A&A, 467, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Evaluation of the function G for fast mode waves
The task is to calculate the function G (41): 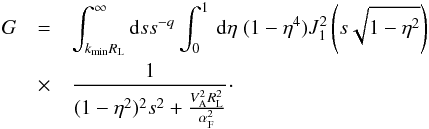 (A.1)First, it is possible to evaluate the term
(A.1)First, it is possible to evaluate the term 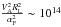 for used plasma parameters (Sect. 5). We then evaluate G in two energy limits.
for used plasma parameters (Sect. 5). We then evaluate G in two energy limits.
Case G(kminRL ≫ 1)
For energies T ≫ 1 we substitute s = xT. Then, (A.1) reads as 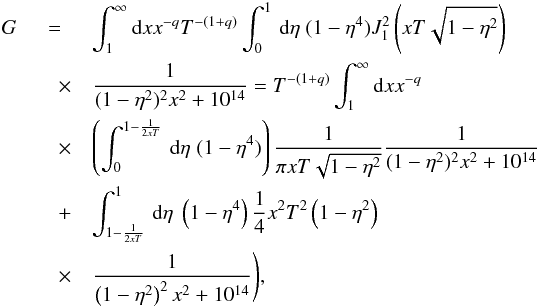 (A.2)where we use the approximations of Bessel functions for large and small arguments (Abramowitz & Stegun 1972):
(A.2)where we use the approximations of Bessel functions for large and small arguments (Abramowitz & Stegun 1972): 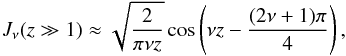 (A.3)implying
(A.3)implying 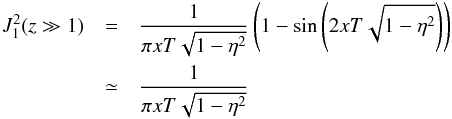 (A.4)(1/ξ ≫ sinξ/ξ) for the argument, z = xT ≪ 1, and
(A.4)(1/ξ ≫ sinξ/ξ) for the argument, z = xT ≪ 1, and 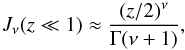 (A.5)implying
(A.5)implying 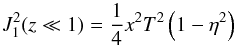 (A.6)for the argument z = xT ≫ 1. We then obtain
(A.6)for the argument z = xT ≫ 1. We then obtain
Next, we simplify further, namely keeping only terms with respect to 1 − η of the lowest order, and we evaluate each integral: 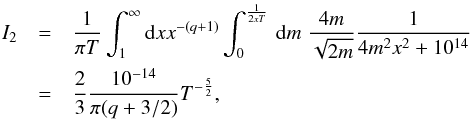 (A.8)
(A.8)
where we substitute m = 1 − η. 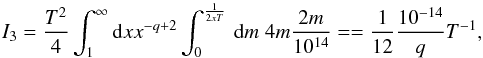 (A.9)where we have used the same substitution as in the previous case and where 1014 ≫ 4m2x2. We note that I2 ≪ I3.
(A.9)where we have used the same substitution as in the previous case and where 1014 ≫ 4m2x2. We note that I2 ≪ I3. 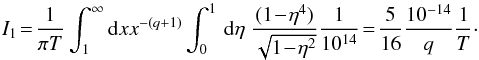 (A.10)Combining all these three integrals, we obtain
(A.10)Combining all these three integrals, we obtain 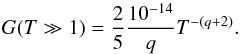 (A.11)
(A.11)
Case G(kmin RL ≪ 1)
For energies T ≪ 1, we use the approximation for Bessel function (A.5). Then, (A.1) reads as 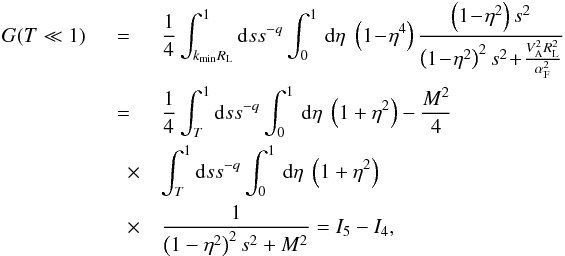 (A.12)where
(A.12)where 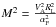 . We then evaluate each integral:
. We then evaluate each integral: 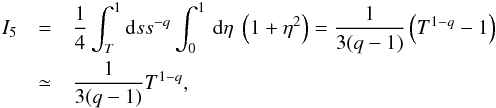 (A.13)since T ≪ 1, and q > 1.
(A.13)since T ≪ 1, and q > 1.
The exact solution of integral I6 reads as 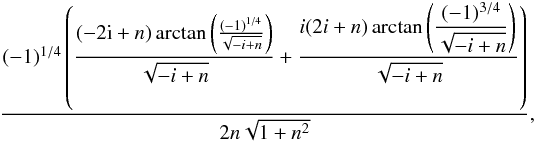 (A.16)where n2 = M2/s2. We can evaluate I6 by
(A.16)where n2 = M2/s2. We can evaluate I6 by 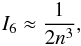 (A.17)which for I4 gives
(A.17)which for I4 gives 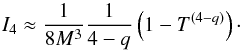 (A.18)To compare I4 and I5 and calculate G(T ≪ 1), we have to consider two cases, which are (1 < q < 4) and steep (4 < q < 6) turbulence spectrum.
(A.18)To compare I4 and I5 and calculate G(T ≪ 1), we have to consider two cases, which are (1 < q < 4) and steep (4 < q < 6) turbulence spectrum.
For (1 < q < 4) the integral 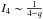 , while
, while 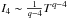 for (4 < q < 6). However, M3 exists in both cases in the denominator of I4, which implies that I4 ≪ I5. According to Eq. (A.12) then:
for (4 < q < 6). However, M3 exists in both cases in the denominator of I4, which implies that I4 ≪ I5. According to Eq. (A.12) then: 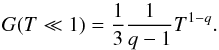 (A.19)
(A.19)
Appendix B: Evaluation of the function G for slow mode waves
The task is to calculate the function G (48),
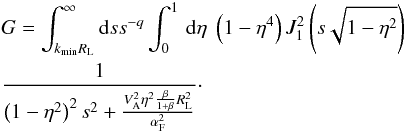 (B.1)and evaluate it in two energy limits.
(B.1)and evaluate it in two energy limits.
Case G(kminRL ≫ 1)
For energies T ≫ 1 we substitute s = xT. Then, (B.1) reads as 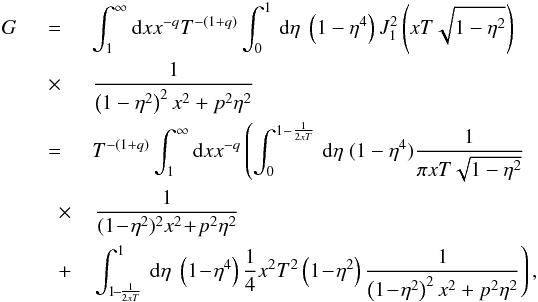 (B.2)where
(B.2)where 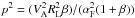 . We have used
. We have used 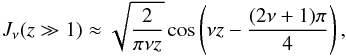 (B.3)implying
(B.3)implying
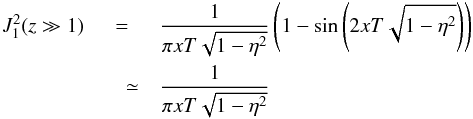 (B.4)(1/ξ ≫ sinξ/ξ) for the argument, z = xT ≪ 1, and
(B.4)(1/ξ ≫ sinξ/ξ) for the argument, z = xT ≪ 1, and 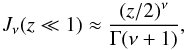 (B.5)implying
(B.5)implying 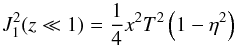 (B.6)for the argument z = xT ≫ 1. We then obtain
(B.6)for the argument z = xT ≫ 1. We then obtain 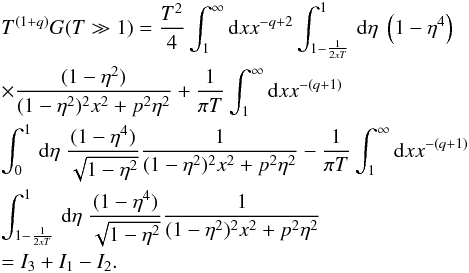 (B.7)Next, we evaluate each integral in turn as in the case of fast mode waves.
(B.7)Next, we evaluate each integral in turn as in the case of fast mode waves.
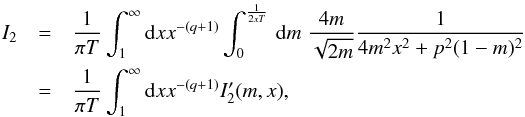 (B.8)where we substitute m = 1 − η.
(B.8)where we substitute m = 1 − η. 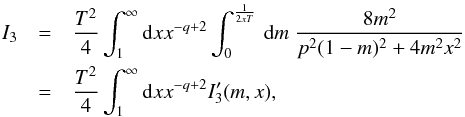 (B.9)where we have used the same substitution as in the previous case.
(B.9)where we have used the same substitution as in the previous case. 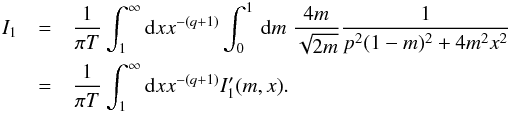 (B.10)To compare functions under integration with respect to m, we write out the following integrals
(B.10)To compare functions under integration with respect to m, we write out the following integrals ![\appendix \setcounter{section}{2} \begin{eqnarray} I'_{2}(m,x)&=&\int _{0}^{\frac{1}{2xT}}\, {\rm d}m \; \frac{4m}{\sqrt{2m}}\frac{1}{4m^{2}x^{2}+p^{2}(1-m)^{2}} \\[2.5mm] &=&\frac{2\sqrt{2}}{p^{2}}\int _{0}^{\frac{1}{2xT}}\, {\rm d}m \; f_{1}, \\[2.5mm] I'_{3}(m,x)&=&\int _{0}^{\frac{1}{2xT}}\, {\rm d}m \; \frac{8m^{2}}{p^{2}(1-m)^{2}+4m^{2}x^{2}}=\frac{8}{p^{2}}\int _{0}^{\frac{1}{2xT}}\, {\rm d}m \; f_{2}, \nonumber\\ \\[2.5mm] I'_{1(m,x)}&= & \int_{0}^{1}{\rm d}m \frac{4m}{\sqrt{2m}}\frac{1}{p^{2}(1-m)^{2}+4m^{2}x^{2}}=\frac{2\sqrt{2}}{p^{2}}\int_{0}^{1}{\rm d}m \;f_{1}, \nonumber\\ \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq253.png) where
where 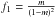 and
and 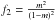 . We have approximated the denominator as (1 − m)2, as long as
. We have approximated the denominator as (1 − m)2, as long as 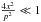 holds (which is ensured by consideration of T ≫ 1). Analyzing f1 and f2 in given intervals of integration we deduce that I2 < I3 < I1. However, this case is not of particular interest, so we make a rough estimation on G.
holds (which is ensured by consideration of T ≫ 1). Analyzing f1 and f2 in given intervals of integration we deduce that I2 < I3 < I1. However, this case is not of particular interest, so we make a rough estimation on G.
Integral 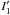 diverges for m = 1, so we integrate to m = b < 1. Combining all, we obtain
diverges for m = 1, so we integrate to m = b < 1. Combining all, we obtain 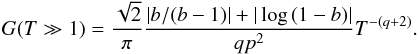 (B.15)
(B.15)
Case G(kminRL ≪ 1)
For energies T ≪ 1, we use the approximation for Bessel function (B.5). Then, (B.1) reads as
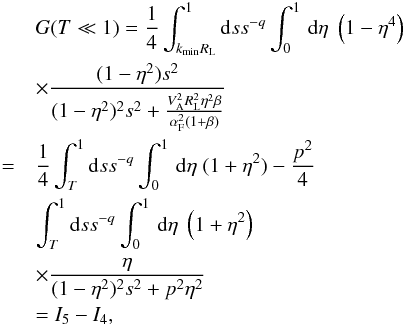 (B.16)where
(B.16)where 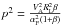 . We then evaluate each integral.
. We then evaluate each integral.
To estimate I4, we write
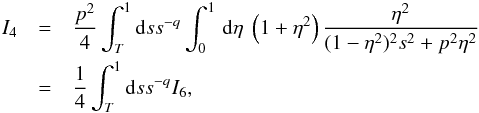 (B.18)where
(B.18)where 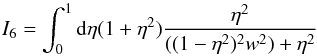 (B.19)and w2 = s2/p2. Here, we compare functions in integrals I5 with respect to η, namely f1 = (1 + η2), and in I6 namely
(B.19)and w2 = s2/p2. Here, we compare functions in integrals I5 with respect to η, namely f1 = (1 + η2), and in I6 namely 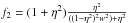 .
.
We find that I5 ≫ I6 for w2 ≫ 1 over the interval [0,1]. For 10-14 < w2 < 1, we still have I5 > I4. Only at 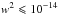 , I5 < I6 (low energy value is caused by this limitation; namely, we consider T ≪ 1). However, this treatment is valid as long as
, I5 < I6 (low energy value is caused by this limitation; namely, we consider T ≪ 1). However, this treatment is valid as long as 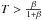 , which is always less than 1.
, which is always less than 1.
As long as I5 dominates, we obtain 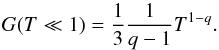 (B.20)
(B.20)
All Figures
 |
Fig. 1 The positron mean free path. The black line represents the mean free path obtained using the slab turbulence model and gyroresonant interactions, which exhibit a cutoff at particle energies less than 2 × 108 eV. The red line is the mean free path obtained using the dynamical magnetic slab turbulence, or the random sweeping slab turbulence model, which exhibit a sharp cutoff at particle energies of 1010 eV. The blue line is the mean free path obtained using isotropic magnetosonic damped plasma wave turbulence, which remains constant for particle energies from 105 eV to 1012 eV. All mean free paths are normalized with respect to the λ1 value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} &&D_{\mu \mu }^{\rm F} \simeq \alpha_{\rm F} (q-1)(k_{\min} R_{\rm L})^{q-1} \left(\frac{\delta B}{B_{0}}\right)^{2}\left(1-\mu^{2}\right)^{\frac{q+1}{2}} \int_{k_{\min} R_{\rm L} \sqrt{1-\mu^{2}}}^{\infty}{\rm d}s s^{-q}\nonumber\\ &&\times \left[\int _{0}^{\min(1,\epsilon/\mu)}\, {\rm d}\eta \; \left(1-\eta^{4}\right) J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \frac{1}{\frac{\alpha_{\rm F}^{2}(1-\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1-\mu^{2})} + V_{\rm A}^{2}}\right. \nonumber\\ &&\left. \!+\!\int _{\min (1,\epsilon/\mu)}^{1}\, {\rm d} \eta \; \left(1-\eta^{4}\right) J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \frac{1}{\frac{\alpha_{\rm F}^{2}(1-\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1-\mu^{2})}+(v\mu\eta)^{2}}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq118.png)
![\begin{eqnarray} &&D_{\mu \mu }^{\rm F}(\mu>\epsilon) \simeq \frac{(q-1)}{\alpha_{\rm F}} \left (k_{\min}R_{\rm L}\right)^{q-1} \left(\frac{\delta B}{B_{0}}\right)^{2} \left(1-\mu^{2}\right)^{\frac{q+3}{2}} \nonumber\\ &&\times \int_{k_{\min}R_{\rm L}\sqrt{1-\mu^{2}}}^{\infty}{\rm d}s s^{-q} \Bigg[\int _{0}^{\epsilon/\mu}\, {\rm d} \eta \; \left(1-\eta^{4}\right) J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \nonumber\\ && + \frac{1}{\left(1-\eta^{2}\right)^{2}s^{2}+\frac{R_{\rm L}^{2}(1-\mu^{2})V_{\rm A}^{2}}{\alpha_{\rm F}^{2}}} +\int _{\epsilon/\mu}^{1}\, {\rm d} \eta \; \left(1-\eta^{4}\right) J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \nonumber\\ && \times \frac{1}{\left(1-\eta^{2}\right)^{2}s^{2}+\frac{R_{\rm L}^{2}(1-\mu^{2})(v\mu\eta)^{2}}{\alpha_{\rm F}^{2}}}\Bigg]\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq121.png)
![\begin{eqnarray} &&D_{\mu \mu }^{\rm F}(\mu<\epsilon)\simeq \alpha_{\rm F} (q-1)(k_{\rm min}R_{\rm L})^{q-1}\left(\frac{\delta B}{B_{0}}\right)^{2} \left(1-\mu^{2}\right)^{\frac{q+1}{2}} \nonumber\\ &&\times \int_{k_{\rm min}R_{\rm L}\sqrt{1-\mu^{2}}}^{\infty}{\rm d}s s^{-q} \left[ \phantom{\frac{1}{\frac{\alpha_{\rm F}^{2}(1-\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1-\mu^{2})}+V_{\rm A}^{2}}}\hspace*{-2.3cm}\int _{0}^{1}\, {\rm d}\eta \; \left(1-\eta^{4}\right)J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \right.\nonumber\\ &&\left. \times \frac{1}{\frac{\alpha_{\rm F}^{2}(1-\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1-\mu^{2})}+V_{\rm A}^{2}}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq124.png)
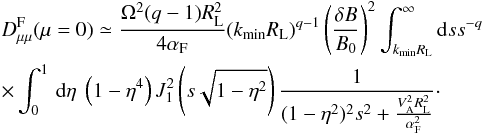
![\begin{eqnarray} D_{\mu \mu }^{\rm S}&\simeq& \frac{\Omega^{2}}{4B_{0}^{2}} \left(1-\mu^{2}\right) \sum_{j=\pm 1} \int_{-\infty}^{\infty}{\rm d}k \,\int _{-1}^1\, {\rm d} \eta \; {\cal R}^j_S(0)g^j(k) J_{1}^{2}(W) \nonumber\\ &\quad \times& \left[\left(1+\eta ^2 \right)\left(1+\mu^{2}\epsilon^{2}\eta^{2}\frac{\beta}{1+\beta}\right) -4\mu j \epsilon \eta\sqrt{\frac{\beta}{1+\beta}}\right], \label{ds6} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq134.png)
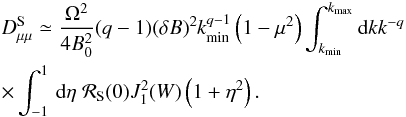
![\begin{eqnarray} &&D_{\mu \mu }^{\rm S} \simeq \alpha_{\rm F} (q-1) (k_{\min} R_{\rm L})^{q-1} \left(\frac{\delta B}{B_{0}}\right)^{2} \left(1-\mu^{2}\right)^{\frac{q+1}{2}} \nonumber\\ &&\times \int_{k_{\min}}^{\infty} {R_{{\rm L}_{\sqrt{1-\mu^{2}}}}}{\rm d}s s^{-q} \left[\int _{0}^{{\min}^{\left(1,\frac{\epsilon}{\mu} \frac{\beta}{1+\beta}\right)}}\, {\rm d} \eta \; \left(1-\eta^{4}\right) \right. \nonumber\\ &&\times \left. J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \frac{1}{\frac{\alpha_{\rm F}^{2}\left(1-\eta^{2}\right)^{2}s^{2}}{R_{\rm L}^{2}(1-\mu^{2})} + V_{\rm A}^{2}\eta^{2}\frac{\beta}{1+\beta}} + \int^{1} _{\min \left(\!1,\frac{\epsilon}{\mu}\!\frac{\beta}{1\!+\!\beta}\!\right)}\right. \nonumber\\ &&\times \!\left. \, \!{\rm d} \eta\! \; \left(1\!-\!\eta^{4}\!\right) \!J_{1}^{2} \!\left(s\!\sqrt{1\!-\!\eta^{2}}\right)\! \frac{1}{\frac{\alpha_{\rm F}^{2}(1\!-\!\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1\!-\!\mu^{2})} \!+ \!(v\mu\eta)^{2}}\!\right]\!, \label{d14} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq143.png)
![\begin{eqnarray} D_{\mu \mu }^{\rm S}(\mu>\epsilon) &\simeq& \frac{(q-1)}{\alpha_{\rm F}} (k_{\min}R_{\rm L})^{q-1} \left(\frac{\delta B}{B_{0}}\right)^{2} \left(1-\mu^{2}\right)^{\frac{q+3}{2}} \nonumber\\ &\quad \times & \int_{k_{\min}} R_{\rm L} \sqrt{1-\mu^{2}}^{\infty}{\rm d}s s^{-q} \nonumber\\ &\quad \times &\left[\phantom{\frac{1}{(1-\eta^{2})^{2}s^{2}+\frac{R_{\rm L}^{2}(1-\mu^{2})(v\mu\eta)^{2}}{\alpha_{\rm F}^{2}}}}\hspace*{-3.7cm}\int _{0}^{\frac{\epsilon\beta}{\mu(1+\beta)}}\, {\rm d}\eta \; \left(1-\eta^{4}\right) J_{1}^{2} \left(s\sqrt{1-\eta^{2}}\right) \right.\nonumber\\ &\quad \times & \left.\frac{1}{(1-\eta^{2})^{2}s^{2}+\frac{R_{\rm L}^{2}(1-\mu^{2})V_{\rm A}^{2}\eta^{2}\frac{\beta}{1+\beta}}{\alpha_{\rm F}^{2}}} \right.\nonumber\\ &\quad &\left. +\int _{\frac{\epsilon\beta}{\mu(1+\beta)}}^{1}\, {\rm d} \eta \; \left(1-\eta^{4}\right) J_{1}^{2}\left(s\sqrt{1-\eta^{2}}\right) \right.\nonumber\\ &\quad \times &\left.\frac{1}{(1-\eta^{2})^{2}s^{2}+\frac{R_{\rm L}^{2}(1-\mu^{2})(v\mu\eta)^{2}}{\alpha_{\rm F}^{2}}}\right]\cdot \label{fp1} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq144.png)
![\begin{eqnarray} && D_{\mu \mu}^{\rm S} (\mu<\epsilon) \simeq \alpha_{\rm F} (q-1) (k_{\min} R_{\rm L})^{q-1} \left( \frac{\delta B}{B_0} \right)^{2} \left(1- \mu^{2} \right)^{\frac{q+1}{2}} \nonumber\\ &\quad \times &\int_{k_{\min}} R_{\rm L} \sqrt{1\!-\!\mu^2}^{\infty}{\rm d}s\, s^{-q}\nonumber\\ &\quad \times & \left[ \int _{0}^{1}\, {\rm d}\eta \; \left(1\!-\!\eta^4\right) J_1^2 \left(s \sqrt{1\!-\!\eta^{2}}\right) \frac{1}{\frac{\alpha_{\rm F}^{2}(1\!-\!\eta^{2})^{2}s^{2}}{R_{\rm L}^{2}(1\!\!-\mu^{2})}\!+\!V_{\rm A}^{2}\eta^{2}\frac{\beta}{1+\beta}}\right], \label{d14b} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq145.png)
![\begin{eqnarray} &&D_{\mu \mu }^{\rm S} (\mu=0) \simeq \frac{\Omega^{2}(q-1)R_{\rm L}^{2}}{4\alpha_{\rm F}} (k_{\min} R_{\rm L})^{q-1} \left(\frac{\delta B}{B_{0}}\right)^{2} \int_{k_{\min}} R_{\rm L}^{\infty}{\rm d}s s^{-q} \nonumber\\ &&\left[\int _{0}^{1}\, {\rm d}\eta \; (1-\eta^{4}) J_{1}^{2}(s\sqrt{1-\eta^{2}})\frac{1}{(1-\eta^{2})^{2}s^{2}+\frac{V_{\rm A}^{2}\eta^{2}\frac{\beta}{1+\beta}R_{\rm L}^{2}}{\alpha_{\rm F}^{2}}}\right]\cdot \label{d24} \end{eqnarray}](/articles/aa/full_html/2013/07/aa21191-13/aa21191-13-eq147.png)