| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321156 | |
| Published online | 10 June 2013 | |
Research Note
Scandium in AmFm stars in the light of new atomic data
1 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jule Janssen, 92190 Meudon, France
e-mail:
georges.alecian@obspm.fr
2 Département de Physique et d’Astronomie, Université de Moncton, Moncton, NB, E1A 3E9, Canada
e-mail:
francis.leblanc@umoncton.ca
3 Université de Lyon, 69003, Université Lyon 1, Observatoire de Lyon, 9 avenue Charles André, 69230 Saint-Genis Laval, France
4 CNRS, UMR 5574, , Centre de Recherche Astrophysique de Lyon, École Normale Supérieure de Lyon, 69007 Lyon, France
e-mail:
gmassacr@ens-lyon.fr
Received: 23 January 2013
Accepted: 24 April 2013
Context. The abundance anomalies observed in AmFm stars are believed to be caused by atomic diffusion below the superficial convection zone. The process by which these anomalies, which are produced in deep layers, propagate toward the stellar surface is well understood. However, it depends on quantities which are not directly observed: the mass-loss flux and the exact position of convections zones. Scandium, which is systematically underabundant at the surface of AmFm stars, is a key element in understanding the interplay between atomic diffusion and the stellar structure and how this structure evolves with time.
Aims. In the light of a new extensive set of atomic data, we calculate much more accurate radiative accelerations of Sc than previously done in the aim to better understand the observed abundance anomalies of this element in AmFm stars.
Methods. Two methods are employed to obtain these radiative accelerations based on the so-called SVP (single-valued parameters) parametric method and the GLAM method while employing this new atomic data.
Results. The radiative accelerations, shown here in a typical Am stellar model, are discussed in the light of the observed anomalies of Sc. Our results are more compatible with the scenario where the scandium depletion is created below the hydrogen convection zone.
Key words: stars: abundances / stars: chemically peculiar / diffusion / atomic processes
© ESO, 2013
1. Introduction
The atmospheres of AmFm chemically peculiar stars exhibit systematic depletion of scandium by about a factor of 5 to 10 (see Smith 1996). This depletion, together with calcium depletion, is among the strongest signatures identifying the stars belonging to the AmFm group. Other metals, like iron group elements for instance, are slightly overabundant in these stars (generally by less than a factor of 10). These abundance anomalies were first explained by atomic diffusion that leads to inhomogeneous elemental distribution as a function of depth below the superficial hydrogen convection zone (Watson 1971; Smith 1971; Michaud et al. 1983; Alecian 1996). However, models including atomic diffusion have to deal with a complex combination of processes like mass loss and structural changes triggered by the modification of abundances caused by atomic diffusion itself.
Indeed, evolution models calculated by Richard et al. (2001) and Richer et al. (2000)1 showed that Fe accumulation (around layers with T ≈ 200 000 K) leads to the appearance of an additional convection zone at some stages of the star’s life on the main sequence. This convection zone, which does not exist in standard models, modifies the way elements are distributed inside the star. Richard et al. (2001) and Richer et al. (2000) have shown that the abundances of iron peak elements observed in AmFm stars are compatible with the existence of an iron convection zone.
Effects of mass loss were also considered by Alecian (1996) in static models and by Vick et al. (2010) in models with evolution (with a new version of the Montreal code). They have shown that a small mass loss (without an additional convection zone due to iron) could also be compatible with observations.
The evolution models mentioned above are relatively accurate and sophisticated, but they do not include scandium because the scandium monochromatic opacity tables needed for its inclusion in the Montreal code were not available. However, LeBlanc & Alecian (2008) have shown that scandium may be considered a key element in discriminating the dominant physical processes lying behind the AmFm stars anomalies. Indeed, according to preliminary estimates of the Sc radiative accelerations (see Alecian 1996), the observed Sc depletion in AmFm stars could be explained if a small mass loss (≈10-14 solar mass per year) exists. Because atomic data for this element were poorly known, LeBlanc & Alecian (2008) used interpolated parameters in their single-valued parameters (SVP) method to calculate radiative accelerations (see Alecian & LeBlanc 2002; LeBlanc & Alecian 2004, hereafter Papers I and II respectively), which is more accurate than the previous estimate. Their results reinforced the arguments in favor of models with small mass loss for AmFm stars.
Recently, Massacrier & Artru (2012) have published new and extensive theoretical atomic data for Sc. The purpose of the present paper is to revisit the study of LeBlanc & Alecian (2008) using this new atomic data to calculate the parameters needed to obtain radiative accelerations by the SVP method, instead of using interpolated values of these parameters. The SVP method allows very fast computation of radiative accelerations and is implemented in some evolution codes (such as the Toulouse evolution code TGEC, see Théado et al. 2012). So, calculations of evolution models including Sc could be considered in the future. To check the accuracy of our new radiative accelerations of Sc, we also considered a second method, which is more accurate, but much heavier to carry out and not implemented in evolution codes. This method, commonly called the GLAM method, is described in Gonzalez et al. (1995).
In Sect. 2 we briefly describe the new atomic data for scandium. In Sect. 3 we give an overview of the SVP and the GLAM methods, and in Sect. 4 we present and discuss our results.
2. New atomic and spectroscopic data
The need for mean opacities in stellar structure and evolution computations involves the production of substantial atomic data as in the OPAL work (Rogers & Iglesias 1992) or the Opacity Project with its associated TIPTOPbase (Seaton et al. 1992; Nahar 2003). Radiative accelerations require monochromatic opacities that can be calculated from these atomic data. However, the data are not accessible (OPAL) or missing for elements that are of minor importance in what concerns the mean opacities, as is the case for scandium in the TIPTOPbase. In that case, one has to turn to other, often incomplete, databases.
Recently, Massacrier & Artru (2012) have performed a large scale analysis of the energy levels and transition data for Sc iii to Sc xxi, i.e. all the ions of scandium except for Sc i and Sc ii. The computations were done in jj-coupling with the Flexible Atomic Code, a relativistic program developped by M.-F. Gu (Gu 2003, 2008). More than twenty thousand fine-structure levels and two million transitions have been made available electronically in the form of tables2 that should allow for accurate computations of radiative accelerations. Their distribution among ions clearly reflects the capacity of the ions to absorb photons according to their half-filled shells or noble gas configurations.
These results were verified against the experimental data found in the NIST database, namely 820 energy levels and 677 transitions with oscillator strength values. The deviation in excitation energies is smaller than 0.2% for Sc xxi to Sc x, 1% for Sc xi to Sc iv, and 1.5% for Sc iii. Oscillator strengths are also faithfully reproduced, though no conclusion can be drawn for some ions, Sc vi for instance, because of the absence of gf values in the NIST databank. This overall agreement leads to a few levels and lines in NIST to be corrected.
Massacrier & Artru (2012) also compared their results with the data found in the linelist of Kurucz3, the largest available set for scandium transitions. Kurucz extended the NIST compilation for Sc iii to Sc ix theoretical oscillator strengths by a factor of ten. The data for Sc vi and Sc viii are consistent, but large discrepancies occur for Sc iii, and for most lines of Sc iv, Sc vii, and Sc ix. This illustrates the continuous need for theoretical atomic data production, that can ideally be validated through cross-checking with experiments.
3. Radiative accelerations
In this section, we briefly describe two methods employed to calculate radiative accelerations (grad). Two independent methods are used to better constrain the radiative accelerations of scandium at certain depths of interest in a typical AmFm star (see Sect. 4). This path was chosen in the hope that it will lead to more conclusive results.
3.1. The single-valued parameters method
The SVP method described in Papers I and II is based on parametric equations of radiative accelerations due to bound-bound (Alecian 1985; Alecian & Artru 1990a) and bound-free (Alecian 1994) transitions. In the SVP method, the radiative accelerations for each ion i due to bound-bound transitions can be calculated with four parameters. The first parameter 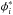 (Eqs. (10) and (20) of Paper I) depends on the strength of the bound-bound transitions through a weighted average of the gf values. The * denotes the fact that this parameter is calculated where the population of the ion is at its maximum. The second parameter
(Eqs. (10) and (20) of Paper I) depends on the strength of the bound-bound transitions through a weighted average of the gf values. The * denotes the fact that this parameter is calculated where the population of the ion is at its maximum. The second parameter 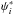 (see Eqs. (14) and (20) of Paper I) depends on the average width of the line profiles and represents the importance of saturation for the ion under consideration. A third parameter
(see Eqs. (14) and (20) of Paper I) depends on the average width of the line profiles and represents the importance of saturation for the ion under consideration. A third parameter 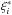 , is related to the ion contribution to the total opacity and will be neglected in this paper since it is of little importance for less abundant elements like Sc. The fourth parameter αi, which characterizes an average Voigt profile of the lines for the ion under consideration, see Eq. (1) of Paper II, is determined by fitting our parametric accelerations to those obtained by a more accurate method (Seaton 1997, see Papers I and II for more details). A parametric formula for the bound-free transitions also exists in which two parameters (ai and bi) are obtained by a fitting procedure (see Papers I and II for the definition of these parameters).
, is related to the ion contribution to the total opacity and will be neglected in this paper since it is of little importance for less abundant elements like Sc. The fourth parameter αi, which characterizes an average Voigt profile of the lines for the ion under consideration, see Eq. (1) of Paper II, is determined by fitting our parametric accelerations to those obtained by a more accurate method (Seaton 1997, see Papers I and II for more details). A parametric formula for the bound-free transitions also exists in which two parameters (ai and bi) are obtained by a fitting procedure (see Papers I and II for the definition of these parameters).
LeBlanc & Alecian (2008) calculated radiative accelerations of Sc by calculating the parameters 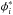 ,
, 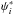 , and αi using an interpolation scheme. This was necessary because of the lack of accurate and complete Sc atomic data. Interpolation was performed between the nearest isoelectronic neighbors with known parameters, calculated with the help of The Opacity Project data (Seaton et al. 1992). The parameters of the ions Sc iii to Sc xx were obtained. Because of a lack of an isoelectronic neighbor (namely Ca i), the parameters of Sc ii directly calculated by Alecian & Artru (1990b) were used to obtain more precise radiative accelerations in stellar layers with low temperatures. The bound-free acceleration was calculated assuming cross-section rates with a ν-3 dependence with the parameters ai and bi also obtained by interpolation.
, and αi using an interpolation scheme. This was necessary because of the lack of accurate and complete Sc atomic data. Interpolation was performed between the nearest isoelectronic neighbors with known parameters, calculated with the help of The Opacity Project data (Seaton et al. 1992). The parameters of the ions Sc iii to Sc xx were obtained. Because of a lack of an isoelectronic neighbor (namely Ca i), the parameters of Sc ii directly calculated by Alecian & Artru (1990b) were used to obtain more precise radiative accelerations in stellar layers with low temperatures. The bound-free acceleration was calculated assuming cross-section rates with a ν-3 dependence with the parameters ai and bi also obtained by interpolation.
The new atomic data for Sc now available and calculated as described in the previous section makes it possible for a more accurate estimation of the radiative accelerations of this element. As in our previous studies (Papers I and II), the values of 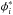 and
and 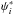 are calculated in the stellar model of interest (see Sect. 4) for each ion i where its population is at its maximum. For numerical expediency, the levels of the ions treated are combined as described in Alecian & Artru (1990a) during these calculations. Since no other precise radiative accelerations of Sc exist (as opposed to the elements treated in Paper II where the radiative accelerations of Seaton 1997 were available), the values of αi are obtained by fitting the radiative accelerations calculated with the SVP method to those calculated in more detail, namely by using the values of φi and ψi calculated in each layer of the underlying stellar model with the atomic data of Massacrier & Artru (2012). A fitting procedure using the GLAM results described below could have been employed, but we prefer to have two independent results for grad which may lead to firmer conclusions rather than having the results of the SVP method depend on those of the GLAM method. The bound-free accelerations are treated similarly to the method used in Paper II where the parameters ai and bi are obtained by a fitting procedure and where the cross-section rates are assumed to have a ν-3 dependence.
are calculated in the stellar model of interest (see Sect. 4) for each ion i where its population is at its maximum. For numerical expediency, the levels of the ions treated are combined as described in Alecian & Artru (1990a) during these calculations. Since no other precise radiative accelerations of Sc exist (as opposed to the elements treated in Paper II where the radiative accelerations of Seaton 1997 were available), the values of αi are obtained by fitting the radiative accelerations calculated with the SVP method to those calculated in more detail, namely by using the values of φi and ψi calculated in each layer of the underlying stellar model with the atomic data of Massacrier & Artru (2012). A fitting procedure using the GLAM results described below could have been employed, but we prefer to have two independent results for grad which may lead to firmer conclusions rather than having the results of the SVP method depend on those of the GLAM method. The bound-free accelerations are treated similarly to the method used in Paper II where the parameters ai and bi are obtained by a fitting procedure and where the cross-section rates are assumed to have a ν-3 dependence.
3.2. The GLAM method
Gonzalez et al. (1995) developed the GLAM method for calculating grad in which the acceleration due to each transition is estimated and summed appropriately to give the total radiative acceleration of a given element. Previous to this study, the opacity due to all other sources except for the transition under consideration (commonly called the background opacity, see Eq. (5) of Gonzalez et al. 1995) was typically crudely estimated. The arrival of more complete atomic data sets such as the Opacity Project data made this improvement possible. The GLAM method distributes the opacity of bound-bound and bound-free transitions of a mixture containing the most abundant elements on a 4000-point frequency grid equally spaced in the interval 0 < u < 20 where 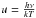 . In this study, we included the elements H, He, C, N, O, Ne, Mg, Si, S, Ar, Ca, and Fe using the Opacity Project data as well as the bound-bound transitions for Sc from Massacrier & Artru (2012). The accelerations are first calculated on a (T,Re) grid where
. In this study, we included the elements H, He, C, N, O, Ne, Mg, Si, S, Ar, Ca, and Fe using the Opacity Project data as well as the bound-bound transitions for Sc from Massacrier & Artru (2012). The accelerations are first calculated on a (T,Re) grid where 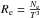 , Ne being the electronic density. The grad for the element of interest in a given stellar model is then obtained by interpolating on this grid.
, Ne being the electronic density. The grad for the element of interest in a given stellar model is then obtained by interpolating on this grid.
Since each transition is treated individually, the GLAM method has the advantage of allowing the inclusion of redistribution of the momentum among the ions. The redistribution scheme used here is discussed in Gonzalez et al. (1995), but is of little importance for the depths of interest here (see Sect. 4). The GLAM method is a detailed computation of radiative accelerations, and so it may be considered more accurate than the SVP method (at least before the application of the fitting procedure), but it is also more demanding for numerical computations.
4. Results and discussion
 |
Fig. 1 Radiative accelerations (in cm s-2) of Sc for a solar abundance vs. the depth (temperature T is in K). The solid line corresponds to the radiative acceleration calculated in this work when using the SVP method, the long-dashed line to the aceleration obtained with the GLAM method, the short-dashed line to the calculation of LeBlanc & Alecian (2008). Also shown are the approximate locations of the bottom of the convection zones of Scenarios A and B. The dotted line represents the local gravity, the dash-dot line the effective gravity gGT as defined by Eq. (8) of Michaud et al. (1976), and the dash-dot-dot line the effective gravity gGT with the (R/r)2 factor and the electronic pressure of our model (see footnote [4]). |
Radiative accelerations for a solar abundance of Sc calculated with the new atomic data discussed in Sect. 2 while using the two independent methods described in Sect. 3 are shown in Fig. 1 compared to the results found by LeBlanc & Alecian (2008) with their interpolation method. These results were calculated in a 1.9 M⊙ stellar model with Teff = 7610 K and an age of 807 Myr (model named 1.9P1 in Talon et al. 2006). The global shape of the acceleration in all of these computations is similar; however, radiative accelerations in the present work are generally larger than those of our previous calculations in layers near the locations where Sc is in Ar-like and Ne-like ionization stages (where the curves present two dips in the figure). The large differences of SVP vs. GLAM near log T = 4.3 are mostly side effects due to the absence of Sc ii in our calculations, and also because the maximum of the population of Sc iii is outside the model so it is not possible to estimate accurately the SVP parameters at this higher boundary. Therefore, the values of grad obtained in the present case by the SVP methods are unreliable above log T ≈ 4.4. However, this has no consequence since these layers are inside the superficial convection zone where atomic diffusion has no effect.
These results are presented in an attempt to verify which of the two scenarios in Sect. 1 is more likely. In AmFm stars, the observed abundances correspond to those in the outer mixed zone. They depend on the incoming flux of elements because of atomic diffusion and mass loss. The surface abundances therefore also depend on the depth of the outer mixed zone. Scenario A supposes that the abundance anomalies come from below a superficial hydrogen convection zone with a small amount of mass loss, while Scenario B assumes that these abundance anomalies come from below a deeper convection zone caused by iron accumulation due to diffusion. The approximate locations of the bottom of the convection zones of Scenario A and Scenario B are shown in Fig. 1. We have also shown in Fig. 1 the effective gravity for scandium, as proposed by Michaud et al. (1976) (the gGT defined by their Eq. (8)), to consider the effect of thermal diffusion4. However, the uncertainty on the thermal diffusion term is higher than for the other terms entering the equations for the diffusion velocity (see Montmerle & Michaud 1976). Comparing radiative accelerations to local gravity (and gGT) can enlighten us about which of the two scenarios is more likely.
Our new calculations using the SVP method show that the radiative acceleration of Sc is still 0.5 dex smaller than local gravity at log T ≈ 4.6 (near the layers where Sc is in the Ar-like configuration). When using the GLAM method, grad of Sc is 0.2 dex smaller than local gravity. Therefore, the solar abundance of Sc cannot be maintained in these layers. This can lead to a depletion of Sc abundance and to the realization of Scenario A. In contrast, Sc radiative acceleration is almost equal to gravity at log T ≈ 5.8 near the layers where Sc is in the Ne-like configuration and where the under-abundance of Sc should form in Scenario B. Indeed, the calculations of Richard et al. (2001) and Richer et al. (2000) found an iron convection zone going down to a depth of log T ≈ 5.4. According to Fig. 1, even if this convection zone went down to where the acceleration of Sc is at its minimum (near log T ≈ 5.8), the acceleration there is too close to the value of gravity and a large underabundance of Sc seems unlikely. The new results presented here therefore favor more vigorously Scenario A compared to the results shown in LeBlanc & Alecian (2008). However, this assertion is weakened if we compare radiative accelerations to the local gravity corrected by thermal diffusion. Indeed gGT is significantly larger than gravity for layers hotter than log T ≈ 5.0, even if at the bottom of the convection zone in Scenario B, radiative acceleration of Sc is still larger than gGT. For layers with log T ≈ 5.8 (around the minimum of the radiative acceleration), thermal diffusion would help scandium to become underabundant, but this underabundance could hardly reach the bottom of the convection zone of Scenario B without mass loss (mass loss has been excluded in this scenario).
These results need to be confirmed since they are done in a static model without taking into account the changes brought about by the diffusion process. In evolution models, the structure of stars changes significantly during their stay on the main sequence and therefore the position of mixing zones may also vary with time. Because the abundance stratification process has to be combined with mass loss, only models describing detailed evolution models could show how the Sc abundance will change during the star’s life on the main sequence. Since evolution models with Sc diffusion are not yet available, we are obliged to use qualitative arguments. More accurate calculations with stellar evolution, and considering scandium, need significant effort in numerical developments. They are foreseen in the near future.
We have computed gGT as given by Michaud et al. (1976) (with a = 4 × 102 as given in their Table 2 for a 2.0 solar mass star), and also calculated the same quantity with two modifications (i) a (R/r)2 factor which seems missing in the term with Teff and (ii) using the electronic pressure computed in our model, rather than the one given by Eq. (9) of Michaud et al. (1976).
Acknowledgments
The authors thank O. Richard for kindly communicating the stellar model used in this paper. This research was partially funded by NSERC and La Faculté des Études Supérieures et de la Recherche de l’Université de Moncton. We also thank RQCHP for computing time. F.L. is grateful for a one month visiting position at the Observatoire de Paris – LUTH and at the Université Denis-Diderot (Paris 7). We acknowledge the financial support of Programme National de Physique Stellaire (PNPS) of CNRS/INSU, France.
References
- Alecian, G. 1985, A&A, 145, 275 [NASA ADS] [Google Scholar]
- Alecian, G. 1986, A&A, 168, 204 [NASA ADS] [Google Scholar]
- Alecian, G. 1994, A&A, 289, 885 [NASA ADS] [Google Scholar]
- Alecian, G. 1996, A&A, 310, 872 [NASA ADS] [Google Scholar]
- Alecian, G., & Artru, M.-C. 1990a, A&A, 234, 323 [NASA ADS] [Google Scholar]
- Alecian, G., & Artru, M.-C. 1990b, A&AS, 83, 379 [NASA ADS] [Google Scholar]
- Alecian, G., & LeBlanc, F. 2002, MNRAS, 332, 891 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, J.-F., LeBlanc, F., Artru, M.-C., & Michaud, G. 1995, A&A, 297, 223 [NASA ADS] [Google Scholar]
- Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2008, Canadian J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- LeBlanc, F., & Alecian, G. 2004, MNRAS, 352, 1329 (Paper II) [NASA ADS] [CrossRef] [Google Scholar]
- LeBlanc, F., & Alecian, G. 2008, A&A, 477, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massacrier, G., & Artru, M.-C. 2012, A&A, 538, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michaud, G., & Charland, Y. 1986, ApJ, 311, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Charland, Y., Vauclair, S., & Vauclair, G. 1976, ApJ, 210, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Tarasick, D., Charland, Y., & Pelletier, C. 1983, ApJ, 269, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Montmerle, T., & Michaud, G. 1976, ApJS, 31, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N. 2003, in The Iron Project and TIPTOPbase: Atomic Data and Opacities for Astrophysics, in Planetary Nebulae: Their Evolution and Role in the Universe, eds. S. Kwok, M. Dopita, & R. Sutherland, IAU Symp., 239, 335 [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2001, ApJ, 558, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, J., Michaud, G., & Turcotte, S. 2000, ApJ, 529, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJ, 401, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1997, MNRAS, 289, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., Zeippen, C. J., Tully, J. A., et al. 1992, Rev. Mex. Astron. Astrofis., 23, 19 [NASA ADS] [EDP Sciences] [Google Scholar]
- Smith, K. C. 1996, Ap&SS, 237, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A. 1971, A&A, 11, 325 [NASA ADS] [Google Scholar]
- Talon, S., Richard, O., & Michaud, G. 2006, ApJ, 645, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Théado, S., Alecian, G., LeBlanc, F., Vauclair, S. 2012, A&A, 546, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vick, M., Michaud, G., Richer, J., & Richard, O. 2010, A&A, 521, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, W. D. 1971, A&A, 13, 263 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Radiative accelerations (in cm s-2) of Sc for a solar abundance vs. the depth (temperature T is in K). The solid line corresponds to the radiative acceleration calculated in this work when using the SVP method, the long-dashed line to the aceleration obtained with the GLAM method, the short-dashed line to the calculation of LeBlanc & Alecian (2008). Also shown are the approximate locations of the bottom of the convection zones of Scenarios A and B. The dotted line represents the local gravity, the dash-dot line the effective gravity gGT as defined by Eq. (8) of Michaud et al. (1976), and the dash-dot-dot line the effective gravity gGT with the (R/r)2 factor and the electronic pressure of our model (see footnote [4]). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


