| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321090 | |
| Published online | 30 May 2013 | |
Statistical and numerical study of asteroid orbital uncertainty
1 Shanghai Astronomical Observatory, 80 Nandan Road, The Chinese Academy of Science, 200030 Shanghai, PR China
2 IMCCE – Observatoire de Paris, UPMC, UMR 8028 CNRS, 77 avenue Denfert-Rochereau, 75014 Paris, France
e-mail: desmars@imcce.fr; bancelin@imcce.fr; hestro@imcce.fr; thuillot@imcce.fr
Received: 11 January 2013
Accepted: 12 March 2013
Context. The knowledge of the orbit or the ephemeris uncertainty of asteroids presents a particular interest for various purposes. These quantities are, for instance, useful for recovering asteroids, for identifying lost asteroids, or for planning stellar occultation campaigns. They are also needed for estimating the close approach of near-Earth asteroids, and the subsequent risk of collision. Ephemeris accuracy can also be used for instrument calibration or for scientific applications.
Aims. Asteroid databases provide information about the uncertainty of the orbits and allow the measure of the quality of an orbit. This paper analyses these different uncertainty parameters and estimates the impact of the different measurements on the uncertainty of orbits.
Methods. We dealt with two main databases, astorb and mpcorb, that provide uncertainty parameters for asteroid orbits. Statistical methods were used to estimate orbital uncertainty and to compare them with parameters from the databases. Simulations were also generated to deal with specific measurements such as the future Gaia mission or present radar measurements.
Results. Relations between the uncertainty parameter and the characteristics of the asteroid (orbital arc, absolute magnitude, etc.) are highlighted. Moreover, a review of the different measuments are compiled and their impact on the accuracy of the orbit is also estimated.
Key words: minor planets, asteroids: general / ephemerides / astrometry
© ESO, 2013
1. Introduction
Asteroids, since the time of their first discovery in the nineteenth century, have raised the need to compute and to predict their position to ensure subsequent detections and observations. While methods for computing orbits or predicting positions of planets and comets had already been developed at that time, the case of asteroids (or minor planets) raised new challenges because no specific assumption could be made about the orbital elements which were completely unknown. This was successfully solved by Gauss (Gauss 1809, 1864) and his method of computing orbits from the knowledge of three topocentric positions. His method, presented as “a judicious balancing of geometrical and dynamical concepts” by Escobal (1965), proved to be remarkably efficient providing – shortly after the discovery of Ceres by Piazzi in 1801, and observations made over only 40 days covering a 3 degree arc – a prediction for the next apparition of Ceres twelve months later, to better than 0.1 degree. Without being exhaustive, one can also mention here the method of Laplace (e.g. Poincaré 1906), based on the knowledge of a position and its derivatives, which shows several similarities to the fundamental scheme (Tisserand & Perchot 1899; Celletti & Pinzari 2005). These methods (Herget 1948; Dubyago 1961; Escobal 1965; Roy 2005; Milani & Gronchi 2010, and reference therein) paved the way for many more discoveries of minor planets or asteroids, and continuous observations of these bodies. The number of known asteroids is still increasing at the end of 2012 there were slightly less than 600 000 catalogued bodies in the astorb database (Bowell 2012). It is interesting to remember the remark extracted from the preface of E. Dubois, the French translator of Gauss’ work (Gauss 1864): “Or il est bien probable que la zone située entre Mars et Jupiter n’est pas encore suffisamment explorée et que le chiffre de 79 auquel on est arrivé, sera encore augmenté. Qui sait ce que réserve l’avenir !!... Bientôt alors les astronomes officiels n’y pourront plus suffire, si des calculateurs dévoués à l’astronomie et à ses progrès ne leur viennent aussi en aide de ce côté1”. Preliminary orbit computations are thus needed to provide some initial knowledge of the celestial object’s orbit. They differ in nature, as an inverse problem, from the direct problem of subsequent position prediction and orbit propagation that can be more complete in terms of correction to the observations and force models.
Nowadays, ephemerides are commonly needed for various practical or scientific uses: to prepare an observation program or space mission rendez-vous, to be able to cross-match a source or to identify a known asteroid observed in a CCD frame, to link two observed arcs as being of the same object, for predicting stellar occultations, for developing planetary ephemerides, for testing new dynamical models and physics, for contributing to local tests of the general relativity, for deriving asteroid masses from close encounters, or non-gravitationnal parameters, etc. During previous centuries these objects were considered planets or minor planets, and analytical or semi-numerical theories could be applied to each body before the advent of modern powerful computers (e.g. Leveau 1880; Brouwer 1937; Morando 1965). Ephemerides are now computed directly by numerical integration of the equation of motions for the orbit propagation using different integrators. Such numerical integration requires the use of a standard dynamical model and associated parameters for all solutions to be consistent, and the knowledge of initial conditions to the Cauchy problem as given by orbital parameters at a reference epoch, which are obtained, as for any solar system object, by a fit to the observations and are updated regularly. The term ephemerides is broadly used for any quantity related to the computation of such orbit propagation of a celestial object, giving its position and motion (spherical cartesian, apparent, astrometric, as seen from various centres, in various reference planes, at various dates, on different time scales, etc.).
In addition to these calculated values from orbit propagation and subsequent transformations generally corresponding to a nominal solution (e.g. least-squares with a standard dynamical model), knowledge of the ephemeris uncertainty, precision, and accuracy is often mandatory as is the case for any physical quantities. It is also often useful to know the degree of confidence one can have in a predicted quantity. Furthermore, the ephemerides uncertainty is needed in the various fields presented above and in particular for planning observations using instruments with a small field of view for instrument calibration purposes, or when one needs to quantify the probability of an impact of a near-Earth object (NEO) with a terrestrial planet, or for efficient planning of stellar occultation campaigns (in particular if it involves a large number of participants and/or large telescopes), etc.
The precision of an ephemeris can be incorrectly reduced to the precision of the observations it is based on. Of course, all things being equal, the higher the precision of the observation the better the theory and ephemerides; but this will not yield an indication of how fast the precision for any predicted or extrapolated quantity is being degraded. Indeed, the precision of the ephemerides is a quantity varying with time; when extrapolating the motion to dates far into the future or in the past (several centuries), the precision will globally be poorer; up to the point where chaotic orbits on a time span of millions of years make such ephemeris prediction unrealistic. An ephemeris uncertainty can be decreased on a short time span – for instance if required by a flyby or space mission to a solar system body – with last-minute observations. However, if no more observations are added in the fitting process, the ephemerides precision will inevitably degrade in time. The accuracy of an ephemeris as the precision of the theory for the dynamical model and its representation can be internal or external. Internal precision refers to the numerical model used (terms of the development in an analytical theory or machine precision in case of numerical integration of the ODE for the equations of motions) or additionally to the representation used to compress such ephemerides (Chebychev polynomials, mixed functions, etc.). External precision refers to the adjustment to the observations and hence to the stochastic and systematic errors involved in the measurements and data reduction, in the validity of the models used to fit and transform the data, in the uncertainty in the considered parameters, etc. We will deal in the following with the external errors, which accounts for most of the uncertainty in present ephemerides of asteroids and other dwarf planets, and small bodies of the solar system.
All ephemerides require observations and measurements related to the dynamical model of the equations of motion. Current ground-based surveys (LINEAR, Catalina, Spacewatch, C9) which where basically designed to detect 90% of the largest NEOs provide most of such data; they are completed by some scientific programs such as radar observations from Arecibo and Goldstone for NEOs, the CFHTLS Ecliptic Survey for the trans-Neptunian objects (Jones et al. 2006) or the Deep Ecliptic Survey (DES) for Kuiper belt objects and Centaurs (Elliot et al. 2005). In the very near future surveys such as Pan-STARRS, Gaia, LSST, will also provide a large number of astrometric positions.
In this paper, we investigate the orbital uncertainty of asteroids in the numerical and statistical way. First, we briefly present the two main databases of orbital parameters of asteroids. In particular, we present and compare uncertainty parameters provided by these databases (Sect. 2).
In Sect. 3 we highlight relations between orbital uncertainty and other asteroid parameters such as dynamical classes of asteroids and magnitude. We specifically study the relation between orbital arc and uncertainty, in particular for short orbital arcs. Finally, in Sect. 4 we present statistical information about astrometric measurements of asteroids and we quantify the impact of astrometric measurements in the radar and the Gaia space mission contexts.
2. Ephemeris uncertainty parameters
The number of discovered asteroids exceeded 590 000 at the beginning of October 2012, and the discovery rate is still about 1800 new asteroids per month2. Currently, four main centres provide asteroid orbital databases (Minor Planet Center; Lowell Observatory; Jet Propulsion Laboratory; Pisa University). In this paper, we deal mainly with two of these databases: astorb from Lowell Observatory (Bowell 2012) and mpcorb from Minor Planet Center (2012b). A total of 590 095 asteroids are compiled in astorb and 590 073 in mpcorb as of October 5, 2012. The two databases provide similar asteroid parameters, in particular:
-
name/number: name or preliminary designation, asteroidnumber;
-
osculating elements: semi-major axis a, eccentricity e, inclination I, mean anomaly M, argument of perihelion ω, longitude of ascending node Ω at reference epoch;
-
magnitude: absolute magnitude H, slope parameter G;
-
observations: number of astrometric observations, arc length or year of first and last observation.
The two databases also provide parameters about predictability of the ephemerides, only one for mpcorb, the U parameter and five parameters for astorb, current ephemeris uncertainty (CEU), rate of change of CEU, next peak ephemeris uncertainty (PEU) and the two greatest PEU.
The uncertainty parameter U is an integer value between 0 and 9, where 0 indicates a very small uncertainty and 9 an extremely large uncertainty. Detailed information about its computation is given in Minor Planet Center (2012d). Briefly, the U parameter is computed thanks to another parameter, RUNOFF, which depends on the uncertainty in the time of passage at perihelion, the orbital period and its uncertainty. RUNOFF expresses the uncertainty in longitude in seconds of arc per decade. The U parameter is derived by a logarithmic relation of RUNOFF. The quality of the orbit can be quickly determined with the uncertainty parameter U.
The astorb database provides five parameters related to the ephemeris uncertainty. In our study, we specifically dealt with two of them, current ephemeris uncertainty (CEU) and the rate of change of CEU. The CEU matches the sky-plane uncertainty σψ at a date3 provided by astorb. A brief description of the uncertainty-analysis technique is presented in Yeomans et al. (1987) and all the details can be found in Muinonen & Bowell (1993). The orbit determination provides the covariance matrix of the orbital elements Λ. Linear transformations then give the covariance matrix Σ in spherical coordinates (in right ascension and declination) 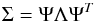 (1)where Ψ is the matrix of partial derivatives between spherical coordinates and orbital elements. Finally, by propagating this covariance matrix at a given date (date of CEU), the sky-plane uncertainty can be determined as the trace of the matrix (Muinonen & Bowell 1993). The CEU is determined in two body linear approximation (Bowell 2012). The rate of change of CEU (noted CEU rate) is in arcsec/day. According to Muinonen & Bowell (1993), in linear approximation uncertainties in spherical coordinates increase linearly with time in the two body approximation.
(1)where Ψ is the matrix of partial derivatives between spherical coordinates and orbital elements. Finally, by propagating this covariance matrix at a given date (date of CEU), the sky-plane uncertainty can be determined as the trace of the matrix (Muinonen & Bowell 1993). The CEU is determined in two body linear approximation (Bowell 2012). The rate of change of CEU (noted CEU rate) is in arcsec/day. According to Muinonen & Bowell (1993), in linear approximation uncertainties in spherical coordinates increase linearly with time in the two body approximation.
2.1. Comparison of the ephemeris uncertainty parameters
The U parameter can be compared to the CEU and its rate of change. Figure 1 shows a correlation between these parameters. Qualitatively and as expected, asteroids with a low U parameter also have a low CEU and CEU rate.
 |
Fig. 1 CEU, CEU rate, U parameter for asteroids in common between the astorb and mpcorb databases. |
The measure of the uncertainty could be provided by only one of these parameters. Nevertheless, these two parameters are not perfect and some problems can appear.
Indeed, the main difficulty with the uncertainty parameters is that they are sometimes not indicated. For mpcorb, 105 399 asteroids (17.9% of the total in the database) have no U parameter at all and 9431 (1.6%) have only a qualitative letter for the U parameter4. In the astorb database, the CEU has not been computed (and appears as 0) for 2585 asteroids (0.44%). Moreover, CEU is determined using the approximate two-body problem. For some critical cases (Earth-approaching asteroids), the uncertainties may have been misestimated by a factor of several (Bowell 2012). As an illustration, we have computed the orbital uncertainty – with methods described in the next section – for the asteroid Apophis which is a well-known Earth approaching Potentially Hazardous Asteroid. The difference between the simplified two-body approximation and the full N-body perturbations is clear (see Fig. 2). The ratio between the two values of uncertainty is close to 1 until 2029 and reaches approximately 105 after the 2029 close approach. The two-body approach does not involve the stretching of the orbital uncertainty and thus yields over-optimistic results.
 |
Fig. 2 Orbital uncertainty in distance of the asteroid Apophis using a two-body approximation and full N-body perturbations. |
2.2. Study of the ephemeris uncertainty parameters
Another problem is that some asteroids have CEU and U parameters in total contradiction. For example, they can have a good CEU (less than 1 arcsec) and a bad U parameter (U = 9) (and conversly). To clarify this situation, we have compared the CEU value to the standard deviation σ obtained by orbital clones for eight selected representative asteroids (two with a bad U and bad CEU, two with bad U and good CEU, two with good U and bad CEU and two with good U and good CEU).
In this context, we have computed the standard deviation provided by clones with two different methods using non-linear extrapolation. The main principle of these methods is to perform a Monte Carlo propagation of the orbit, i.e. to compute clones of initial conditions around the nominal orbit, providing as many orbits as possible. The first method (Monte Carlo using covariance matrix, MCCM) consists in adding a random noise to the set of nominal initial conditions using the standard deviation and correlation of these parameters thanks to the covariance matrix. The second one, uses the bootstrap resampling method (BR) directly on the observations, and consists in determining a new set of initial conditions by fitting to a bootstrap set of observations. These two methods, one parametric and one non-parametric, have been used previously in Desmars et al. (2009) for the study of the precision of planetary satellites ephemerides.
For this test, we computed 1000 clones of orbital initial conditions of each representative asteroid. Then we calculated the standard deviation σ of the angular separation s in the plane-of-sky at the date of CEU, which represents the angular deviation of an orbit to the nominal one, defined as 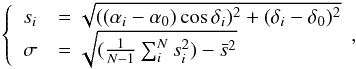 (2)where i denotes the number of the clone, the subscript 0 refers to the nominal orbit,
(2)where i denotes the number of the clone, the subscript 0 refers to the nominal orbit, 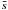 is the mean, and N is the total number of clones computed.
is the mean, and N is the total number of clones computed.
Table 1 gives the comparison between the U parameter, CEU, and standard deviation provided by these orbital clones for the two methods.
Comparison of the U parameter, the CEU and standard deviation σ obtained from orbital clones around the nominal orbits, with two different methods (MCCM and BR, see text).
For these representative asteroids, the CEU is often close to the standard deviation computed here, whereas the U parameter is misestimated for at least four representative asteroids. Moreover, we stress that the U parameter provides a number which is not related to a physical value (a distance or an angle).
In light of the previous tests for several particular cases, and of Fig. 1 for the general purpose, the CEU seems to be a good and practical parameter for estimating the accuracy and predictability of an asteroid orbit, as CEU is quickly computable, precise, and provides a physical value (an angle).
3. Relations between CEU and physical or orbital parameters
As the CEU seems to be a useful parameter for measuring the orbital uncertainty, we will hereafter use this parameter and highlight several relations between CEU and orbital parameters.
3.1. Relation between absolute magnitude, orbital arc and CEU
Generally, asteroids can be classified in dynamical groups. We propose, for the sake of simplicity, to gather the asteroids into the following three main groups defined as5
-
A-NEA (near-Earth asteroids): asteroid with perihelionq ≤ 1.3 AU. It represents asteroids in the inner zone of the solar system. This group includes the Aten, Apollo, Amor, and inner Earth orbit (IEO). There are 9144 objects in A-NEA group in astorb. In this category, PHA are asteroids that present a risk of devastating collision (i.e. with H ≤ 22 and a minimum orbital intersection distance, MOID < 0.05 AU).
-
B-MBA (main belt asteroids): asteroid with perihelion q > 1.3 AU and semi-major axis a ≤ 5.5 AU, representing asteroids in the intermediate zone. Thus Trojans are considered B-MBA in the following. There are 579 208 B-MBAs in astorb.
-
C-TNO (trans-Neptunian objects): asteroid with perihelion q > 1.3 AU and semi-major axis a > 5.5 AU, representing asteroids in the outer zone of the solar system. Thus Centaurs, asteroids between Jupiter and Neptune, are included in C-TNO. There are 1743 C-TNOs in astorb.
Figure 3 represents the absolute magnitude H, CEU, and the length of the orbital arc given in astorb for all the asteroids. Each group defined previously appears to be clearly distinguishable: C-TNOs in the left part (crosses), B-MBAs in middle part (small squares) and A-NEAs in right part (bullets). Large C-TNOs (larger than ≈45 km corresponding to absolute magnitude 8, depending on albedo) with short arcs and small A-NEAs (approximately smaller than 5 km whatever the albedo of the asteroid larger than 0.05, using the relation between magnitude and size (Minor Planet Center 2012c) with short arcs also appear.
 |
Fig. 3 H magnitude, CEU, and orbital arc for asteroids from astorb. The crosses indicate C-TNO, small squares B-MBA and bullets A-NEA. When H or CEU are unknown they are represented on the plot with the value H = 35 or CEU = 109, in contrast to the convention adopted in astorb database where H = 14. |
One also notes that for all the objects a correlation between the value of CEU, the length of orbital arc, and the number of observations can be identified. In Fig. 4, this correlation appears clearly. We can identify three groups related to the length of the arc
-
arc <10 days: these asteroids are barely observed(fewer than 10 observations), corresponding mostly to thediscovery period, and have a high CEU (between 1 and 107 arcsec). Moreover, the CEU does not decrease much on this graph with increasing orbital arc (see Sect. 3.3 for a discussion of this statement);
-
10 days ≤ arc <250 days: these asteroids are not observed often (fewer than 100 observations) and have a high CEU (between 1 and 106 arcsec);
-
250 days ≤ arc <8000 days: these asteroids are also not observed often but have a better CEU (between 0.1 and 100 arcsec);
-
8000 days ≤ arc: these asteroids all have a large number of observations (more than 100 observations) and have a good CEU (between 0.01 and 10 arcsec).
The gap in orbital arc apparent around 250 days means that when an asteroid is discovered, it is rarely observed for more than 250 days. Beyond this period, the asteroid is in an unfavourable configuration to be observed because of its small solar elongation (conjunction) and can be observed again only after its passage behind the Sun. Two peaks can also be observed in Fig. 4 at orbital arcs longer than 10 000 days, one for arcs of 19 000 days and another, more spread out, for approximately 14 000 days. These peaks can be explained by an important number of objects with an orbital arc of this dimension. Many asteroids (∼1500) were discovered in 1960 with the 1.22 m telescope of Mt. Palomar, and also in 1973. Because these asteroids have been observed recently (in the late 2000 s), their orbital arcs correspond approximately to 14 000 days (the period 1973–2012) and to 19 000 days (the period 1960–2012). These objects now have various CEU corresponding to the peaks.
 |
Fig. 4 Relation between the length of the orbital arc, CEU, and the number of observations for all asteroids. |
With these considerations, asteroids can be classified in 12 groups according to their orbital arcs, their dynamical classes (A-NEA, B-MBA, C-TNO), and their CEU (given the correlation between CEU and length of arc). Table 2 gives the number and the median6 CEU for each group. Asteroids with undetermined CEU (about 2585 asteroids with CEU = 0 in astorb) are not taken into account.
Different classes of ephemeris precision as given by their median CEU and length of arc.
3.2. Relation between orbital arc and CEU
Figure 4 shows that the decrease in the CEU is correlated to the increase in the orbital arc. Moreover, the increasing rate of the CEU appears different with varying orbital arc. We have computed an empirical relation for this improvement rate for each of the groups defined in the previous section. For each group, a linear regression can be computed between CEU and the length of orbital arc (as shown in Fig. 5) and we have the relation 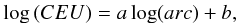 (3)where a and b are given in Table 3 and Fig. 5 for each groups.
(3)where a and b are given in Table 3 and Fig. 5 for each groups.
If the orbital arc is smaller than ten days7, the CEU is very large and does not improve much when the length of arc becomes larger (see also Sect. 3.3). However, in this case, observations remain useful to avoid loosing the object. Between 10-day and 250-day arcs, the CEU is clearly improved when the length of arc increases. For asteroids with an orbital arc between 250 and 8000 days, the CEU is smaller than 100 arcsec and is still much improved when the length of arc becomes greater. If the orbital arc is greater than 8000 days, then the CEU is not much improved and reaches its typical minimum value of about 0.1–0.2 arcsec.
As noted previously, in the short-arc group (orbital arc less than 10 days) the CEU does not decrease quickly while the orbital arc increases. It is unclear however, if this is associated with the population on average or on each individual arc. In the second case it could be a surprising result so we highlight the trend in the following section.
3.3. Evolution of CEU for short orbital arcs
In this section we investigate the evolution of the CEU as a function of the orbital arc for a single object. We try to highlight the time spent on improving the quality of the orbit after its discovery. A previous work in Virtanen & Muinonen (2006) studied the time evolution of the orbital-element uncertainty of the asteroid 2004 AS1 together with the evolution of the impact risk assessment. For this purpose, the authors used the volume of variation (VoV) technique which is a nonlinear Monte Carlo technique (Muinonen et al. 2006).
In this context, we computed the orbital uncertainty of an asteroid by considering a variable (and short) length of orbital arc. For our work, six test case objects were considered: (31 824) Elatus and (2060) Chiron for Centaur asteroids; 1 Ceres and 8 Flora for MBAs; 1866 Sisyphus and 4179 Toutatis (PHA) for NEOs. First, we performed a preliminary orbit determination using the Gauss method. The Gauss method converged two days after discovery for all cases except for Chiron and Ceres which converged one day after discovery. To assess the uncertainty of the orbit, we used the differential correction method. All of these computations were performed using the OrbFit4.2 package8. Then, for each arc, we computed 1001 clones of the nominal orbit from a multivariate Gaussian distribution given by the covariance matrix (obtained from the procedure described above). Each clone orbit was then directly propagated at the date of computation of CEU with the Monte Carlo technique. The Lie integrator (Bancelin et al. 2012c) was used to perform this propagation. Thus, we were able to compute the standard deviation σ using (Eq. (2)) that we assumed to match with the definition of the CEU. If the Gauss method and/or orbital improvement failed or if the σ value obtained was large (greater that 107), then the CEU was considered indeterminate and was set to 107. Obviously, some asteroids considered in this study have an indeterminate CEU at the epoch of their discovery (Fig. 6). For Chiron and Ceres, a preliminary solution was obtained but the uncertainty on the orbit was too large. For the NEOs, the Gauss method converged two days after the discovery and the differential correction succeeded. For the MBAs, it is defined after three days whereas for the Centaurs, the uncertainty is not defined up to ten days. Then, the orbital uncertainty drops almost linearly for all the objects; for the Centaur asteroids, it goes below 100–1000 arcsec for an arc length 800–1000 days. This is a consequence of the lack of observations because they are distant objects and they have a slow apparent motion. For the other asteroids, the orbital uncertainty decreases linearly and goes below 100 arcsec. One can see that its variation for the asteroid Toutatis has a stranger behaviour than the others because the sharp drop of the uncertainty value occurs around the 14th day.
 |
Fig. 5 Relation between the length of the orbital arc and CEU for all asteroids, and slope for the four classes identified (red for arc<10 d, green for 10d ≤ arc < 250 d, blue for 250 d ≤ arc < 8000 d, and orange for arc ≥ 8000 d). |
 |
Fig. 6 Variation of the orbital uncertainty as a function of the arc length for six single objects. The axes are expressed in a logarithmic scale. |
This test shows that, except for the distant objects (Centaurs), observations performed after their discovery (until ∼6 days) will mostly avoid the loss of the object than improve its orbit, as the rate of change is not that significant. However, continuous observations performed after ∼6 days will allow a significant orbit improvement as the rate is much steeper.
4. Astrometric measurements
In this section, we first described the different types of measurement of asteroid position, then we estimate the effect of specific measurements (optical observations, radar, or future Gaia observations) in the improvement of the orbit.
4.1. Presentation
The position of an asteroid can be determined by many types of measurements. The Minor Planet Center provides all the measurements related to asteroids for numbered and unnumbered asteroids (Minor Planet Center 2012a). As of September 30, 2012, 94 082 128 observations are available on the database. Table 4 gives the statistics on the different kind of measurements provided by the MPC database, in particular their percentage and the time span.
Historically, the first observations of asteroids were made with micrometers during the 19th century. In the latter part of that century, photographic plates allowed a better measurement of asteroid position. In the mid-1980s, the CCD revolutionized astrometric measurement thanks to better sensitivity, stability, dynamic range, and ease of extracting astrometric measurements. Consequently, most of the measurement in the MPC database come from CCD. Space observations by instruments such as the Hubble Space Telescope, Spitzer, and particularly Wide-field Infrared Survey Explorer (WISE) also provide an important number of measurements.
In addition to the different types of measurements mentioned above, some observations can appear as secondary or marginal for different reasons; even if precise, they can have a lower impact on the orbital models. For example, the space mission Hipparcos also provides geocentric data (Hestroffer et al. 1998). Radar measurements are not very common, but give the most accurate measurements for asteroids. They can also provide physical characteristics such as shape. Astrometric positions can also be deduced from stellar occultations.
Statistics of different measurements provided by the MPC database for numbered and unnumbered asteroids.
Accuracy of measurements for numbered asteroids from the AstDyS2 database.
The accuracy of each measurement can be obtained thanks to the AstDyS website (AstDyS 2012). For each numbered asteroid, this website provides an observation file indicating the residual (O–C) of each measurement. All the observations of all numbered asteroids9 have been compiled and the accuracy of each measurement has been estimated by computing a weighted10 root mean square of all the residuals of the measurement.
Table 5 provides the number, the percentage of accepted measurement, and the estimated accuracy for each kind of observation. After radar measurements, observations derived from occultations and Hipparcos geocentric observations appear to be the most accurate (about 0.08–0.15 arcsec). Recent measurements such as CCD observations or meridian circle observations are accurate to between 0.2–0.4 arcsec. Older measurements, such as photographic or micrometric measures, are less accurate (1.0–1.8 arcsec). Surprisingly, observations from spacecraft (HST, Spitzer or WISE) are not any more accurate than ground-based data. Nevertheless, WISE was designed for asteroid detection and the mission has detected 157 000 asteroids, including more than 500 NEO (Mainzer et al. 2011).
4.2. Impact of astrometric measurements on orbit uncertainty – the Apophis example
In order to quantify the impact of a type of measurement on the orbital uncertainty of an asteroid, we specifically dealt with the asteroid Apophis. This particular object belongs to the PHA family and is known to be the most threatening object of the last decade since it is the only asteroid that reached level 4 of the Torino scale for potential impact with the Earth in April 2029 (Sansaturio & Arratia 2008). Since new observations (optical and radar) ruled out every possibility of impact in 2029, this threat turned out to be a close encounter within 5.64 R⊕ of the Earth. But this close encounter is so deep that the asteroid will move from the Aten family orbit to the Apollo family orbit. Besides, its orbit will become chaotic and new possibilities of collision with the Earth after 2029 will appear. The most accepted collision date is in 2036 for which the risk was estimated, at the date of the last observations available in 2012, with a probability of ∼10-6. This date is also important because of the size of the keyhole, the region in the B-plane (Valsecchi et al. 2003) of 2029 where the asteroid has to pass in order to collide with the Earth in the future. The size of the 2036 keyhole is estimated at ∼600 m. In the B-plane we can represent the state of the asteroid, located by two geocentric coordinates (ξ and ζ), at the date of close encounter, and also its uncertainty (σξ and σζ) and the relative position of the keyhole with respect to the nominal solution. More often than not, the uncertainty region is a 3σ ellipse centred on the nominal solution and its size is directly linked to the observations used. Therefore, the position of the keyhole compared with the size of the ellipse uncertainty is also important for quantifying the risk of future collision (Chesley 2006; Kochetova et al. 2009; Bancelin et al. 2012a).
4.2.1. Past observations
In this section, we deal first with the impact of the observations of Apophis (from 2004 to 2008), available at MPC-UAI, on the uncertainty region. We propagated the equations of motion (as well as the variational equations) of Apophis until 2029 considering the gravitational perturbations of all the planets, also including the gravitational perturbations of the Moon, Ceres, Pallas, and Vesta. Relativistic accelerations were also taken into account. The uncertainty of the nominal orbit was propagated using a linear propagation of the initial covariance matrix in order to assess the evolution of the orbit uncertainty. We performed this test using two different sets of observations. The first uses only optical data from 2004–2008 and the second uses optical and radar data (five radar measurements – ranging and Doppler measurements – were performed at Arecibo in 2005 and 2006). This test was done to highlight the impact of radar data on the current orbit uncertainty.
First, we represent in Fig. 7, the current position uncertainty of Apophis until the date of close encounter, when considering optical data only or optical and radar data. One can see that the uncertainty is improved by a factor of more than 2 when considering radar data. This is not a surprise as radar data are very accurate measurements.
 |
Fig. 7 Position uncertainty on the geocentric distance of Apophis after fitting to optical observations (solid line) and optical and radar data observations (dashed line). |
This improvement can also be illustrated by the evolution of the uncertainty on the 2029 B-plane. Table 6 shows the value of the nominal position (ξ and ζ) and the uncertainty (σξ and σζ). The uncertainty on the geocentric distance Δ is also given through the value of σΔ. One can see that radar measurements enable to decrease the uncertainty on the main component ζ and on Δ by a factor of more than 2, while the uncertainty on the ξ component remains almost unchanged.
Uncertainty (σξ and σζ) on the 2029 B-plane of Apophis considering optical data only or optical and radar data.
One should note that if the arc data increases thanks to optical measurements and without radar data, the orbital improvement using ranging and/or doppler measurements could not be that significant. For instance, Apophis has additional optical observations from 2011–2012. Considering those data combined with the radar measurements, the uncertainty on the distance drops to 154 km. If we ignore the radar data, this uncertainty value is 177 km.
4.2.2. Future observations
Gaia is an astrometric mission that will be launched in October 2013. Its aim is to provide a 3D-map of our Galaxy. There are many scientific outcomes from this mission and the satellite will be able to map thousands of main belt asteroids (MBAs) and near-Earth objects (NEOs) in our solar system down to magnitude 20. The high precision astrometry (0.3–5 mas of accuracy on a transit level) will allow orbital improvement, mass determination, and better accuracy in the prediction and ephemerides of PHAs. During the five-year mission, Gaia may observe the asteroid Apophis several times (Bancelin et al. 2012b). We performed some tests to quantify the impact of future measurements (optical, radar, or space data) on Apophis orbit when the new data are outside the period of observations. Apophis will have favourable observation conditions in 2013 and 2021 because it will be at a distance of less than 0.1 AU. In this context, we have considered five sets of possible measurements:
-
S1: using all optical and radar data available (2004–2012);
-
S2: using set S1 with additional Gaia data (over the period 2013–2018) with 5 mas accuracy;
-
S3: using set S1 with one additional future radar measurement in 2013 with 1 μs accuracy (measurement of a timing echo);
-
S4: using set S1 with one future optical observation done in 2013 with 0.1 arcsec accuracy;
-
S5: using set S1 and the case that Gaia would provide only one observation with 5 mas accuracy.
Figure 8 shows that the Gaia data enable the position uncertainty to be reduced to the kilometer level (set S2) and this value to be maintained until the close approach of 2029. For comparison, the effect of future accurate measurements (radar and optical) can be comparable to the impact of one future Gaia data.
 |
Fig. 8 Evolution of the position uncertainty (given by its geocentric distance) of the asteroid Apophis considering several different sets of observations. |
In the same context, we have quantified the uncertainty in the B-plane of 2029. While the effect of one additional Gaia data point (set S5) can be compared to the effect of one radar measurement (set S3), one set of Gaia observations (set S2) can bring the uncertainties to around the kilometer level (Table 7).
Uncertainty (σξ,σζ) on the 2029 B-plane of Apophis considering various sets Si of future observations (see text).
4.3. Impact of Gaia stellar catalogue on orbit uncertainty
The space mission Gaia will provide not only accurate observations of asteroid positions, but also, and especially, an astrometric stellar catalogue. The Gaia catalogue (Mignard et al. 2007) will provide unbiased positions of a billion stars up to magnitude 20 and with an accuracy depending on magnitude (7 μas at ≤10 mag, 12–25 μas at 15 mag, and 100–300 μas at 20 mag). With this stellar catalogue, a new era of astrometry will be possible. New processes of reduction of new and archived observations will be necessary, such as a propagation model to the third order for the proper motion of stars, differential aberration, atmospheric absorption, colour of stars, etc. With these corrections, an accuracy of 10 mas is expected on the position of any asteroid deduced from the Gaia stellar catalogue. In particular, it will be possible to reduce future and past observations with this catalogue, even if it seems obvious that all the observations for all the asteroids could not be reduced again.
In this section we studied the impact of this new reduction in the orbit uncertainty and we considered the case of Apophis and assumed its current observations: 1518 optical observations and 7 radar measurements from 2004 to 2012.
We assumed that a variable part of the optical observations could be reduced again with the Gaia stellar catalogue (i.e. with an accuracy of 10 mas systematically) and we computed in Fig. 9, the position uncertainty from 2000 to 2050 depending on a percentage of reduced observations with the Gaia stellar catalogue (0%, 10%, 25%, 50% and 100%). The case of 0% means that none of the optical observations could be reduced again and represents the current position uncertainty by considering the current accuracy of the observations; 100% means that all the observations could be reduced with the Gaia stellar catalogue.
 |
Fig. 9 Evolution of the position uncertainty of the asteroid Apophis by considering that a certain percentage of optical observations could be reduced with the Gaia stellar catalogue, i.e. with an accuracy of 10 mas (see text). |
The variation of the uncertainty is the same for all the cases but the amplitude is different (Fig. 9). With the current accuracy of observations, the uncertainty of the Apophis orbit is about 10 to 100 km in geocentric distance from 2000 to 2029 and then sharply increases after the 2029 Earth close approach. While the percentage of observations reduced with the Gaia stellar catalogue increases, the uncertainty of the orbit decreases. Figure 9 shows that if only 10% of observations were reduced with the Gaia stellar catalogue, the accuracy of the position would be 20 times smaller than with current observations. If the percentage reaches 50%, the position uncertainty would be 40 times smaller. Finally, if all the optical observations of Apophis could be reduced again with the Gaia catalogue then the orbit accuracy would be 50 times better than with current observations.
When just a few observations can be reduced again, the choice of the first and last observations appears opportune. We have compared this case with a random choice of the same number of observations reduced by the Gaia stellar catalogue. The selection of the first and last observations provides the best accuracy by virtually increasing the length of the orbital arc, bringing more important constraints on the orbital motion of the asteroid.
Consequently, we assumed that a small number of the optical observations could be reduced again with the Gaia stellar catalogue and we computed the accuracy of the orbit from 2000 to 2050. We dealt with five situations:
-
current observations with their current accuracy;
-
the first and the last observations reduced with the Gaia stellar catalogue i.e. with a conservative accuracy of 10 mas;
-
the first five and the last five observations reduced with the Gaia stellar catalogue;
-
the first ten and the last ten observations reduced with the Gaia stellar catalogue;
-
all observations reduced with the Gaia stellar catalogue.
Figure 10 shows that even if only a few first and last observations could be reduced by the Gaia stellar catalogue, the position uncertainty of Apophis would be significantly reduced. In particular, if only two observations (first and last) were reduced again with the Gaia catalogue, then the orbital accuracy would be five times better than with the current precision of observations. By reducing ten (first five and last five) or twenty (first ten and last ten) optical observations of Apophis, the quality of the orbit would also be improved.
 |
Fig. 10 Evolution of the position uncertainty of asteroid Apophis considering different quantities of first and last observations reduced by the Gaia stellar catalogue (see text). |
The Gaia stellar catalogue will be very useful for astrometry because with only a few observations reduced with this catalogue, the quality of the orbit will be greatly improved. For asteroids and in particular PHAs, it will help to considerably refine the orbit and the impact probability during close approaches.
5. Conclusion
Orbital uncertainty parameters can be useful for recovering asteroids, for instrument calibration, and for scientific applications. They are also important for estimating the conditions of asteroid close approaches from Earth and their impact probability.
In this study, we particularly dealt with the current ephemeris uncertainty provided by the astorb database and the U parameter from the mpcorb database. In practice, the CEU shows some advantages because it is quickly computable, precise, and provides a physical value (an angle). Relations between CEU, H magnitude, orbital arc, and dynamical group have been identified. In particular, empirical linear relation between the CEU and the orbital arc have been highlighted. The CEU significantly increases while the orbital arc increases when the orbital arc is between 10 and 250 days and more moderately for 250–8000 day arcs. For orbital arcs larger than 8000 days, the CEU does not improve much and reaches about 0.1–0.2 arcsec. For short arc asteroids (less than 10 days), the CEU is sometimes hard to compute and remains large while the orbital arc increases.
Finally, we present statistical data about astrometric measurements. Most asteroid observations (about 94%) come from CCD frames. Presently, radar measurements are more precise with an accuracy of about 3.3 km in distance and 6.7 km s-1 in velocity. Unfortunately, these measurements are still rare and are mostly limited to PHAs (during close approaches). The CCD frames remain relatively accurate (0.4 arcsec) and are quite numerous. These measurements provide the astrometry for most asteroids. The bias in stellar catalogues remains the main cause of uncertainty.
Nowadays, there are two ways to improve orbit uncertainty. One way is to increase the length of the orbital arc. We have shown how fast CEU decreases while the orbital arc increases. In this context it is necessary to provide asteroid observations by performing new observations or dataming. The second way is to improve the accuracy of the measurements. Radar measurements appear the most accurate, but they remain few in number.
The Gaia mission will be a revolution for asteroid dynamic and astrometry. The satellite will provide several tens of observations for most asteroids. For PHAs, in particular the asteroid Apophis, we have shown that Gaia observations will help to improve orbit accuracy and to refine its impact probability during close approaches. In the B-plane, Gaia will decrease the uncertainty at the kilometer level instead of the current 10 km level. Moreover, with the Gaia stellar catalogue, it will be possible to reduce future and past observations with a very high level of accuracy (about 10 mas). Even if only a few of the older observations could be reduced with this catalogue, the orbit quality will be about five times better than it is currently. In the extreme case where all observations can be reduced, the orbit uncertainty will be about 50 times smaller than it is currently.
“It is likely that the zone between Mars and Jupiter is not yet sufficiently explored and that the number of 79 that has been reached will still be increased. Who knows what the future will hold for us!! Soon official astronomers will not suffice, if some human computers devoted to astronomy and its progress do not come to their rescue also on that side.” It is clear that two centuries later modern electronic computing machines came to the rescue and are now impossible to circumvent.
In the mpcorb database, the U parameter can be indicated as a letter. If U is indicated as “E”, it means that the orbital eccentricity was assumed. For one-opposition orbits, U can also be “D” if a double (or multiple) designation is involved or “F” if an assumed double (or multiple) designation is involved (Minor Planet Center 2012d).
Acknowledgments
This study was partly supported by contract ESA/22885/ 09/F/MOS/100409-R from the European Space Agency.
References
- AstDyS. 2012, Asteroids Dynamics Site, http://hamilton.dm.unipi.it/astdys [Google Scholar]
- Bancelin, D.,Colas, F.,Thuillot, W.,Hestroffer, D., &Assafin, M. 2012a, A&A, 544, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bancelin, D.,Hestroffer, D., &Thuillot, W. 2012b, Planet. Space Sci., 73, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bancelin, D.,Hestroffer, D., &Thuillot, W. 2012c, Celest. Mech. Dyn. Astron., 112, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Bowell, E. 2012, The asteroid orbital elements database, ftp://ftp.lowell.edu/pub/elgb/astorb.html [Google Scholar]
- Brouwer, D. 1937, Transactions of the Astronomical Observatory of Yale University, 6, 173 [NASA ADS] [Google Scholar]
- Celletti, A., &Pinzari, G. 2005, Celest. Mech. Dyn. Astron., 93, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R. 2006, in Asteroids, Comets, Meteors, eds. L. Daniela, M. Sylvio Ferraz, & F. J. Angel, IAU Symp., 229, 215 [Google Scholar]
- Desmars, J.,Arlot, S.,Arlot, J.,Lainey, V., &Vienne, A. 2009, A&A, 499, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubyago, A. D. 1961, The Determination of Orbits (New York: The Macmillan Company) [Google Scholar]
- Elliot, J. L.,Kern, S. D.,Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Escobal, P. R. 1965, Methods of orbit determination (New York: Wiley) [Google Scholar]
- Gauss, C. F. 1864, Théorie du mouvement des corps célestes parcourant des sections coniques autour du soleil / trad. du Theoria motus de Gauss; suivie de notes, par E. Dubois (Paris: A. Bertrand, 1855; trad. E.-P. Dubois; in 8), 380 [Google Scholar]
- Gauss, K. F. 1809, Theoria motus corporum coelestium in sectionibus conicis solem ambientium. (Hamburgi, Sumtibus F. Perthes, & I. H. Besser) [Google Scholar]
- Herget, P. 1948, The computation of orbits (Michigan: Lithoprinted from copy by Edwards Brothers, Inc.) [Google Scholar]
- Hestroffer, D.,Morando, B.,Hog, E., et al. 1998, A&A, 334, 325 [NASA ADS] [Google Scholar]
- Jones, R. L.,Gladman, B.,Petit, J.-M., et al. 2006, Icarus, 185, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Kochetova, O. M.,Chernetenko, Y. A., &Shor, V. A. 2009, Sol. Syst. Res., 43, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Leveau, G. 1880, Annales de l’Observatoire de Paris, 15, A1 [NASA ADS] [Google Scholar]
- Mainzer, A.,Bauer, J.,Grav, T., et al. 2011, ApJ, 731, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F.,Cellino, A.,Muinonen, K., et al. 2007, Earth Moon and Planets, 101, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., & Gronchi, G. F. 2010, Theory of Orbital Determination (Cambridge University Press) [Google Scholar]
- Minor Planet Center 2012a, MPCAT-OBS: Observation Archive, http://www.minorplanetcenter.net/iau/ECS/MPCAT-OBS/MPCAT-OBS.html [Google Scholar]
- Minor Planet Center 2012b, MPCORB database, http://minorplanetcenter.net/iau/MPCORB.html [Google Scholar]
- Minor Planet Center 2012c, Relation between size, albedo and magnitude, http://www.minorplanetcenter.org/iau/lists/Sizes.html [Google Scholar]
- Minor Planet Center. 2012d, Uncertainty parameter U, http://www.minorplanetcenter.net/iau/info/UValue.html [Google Scholar]
- Morando, B. 1965, Bull. Astron., 1, 331 [Google Scholar]
- Muinonen, K., &Bowell, E. 1993, Icarus, 104, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K.,Virtanen, J.,Granvik, M., &Laakso, T. 2006, MNRAS, 368, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Poincaré, H. 1906, Bull. Astron., Ser. I, 23, 161 [Google Scholar]
- Roy, A. E. 2005, Orbital motion, fourth edn. (Bristol and Philadelphia: IoP) [Google Scholar]
- Sansaturio, M. E., &Arratia, O. 2008, Earth Moon and Planets, 102, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Tisserand, F., & Perchot, J. 1899, Leçons sur la détermination des orbites (Paris: Gauthier-Villars), 124 [Google Scholar]
- Valsecchi, G. B.,Milani, A.,Gronchi, G. F., &Chesley, S. R. 2003, A&A, 408, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, J., &Muinonen, K. 2006, Icarus, 184, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Yeomans, D. K.,Ostro, S. J., &Chodas, P. W. 1987, AJ, 94, 189 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of the U parameter, the CEU and standard deviation σ obtained from orbital clones around the nominal orbits, with two different methods (MCCM and BR, see text).
Different classes of ephemeris precision as given by their median CEU and length of arc.
Statistics of different measurements provided by the MPC database for numbered and unnumbered asteroids.
Uncertainty (σξ and σζ) on the 2029 B-plane of Apophis considering optical data only or optical and radar data.
Uncertainty (σξ,σζ) on the 2029 B-plane of Apophis considering various sets Si of future observations (see text).
All Figures
 |
Fig. 1 CEU, CEU rate, U parameter for asteroids in common between the astorb and mpcorb databases. |
| In the text | |
 |
Fig. 2 Orbital uncertainty in distance of the asteroid Apophis using a two-body approximation and full N-body perturbations. |
| In the text | |
 |
Fig. 3 H magnitude, CEU, and orbital arc for asteroids from astorb. The crosses indicate C-TNO, small squares B-MBA and bullets A-NEA. When H or CEU are unknown they are represented on the plot with the value H = 35 or CEU = 109, in contrast to the convention adopted in astorb database where H = 14. |
| In the text | |
 |
Fig. 4 Relation between the length of the orbital arc, CEU, and the number of observations for all asteroids. |
| In the text | |
 |
Fig. 5 Relation between the length of the orbital arc and CEU for all asteroids, and slope for the four classes identified (red for arc<10 d, green for 10d ≤ arc < 250 d, blue for 250 d ≤ arc < 8000 d, and orange for arc ≥ 8000 d). |
| In the text | |
 |
Fig. 6 Variation of the orbital uncertainty as a function of the arc length for six single objects. The axes are expressed in a logarithmic scale. |
| In the text | |
 |
Fig. 7 Position uncertainty on the geocentric distance of Apophis after fitting to optical observations (solid line) and optical and radar data observations (dashed line). |
| In the text | |
 |
Fig. 8 Evolution of the position uncertainty (given by its geocentric distance) of the asteroid Apophis considering several different sets of observations. |
| In the text | |
 |
Fig. 9 Evolution of the position uncertainty of the asteroid Apophis by considering that a certain percentage of optical observations could be reduced with the Gaia stellar catalogue, i.e. with an accuracy of 10 mas (see text). |
| In the text | |
 |
Fig. 10 Evolution of the position uncertainty of asteroid Apophis considering different quantities of first and last observations reduced by the Gaia stellar catalogue (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


