| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321040 | |
| Published online | 11 June 2013 | |
The hydrodynamics of astrophysical jets: scaled experiments and numerical simulations
1 Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, 20156 Milano, Italy
e-mail:
belan@aero.polimi.it
2 Dipartimento di Fisica, Università degli Studi di Torino, via Pietro Giuria 1, 10125 Torino, Italy
e-mail:
silvano.massaglia@unito.it
3 Dipartimento di Ingegneria Meccanica e Aerospaziale, Politecnico di Torino, 10129 Torino, Italy
e-mail:
daniela.tordella@polito.it
4 Retired, formerly Dipartimento di Ingegneria Aerospaziale, Politecnico di Milano, 20156 Milano, Italy
e-mail:
deponte@aero.polimi.it
Received: 4 January 2013
Accepted: 12 April 2013
Context. In this paper we study the propagation of hypersonic hydrodynamic jets (Mach number >5) in a laboratory vessel and make comparisons with numerical simulations of axially symmetric flows with the same initial and boundary conditions. The astrophysical context is that of the jets originating around young stellar objects (YSOs).
Aims. In order to gain a deeper insight into the phenomenology of YSO jets, we performed a set of experiments and numerical simulations of hypersonic jets in the range of Mach numbers from 10 to 20 and for jet-to-ambient density ratios from 0.85 to 5.4, using different gas species and observing jet lengths of the order of 150 initial radii or more. Exploiting the scalability of the hydrodynamic equations, we intend to reproduce the YSO jet behaviour with respect to jet velocity and elapsed times. In addition, we can make comparisons between the simulated, the experimental, and the observed morphologies.
Methods. In the experiments the gas pressure and temperature are increased by a fast, quasi-isentropic compression by means of a piston system operating on a time scale of tens of milliseconds, while the gas density is visualized and measured by means of an electron beam system. We used the PLUTO software for the numerical solution of mixed hyperbolic/parabolic conservation laws targeting high Mach number flows in astrophysical fluid dynamics. We considered axisymmetric initial conditions and carried out numerical simulations in cylindrical geometry. The code has a modular flexible structure whereby different numerical algorithms can be separately combined to solve systems of conservation laws using the finite volume or finite difference approach based on Godunov-type schemes.
Results. The agreement between experiments and numerical simulations is fairly good in most of the comparisons. The resulting scaled flow velocities and elapsed times are close to the ones shown by observations. The morphologies of the density distributions agree with the observed ones as well.
Conclusions. The laboratory and the simulated hypersonic jets are all pressure matched, i.e. their axial regions are almost isentropic at the nozzle exit. They maintain their collimation for long distances in terms of the initial jet radii, without including magnetic confinement effects. This yields a qualitatively good agreement with the observed YSO jet morphologies. It remains to be seen what happens when non-axially symmetric perturbations of the flow are imposed at the nozzle, both in the experiment and in the simulation.
Key words: ISM: jets and outflows / hydrodynamics / stars: winds, outflows / Herbig-Haro objects / shock waves
© ESO, 2013
1. Introduction
Astrophysical jets are observed in the Universe in a large variety of environments and under a wide range of sizes and powers. They are generated in active galactic nuclei (AGNs), can travel up to a few thousands of Megaparsecs, and reach the largest powers observed in the Universe (up to ~1047 − 48 erg s-1, Zanni et al. 2003; Godfrey & Shabala 2013). Astrophysical jets can be found in giant molecular clouds, emanating in the vicinities of young stellar objects (YSOs), and reaching distances of some parsecs (Reipurth & Bally 2001). They are also located near neutron stars in galactic X-ray binary star systems, such as GRS 1915+105, that behave as microquasars generating relativistic jets (Fender 2004). Astrophysical jets can be found in the asymptotic giant branch (post-AGB) stars as well in pre-planetary and planetary nebulae. Opposite, precessing jets are observed in the SS433 binary source, leading to a peculiar phenomenology (Frank 2011). A jet-like structure is observed, at X-ray energies, inside the Crab Nebula departing from the embedded pulsar (Hester 2008). Finally, jets can be at the base of the phenomenology of gamma-ray bursts, observed at the highest radiation energies, that are still elusive phenomena because of their extreme distances (Granot 2006).
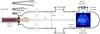 |
Fig. 1 Experimental setup. The total vessel length depends on the number of assembled sections. The set of de Laval nozzles used in this work is shown on the left. All the nozzles have the same converging section and throat (radius = 1 mm), whilst the diverging section depends on the Mach number of the design. The output radii rn are 12.0, 35.7, and 60.9 mm. |
The hypersonic jets are, of course, also of great interest in aero- and astronautical applications; however, many works are mainly focused on the jet near field, on the thrust obtained by means of jets, on jet-body interactions, and other applied issues. There is a great deal of literature on these topics, from the early works of Love et al. (1959) or Ashkenas & Sherman (1966), but it is very hard to find experimental works about the long scale behaviour of free hypersonic jets. Often the jets are compressible but not hypersonic, or, if hypersonic, they are underexpanded (see e.g. Bulent & Volkan 2002; Belan et al. 2010). Studies on the mid-term field of nearly isentropic laboratory jets up to Mach 2 can be found only in two papers by Zaman (1998, 1999). For these reasons, this work can also help to clarify some aspects of the basic fluid dynamics of these flows.
We have seen in recent years many experiments that try to reproduce in the laboratory at least some aspects of astrophysical phenomena. In the domain of radiative hydrodynamics, experiments have been carried out to understand the physics of radiative shocks in accretion flows about young stars from the analyses of the emitted spectra (Rus et al. 2002; Gonzàlez et al. 2009), to study the formation and evolution of magnetized accretion disks (Bellan et al. 2005), and to examine different aspects of the complex physics of stellar and galactic jets (Bellan et al. 2009). Different techniques have been employed, to study laboratory simulations of astrophysical jets, i.e. high-power lasers (Hartigan et al. 2009; Gregory et al. 2009; Falize et al. 2011), radial wires, and foil Z-pinch (Lebedev et al. 2005; Suzuki-Vidal et al. 2010). These experiments reproduce some features of the actual YSO jets such as jet velocities, temperatures, and cooling effects. Comparisons between laboratory jets produced by pulsed-power Z-pinch machines with simulations have been discussed by Ciardi et al. (2009). The disadvantage of these techniques is their inability to produce long collimated jets, where long means orders of magnitude longer than the width of the formation region.
Experimental configurations.
Hypersonic hydrodynamic flows in a vacuum vessel have recently been studied in the laboratory and by numerical means (Tordella et al. 2011; Belan et al. 2010). The hydrodynamic approach aims to highlight the compressibility effects, that observations show to be of the utmost importance in jets. In fact, observational data give clear evidence of shocked emission from structures that form at the jet’s head; on the jet axis we also observed series of aligned emission knots. Knot formation was evident ever since the early numerical studies of astrophysical jets by Norman et al. (1982), and were interpreted as shocks originated by jet compression or velocity variations in the jet, and/or by the nonlinear evolution of shear-layer instabilities (Massaglia et al. 1992; Micono et al. 2000). These structures are particularly well studied in YSO jets, because of the rich diagnostics supplied by the spectral line emission, and allow us to constrain well the values of the jet Mach numbers, between 10 and 40, and jet-to-ambient density ratios, in the range 1–10. It is, therefore, extremely interesting for us to be able to generate and study in the laboratory jets with Mach numbers and jet-to-ambient density ratios that are close to the ones inferred for YSO jets. It is worth noticing that, while the absolute velocities of the plasma jets produced in Z-pinch machines are fairly close to the velocity of the actual YSO jets, ~200 km s-1, they have densities that exceed the ambient density by orders of magnitude, typically jet electron density ~5 × 1018 cm-3 propagating in a vacuum (Lebedev et al. 2004).
In this paper we carry out a systematic analysis of hydrodynamic hypersonic jets, exploring the range of Mach numbers 10, 15, and 20 and different jet-to-ambient density ratios, carrying out comparisons between experimental and numerical results. The plan of the paper is the following: in Sects. 2 and 3 we describe the experimental and numerical setups, in Sect. 4 we present the results obtained, that are discussed in Sect. 5. Conclusions are drawn in Sect. 6.
2. Experimental setup
The laboratory experiment was carried out using facilities designed and built specifically for the generation and display of hypersonic jets. Detailed information can be found in the work of Belan et al. (2008, 2010, 2011, 2012), including descriptions of the configurations and improvements adopted in different experiments. The jets under test in this work were obtained by means of suitable de Laval nozzles and were propagated along the longitudinal axis of a modular cylindrical vacuum vessel. A sample setup is shown in Fig. 1. Visualizations and measurements are based on the electron beam technique, which is described in detail later.
The available set of nozzles was specially designed for monoatomic gas flows, taking account of the real flow properties, including viscous boundary layer and heat exchange effects. These calculations yield the momentum and temperature evolution in the viscous layer near the nozzle wall. It is important to recall here that the viscous layer undergoes an unavoidable transition to turbulence in the divergent part of the nozzle. Each de Laval nozzle is designed for a nominal Mach number, which is obtained by imposing a given stagnation-to-ambient pressure ratio p0/pa in such a way as to match the jet pressure pj at the nozzle exit and the ambient pressure pa. Slight adjustments of the pressure ratios are possible, so that all the jets are generated under matched or nearly matched pressure conditions, i.e. the jet pressure pj at the nozzle exit is close to the ambient pressure pa, in the range pa ± 20%. This permits the production of jets with different Mach numbers by means of the same nozzle; for example, the nozzle designed nominally for Mach 10 can be used to create jets in the range 7.5 < M < 12.5 (see also Table 1). Because of the boundary layer within the nozzles, the actual jet diameter is less than the diameter of the nozzle exit section. A proper definition for the reference jet diameter r0 at the nozzle output can be given by observing that in the present experiment the information is mainly obtained from density-dependent measurements. For this reason, r0 will be identified as the radius at which the density is reduced by 0.5 times the difference between the axial value and the minimum value at the nozzle boundary. This definition is a generalized form of the half density-half width criterion, and can be extended to the far field for any value of the density ratio, assuming as jet radius the point of half width between the central maximum and the external minimum, as shown in Fig. 2.
 |
Fig. 2 Output density curve and actual jet width under matched conditions. Upper panel: density and jet sketch at the output of the Mach 10 nozzle. Mid panel: density profiles and jet widths in the near and far fields for an underdense jet. Lower panel: density profiles and jet widths in the near and far fields for an overdense jet. |
The gas is fed to the nozzles by a fast piston system purposely designed, which compresses the gas to stagnation pressure in the 0.04 to 0.7 MPa (0.4–7 bar) range. At the same time, the piston raises the gas temperature, increasing significantly the gas enthalpy. The piston is a purely mechanical system, machined at a high level of precision which ensures a good repeatability to the jet production. The repeatability is high when considering global variables such as the time variation of the mass flow and the large scale structures. It is, naturally, less good on fine morphological details highly dependent on the boundary conditions at the nozzle output (Tordella et al. 2011; Belan et al. 2012). In particular, the mass flow curves show that the nominal mass flow of the jet can be reached after a certain transient time elapses. All the results presented in this work were obtained by satisfying this condition, i.e. the data were only collected when the mass flow was close to the asymptotic value for a given Mach number and pressure ratio p0/pa.
The jets under study were created inside a modular vacuum vessel; up to five cylindrical sections having a diameter of 0.5 m were available. These can be assembled together, giving a maximum available length for the spatial evolution of the jets of about 3.3 m, corresponding at least to 150 jet radii. A set of pumps was used to lower the internal pressure, that can reach a minimum level about 0.5–1 Pa. Pressures inside the vessel were monitored by 0.25% accuracy transducers. The vessel diameter is typically much larger than the jet diameter in all tests, so the lateral wall effects are negligible and the jets can be considered free jets until they hit the end of the vessel. The ambient pressure inside the vessel were controlled by means of a valve system which sets the desired ambient density (at pressures in the range 1.5 to 100 Pa) generally using a gas different from the gas flowing in the jet. The use of different gases for the jet (He, Ar, Xe) and the ambient (He, Ar, Xe, air) allowed us to set the jet-to-ambient density ratio η = ρj/ρa over a wide range, from underdense conditions (η < 1) to very overdense conditions (η ≫ 1).
The vessel modularity gives the advantage of fitting the total length to the needs of the individual tests. In general, for the sake of studying the jets evolution over long distances, a longer size is needed to follow the development of jets with higher Mach numbers, because of their larger diameter. Thus, the general setup depends on the nozzle in use. The main parameters, including the matched pressure ratios which are known with very good accuracy, as well as reference lengths and domain lengths, are listed in Table 1. The vessel lengths vary depending on the number of sections and on the nozzle length.
Visualizations and measurements are based on the electron beam method, thanks to an electron gun specifically designed and built in the laboratory. Detailed descriptions of this method, well known in experimental fluid mechanics, can be found in Muntz (1968) and Bütefisch & Vennemann (1974). The device is equipped with a deflection system to create an electron sheet, adjustable up to 2 mA at 20 kV. It was operated in continuous mode, i.e. it was turned on before the piston start and switched off at the end of the experiment. However, because of the high speed of the jets, the total working time of the electron gun was of the order of a few seconds for each test. The power of the beam can be easily obtained as the product of the current and the voltage. In a typical test the electron gun was not used at the maximum power; a power of 1 mA × 16 kV = 16 W can usually be assumed as a reference. This value can be compared to the power of the jets to estimate the perturbation due to the measurement method. It turned out that the beam-to-jet power or energy ratio was typically of the order of 1/200 or better.
The electron sheet intercepted the jet being tested and generated a plane fluorescent section of the flow, shown from above in Fig. 1. These 2D sections were then acquired as digital images by an intensified high-speed camera. Several cameras have been tested and used up to now, reaching speeds up to 8100 frames per second (fps). The image resolution was typically 512 × 512. The camera with the top performance in use acquires these images by means of a 32 × 20 mm CMOS (Complementary Metal-Oxide Semiconductor) sensor that receives light from an intensifier having a sensitive photo-cathode with a diameter of 25 mm. The time exposure was forced by the extreme conditions of this experiment where two opposite needs must be balanced, namely a short exposure to obtain sharp images and a long exposure to obtain a sufficient light level. In general, the longest exposure compatible with the frame rate was selected, i.e. the inverse of the frame rate minus the readout time. For example, at 8100 fps the exposure is 122.3 μs; at 4000 fps it is 248.9 μs. Since phenomena taking place over much shorter times are unavoidably blurred by the system, these time values can be considered close to the temporal resolution. The spatial resolution instead can be quantified reporting the visible jet width of the original images in pixels. This value ranges approximately from 30 to 100 pixels and it can be easily converted to millimetres value by the optical magnifying factor. This factor depends on the specific setup for each experimental session, but, in general, it is of the order of unity.
Besides visualizations, flow structure velocities and gas densities can be measured through image processing. Measurements of velocities can be obtained by special correlation techniques, applied to the typical macroscopic structures appearing in the jet morphology, such as the head bow-shock and the secondary moving shocks. A detailed description of the correlation techniques in use is beyond the scope of this work (see, e.g. Tordella et al. 2011). However, the main points are summarized here. Considering two consecutive frames as monochromatic pixel matrices Aij and Bij, and extracting two rows aj and bj containing the information about the moving structure, the displacement of this structure is obtained by calculating a correlation product of the kind
![$$ h_k = \sum_j \left[ a_j \cup R(b_j)\right] \left[b_{k+j} \cup R(a_{k+j})\right], $$](/articles/aa/full_html/2013/06/aa21040-13/aa21040-13-eq28.png) where R is a reflection operator that reverses the order of the elements in a pixel row. The resulting vector hk, which can also be expressed as a convolution product, has a maximum at kmax = s, where s (in pixels) is the structure shift between the two images. Then, dividing by the interframe time, the s/t ratio becomes a measure of the structure velocity. When this velocity is known, two consecutive images containing the same structure can be juxtaposed after shifting the second one by s pixels. This procedure can be repeated making use of different velocity measurements (head velocity, instability waves), leading to partial reconstructions of the jet morphology, consisting of juxtaposed parts (slices) of adjacent frames. Of course, this kind of reconstruction has a physical meaning only if the changes in the structure properties are slow compared to the interframe time, so that it cannot be performed over an arbitrarily large number of frames, to avoid a frozen representation of the flow under test. For these reasons, the presented results have been obtained by juxtaposing small numbers of slices (less than 15) coming from wide frames (about 0.4 m each) obtained by wide angle lenses.
where R is a reflection operator that reverses the order of the elements in a pixel row. The resulting vector hk, which can also be expressed as a convolution product, has a maximum at kmax = s, where s (in pixels) is the structure shift between the two images. Then, dividing by the interframe time, the s/t ratio becomes a measure of the structure velocity. When this velocity is known, two consecutive images containing the same structure can be juxtaposed after shifting the second one by s pixels. This procedure can be repeated making use of different velocity measurements (head velocity, instability waves), leading to partial reconstructions of the jet morphology, consisting of juxtaposed parts (slices) of adjacent frames. Of course, this kind of reconstruction has a physical meaning only if the changes in the structure properties are slow compared to the interframe time, so that it cannot be performed over an arbitrarily large number of frames, to avoid a frozen representation of the flow under test. For these reasons, the presented results have been obtained by juxtaposing small numbers of slices (less than 15) coming from wide frames (about 0.4 m each) obtained by wide angle lenses.
Density measurements in extended spatial regions are possible because of the proportionality between gas density and light intensity in the working pressure range. The working conditions in the vacuum vessel permit the use of the well-known relation 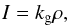 (1)where I is the light intensity taken from a subregion of the image and kg is a constant relevant to the tested gas (Brown & Miller 1957; Muntz 1968; Bütefisch & Vennemann 1974). The constant kg was obtained from direct calibrations performed on each tested gas (Belan et al. 2008).
(1)where I is the light intensity taken from a subregion of the image and kg is a constant relevant to the tested gas (Brown & Miller 1957; Muntz 1968; Bütefisch & Vennemann 1974). The constant kg was obtained from direct calibrations performed on each tested gas (Belan et al. 2008).
3. Numerical setup
We solved numerically the hydrodynamic ideal equations, Eqs. (1)–(3) (Sect. 5). The simulations were carried out on a 2D domain in cylindrical coordinates (r, z), which were normalized over the initial jet effective radius r0 (Fig. 2). The z axis represents the longitudinal direction of the jet. Because of the axial symmetry of the problem, we will consider a domain going from r = 0 to r = Rvessel.
The domain chosen depends on the nominal jet Mach number considered: for the cases with the M = 10 nozzle, we have assumed a domain of 31 × 310 r0 including 128 × 1280 zones; for the cases with the M = 15 nozzle, the domain was 16.5 × 165 r0 with the same number of grid zones; for the cases with the M = 20 nozzle, we had 12.5 × 150 r0 including 128 × 1500 zones. Exploiting the axial symmetry, half of the domains reported in Table 1 were chosen to carry out the numerical calculations.
We imposed reflective boundary conditions on the axis of the jet and at z = zvessel. At r = Rvessel we imposed that the flow velocity must be zero. We verified that this condition mimics the experimental behaviour at best. The jet was injected at the boundary z = 0 and the temporal dependence of the physical quantities was carefully modeled (Tordella et al. 2011).
We employed the PLUTO numerical code by Mignone et al. (2007)1 for the solution of hypersonic flows. The code provides a multiphysics, multialgorithm modular environment which is particularly oriented towards the treatment of astrophysical flows in the presence of discontinuities. Different modules and algorithms may be independently selected to properly describe Newtonian, relativistic, magnetohydrodynamic (MHD), or relativistic MHD fluids. In this case, Newtonian ideal hydrodynamics was used. This module exploits a general framework to integrate a system of conservation laws, built on modern Godunov-type shock-capturing schemes.
4. Results
A large set of jets was studied in the experimental investigation. The Mach numbers range from 7 to 21, and the density ratio η from 0.5 to more than 100. For a number of jets, also the corresponding numerical simulations have been realized.
4.1. Morphologies
This section presents the different morphologies observed at some significant density ratios and Mach numbers, selected as follows: Figs. 3 to 5 show three sets of jets, chosen in order to present slightly underdense, slightly overdense, and overdense jets. For each set, three different Mach numbers are selected, and for each jet the laboratory visualization is compared with the numerical simulation. In the visualizations, thanks to the electron beam technique, the light intensity is proportional to the local density, whereas in the corresponding numerical simulations the density maps are intentionally produced for the sake of comparison with the experiment, even if the simulations may easily produce maps for many other quantities.
Each experimental image is obtained by juxtaposing the time-correlated frames on a short time range including the instant chosen for the corresponding numerical image, as explained in Sect. 2. This treatment was introduced because of the limitation in size of the optical window in the experiment (Fig. 1) which even by using wide angle lenses cannot be larger than about 0.4 m. This extends the jet image over a wider spatial range that of a single camera frame, but limits the number of frames to maintain the right physical meaning of these reconstructions. The resulting image was then compared to the corresponding numerical simulation, which is inherently a fixed-time representation of the same phenomenon over the complete spatial domain.
 |
Fig. 3 Set of three slightly underdense jets of He in Xe: from top to bottom, η = 0.85, 0.9, and 0.9, Mach number = 10.0, 13.5, and 18.0. Length is expressed in r0 units (effective or reference jet radius) and time in τ units, i.e sound crossing time over jet radius. The numerical density scale refers to the unperturbed ambient density. |
Figure 3 shows three light, underdense jets, having similar density ratios <1 and Mach numbers from 10 to 18. Many known properties are visible both in the experiments and in the simulations, namely the presence of a large cocoon, the possible appearance of compression knots along the jet core, and the increasing bluntness of the jet head for decreasing Mach numbers. However, the last property must be considered by keeping in mind that head shape changes continuously with time, owing to the beam pumping phenomenon (Kössl & Müller 1988; Massaglia et al. 1996; Tordella et al. 2011). The hypersonic material at the jet’s head interacts with the ambient one forming a strong shock (called Mach disk). The back-flowing, shocked jet material inflates an expanding over-pressured region called a cocoon, that in turn squeezes the jet and drives shock waves into it which assume the characteristic biconical shape on the axis. These shocks modify the structure of the jet head, including the bow shock that precedes the Mach disk, and affect its propagation velocity into the ambient medium. It is also important to note that the experimental observation of the head structure and of the knots was difficult because of the finite, non-negligible exposure time of the camera, which is necessary for getting enough light. This produced an unavoidable image blur effect since the displacement of the structures under study was not always negligible during a typical exposure time. This effect is also discussed in Sect. 4.2.
A simple quantitative comparison between experiments and simulations can be made by measuring the jet head velocity Vexp. The results are in Table 2 and agree well with the numerical results Vnum, slightly less well at the lowest Mach number. For the experimental images, the results were obtained by means of the above mentioned correlation technique. In this and in the following tables, the accuracy reported for the simulated velocity is mainly due to the errors introduced by setting the accessory conditions of the simulations in such a way as to reproduce the experimental cases under investigation. The inherent accuracy of the PLUTO code, instead, is several orders of magnitude better than the experimental one. In the laboratory image at Mach 18 (Fig. 3), one can see a non-axially symmetric displacement of the jet core, which cannot be reproduced in the related two-dimensional axisymmetric numerical simulation (lower panel).
This property must be numerically investigated by considering a three-dimensional domain in further studies. At the moment, we might interpret this observation as an effect of the higher Reynolds number at the nozzle exit that disrupts the symmetry of the mean base flow. In particular, one must consider the effects associated to the viscous and turbulent boundary layer developing along the inner surface of the long de Laval nozzle necessary to generate the Mach 20 jets (see Fig. 1). This long layer can act as a source of excitation for the long transversal perturbation observed in this image. However, whether this behaviour at high Mach numbers is an effect of the injection mechanism adopted or is the result of the growth of intrinsic non-axially symmetric jet modes remains to be investigated.
 |
Fig. 4 Set of three slightly overdense jets of He in Xe: from top to bottom, η = 1.2, 1.35, and 1.4, Mach number = 11.0, 16.0, and 18.0. |
 |
Fig. 5 Set of three overdense jets of He: from top to bottom, ambient is air, air, and He; η = 4.4, 4.6, and 5.4; Mach number = 7.0, 14.3, and 17.9. |
Figure 4 shows three slightly overdense jets, having similar density ratios >1 and Mach numbers from 11 to 18. Again, both in the experiments and in the simulations, a cocoon and some compression knots are visible, whereas the jet head is blunter for lower Mach numbers. Compared to the underdense jets, here the higher density ratio causes a slight decrease of the cocoon and jet head sizes. The comparison between experimental and numerical jet head velocities is shown in Table 3; in this case the agreement is also fair, worsening at the highest Mach number.
Figure 5 shows three overdense jets, with similar density ratios ~5 and Mach numbers from 7 to 17.9. Unlike the previous cases where He jets travel in Xe ambients, here the He jets travel in different ambients, made of air or He, a necessary choice in order to obtain the desired density ratios, as explained in Sect. 2. The presence of a different ambient gas does not prevent the comparison with the previous cases since the ambient is not accelerated enough to introduce secondary effects due, for example, to the molecular structure of the ambient gas. In this case, as expected, the backward flow zone related to the cocoon formation has a definitely smaller size and the compression zones, when present, are narrowly spaced, so that they cannot be resolved by the experimental technique. The jet head structure is smaller than in the previous cases – it must not be confused with the bow shock, which reaches the boundaries of the domain. Unfortunately, at the lowest Mach number presented in this figure, the formation of a proper head structure is hampered by the pressure ratio pj/pa, which in this particular case turns out to be 0.77, i.e. at the very limit of the value allowed for a nearly matched condition. The comparison between experimental and numerical jet head velocities is shown in Table 4, excluding the lowest Mach number jet for the reasons mentioned above; even in this case there is a good agreement.
It is worth noting that pressure matched hypersonic hydrodynamic jets maintained their collimation up to large distances from the launching region, at least within the physical limits of the walls of the chamber. We note, however, that these jets were undisturbed in their propagation, apart from the self-induced non-axisymmetric long wave instability seen in the case of the underdense jet at Mach number 18 and Reynolds number ~105, see discussion above. It would be interesting, also from the astrophysical point of view, to modify the experimental setup to introduce some controlled non-axial perturbations in the flow at the nozzle exit, in particular to understand which part of the evolution is more influenced by the boundary condition at the nozzle.
4.2. Effects of the exposure time
In Fig. 6 we show what one obtains when the effect of the finite experimental exposure time is taken into account in the simulated density distribution. This figure was created by superimposing density maps taken in a time interval of the order of the exposure time, so that at each point the density has a time-averaged value. The case under investigation is the He jet in Xe ambient at the centre of Fig. 4 (η =1.35 and M = 16.0). One can see that the simulated density map of Fig. 6 is more similar to the experimental image than the original simulation, which is an instantaneous representation of the field. The time interval used to create this density map, 28τ < t < 33τ, is of the order of the exposure time, and must not be confused with the time interval 26τ < t < 56τ used to extract and juxtapose frames from the sequence of images, which is definitely larger for the sake of comparison with the numerical images. Another minor reason for blur, however, cannot be accounted for in Fig. 6, and it is due to the finite time needed for the excitation of molecules by the electron beam, so that the light emission is delayed while the molecules drift downstream of the excitation point.
 |
Fig. 6 Simulation of the overdense jet at centre of Fig. 4 (Mach number = 16) obtained by averaged superposition of density maps over a time interval of the order of the experimental image exposure. |
4.3. Density measurements
Another kind of quantitative result is given in Fig. 7, where the proportionality law (Eq. (1)) between the fluorescent light intensity and the gas density is used to measure density values along the axes of the three slightly overdense jets in Fig. 4. The proportionality constant for each gas species is known by calibration. Whenever possible, the results were obtained by using different values of this constant for different gas species (the inner zone of the jet heads, namely the region between the bow shock and the terminal shock or Mach disk, cannot be analyzed because it contains two mixed gas species, it is represented in Fig. 7 as an empty space between vertical dashed lines). The output density values were corrected to account for the image background noise and the final curves were compared with the relevant numerical ones. The results, given in terms of the density ratio η referred to the unperturbed ambient, show that the experimental technique is capable of reproducing the large scale density variations, whereas the small scale details are lost. However, the small scale structures exhibit turbulent temporal variations that are just barely reproducible. That is, even a higher time resolution of the camera that produces less blur in the experimental images would probably reveal different small scale variations at each repetition of the same jet.
 |
Fig. 7 Numerical (thin lines) and experimental (thick lines) axial densities for the 3 slightly overdense jets of Fig. 4. Densities are expressed in nondimensional form as density ratios η referred to the unperturbed ambient. The space between vertical dashed lines is a non-measurable zone, see the text, Sect. 4.3. |
5. Discussion
Physical parameters for the laboratory helium jets.
The ideal hydrodynamic equations, in absence of dissipation effects and radiative cooling, can be written as 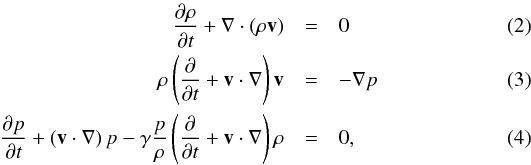 where v, p, and ρ are the fluid velocity, pressure, and density, and γ is the ratio of specific heats. These equations are invariant under the transformation (Ryutov et al. 1999)
where v, p, and ρ are the fluid velocity, pressure, and density, and γ is the ratio of specific heats. These equations are invariant under the transformation (Ryutov et al. 1999) 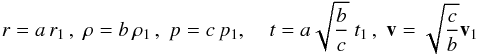 (5)where a, b, and c are arbitrary positive numbers (Euler similarity).
(5)where a, b, and c are arbitrary positive numbers (Euler similarity).
To apply the Euler similarity, the system must have large Reynolds and Peclet numbers (Re and Pe) with respect to unity and a small localization parameter (K or Knudsen number, the ratio of the collisional mean-free-path to the typical scale length of the system). We recall that the definitions for these parameters are 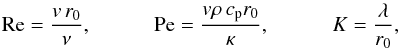 (6)where ν is the kinematic viscosity, cp the heat capacity, κ the thermal conductivity, λ the collisional mean-free-path, and ρ the mass density, and where we have taken the radius r0 as typical scale of the system.
(6)where ν is the kinematic viscosity, cp the heat capacity, κ the thermal conductivity, λ the collisional mean-free-path, and ρ the mass density, and where we have taken the radius r0 as typical scale of the system.
To verify whether the hypersonic flows generated in the laboratory are Euler similar to YSO jets we recall some fiducial values of length, density, and pressure of the astrophysical objects (Teşileanu et al. 2012): jet radius 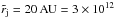 m, temperature
m, temperature 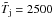 K, and particle density (mostly Hydrogen)
K, and particle density (mostly Hydrogen) 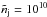 m-3, thus the mass density is ~10-17 Kg m-3. The pressure can then be obtained by the ideal gas law as ~3 × 10-10 Pa. As reported in Sect. 1, observational data include Mach numbers approximately ranging from 10 to 40 and density ratios from 1 to 10.
m-3, thus the mass density is ~10-17 Kg m-3. The pressure can then be obtained by the ideal gas law as ~3 × 10-10 Pa. As reported in Sect. 1, observational data include Mach numbers approximately ranging from 10 to 40 and density ratios from 1 to 10.
The corresponding values for laboratory flows can be essentially expressed by the effective radius range 8 × 10-3 < r0 < 22 × 10-3 m, the Mach number range 7 < M < 18, and the density ratio range 0.85 < η < 5.4. Temperatures, densities and pressures are respectively in the order of ~10 K, ~10-4 Kg m-3, and ~5 Pa. The Reynolds number of the experimental flows is of the order of 104 for the jets emerging from the Mach 10 nozzle, and of the order of (or larger than) 105 for the higher Mach nozzles, while the Peclet Number is Pe ~ 102 − 103. The Knudsen number turns out to be K ~ 10-3 − 10-2. It is interesting to note that, in the case of YSO jets, the values for Re and Pe are huge and K also attains values ~10-2 − 10-3. This confirms that the ideal Euler equations, Eqs. (1)–(3) are a good description of the dynamics of the flows under discussion.
We can now estimate the constants a, b, and c (Eq. (5)) and, given the gas velocities and evolution times, derive the similarity values for YSO jets. In this case, r,ρ, and p correspond to the astrophysical values 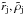 , and
, and 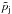 while r1,ρ1, and p1 correspond to the laboratory values of r0,ρj, and pj listed in Table 5. The values for jet flow velocity Vj, on-axis and at nozzle output, are listed in Table 5 as well. The flow velocity is simply derived from the relation
while r1,ρ1, and p1 correspond to the laboratory values of r0,ρj, and pj listed in Table 5. The values for jet flow velocity Vj, on-axis and at nozzle output, are listed in Table 5 as well. The flow velocity is simply derived from the relation 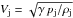 . We recall that the elapsed time tj is the time for the jet head to reach the end of the vessel. The last column also reports the time scale of the jets (sound crossing time over radius).
. We recall that the elapsed time tj is the time for the jet head to reach the end of the vessel. The last column also reports the time scale of the jets (sound crossing time over radius).
The results for the Euler similar, scaled values are listed in Table 6. We see that the values for the jet velocities VES range between 80 and about 140 km s-1 and the scaled times 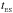 considered from about 400 up to 5000 years. We recall that YSO jets velocities are typically in the range ~100–400 km s-1 and their lifetime lasts ~ 104 − 105 ys. Thus the values for the velocities are close to the actual observed values for slow YSO jets, while the simulated times cover a sizable fraction of the life-span of the astrophysical objects.
considered from about 400 up to 5000 years. We recall that YSO jets velocities are typically in the range ~100–400 km s-1 and their lifetime lasts ~ 104 − 105 ys. Thus the values for the velocities are close to the actual observed values for slow YSO jets, while the simulated times cover a sizable fraction of the life-span of the astrophysical objects.
Euler similar, scaled physical parameters for the laboratory helium jets.
6. Conclusions
The experimental facility and instrumentation have been shown to fit the experimental requirements and to give valid results for the aim they were designed and assembled for. Both experiments and numerical simulations have shown detailed aspects of the head bow shock, its bluntness versus Mach number and the shape of the cocoon as a function of the density ratio. In this sense the use of gases of strong density difference, such as helium and xenon has been very important. We note that both the experiments and the numerical simulations agree well in most cases. Moreover, the Euler similar scaled flows that we reproduced in the laboratory are characterized by velocities that also agree well with YSO jets values. The physical characteristics of simulated jets, i.e. head and jet velocities, bow-shock, and cocoon morphologies that we discuss in the paper are intentionally limited to the ones that can be obtained either by direct measurements or that are derived in the laboratory experiments, and are thus subjects of comparison. These experiments suggest once again that the PLUTO code may be considered a valid tool for HD simulations of astrophysical jets, as a useful tool for further investigations. Physical elements, such as radiative cooling which is important in determining the jet emission details, and magnetic fields which are important in determining the outflow launching, are absent in our investigation. However, we can say that the basic features of the jet dynamics are well described by the HD treatment alone, and it is therefore reasonable to assume that fluid dynamics may explain the major characteristics of the behaviour of YSO gas jets with respect to morphology and collimation.
We are almost at the limits of the experimental instrumentation capabilities. It is difficult to imagine cameras with higher performance in resolution or sensitivity and acquisition time, or to imagine increasing the electron beam characteristics beyond 2 mA without increasing the beam width, or voltage, going into X-ray emission. A significant change could be achieved by using different measurements techniques, like molecular tagging velocimetry or laser interferometry; of course these techniques might be considered radical, long term modifications of the existing setup. Another progress in the facility would be to increase the temperature of the gas jet. The facility now has the advantage of being economically manageable and low-energy, while the major modifications to the whole system needed to heat the gas jet would require a very high cost.
Acknowledgments
The authors wish to thank Andrea Milanese of the LA.S.T. Laboratory (Politecnico di Milano). They also thank the anonymous referee whose careful comments have helped to improve the paper.
References
- Ashkenas, H., & Sherman, F. S. 1966, in Rarefied gas dynamics, ed. J. A. deLeeuw (NY: Academic) [Google Scholar]
- Belan, M., De Ponte, S., & Tordella, D. 2008, Exp. Fluids, 45, 501 [CrossRef] [Google Scholar]
- Belan, M., De Ponte, S., & Tordella, D. 2010, Phys. Rev. E, 82, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Belan, M., De Ponte, S., Tordella, D., et al. 2011, Ap&SS, 336, 9 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Belan, M., Mirzaei, M., De Ponte, S., & Tordella, D. 2012, EPJ Web Conf., 25, 01056 [CrossRef] [EDP Sciences] [Google Scholar]
- Bellan, P. M., You, S., & Hsu, S. C. 2005, Ap&SS, 298, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Bellan, P. M., Livio, M., Kato, et al. 2009, Phys. Plasmas, 16, 4 [CrossRef] [Google Scholar]
- Brown, L. O., & Miller, N. 1957, Trans. Faraday Soc., 53, 748 [CrossRef] [Google Scholar]
- Bülent Yüceil, K., & Volkan Ötügen, M. 2002, Phys. Fluids, 14, 4206 [NASA ADS] [CrossRef] [Google Scholar]
- Bütefisch, K. A., & Vennemann, D. 1974, Prog. Aer. Sci., 15, 217 [CrossRef] [Google Scholar]
- Ciardi, A., Lebedev, S. V., Frank, A., et al. 2009, ApJ, 691, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Falize, É., Michaut, C., & Bouquet, S. 2011, ApJ, 730, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. 2004, ARA&A, 42, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A. 2011, Asymmetric Planetary Nebulae 5 conference, Bowness-on-Windermere, UK, 20–25 June 2010, eds. A. A. Zijlstra, F. Lykou, I. McDonald, & E. Lagadec, Jodrell Bank Centre for Astrophysics [Google Scholar]
- Godfrey, L. E. H., & Shabala, S. S. 2013, ApJ, 767, 12 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Audit, E., & Stehlé, C. 2009, A&A, 497, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granot, J. 2007, Rev. Mex. Astron. Astrophys. (Serie de Conferencias), 27, 140 [Google Scholar]
- Gregory, C. D., Howe, J., Loupias, B., et al. 2009, Ap&SS, 322, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Foster, J. M., Wilde, B. H., et al. 2009, ApJ, 705, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J., 2008, ARA&A, 46, 127 [Google Scholar]
- Kössl, D., & Müller, E. 1988, A&A, 206, 204 [NASA ADS] [Google Scholar]
- Lebedev, S. V., Ampleford, D. J., Ciardi, A., et al. 2004, ApJ, 616, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Lebedev, S. V., Ciardi, A., Ampleford, D. J., et al. 2005, MNRAS, 361, 97 [Google Scholar]
- Love, E. S., Grigsby, C., Lee, L., & Woodling, M. 1959, NASA Tech. rep. TR R-6 [Google Scholar]
- Massaglia, S., Trussoni, E., Bodo, G., Rossi, P., & Ferrari, A. 1992, A&A, 260, 243 [NASA ADS] [Google Scholar]
- Massaglia, S., Bodo, G., & Ferrari, A. 1996, A&A, 307, 997 [NASA ADS] [Google Scholar]
- Micono, M., Bodo, G., Massaglia, S., et al. 2000, A&A 360, 795 [NASA ADS] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Muntz, E. P. 1968, AGARDograph, 132 [Google Scholar]
- Norman, M. L., Winkler, K.-H. A., Smarr, L., & Smith, M. D. 1982, A&A, 113, 285 [NASA ADS] [Google Scholar]
- Reipurth, B., & Bally, J. 2001, ARA&A, 39, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Rus, B., Mocek, T., Prag, A. R., et al. 2002, PRA, 66, 063806 [NASA ADS] [CrossRef] [Google Scholar]
- Ryutov, D., Drake, R. P., Kane, J., et al. 1999, ApJ, 518, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki-Vidal, F., Hall, G. N., Bland, S. N., et al. 2010, Phys. Plasmas, 17, 112708 [NASA ADS] [CrossRef] [Google Scholar]
- Teşileanu, O., Mignone, A., Massaglia, S., & Bacciotti, F. 2012, ApJ, 746, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Tordella, D., Belan, M., Massaglia, S., et al. 2011, NJP, 13, 043011 [NASA ADS] [CrossRef] [Google Scholar]
- Tzeferacos, P., Ferrari, A., Mignone, A., et al. 2009, MNRAS, 400, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Zaman, K. B. M. Q. 1998, Phys. Fluids, 10, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Zaman, K. B. M. Q. 1999, J. Fluid Mech., 383, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., Bodo, G., Rossi, P., et al. 2003, A&A, 402, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Experimental setup. The total vessel length depends on the number of assembled sections. The set of de Laval nozzles used in this work is shown on the left. All the nozzles have the same converging section and throat (radius = 1 mm), whilst the diverging section depends on the Mach number of the design. The output radii rn are 12.0, 35.7, and 60.9 mm. |
| In the text | |
 |
Fig. 2 Output density curve and actual jet width under matched conditions. Upper panel: density and jet sketch at the output of the Mach 10 nozzle. Mid panel: density profiles and jet widths in the near and far fields for an underdense jet. Lower panel: density profiles and jet widths in the near and far fields for an overdense jet. |
| In the text | |
 |
Fig. 3 Set of three slightly underdense jets of He in Xe: from top to bottom, η = 0.85, 0.9, and 0.9, Mach number = 10.0, 13.5, and 18.0. Length is expressed in r0 units (effective or reference jet radius) and time in τ units, i.e sound crossing time over jet radius. The numerical density scale refers to the unperturbed ambient density. |
| In the text | |
 |
Fig. 4 Set of three slightly overdense jets of He in Xe: from top to bottom, η = 1.2, 1.35, and 1.4, Mach number = 11.0, 16.0, and 18.0. |
| In the text | |
 |
Fig. 5 Set of three overdense jets of He: from top to bottom, ambient is air, air, and He; η = 4.4, 4.6, and 5.4; Mach number = 7.0, 14.3, and 17.9. |
| In the text | |
 |
Fig. 6 Simulation of the overdense jet at centre of Fig. 4 (Mach number = 16) obtained by averaged superposition of density maps over a time interval of the order of the experimental image exposure. |
| In the text | |
 |
Fig. 7 Numerical (thin lines) and experimental (thick lines) axial densities for the 3 slightly overdense jets of Fig. 4. Densities are expressed in nondimensional form as density ratios η referred to the unperturbed ambient. The space between vertical dashed lines is a non-measurable zone, see the text, Sect. 4.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


