| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 6 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220854 | |
| Published online | 29 May 2013 | |
Research Note
Using hierarchical octrees in Monte Carlo radiative transfer simulations
1
Sterrenkundig Observatorium, Universiteit Gent,
Krijgslaan 281,
9000
Gent,
Belgium
e-mail:
waad.saftly@ugent.be
2
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
3
National Astronomical Observatories, Chinese Academy of Sciences,
100012
Beijing, PR
China
4
Astronomical Observatory, Volgina 7, 11060
Belgrade,
Serbia
5
Isaac Newton Institute of Chile, Yugoslavia Branch, Volgina 7, 11060
Belgrade,
Serbia
Received: 5 December 2012
Accepted: 3 April 2013
A crucial aspect of 3D Monte Carlo radiative transfer is the choice of the spatial grid used to partition the dusty medium. We critically investigate the use of octree grids in Monte Carlo dust radiative transfer, with two different octree construction algorithms (regular and barycentric subdivision) and three different octree traversal algorithms (top-down, neighbour list, and the bookkeeping method). In general, regular octree grids need higher levels of subdivision compared to the barycentric grids for a fixed maximum cell mass threshold criterion. The total number of grid cells, however, depends on the geometry of the model. Surprisingly, regular octree grid simulations turn out to be 10 to 20% more efficient in run time than the barycentric grid simulations, even for those cases where the latter contain fewer grid cells than the former. Furthermore, we find that storing neighbour lists for each cell in an octree, ordered according to decreasing overlap area, is worth the additional memory and implementation overhead: using neighbour lists can cut down the grid traversal by 20% compared to the traditional top-down method. In conclusion, the combination of a regular node subdivision and the neighbour list method results in the most efficient octree structure for Monte Carlo radiative transfer simulations.
Key words: radiative transfer / methods: numerical
© ESO, 2013
1. Introduction
Cosmic dust is present in and around many astrophysical systems, ranging from planetary and stellar atmospheres to the diffuse interstellar medium in galaxies. Dust grains have a profound effect on the radiation field, as they efficiently scatter, absorb, and re-emit radiation from these sources. Radiative transfer calculations are required if we want to understand the intrinsic properties of dusty objects, or predict the observable properties of artificial systems simulated using hydrodynamical simulations. In the past decade, several codes have been developed that can handle the full dust radiative transfer problem in a general 3D geometry; for a general overview of 3D dust radiative transfer we refer to Steinacker et al. (2013).
Virtually all 3D radiative transfer codes are based on the Monte Carlo technique1 (e.g. Gordon et al. 2001; Juvela & Padoan 2003; Wolf 2003; Jonsson 2006; Pinte et al. 2006; Baes et al. 2011; Robitaille 2011). In Monte Carlo dust radiative transfer simulations, the dusty medium is divided into a large number of tiny grid cells. Each of these cells is typically characterized by a constant dust density, temperature, radiation field, etc. Their size sets the effective resolution of the simulation. On the one hand, it is useful to maximize the number of cells, in order to obtain the highest resolution possible. On the other hand, the memory requirements and run time of the simulation scales as 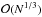 to
to 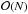 with N the number of grid cells, which puts a limit to this number. The choice of the grid structure is, therefore, a crucial ingredient of a modern 3D radiative transfer simulation. Ideally, the size of the grid cells should be linked to the dust mass, optical depth or temperature of the dusty medium: the cells should be small where the dust density is high or the radiation field shows a large gradient, and they can be bigger where the dust density is low and the radiation field does not change significantly.
with N the number of grid cells, which puts a limit to this number. The choice of the grid structure is, therefore, a crucial ingredient of a modern 3D radiative transfer simulation. Ideally, the size of the grid cells should be linked to the dust mass, optical depth or temperature of the dusty medium: the cells should be small where the dust density is high or the radiation field shows a large gradient, and they can be bigger where the dust density is low and the radiation field does not change significantly.
The most popular candidate for such grid structures are hierarchical octree grids, in which the 3D space is partitioned by recursively subdividing it into eight subcubes. Octrees are widely used in all areas of science and engineering, especially in computer graphics and 3D game engines (Jackins & Tanimoto 1980). In astronomy, they are most popular in N-body and hydrodynamics codes (Barnes & Hut 1986; Hernquist 1987; Hernquist & Katz 1989; Teyssier 2002; Springel 2005). Octree grid structures, or more general hierarchical grid-in-grid structures, have now been implemented in several Monte Carlo dust radiative transfer codes (e.g. Kurosawa & Hillier 2001; Wolf 2003; Harries et al. 2004; Jonsson 2006; Bianchi 2008; Niccolini & Alcolea 2006; Robitaille 2011; Heymann & Siebenmorgen 2012; Lunttila & Juvela 2012), and UV ionization and Lyα transfer codes (e.g. Tasitsiomi 2006; Laursen et al. 2009).
In this Research Note we investigate two different aspects of the use of octree grid structures in 3D Monte Carlo radiative transfer simulations. The first aspect concerns the construction of the grid, and more specifically the way dust cells are subdivided. All radiative transfer codes with octree dust grids subdivide the cells in a regular way, whereas we investigate whether a barycentric subdivision is more efficient. Second, we concentrate on the traversal of photon packages through the dust grid. Most Monte Carlo codes use a simple top-down method to traverse the octree. Other bottom-up octree traversal algorithms have been developed in the field of computer graphics and it remains to be investigated whether these might be more efficient in the context of radiative transfer simulations. In Sect. 2 we present the algorithms proposed for the construction of the octree and the traversal of photon packages through the octree. In Sect. 3 we present three different test models on which we test the different algorithms. In Sect. 4 we present the results of our simulations, and in Sect. 5 we present the conclusion.
2. Octree algorithms
2.1. Construction of the octree grid
We have implemented an octree dust grid structure in the SKIRT Monte Carlo radiative transfer code (Baes et al. 2003, 2011) based on a dust mass threshold, in the sense that each dust cell (i.e. each leaf node in the tree) can contain at most a fraction δmax of the total dust mass in the system. The construction of the octree grid is done as it is in most other radiative transfer codes with octrees (Kurosawa & Hillier 2001; Wolf 2003; Harries et al. 2004; Bianchi 2008) and is very straightforward. We create a list of nodes over which we run a loop. The first node in the list is a cuboidal root node that encloses the entire dusty medium. While running the loop, we test whether each node should be subdivided by calculating the ratio δ = M/Mtot, where M is the estimated dust mass in the node (determined using a Monte Carlo integration) and Mtot is the total dust mass in the system. If δ < δmax there is no subdivision, the node is a leaf node and hence an actual dust cell. On the other hand, if δ > δmax, we partition the node into eight subnodes and append them at the end of the node list. In either case, we subsequently move to the next node in the node list and repeat the same test. This loop is repeated until the entire list of nodes is finished.
2.2. Octree subdivision
Standard octree algorithms subdivide each node by taking the centre of the node as the subdivision point, such that all eight subnodes of a node have the same size (and in general, all nodes corresponding to the same level of subdivision have exactly the same dimensions). We denote this method as regular subdivision. One might wonder whether this is the ideal situation. In a node with a large density gradient, applying a regular subdivision might result in a set of eight subnodes in which nearly all the dust mass is concentrated in only one of the subnodes, which might lead to frequent nested subdivision. An alternative could be to choose the division point of the node such that the mass distribution is divided more or less equally over the eight subnodes. This can be achieved by choosing the barycentre rather than the geometrical centre of the node as the subdivision point. With a barycentric subdivision, one would expect to be able to zoom in faster on high density regions. It is straightforward to see that both the memory penalty and the computational cost are minimal compared to the complete simulation memory requirement and run time.
2.3. Octree traversal
During a Monte Carlo simulation, the life cycle of every photon package implies the calculation of several random straight paths through the dust grid. This essentially comes down to the determination of the ordered list of dust cells that the path intersects and the physical distance covered in each individual cell. As a Monte Carlo simulation typically follows many millions of photon packages, it is obvious that this task should be implemented as efficiently as possible.
The grid traversal is a loop that consists of a repetition of two simple steps. The first step is to determine in which cell the initial path position is located, and the next step is to follow the path to the boundary of the cell while recording the covered distance. While the second step is straightforward, the first step is less so in an octree grid structure. Actually, the traversal of rays in octrees has been a topic of investigation in the computer graphics literature (e.g. Glassner 1984; Amanatides & Woo 1987; Samet 1989, 1990; Agate et al. 1991; Revelles et al. 2000; Frisken & Perry 2002). Loosely based on these methods, we have implemented three different methods to perform octree traversal as appropriate for Monte Carlo radiative transfer simulations.
The most straightforward method to traverse an octree grid is a top-down method (Glassner 1984). The idea of this method is simple: once a photon package hits the boundary of a cell and we have determined the new position (which is now in a yet unidentified cell), we start from the root node and descend the tree. For every node along the tree, we determine in which of its subnodes the new position is located. This loop ends when the node is a leaf node, i.e. an actual dust cell. This top-down method is very easy to implement, and it does not depend on whether the subdivision is regular or barycentric. This algorithm is implemented in most Monte Carlo radiative transfer codes that operate on octree grids (e.g. Kurosawa & Hillier 2001; Bianchi 2008).
An alternative method of traversing an octree makes use of a list of the neighbouring cells of each node. This method was first advocated by Samet (1989, 1990) in the frame of computer graphics ray-tracing. Instead of blindly looking for the cell that contains the position of the photon package once it has traversed a cell wall, we make use of the fact that the yet unknown cell is a neighbour of the previous dust cell. In our implementation, every dust cell contains six different lists (one for each cell wall) with pointers to the neighbouring cells, ordered by decreasing area of overlap. If we know through which wall the photon package has escaped the previous cell, we just have to go down the corresponding list of neighbour cells. This algorithm is straightforward and simple to implement, and again is applicable both to regular and barycentric octree grids. The additional memory usage of this method is usually not a problem: six pointer lists need to be stored for each cell (one list for every cell wall). For typical dust radiative transfer simulations that require the storage of many properties per cell, this is a negligible addition. Moreover, the neighbour lists can be created in a very straightforward way during the construction of the octree grid, with very limited computational overhead. For the computations we discuss in this work, the computational overhead is less than 1 per cent of the simulation time; for realistic simulations, the relative overhead will be even much smaller.
Finally, we explored a third method of traversing an octree grid that is inspired by the work of Frisken & Perry (2002) and which we denote as the bookkeeping method. One of the drawbacks of the top-down method is that, for every passage through a wall, the search for the new cell has to start from the root node. This is unfortunate, as we often know in which branch of the tree the next position will be: indeed each node in the octree has a place-awareness, i.e. the knowledge of its position as a subnode with respect to its sibling nodes. If a transition is internal, i.e. if the path crosses a cell wall that does not leave the parent cell, we know that the next cell is one of its siblings (or its children if the sibling is not a leaf node). A slightly more difficult case occurs when the transition through a wall is not an internal transition. One option could be to start the search then from the root node as in the standard top-down method. An alternative, which we have implemented, is to iteratively go up the tree starting from the current node until the transition is an internal transition, and then iteratively descend the tree until the node is a leaf node. Of the three methods presented, this method is the most complex in terms of implementation. However, it is still very manageable, it implies no memory overhead or additional computations, and it is, again, applicable to regular as well as barycentric octree grids.
3. Test models
To test these algorithms, we have considered three different challenging test models. They were chosen to accommodate a variety of possible geometries that can be encountered in realistic 3D Monte Carlo radiative transfer simulations.
Our first model is an idealized model for a disc galaxy with a three-armed logarithmic spiral structure. This model is completely analytical and is inspired by the models used by Misiriotis et al. (2000) and Schechtman-Rook et al. (2012). Stars in the model galaxy are distributed in two components: a double-exponential disk with a spiral arm perturbation, and a flattened Sérsic bulge. The dust is only distributed in a double-exponential disc; with a spiral perturbation. For the parameters of the stellar and dust distribution, we used typical values applicable for spiral galaxies (Kregel et al. 2002; Hunt et al. 2004; Cortese et al. 2012); for other parameters, we were specifically inspired by the results obtained from radiative transfer fits to nearby edge-on spiral galaxies (Xilouris et al. 1999; Bianchi 2007; Baes et al. 2010) and (MacLachlan et al. 2011). An illustration of the dust density in the central plane of the galaxy is shown on the top left panel of Fig. 1.
 |
Fig. 1 Illustration of the geometry and the octree grid structures for the three test models: the logarithmic spiral galaxy (top row), the AGN torus (middle row), and the galaxy from an SPH simulation (bottom row). In each row, the left column represents a cut through the dust density. For the two galaxy models, this cut corresponds to the xy plane; for the AGN torus model it is a cut through the xz plane. The central and right columns are cuts through the octree grids corresponding to the same planes, and correspond to the regular and barycentric subdivision recipes, respectively. The different shades of gray in the middle and right columns illustrate the density of the cells: darker gray means higher density. |
Statistics of the different models and grids.
Our second test model is a model for the central region of an active galactic nucleus (AGN), and consists of a central, isotropic source surrounded by an optically thick dust torus. It is similar to the AGN torus models presented by Stalevski et al. (2012), in that it consists of a number of compact and optically thick clumps embedded in a smooth interclump medium. Contrary to the approach adopted by Stalevski et al. (2012), where the two-phase clumpy medium was generated in a statistical way by applying a clumpiness algorithm (Boissé 1990; Witt & Gordon 1996; Wolf et al. 1998), we now consider a torus model consisting of a smooth distribution of dust to which we add 4000 individual clumps (as in Bianchi 2008). An illustration of the dust density in the xz plane of the model is shown on the central left panel of Fig. 1.
The last test model we use is a completely numerical spiral galaxy model created by means of a hydrodynamic simulation. The galaxy model we consider is the 1 Gyr snapshot of model run number 6 from Rahimi & Kawata (2012), which represents an M33-sized late-type spiral galaxy. It was run using the N-body/SPH code GCD+ (Kawata et al. 2012) in a fixed dark matter halo, and includes self-gravity, hydrodynamics, radiative cooling, star formation, supernova feedback, metal enrichment and metal diffusion. The snapshot is characterized by 410 372 stellar particles and 189 628 gas particles. For the calculation of the dust mass density distribution, we follow the approach of Jonsson et al. (2010) and assume that, at every position in the galaxy, a fixed fraction of the metal content is locked in dust grains. To obtain the dust density at a given position, we interpolate the metal density over the SPH gas particles and use a metal depletion in the dust grains of 40% (Dwek 1998). The resulting dust mass density in the equatorial plane of the galaxy can be seen in the bottom left panel of Fig. 1. The holes and bubbles caused by the feedback from supernovae and stellar winds are clearly visible.
4. Results
In this section we compare the statistics on the number of cells in the different models, and the efficiency of the path calculations within the different grids. We stress that the different grid structures for the six models (i.e. three geometries, each with regular and barycentric octree subdivision) have been constructed based on exactly the same criterion (δmax = 10-6).
Intuitively, one would expect that the barycentric subdivision is more efficient in following the mass distribution. When a node is subdivided with the barycentre as the subdivision point, the mass of the parent node is redistributed more or less equally among the eight child subnodes. This means that the subdivision needs to be repeated less often in the barycentric case compared to the regular case. This is confirmed in Row 5 of Table 1, which shows that the average level of a cell in the barycentric grids is about 7.6, whereas it is about 8.6 for the regular grids.
Surprisingly at first sight, this does not systematically lead to a smaller total number of cells in the barycentric grids compared to the equivalent regular octree grids (Row 4 of Table 1). For the spiral galaxy model, the smoothest of the three test geometries, the barycentric grid contains some 3% fewer cells than the regular grid. For the AGN torus and the SPH galaxy models, with their strong density gradients, the barycentric grids contains more cells than the regular grids, with differences of 11% and 2% respectively.
To understand this, consider a subnode with δ = 10 δmax and a strong density gradient within the cell. In the barycentric octree, this cell will be subdivided and each of the subnodes will contain approximately δ ≈ 1.25 δmax, which means they will all be subdivided again, resulting in 64 cells in total. In a regular grid, it is possible that one subnode contains most of the mass and the remaining seven subnodes do not need to subdivided again. Most probably, several (but not all) of the children of this one subnode will have to subdivided again. This could lead to a set of leaf cells with, on average, a deeper level of subdivision, but the total number of cells could be either less or more compared to the barycentric grid, subtly depending on the distribution of the density within the cell.
The main goal of this Research Note is to find the most efficient algorithm for the grid construction and traversal. We tested the efficiency by doing accurate timings of the Monte Carlo routine, for each of the 18 models in our test suite (i.e. for the three geometries, the two grid subdivision methods, and the three grid traversal algorithms). Obtaining precise and repeatable timings is trickier than it might seem, as even in single-thread simulations modern hardware features can complicate matters. We performed our timing tests on a server installed in a temperature-controlled room, in a single execution thread on otherwise idle computers. Numbering the 18 tests from 1 to 18, we ran the sequence 1–18, 1–18, 18–1. The timing variations between the three runs turned out to be less than 2 s for each simulation, well below the differences between the various methods.
The average run times for each of the different runs2 can be found in the top three rows of Table 1. Ignoring intricacies such as loop overhead, the run time of each simulation can schematically be written as ![\begin{eqnarray} t_{\text{run}} = N_{\text{pp}} \langle N_{\text{path}}\rangle \left[ \langle t_{\text{launch}}\rangle + \langle N_{\text{cross}}\rangle \Bigl( \langle t_{\text{id}}\rangle + \langle t_{\text{cross}} \rangle \Bigr) \right] , \end{eqnarray}](/articles/aa/full_html/2013/06/aa20854-12/aa20854-12-eq16.png) (1)where Npp is the total number of photon packages in the simulation, ⟨ Npath ⟩ is the average number of random straight paths in a photon package, ⟨ tlaunch ⟩ is the average time needed to generate the starting location and orientation of a path, ⟨ Ncross ⟩ is the average number of cells crossed by a path, ⟨ tid ⟩ is the average time necessary to identify the next cell along the path, and ⟨ tcross ⟩ is the average time necessary to cross this cell (i.e. to find the exit point and the covered pathlength within the cell). Of these six factors, Npp is the same for all runs, and ⟨ tcross ⟩ is nearly identical (tiny differences can occur because of cache misses). The quantities ⟨ Npath ⟩ and ⟨ tlaunch ⟩ are similar for all runs corresponding to a given test model. Furthermore, ⟨ tlaunch ⟩ is expected to be small compared to the grid traversal, which was indeed confirmed in separate timing experiments. For a fixed geometry, the differences in run time are therefore dominated by differences in ⟨ Ncross ⟩ and ⟨ tid ⟩, where the former depends only on the grid subdivision method (regular or barycentric), and the latter depends on both the grid subdivision method and the grid traversal method.
(1)where Npp is the total number of photon packages in the simulation, ⟨ Npath ⟩ is the average number of random straight paths in a photon package, ⟨ tlaunch ⟩ is the average time needed to generate the starting location and orientation of a path, ⟨ Ncross ⟩ is the average number of cells crossed by a path, ⟨ tid ⟩ is the average time necessary to identify the next cell along the path, and ⟨ tcross ⟩ is the average time necessary to cross this cell (i.e. to find the exit point and the covered pathlength within the cell). Of these six factors, Npp is the same for all runs, and ⟨ tcross ⟩ is nearly identical (tiny differences can occur because of cache misses). The quantities ⟨ Npath ⟩ and ⟨ tlaunch ⟩ are similar for all runs corresponding to a given test model. Furthermore, ⟨ tlaunch ⟩ is expected to be small compared to the grid traversal, which was indeed confirmed in separate timing experiments. For a fixed geometry, the differences in run time are therefore dominated by differences in ⟨ Ncross ⟩ and ⟨ tid ⟩, where the former depends only on the grid subdivision method (regular or barycentric), and the latter depends on both the grid subdivision method and the grid traversal method.
The first clear result that we find from a comparison of the run times listed in Table 1, is that for all simulations in our suite, the neighbour list algorithm is the fastest method to traverse photon packages through the dust grid. It is faster than the other two methods, which are almost equally efficient, by about 20%. For the neighbour list method, ⟨ tid ⟩ is proportional to the number of neighbouring dust cells that needs to be tested every time a cell is crossed. In this respect, it is important to make the distinction between the average number of neighbours of each cell wall (Row 9 in Table 1), the average number of neighbours of every wall crossed (Row 10) and the number of neighbours that need to be tested for each crossing (Row 11). These statistics turn out to be substantially different, because some cells are crossed more often than others and because neighbouring cells with the largest overlap area are tested first in the neighbour search algorithm. The ordering of the neighbour list by overlapping surface area makes the neighbour list algorithm extremely efficient.
Another remarkable result is that simulations with a barycentric grid are always slower than the corresponding simulations with a regular grid, even if the number of cells in the barycentric grid is smaller than in the regular grid. At first sight, this is surprising. Consider, for example, the top-down method, where ⟨ tid ⟩ is proportional to the average level of every cell crossed. As the average level of each cell in a barycentric grid is lower than in a regular grid (Rows 5 and 6 in Table 1), one would expect the barycentric grid to be more efficient than the regular grid. However, the difference in ⟨ Ncross ⟩, i.e. the average number of cells crossed per path, means that the opposite is true. Row 8 of Table 1 shows that ⟨ Ncross ⟩ is indeed systematically larger for the barycentric octrees compared to the corresponding regular octrees. The reason for the difference in ⟨ Ncross ⟩ (and so in efficiency) is geometrical in nature. By construction, barycentric grids are more irregular in structure, with more neighbours per cell wall. In a regular grid, every cell has, on average, only 1.03 neighbours per wall, whereas the barycentric grid cells have, on average, 1.86 neighbours per wall. Having more neighbours and a more irregular distribution also leads to shorter paths crossed per cell and so more cells along each path.
5. Discussion and conclusion
In this Research Note, we have critically investigated the use of hierarchical octree grids to partition a dusty medium in the frame of 3D dust radiative transfer codes, but the results are equally applicable to other Monte Carlo transport problems. Octree grids can refine the gridding in higher density regions without the need to create undesirable dust cells in low density regions. We have implemented a flexible octree structure in the 3D Monte Carlo code SKIRT (Baes et al. 2003, 2011), which allows for either a regular or a barycentric iterative subdivision of the cells. We implemented two alternative methods for octree traversal (neighbour list search and bookkeeping), and we compared them with a more straightforward top-down method. We ran simulations on three representative astrophysical models (spiral galaxy model, clumpy AGN torus, and galaxy from SPH simulation) to test the efficiency of the octree construction types and the traversal methods in typical Monte Carlo radiative transfer environments.
Our main conclusions are the following:
-
1.
A barycentric subdivision leads to a lower average level ofsubdivision compared to regular subdivision. This, however,does not directly imply that barycentric octree grids containfewer dust cells than the corresponding regular grids.
-
2.
The neighbour list method is consistently the most efficient way to calculate paths through an octree, with a 20% advantage compared to the other two methods. The efficiency of the neighbour list method is achieved in part by ordering the neighbour lists according to decreasing overlap area.
-
3.
Octree traversal is less efficient in barycentric octrees than in the corresponding regular octrees in all cases, even for simulations in which the regular grid contains more grid cells. The reason is the average number of grid cells crossed by a path, which is significantly larger in barycentric grids compared to the corresponding regular octree grids.
Based on the above, we conclude that, while they are designed to follow the mass distribution more closely, barycentric octree grids are less efficient than regular octree grids, and we strongly recommend the neighbour list method as the preferred method to traverse octrees in the frame of 3D radiative transfer simulations.
Taking a step back, the underlying goal of this research is to find better ways for partitioning a dusty medium into cells in the context of a 3D Monte Carlo RT simulation. We have considered a criterion based on the mass in each cell. Is this the best possible criterion? One could consider an alternative criterion based on the density gradient within each cell. This may be particularly interesting for a density distribution with strong gradients or sharp boundaries such as the AGN torus model, where the barycentric grid subdivision results in large elongated grid cells in regions with a sharp boundary (see Fig. 1). Furthermore, for radiative transfer simulations including thermal emission, the ideal grid depends not only on the dust density, but also on the mean intensity of the radiation field, which can only be determined through the radiative transfer simulation itself. Possible ways to deal with this include using knowledge of the source function when constructing the dust grid (Stamatellos & Whitworth 2005), or refining the grid structure based on low-resolution pre-calculations (Niccolini & Alcolea 2006). The most general approach is probably to use an iterative scheme for the determination of the grid: start with an initial grid structure derived from the dust density field (based on total mass and/or density gradient), determine the radiation field in every cell using the radiative transfer simulation, and iteratively refine/redetermine the grid based on the properties of the cell-to-cell variance of the radiation field. This is beyond the scope of the present Research Note and may be investigated in future work.
Monte Carlo techniques have been applied to different 3D transport problems, including neutron, neutrino, UV ionizing radiation, and Lyα radiation transport (e.g. Ciardi et al. 2001; Wood et al. 2004; Verhamme et al. 2006; Tasitsiomi 2006; Laursen et al. 2009; Abdikamalov et al. 2012). The focus of this Research Note is on dust radiative transfer, but the results are equally applicable to other Monte Carlo transport problems.
Octree construction times are not considered in this table. In the current SKIRT implementation (which was not optimized for octree construction, as this needs to be done only once for each simulation), the octree construction time is a few minutes at most (depending on the complexity of the dust density field), whereas a typical full-scale radiative transfer simulation can last several hours. In other applications where the efficiency of the octree construction is important, more advanced tree construction algorithms can be applied (Sundar et al. 2008; Burstedde et al. 2011).
Acknowledgments
We thank the referee for his/her constructive referee report that improved the content and presentation of this Research Note. W.S. acknowledges the support of Al-Baath University and The Ministry of High Education in Syria in the form of a research grant. This work fits in the CHARM framework (Contemporary physical challenges in Heliospheric and AstRophysical Models), a phase VII Interuniversity Attraction Pole (IAP) programme organised by BELSPO, the BELgian federal Science Policy Office. M.S. acknowledges the support of the Ministry of Education, Science and Technological Development of the Republic of Serbia through the projects “Astrophysical Spectroscopy of Extragalactic Objects” (176001) and “Gravitation and the Large Scale Structure of the Universe” (176003).
References
- Abdikamalov, E., Burrows, A., Ott, C. D., et al. 2012, ApJ, 755, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Agate, M., Grimsdale, R. L., & Lister, P. F. 1991, in Advances in Computer Graphics Hardware IV, Eurographics’89 Workshop, (London, UK: Springer-Verlag), 61 [Google Scholar]
- Amanatides, J., & Woo, A. 1987, in Eurographics, 87, 3 [Google Scholar]
- Baes, M., Davies, J. I., Dejonghe, H., et al. 2003, MNRAS, 343, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Fritz, J., Gadotti, D. A., et al. 2010, A&A, 518, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baes, M., Verstappen, J., De Looze, I., et al. 2011, ApJS, 196, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S. 2007, A&A, 471, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S. 2008, A&A, 490, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissé, P. 1990, A&A, 228, 483 [NASA ADS] [Google Scholar]
- Burstedde, C., Wilcox, L. C., & Ghattas, O. 2011, SIAM J. Sci. Comput., 33, 1103 [CrossRef] [MathSciNet] [Google Scholar]
- Ciardi, B., Ferrara, A., Marri, S., & Raimondo, G. 2001, MNRAS, 324, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Ciesla, L., Boselli, A., et al. 2012, A&A, 540, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Frisken, S. F., & Perry, R. N. 2002, J. Graphics Tools, 7, 2002 [Google Scholar]
- Glassner, A. S. 1984, IEEE Comput. Graph. Appl., 4, 15 [Google Scholar]
- Gordon, K. D., Misselt, K. A., Witt, A. N., & Clayton, G. C. 2001, ApJ, 551, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J., Monnier, J. D., Symington, N. H., & Kurosawa, R. 2004, MNRAS, 350, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1987, ApJS, 64, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., & Katz, N. 1989, ApJS, 70, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Heymann, F., & Siebenmorgen, R. 2012, ApJ, 751, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Pierini, D., & Giovanardi, C. 2004, A&A, 414, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackins, C. L., & Tanimoto, S. L. 1980, Computer Graphics and Image Processing, 14, 249 [CrossRef] [Google Scholar]
- Jonsson, P. 2006, MNRAS, 372, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jonsson, P., Groves, B. A., & Cox, T. J. 2010, MNRAS, 403, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M., & Padoan, P. 2003, A&A, 397, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawata, D., Okamoto, T., Gibson, B. K., Barnes, D. J., & Cen, R. 2012, MNRAS, 115 [Google Scholar]
- Kregel, M., van der Kruit, P. C., & de Grijs, R. 2002, MNRAS, 334, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., & Hillier, D. J. 2001, A&A, 379, 336 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laursen, P., Razoumov, A. O., & Sommer-Larsen, J. 2009, ApJ, 696, 853 [Google Scholar]
- Lunttila, T., & Juvela, M. 2012, A&A, 544, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacLachlan, J. M., Matthews, L. D., Wood, K., & Gallagher, J. S. 2011, ApJ, 741, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Misiriotis, A., Kylafis, N. D., Papamastorakis, J., & Xilouris, E. M. 2000, A&A, 353, 117 [NASA ADS] [Google Scholar]
- Niccolini, G., & Alcolea, J. 2006, A&A, 456, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahimi, A., & Kawata, D. 2012, MNRAS, 422, 2609 [NASA ADS] [CrossRef] [Google Scholar]
- Revelles, J., Ureña, C., & Lastra, M. 2000, J. of WSCG, 8, 212 [Google Scholar]
- Robitaille, T. P. 2011, A&A, 536, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samet, H. 1989, Computers and Graphics, 13, 445 [CrossRef] [Google Scholar]
- Samet, H. 1990, Applications of spatial data structures: Computer graphics, image processing, and GIS (Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc.) [Google Scholar]
- Schechtman-Rook, A., Bershady, M. A., & Wood, K. 2012, ApJ, 746, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Fritz, J., Baes, M., Nakos, T., & Popović, L. Č. 2012, MNRAS, 420, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2005, A&A, 439, 153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinacker, J., Baes, M., & Gordon, K. D. 2013, ARA&A, 51, in press [Google Scholar]
- Sundar, H., Sampath, R. S., & Biros, G. 2008, SIAM J. Sci. Comput., 30, 2675 [CrossRef] [Google Scholar]
- Tasitsiomi, A. 2006, ApJ, 645, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Schaerer, D., & Maselli, A. 2006, A&A, 460, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witt, A. N., & Gordon, K. D. 1996, ApJ, 463, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S. 2003, Comp. Phys. Comm., 150, 99 [Google Scholar]
- Wolf, S., Fischer, O., & Pfau, W. 1998, A&A, 340, 103 [NASA ADS] [Google Scholar]
- Wood, K., Mathis, J. S., & Ercolano, B. 2004, MNRAS, 348, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Xilouris, E. M., Byun, Y. I., Kylafis, N. D., Paleologou, E. V., & Papamastorakis, J. 1999, A&A, 344, 868 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Illustration of the geometry and the octree grid structures for the three test models: the logarithmic spiral galaxy (top row), the AGN torus (middle row), and the galaxy from an SPH simulation (bottom row). In each row, the left column represents a cut through the dust density. For the two galaxy models, this cut corresponds to the xy plane; for the AGN torus model it is a cut through the xz plane. The central and right columns are cuts through the octree grids corresponding to the same planes, and correspond to the regular and barycentric subdivision recipes, respectively. The different shades of gray in the middle and right columns illustrate the density of the cells: darker gray means higher density. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


