| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220547 | |
| Published online | 07 June 2013 | |
Non-perturbative effect of rotation on dipolar mixed modes in red giant stars
1 Institut d’Astrophysique et de Géophysique de l’Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
2 Observatoire de Paris, LESIA, CNRS UMR 8109, 92195 Meudon, France
e-mail: rhita-maria.ouazzani@obspm.fr
3 Georg-August-Universität Göttingen, Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 12 October 2012
Accepted: 13 March 2013
Context. The space missions CoRoT and Kepler provide high-quality data that allow us to test the transport of angular momentum in stars by the seismic determination of the internal rotation profile.
Aims. Our aim is to test the validity of seismic diagnostics for red giant rotation that are based on a perturbative method and to investigate the oscillation spectra when the validity does not hold.
Methods. We use a non-perturbative approach implemented in the ACOR code that accounts for the effect of rotation on pulsations and solves the pulsation eigenproblem directly for dipolar oscillation modes.
Results. We find that the limit of the perturbation to first order can be expressed in terms of the rotational splitting compared to the frequency separation between consecutive dipolar modes. Above this limit, non-perturbative computations are necessary, but only one term in the spectral expansion of modes is sufficient as long as the core rotation rate remains significantly smaller than the pulsation frequencies. Each family of modes with different azimuthal symmetry, m, has to be considered separately. In particular, in case of rapid core rotation, the density of the spectrum differs significantly from one m-family of modes to another, so that the differences between the period spacings associated with each m-family can constitute a promising guideline toward a proper seismic diagnostic for rotation.
Key words: asteroseismology / stars: interiors / stars: solar-type / stars: oscillations / stars: rotation / stars: low-mass
© ESO, 2013
1. Introduction
Seismic measurements of rotation profiles inside the Sun as well as stars provide tight constraints on models of transport of angular momentum (Pinsonneault et al. 1989; Zahn 1992; Zahn et al. 1997; Talon & Charbonnel 2008, and references therein). In particular, stars in late stages of evolution, due to the highly condensed core, oscillate with non-radial modes that have a mixed character: they behave as p modes in the envelope and as g modes in the core. These modes, also known as mixed modes, are of particular interest for the determination of the rotation profile throughout the star, as they carry the signature of the star’s innermost layers and are detectable at the surface. The CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010) spacecrafts have dramatically improved the quality of the available asteroseismic data. Several recent studies reported the detection of mixed modes that are split by rotation in a subgiant (Deheuvels et al. 2012) and in several red giants (Beck et al. 2012; Mosser et al. 2012b,a) observed with Kepler. A large number of these stars exhibit frequency spectra that show a quite simple structure where symmetric patterns around axisymmetric modes are easily identified. They are interpreted as multiplets of modes split by rotation. The rotational splittings, i.e. the frequency spacing related to the lift of degeneracy caused by rotation, is then used to determine the core rotation. The values of the corresponding splittings are quite small and the use of the lowest order approximation to derive the splittings from stellar models can be justified. Such studies have led to the determination of unexpectedly low central rotation frequencies (of few hundreds of nHz). These results are in strong disagreement with the core rotation frequencies predicted by evolutionary models, which are of the order of few dozens of μHz (Eggenberger et al. 2012; Marques et al. 2013). They show that the transport processes currently included in stellar models are not able to spin down the core of red giant stars enough to explain the slowly core-rotating red giants. On the other hand, a large set of red giant stars shows complex frequency spectra (Mosser et al. 2012a), in particular with non-symmetric multiplets and therefore are likely rotating fast. Their rotation must then be investigated with non-perturbative methods.
In this context, we first report on the relevance of using a first-order approach for the inference of rotation from seismic spectra of red giant stars with slowly to rapidly rotating cores. When not relevant, we adopt the non-perturbative approach to shed light on the behaviour of splitted mixed modes in the spectra of red giants.
2. Theoretical frequency spectra for red giants
 |
Fig. 1 Pulsation frequencies in the inertial frame ν (in μHz) versus core rotation frequency Ωc/2π (in μHz) for dipolar multiplets. Red curves refer to m = − 1 (prograde) modes, green curves to m = 0 modes (axis-symmetric), and blue curves to m = 1 (retrograde) modes, for central rotation frequency ranging from 0 to 100 μHz. |
This work is based on the study of a model, (model M1with mass 1.3 M⊙ and radius 3.6 R⊙) at the bottom of the red giant branch. The stellar model is computed with the CESTAM code (Code d’Évolution Stellaire, avec Transport, Adaptatif et Modulaire, Marques et al. 2013). Transport of angular momentum induced by rotation according to Zahn (1992) is included. The central rotation rate in this model is Ωc/2π ≃ 180 μHz, while the surface convective region rotates at a rate of 1 μHz. The distortion of the model due to the centrifugal force can be neglected everywhere in red giant stars. For the model M1, scaling laws (Kjeldsen & Bedding 1995) give a frequency of maximum power around νmax = 289 μHz and a large separation of Δν = 23 μHz. We then compute frequencies ranging between νmax ± 2Δν. In this frequency range, the impact of the Coriolis force remains small except in the very inner layers of the star, where it can significantly affect the modes. In order to investigate the effect of core rotation on the frequency spectrum, we compute sets of frequencies for model M1 for a sequence of rotation profiles. This sequence is obtained by dividing the whole rotation profile given by CESTAM for model M1 by constant factors. The oscillation frequencies are calculated by the non-perturbative pulsation code ACOR (Adiabatic Code of Oscillations including Rotation, Ouazzani et al. 2012). The eigenmodes are obtained as a result of the coupling of spherical harmonics. In what follows, taking M coupling terms means expansion on the ℓ = 1,3,...,2M + 1 spherical harmonics for the scalars and the poloidal velocity component and ℓ = 2,4,...,2M + 2 for the toroidal velocity component.
Figure 1 shows the frequencies of several dipolar (ℓ = 1) multiplets with increasing rotation frequency, computed using one coupling term (M = 1) in the spectral expansion. Starting at a low rotation rate, prograde (m = − 1) modes are shifted towards higher frequencies in the inertial frame due to the combined action of the Doppler effect and the Coriolis force. In contrast, retrograde (m = + 1) modes are shifted towards lower frequencies. Crossings between modes of different symmetry occur approximately at Ωc/2π ≳ 8 μHz (for model M1). As a result, for core rotation frequencies above 8 μHz, modes of different m are no longer gathered by original multiplets, i.e. triplets of modes which have the same degenerate frequency without rotation.
The choice of M = 1 coupling term in the spectral expansion is indeed sufficient for most of the rotation profiles investigated here. This is illustrated in Fig. 2, which shows the impact of the number of spherical harmonics used in the eigenmode expansion. Figure 2 present the results of non-perturbative calculations using three coupling terms (M = 3). Most modes are clearly dominated by their ℓ = 1 component (Fig. 2, top). Figure 2 (bottom) shows that the frequency difference between calculations including one and three spherical harmonics is smaller then the frequency difference between two consecutive mixed modes (for Ωc/2π < 100 μHz by two orders of magnitude). From now on, we adopt M = 1.
 |
Fig. 2 Top: ratio between the contributions to kinetic energy of the ℓ = 3 component and the ℓ = 1 component of a dominated ℓ = 1 mode. Bottom: difference between the pulsation frequencies computed with three coupling terms (M = 3) and with one coupling term (M = 1), divided by the frequency separation between two consecutive mixed modes. Computed for the triplet indicated in thick lines in Fig. 1. |
The trapping of modes essentially depends on their frequency (see, for instance, Unno et al. 1989). As seen in Fig. 1, when Ωc increases, so does the frequency difference between the three members of a triplet. The trapping of these members can be significantly different, to such an extent that they end up with very different p-g natures. This is illustrated in Fig. 3, where the kinetic energy corresponding to modes of different m around νmax is plotted. It gives an indication of the p-g nature of modes: the p-dominated modes (referred as p-m modes) correspond to the minima of energy, while the g-dominated ones (g-m modes) are associated with the maxima. The three modes circled in black belong to the same original multiplet and show different p-g natures. The prograde and the retrograde modes are g-m modes, while the m = 0 mode is a p-m mode. This change of nature induced by rotation, which depends on the azimuthal order, can also be characterized by the number of nodes in the p-mode cavity (np) and in the g-mode cavity (ng), calculated according to the Cowling approximation (Cowling 1941). As shown in Fig. 3, the np and ng values of the members of an original triplet are modified differently. These gains (for m = 0,1 modes) or losses (for m = − 1 modes) of nodes occur during gravito-acoustic avoided crossings. When the rotation rate increases and the frequencies of two modes of same symmetry become very close, they avoid crossing each other and they exchange natures. These avoided crossings need to be taken into account all the more because they mainly affect the p-m modes that are the most likely to be observed. Therefore, modes of different azimuthal order m probe the stellar interior differently. Even if they belong to the same triplet with radial order n and degree ℓ, they can be of very different nature. Therefore using the rotational splitting δωn,ℓ = (ωn,ℓ,m − ωn,ℓ, − m)/2m to determine the rotation rate is questionable for red giants.
3. Slowly to moderately core rotating red giants
For models with Ωc/2π ≤ 8 μHz (see Fig. 1), the frequencies behave linearly with respect to Ωc. In this range, the sectorial modes (ℓ = | m |) are symmetrically distributed around the axisymmetric modes and have the same radial order.
 |
Fig. 3 For a central rotation frequency of 20 μHz, kinetic energy of modes around a p-m mode as a function of the mode frequency. The three modes circled in black belong to the same original triplet. Inside the parentheses are the number of nodes in the p cavity and in the g cavity. |
In this case, a first-order perturbation approach approximates well the effects of rotation on the mode frequencies. The pulsation ωn,ℓ,m is then given by 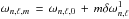 (Cowling & Newing 1949; Ledoux 1949), where the first-order rotational splitting
(Cowling & Newing 1949; Ledoux 1949), where the first-order rotational splitting 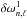 is expressed as a weighted measure of the star rotation rate:
is expressed as a weighted measure of the star rotation rate: 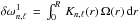 , where Kn,ℓ(r) are the rotational kernels of the modes. They depend on the equilibrium structure and on the eigenfunctions of the unperturbed modes (see e.g. Goupil 2009, and references therein). This formulation relies on two main assumptions. First, only the Coriolis force is significant and accounting for its contribution to order O(Ω/ωn,ℓ) is enough. Second, it is derived from a variational principle (see e.g. Lynden-Bell & Ostriker 1967), which requires that the eigenfunction of the mode perturbed by rotation is close to the eigenfunction of the corresponding unperturbed mode. This is the case for model M1 for Ωc/2π < 8 μHz.
, where Kn,ℓ(r) are the rotational kernels of the modes. They depend on the equilibrium structure and on the eigenfunctions of the unperturbed modes (see e.g. Goupil 2009, and references therein). This formulation relies on two main assumptions. First, only the Coriolis force is significant and accounting for its contribution to order O(Ω/ωn,ℓ) is enough. Second, it is derived from a variational principle (see e.g. Lynden-Bell & Ostriker 1967), which requires that the eigenfunction of the mode perturbed by rotation is close to the eigenfunction of the corresponding unperturbed mode. This is the case for model M1 for Ωc/2π < 8 μHz.
Between 8 and 20 μHz (Fig. 1), the mode frequencies seem to behave linearly with Ωc, but are no longer gathered by original multiplets. Figure 4 (top) displays the apparent rotational splittings, taking half the difference between the closest modes of opposite azimuthal order m = ± 1. The values taken by the apparent rotational splittings range from few hundreds nHz to 2 μHz. This is of the order of the splittings measured in observed spectra. Because the apparent multiplets occur by “accident”, the curve in Fig. 4 (top) does not, and usually cannot, follow the particular “V” pattern around the p-m modes as observed for some slowly rotating red giants (see for observations Beck et al. 2012; Mosser et al. 2012b). This V pattern has the same origin as the modulation seen for mode inertia (Goupil et al. 2013) that is due to the trapping of modes (see Dziembowski et al. 2001; Dupret et al. 2009). The “V” pattern can then constitute a strong indication that the selection of multiplet has been done correctly in observed spectra. Figure 3 confirms that modes which belong to the same original multiplet (circled in black) are found in different apparent multiplets, and show quite different p-g natures. Figure 4 (bottom) compares the original splittings, i.e. half the differences between frequencies of modes from the same original triplet with opposite m, with the splittings given by the first-order approach. The g-m modes (e.g. at 277 μHz and 303 μHz) have the largest splittings. For such modes, both computations give very close results (with a discrepancy of ~4%). The p-m modes (e.g. at 290 μHz and 315 μHz) have the smallest splittings and show the expected V shape variation. For these modes, the discrepancies can reach 30%. This is due to the trapping of these modes, which differs from one m to the other. We note that original splittings including three terms (M = 3) in the non-perturbative calculations give relative differences lower than 10-6 when compared with results of computations using two 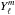 (Fig. 2).
(Fig. 2).
 |
Fig. 4 For the model M1 and a central rotation frequency of 20 μHz, Top: spacing between two closest modes of opposite azimuthal order m = ± 1, i.e. apparent rotational splitting. Bottom: spacing between prograde and the retrograde modes which belong to the same original multiplet (grey, crosses) and splittings computed with the first-order perturbative method (green, plus signs). |
Therefore, for a rotation between 8 and 20 μHz, the fact that the multiplets are correctly selected can be assumed if the splitting given by apparent triplets do follow the V pattern. If so, the first-order approach provides an order of magnitude estimate of the core rotation rate, but non-perturbative modelling is required for accurate quantitative conclusions on the rotational profile from p-m modes.
4. Rapidly core rotating red giants
For Ω > 20 μHz, the mode frequencies no longer behave linearly with the rotation rate (see Fig. 1). This is due not only to higher order effects that come into play, but also to the trapping of modes that is modified by rotation. Modes which belong to the same original multiplet do not have the same radial distribution. Under these circumstances, the notion of rotational splitting as defined by 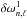 is no longer relevant, and cannot be simply related to the rotation profile. Figure 5 (top) shows the kinetic energy of pulsating modes for a core rotation rate of 140 μHz. The large separation, as measured by the difference between consecutive p-m modes with minimum kinetic energies, is conserved. The higher kinetic energy of prograde modes indicates that they are more of g nature than retrograde or axisymmetric ones. This is due to the shift in frequency induced by rotation that brings, in the same frequency range, modes which belong to very different parts of the zero rotation spectrum (see Fig. 1).
is no longer relevant, and cannot be simply related to the rotation profile. Figure 5 (top) shows the kinetic energy of pulsating modes for a core rotation rate of 140 μHz. The large separation, as measured by the difference between consecutive p-m modes with minimum kinetic energies, is conserved. The higher kinetic energy of prograde modes indicates that they are more of g nature than retrograde or axisymmetric ones. This is due to the shift in frequency induced by rotation that brings, in the same frequency range, modes which belong to very different parts of the zero rotation spectrum (see Fig. 1).
Figure 5 (top) shows that, in the same range of frequency, there are more m = − 1 modes than m = 0 modes, and in turn, there are more m = 0 modes than m = + 1 ones. In order to highlight this difference in distribution, the period spacings are plotted for each m value in Fig. 5 (bottom). In this diagram, the families of modes of different azimuthal orders clearly show different values of period spacing, ranging from the lowest for the prograde modes to the highest for the retrograde ones. We note that this phenomenon appears only for a rotation high enough that the distributions of the three m-families of modes become clearly different (Ωc ~ 100 μHz for model M1). If one is able to measure three different values of period spacings in a observed spectrum, one is able to identify the values of the azimuthal order. Moreover, based on our study of synthetic spectra, we find that the differences between the values of period spacings increase with Ωc and can therefore constitute a guideline toward a constraint on the rotation profile.
5. Discussions and conclusions
 |
Fig. 5 For a central rotation frequency of 140 μHz, top: pulsation modes’ kinetic energy with respect to their frequency. Bottom: period spacing with respect to the pulsation frequency. |
Some observed spectra of red giant stars show structures with nearly symmetric spacings around axisymmetric modes. For this kind of spectra, we found that one can figure out if these apparent multiplets correspond to the original splittings by plotting the apparent splittings as a function of the axisymmetric modes’ frequencies. If the resulting curve follows the V pattern, then it is reasonable to assume that the triplets are correctly selected, and quantitative information on rotation can be derived from the observed splittings. This corresponds to a low-rotation regime, when the splitting is smaller than the frequency spacing between two consecutive modes of same m, i.e. for Ωc/(2π)/(ΔP/P2) ≲ 2.
If the apparent splittings do not follow the V pattern, the triplets overlap. The star is therefore located in the regime of moderate rotation. The frequency differences between the original triplet members are large enough that the trapping properties differ from one member to another. However, if it is still possible to select correctly the original triplets (as done in Mosser et al. 2012a), the first-order approach could be used for a first guess of the core rotation rate. Non-perturbative calculations are nevertheless required for a precise determination, particularly because of the avoided crossings that p-m modes undergo. This rotation regime corresponds to values Ωc/(2π)/(ΔP/P2) between two and five.
Finally, some observed spectra of red giants do not show any regular or close-to-regular structures. We expect these spectra to correspond to rapid rotators. In this case, modes of different azimuthal orders have a very different nature. The concept of rotational splitting of modes with the same radial distribution and different m is no longer relevant, and one should consider separately sub-spectra associated with each value of m. Provided that the rotation is high enough to give rise to clearly different distributions with respect to m, the differences between the period spacings associated with m allows the azimuthal order to be identified, thereby offering the promising opportunity of deriving a proper seismic diagnostic. That corresponds to the very rapid rotation case, i.e. for Ωc/(2π)/(ΔP/P2) ≳ 20. An intermediate case remains, where the rotational splitting is no longer a relevant seismic diagnostic, but where the rotation is too slow to allow to distinguishing among three different period spacings associated with the m-families of modes (for Ωc/(2π)/(ΔP/P2) between 5 and 20). Establishing a diagnostic in this regime is an important issue, which needs to be adressed in a forthcoming paper.
It can be surprising that the perturbative approach gives inaccurate results when Ω/(2π)/(ΔP/P2) < 20, while non-perturbative models where the spectral expansions are limited to one term (plus the toroidal component) give fairly accurate enough results. This can be understood with the help of the following equation: Ω(r)/2π ~ Δν ≪ νmax. In the frequency range of interest here, the rotation frequency remains significantly lower than νmax throughout the whole star and thus lower than the pulsation frequencies. Hence, the Coriolis terms are smaller than other terms in the equation of motion and the coupling of ℓ = 1 modes with ℓ = 3,5,... components is small. However the rotational splitting is not small compared to the large separation Δν. This implies that the trapping of each member of a same triplet can be very different, as illustrated in Fig. 3. Using the variational principle to model rotational splittings is thus not justified because the eigenfunctions are too different. The only way to properly model the effect of rotation on oscillations is to solve separately the differential equations associated with each member of the multiplet.
To sum up, the major impact of moderate rotation on red giants’ spectra is the modification of the trapping that depends on m. While the cavities here are not considered to be modified by rotation, it is the way modes probe them which differs from one member of a multiplet to another. In such a case, the first-order perturbative approach gives inaccurate results and the m-families of modes carry different information on the stellar interior. Only methods which compute these m-sub-spectra independently, i.e. non-perturbative methods, are appropriate for studying moderately to rapidly core rotating red giants.
Acknowledgments
R.M.O. thanks Benoît Mosser for fruitful discussions.
References
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP, 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Cowling, T. G., & Newing, R. A. 1949, ApJ, 109, 149 [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goupil, M. J. 2009, in The Rotation of Sun and Stars (Berlin: Springer Verlag), Lect. Notes Phys., 765, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J., Mosser, B., Marques, J. P., et al. 2013, A&A, 549, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Ledoux, P. 1949, Mem. Soc. Roy. Sci. Liege, 9, 3 [NASA ADS] [Google Scholar]
- Lynden-Bell, D., & Ostriker, J. P. 1967, MNRAS, 136, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012a, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Dupret, M.-A., & Reese, D. R. 2012, A&A, 547, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Talon, S., & Charbonnel, C. 2008, A&A, 482, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars (Tokyo, Japan: University of Tokyo Press) [Google Scholar]
- Zahn, J. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [Google Scholar]
All Figures
 |
Fig. 1 Pulsation frequencies in the inertial frame ν (in μHz) versus core rotation frequency Ωc/2π (in μHz) for dipolar multiplets. Red curves refer to m = − 1 (prograde) modes, green curves to m = 0 modes (axis-symmetric), and blue curves to m = 1 (retrograde) modes, for central rotation frequency ranging from 0 to 100 μHz. |
| In the text | |
 |
Fig. 2 Top: ratio between the contributions to kinetic energy of the ℓ = 3 component and the ℓ = 1 component of a dominated ℓ = 1 mode. Bottom: difference between the pulsation frequencies computed with three coupling terms (M = 3) and with one coupling term (M = 1), divided by the frequency separation between two consecutive mixed modes. Computed for the triplet indicated in thick lines in Fig. 1. |
| In the text | |
 |
Fig. 3 For a central rotation frequency of 20 μHz, kinetic energy of modes around a p-m mode as a function of the mode frequency. The three modes circled in black belong to the same original triplet. Inside the parentheses are the number of nodes in the p cavity and in the g cavity. |
| In the text | |
 |
Fig. 4 For the model M1 and a central rotation frequency of 20 μHz, Top: spacing between two closest modes of opposite azimuthal order m = ± 1, i.e. apparent rotational splitting. Bottom: spacing between prograde and the retrograde modes which belong to the same original multiplet (grey, crosses) and splittings computed with the first-order perturbative method (green, plus signs). |
| In the text | |
 |
Fig. 5 For a central rotation frequency of 140 μHz, top: pulsation modes’ kinetic energy with respect to their frequency. Bottom: period spacing with respect to the pulsation frequency. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


