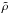| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220467 | |
| Published online | 13 June 2013 | |
Polarization of Saturn’s moon Iapetus
III. Models of the bright and the dark sides
1 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
e-mail: ejeta@mps.mpg.de
2 Institut für Geophysik und extraterrestishe Physik, TU Braunschweig, Mendelssohn str.3, 38106 Braunschweig, Germany
3 Department of Physics, PO Box 64, University of Helsinki, 00014 Helsinki, Finland
4 Finnish Geodetic Institute, PO Box 15, 02431 Masala, Finland
5 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
6 Department of Astronomy, College Park, MD, 20742, University of Maryland, USA
7 SRON Netherlands Institute for Space Research, 3584 Ultrecht, The Netherlands
8 INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received: 30 September 2012
Accepted: 12 March 2013
Context. Like many other atmosphereless solar system bodies, Iapetus exhibits a phenomenon of negative polarization at small phase angles, which can be modeled using theoretical approaches that consider interaction of light with a complex medium.
Aims. To retrieve information on the nature of Iapetus’ surface material, we carried out theoretical modeling analyses for the observed polarization of its two sides.
Methods. We applied two light-scattering models. The first modeling approach is based on the utilization of the phenomenological single-particle scattering matrix parametrization using the double Henyey-Greenstein (2HG) scattering phase function to characterize the resulting multiple scattering by a medium composed of such discrete scatterers. With this approach we carried out radiative-transfer coherent-backscattering (RT-CB) computations for a random medium composed of phenomenological fundamental scatterers. The second model, called the multiple sphere T-matrix method, is based on the exact solutions of the Maxwell equations. Employing this method, we carried out simulations of the scattering and absorption properties of light by a medium represented by a spherical volume of randomly positioned monodisperse particles. The modeling entails physical characteristics of the particulate surface, such as the porosity of the medium; the number of constituent particles; the size, and optical properties of the scatterers.
Results. While our RT-CB model suggests geometric albedo values in the neighborhood of 0.40 for Iapetus’ trailing side and ~0.10 for the leading one, our T-matrix model retrieves particles of radius ~0.10 ≤ r ≤ 0.20 μm for both Iapetus’ leading and trailing surface materials.
Key words: polarization / planets and satellites: surfaces / scattering / methods: numerical / techniques: polarimetric / radiative transfer
© ESO, 2013
1. Introduction
The scattering and absorption properties of surface particles of atmosphereless solar system objects often display a strong dependence on their size, shape, orientation, and refractive indices (e.g., Muinonen et al. 2010). Hence, analyses of polarization measurements of solar radiation scattered by these bodies offer means of obtaining otherwise inaccessible information about their surface properties. The degree of linear polarization varies with the phase angle (and thus the phase curve) and also with the wavelength. At phase angles less than the inversion angle (where the polarization changes in sign), atmosphereless solar system objects exhibit a phenomenon of negative polarization: a peculiar case of a partially linearly polarized scattered light P = (I⊥ − I∥)/(I⊥ + I∥), where the intensity component of the electric field vector parallel to the scattering plane I∥ predominates over the perpendicular component I⊥.
For many types of solar system bodies, negative polarization is often manifested as a wide, nearly symmetric and parabolically shaped branch with its minimum located at a phase angle α ≈ 3.0 − 15.0°, also known as the regular negative polarization branch (Rosenbush et al. 2006, references therein). On the other hand, high albedo objects, such as the Galilean satellites and the E-type asteroids (Rosenbush et al. 1997, 2005, 2009; Rosenbush & Kiselev 2005), exhibit a narrow, asymmetric spike of negative polarization with a minimum at α ≈ 0.20° to 2.0°, superimposed on the regular negative polarization branch, named the polarization opposition effect.
The polarization measurements for the trailing side of Iapetus seem to display the polarization opposition effect despite a lack of sufficient measurements at phase angles ≤1.0°, while those of its leading side seem to exhibit only the regular branch of negative polarization (Ejeta et al. 2012, 2013); hereinafter referred to as Paper I and Paper II, respectively.
Among the physical mechanisms potentially contributing to the negative linear polarization observed at small phase angles for particulate media, the coherent backscattering mechanism is the most relevant one (e.g., Mishchenko 1993; Shkuratov et al. 1994; Mishchenko et al. 2000, 2002; Muinonen et al. 2002). Coherent backscattering, as a multiple scattering mechanism for scattering orders higher or equal to the second, is the constructive interference of waves (near exact backscattering direction) in a random medium passing through the same scatterers in opposite directions. Moreover, while single-particle scattering of light by individual particles also contributes to negative polarization branches (Shkuratov et al. 2006; Muinonen et al. 2007), it is believed to have a minor effect at small phase angles (e.g., Muinonen et al. 2009). Besides, Petrova et al. (2007) consider what they called the near-field effects as a contributing mechanism to negative polarization, in particular, in the case of a densely packed medium.
In this paper, we provide analyses of simulation of light scattering by a particulate medium using two modeling approaches, to explain the polarization measurements of Iapetus that have already been reported in Papers I and II. As a first modeling approach, we performed the radiative-transfer coherent-backscattering (RT-CB) computations for a complex random medium composed of phenomenological fundamental scatterers. This modeling approach is based on the treatment formulated by Muinonen & Videen (2012). The second modeling approach we applied is called the multiple sphere T-matrix (MSTM) method, which is based on numerically exact solutions of the Maxwell equations simulating electromagnetic scattering by a medium consisting of large numbers of randomly positioned particles. This approach of modeling has already been applied to polarimetric observations of the Galilean satellite Europa (e.g., Mishchenko et al. 2009). For numerical comparison of the RT-CB and MSTM methods, we refer to the work by Muinonen et al. (2012).
In Sects. 2 and 3, we provide model formulations and results from the RT-CB and the MSTM modeling approaches, respectively. In Sect. 4, the results and effects of each input parameter of the respective models on the polarimetric phase curve will be separately discussed in detail. In Sect. 5, we conclude the paper by our main findings of the work and its future prospects.
2. Radiative-transfer Coherent-backscattering model (RT-CB)
Multiple scattering in a complex random medium can be studied in terms of a single scatterer, with the single scatterer represented by modified electric dipole scatterers (Muinonen et al. 2010). As an extension to this modeling approach, the current model applied here treats the multiple scattering by a random medium consisting of phenomenological fundamental scatterers (modified from pure electric and magnetic dipole scatterers), where the single-scattering matrix of these discrete scatterers can be parametrized by the use of an empirical double Henyey-Greenstein scattering phase function P2HG (e.g., Muinonen & Videen 2012). Thus, the RT-CB modeling approach, based on a Monte Carlo method to compute the coherent backscattering contribution near the exact backscattering direction, is employed here to characterize multiple scattering by a medium composed of phenomenological fundamental scatterers. Moreover, as shown below, the relative scattering matrix for the component modified from the electric dipole scatterer is the same as the relative Rayleigh scattering matrix, whereas for the scatterer modified from the magnetic dipole it is with an opposite sign.
As given in Muinonen & Videen (2012), the average single-scattering matrix can be approached by a weighted sum of the scattering matrices for the modified electric dipole scatterers S+ and the modified magnetic dipole scatterer S− as ![\begin{equation} P(\theta)\propto \frac{f(\theta)} {\frac{3}{4}(1+\cos^{2}\theta)}[w_{+}P_{+}(\theta)+(1-w_{+})P_{-}(\theta)], \label{scam} \end{equation}](/articles/aa/full_html/2013/06/aa20467-12/aa20467-12-eq17.png) (1)where w+ is the normalized weight of scatterers S+ yielding a positively polarized component, 1 − w+ is that of S− resulting in a negatively polarized component; and the Mueller matrices P+ and P− are, respectively,
(1)where w+ is the normalized weight of scatterers S+ yielding a positively polarized component, 1 − w+ is that of S− resulting in a negatively polarized component; and the Mueller matrices P+ and P− are, respectively, 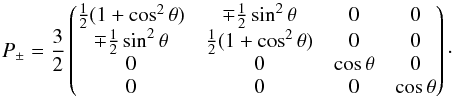 (2)The normalized weight factor w+ can be written as a function of another parameter:
(2)The normalized weight factor w+ can be written as a function of another parameter: 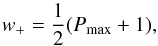 (3)where Pmax describes the maximum degree of linear polarization that would be obtained in single scattering at a scattering angle θ = 90.0°.
(3)where Pmax describes the maximum degree of linear polarization that would be obtained in single scattering at a scattering angle θ = 90.0°.
The 2HG single-scattering phase function f(θ), and its asymmetry parameter g are given by 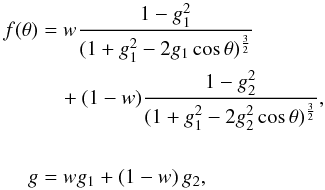 (4)where g1 and g2 describe the increase towards the forward-scattering direction and the increase from intermediate scattering angles towards the backward-scattering direction, respectively; w is the normalized weight of the first Henyey-Greenstein function (g1) and 1 − w is that of g2; g is the asymmetry parameter of the full 2HG phase function.
(4)where g1 and g2 describe the increase towards the forward-scattering direction and the increase from intermediate scattering angles towards the backward-scattering direction, respectively; w is the normalized weight of the first Henyey-Greenstein function (g1) and 1 − w is that of g2; g is the asymmetry parameter of the full 2HG phase function.
Assuming that the attenuation due to extinction is exponential within the random media and can be described by the extinction mean-free-path length ℓ (e.g., Muinonen 2004; Muinonen & Videen 2012), the multiple-scattering problem can be formulated in terms of six parameters: the single-scattering albedo 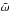 , which describes the fraction of scattering to absorption (scattering cross section divided by the extinction cross section), and is an additional free parameter of the single scatterer; the maximum degree of linear polarization in single-scattering Pmax; the total g, forward g1, and backward g2 asymmetry parameters of the empirical 2HG single-scattering phase function; and the extinction mean-free-path length ℓ describing wave propagation in the multiple-scattering medium.
, which describes the fraction of scattering to absorption (scattering cross section divided by the extinction cross section), and is an additional free parameter of the single scatterer; the maximum degree of linear polarization in single-scattering Pmax; the total g, forward g1, and backward g2 asymmetry parameters of the empirical 2HG single-scattering phase function; and the extinction mean-free-path length ℓ describing wave propagation in the multiple-scattering medium.
In these RT-CB computations, we have carried out a systematic mapping, with a course over the phase space of the parameters, to map the full range of plausible solutions. Each numerical computation has been carried out with 200 000 incident rays.
3. Multiple-sphere T-matrix method (MSTM)
This approach is an extension of Lorenz-Mie theory to the multiple-sphere system and calculates the time-harmonic electromagnetic scattering properties of a group of spheres (Mackowski & Mishchenko 1996, 2011). The formulation considers the total field exciting the spheres as the superposition of the incident field and the scattered fields from each of the spheres. The formal solution for the scattered field by the sphere ensemble would be determined numerically from a system of linear relations between the incident and the scattered field coefficients, which result from application of the continuity conditions at the surface of each sphere (Mackowski & Mishchenko 2011). The scattering process is fully described by the following scattering matrix (e.g., Mishchenko et al. 2009): 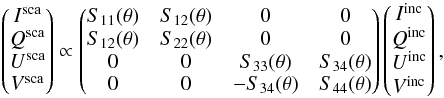 (5)where the phase angle α = π − θ (θ is the scattering angle). Note that, S21 = S12, and S43 = − S34. The relation given by Eq. (5) represents the normalized scattering matrix transforming the Stokes parameters I,Q,U,V of the incident light into those of the scattered light upon scattering by the entire particulate volume. Moreover, the scattering matrix indicated in Eq. (5) is for a random orientation of the cluster (with respect to the incident field). For the purpose of utilizing this approach, we considered a spherical volume of radius R consisting of N non-overlapping randomly positioned monodisperse spherical particles of radius r (e.g., Mishchenko et al. 2009; Dlugach et al. 2011). As noted in Dlugach et al. (2011), the corresponding volume fraction (the packing density) inside the scattering medium is defined as the ratio of cumulative volume of the constituent particles to the volume of the sphere enclosing all constituent particle centers, i.e.,
(5)where the phase angle α = π − θ (θ is the scattering angle). Note that, S21 = S12, and S43 = − S34. The relation given by Eq. (5) represents the normalized scattering matrix transforming the Stokes parameters I,Q,U,V of the incident light into those of the scattered light upon scattering by the entire particulate volume. Moreover, the scattering matrix indicated in Eq. (5) is for a random orientation of the cluster (with respect to the incident field). For the purpose of utilizing this approach, we considered a spherical volume of radius R consisting of N non-overlapping randomly positioned monodisperse spherical particles of radius r (e.g., Mishchenko et al. 2009; Dlugach et al. 2011). As noted in Dlugach et al. (2011), the corresponding volume fraction (the packing density) inside the scattering medium is defined as the ratio of cumulative volume of the constituent particles to the volume of the sphere enclosing all constituent particle centers, i.e., 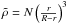 .
.
A pool of RT-CB models.
 |
Fig. 1 Degree of linear polarization, − P21/P11, versus phase angle α, obtained using the RT-CB model, along with the respective geometric albedo values pMS retrieved in each computation run. The top panel(a) shows comparison of polarization measurements of Iapetus’ trailing side (circles with error bars) with the RT-CB model, while the bottom panel (b) shows comparison of the model with the polarization measurements of Iapetus’ leading side. |
If unpolarized incident light (i.e., Qinc = Uinc = Vinc = 0) of irradiance Iinc is incident on the particles, the scattering matrix of Eq. (5) yields the Stokes parameters of the scattered light given by 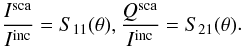 (6)Also known as the phase function, S11(θ) specifies the angular distribution of the scattered light intensity by the entire particulate volume, provided that the incident light is unpolarized. Hence, the corresponding degree of linear polarization is given by
(6)Also known as the phase function, S11(θ) specifies the angular distribution of the scattered light intensity by the entire particulate volume, provided that the incident light is unpolarized. Hence, the corresponding degree of linear polarization is given by 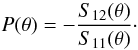 (7)The MSTM code1 has been executed on a parallel computer platform, the Nahalem Cluster at Gesellschaft für wissenschaftliche Datenverarbeitung mbH Göttingen (GWDG), using up to 64 cores. This computing resource has allowed us to calculate scattering properties for random orientations of targets containing up to 1200 spheres. Depending on the value of particle size parameter and volume fraction, the computation takes from a couple of hours to five days. However, as the particle size parameter gets higher (≥ 0.60 μm), very long execution times are required (~ 725.0 h). We varied all the parameters of the model one at a time to investigate their respective effects on the polarimetric phase function, as described in the next section.
(7)The MSTM code1 has been executed on a parallel computer platform, the Nahalem Cluster at Gesellschaft für wissenschaftliche Datenverarbeitung mbH Göttingen (GWDG), using up to 64 cores. This computing resource has allowed us to calculate scattering properties for random orientations of targets containing up to 1200 spheres. Depending on the value of particle size parameter and volume fraction, the computation takes from a couple of hours to five days. However, as the particle size parameter gets higher (≥ 0.60 μm), very long execution times are required (~ 725.0 h). We varied all the parameters of the model one at a time to investigate their respective effects on the polarimetric phase function, as described in the next section.
4. Results and discussions
 |
Fig. 2 Degree of linear polarization, − S12/S11, versus phase angle α for water ice (m = 1.30) of different volume fractions Vf, obtained using T-matrix method. It can be seen from all panels of the cases (a) and (b) that larger particle sizes x lead to deeper polarization curve, for the considered number of particles (N = 500). |
 |
Fig. 3 Same as Fig. 2 for a medium of refractive index m = 1.30 + i 0.20 and different volume fractions, showing that larger particle size x leads to deeper polarization curve (a); and for media with refractive indices m = 1.30 + i (0.0 ≤ mi ≤ 0.20) and different volume fractions, showing that negative polarization decreases monotonically with increasing imaginary part of the refractive index mi(b). |
 |
Fig. 4 Same as Fig. 2 for media of refractive indices m = (1.30 ≤ mr ≤ 2.70) + i (0.20 ≤ mi ≤ 0.30) having different particle sizes x, under similar volume fractions. It can be seen from panels (a) and (b) that as the real part of the refractive index mr increases, the negative polarization curves get deeper, with almost identical features in each of the cases. Furthermore, the minimum of polarization angle αmin, is independent of mr. However, as mr keeps increasing, the polarization turns out to be positive (c). |
 |
Fig. 5 Same as Fig. 2 for water ice of different particle sizes x(a) and for media with refractive indices m = 1.30 + i (0.02 ≤ mi ≤ 0.20) having similar particle sizes x(b). In both cases, for the considered number of particles N, the polarization curve gets deeper as the volume fraction Vf increases, with the αmin shifting towards higher phase angles. |
 |
Fig. 6 Same as Fig. 2 for media of water ice (m = 1.30) with similar particle sizes x and different volume fractions. It can be seen from both the top and bottom panels that a higher number of constituent particles N leads to a deeper polarization curve, i.e., the particle packing density |
 |
Fig. 7 Degree of linear polarization versus phase angle, obtained using the T-matrix method for medium of m = 1.30 + i 0.02 and particle size x = ~ 1.20, compared to measurements of Iapetus’ trailing side (top panel); and for a medium with refractive index m = 2.61 + i 0.20 and particle size x = 0.74 compared to measurements of Iapetus’ leading side (bottom panel). |
Table 1 shows systematic study of the variations of the RT-CB model parameters in the neighborhood of the “reference solution”, along with the retrieved geometric albedo pMS in each computation run. Figure 1 represents the RT-CB model fits to measurements of the trailing (a) and leading (b) sides of Iapetus.
Figures 2 to 6 show the analyses of the effects of each model parameter (i.e., particle size, refractive indices, packing density, number of constituent particles) on the polarimetric phase curve using the T-matrix method. Figure 7 shows the best-fit models using T-matrix for the leading and the trailing side measurements of Iapetus.
4.1. Retrieved parameters from the RT-CB modeling approach
In our treatment of the modeling approach using the RT-CB model discussed above, the model that can explain our measurements of Iapetus’ leading hemisphere is the one with the following parameters: g, g1, g2 = 0.45, 0.75, −0.20, respectively; 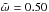 , ℓ = 2.0, and Pmax = 0.60. As can be seen from Table 1, for the same value of all other parameters, a change in the g parameter from 0.50 to 0.45 leads to an increase in geometric albedo from 0.07 to 0.08, thereby making the polarization minimum deeper (Fig. 1b).
, ℓ = 2.0, and Pmax = 0.60. As can be seen from Table 1, for the same value of all other parameters, a change in the g parameter from 0.50 to 0.45 leads to an increase in geometric albedo from 0.07 to 0.08, thereby making the polarization minimum deeper (Fig. 1b).
In the case of the trailing hemisphere (Fig. 1a), the indicated geometric albedo value of 0.42 corresponds to the model parameters of g = 0.50, g1 = 0.80, g2 = − 0.20, Pmax = 0.40, ℓ = 40, 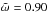 (Table 1). This results in a sharp polarimetric surge close to the backscattering direction due to the coherent backscattering effect (e.g., Muinonen et al. 2010). In addition, the single-scattering albedo
(Table 1). This results in a sharp polarimetric surge close to the backscattering direction due to the coherent backscattering effect (e.g., Muinonen et al. 2010). In addition, the single-scattering albedo 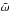 has a direct relationship with the geometric albedo (see Table 1). In this model, the position of the minimum polarization is controlled by the extinction mean free path of the medium. Moreover, we note that (see Table 1) the geometric albedo values of Iapetus’ two sides retrieved from this model differ by roughly a factor of five. As can be seen from Fig. 1, the value of the inversion angle for Iapetus’ leading and trailing sides are ~ 13.50° and ~ 7.50°, respectively.
has a direct relationship with the geometric albedo (see Table 1). In this model, the position of the minimum polarization is controlled by the extinction mean free path of the medium. Moreover, we note that (see Table 1) the geometric albedo values of Iapetus’ two sides retrieved from this model differ by roughly a factor of five. As can be seen from Fig. 1, the value of the inversion angle for Iapetus’ leading and trailing sides are ~ 13.50° and ~ 7.50°, respectively.
It can be seen from Table 1 that the single-scattering albedo 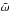 for Iapetus’ trailing side is higher than that of its leading one, thus favoring more multiple scattering. This in turn leads to more pronounced backward lobe g2 (in absolute terms) than what is obtained for the leading hemisphere. It cannot be clearly established whether the maximum degree of linear polarization in single-scattering Pmax (which is higher for Iapetus’ leading side than that of its trailing one) is because of the effect of albedo or the grain size. In fact, according to our T-matrix results, discussed in the following section, the grain size difference for Iapetus’ two sides is insignificant, although it is slightly higher for the trailing side. Based on this modeling approach, the fact that the mean free path ℓ for Iapetus’ trailing side is relatively longer than that for the leading one may indicate the surface on the trailing side is less compact than the surface on the leading one.
for Iapetus’ trailing side is higher than that of its leading one, thus favoring more multiple scattering. This in turn leads to more pronounced backward lobe g2 (in absolute terms) than what is obtained for the leading hemisphere. It cannot be clearly established whether the maximum degree of linear polarization in single-scattering Pmax (which is higher for Iapetus’ leading side than that of its trailing one) is because of the effect of albedo or the grain size. In fact, according to our T-matrix results, discussed in the following section, the grain size difference for Iapetus’ two sides is insignificant, although it is slightly higher for the trailing side. Based on this modeling approach, the fact that the mean free path ℓ for Iapetus’ trailing side is relatively longer than that for the leading one may indicate the surface on the trailing side is less compact than the surface on the leading one.
4.2. Analysis from MSTM method
For the modeling approach using the MSTM method, the effect of each model parameter can be described as follows: Figs. 2 and 3 demonstrate the effect of particle size parameter on the polarization phase function for absorbing and non-absorbing media, respectively. In both cases, it can be seen that higher particle size parameter yields a deeper polarization curve. As evident from panel (b) of Fig. 3, the effect of increase in the imaginary part of the refractive index of a material leads to a decrease in the depth of the negative linear polarization branch. This result is well consistent with the studies by Zubko et al. (2009), who investigated the influence of material absorption on light scattering of wavelength-sized agglomerated debris particles of refractive indices m = 1.50 + i (0.0 ≤ mi ≤ 1.30). Moreover, Dlugach et al. (2011) have reported that the depth of the negative polarization branch decreases monotonously with increasing mi for materials of refractive index m = 1.31 + i ( 0.0 ≤ mi ≤ 0.30). This effect is attributed to a decreasing contribution of multiple scattering with increasing absorption, since absorption is believed to terminate long scattering paths and thus can be expected to reduce the range of phase angles affected by coherent backscattering (Dlugach et al. 2011, references therein). However, we remark that the depth of the negative polarization curve with increasing absorption may not always follow the same behavior (it can either increase or decrease depending on the particle packing density and real part of the refractive index), as noted by Dlugach et al. (2011), who also investigated the case m = 1.50 + i ( 0.0 ≤ mi ≤ 0.30) for different particle packing densities.
Figure 4 shows the influence of the real part of the refractive index on the polarization phase curve. It can be seen that higher values of the real part of the refractive index result in a deeper polarization phase curve, with the features almost identical in each of the cases (a) and (b) of Fig. 4. Moreover, the phase angle of polarization minimum is independent of the real part of the refractive index, showing in this respect consistency with the notion of Dlugach et al. (2011). However, at the same time as the real part of the refractive index increases, the polarization turns out to be positive, as seen in Fig. 4c.
Figure 5 demonstrates the effect of volume fraction on the polarization phase curve for a non-absorbing medium. As the volume fraction increases, the negative polarization becomes deeper, while the corresponding angular position of the polarization minimum shifts towards higher phase angle.
Moreover, as can be seen from the top and bottom panels of Fig. 3b, for a similar imaginary part of the refractive indices, the influence of increase in average volume fraction Vf of a particle in absorbing medium also leads to a deeper polarization curve, with the polarization minimum slightly shifting towards the inversion point with increasing volume fraction. We note that Petrova & Tishkovets (2011) have also reported a similar general behavior of shift of the polarization minimum towards the inversion angle under the influence of increase in packing density for absorbing medium. However, in an absorbing medium, the effect of packing density may cause the polarization to be shallower or deeper, depending on the relation between the sizes of the constituent particles and the real part of the refractive index (Petrova & Tishkovets 2011, references therein).
Figure 6 indicates the influence of the number of constituent particles for different volume fractions of the media, showing that a higher number of particles leads to a deeper negative polarization curve, with the corresponding phase angle of minimum polarization shifting slightly towards smaller phase angles.
Clark et al. (2012) have suggested that metallic iron and iron oxide (hematite) are the dominant component of the observed spectral properties of Iapetus’ leading side surface material. Hence, to verify whether these suggested surface materials are consistent with the polarization behaviors observed for Iapetus’ leading side, we made several computations over a phase space of particle size parameter with a given particle packing density for a mixture hematite with metallic iron and water ice (Fe2O3 + H2O + Fe). Before attaining the best fit model of Fig. 7, we performed computations for the cases: i) x = 2.22, 2.96, 3.0 with N = 500, and Vf = 0.05; ii) x = 1.40, 1.50 with Vf = 0.02, and N = 500; iii) x = 2.0, with Vf = 0.01, and N = 500; iv) x = 2.96, with Vf = 0.10 and N = 500.
The surface material of Iapetus’ trailing side is claimed to be mostly (~ 98.0%) pure water ice (Clark et al. 2012, references therein). Thus, in our case, the small absorption component is mimicked through the imaginary part of the refractive index of water ice, i.e., we used a refractive index value of (m = 1.304 + i 0.02). The refractive index value used for Iapetus’ leading side is computed using the Maxwell Garnett mixing rule, according to the information given in Clark et al. (2012). That is, it is obtained using the mixture of 93.7% Fe2O3 (m = 2.6915 + i 0.043) + 1.3% H2O (m = 1.304 + i 0.0) + 5.0% Fe (m = ~3.07 + i 3.84), yielding an effective refractive index of m = (2.61 + i 0.20) | λ = 0.85 μm.
The refractive index of iron is from Ordal et al. (1985), water ice from Warren & Brandt (2008), and that of hematite corresponds to the value used by Buratti et al. (2005). Hence, we obtained the model parameters of Fig. 7 (i.e., x, N, and Vf) through careful assessment of their effects on the polarization phase curve. From Fig. 7, it can be seen that the corresponding volume-size parameter KR for Iapetus’ leading side is ~ 39.0, while it is ~ 76.0 for the trailing one. This significant difference in the values of KR between the two sides is due to the fact that the minimum of polarization αmin (which is higher for the leading side) is inversely proportional to KR, as pointed out by Mishchenko et al. (2009). It can also be seen from Fig. 7 that the inversion angle for Iapetus’ leading, and trailing sides are ~ 11.0° and ~ 7.0°, respectively.
5. Conclusions
To obtain information on the nature of Iapetus’ surface material, we applied two modeling approaches of light scattering. As a first modeling treatment, we carried out numerical RT-CB computations for random media of discrete scatterers, with the single-scattering matrix of the scatterers parametrized using the concept of the phenomenological fundamental scatterer. The second modeling approach we performed is simulation of time-harmonic electromagnetic scattering by a medium consisting of a group of randomly positioned spheres, employing the MSTM method. Our main results from these two modeling approaches are summarized as follows:
-
For materials suggested by Clarket al. (2012) as predominantcomponents of Iapetus’ surface, our T-matrix model indicates particles of size ~0.10 ≤ x ≤ 0.20 μm (radius) for both its leading and trailing sides, in agreement with the value reported by the same authors.
-
The geometric albedo values of Iapetus’ two sides, retrieved from our RT-CB modeling, differ by roughly a factor of five, i.e., (~0.40) for the trailing hemisphere and (~0.08) for the leading one. The geometric albedo value for the trailing side of Iapetus is quite consistent with the value reported by Spencer & Denk (2010), which is 0.39, while the value for the leading side is higher than the corresponding value reported by the same author, which is 0.04. We emphasize that even though, as can be seen from Fig. 1b, the RT-CB simulation resulting in a geometric albedo of ~0.08 can well explain the polarization of Iapetus’ leading side, additional simulations may still be needed to arrive at a more solid estimate for its geometric albedo.
-
The relatively longer mean free path ℓ for Iapetus’ trailing side, as compared to that for the leading one, might indicate that the surface material on the trailing side is less compact than on the leading side.
-
Comparison of the two best-fit models, i.e., the T-matrix and the RT-CB, shows that while the result from the two models for Iapetus’ leading side are similar, the RT-CB model succeeded better in fitting measurements of the trailing one than the T-matrix, as can be seen from Figs. 1 and 7, and possibly the same for polarimetric measurements of objects that potentially exhibit the polarization opposition effect at very small phase angles. This is due to the fact that in order to achieve a position of polarization minimum at αmin ≤ 5.0°, the volume size parameter KR needs to be higher in the case of T-matrix, which in turn requires very long execution time. However, in the case of the RT-CB computations, it is controlled by the transport mean free path and is relatively easy to achieve.
-
The inversion angle for Iapetus’ leading side determined from our models is ~11.0−13.50°; while that of its trailing side is ~7.0−7.50°. The latter value is consistent with that for Saturn’s rings, which is ~7.0−8.0° (e.g., Dollfus 1996).
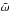 , ℓ, pMS) of the RT-CB best-fit model (Fig. 1) for the case of a distribution of non-spherical scatterers of different materials (i.e., polydisperse media). Further steps in RT-CB modeling (beyond the scope of the present study) can include the interpretation of the phenomenological fundamental scattering characteristics in terms of exact solutions of the Maxwell equations. Such future studies would help to further investigate the nature of Iapetus’ surface material.
, ℓ, pMS) of the RT-CB best-fit model (Fig. 1) for the case of a distribution of non-spherical scatterers of different materials (i.e., polydisperse media). Further steps in RT-CB modeling (beyond the scope of the present study) can include the interpretation of the phenomenological fundamental scattering characteristics in terms of exact solutions of the Maxwell equations. Such future studies would help to further investigate the nature of Iapetus’ surface material.
Acknowledgments
All computation results presented in this work were performed on the Nahalem Cluster at Gesellschaft für wissenschaftliche Datenverarbeitung mbH Göttingen (GWDG). We are grateful to the GWDG staff for their support with our enquiries. We are also thankful to the anonymous referee for the help in reviewing this paper.
References
- Buratti, B. J., Cruikshank, D. P., Brown, R. H., et al. 2005, ApJ, 622, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, R. N., Cruikshank, D. P., Juamann, R., et al. 2012, Icarus, 218, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Dlugach, J. M., Mishchenko, M. I., Liu, L., & Mackowski, D. W. 2011, J. Quant. Spectr. Rad. Transf., 112, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Dollfus, A. 1996, Icarus, 124, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Ejeta, C., Boehnhardt, H., Bagnulo, S., & Tozzi, G. P. 2012, A&A, 537, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ejeta, C., Boehnhardt, H., Bagnulo, S., et al. 2013, A&A, 549, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackowski, D. W., & Mishchenko, M. I. 1996, J. Opt. Soc. Am., 13, 2266 [NASA ADS] [CrossRef] [Google Scholar]
- Mackowski, D., & Mishchenko, M. I. 2011, J. Quant. Spectr. Rad. Transf., 112, 2182 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I. 1993, ApJ, 411, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., Luck, J. M., & Nieuwenhuizen, T. M. 2000, J. Opt. Soc. Am., 17, 888 [Google Scholar]
- Mishchenko, M., Tishkovets, V., & Litvinov, P. 2002, in Optics of Cosmic Dust, ed. G. Videen & M. Kocifaj, 239 [Google Scholar]
- Mishchenko, M. I., Dlugach, J. M., Liu, L., et al. 2009, ApJ, 705, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K. 2004, Waves in Random Media, 14, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., & Videen, G. 2012, J. Quant. Spectr. Rad. Transf., 113, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Piironen, J., Shkuratov, Y. G., Ovcharenko, A., & Clark, B. E. 2002, Asteroids III, 123 [Google Scholar]
- Muinonen, K., Tyynela, J., Zubko, E., Videen, G., & Shkuratov, Y. G. 2007, in AAS/Division for Planetary Sciences Meeting Abstracts #39, BAAS, 38, 469 [Google Scholar]
- Muinonen, K., Penttilä, A., Cellino, A., et al. 2009, Meteor. Planet. Sci., 44, 1937 [Google Scholar]
- Muinonen, K., Tyynelä, J., Zubko, E., & Videen, G. 2010, Earth Planets Space, 62, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Mishchenko, M. I., Dlugach, J. M., et al. 2012, ApJ, 760, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Ordal, M. A., Bell, R. J., Alexander, R. W., Long, L. L., & Querry, M. R. 1985, Appl. Opt., 24 [Google Scholar]
- Petrova, E. V., & Tishkovets, V. P. 2011, J. Quant. Spectr. Rad. Transf., 112, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Petrova, E. V., Tishkovets, V. P., & Jockers, K. 2007, Icarus, 188, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., & Kiselev, N. N. 2005, Icarus, 179, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Avramchuk, V. V., Rosenbush, A. E., & Mishchenko, M. I. 1997, ApJ, 487, 402 [Google Scholar]
- Rosenbush, V. K., Kiselev, N. N., Shevchenko, V. G., et al. 2005, Icarus, 178, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V., Kiselev, N., & Avramchuk, V. 2006, J. Quant. Spectr. Rad. Transf., 100, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Shevchenko, V. G., Kiselev, N. N., et al. 2009, Icarus, 201, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y. G., Muinonen, K., Bowell, E., et al. 1994, Earth Moon and Planets, 65, 201 [Google Scholar]
- Shkuratov, Y., Bondarenko, S., Ovcharenko, A., et al. 2006, J. Quant. Spectr. Rad. Transf., 100, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., & Denk, T. 2010, Science, 327, 432 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Warren, S. G., & Brandt, R. 2008, J. Geophys. Res., 113 [Google Scholar]
- Zubko, E., Kimura, H., Shkuratov, Y., et al. 2009, J. Quant. Spectr. Rad. Transf., 110, 1741 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Degree of linear polarization, − P21/P11, versus phase angle α, obtained using the RT-CB model, along with the respective geometric albedo values pMS retrieved in each computation run. The top panel(a) shows comparison of polarization measurements of Iapetus’ trailing side (circles with error bars) with the RT-CB model, while the bottom panel (b) shows comparison of the model with the polarization measurements of Iapetus’ leading side. |
| In the text | |
 |
Fig. 2 Degree of linear polarization, − S12/S11, versus phase angle α for water ice (m = 1.30) of different volume fractions Vf, obtained using T-matrix method. It can be seen from all panels of the cases (a) and (b) that larger particle sizes x lead to deeper polarization curve, for the considered number of particles (N = 500). |
| In the text | |
 |
Fig. 3 Same as Fig. 2 for a medium of refractive index m = 1.30 + i 0.20 and different volume fractions, showing that larger particle size x leads to deeper polarization curve (a); and for media with refractive indices m = 1.30 + i (0.0 ≤ mi ≤ 0.20) and different volume fractions, showing that negative polarization decreases monotonically with increasing imaginary part of the refractive index mi(b). |
| In the text | |
 |
Fig. 4 Same as Fig. 2 for media of refractive indices m = (1.30 ≤ mr ≤ 2.70) + i (0.20 ≤ mi ≤ 0.30) having different particle sizes x, under similar volume fractions. It can be seen from panels (a) and (b) that as the real part of the refractive index mr increases, the negative polarization curves get deeper, with almost identical features in each of the cases. Furthermore, the minimum of polarization angle αmin, is independent of mr. However, as mr keeps increasing, the polarization turns out to be positive (c). |
| In the text | |
 |
Fig. 5 Same as Fig. 2 for water ice of different particle sizes x(a) and for media with refractive indices m = 1.30 + i (0.02 ≤ mi ≤ 0.20) having similar particle sizes x(b). In both cases, for the considered number of particles N, the polarization curve gets deeper as the volume fraction Vf increases, with the αmin shifting towards higher phase angles. |
| In the text | |
 |
Fig. 6 Same as Fig. 2 for media of water ice (m = 1.30) with similar particle sizes x and different volume fractions. It can be seen from both the top and bottom panels that a higher number of constituent particles N leads to a deeper polarization curve, i.e., the particle packing density |
| In the text | |
 |
Fig. 7 Degree of linear polarization versus phase angle, obtained using the T-matrix method for medium of m = 1.30 + i 0.02 and particle size x = ~ 1.20, compared to measurements of Iapetus’ trailing side (top panel); and for a medium with refractive index m = 2.61 + i 0.20 and particle size x = 0.74 compared to measurements of Iapetus’ leading side (bottom panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.