| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201220957 | |
| Published online | 26 April 2013 | |
Radiative association of He+2 revisited
1
Charles University in Prague, Faculty of Mathematics and Physics,
Department of Chemical Physics and Optics, Ke Karlovu 3, 12116 Prague 2, Czech Republic
e-mail:
lucie.augustovicova@mff.cuni.cz
2
Institute of Organic Chemistry and Biochemistry, Academy of
Sciences of the Czech Republic, Flemingovo nám. 2, 16010 Prague 6, Czech Republic
e-mail:
vladimir.spirko@marge.uochb.cas.cz
3
Max-Planck-Institute of Astrophysics, Postfach 1371, 85741
Garching,
Germany
e-mail:
wpk@mpa-garching.mpg.de
4
Charles University in Prague, Faculty of Mathematics and Physics,
Department of Chemical Physics and Optics, Ke Karlovu 3, 12116 Prague 2, Czech Republic
e-mail:
pavel.soldan@mff.cuni.cz
Received:
19
December
2012
Accepted:
13
March
2013
Aims. Rate coefficients for spontaneous and stimulated radiative association of the He+2 molecular ion are presented as a function of temperature, considering the association with rotational-vibrational states of the ground X electronic state from the continuum states of the lowest three excited A,C, and E electronic states.
Methods. The rate coefficients are obtained from the cross sections for radiative association, which are calculated by solving the Schrödinger equation for bound and continuum states supported by the corresponding Born-Oppenheimer potential energy curves.
Results. The rate coefficients for the A → X spontaneous process are in excellent agreement with previous calculations. For temperatures up to about 10 000 K, the spontaneous C → X and E → X processes are dominant, exceeding the A → X rate coefficient by several orders of magnitude. Stimulation of the radiative association by black-body radiation has significant influence only on the A → X process at temperatures below 1000 K. The black-body radiation temperature would have to be well above 50 000 K in order to have any noticeable effect on the C → X and E → X processes.
Key words: molecular processes
© ESO, 2013
1. Introduction
The small diatomic ions H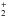 or HeH+ and
or HeH+ and 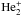 are assumed to be
significantly abundant in the atmospheres of white dwarf stars, either in the
hydrogen-dominated DA-type stars or the less numerous helium-rich ones, respectively (Koester & Chanmugam 1990). Continuous absorption
by these ions has been shown to be a major source of the opacity in the ultraviolet
continuum of these stars (Stancil 1994). With their
one-dimensional potentials originating from solutions of a small few-electron problem, these
ions can be treated on very high theoretical accuracy levels and are therefore ideal test
cases for comparisons between theory and results obtained from laboratory experiments or
observations.
are assumed to be
significantly abundant in the atmospheres of white dwarf stars, either in the
hydrogen-dominated DA-type stars or the less numerous helium-rich ones, respectively (Koester & Chanmugam 1990). Continuous absorption
by these ions has been shown to be a major source of the opacity in the ultraviolet
continuum of these stars (Stancil 1994). With their
one-dimensional potentials originating from solutions of a small few-electron problem, these
ions can be treated on very high theoretical accuracy levels and are therefore ideal test
cases for comparisons between theory and results obtained from laboratory experiments or
observations.
There have been numerous accurate theoretical studies of the
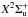 ground electronic
state of the
ground electronic
state of the  ion,
culminating in the highly accurate calculations of its adiabatic potential energy curve by
Cencek & Rychlewski (1995) and most recently
in calculations of the ground state potential including adiabatic corrections by Tung et al. (2012). Theoretical studies on a similar high
accuracy level of the excited states are less frequent, which is partly due to the fact that
within the adiabatic approximation these states undergo numerous avoided curve crossings.
The first serious attempt to clear up the situation for the lowest six
ion,
culminating in the highly accurate calculations of its adiabatic potential energy curve by
Cencek & Rychlewski (1995) and most recently
in calculations of the ground state potential including adiabatic corrections by Tung et al. (2012). Theoretical studies on a similar high
accuracy level of the excited states are less frequent, which is partly due to the fact that
within the adiabatic approximation these states undergo numerous avoided curve crossings.
The first serious attempt to clear up the situation for the lowest six
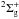 excited
states went beyond the adiabatic Born-Oppenheimer approximation, evaluating in addition to
the adiabatic potential curves the non-adiabatic matrix elements at the avoided crossings
and thus constructing approximate diabatic potential curves (Metropoulos et al. 1987). Other extended calculations focused later on the
Born-Oppenheimer potentials of the low-lying
excited
states went beyond the adiabatic Born-Oppenheimer approximation, evaluating in addition to
the adiabatic potential curves the non-adiabatic matrix elements at the avoided crossings
and thus constructing approximate diabatic potential curves (Metropoulos et al. 1987). Other extended calculations focused later on the
Born-Oppenheimer potentials of the low-lying 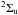 ,
,
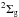 ,
,
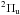 , and
, and
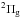 states (Ackermann & Hogreve 1991; Bawagan & Davidson 1997). Recently, a two-state study of the
ground and first excited states was performed, which included an exact treatment of all
adiabatic correction terms (Xie et al. 2005).
states (Ackermann & Hogreve 1991; Bawagan & Davidson 1997). Recently, a two-state study of the
ground and first excited states was performed, which included an exact treatment of all
adiabatic correction terms (Xie et al. 2005).
Stancil et al. (1993) have studied the spontaneous
radiative-association formation of 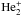 from collisions
of He+ ions with He atoms in their ground state and discussed possible
astrophysical implications of this reaction in attempts to model abundances in SN 1987A
ejecta and in the planetary nebula NGC 7027. They came to the conclusion that the formation
of
from collisions
of He+ ions with He atoms in their ground state and discussed possible
astrophysical implications of this reaction in attempts to model abundances in SN 1987A
ejecta and in the planetary nebula NGC 7027. They came to the conclusion that the formation
of 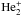 in the early
Universe does not have any interesting consequences. In contrast, the helium-containing
small molecular ions HeH+ and
in the early
Universe does not have any interesting consequences. In contrast, the helium-containing
small molecular ions HeH+ and 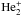 are known to
be highly abundant in the atmospheres of He-rich white dwarf stars (Gaur et al. 1988, 1992) and some
planetary nebulae (Black 1978; Flower & Roueff 1979; Stancil
1994). It was demonstrated, for instance, that HeH+ can affect
significantly the photosphere of such stars (Harris et al.
2004) and that the resulting increased opacity will lengthen their cooling time
(Fontaine et al. 2001). The same holds for
contributions from He + He+ collisional absorption and
are known to
be highly abundant in the atmospheres of He-rich white dwarf stars (Gaur et al. 1988, 1992) and some
planetary nebulae (Black 1978; Flower & Roueff 1979; Stancil
1994). It was demonstrated, for instance, that HeH+ can affect
significantly the photosphere of such stars (Harris et al.
2004) and that the resulting increased opacity will lengthen their cooling time
(Fontaine et al. 2001). The same holds for
contributions from He + He+ collisional absorption and
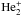 photo-dissociation processes (Ignjatovic et al.
2009). Since temperatures in these objects are very high, investigations of possible
interactions between excited He atoms and He+ ions or protons seem to be
appropriate.
photo-dissociation processes (Ignjatovic et al.
2009). Since temperatures in these objects are very high, investigations of possible
interactions between excited He atoms and He+ ions or protons seem to be
appropriate.
On this background the present study intends to go beyond the previous work of Stancil et al. (1993), investigating the different
radiative-association formation processes of 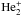 , which can be
formulated with the lowest three excited
, which can be
formulated with the lowest three excited 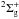 states
acting as reactant channels. They are described as
states
acting as reactant channels. They are described as ![\begin{eqnarray} & A{^2}\left[\mathrm{He} (1^{1}S)\, + \mathrm{He}^{+}\right]_{\rm g} \rightarrow \mathrm{He}_{2}^{+}(X^{2}\Sigma^{+}_{\rm u})\, + \,h\nu & (A\rightarrow X) \label{AX} \\ & C{^2}\left[\mathrm{He} (2^{3}S)\, + \mathrm{He}^{+}\right]_{\rm g} \rightarrow \mathrm{He}_{2}^{+}(X^{2}\Sigma^{+}_{\rm u})\, + \,h\nu & (C\rightarrow X) \label{CX} \\ & E{^2}\left[\mathrm{He} (2^{1}S)\, + \mathrm{He}^{+}\right]_{\rm g} \rightarrow \mathrm{He}_{2}^{+}(X^{2}\Sigma^{+}_{\rm u})\, + \,h\nu & (E\rightarrow X), \label{EX} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20957-12/aa20957-12-eq19.png) where
2 [...] g means a doublet g
submanifold of the corresponding collisional continuum. According to this scheme, reactions
start from collisions of He in one of the lowest three atomic levels
(11S, 23S,
21S) with He+ ions and proceed via resonance and
continuum states of the excited
where
2 [...] g means a doublet g
submanifold of the corresponding collisional continuum. According to this scheme, reactions
start from collisions of He in one of the lowest three atomic levels
(11S, 23S,
21S) with He+ ions and proceed via resonance and
continuum states of the excited 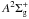 ,
,
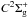 , and
, and
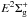 potentials of the
collisional complex to form under spontaneous photon emission the molecular-ion ground state
potentials of the
collisional complex to form under spontaneous photon emission the molecular-ion ground state
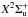 . These processes are
characterized in the above scheme as A → X,
C → X, or E → X,
respectively. Apart from spontaneous emission, processes stimulated by the background
radiation with frequency νb (Stancil & Dalgarno 1997; Zygelman et al.
1998) are also considered:
. These processes are
characterized in the above scheme as A → X,
C → X, or E → X,
respectively. Apart from spontaneous emission, processes stimulated by the background
radiation with frequency νb (Stancil & Dalgarno 1997; Zygelman et al.
1998) are also considered: 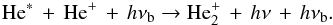 (4)The
underlying information necessary for the present dynamics calculations, i.e. potential
energy data for the different
(4)The
underlying information necessary for the present dynamics calculations, i.e. potential
energy data for the different 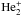 states and the
dipole transition data, is calculated on a high accuracy level of ab initio theory (details
of these calculations and a discussion of the methodology used will be collected in a
separate paper (Augustovičová et al., in prep.).
states and the
dipole transition data, is calculated on a high accuracy level of ab initio theory (details
of these calculations and a discussion of the methodology used will be collected in a
separate paper (Augustovičová et al., in prep.).
2. Methods
In quantum mechanics, the cross sections for radiative association of a diatomic molecule
in the presence of black-body radiation can be expressed as a sum over allowed transitions
between a continuum state with a positive energy E and orbital angular
momentum N′ to bound rovibrational states with vibrational
quantum number v′′ and orbital angular momentum
N′′ (Zygelman &
Dalgarno 1990): 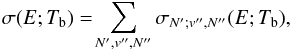 (5)where the temperature
Tb characterizes the black-body radiation field. In the case
of dipole moment transitions, the individual cross sections can be expressed as (Stancil & Dalgarno 1997)
(5)where the temperature
Tb characterizes the black-body radiation field. In the case
of dipole moment transitions, the individual cross sections can be expressed as (Stancil & Dalgarno 1997) ![\begin{eqnarray} \label{sigind} \sigma_{N';v'',N''}(E;T_{\rm b}) = \frac{1}{4\pi\epsilon_{0}} \frac{64}{3}\frac{\pi^5}{c^3\,k^2}\,p\,\nu^{3}_{E;v'',N''}\,S_{N',N''}\,M_{E,N';v'',N''}^2 \nonumber \\ \times \left[\frac{1}{1-\exp{(-h \nu_{E;v'',N''} / k_{\rm B} T_{\rm b})}}\right], \end{eqnarray}](/articles/aa/full_html/2013/05/aa20957-12/aa20957-12-eq34.png) (6)where
c is the speed of light in a vacuum,
k2 = 2μE/ħ2,
μ is the “reduced mass” of the molecular ion
(μ = 3647.89986 AU for 4
(6)where
c is the speed of light in a vacuum,
k2 = 2μE/ħ2,
μ is the “reduced mass” of the molecular ion
(μ = 3647.89986 AU for 4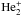 ),
p is the probability of approach in the initial electronic state
(p = 1/2 for A → X
and E → X and p = 1/6
for C → X), and
νE;v′′,N′′
is the emitted photon frequency,
hνE;v′′,N′′ = E + ▵ E − Ev′′,N′′,
where ▵ E = 0 cm-1 for A → X,
▵ E = 19.8176 eV for C → X and
▵ E = 20.6164 eV for E → X (Ralchenko et al. 2010).
),
p is the probability of approach in the initial electronic state
(p = 1/2 for A → X
and E → X and p = 1/6
for C → X), and
νE;v′′,N′′
is the emitted photon frequency,
hνE;v′′,N′′ = E + ▵ E − Ev′′,N′′,
where ▵ E = 0 cm-1 for A → X,
▵ E = 19.8176 eV for C → X and
▵ E = 20.6164 eV for E → X (Ralchenko et al. 2010).
For a homonuclear diatomic molecule within the Hund’s case (a) spin-less approximation, the
dipole moment transitions between Σg and Σu states are governed by the
rotational selection rules
▵ N = N′ − N′′ = ∓ 1.
Thus there are only two branches and the only non-zero Hönl-London coefficients are
SN′,N′ + 1 = N′ + 1
and
SN′,N′ − 1 = N′,
respectively. 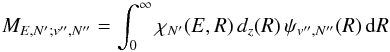 (7)is the matrix
element of the transition dipole moment function
dz(R) between the initial
continuum radial wave function
χN′(E,R) for the
partial wave N′ and the final bound-state radial wave function
ψv′′,N′′(R).
The above formula (6) is derived for the
energy-normalized continuum wave function
χN′(E,R):
(7)is the matrix
element of the transition dipole moment function
dz(R) between the initial
continuum radial wave function
χN′(E,R) for the
partial wave N′ and the final bound-state radial wave function
ψv′′,N′′(R).
The above formula (6) is derived for the
energy-normalized continuum wave function
χN′(E,R):
![\begin{equation} \chi_{N'}(E,R) \sim \left(\frac{2\mu}{\hbar^{2}\pi k}\right)^{1/2}\sin\left[kR - \frac{1}{2}\,N'\pi + \delta_{N'}(E)\right] \quad \mbox{for } R\rightarrow\infty, \end{equation}](/articles/aa/full_html/2013/05/aa20957-12/aa20957-12-eq59.png) (8)where
δN′(E) is the
phase shift and
(8)where
δN′(E) is the
phase shift and 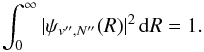 (9)Moreover, in the case of a
homonuclear diatomic molecule with zero nuclear spin (such as
4
(9)Moreover, in the case of a
homonuclear diatomic molecule with zero nuclear spin (such as
4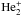 ), symmetry
requires that only even N′ levels are populated in the
Σg electronic states and only odd N′′ levels are
populated in the Σu electronic states. Thus the sum in Eq. (5) goes only over even
N′, and then the Hönl-London coefficients conveniently arrange
that it also goes only over odd N′′.
), symmetry
requires that only even N′ levels are populated in the
Σg electronic states and only odd N′′ levels are
populated in the Σu electronic states. Thus the sum in Eq. (5) goes only over even
N′, and then the Hönl-London coefficients conveniently arrange
that it also goes only over odd N′′.
The radial wave functions may be determined by numerical integration of the Schrödinger
equations ![\begin{eqnarray} \left[-\frac{\hbar^{2}}{2\mu}\frac{\mathrm{d}^2}{\mathrm{d}R^2} + \frac{\hbar^{2}}{2\mu}\frac{N'(N'+1)}{R^{2}} + U_{\rm C}(R)\right]\chi_{N'}(E,R) & = & \nonumber \\ E\,\chi_{N'}(E,R), & & \label{SES} \\ \left[-\frac{\hbar^2}{2\mu}\frac{\mathrm{d}^2}{\mathrm{d}R^2} + \frac{\hbar^{2}}{2\mu}\frac{N''(N''+1)}{R^{2}} + U_{\rm B}(R)\right]\psi_{v'',N''}(R) &= & \nonumber \\ E_{v'',N''}\,\psi_{v'',N''}(R), & & \label{SEF} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20957-12/aa20957-12-eq62.png) where
UC(R) and
UB(R) are the potential energy functions
supporting the initial continuum state E, N′
and the final bound state
v′′, N′′,
respectively. The wave functions
χN′(E,R) and
ψv′′,N′′(R)
were calculated by numerical integration of the radial Schrödinger equation using the
Numerov-Cooley method (Numerov 1933; Cooley 1961). Resonance positions and tunneling widths
were calculated employing the computer program LEVEL 7.7 (Le
Roy 2005) and making use of the Airy-function boundary condition at the outermost
classical turning point (Le Roy & Liu 1978)
and the uniform semiclassical method (Connor & Smith
1981; Huang & Le Roy 2003).
where
UC(R) and
UB(R) are the potential energy functions
supporting the initial continuum state E, N′
and the final bound state
v′′, N′′,
respectively. The wave functions
χN′(E,R) and
ψv′′,N′′(R)
were calculated by numerical integration of the radial Schrödinger equation using the
Numerov-Cooley method (Numerov 1933; Cooley 1961). Resonance positions and tunneling widths
were calculated employing the computer program LEVEL 7.7 (Le
Roy 2005) and making use of the Airy-function boundary condition at the outermost
classical turning point (Le Roy & Liu 1978)
and the uniform semiclassical method (Connor & Smith
1981; Huang & Le Roy 2003).
Molecular characteristics of the potential energy curves used in the cross-section
calculations of the 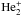 radiative
association.
radiative
association.
For evaluation of the continuum and bound-state wave functions in Eqs. (10, 11) and the dipole moment matrix elements in Eq. (7), it is necessary to have either analytical or numerical representation
of the potential energy and dipole moment functions. We chose numerical representation by
the one-dimensional reciprocal-power reproducing kernel Hilbert space (RP-RKHS)
interpolation method (Ho & Rabitz 1996). This
method allows not only for qualitatively correct extrapolation in the long-range region of
the A + A+ interaction potential
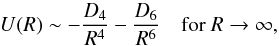 (12)but also for the use of
predetermined values of long-range coefficients (Ho
& Rabitz 2000). In the case of potential energy curves U,
the interpolation was done with respect to r2 (Soldán & Hutson 2000) using RP-RKHS parameters
m = 1 and n = 2, the coefficient
D4, which is equal to
αd/2, was kept fixed to the values given by
static dipole polarisabilities
αd [He(11S)] = 1.383191 AU (Pachucki & Sapirstein 2000),
αd [He(23S)] = 800.31633 AU and
αd [He(21S)] = 315.631468 AU (Yan & Babb 1998). Very accurate interaction
energies of the ground
(12)but also for the use of
predetermined values of long-range coefficients (Ho
& Rabitz 2000). In the case of potential energy curves U,
the interpolation was done with respect to r2 (Soldán & Hutson 2000) using RP-RKHS parameters
m = 1 and n = 2, the coefficient
D4, which is equal to
αd/2, was kept fixed to the values given by
static dipole polarisabilities
αd [He(11S)] = 1.383191 AU (Pachucki & Sapirstein 2000),
αd [He(23S)] = 800.31633 AU and
αd [He(21S)] = 315.631468 AU (Yan & Babb 1998). Very accurate interaction
energies of the ground 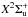 state (Tung et al. 2012) were exploited as known data points for
the interpolation. We calculated ab initio interaction energies for the excited states
state (Tung et al. 2012) were exploited as known data points for
the interpolation. We calculated ab initio interaction energies for the excited states
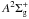 ,
,
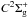 , and
, and
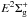 and the corresponding
transition dipole moment values employing the multi-reference configuration interaction
method (combined with a very large electron basis set) as implemented in the quantum
chemistry program suite MOLPRO (Werner et al. 2010).
Further details of these extensive quantum chemistry calculations will be published later
elsewhere (Augustovičová et al., in prep.).
and the corresponding
transition dipole moment values employing the multi-reference configuration interaction
method (combined with a very large electron basis set) as implemented in the quantum
chemistry program suite MOLPRO (Werner et al. 2010).
Further details of these extensive quantum chemistry calculations will be published later
elsewhere (Augustovičová et al., in prep.).
Having obtained the corresponding cross sections (5), the rate coefficients for formation of a molecule by (spontaneous and
stimulated) radiative association at temperature T is then defined by
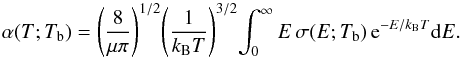 (13)To evaluate this
integral as accurately as possible, we followed the approach of Augustovičová et al. (2012), where contributions from wide and narrow
resonances are treated separately from the background contribution. This method was
successfully used for very recent calculations of radiative-association rate coefficients of
the molecular ion LiHe+ (Augustovičová et al.
2012).
(13)To evaluate this
integral as accurately as possible, we followed the approach of Augustovičová et al. (2012), where contributions from wide and narrow
resonances are treated separately from the background contribution. This method was
successfully used for very recent calculations of radiative-association rate coefficients of
the molecular ion LiHe+ (Augustovičová et al.
2012).
3. Results and discussion
Using the high-level calculations of Tung et al.
(2012) for the 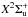 state as reference,
we calculated the potentials of the three lowest
state as reference,
we calculated the potentials of the three lowest 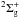 states on
a comparable accuracy level. In Table 1 some data
characterizing the three excited states potentials are summarized. For the
A state, degenerate with the X state at dissociation,
the equilibrium bond distance Re and the dissociation energy
states on
a comparable accuracy level. In Table 1 some data
characterizing the three excited states potentials are summarized. For the
A state, degenerate with the X state at dissociation,
the equilibrium bond distance Re and the dissociation energy
 are in perfect agreement with previous accurate results obtained by Xie et al. (2005) and those of Carrington
et al. (1995). Relative to the results of Xie et
al. (2005), the present Re is smaller by less than 0.3
percent and
are in perfect agreement with previous accurate results obtained by Xie et al. (2005) and those of Carrington
et al. (1995). Relative to the results of Xie et
al. (2005), the present Re is smaller by less than 0.3
percent and  is larger by less than 1 percent. For the C state,
Re and
is larger by less than 1 percent. For the C state,
Re and  can be compared with earlier calculations by Ackermann
& Hogreve (1991), which were performed at a lower accuracy level. Whereas
the difference in Re is only about 0.9 percent,
can be compared with earlier calculations by Ackermann
& Hogreve (1991), which were performed at a lower accuracy level. Whereas
the difference in Re is only about 0.9 percent,
 differs considerably more: 9173 cm-1 compared to 8565 cm-1. For the
E state, accurate results for comparison are not available. Quantitative
comparisons with the corresponding basic data used in the white dwarf atmosphere studies of
Stancil et al. (1993), Stancil (1994), and Ignjatovic et al.
(2009) are not possible, because explicit numerical results are not given there.
However, the qualitative agreement with these studies is very good. The
differs considerably more: 9173 cm-1 compared to 8565 cm-1. For the
E state, accurate results for comparison are not available. Quantitative
comparisons with the corresponding basic data used in the white dwarf atmosphere studies of
Stancil et al. (1993), Stancil (1994), and Ignjatovic et al.
(2009) are not possible, because explicit numerical results are not given there.
However, the qualitative agreement with these studies is very good. The
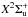 potential energy
curve of Tung et al. (2012) supports 409
rotational-vibrational bound states as opposed to 411 states found by Stancil et al. (1993). Our maximum rotational quantum numbers differ from
those presented by Stancil (1994) for four
vibrational states (for v = 1,11,20, and
23 our Nmax are 55, 35, 13, and 3, respectively). The
potential energy
curve of Tung et al. (2012) supports 409
rotational-vibrational bound states as opposed to 411 states found by Stancil et al. (1993). Our maximum rotational quantum numbers differ from
those presented by Stancil (1994) for four
vibrational states (for v = 1,11,20, and
23 our Nmax are 55, 35, 13, and 3, respectively). The
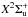 potential energy
curve of Tung et al. (2012), our
potential energy
curve of Tung et al. (2012), our
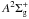 potential energy
curve, and our transition dipole moment function connecting these two states also seem to
agree very well with the corresponding function plots of Ignjatovic et al. (2009) with no visible differences.
potential energy
curve, and our transition dipole moment function connecting these two states also seem to
agree very well with the corresponding function plots of Ignjatovic et al. (2009) with no visible differences.
 |
Fig. 1 Cross sections for spontaneous (Tb = 0 K) radiative
association of |
Cross sections for a spontaneous (Tb = 0 K) radiative
association are shown graphically in Fig. 1. The cross
sections for the C → X and
E → X processes are several orders of magnitude larger
than the cross sections for the A → X process because of
their rather large ▵ E. For these two processes one can also see the
high-energy resonance structures. These are consequences of the avoided crossings with
higher 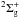 electronic states, which result in local potential energy minima in the short-range region
(for R between 1 a0 and
2.5 a0) (Metropoulos et al.
1987). The corresponding potential energy wells then support many shape resonances
in the high-energy region (between 1.7 eV and 6.2 eV and between 6.5 eV and 7.9 eV for the
C → X and E → X
processes, respectively). The low-energy resonance structure in the radiative-association
cross sections, which is created by the quasi-bound states trapped behind the centrifugal
barrier, is the richest for the C → X process. Only
quasi-bound states, which have a symmetry-allowed (i.e. for which the corresponding
Hönl-London coefficient is non-zero) bound-state partner supported by the
electronic states, which result in local potential energy minima in the short-range region
(for R between 1 a0 and
2.5 a0) (Metropoulos et al.
1987). The corresponding potential energy wells then support many shape resonances
in the high-energy region (between 1.7 eV and 6.2 eV and between 6.5 eV and 7.9 eV for the
C → X and E → X
processes, respectively). The low-energy resonance structure in the radiative-association
cross sections, which is created by the quasi-bound states trapped behind the centrifugal
barrier, is the richest for the C → X process. Only
quasi-bound states, which have a symmetry-allowed (i.e. for which the corresponding
Hönl-London coefficient is non-zero) bound-state partner supported by the
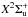 electronic state,
contribute to rate coefficients. The resonance structures relevant for the studied processes
are summarized in Table 2. The corresponding rate
coefficients for the spontaneous radiative association are shown graphically in Fig. 2, and their values, evaluated at selected temperatures,
are provided in Table 3. Our results for the
A → X process are in excellent agreement with the
results of Stancil et al. (1993), indicating thus
that in this case the rate coefficients are not very sensitive to the potentials used. For
temperatures up to about 10 000 K, the processes C → X and
E → X are dominant, exceeding the
A → X rate coefficient by several orders of magnitude
and thus mimicking the cross-section behaviour.
electronic state,
contribute to rate coefficients. The resonance structures relevant for the studied processes
are summarized in Table 2. The corresponding rate
coefficients for the spontaneous radiative association are shown graphically in Fig. 2, and their values, evaluated at selected temperatures,
are provided in Table 3. Our results for the
A → X process are in excellent agreement with the
results of Stancil et al. (1993), indicating thus
that in this case the rate coefficients are not very sensitive to the potentials used. For
temperatures up to about 10 000 K, the processes C → X and
E → X are dominant, exceeding the
A → X rate coefficient by several orders of magnitude
and thus mimicking the cross-section behaviour.
Resonance situation overview for the three studied processes of the
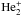 radiative
association.
radiative
association.
Cross sections and rate coefficients for the stimulated radiative-association A → X process are shown graphically for different black-body radiation temperatures Tb in Figs. 3 and 4, respectively. The difference in cross sections between the limit (Tb = 0 K and Tb = 10 000 K) cases starts to be washed out at collision energies around E = 1 eV. However, at lower energies the difference is almost two orders of magnitude in favour of the stimulated process. The difference in the corresponding rate coefficients at low temperatures (around T = 10 K) reaches two orders of magnitude, although it decreases rapidly with increasing temperature until it becomes negligible at temperatures around T = 10 000 K. The cross sections and rate coefficients for the stimulated C → X and E → X processes do not vary significantly with the black-body radiation temperatures. This is caused by very large ▵ E for these processes, which negates the effect of the black-body radiation temperature in Eq. (6). Consequently one would need the black-body radiation temperature around Tb = 50 000 K to see an increase by merely 1% in the cross sections or rate coefficients.
 |
Fig. 2 Rate coefficients for spontaneous (Tb = 0 K) radiative
association of |
Values of the total rate coefficients for the three spontaneous processes of the
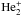 radiative
association.
radiative
association.
 |
Fig. 3 Cross sections for the stimulated radiative association
A → X process in
|
 |
Fig. 4 Rate coefficients for the stimulated radiative association
A → X process in
|
4. Conclusion
Radiative association formation of the ground 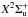 electronic state of
electronic state of
 by spontaneous
or stimulated photon emission was investigated considering the lowest three excited
by spontaneous
or stimulated photon emission was investigated considering the lowest three excited
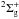 electronic states (
electronic states (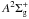 ,
,
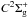 ,
,
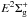 ) as initial reactant
channels. The cross sections for spontaneous radiative association via the
A → X, C → X, and
E → X processes were calculated as functions of the
collision energy. The corresponding rate coefficients for the formation of
) as initial reactant
channels. The cross sections for spontaneous radiative association via the
A → X, C → X, and
E → X processes were calculated as functions of the
collision energy. The corresponding rate coefficients for the formation of
 in the ground
in the ground
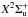 electronic state were
determined as functions over a wide range of temperatures. For the
A → X process, the results were found to be in excellent
agreement with those of Stancil et al. (1993).
Whereas at low temperatures the C → X process is by far
the most efficient one (its rate coefficient is more than six orders of magnitude larger
than for A → X), the
E → X process becomes more efficient at very high
temperatures (in the range of 104 to 105 K) with rate coefficients
more than an order of magnitude larger than for A → X.
Stimulation of the radiative association by black-body radiation was shown here to be
important for the A → X reaction at temperatures up to
about 1000 K. For background radiation temperatures of a few thousand K, the increase of the
rate coefficient in this temperature range can be by about an order of magnitude and more.
electronic state were
determined as functions over a wide range of temperatures. For the
A → X process, the results were found to be in excellent
agreement with those of Stancil et al. (1993).
Whereas at low temperatures the C → X process is by far
the most efficient one (its rate coefficient is more than six orders of magnitude larger
than for A → X), the
E → X process becomes more efficient at very high
temperatures (in the range of 104 to 105 K) with rate coefficients
more than an order of magnitude larger than for A → X.
Stimulation of the radiative association by black-body radiation was shown here to be
important for the A → X reaction at temperatures up to
about 1000 K. For background radiation temperatures of a few thousand K, the increase of the
rate coefficient in this temperature range can be by about an order of magnitude and more.
Acknowledgments
L.A. acknowledges funding from the Grant Agency of the Charles University in Prague – GAUK (Grant no. 550112). L.A. and V.Š. also appreciate support of the Czech Science Foundation – GAČR (Grant No. P208/11/0436).
References
- Ackermann, J., & Hogreve, H. 1991, Chem. Phys., 157, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Augustovičová, L., Špirko, V., Kraemer, W. P., & Soldán, P. 2012, Chem. Phys. Lett., 531, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bawagan, A. D. O., & Davidson, E. R. 1997, Chem. Phys. Lett., 266, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. 1978, ApJ, 222, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Carrington, A., Pyne, C. H., & Knowles, P. J. 1995, J. Chem. Phys., 102, 5979 [NASA ADS] [CrossRef] [Google Scholar]
- Cencek, W., & Rychlewski, J. 1995, J. Chem. Phys., 102, 2533 [NASA ADS] [CrossRef] [Google Scholar]
- Connor, J. N. L., & Smith, A. D. 1981, Mol. Phys., 43, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Cooley, J. W. 1961, Math. Comput., 15, 363 [Google Scholar]
- Flower, D., & Roueff, E. 1979, A&A, 72, 361 [NASA ADS] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, V. P., Tripathi, B. M., Joshi, G. C., & Pande, M. C. 1988, Ap&SS, 147, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, V. P., Joshi, G. C., & Pande, M. C. 1992, Ap&SS, 197, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G., Lynas-Gray, A., Miller, S., & Tennyson, J. 2004, ApJ, 617, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, T. S., & Rabitz, H. 1996, J. Chem. Phys., 104, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, T. S., & Rabitz, H. 2000, J. Chem. Phys., 113, 3960 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y., & Le Roy, R. J. 2003, J. Chem. Phys., 119, 7398 [NASA ADS] [CrossRef] [Google Scholar]
- , erratum 2007, J. Chem. Phys., 126, 9904 [Google Scholar]
- Ignjatovic, L. M., Mihajlov, A. A., Sakan, N. M., Dimitrijevic, M. S., & Metropoulos, A. 2009, MNRAS, 396, 2201 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., & Chanmugam, G. 1990, Rep. Prog. Phys., 837, 53 [Google Scholar]
- Le Roy, R. J. 2005, LEVEL 7.7: A Computer Program for Solving the Radial Schrödinger Equation CPRR-661 [Google Scholar]
- Le Roy, R. J., & Liu, W. 1978, J. Chem. Phys., 69, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Metropoulos, A., Nicolaides, C. A., & Buenker, R. J. 1987, Chem. Phys., 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Numerov, B. 1933, Math. Comput., 2, 188 [Google Scholar]
- Pachucki, K., & Sapirstein, J. 2000, Phys. Rev. A, 63, 504 [CrossRef] [Google Scholar]
- Ralchenko, Y., Kramida, A. E., Reader, J., & Team, N. A. 2010, NIST Atomic Spectra Database (version 3.1.5), see http://physics.nist.gov/asd3 [Google Scholar]
- Soldán, P., & Hutson, J. M. 2000, J. Chem. Phys., 112, 4415 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C. 1994, J. Quant. Spec. Radiat. Transf., 51, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., & Dalgarno, A. 1997, ApJ, 479, 543 [Google Scholar]
- Stancil, P. C., Babb, J. F., & Dalgarno, A. 1993, ApJ, 414, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Tung, W., Pavanello, M., & Adamowicz, L. 2012, J. Chem. Phys., 136, 104309 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Manby, R. R., et al. 2010, Molpro, version 2010.2. A package of ab initio programs, see http://www.molpro.net [Google Scholar]
- Xie, J., Poirier, B., & Gellene, G. 2005, J. Chem. Phys., 122, 310 [Google Scholar]
- Yan, Z., & Babb, J. F. 1998, Phys. Rev. A, 58, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Zygelman, B., & Dalgarno, A. 1990, ApJ, 365, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Zygelman, B., Stancil, P. C., & Dalgarno, A. 1998, ApJ, 508, 151 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Molecular characteristics of the potential energy curves used in the cross-section
calculations of the 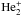 radiative
association.
radiative
association.
Resonance situation overview for the three studied processes of the
 radiative
association.
radiative
association.
Values of the total rate coefficients for the three spontaneous processes of the
 radiative
association.
radiative
association.
All Figures
 |
Fig. 1 Cross sections for spontaneous (Tb = 0 K) radiative
association of |
| In the text | |
 |
Fig. 2 Rate coefficients for spontaneous (Tb = 0 K) radiative
association of |
| In the text | |
 |
Fig. 3 Cross sections for the stimulated radiative association
A → X process in
|
| In the text | |
 |
Fig. 4 Rate coefficients for the stimulated radiative association
A → X process in
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


