| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220803 | |
| Published online | 16 May 2013 | |
Laboratory measurement of optical constants of solid SiO and application to circumstellar dust
1 Universität Heidelberg, Kirchhoff-Institut für Physik, Im Neuenheimer Feld 227, 69120 Heidelberg, Germany
2 Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
e-mail: gail@uni-heidelberg.de
3 Universität Heidelberg, Institut für Geowissenschaften, Im Neuenheimer Feld 234–236, 69120 Heidelberg, Germany
Received: 28 November 2012
Accepted: 13 March 2013
Context. Silicate minerals belong to the most abundant solids that form in cosmic environments. Their formation requires that a sufficient number of oxygen atoms per silicon atom are freely available. For the standard cosmic element mixture this can usually be taken for granted, but it becomes a problem at the transition from the oxygen-rich chemistry of M-stars to the carbon-rich chemistry of C-stars. In the intermediate type S-stars, most of the oxygen and carbon is consumed by formation of CO and SiO molecules, and left-over oxygen to build SiO4-tetrahedrons in solids becomes scarce. Under such conditions SiO molecules from the gas phase may condense into solid SiO. The infrared absorption spectrum of solid SiO differs from that of normal silicates by the absence of Si-O-Si bending modes around 18 μm whereas the absorption band due to Si-O bond stretching modes at about 10 μm is present. Observations show that exactly this particular characteristic can be found in some S-star spectra.
Aims. We demonstrate that this observation may be explained by the formation of solid SiO as a major dust component at C/O abundance ratios close to unity.
Methods. The infrared absorption properties of solid SiO are determined by laboratory transmission measurements of thin films of SiO produced by vapour deposition on a Si(111) wafer in the range between 100 cm-1 and 5000 cm-1 (2 μm and 100 μm). From the measured spectra the dielectric function of SiO is derived by using a Brendel-oscillator model, particularly suited to the representation of optical properties of amorphous materials. The results are used in model calculations of radiative transfer in circumstellar dust shells with solid SiO dust in order to determine the spectral features due to SiO dust.
Results. Comparison of synthetic and observed spectra shows that reasonable agreement is obtained between the main spectral characteristics of emission bands due to solid silicon monoxide and an emission band centred on 10 μm, but without the accompanying 18μm band, observed in some S-stars. We propose that solid SiO is the carrier material of this 10 μm spectral feature.
Key words: circumstellar matter / stars: mass-loss / stars: chemically peculiar / stars: AGB and post-AGB
© ESO, 2013
1. Introduction
Silicon monoxide, SiO, is one of the most abundant and stable molecules encountered in space. It is found to be present in many astronomical objects by observing its infrared molecular bands. Usually (but not exclusively) it is found in objects where rather warm (T > 1000 K) gaseous material exists, such as in circumstellar dust shells. At lower temperatures the SiO molecules tend to associate with Mg, Fe, and O (available as H2O) from the gas phase to form solid magnesium-iron silicates – the main components of cosmic dust – and some additional minor condensed phases also bearing Al and/or Ca. Alternatively the SiO molecules may also condense to a solid material of their own, the silicon monoxide solid. Solid SiO is a well known material of significant technical importance, since it is widely used for optical purposes as anti-reflection coating. Despite its technical use, the properties of SiO are not well known, and its lattice structure remains enigmatic.
In astrophysics, solid SiO has not yet been detected as a separate dust component. In the early discussions on the nature of interstellar medium (ISM) dust, it was taken into consideration as a possible ISM dust component (Duley et al. 1978; see also Millar 1982, and references therein), until amorphous silicates (olivine, pyroxene) were identified as carriers of the observed infrared features at 9.7 μm and 18 μm. The formation of silicon monoxide has been thought, however, to be an important intermediate step in the formation of silicate dust for the following reasons:
-
The backbone of the silicate mineral structure is the SiO4-tetrahedron with four oxygen atoms attached to a silicon atom. The silicate minerals detected in space are usually identified by the stretching and bending vibrational modes of this particular structure.
-
On the molecular level there are no gas phase species with a comparable structure (at least not in detectable amounts).
It is necessary, therefore, that the initial stages of the condensation of silicates involve some different kind of material. Because of the high abundance of SiO molecules in matter with standard cosmic elemental abundances, it has been speculated since the early 1980s that condensation of SiO may be the very initial step of silicate formation (Nuth & Donn 1982; Gail & Sedlmayr 1986, 1998a,b; Nuth & Ferguson 2006; Reber et al. 2006). It is assumed that silicon monoxide clusters are initially formed that serve as seed particles for growth of the silicates.
The possibility exists, however, that the silicon monoxide seeds finally grow to a dust species of their own in a number of cases. The formation of silicates requires the free availability of enough oxygen to build the SiO4-tetrahedrons in silicates. This is usually not a problem since the oxygen abundance in the standard cosmic element mixture is about twice the carbon abundance and about sixteen-fold the silicon abundance (cf. Lodders et al. 2009). Even after formation of the extremely stable CO and SiO molecules, enough oxygen remains available to form the SiO4-tetrahedrons of silicate minerals from SiO. However, this does not hold during the whole lifetime of stars. During the evolution of low- and intermediate-mass stars on the asymptotic giant branch (AGB) the C/O abundance ratio stepwise increases once “third dredge-up” starts to operate. In a number of steps this drives the C/O abundance ratio to values exceeding unity, thereby passing through a stage where the C/O ratio is close to unity. During this stage the stars show the characteristic chemical peculiarities of the S-stars. Then almost all oxygen is used up by the formation of CO and SiO, and with increasing C/O abundance ratio only a decreasing fraction of the SiO molecules can finally be converted into silicate dust because of the decreasing fraction of oxygen left over after SiO and CO formation. Since it is possible to form a solid material with chemical composition SiO by condensating SiO vapour, the possibility arises of forming this kind of material in stellar outflows from S-stars where the available oxygen becomes scarce due to “third dredge-up”.
Recently some observational results for infrared emission from dust in S-stars have been published that show spectral characteristics that cannot be explained by the standard amorphous silicate dust (Hony et al. 2009; Sacuto et al. 2008; Smolders et al. 2012). For these stars the emission feature at about 10 μm is as strong as usual, but the concomitant feature of silicate dust at 18 μm is very weak or even seems to be missing entirely. By inspecting the spectra published by Chen & Kwok (1993), one finds some additional objects sharing this special property. In our opinion this property is a clear signature of the emission from solid silicon monoxide dust. In this material one has Si-O bonds as in silicates, which give rise to the stretching vibrations that are the origin of the broad 10 μm feature of amorphous silicates, but one has no Si-O-Si bending modes as in SiO4-tetrahedrons, which are the origin of the 18 μm feature of silicates. Theoretically, this feature does not exist for solid silicon monoxide, but in practice, since solid silicon monoxide is prone to disintegrate into silicon nano-clusters and SiO2 (e.g. Hohl et al. 2003; van Hapert et al. 2004), the 18 μm feature is not completely absent but weak. In S-stars with some oxygen left over after formation of CO and SiO molecules, part of the SiO may form some silicate material, whereas the bulk of the SiO molecules condense into solid silicon monoxide. This would give rise to an unusually weak 18 μm feature compared to the 10 μm feature.
In this paper we attempt to show that the observational finding of S-stars with strong 10 μm emission feature and a weak or absent 18 μm feature can be explained by condensation of solid silicon monoxide in their outflows at C/O abundance ratios close to unity where chemically available oxygen is lacking to form silicates. For this purpose we calculate radiative transfer models of circumstellar dust shells with silicon monoxide dust and compare the resulting spectra with published spectra of S-stars.
For these radiative transfer calculations one needs the dielectric function of solid silicon monoxide to calculate the extinction coefficient. Because this material is used for optical purposes the complex index of refraction is known from the middle infrared to the extreme UV and data are listed, e.g., in Palik (1985). More recent determinations are given by Tazawa et al. (2006). During the course of our laboratory studies on materials of astrophysical interest (Klevenz 2009; Wetzel 2012), the far-infrared optical properties have been determined with high accuracy. We briefly describe the measurements and their results in this paper. In particular, the dielectric function is determined by fitting a Brendel-oscillator model (Brendel & Bormann 1992) to experimental results. This model is particularly suited to describing infrared optical properties of amorphous materials in contrast to the widely used Lorentz-oscillator model that is more suited to crystalline materials. The 10 μm feature of silicon monoxide is always diffuse like the corresponding feature of amorphous silicate materials. The lattice structure of solid silicon monoxide is not well known, but a crystalline phase does not seem to exist.
The plan of this paper is as follows. In Sect. 2 we briefly describe our laboratory measurements of the optical properties of solid SiO and the results for the dielectric function. In Sect. 3 we give our arguments why solid SiO could form in outflows from S-stars. Section 4 describes the radiative transfer models and gives the results.
2. Optical properties of SiO
To study the mid-infrared (MIR) optical properties of SiO spectroscopic transmittance, measurements were performed in situ on condensed SiO films produced by evaporation under UHV conditions. After the experiment the film was measured ex situ in the far-infrared (FIR). The dielectric function of solid SiO is derived via Brendel-oscillator fits to the experimental IR spectra.
2.1. Experimental setup
The experiments were performed under UHV conditions (base pressure <10-10 mbar). IR spectra were taken in the MIR range between 500 cm-1 and 5000 cm-1 with a Fourier-transform IR spectrometer (Bruker IFS66v/S with deuterium triglycine sulfate (DTGS) detector and evacuated beam path (4 mbar)). The IR spectra were measured in transmittance geometry at normal incidence of light. A floating zone Si(111) wafer with dimensions of 10 × 10 mm2 and a thickness of 0.740 mm and high resistivity was used as transparent substrate. Spectra were taken in situ, i.e., during the growth of the evaporated film on the substrate (spectral resolution of 4 cm-1), and normalized to the spectrum of the bare Si(111) taken directly before deposition. This method allows monitoring the whole growth process and detecting changes due to the film growth.
 |
Fig. 1 Relative transmittance spectra of SiO on Si(111) are shown for increasing film thicknesses up to 57 nm. The thickness change between two shown spectra is about 6.3 nm. The strong peak at 983 cm-1 is attributed to the asymmetric Si-O stretching vibration (Cachard et al. 1971). For such film thicknesses, there is clearly no shift in that peak. SiO oscillator positions are indicated by dashed lines. |
Commercial SiO (Mateck, silicon monoxide, SiO, 99.9% pure, − 325 mesh, CAS no. 10097-28-6) was evaporated from a tantalum Knudsen cell heated by electron bombardment. The background pressure measured during evaporation away from the SiO molecular beam did not exceed 1 × 10-9 mbar. The SiO deposition rate was determined before and after the spectroscopic experiment with a quartz crystal microbalance with a relative error up to 5%. This error is caused by the uncertainty in the density of the evaporated film in the thickness calculation for which the density of bulk SiO (2.18 g/cm3) was taken (Hass & Salzberg 1954). Further experimental details can be found in Wetzel et al. (2012a).
In addition to the in situ measurement in the MIR that was explained above we also characterized the sample in the far-infrared (FIR) after transferring it to ambient conditions. These ex situ measurements in the range between 100 cm-1 and 600 cm-1 were performed in the sample compartment of a Bruker Vertex80v with a special FIR-DTGS detector and a mylar beam splitter. The sample compartment and beam path was evacuated to 3 mbar during the measurement. The MIR and FIR measurements show a good match in the overlapping region and can be easily connected as shown in Wetzel (2012). With this method we can obtain experimental IR spectra in the range between 100 cm-1 and 5000 cm-1 (2 μm and 100 μm).
2.2. Results
In Fig. 1 relative transmittance spectra of SiO with increasing film thicknesses are shown. The films were produced by SiO evaporation and subsequent condensation on a Si(111) substrate hold at 300 K. Two broad features develop with growing film thickness. The stronger one at 983 cm-1 is assigned to the asymmetric stretching mode of the oxygen atom in a Si-O-Si bridge against the Si-neighbour atoms (Philipp 1971; Chabal et al. 2002; Queeney et al. 2004; Cachard et al. 1971; Lehmann et al. 1983, 1984). The much weaker structure at approximately 715 cm-1 corresponds to the Si stretching mode, a mode with dominating Si displacement (Lehmann et al. 1983), sometimes called “bending" mode in the literature. It is important to note that already from 1 nm the IR spectral features of the evaporated SiO films no longer change (Klevenz et al. 2010b). Accordingly, the IR dielectric function of the evaporated film already resembles that of bulk SiO (Hjortsberg & Granqvist 1980; Tazawa et al. 2006; Klevenz et al. 2010a). After the in situ measurement the SiO film with the final film thickness auf 57 nm was measured in the FIR. In Fig. 2 the composed spectrum from both measurements is shown where a third strong peak at 384 cm-1 caused by the rocking mode can be identified.
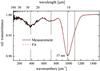 |
Fig. 2 Normal transmittance measurement of an evaporated SiO film (black solid line) with 57 nm thickness shown together with the best fit by a Brendel-model of the dielectric function as described in the text. Peak positions are indicated by dashed lines. |
2.3. Dielectric function
For thin dielectric films with the thickness d of the film that is much smaller than the wavelength λ (d ≪ λ), approximate formulas for the transmittance can be derived based on the Fresnel equations (Berreman 1963). For a thin layer on a thick (non-interfering) substrate the normal transmittance (φ = 0°) is given by (Lehmann 1988; Teschner & Hübner 1990) 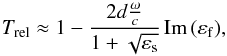 (1)with ω = 2πc/λ, εs as the dielectric function of the substrate and εf as the dielectric function of the film. In transmittance measurements under normal incidence (φ = 0°), therefore, only the transverse optical (TO) modes can be observed with frequency at the maximum of the imaginary part of the dielectric function ε and with a dynamic dipole moment parallel to the surface.
(1)with ω = 2πc/λ, εs as the dielectric function of the substrate and εf as the dielectric function of the film. In transmittance measurements under normal incidence (φ = 0°), therefore, only the transverse optical (TO) modes can be observed with frequency at the maximum of the imaginary part of the dielectric function ε and with a dynamic dipole moment parallel to the surface.
To determine the dielectric function of SiO in the IR from such thin film measurements, an appropriate model for the dielectric function has to be used. A simple Lorentz-oscillator model cannot be applied in our case owing to the amorphous character of the film. The model introduced by Brendel & Bormann (1992) accounts for the amorphous structure of a material by assuming that the different IR modes can be represented by Lorentz-oscillators, but with randomly shifted resonance frequencies that are distributed according to a Gaussian probability distribution. The dielectric function in the IR is therefore assumed in this model to be given by the relation 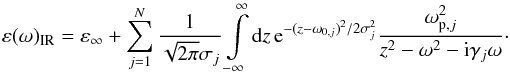 (2)It consists of a dielectric background ε∞ and N distributions of Lorentz oscillators with resonance frequencies ω0,j, damping constants γj, plasma frequencies ωp,j, and with standard deviations σj of the Gaussian probability distributions.
(2)It consists of a dielectric background ε∞ and N distributions of Lorentz oscillators with resonance frequencies ω0,j, damping constants γj, plasma frequencies ωp,j, and with standard deviations σj of the Gaussian probability distributions.
 |
Fig. 3 Dielectric function obtained from the best fit with four Brendel oscillators to the transmittance data shown in Fig. 2. |
The composed spectrum of Fig. 2 was fitted with such a Brendel dielectric function using four oscillators, similar to a procedure for SiO2 (Kirk 1988), which results in very good agreement. We performed the spectral fits in the range between 100 cm-1 and 1400 cm-1 using the software package SCOUT (Theiss 2011). For the high-frequency limit ε∞ of the dielectric function, a value of 3.61 was taken from the literature (Hjortsberg & Granqvist 1980). Since the oscillator damping constant γ cannot be properly determined from fits to vibration spectra of disordered solids (cf. Ishikawa et al. 2000), we fixed the value of γ to the resolution of our measurement of 4 cm-1. Nearly the same kind of procedure has already been reported in the literature (Ishikawa et al. 2000; Brendel & Bormann 1992; Grosse et al. 1986; Naiman et al. 1985). The result of the best fit is also plotted in Fig. 2, and the corresponding dielectric function of SiO in the IR is shown in Fig. 3. Our parameters of the best fit for the oscillator model are given in Table 1.
This result for a substrate temperature of 300 K confirms our previously published data (Klevenz et al. 2010a,b; Wetzel et al. 2012a) but extends the wavelength range into the far-infrared.
Brendel oscillator parameters for the dielectric function from the temperature dependent condensation and annealing experiments of Wetzel et al. (2012a).
2.4. Temperature dependence
Other substrate temperatures than 300 K result in shifted peak positions. This is discussed in detail in Wetzel et al. (2012a). In Table 2 the corresponding oscillator parameters for temperatures from 40 K to 873 K are summarized. It is important to note that the rocking mode around 400 cm-1 was not measured in the experiments of Wetzel et al. (2012a), so the data for temperatures different from 300 K are only valid above 500 cm-1. For temperatures below 350 K, the oscillator data are taken from condensation experiments, and the results for temperatures above 350 K are based on annealing experiments in which a 100 nm-thick SiO film was annealed at a number of gradually increased temperatures for 100 min. To take the observed splitting of the peak around 730 cm-1 for higher temperatures into account, the data were re-evaluated with two oscillators for the Si stretching mode. In Fig. 4 relative transmittance spectra at 300 K of SiO and SiO2 are compared to the spectrum of a SiO film that was annealed at 873 K. The splitting of the Si stretching mode is clearly visible, and the peak (3a) around 800 cm-1 gets stronger compared to the peak 3b with increasing temperature indicating the partial decomposition of SiO into Si and SiO2 (Wetzel et al. 2012a).
 |
Fig. 4 Simulated spectra at 300 K for SiO (oscillator data from Table 1) and SiO2 (oscillator data from Wetzel 2012) compared to the measurement of a SiO film that was annealed at 873 K. The spectra are shifted against each other, and the dashed lines indicate the oscillator position of the Si stretching mode of SiO and SiO2, respectively. |
 |
Fig. 5 Fit of the coefficients of the Brendel oscillator model for the dielectric function of solid SiO at a number of temperatures by a linear temperature variation. The various data points correspond to data from Tables 1 and 2 for oscillator parameters at different temperatures. Full lines show the linear fit (3). The vertical dotted line indicates the limit between the temperature ranges where data are obtained either from thin films made by vapour deposition on a substrate with given temperature or from thin films deposited at low temperature and annealed at high temperatures. |
Fit coefficients for the temperature dependent oscillator parameters of the Brendel model for the dielectric function.
2.5. Absorption efficiency
The data for the coefficients of the Brendel oscillator model at different temperatures given in Tables 1 and 2 are fitted with a linear relation 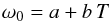 (3)(and analogous for ωp and σ) by the least square method using the corresponding option in gnuplot1. The coefficients a and b are given in Table 3 and the fit is shown in Fig. 5. The complex dielectric function ελ(T) is calculated for different temperatures from the Brendel oscillator model with temperature-dependent parameters given by these approximations, including the fourth oscillator from Table 1, which is treated as temperature-independent because no data for its temperature dependence are presently available.
(3)(and analogous for ωp and σ) by the least square method using the corresponding option in gnuplot1. The coefficients a and b are given in Table 3 and the fit is shown in Fig. 5. The complex dielectric function ελ(T) is calculated for different temperatures from the Brendel oscillator model with temperature-dependent parameters given by these approximations, including the fourth oscillator from Table 1, which is treated as temperature-independent because no data for its temperature dependence are presently available.
We have calculated the dielectric function ε(ω) according to Eq. (2) for a set of temperatures and, from this, the absorption efficiencies 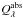 of spherical grains by means of Mie-theory (see Bohren & Huffman 1983). Figure 6 shows the result for the spectroscopically relevant wavelength range for particles with radius of 0.1 μm and for a number of different temperatures. The absorption spectrum is clearly dominated by the strong Si-O bond stretching mode. This feature peaks at a wavelength close to 10 μm for completely amorphous material formed at very low temperatures. From the other oscillators only subordinate variations of
of spherical grains by means of Mie-theory (see Bohren & Huffman 1983). Figure 6 shows the result for the spectroscopically relevant wavelength range for particles with radius of 0.1 μm and for a number of different temperatures. The absorption spectrum is clearly dominated by the strong Si-O bond stretching mode. This feature peaks at a wavelength close to 10 μm for completely amorphous material formed at very low temperatures. From the other oscillators only subordinate variations of 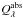 result. The peak position of the strong absorption band depends on the temperature up to which the material has been heated or at which it has been formed and shifts towards shorter wavelengths with increasing temperature. This change of
result. The peak position of the strong absorption band depends on the temperature up to which the material has been heated or at which it has been formed and shifts towards shorter wavelengths with increasing temperature. This change of 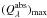 with temperature is caused by a partial decomposition of the solid SiO into a SiO2 matrix and nano-m sized Si clusters (Hohl et al. 2003) at elevated temperature. The peak position of the absorption feature shifts by this change in micro-structure in the direction towards the peak position of the corresponding SiO2 feature at 8.6 μm if temperatures increase.
with temperature is caused by a partial decomposition of the solid SiO into a SiO2 matrix and nano-m sized Si clusters (Hohl et al. 2003) at elevated temperature. The peak position of the absorption feature shifts by this change in micro-structure in the direction towards the peak position of the corresponding SiO2 feature at 8.6 μm if temperatures increase.
It has to be observed that the temperature does not correspond to the actual temperature of a dust particle in a circumstellar environment but to the highest temperature that the particle has seen so far. A second point to be observed is that the peak position of the absorption band shifts somewhat if particles are not spherical, usually to longer wavelengths (e.g. Henning & Mutschke 2010).
3. Astrophysical applications
In this section we discuss the possibility that solid silicon monoxide might be an important dust species in the dust shells of S-stars.
3.1. S-stars
Low- and intermediate-mass stars from the range of initial masses below ≈8 M⊙ evolve until the very end of their lives to the thermally pulsing asymptotic giant branch (TP-AGB) where they are composed of an electron-degenerated core of carbon and some oxygen, resulting from He-burning, an overlying layer of mainly He, itself resulting from H-burning via the CNO-cycle and an enormously extended hydrogen rich envelope. On the TP-AGB the stars alternatively burn either (i) H in a shell source at the interface between the H-rich envelope and the He layer for a period of several thousand years or (ii) He in a shell-source at the interface between the He layer and the carbon-oxygen core for a period of about 200 yr. During the short burning phase of He (the thermal pulse), the He layer is fully convective from bottom to top for part of the time and distributes freshly synthesized carbon from the He-burning shell at the bottom of the He layer over the whole layer. Somewhat later in the pulse phase, the convection zone of the fully convective hydrogen envelope briefly dips into the upper parts of the He layer and mixes some carbon-rich material into the outer envelope. As a result, after each thermal pulse the carbon abundance of the envelope increases stepwise. The oxygen abundance in the envelope remains almost unchanged by this process because only very little oxygen is synthesized by He-burning in TP-AGB stars. Thus, the carbon-to-oxygen abundance ratio (C/O) in the envelope changes from its initial value of ≈0.5, corresponding to the C/O of the cosmic standard element mixture (see, e.g., Lodders et al. 2009), to C/Os far exceeding a value of unity.
 |
Fig. 6 Absorption efficiency |
For most of the stars on the TP-AGB, the C/O falls – after mixing carbon from the core into the envelope during a thermal pulse – for one or two inter-pulse phases into the critical range between about 0.9 and 1.0 where the chemical composition of the material in the stellar photosphere dramatically changes from an oxygen-compound-dominated composition for a C/O below 0.9 and a hydrocarbon-dominated composition for a C/O exceeding 1.0. This switching of the chemical composition is brought about by the extraordinary stability of the CO molecule that by its formation almost completely consumes the less abundant of the two elements C and O. Only part of the TP-AGB stars leap over the critical range of C/O abundance ratios during a single thermal pulse.
In the intermediate abundance range of C/O ratios between 0.9 and 1.0, the stellar spectrum is dominated by molecular bands of some low-abundance elements that are seen neither in M-Stars (C/O ≲ 0.9) nor in C-stars (C/O ≳ 1.0). These stars are the so-called S-stars. They are much less abundant than M-stars or C-stars since stars on the TP-AGB suffer numerous thermal pulses, but only during one or two inter-pulse phases are they S-stars.
For these S-stars the material that flows out from the stellar surface can form neither the silicate dust that is seen in circumstellar dust shells around M-stars nor the graphite and SiC dust seen in dust shells around C-stars. This is because the excess oxygen over carbon, which is not bound in CO molecules, is too rare to combine with all of the silicon to the SiO4-tetrahedrons that form the backbone of silicate minerals. At the same time no excess carbon is available to form solid carbon.
The details of the chemistry of dust formation in outflows from S-stars is discussed in Ferrarotti & Gail (2002). Because of the very high bond energy of the SiO molecule – not as high as for CO, but also exceptionally high – the silicon is bound in this molecule, and the excess of the oxygen not bound in SiO and CO forms H2O. Some quantities of silicate dust may be formed in outflows from S-stars if C/O is not too close to unity, because then SiO molecules react with the leftover H2O and with Mg (and/or Fe). Indeed, weak emission bands showing the characteristic two peaks around 9.7 μm and 18 μm are seen in the infrared spectrum of a number of S-stars (Chen & Kwok 1993; Lloyd Evans & Little-Marenin 1999). It is argued by Ferrarotti & Gail (2002) that iron dust also may be formed and may be an abundant dust species for S-stars. This dust would be hard to detect observationally for optically thin dust shells, since its smooth and featureless extinction would act as a more or less grey opacity source. For optically thick shells, it is likely that this is mistaken to be carbon dust because of largely indistinguishable extinction properties of iron and carbon dust.
3.2. Why solid silicon monoxide?
If the abundance of excess oxygen not bound in CO and SiO tends to zero for C/O approaching unity, the possibility exists that SiO molecules start to condense as a solid of their own. This has not yet seriously been considered as a dust component in circumstellar dust shells, though it was discussed several times whether it could be the first condensate to form the necessary seed particles for silicate dust formation (Nuth & Donn 1982; Gail & Sedlmayr 1986, 1998a,b; Nuth & Ferguson 2006; Reber et al. 2006). This is a crucial question for cosmic dust formation since it is not possible to form the necessary seed particles for silicate dust growth from a material with the composition and lattice structure of one of the many silicate minerals.
The main reason solid SiO was not considered as one of the major dust materials in circumstellar shells was the seemingly high vapour pressure from which one predicts a rather low condensation temperature under the low-pressure conditions of circumstellar dust shells. New determinations of the vapour pressure of solid SiO (Ferguson & Nuth 2008, 2012; Wetzel et al. 2012b) have now shown that the older measurements were seriously in error and had strongly overestimated the vapour pressure. Our own results (Wetzel et al. 2012b, Gail et al., in prep.) can be approximated by a vapour pressure formula for the equilibrium pressure of SiO molecules over solid silicon monoxide 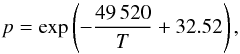 (4)where the pressure is in units of dyn cm-2 (as usual in astrophysics). Our results (Wetzel et al. 2012b) extend the range of measured vapour pressures down to the pressure range relevant to circumstellar dust shells. Only moderate extrapolation of vapour pressures measured at higher temperatures in the laboratory to the lower temperatures of circumstellar dust condensation is required. The details will be discussed in a separate paper.
(4)where the pressure is in units of dyn cm-2 (as usual in astrophysics). Our results (Wetzel et al. 2012b) extend the range of measured vapour pressures down to the pressure range relevant to circumstellar dust shells. Only moderate extrapolation of vapour pressures measured at higher temperatures in the laboratory to the lower temperatures of circumstellar dust condensation is required. The details will be discussed in a separate paper.
 |
Fig. 7 Stability limits against vaporization of some refractory compounds formed from an oxygen-rich element mixture with cosmic standard element abundances, and of solid SiO. Dashed line: typical pressure-temperature combinations in an outflowing gas element for a stellar wind model with stationary outflow and Ṁ = 5 × 10-6 M⊙ yr-1 (here for an M-star). Most parts of the dust condensation occur around the knee where the velocity turns from subsonic (horizontal part of the curve) to highly supersonic (steep descending part of the curve) outflow. Pressures are typically 10-8 bar to 10-10 bar in the region of main dust growth. |
Figure 7 shows the resulting stability limit against evaporation in chemical equilibrium for the astrophysically important silicates, for solid iron, and for solid SiO, calculated by using the new results for the vapour pressure of solid SiO and thermochemical data from Barin (1995) for the other materials, for the case of standard cosmic element abundances (Asplund et al. 2005; Lodders et al. 2009). At C/Os close to unity, no silicates can be formed in S-stars because of a lack of freely available oxygen to convert a significant fraction of the SiO molecules from the gas phase into the SiO4-tetrahedrons in silicate minerals (e.g., for a C/O ratio of 0.95 only about 20% of the Si can condense as silicate dust). Then the SiO molecules may condense instead into solid disordered SiO. At a typical pressure of p = 10-8 bar → p = 10-10 bar in the dust condensation layer of circumstellar dust shells (see Fig. 7), the SiO would become stable against evaporation at about 950 K → 1050 K. This is high enough that such dust could be observed as warm dust in a circumstellar dust shell. Solid SiO is thus a candidate dust material to be observed in S-stars.
A lack of oxygen to form normal silicates may also be encountered in massive supergiants if the outer layers are peeled off by mass loss and material that has burned H via the CNO-cycle and evolved to isotopic equilibrium appears at the surface. Then the O abundance may drop to values close to the Si abundance, and solid SiO may also form in the outflows from such stars.
Whether this material really forms can be tested observationally. The absorption properties of solid SiO are sufficiently different from normal silicate materials that they can be distinguished by their spectral features. Amorphous olivine and pyroxene both show two strong absorption features centred on 9.7 μm and 18 μm, which are usually observed as emission features in the infrared spectra from circumstellar dust shells. For SiO the strong feature at 18 μm is missing because this corresponds to rocking modes in the SiO4-tetrahedron, but a strong feature at about 10 μm is present because this originates from Si-O bond stretching vibrations. As a result, the presence of a strong 10 μm feature without a strong 18 μm feature is diagnostic for solid SiO.
These characteristics have, indeed, been observed for a number of S-star spectra (Hony et al. 2009; Smolders et al. 2012), and one may speculate that they result from solid SiO as a major dust component in such dust shells. To test this hypothesis we performed radiative transfer calculations using our new results for the dielectric function of SiO.
Some data used for calculating the opacity of the dust species considered in the model calculations and the corresponding key elements.
3.3. Growth of silicon monoxide grains
Now we turn to the question whether growth of silicon monoxide is kinetically possible. Consider the simple approximation of a spherical dust grain co-moving with the outflowing gas collects SiO molecules from the gas phase. For simplicity we neglect evaporation. The equation of growth of radius a for a single grain is 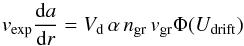 (5)if we introduce by dr = vexpdt the radial coordinate instead of time as an independent variable, vexp being the outflow velocity.
(5)if we introduce by dr = vexpdt the radial coordinate instead of time as an independent variable, vexp being the outflow velocity.
The meaning of the quantities in the growth equation is as follows: Vd is the volume of one chemical formula unit in the condensed phase 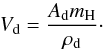 (6)Here Ad is the atomic weight of the condensed phase and ρd its mass density. Numerical values are given in Table 4.
(6)Here Ad is the atomic weight of the condensed phase and ρd its mass density. Numerical values are given in Table 4.
The quantity α is the growth coefficient. This seems to be first measured by Gunther (1958) who found a rather low value of α ≈ 4 × 10-3 in the temperature range 1200 K → 1500 K. Rocabois et al. (1992) made a new determination of the vapour pressure and of the evaporation coefficient α of SiO and found that their results for α can be approximated by 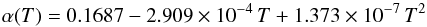 (7)in the temperature range 1175 K to 1410 K. Similar results for α are found by Ferguson & Nuth (2008, 2012) and are essentially confirmed by our own measurements (Wetzel et al. 2012b, Gail et al., in prep.) which can be approximated by
(7)in the temperature range 1175 K to 1410 K. Similar results for α are found by Ferguson & Nuth (2008, 2012) and are essentially confirmed by our own measurements (Wetzel et al. 2012b, Gail et al., in prep.) which can be approximated by 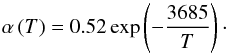 (8)Extrapolating these results down to a temperature of 1000 K results in α ≈ 0.013. This value is used in the following considerations.
(8)Extrapolating these results down to a temperature of 1000 K results in α ≈ 0.013. This value is used in the following considerations.
The quantity ngr is the particle density of the growth species. If we concentrate on the initial growth phase where not much of the growth species has been consumed from the gas phase, we can approximate ngr by 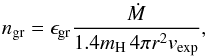 (9)where ϵgr is the element abundance of the element (Si in our case) that determines the gas-phase abundance of the growth species. The second quantity on the right hand side is the density of H nuclides in a spherically symmetric, stationary outflow with velocity vexp and mass-loss rate Ṁ.
(9)where ϵgr is the element abundance of the element (Si in our case) that determines the gas-phase abundance of the growth species. The second quantity on the right hand side is the density of H nuclides in a spherically symmetric, stationary outflow with velocity vexp and mass-loss rate Ṁ.
The quantity 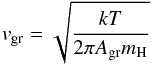 (10)is the thermal velocity of the growth species (SiO molecules in our case) and Agr their molecular weight, while
(10)is the thermal velocity of the growth species (SiO molecules in our case) and Agr their molecular weight, while 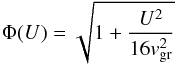 (11)is a correction factor for particle drift relative to the gas with relative velocity U. If U ≫ 4vgr the particle drift is supersonic with respect to the thermal velocity of the growth species (not the carrier gas!); then
(11)is a correction factor for particle drift relative to the gas with relative velocity U. If U ≫ 4vgr the particle drift is supersonic with respect to the thermal velocity of the growth species (not the carrier gas!); then 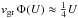 . Typical values of all these quantities required for calculating SiO growth are given in Table 5.
. Typical values of all these quantities required for calculating SiO growth are given in Table 5.
Data used for calculation of silicon monoxide growth.
For the following we assume the outflow velocity vexp in the region of dust growth to be constant. This is not completely correct since dust condensation results in an acceleration of the wind, but the velocity increase is moderate if we consider S-stars. It increases from a velocity of about the sonic velocity (2 km s-1–3 km s-1) at the inner edge of the dust shell to the final outflow velocity that is at most 10 km s-1 for S-stars (e.g. Ramstedt et al. 2006). Then integrating from the inner radius Rc of the dust shell, where dust commences to grow, to infinity we obtain 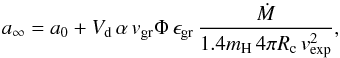 (12)where a0 is the radius of the seed nuclei for dust growth and a∞ the grain radius at infinity. This equation requires that the grain radius a∞ remains smaller than the maximum radius amax, attained if all condensable material is condensed, because the consumption of the growth species is neglected in Eq. (5). The maximum possible radius to which a particle may grow in the outflow is given by
(12)where a0 is the radius of the seed nuclei for dust growth and a∞ the grain radius at infinity. This equation requires that the grain radius a∞ remains smaller than the maximum radius amax, attained if all condensable material is condensed, because the consumption of the growth species is neglected in Eq. (5). The maximum possible radius to which a particle may grow in the outflow is given by 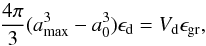 (13)if ϵd is the number of dust grains per hydrogen nucleus. This quantity is not precisely known, so we assume a value of 5 × 10-13 that is a typical value found by observations (Knapp 1985).
(13)if ϵd is the number of dust grains per hydrogen nucleus. This quantity is not precisely known, so we assume a value of 5 × 10-13 that is a typical value found by observations (Knapp 1985).
We can now write 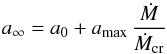 (14)with
(14)with 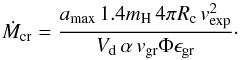 (15)The mass-loss rate Ṁ has to be lower than Ṁcr in order for our assumption to be valid that there is no strong depletion of the gas phase from condensable material.
(15)The mass-loss rate Ṁ has to be lower than Ṁcr in order for our assumption to be valid that there is no strong depletion of the gas phase from condensable material.
Basic parameters of the dust-shell models
For applying this to silicon monoxide condensation we have to specify the values of vexp, Rc, and Φ. All other quantities are given in Table 5. For the outflow velocity we assume a value of vexp = 3 km s-1, which is slightly higher than the sound velocity of the gas, since most of the grain growth proceeds before the gas is accelerated to highly supersonic outflow velocities; otherwise, further growth is suppressed by rapid dilution of the gas. For Rc we assume a value Rc = 3 × 1014 cm, corresponding to about eight stellar radii, see Table 6. For the drift velocity we assume the same value as for vexp since typical drift velocities usually are close to the sonic velocity of the gas, except for very high mass-loss rates where they are much less. With these estimated values we obtain 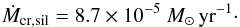 (16)This shows that significant condensation of solid silicon monoxide is kinetically possible, at least for mass-loss rates exceeding 10-6 M⊙.
(16)This shows that significant condensation of solid silicon monoxide is kinetically possible, at least for mass-loss rates exceeding 10-6 M⊙.
The result for Ṁcr,sil depends on the rather uncertain value of α that is determined from extrapolating laboratory measured values (which decrease with decreasing temperature) to much lower temperatures. The value of 0.013 at 1000 K determined this way may be too low. In this case Ṁcr,sil would be overestimated, and the growth of solid silicon monoxide may be even more favourable than in the estimate above.
4. Radiative transfer model for dust shells
4.1. Opacity
The spectral energy distribution of the emission from circumstellar dust shells is determined by the composition of the dust mixture and the properties of the different dust species. Here we concentrate on the special question whether the unusual feature at 10 μm detected in some S-stars could result from solid SiO. Since this feature is the most prominent dust feature in the objects where it has been detected so far (Hony et al. 2009), it also appears to be the most abundant dust species in these objects, apart from possible contributions to opacity from dust species with structure-less pure continuous extinction, such as iron dust grains. Therefore we concentrate on models with solid silicon monoxide as the sole dust component.
In our model calculations we assume the opacity in the shell to be completely determined by the dust components; no contribution of the gas phase is considered. The dust particles are assumed to be small spheres of radius a. The absorption and scattering coefficients of the different dust components, characterized by an index i, are then given by 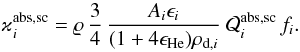 (17)The quantity Ai is the molecular weight corresponding to the chemical formula of the condensed phase, ϵi is the elemental abundance of a characteristic key element that is required to form the condensed phase, and fi is the fraction of the atoms of this element that are really condensed into the solid phase, ρd,i is the mass density of the solid. The quantities
(17)The quantity Ai is the molecular weight corresponding to the chemical formula of the condensed phase, ϵi is the elemental abundance of a characteristic key element that is required to form the condensed phase, and fi is the fraction of the atoms of this element that are really condensed into the solid phase, ρd,i is the mass density of the solid. The quantities 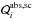 are the absorption and scattering efficiencies, divided by the particle radius a. These quantities are calculated by means of Mie-theory (see Bohren & Huffman 1983) from the dielectric function of the dust material. The basic data used in the calculation of dust extinction are given in Table 4.
are the absorption and scattering efficiencies, divided by the particle radius a. These quantities are calculated by means of Mie-theory (see Bohren & Huffman 1983) from the dielectric function of the dust material. The basic data used in the calculation of dust extinction are given in Table 4.
With respect to the particle shape we consider spherical grains and ellipsoids. If the grains are not spherical, the absorption band profiles of dust grains are distorted, and their centre is shifted compared to the case of spherical grains. SiO grains formed in laboratory condensation experiments from the gas phase generally seem to be almost spherical (Kamitsuji et al. 2004, their Fig. 1a). Though there seems to be no immediately obvious reason why this should be different for the tiny grains condensed in a circumstellar shell and for nanometre-sized laboratory condensed grains, there are indications from presolar silicate dust grains that there are noticeable deviations from sphericity (Vollmer et al. 2009; Bose et al. 2010). Therefore we also use the continuous distribution of ellipsoids (see, e.g., Bohren & Huffman 1983), in order to account for possible non-sphericity effects.
With respect to the particle size we assume the canonical value of a = 0.1 μm that seems to be typical of dust grains in circumstellar shells (e.g. Kruszewski et al. 1968; Jura 1996; Serkowski & Shawl 2001). Without calculating a complete model for the dust shell including hydrodynamics and dust growth, the grain radius cannot be specified more precisely. Fortunately, for the FIR spectral region, the opacity does not depend on the grain size a since circumstellar grains are in any case much smaller than the wavelength λ in the far infrared. Only for the absorption of stellar radiation might there be a slight dependency on grain size since in the optical and near UV spectral region the grains may satisfy only marginally the condition 2πa/λ ≪ 1 that particles can be considered as small.
 |
Fig. 8 Absorption and scattering coefficient per unit mass of some dust species in a dusty gas with standard cosmic element abundances. Full line: solid SiO at low temperature. Dashed line: amorphous olivine. Dotted line: amorphous pyroxene. |
For the purpose of model calculations of dust shells of cool giant stars, one needs optical data for the dust species at least in the wavelength range from about 0.4 μm to about 100 μm in order to cover (i) the wavelength range of the stellar radiation field from the ultraviolet to the MIR, and (ii) to cover the wavelength range of dust emission from the shell that ranges from the near infrared to the sub-mm region. Our own measurements discussed in Sect. 2 cover only the mid- to far-IR wavelength range. Therefore we have to augment our data by data from other sources to cover also the spectral region from NIR to UV.
For the visible to far-ultraviolet spectral regions (λ ≤ 0.8 μm), we used data for solid SiO listed in Palik (1985). The real part of the complex index of refraction of our infrared extinction data and the data given in Palik fit nicely in the NIR where they overlap. The imaginary part becomes very small in the wavelength region below 8 μm in our results, and it is omitted in the range between 8 and 0.8 μm in the listing of Palik. In this region the absorption coefficient of solid SiO would become many orders of magnitude smaller than the scattering coefficient (or would vanish at all if data of Palik are used). To avoid numerical problems in solving the radiative transfer problem, we arbitrarily increase the absorption in the wavelength range 0.8 to 8 μm by assuming that the dust material contains tiny inclusions of pure iron particulates with a volume-filling factor of fV = 10-3 and calculating the average dielectric function ⟨ ε ⟩ for this composite material from the Maxwell-Garnett mixing rule (cf., e.g., Bohren & Huffman 1983) 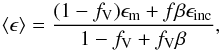 (18)where
(18)where 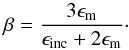 (19)Here ϵm is the bulk dielectric function of the matrix material (solid SiO in our case) and ϵinc the bulk dielectric function of the material forming the inclusions (solid iron in our case).
(19)Here ϵm is the bulk dielectric function of the matrix material (solid SiO in our case) and ϵinc the bulk dielectric function of the material forming the inclusions (solid iron in our case).
This kind of additional absorption by impurities has no influence on the calculated temperature of dust grains since this is determined by the strong absorption at λ < 0.8 μm and also has no influence on the calculated radiation field. It is unlikely that any real dust material is pure and ideally transparent, and nano-sized iron inclusions are fundamental constituents of, e.g., GEMS (e.g. Bradley 2010).
The resulting mass-absorption and scattering coefficients of small particles of solid SiO are shown in Fig. 8. They are calculated according to Eq. (17) using the data given in Table 4 and calculating optical constants for SiO according to the Brendel-model for the dielectric function of amorphous materials, Eq. (2), using constants from Table 1, and following the procedure described above.
Brendel & Bormann (1992) have shown that the integral in Eq. (2) can be solved in terms of the complex probability functions and Gaussians. We did not make use of this in our opacity calculations but preferred to evaluate the integrals numerically since evaluation of the analytic expressions seems to be numerically more expensive because of their complicated structure.
Also mass-absorption and scattering coefficients of amorphous olivine and pyroxene are shown for comparison2, which are the main dust species in circumstellar dust of M-stars. It is seen that solid SiO indeed shows a prominent absorption feature centred on about 10 μm and only some weak structure on the long-wavelength side.
4.2. Model calculations
Using the above opacity description we have calculated radiative transfer models of circumstellar dust shells with solid SiO as the dust component for a range of mass-loss rates in order to determine the spectral features that would result from solid silicon monoxide. The essentials of the model of the dust shell and of the radiative transfer calculations are briefly described in Appendix A.
A fundamental parameter of the model is the location of the inner boundary of the dust shell, Ri, that depends on the mechanism by which the dust forms from the gas phase by nucleation and subsequent grain growth. About the details of these processes almost nothing is known, and we have recourse to the simple assumption that the dust suddenly appears at some prescribed dust temperature Tc, and the fraction fSiO of material condensed into the solid phase is constant across the dust shell. This is the kind of approximation on which most existing models of circumstellar dust shells are based. For temperature Tc, we assume a value of 700 K for silicon monoxide dust because the temperature where solid SiO becomes stable against vaporization is about 1000 K under conditions in circumstellar dust shells, see Sect. 3.2, and because in dust shells this temperature probably is somewhat lower if some super-cooling of the outflowing material should be required for the onset of nucleation and condensation. Calculations with Tc = 800 K result in model spectra that are not significantly different. The old results of Gail & Sedlmayr (1986) seem to indicate a temperature for onset of SiO condensation as low as 600 K, but this conclusion can no longer be maintained since that calculation is based on older vapour-pressure measurements of solid SiO for which it is now known that they have to be revised downwards substantially (Ferguson & Nuth 2008; Wetzel et al. 2012b; Ferguson & Nuth 2012), which increases the condensation temperature.
For the basic parameters Teff, L∗, Vexp, we use representative average values, since we do not intend to model individual stars but to only perform some explorative calculations. For the effective temperature of the central star we choose a value of 2700 K. This seems to be a representative value for S stars (e.g. Kerschbaum & Hron 1998; Kerschbaum 1999). The luminosity is chosen to be L = 104 L⊙, which is typical of stars at the uppermost part of the TP-AGB, where one expects AGB-stars to pass through the stage of S-stars. Observed values given in the literature for stars with substantial mass-loss rate are within this order of magnitude or slightly less (e.g. Jorissen & Knapp 1998; Groenewegen & de Jong 1998; Ramstedt et al. 2006). The observed expansion velocities Vexp of S-stars vary between a few km s-1 and about 20 km s-1 and are typically between 5 km s-1 and 10 km s-1 (Groenewegen & de Jong 1998; Ramstedt et al. 2006). We use a value of 10 km s-1. The observed mass-loss rates of S-stars vary over a wide range between values as low as a few times 10-8 M⊙ yr-1 up to ≈10-5 M⊙ yr-1 (e.g. Groenewegen & de Jong 1998; Ramstedt et al. 2006; Guandalini 2010). We consider Ṁ as free parameter and calculate models for different values of the mass-loss rate.
The basic model parameters of the calculations are shown in Table 6. The calculations are done for spherical dust grains of radius 0.1 μm and for a continuous distribution of ellipsoids with the same volume as the spherical grains.
4.3. Results for spectral energy distribution
Models are calculated for mass-loss rates ranging from Ṁ = 3 × 10-7 M⊙ yr-1 to Ṁ = 1 × 10-5 M⊙ yr-1 with solid silicon monoxide as the sole opacity source. Figure 9 shows the resulting spectral energy distribution of the radiation emitted by the star and its dust shell. Since we assumed for the star a blackbody radiation field, the strong structure of cool stellar spectra resulting from molecular absorption bands is missing in our models. This simplifies the identification of the dust features in the spectrum. Emission from warm dust is seen only at wavelengths longer than 8 μm since the absorption coefficient of solid SiO is weak at shorter wavelengths, see Fig. 8. The prominent absorption band around 10 μm is clearly seen as a strong emission feature in all of the spectra. Some structure is seen in the spectrum at longer wavelengths, but there is no strong emission feature around 18 μm.
 |
Fig. 9 Synthetic spectra of models of circumstellar dust shells with solid silicon monoxide dust particles for different mass-loss rates from Ṁ = 3 × 10-7 M⊙ yr-1 to Ṁ = 1 × 10-5 M⊙ yr-1. Dotted line: stellar radiation. |
 |
Fig. 10 Calculated energy flux from star and dust shell for solid SiO as absorber for spherical grains (dotted line) and using a distribution of particle shapes (CDE) (dashed line), subtracted by the black-body emission from the star for different mass-loss rates (in units M⊙ yr-1), and averaged emission profile of S-stars from Hony et al. (2009) (full lines). The line profile are scaled and shifted in arbitrary units such that the maxima and bottom line of observed and calculated profiles coincide and are of comparable height. In the case of Ṁ = 1 × 10-6 M⊙ yr-1 a profile is added where additionally condensation of corundum is considered (dash-dotted line). |
This is similar to what is found in a number of S-star spectra. Figure 10 shows a more close-up view of our synthetic spectra in the wavelength region between 5 μm and 25 μm. For clarity the blackbody radiation field of the star is subtracted from the synthetic spectra and the resulting emission profiles are shifted relative to each other and scaled to approximately comparable peak heights. The calculations are done for spherical grains and for a continuous distribution of ellipsoids (see Bohren & Huffman 1983). These emission profiles reflect the peculiar characteristics of the emission coefficient of amorphous solid silicon monoxide: A strong emission band centred at ≈10 μm and a missing strong feature around 18 μm. For the highest mass-loss rates, some structure is seen in the 15 to 25 μm wavelength region, which, however, is dissimilar to the 18 μm feature of silicates. Figure 10 also shows one of the two different profiles of the emission bands around 10 μm observed in S-stars where none or only a very weak 18 μm feature is observed. The data are taken from Fig. 6 of Hony et al. (2009). The profile in Fig. 10 corresponds to the lower one in Fig. 6 of Hony et al. (2009). This profile is scaled such that the peak value coincides with that of the synthetic emission profiles in our models.
The upper profile of Fig. 6 of Hony et al. (2009) is not considered since it peaks at a significantly higher wavelength. It may result from a different kind of material or a complex superposition of emission bands from several materials.
4.4. Discussion
The calculated line profiles for a distribution of ellipsoids show some similarity with the average profile derived in Hony et al. (2009), which peaks at 10 μm. The peak position does not match exactly, but probably within the limit of errors with which such averaged profiles can be determined. For spherical grains the calculated line profiles are located at somewhat shorter wavelengths than the observed profile. They do not match observations well, but this is a well known problem if one assumes particles that are exactly spherical (see, e.g., Lindsay et al. 2013, for a detailed discussion of this).
The broad extension to the long-wavelength side of the observed profile, however, does not agree with the shape of our profiles. The strong asymmetry of the observed profile is conspicuous. This may have a number of reasons. Either the observed profile is the superposition of the strong 10 μm emission feature of solid silicon monoxide with one or more absorption bands of additional dust materials centred on somewhat longer wavelengths, or the properties of solid silicon monoxide deposited under conditions in circumstellar shells differ from that of the material obtained in our laboratory experiments by PVD.
With respect to a contribution by some other materials, the most likely candidates are hibonite (CaAl6O19) with a strong absorption band centred on 12.3 μm, spinel (MgAl2O4) with a strong absorption band centred on 13 μm, or corundum (Al2O3) with a strong and broad band peaking at 11 μm. Such materials probably would start to condense at higher temperatures than solid SiO because of their lower vapour pressure. They would use up only small amounts of the oxygen because of the much lower element abundances of Al and Ca compared to that of Si. This would not noticeably compete with SiO condensation under conditions where oxygen is scarce.
Explorative calculations for hibonite (optical data from Mutschke et al. 2002) and spinel (optical data from Palik 1985) showed that their main absorption band would always be seen as a strong separate band, which does not seem to be found in spectra of S-stars with a strong 10 μm feature. The rather broad corundum feature (optical data from Koike et al. 1995) is a better candidate. Figure 10 shows a Ṁ = 1 × 10-6 M⊙ yr-1 model where corundum is included as absorber (assumed condensation temperature Tc = 1300 K). This obviously strongly widens the long-wavelength side of the SiO profile, but results in somewhat too strong a filling-up of the observed dip of the emission profile around about 15 μm.
Forsterite may also contribute somewhat to the observed profile and increase its width and asymmetry. If the oxygen abundance somewhat exceeds the critical abundance limit ϵO,crit = ϵC − ϵSi + ϵS (where O is completely bound by CO and by that fraction of Si, which is bound in SiO and not in SiS), then some oxygen is left over to form silicates. However, it seems impossible to reproduce the observation with a mixture of solid SiO and silicates, because if more than a few per cent of the Si forms a silicate, the 18 μm feature becomes clearly visible. On the other hand, additional formation of silicates besides solid SiO could explain the sources with a marked 10 μm feature but only a weak 18 μm feature, which is frequently found within the population of S-stars.
Possibly one could reproduce the observed band structure of the stars under consideration by a mixture of the oxides and silicates with solid SiO, but this is beyond the scope of this paper. Another possibility for the strong asymmetry of the observed profile may be that the material formed in stellar outflows is more strongly disordered than the material formed in our laboratory experiments. A significantly stronger damping constant γj would also result in an asymmetric and much broader line profile. However, test calculations with strongly increased values of γj showed that the observed band shape cannot be explained in this way.
Finally some remarks are needed on the structure of SiO. At low temperatures this material slowly decomposes into silicon nano-clusters embedded in a SiO2 matrix (Kamitsuji et al. 2004). The material called silicon monoxide then in truth is an intimate mixture of two different phases which is inhomogeneous on scales of a few nanometres. The absorption peak then shifts to the characteristic peak of SiO2 at 9.2 μm (see Sect. 2.4). Clearly, such a decomposition did not occur for our silicon monoxide films for temperatures below 800 K. Decomposition times have been measured for the closely related material Si2O3 in the laboratory by, e.g., Nuth & Donn (1984). If this can be taken as representative of solid SiO the decomposition would be slow enough at the temperatures of interest (≲750 K) that solid SiO can survive long enough to be observable.
5. Conclusions
This paper reports on laboratory studies of the infrared optical properties of solid silicon monoxide. The dielectric function ε was derived from transmission measurements of thin films obtained by evaporation of commercially available solid SiO and depositing its vapour on a cold substrate. A Brendel oscillator model is fitted to the results of the transmission measurements to determine ε(ω).
Solid silicon monoxide is a material that has been speculated on different occasions to be involved in the formation process for silicate dust in circumstellar environments, such as accretion disks around protostars or dust shells around AGB stars. In this paper we study the possibility that solid silicon monoxide forms a separate dust component in circumstellar dust shells if not enough oxygen is available to build the SiO4-tetrahedrons of normal silicate dust material. This would apply, for instance, to S-stars with a C/O abundance ratio very close to unity.
The characteristic property of this SiO dust would be a broad and structure-less emission feature centred on about 10 μm, resulting from Si-O bond stretching vibrations. It is similar to the 9.7 μm feature of amorphous silicates, but is missing an 18 μ feature resulting from O-Si-O bending modes in a SiO4-tetrahedron. Such peculiar cases have, indeed, been detected for some S-stars (Hony et al. 2009; Smolders et al. 2012). We propose that we see solid silicon monoxide in these stars as an abundant dust component. Radiative transfer calculations for circumstellar dust shells were performed using our new data on the dielectric function of solid SiO to calculate the emission band structure due to SiO dust.
The resulting emission feature at 10 μm was compared with one of the two average emission profiles derived in Hony et al. (2009). The profile of the emission feature obtained in the model calculation peaks at about just the same wavelength as the observed feature, which makes its identification very likely as due to solid SiO. However, the observed profile is much more extended to longer wavelengths than the synthetic profile, which either may result from blending the band from solid SiO with emission bands from a number of additional minor dust species (corundum, hibonite, etc.) or shows that the laboratory produced amorphous SiO films have a somewhat different lattice structure than the material condensed in stellar outflows.
More work is required to explain the asymmetry of the observed peculiar 10 μm feature in some S-stars before the identification of solid silicon monoxide as carrier material of this feature can be considered safe, but at least this explanation can presently be considered as the most likely one.
Data for silicates with x = 0.7, from the Jena-St. Petersburg data basis, accessible via: http://www.mpia-hd.mpg.de/HJPDOC/
Acknowledgments
This work was supported in part by “Forschergruppe 759” and special research program SPP 1385, which both are supported by the “Deutsche Forschungsgemeinschaft (DFG)”.
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash (San Francisco: Astron. Soc. of the Pacific), ASP Conf. Ser., 336, 25 [Google Scholar]
- Barin, I. 1995, Thermochemical Data of Pure Substances, 3rd edn., Vol. I, II (Weinheim: VCH Verlagsgesellschaft) [Google Scholar]
- Berreman, D. W. 1963, Phys. Rev., 130, 2193 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by Small Particles (New York: John Wiley & Sons) [Google Scholar]
- Bose, M., Floss, C., & Stadermann, F. J. 2010, ApJ, 714, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, J. 2010, in Astromineralogy, ed. T. K. Henning (Berlin: Springer), Lecture Notes in Physics, 815, 259 [Google Scholar]
- Brendel, R., & Bormann, D. 1992, J. Appl. Phys., 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cachard, A., Roger, J. A., Pivot, J., & Dupuy, C. H. S. 1971, Phys. Stat. Sol. A, 5, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Chabal, Y. J., Raghavachari, K., Zhang, X., & Garfunkel, E. 2002, Phys. Rev. B, 66, 161315 [Google Scholar]
- Chen, P. S., & Kwok, S. 1993, ApJ, 416, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W., Maclean, S., & Millar, T. J. 1978, Ap&SS, 53, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, F. T., & Nuth, J. A. 2008, J. Chem. Eng. Data, 53, 2824 [CrossRef] [Google Scholar]
- Ferguson, F. T., & Nuth, J. A. 2012, J. Chem. Eng. Data, 57, 721 [CrossRef] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2002, A&A, 382, 256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1986, A&A, 166, 225 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1998a, in The Molecular Astrophysics of Stars and Galaxies, eds. T. W. Hartquist, & D. A. Williams (Oxford: Oxford University Press), 285 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1998b, Faraday Discussion, 109, 303 [Google Scholar]
- Groenewegen, M. A. T., & de Jong, T. 1998, A&A, 337, 797 [NASA ADS] [Google Scholar]
- Grosse, P., Harbecke, B., Heinz, B., & Meyer, R. 1986, Appl. Phys. A, 39, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Guandalini, R. 2010, A&A, 513, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunther, K. G. 1958, Glastechn. Ber., 31, 9 [Google Scholar]
- Hass, G., & Salzberg, C. D. 1954, J. Opt. Soc. Am., 44, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Mutschke, H. 2010, J. Nanophotonics, 4, 041580 [NASA ADS] [CrossRef] [Google Scholar]
- Hjortsberg, A., & Granqvist, C. G. 1980, Appl. Opt., 19, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Hohl, A., Wieder, T., van Aken, P., et al. 2003, J. Non-Crystal. Solids, 320, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Hony, S., Heras, A. M., Molster, F. J., & Smolders, K. 2009, A&A, 501, 609 [Google Scholar]
- Ishikawa, K., Suzuki, K., & Okamura, S. 2000, J. Appl. Phys., 88, 7150 [NASA ADS] [CrossRef] [Google Scholar]
- Jorissen, A., & Knapp, G. R. 1998, A&AS, 129, 363 [Google Scholar]
- Jura, M. 1996, ApJ, 472, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Kamitsuji, K., Ueno, S., Suzuki, H., et al. 2004, A&A, 422, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerschbaum, F. 1999, A&A, 351, 627 [NASA ADS] [Google Scholar]
- Kerschbaum, F., & Hron, J. 1998, A&A, 308, 489 [Google Scholar]
- Kirk, C. T. 1988, Phys. Rev. B, 38, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Klevenz, M. 2009, Ph.D. Thesis, University of Heidelberg [Google Scholar]
- Klevenz, M., Wetzel, S., Möller, M., & Pucci. 2010a, Appl. Spectrosc., 64, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Klevenz, M., Wetzel, S., Trieloff, M., Gail, H. P., & Pucci. 2010b, Phys. Stat. Sol. B, 247, 2179 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R. 1985, ApJ, 293, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Koike, C., Kaito, C., Yamamoto, T., et al. 1995, Icarus, 114, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Kruszewski, A., Gehrels, T., & Serkowski, K. 1968, AJ, 73, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, A. 1988, Phys. Stat. Sol. B, 148, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, A., Schumann, L., & Hübner, K. 1983, Phys. Stat. Sol. B, 117, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, A., Schumann, L., & Hübner, K. 1984, Phys. Stat. Sol. B, 121, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsay, S. S., Wooden, D. H., Harker, D. E., et al. 2013, ApJ, 766, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd Evans, T., & Little-Marenin, I. R. 1999, MNRAS, 304, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, in Landolt-Börnstein, New Series, Group IV, ed. J. E. Trümper (Berlin: Springer), 4, 560 [Google Scholar]
- Lucy, L. 1964, in Proc. of the first Harvard-Smithonian Conf. on Stellar Atmospheres, eds. E. H. Avrett, O. Gingerich, & C. A. Whitney, Smithonian Astrophysical Observatory Special Report No. 167 (Cambridge, MA: Smithonian Astrophysical Observatory), 93 [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres (San Francisco: Freeman & Co) [Google Scholar]
- Millar, T. J. 1982, Ap&SS, 86, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mutschke, H., Posch, T., Fabian, D., & Dorschner, J. 2002, A&A, 392, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naiman, M. L., Kirk, C. T., Emerson, B. L., Taitel, J. B., & Senturia, S. D. 1985, J. Appl. Phys., 58, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A., & Donn, B. 1982, J. Chem. Phys., 77, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A., & Donn, B. 1984, J. Geophys. Res., 89, 657 [Google Scholar]
- Nuth, J. A., & Ferguson, F. T. 2006, ApJ, 649, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Palik, E. D. 1985, Handbook of Optical Constants in Solids (New York: Academic Press) [Google Scholar]
- Philipp, H. 1971, J. Phys. Chem. Solids, 32, 1935 [Google Scholar]
- Queeney, K. T., Herbots, N., Shaw, J. M., Atluri, V., & Chabal, Y. J. 2004, Appl. Phys. Lett., 84, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Ramstedt, S., Schöier, F. L., Olofson, H., & Lundgren, A. A. 2006, A&A, 454, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reber, A. C., Clayborne, P. A., Reveles, J. U., et al. 2006, Nano Letters, 6, 1190 [Google Scholar]
- Rocabois, P., Chatillon, C., & Bernard, C. 1992, Rev. Int. Hautes Tempér. Réfract., 28, 37 [Google Scholar]
- Sacuto, S., Jorissen, A., Cruzalèbes, P., et al. 2008, A&A, 482, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serkowski, K., & Shawl, S. J. 2001, AJ, 122, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Smolders, K., Neyskens, P., Blommaert, J. A. D. L., et al. 2012, A&A, 540, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tazawa, M., Kakiuchida, G., Xu, P. J., & Arwin, H. 2006, J. Electroceram., 16, 511 [CrossRef] [Google Scholar]
- Teschner, U., & Hübner, K. 1990, Phys. Stat. Sol. (B), 159, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Theiss, M. 2011, SCOUT – software package for optical spectroscopy V3.48 [Google Scholar]
- van Hapert, J. J., Vredenberg, A. M., van Faassen, E. E., et al. 2004, Phys. Rev. B, 69, 245202 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, C., Hoppe, P., Stadermann, F. J., Floss, C., & Brenker, F. E. 2009, Geochim. Cosmochim. Acta, 73, 7127 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, S. 2012, Ph.D. Thesis, Heidelberg University [Google Scholar]
- Wetzel, S., Klevenz, M., Pucci, A., & Gail, H.-P. 2012a, Appl. Spectrosc., 66, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, S., Pucci, A., & Gail, H.-P. 2012b, J. Chem. Eng. Data, 57, 1594 [CrossRef] [Google Scholar]
Appendix A: Radiative transfer model
Model spectra of S-stars are calculated using a simple code for modelling radiative transfer in circumstellar dust shells. The basic assumptions on the structure of the dust shell follow the conventional assumptions: a spherically symmetric mass distribution around the central star, with inner radius Ri and outer radius Ra. The outflow is assumed to be stationary and the outflow velocity vexp to be independent of distance r from the centre. The radial distribution of mass density in this case is 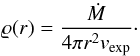 (A.1)Here Ṁ is the mass-loss rate that is also assumed to be constant.
(A.1)Here Ṁ is the mass-loss rate that is also assumed to be constant.
With given opacities (see Sect. 4.1), the radiative transfer equation in spherical symmetry 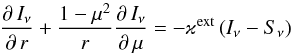 (A.2)is solved by the so-called p-z-method (cf. Mihalas 1978). The source function Sν and the total extinction coefficient ϰext are
(A.2)is solved by the so-called p-z-method (cf. Mihalas 1978). The source function Sν and the total extinction coefficient ϰext are
The sum runs over all dust species. The angular distribution of the scattering term is the one for small particles. The temperatures Ti of the dust species are determined so as to satisfy radiative equilibrium ![\appendix \setcounter{section}{1} \begin{equation} \int_0^\infty{\rm d}\nu\,\varkappa_i^{\rm abs}\left[J_\nu-B_\nu(T_i)\right]=0 \end{equation}](/articles/aa/full_html/2013/05/aa20803-12/aa20803-12-eq202.png) (A.5)for each species by applying an Unsöld-Lucy temperature correction procedure (see Lucy 1964) adapted to the spherically symmetric case. This requires an iteration procedure for determing all temperatures Ti. This iteration is combined with a simple iteration scheme (successive over-relaxation) with respect to Jν and Kν in the scattering contribution of the source function.
(A.5)for each species by applying an Unsöld-Lucy temperature correction procedure (see Lucy 1964) adapted to the spherically symmetric case. This requires an iteration procedure for determing all temperatures Ti. This iteration is combined with a simple iteration scheme (successive over-relaxation) with respect to Jν and Kν in the scattering contribution of the source function.
The inner radius Ri of the dust shell is fixed by the requirement that the most stable of the dust species appears at some prescribed temperature Tc. Since it is not known in advance at which radius this condition is satisfied, an additional iteration procedure is required to determine Ri. The outer radius Ra is always taken at 105 stellar radii.
The radiation field of the central star is approximated by a black body radiation field.
All Tables
Brendel oscillator parameters for the dielectric function from the temperature dependent condensation and annealing experiments of Wetzel et al. (2012a).
Fit coefficients for the temperature dependent oscillator parameters of the Brendel model for the dielectric function.
Some data used for calculating the opacity of the dust species considered in the model calculations and the corresponding key elements.
All Figures
 |
Fig. 1 Relative transmittance spectra of SiO on Si(111) are shown for increasing film thicknesses up to 57 nm. The thickness change between two shown spectra is about 6.3 nm. The strong peak at 983 cm-1 is attributed to the asymmetric Si-O stretching vibration (Cachard et al. 1971). For such film thicknesses, there is clearly no shift in that peak. SiO oscillator positions are indicated by dashed lines. |
| In the text | |
 |
Fig. 2 Normal transmittance measurement of an evaporated SiO film (black solid line) with 57 nm thickness shown together with the best fit by a Brendel-model of the dielectric function as described in the text. Peak positions are indicated by dashed lines. |
| In the text | |
 |
Fig. 3 Dielectric function obtained from the best fit with four Brendel oscillators to the transmittance data shown in Fig. 2. |
| In the text | |
 |
Fig. 4 Simulated spectra at 300 K for SiO (oscillator data from Table 1) and SiO2 (oscillator data from Wetzel 2012) compared to the measurement of a SiO film that was annealed at 873 K. The spectra are shifted against each other, and the dashed lines indicate the oscillator position of the Si stretching mode of SiO and SiO2, respectively. |
| In the text | |
 |
Fig. 5 Fit of the coefficients of the Brendel oscillator model for the dielectric function of solid SiO at a number of temperatures by a linear temperature variation. The various data points correspond to data from Tables 1 and 2 for oscillator parameters at different temperatures. Full lines show the linear fit (3). The vertical dotted line indicates the limit between the temperature ranges where data are obtained either from thin films made by vapour deposition on a substrate with given temperature or from thin films deposited at low temperature and annealed at high temperatures. |
| In the text | |
 |
Fig. 6 Absorption efficiency |
| In the text | |
 |
Fig. 7 Stability limits against vaporization of some refractory compounds formed from an oxygen-rich element mixture with cosmic standard element abundances, and of solid SiO. Dashed line: typical pressure-temperature combinations in an outflowing gas element for a stellar wind model with stationary outflow and Ṁ = 5 × 10-6 M⊙ yr-1 (here for an M-star). Most parts of the dust condensation occur around the knee where the velocity turns from subsonic (horizontal part of the curve) to highly supersonic (steep descending part of the curve) outflow. Pressures are typically 10-8 bar to 10-10 bar in the region of main dust growth. |
| In the text | |
 |
Fig. 8 Absorption and scattering coefficient per unit mass of some dust species in a dusty gas with standard cosmic element abundances. Full line: solid SiO at low temperature. Dashed line: amorphous olivine. Dotted line: amorphous pyroxene. |
| In the text | |
 |
Fig. 9 Synthetic spectra of models of circumstellar dust shells with solid silicon monoxide dust particles for different mass-loss rates from Ṁ = 3 × 10-7 M⊙ yr-1 to Ṁ = 1 × 10-5 M⊙ yr-1. Dotted line: stellar radiation. |
| In the text | |
 |
Fig. 10 Calculated energy flux from star and dust shell for solid SiO as absorber for spherical grains (dotted line) and using a distribution of particle shapes (CDE) (dashed line), subtracted by the black-body emission from the star for different mass-loss rates (in units M⊙ yr-1), and averaged emission profile of S-stars from Hony et al. (2009) (full lines). The line profile are scaled and shifted in arbitrary units such that the maxima and bottom line of observed and calculated profiles coincide and are of comparable height. In the case of Ṁ = 1 × 10-6 M⊙ yr-1 a profile is added where additionally condensation of corundum is considered (dash-dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\appendix \setcounter{section}{1} \begin{eqnarray} &&S_\nu=\sum\limits_{i=1}^I\left\{{\varkappa_i^{\rm abs}\over \varkappa^{\rm ext}} B_{i,\nu}(T_i)\!+\!{\varkappa_i^{\rm sc}\over \varkappa^{\rm ext}} {3\over 8}\left[(3-\mu^2)J_\nu\!+\!(3\mu^2-1)K_\nu\right]\right\}~~~~~~~~~\\ &&\varkappa^{\rm ext}=\sum\limits_{i=1}^I\left(\varkappa_i^{\rm abs}+ \varkappa_i^{\rm sc}\right). \end{eqnarray}](/articles/aa/full_html/2013/05/aa20803-12/aa20803-12-eq200.png)