| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 22 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201220654 | |
| Published online | 22 April 2013 | |
ODIN: a new model and ephemeris for the Pluto system⋆,⋆⋆
1 Institut de Mécanique Céleste et de Calcul des Éphémérides – Observatoire de Paris, UMR 8028 CNRS, Université Pierre et Marie Curie, Université Lille 1, 77 avenue Denfert Rochereau, 75014 Paris, France
e-mail: beauvalet@imcce.fr
2 Institut Polytechnique des Sciences Avancées IPSA, 7-9 rue Maurice Grandcoing, 94200 Ivry-sur-Seine, France
Received: 29 October 2012
Accepted: 6 February 2013
Because of Pluto’s distance from the Sun, the Pluto system has not yet completed a revolution since its discovery, hence an uncertain heliocentric distance. In this paper, we present the fitting of our dynamical model ODIN (Orbite, Dynamique et Intégration Numérique) to observations. The small satellites P4 and P5 are not taken into account. We fitted our model to the measured absolute coordinates (RA, DEC) of Pluto, and to the measured positions of the satellites relative to Pluto. The masses we found for the bodies of the system are consistent with those of previous studies. Yet the masses of the small satellites Nix and Hydra are artificially constrained by the number of observations of Charon. The best way to improve the determination of their masses would be to use observations of P4 and P5, but there are still not enough published observations. Concerning the heliocentric distance of the system, we compared the value we obtained using ODIN and those of other models. The difference between the models far exceeds the uncertainty needed (about 1000 km) for the mission New Horizons. A new astrometric reduction of old photographic plates may be an efficient way to constrain this distance. The ephemeris for Pluto’s satellites is available on the web page of the IMCCE at http://www.imcce.fr/hosted_sites/saimirror/nssreq9hf.htm. The complete version of the ephemeris is available as a SPICE kernel at http://www.imcce.fr/~beauvalet/.
Key words: celestial mechanics / ephemerides / planets and satellites: fundamental parameters / Kuiper belt: general / planets and satellites: individual: Pluto / methods: numerical
Appendices A and B are available in electronic form at http://www.aanda.org
Table A.2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A14
© ESO, 2013
1. Introduction
Pluto was discovered in 1930. Because its period of revolution is about 248 years, it has not yet completed an entire revolution. As a consequence, its distance to the Sun is not accurately known.
Pluto has a unique trait among the dwarf planets: a very massive satellite. Its main satellite Charon has a mass of one tenth of Pluto’s, while the mass of the other satellites, Nix, Hydra, P4, and P5, are nearly negligible. Because of this mass ratio, the center of mass of the system is outside of Pluto. Pluto’s motion is the result of the combination of its motion around the Sun, and its motion around the barycenter of its system. This situation is the same for planets, except that the center of mass then lies inside the system’s most massive object. In the case of Pluto, the motion around the Sun is heavily disturbed by Charon. Thus any modeling of Pluto’s motion needs to include these perturbations. Up to now, there have been studies separating the satellites (Tholen et al. 2008) and the dwarf planet’s motion (Folkner et al. 2008; Fienga et al. 2011). Our goal here is to provide a single dynamical model for the system and to build a coherent physical approach to its dynamics.
Besides focusing on the motion of the objects in the system, one must consider the difficult problem of their masses. The masses of Pluto and Charon are relatively well known, since they are the largest of the system. Instead, Nix and Hydra have very small masses. In a previous article (Beauvalet et al. 2012), we showed that the values of the masses given in Tholen et al. (2008) for Nix and Hydra are at the very limit of what could be detected from observations.
The purpose of this paper is to present our results for the masses of the system bodies and for their motion by fitting our model to observations. First, we will briefly present our dynamical model. Then we will present the observations to which our model was fitted, as well as the physical corrections we applied. Finally, we will present the results of the fitting process, the residuals and the determined physical parameters.
Properties of the observations to which ODIN was fitted.
2. Dynamical model: ODIN
We specifically developed the numerical model ODIN (Orbite, Dynamique et Intégration Numérique) to study the orbit of multiple systems (Beauvalet et al. 2012, 2013). We integrated the equations of motion of the bodies in the Pluto system with ODIN, using the barycenter of the solar system as the center of the reference frame; the inertial axes coincided with the ICRF (International Celestial Reference Frame). We also included the perturbations caused by the Sun and the planets. Because we found the second order harmonics of the gravity fields of Pluto and Charon to be non-detectable with observations (Beauvalet et al. 2012), we did not take them into account. As a result, the equations of motion consisted only in the gravitational interactions between the center of mass of the bodies and their interaction with the main bodies of the solar system 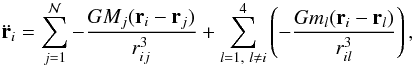 (1)where i is an integrated body, j is the Sun or a planet, l is a body of Pluto’s system, Mj is the mass of the body j, ml is the mass of the body l, rj is the position vector of the body j with respect to the solar system barycenter, and rij is the distance between bodies i and j.
(1)where i is an integrated body, j is the Sun or a planet, l is a body of Pluto’s system, Mj is the mass of the body j, ml is the mass of the body l, rj is the position vector of the body j with respect to the solar system barycenter, and rij is the distance between bodies i and j.
Properties of the observations of the satellites to which ODIN was fitted.
Our model was fitted to the observations using the least squares method. We may approximate the relationship between the calculated residuals and the model parameter errors by its linear part 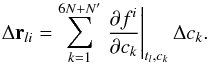 (2)To obtain the needed partial derivatives, we used Newton’s second law
(2)To obtain the needed partial derivatives, we used Newton’s second law 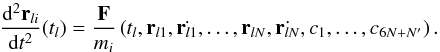 (3)Assuming that the derivations with respect to time and to a dynamical parameter are independent, we determined the differential equations (Lainey et al. 2004)
(3)Assuming that the derivations with respect to time and to a dynamical parameter are independent, we determined the differential equations (Lainey et al. 2004) ![\begin{equation} \frac{\partial}{\partial c_l}\left(\frac{\mathrm{d}^2 \vec{r}_i}{\mathrm{d}t^2}\right)=\frac{1}{m_i}\left[\sum_j\left( \frac{\partial\vec{F}_i}{\partial \vec{r}_j}\frac{\partial \vec{r}_j}{\partial c_l} + \frac{\partial\vec{F}_i}{\partial \dot{\vec{r}}_j}\frac{\partial \dot{\vec{r}}_j}{\partial c_l}\right) + \frac{\partial\vec{F}_i}{\partial c_l}\right]\textrm{,} \end{equation}](/articles/aa/full_html/2013/05/aa20654-12/aa20654-12-eq11.png) (4)where cl is a parameter we need to adjust. We numerically integrated these equations alongside the equations of motion. Note that our model can be fitted to both resolved and unresolved observations of Pluto’s system in right ascension (RA) and declination (Dec) spherical coordinates, and to the relative observations of Pluto’s satellites.
(4)where cl is a parameter we need to adjust. We numerically integrated these equations alongside the equations of motion. Note that our model can be fitted to both resolved and unresolved observations of Pluto’s system in right ascension (RA) and declination (Dec) spherical coordinates, and to the relative observations of Pluto’s satellites.
3. Observations used
We used sets of observations taken from 1914 to 2011 and because this time span is so large, the number of observations and their accuracy changes significantly between the different sets. Over this period, there is a gap in both the precision and the number of observations because of the introduction of CCD targets.
3.1. Photographic observations
The photographic observations were taken in various observatories. Those we used are provided in the Planetary Ephemeris Data by the 4th Commission of the International Astronomical Union. The description of these observations is given in Table 1. They span from 1914 to 1993; the observations from 1914 to 1929 are pre-discovery observations. With these observations, Pluto and its satellites are not resolved, so we only have access to the photocenter of the system.
3.2. CCD observations
The CCD observations also come from various sources. Among them, two sets have never been used before for the production of Pluto ephemerides: those from the Observatoire de Haute-Provence (OHP) and those from the Pic du Midi. The description of these observations is given in Table 1.
3.2.1. OHP observations
The OHP observations of Pluto have been regularly taken with the 120 cm telescope (f = 7.2 m) since 1997. They are not resolved and only provide the photocenter of the system. The field of view is 11.8′ × 11.8′ and the camera resolution is 0.69 arcsec per pixel. For the measurement process, we used the method described in Robert et al. (2011) and Robert (2011). Thus, the following steps were implemented: image calibration, background estimation, data extraction with the Source Extractor software (Bertin & Arnouts 1996). Then we corrected all the known spherical effects: parallax, aberration, relative deflection effects, and total atmospheric refraction. Finally we identified the UCAC2 stars (Zacharias et al. 2004).
The astrometric reduction was performed by using first-order equations modeling two scale factors, orientations, and offsets, in order to separate the contributions of the different effects. The obtained astrometric positions are available in electronic form at the CDS.
3.2.2. Pic du Midi observations
The Pic du Midi observations of Pluto were taken with the 105 cm telescope (f = 17.2 m) in July 2011, with a 7′ × 7′ field of view and a resolution of 0.17 arcsec par pixel. We have only three nights of observations, but the excellent seeing (mean value of 0.9′′) allowed us good precision. The astrometric reduction was performed with the PRISM software, using the UCAC2 astrometric catalog. The obtained astrometric positions are given in Table A.1.
3.2.3. Observations of the satellites
The maximum separation between Pluto and Charon is 0.9′′. Because of this, the first resolved observations of the system were taken with the Hubble Space Telescope (HST) in 1992. This first set of images spans between 1992 and 1993. Afterward, most of the satellite observations were taken with the HST, except for a few observations taken with the VLT. The description of these observations is in Table 2.
3.3. Stellar occultations
Pluto’s orbit is currently crossing the Galactic plane. As a consequence, stellar occultations have been observed since 2005. These observations provide the most precise astrometry. In this case, we are dominated by the catalog errors. Between 2005 and the publication date of this article, only occultations by Pluto and Charon have been observed successfully.
4. Fitting to the observations
4.1. Phase correction
Pluto’s system is usually observed near opposition. Moreover, its mean distance to the Sun is currently about 30 AU. As a result, the phase angle of the system is always quite low, at most about 2°. To correct for the phase effect, we used the same method as Lindegren (1977). To do this, we considered that Pluto and Charon have a homogeneous surface. We only corrected the observations of Pluto and Charon for the phase effect. As the maximum phase angle of the system is about 2°, the consequence on Nix and Hydra is negligible since the angular size of these objects is a few mas. The difference between the photocenter and the center of mass will then be 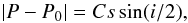 (5)where C is a function of the diffusion law, s is the object angular radius, and i the phase angle. Then we obtain
(5)where C is a function of the diffusion law, s is the object angular radius, and i the phase angle. Then we obtain 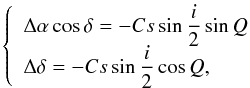 (6)where Q is the position angle of the intensity equator. Supposing that the object is a Lambertian sphere, the value of C varies between 0.5 and 1, depending on the limb darkening (Lindegren 1977). A mean value of 0.75 provides satisfying results.
(6)where Q is the position angle of the intensity equator. Supposing that the object is a Lambertian sphere, the value of C varies between 0.5 and 1, depending on the limb darkening (Lindegren 1977). A mean value of 0.75 provides satisfying results.
4.2. System photocenter
Most of the observations of the system are unresolved. The first resolved observations were speckle observations in 1985, which were not included in our fit (Baier & Weigelt 1987). Because of Charon’s size compared to Pluto, the photocenter of the system can be very different from Pluto’s photocenter. As a result, we needed to estimate the position of the photocenter of the system, which depends on the position of Charon, the other satellites being too faint to be taken into account.
We considered that Pluto and Charon are homogeneous spheres and we neglected the center-border effect. We also neglected the inhomogeneity of Pluto’s and Charon’s albedo. The non-uniformity of both of the objects’ surfaces causes a slight change in corresponding photocenters, but these changes are negligible if we compare with the precision of the non-resolved observations. The photocenter of the system will then be the barycenter of the positions of Pluto and Charon, weighted by their luminosities. As a result, the coordinates of the photocenter of the system are ![\begin{equation} \left\{ \begin{array}{l} \displaystyle\alpha_{\rm pho}=\frac{A_{\rm P}.R_{\rm P}^2.\alpha_{\rm P}+A_{\rm C}.R_{\rm C}^2.\alpha_{\rm C}}{A_{\rm P}.R_{\rm P}^2+A_{\rm C}.R_{\rm C}^2}\\[1mm] \displaystyle\delta_{\rm pho}=\frac{A_{\rm P}.R_{\rm P}^2.\delta_{\rm P}+A_{\rm C}.R_{\rm C}^2.\delta_{\rm C}}{A_{\rm P}.R_{\rm P}^2+A_{\rm C}.R_{\rm C}^2}, \end{array}\right. \end{equation}](/articles/aa/full_html/2013/05/aa20654-12/aa20654-12-eq24.png) (7)where AP and Ac are the albedos of Pluto and Charon, respectively, and RP and RC the radii of Pluto and Charon, respectively.
(7)where AP and Ac are the albedos of Pluto and Charon, respectively, and RP and RC the radii of Pluto and Charon, respectively.
4.3. Center correction
The last two estimations of Charon’s semi-major axis (Tholen & Buie 1997; Tholen et al. 2008) do not have a coherent value. The main difference between these estimations is the observation sets used. The value from Tholen & Buie (1997) was obtained thanks to the HST set of 1992−1993, while the solution from Tholen et al. (2008) was dominated by the HST set of 2002−2003. The double stellar occultation of 2010 gave a distance between Pluto and Charon more consistent with the value from Tholen & Buie (1997). According to Buie et al. (2012), the reason for this difference seems to be a problem in determining the position of Pluto’s center because of the non-uniform albedo of the dwarf planet. The positions of Charon in Buie et al. (2012) take into account the latest modeling of Pluto’s albedo to correct this bias on all the observations.
Because of the faintness of Nix and Hydra, their position is obtained from stacked images. The positions of Charon in Buie et al. (2012) are the positions in every independent image. As a consequence, we do not have a measured position of Charon at the mean time of the stacked images. We used observations around the needed date and a polynomial interpolation to obtain the positions of Charon. Comparing the calculated positions and those given in Buie et al. (2006), we deduced the shift in Pluto’s center and corrected the positions of Nix and Hydra.
4.3.1. Other corrections
The other effects we corrected for are not specific to our model, and as such, will not be fully developed.
Light-time and aberration.
Because of Pluto’s distance from the Sun, we included light-time correction in our model. The mean value of the light-time distance between the Earth and Pluto is currently about 4 h. The light-time value is obtained by iterating the following formula which easily gives a good value of the light-time 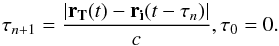 (8)To correct the aberration, we do not take into account the position of Earth at time t but at t − τ. As a result, the light-time value becomes
(8)To correct the aberration, we do not take into account the position of Earth at time t but at t − τ. As a result, the light-time value becomes 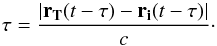 (9)
(9)
Catalogs and reference frame.
Most of the oldest observations are given in the B1950 reference frame. The transformation from the B1950 to the J2000 reference frame is performed with the procedure given in Aoki et al. (1983). The transformation between the FK5 catalog and the Hipparcos catalog is performed with the IAU SOFA library (IAU SOFA Board 2010). The transformations between the time scales used is performed with the SPICE library (Acton 1996).
4.4. Weight of the observations
4.4.1. Pluto
About one hundred years of observations of the Pluto system are available. This large timespan covers most of the evolution of astronomical observations from photographic plates at the beginning of the 20th century to the use of adaptive optics and HST. As a result, we had to consider each set of observations separately. For most of the ground based observations, we did not have any clues about their precision. So we decided to weight observations with the root mean square of their residuals. The root mean square used was the one we obtained after eliminating the biased observations. We gave a uniform uncertainty of 10 mas to the stellar occultations, coming from the approximate precision of the star positions in the catalogs.
4.4.2. Satellites
We used the same uncertainties as those in Buie et al. (2006): 6 mas for Charon, 15 mas for Nix, and 9 mas for Hydra for the 2002−2003 observations. Those of Charon from the 1992−1993 set had a 10 mas uncertainty. We gave them a bigger uncertainty than those of the 2002−2003 set because, apart from the semi-major axis and the eccentricity, the elliptic elements of Charon from the latest set were closer to the value deduced using stellar occultations.
5. Results of the fitting
Because of the small perturbations caused by the rest of the solar system on the satellites, we first fitted the motion of the satellites and then we used this first solution to fit the heliocentric motion of the system.
5.1. Satellites
We first fitted the initial state vectors and masses in our model to the satellite observations given in Buie et al. (2006). After determining a preliminary solution, we added the observations given in Tholen & Buie (1997). The obtained residuals of the satellites are given in Figs. B.1 to B.6, while the masses and initial positions and velocities are given in Tables 3 and 4. We rejected the observations whose residuals were larger than 3σ. The new observations in Buie et al. (2012) improved the error bars when compared with the results obtained from the previous set of observations available. This improvement is discussed more thoroughly later, as there is serious cause for concern because of most probable non-Gaussian errors of the observations.
Masses of Pluto and satellites.
Initial positions and velocities for Pluto’s satellites at JD = 2 452 600.5.
Mean value and standard deviation for the residuals with ODIN, DE421 and INPOP08 ephemerides.
We compared our semi-major axis results with those in Tholen et al. (2008). The differences are mainly due to the error regarding the center of Pluto in the 2002−2003 observations. We can draw the same conclusion when comparing the eccentricities. These results are closer to the Charon occultations of 2005 and 2011. At the present time, without other observations available, we cannot have a definite idea of Charon’s eccentricity. Now, considering the fact that Pluto and Charon are in a double spin-orbit resonance, it is highly probable that the system has reached an equilibrium status and that Charon’s eccentricity is nearly zero (Stern & Spencer 2003). The post-fit residuals are quite close to those given in Tholen et al. (2008) for Nix and Hydra, in spite of the very different masses we found. This result is not surprising since we found in a previous article (Beauvalet et al. 2012) that their estimated masses could not be constrained with the observations then available. The masses of the small satellites are much more constrained than in the estimation in Beauvalet et al. (2012). This situation is caused by the data released in Buie et al. (2012). The positions provided in this paper are only those of Charon. By constraining Pluto and Charon, we indirectly constrained Nix and Hydra. We obtained a similar result when studying the contribution of the future astrometric satellite Gaia (Beauvalet et al. 2013) which will only observe Charon.
Now we must use some caution concerning the constraints given by the least squares method with the masses of Nix and Hydra. The obtained accuracy is heavily influenced by the number of observations of Charon. The masses of Nix and Hydra are very small, and as such, the satellites have hardly any influence on the trajectory of Charon. The values of the masses found come mainly from the interactions between Nix and Hydra. As a consequence, the statistical uncertainty now obtained is far smaller than without the observations from Buie et al. (2012), yet the masses remain extremely close. We have given the value of the masses and attached uncertainties obtained in this case in Table 3. The difference in the mass of Charon between the two fittings comes from the scale factor problem explained in Sect. 4.3.
The number of observations of Charon that we have strongly constrains the perturbations that Charon has on the two other satellites. As a consequence, the perturbations on the motion of the two satellites are, in our model, only caused by their respective masses. The observations involved are mainly from one set of observations, which means that the value of the masses found will depend strongly on the systematic errors of this set. In the absence of any estimation of these systematic errors, we have assumed that the noise of the observations was Gaussian, though this is probably not the case. As a consequence, the uncertainty regarding Nix’s and Hydra’s masses is probably very optimistic and does not reflect the problem of the accuracy of the value.
Recent results from Youdin et al. (2012) obtained when supposing long-term stability of the P4 orbit suggest that Nix’s and Hydra’s masses should be lower than 0.003 km3 s-2 and 0.006 km3 s-2, respectively. The mass of Nix is the lowest possible value from our study, but the value of Hydra’s mass is far lower than its lowest estimation considering the error bars given in Table 3, i.e. 0.055 km3 s-2. This huge difference casts further doubt over our error bars since our own masses seem inconsistent with the long-term orbital stability of P4. If the long-term stability of the system is proved, our lack of accuracy on the determination of the masses would come from the non-Gaussian errors of the observations. If the masses of Nix and Hydra are indeed in the same order of magnitude as the value found from our fitting, then we could question the long-term stability of the smallest satellites in the Pluto system.
5.2. Heliocentric motion of the system
The post-fit residuals are given in the Figs. B.7 to B.28, available only in the electronic version of the article. The elliptic elements are given in Table 6, while the corresponding initial positions and velocities are given in Table 7. The semi-major axis differs by 0.2% from that given by DE423 (Folkner 2010) for the same date. A more complete comparison between the Jet Propulsion Laboratory ephemeris of Pluto and our own fitted model is given in Table 5 with the standard deviation and mean value of the residuals obtained with the two theories. The residuals of both theories are quite close considering their statistics.
Initial elliptic elements of Pluto at JD = 2 452 600.5, reference plane: Mean Earth Equator J2000.
 |
Fig. 1 Evolution of the difference in the heliocentric distance of Pluto between DE421 and other models. |
Initial position and velocities of Pluto at JD = 2 452 600.5, reference plane: Mean Earth Equator J2000.
Concerning the specific issue of the stellar occultations, the residuals obtained with the DE418 theory (Assafin et al. 2010), show that the declination has a clear trend. The equivalent figure for our own residuals is shown in Figs. B.27 and B.28. The trend of the declination is mainly absorbed. It would have been possible to reduce this trend even more by considering that the precision of the occultations is greater than we considered, yet we chose to keep a reasonable precision because of the number of data when compared with other sets. The new data that comes from future occultations will enable a new fit that will probably reduce this trend, while keeping a reasonable precision for occultations.
Concerning the residuals in right ascension for these occultations, we were not able to reduce the width of the residuals. We still do not know the cause of these strong residuals when compared with those in declination. A bad model for Charon’s motion would not cause the same pattern for both theories, since there is no reason for our model of Charon to be the same. Errors on the position of the occulted star is possible, yet the star position is always determined with careful preliminary astrometry and the occultations do not depend on the albedos of the objects.
5.3. Heliocentric distance of the system
Since its discovery, Pluto has not completed an entire revolution around the Sun. As a consequence, its distance to the Sun is not accurately known. The least squares method provides a statistical uncertainty of the fitted semi-major axis, yet this uncertainty is based on the hypothesis that the errors of the observations follow a Gaussian law. This is clearly not the case when considering the systematic errors which might affect the observations. As a consequence, this uncertainty is only linked to the residuals and to the correlations between the parameters in the model. What we need to know is the external precision of the ephemeris, that is, the error we make because of the differences between the real motion we try to determine and our model.
To have a clear indication of the external precision of the distance of Pluto to the Sun, we need to compare the heliocentric distance given by different theories which give comparable residuals. For this purpose, we compared the heliocentric distance of Pluto to the Sun with different theories: ODIN, DE421 (Folkner et al. 2008), DE423 (Folkner 2010), INPOP08 (Fienga et al. 2009), and INPOP10 (Fienga et al. 2011). These ephemerides are based on three different models. They are fitted to similar sets of observations, but with few differences. The differences on the heliocentric distance will be a lower estimation of the external precision of Pluto’s motion.
The result is shown in Fig. 1. As we can see, there is a large discrepancy between the models, while all of them give comparable residuals. This situation has a direct consequence in the near future. The New Horizons spacecraft needs a precision of about 1000 km (Richard Binzel, private communication) on the heliocentric distance of Pluto in order to begin its observation sequence at the right time. For 2015, the most recent calculations can show differences of up to 5000 km. Even when comparing the two models with the smallest difference in distance, ODIN and DE421/423, we still have a difference of about 4000 km.
The best way to try to reduce this uncertainty would be either to increase the number of observations or to improve the accuracy of those already existing. The first possible way is to go on fitting Pluto to the new observations taken every year. But the fly-by of New Horizons is due in 2015. It is doubtful that a few years of observations will be useful to constrain the models. The second source of improvement would be to make a new reduction of the observations taken with photographic plates. The residuals of these observations are greater than those of the CCD observations and span many decades. Reducing the uncertainties attached to the old observations would naturally reduce the differences between the positions given by the different models.
In order to have a first approach of the influence of those old observations on the heliocentric distance of Pluto, we created alternative catalogs and fitted our model to it. These alternative catalogs have been created by randomly removing up to half of the photographic observations we used. We then compared the resulting heliocentric distances of Pluto. At most, the heliocentric distance in 2015 will have a difference of 2500 km when compared to the model fitted to all the available observations, showing the influence of the photographic observations in the modeling. A similar procedure for the CCD observations leads to a difference of at most 750 km. A new reduction of the old photographic plates appears to be the best way to constrain the heliocentric distance of the system, but the influence of the CCD observations is far from being negligible.
6. Conclusion
We developed ODIN, a numerical model dedicated specifically to the study of multiple systems. After fitting our model to observations of Pluto’s system, we obtained a dynamical solution for Pluto’s heliocentric motion and for the plutocentric motion of the satellites. This dynamical solution provided similar results to those obtained with other dynamical models. The masses of the bodies of the system are consistent with about 1.5σ uncertainty to previous estimations. The uncertainties we obtained from the least squares fitting for the masses of Nix and Hydra are probably too optimistic, since we assumed a Gaussian noise of the observations, which is unlikely. The improvement on the statistic error bars comes from the huge number of observations of Charon we have when compared with the number of observations of the two small satellites. If the only observations available continue to be those of Charon, Nix, and Hydra, we will not be able to put strong constraints to the masses of Nix and Hydra before the arrival of New Horizons (Beauvalet et al. 2012). The ephemeris for Pluto’s satellites is available on the web page of the IMCCE at http://www.imcce.fr/hosted_sites/saimirror/ nssreq9hf.htm. The complete version of the ephemeris is available as a SPICE kernel at http://www.imcce.fr/~beauvalet/.
We did not take into account the recently discovered satellites P4 (Showalter et al. 2011) and P5 (Showalter et al. 2012) in our model because of the very few published observations. With P4 orbiting around Pluto with its semi-major axis between Nix and Hydra, and P5 orbiting between Charon and Nix, we might efficiently detect the masses of Nix and Hydra.
Concerning the heliocentric motion of Pluto’s system, we found that the heliocentric distance of Pluto is known with less precision than we expected. The New Horizons probe needs an accuracy of about 1000 km on the heliocentric distance of Pluto. Even though the expected precision of the different available ephemerides is lower than this threshold, the differences between the models are far greater. The different models have similar results for the most recent observations. The oldest observations of the system have far greater residuals. A new reduction of these old observations would certainly reduce these residuals and then constrain well enough the heliocentric distance of Pluto.
Online material
Appendix A: Astrometric data from Observatoire du Pic du Midi
Astrometry from the observations at Pic du Midi in 2011. Topocentric observations.
Appendix B: Post-fit residuals
 |
Fig. B. 1 Post-fit residuals of Charon in right ascension. |
 |
Fig. B. 2 Post-fit residuals of Charon in declination. |
 |
Fig. B. 3 Post-fit residuals of Nix in right ascension. |
 |
Fig. B. 4 Post-fit residuals of Nix in declination. |
 |
Fig. B. 5 Post-fit residuals of Hydra in right ascension. |
 |
Fig. B. 6 Post-fit residuals of Hydra in declination. |
 |
Fig. B. 7 Post-fit residuals in right ascension of photographic plates from 1914 to 1987. |
 |
Fig. B. 8 Post-fit residuals in declination of photographic plates from 1914 to 1987. |
 |
Fig. B. 9 Post-fit residuals in right ascension of photographic plates of Pulkovo Observatory. |
 |
Fig. B. 10 Post-fit residuals in declination of photographic plates of Pulkovo Observatory. |
 |
Fig. B. 11 Post-fit residuals in right ascension of photographic plates of A. J. Dyer Observatory, Lick Observatory and Mink observations. |
 |
Fig. B. 12 Post-fit residuals in declination of photographic plates of A. J. Dyer Observatory, Lick Observatory and Mink observations. |
 |
Fig. B. 13 Post-fit residuals in right ascension of photographic plates of Tokyo, Bordeaux and Flagstaff. |
 |
Fig. B. 14 Post-fit residuals in declination of photographic plates of Tokyo, Bordeaux and Flagstaff. |
 |
Fig. B. 15 Post-fit residuals in right ascension of photographic plates from Gemmo & Barbieri (1994) and USNO. |
 |
Fig. B. 16 Post-fit residuals in declination of photographic plates from Gemmo & Barbieri (1994) and USNO. |
 |
Fig. B. 17 Post-fit residuals in right ascension of photographic plates of Bordeaux. |
 |
Fig. B. 18 Post-fit residuals in declination of photographic plates of Bordeaux. |
 |
Fig. B. 19 Post-fit residuals in right ascension of FASTT observations. |
 |
Fig. B. 20 Post-fit residuals in declination of FASTT observations. |
 |
Fig. B. 21 Post-fit residuals in right ascension of Table Mountain observations. |
 |
Fig. B. 22 Post-fit residuals in declination of Table Mountain observations. |
 |
Fig. B. 23 Post-fit residuals in right ascension of Haute Provence Observatory observations. |
 |
Fig. B. 24 Post-fit residuals in declination of Haute Provence Observatory observations. |
 |
Fig. B. 25 Post-fit residuals in right ascension of Pic du Midi Observatory observations. |
 |
Fig. B. 26 Post-fit residuals in declination of Pic du Midi Observatory observations. |
 |
Fig. B. 27 Post-fit residuals in right ascension of stellar occultations. |
 |
Fig. B. 28 Post-fit residuals in declination of stellar occultations. |
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, S., Soma, M., Kinoshita, H., & Inoue, K. 1983, A&A, 128, 263 [NASA ADS] [Google Scholar]
- Assafin, M., Camargo, J. I. B., Vieira Martins, R., et al. 2010, A&A, 515, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baier, G., & Weigelt, G. 1987, A&A, 174, 295 [NASA ADS] [Google Scholar]
- Barbieri, C., Capaccioli, M., Ganz, R., & Pinto, I. G. 1972, AJ, 77, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Barbieri, C., Capaccioli, M., & Pinto, G. 1975, AJ, 80, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Barbieri, C., Benacchio, L., Capaccioli, M., Pinto, G., & Schoenmaker, A. A. 1979, AJ, 84, 1890 [NASA ADS] [CrossRef] [Google Scholar]
- Barbieri, C., Benacchio, L., Capaccioli, M., & Gemmo, A. G. 1988, AJ, 96, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Beauvalet, L., Lainey, V., Arlot, J.-E., & Binzel, R. 2012, A&A, 540, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beauvalet, L., Lainey, V., Arlot, J.-E., et al. 2013, Planet. Space Sci., in press [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buie, M. W., Grundy, W. M., Young, E. F., Young, L. A., & Stern, S. A. 2006, AJ, 132, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Tholen, D. J., & Grundy, W. M. 2012, AJ, 144, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, C. J., Hubbard, E. C., & Oesterwinter, C. 1967, AJ, 72, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Debehogne, H., & de Freitas Mourao, R. R. 1988, AJ, 96, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Debehogne, H., Machado, L. E., Caldeira, J. F., Vieira, G. G., & Netto, E. R. 1981, A&AS, 46, 131 [NASA ADS] [Google Scholar]
- Fienga, A., Laskar, J., Morley, T., et al. 2009, A&A, 507, 1675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Laskar, J., Kuchynka, P., et al. 2011, Celest. Mech. Dyn. Astron., 111, 363 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Folkner, W. M. 2010, Tech. rep., Jet Prop. Lab. Interoffice Memo. IOM 343R-10-001 [Google Scholar]
- Folkner, W. M., Williams, J. G., & Boggs, D. H. 2008, Tech. rep., Jet Prop. Lab. Interoffice Memo. 343R-08-003 [Google Scholar]
- Gemmo, A. G., & Barbieri, C. 1994, Icarus, 108, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Hardie, R. H., Marcialis, R. L., Wilson, J. W., & Furman, W. R. 1985, AJ, 90, 2643 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, R. S., & Walker, R. L. 1984, AJ, 89, 889 [NASA ADS] [CrossRef] [Google Scholar]
- IAU SOFA Board. 2010, IAU SOFA Software Collection [Google Scholar]
- Jensen, K. S. 1979, A&AS, 36, 395 [NASA ADS] [Google Scholar]
- Klemola, A. R., & Harlan, E. A. 1982, AJ, 87, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Klemola, A. R., & Harlan, E. A. 1984, AJ, 89, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Klemola, A. R., & Harlan, E. A. 1986, AJ, 92, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Duriez, L., & Vienne, A. 2004, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 1977, A&A, 57, 55 [NASA ADS] [Google Scholar]
- Rapaport, M., Teixeira, R., Le Campion, J. F., et al. 2002, A&A, 383, 1054 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, V. 2011, Ph.D. Thesis, Observatoire de Paris [Google Scholar]
- Robert, V., de Cuyper, J.-P., Arlot, J.-E., et al. 2011, MNRAS, 415, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Rylkov, V. P., Vityazev, V. V., & Dement’eva, A. A. 1995, Astron. Astrophys. Trans., 6, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Showalter, M. R., Hamilton, D. P., Stern, S. A., et al. 2011, Central Bureau Electronic Telegrams, 2769, 1 [Google Scholar]
- Showalter, M. R., Weaver, H. A., Stern, S. A., et al. 2012, IAU Circ., 9253, 1 [NASA ADS] [Google Scholar]
- Sicardy, B., Ageorges, N., Marco, O., et al. 2006, IAU Electronic Telegram [Google Scholar]
- Stern, A., & Spencer, J. 2003, Earth Moon and Planets, 92, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., & Buie, M. W. 1997, Icarus, 125, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., Buie, M. W., Grundy, W. M., & Elliott, G. T. 2008, AJ, 135, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2005, IAU Circ., 8625, 1 [NASA ADS] [Google Scholar]
- Youdin, A. N., Kratter, K. M., & Kenyon, S. J. 2012, ApJ, 755, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., de Sanctis, G., & Ferreri, W. 1980, A&AS, 41, 29 [NASA ADS] [Google Scholar]
- Zappala, V., de Sanctis, G., & Ferreri, W. 1983, A&AS, 51, 385 [NASA ADS] [Google Scholar]
All Tables
Mean value and standard deviation for the residuals with ODIN, DE421 and INPOP08 ephemerides.
Initial elliptic elements of Pluto at JD = 2 452 600.5, reference plane: Mean Earth Equator J2000.
Initial position and velocities of Pluto at JD = 2 452 600.5, reference plane: Mean Earth Equator J2000.
Astrometry from the observations at Pic du Midi in 2011. Topocentric observations.
All Figures
 |
Fig. 1 Evolution of the difference in the heliocentric distance of Pluto between DE421 and other models. |
| In the text | |
 |
Fig. B. 1 Post-fit residuals of Charon in right ascension. |
| In the text | |
 |
Fig. B. 2 Post-fit residuals of Charon in declination. |
| In the text | |
 |
Fig. B. 3 Post-fit residuals of Nix in right ascension. |
| In the text | |
 |
Fig. B. 4 Post-fit residuals of Nix in declination. |
| In the text | |
 |
Fig. B. 5 Post-fit residuals of Hydra in right ascension. |
| In the text | |
 |
Fig. B. 6 Post-fit residuals of Hydra in declination. |
| In the text | |
 |
Fig. B. 7 Post-fit residuals in right ascension of photographic plates from 1914 to 1987. |
| In the text | |
 |
Fig. B. 8 Post-fit residuals in declination of photographic plates from 1914 to 1987. |
| In the text | |
 |
Fig. B. 9 Post-fit residuals in right ascension of photographic plates of Pulkovo Observatory. |
| In the text | |
 |
Fig. B. 10 Post-fit residuals in declination of photographic plates of Pulkovo Observatory. |
| In the text | |
 |
Fig. B. 11 Post-fit residuals in right ascension of photographic plates of A. J. Dyer Observatory, Lick Observatory and Mink observations. |
| In the text | |
 |
Fig. B. 12 Post-fit residuals in declination of photographic plates of A. J. Dyer Observatory, Lick Observatory and Mink observations. |
| In the text | |
 |
Fig. B. 13 Post-fit residuals in right ascension of photographic plates of Tokyo, Bordeaux and Flagstaff. |
| In the text | |
 |
Fig. B. 14 Post-fit residuals in declination of photographic plates of Tokyo, Bordeaux and Flagstaff. |
| In the text | |
 |
Fig. B. 15 Post-fit residuals in right ascension of photographic plates from Gemmo & Barbieri (1994) and USNO. |
| In the text | |
 |
Fig. B. 16 Post-fit residuals in declination of photographic plates from Gemmo & Barbieri (1994) and USNO. |
| In the text | |
 |
Fig. B. 17 Post-fit residuals in right ascension of photographic plates of Bordeaux. |
| In the text | |
 |
Fig. B. 18 Post-fit residuals in declination of photographic plates of Bordeaux. |
| In the text | |
 |
Fig. B. 19 Post-fit residuals in right ascension of FASTT observations. |
| In the text | |
 |
Fig. B. 20 Post-fit residuals in declination of FASTT observations. |
| In the text | |
 |
Fig. B. 21 Post-fit residuals in right ascension of Table Mountain observations. |
| In the text | |
 |
Fig. B. 22 Post-fit residuals in declination of Table Mountain observations. |
| In the text | |
 |
Fig. B. 23 Post-fit residuals in right ascension of Haute Provence Observatory observations. |
| In the text | |
 |
Fig. B. 24 Post-fit residuals in declination of Haute Provence Observatory observations. |
| In the text | |
 |
Fig. B. 25 Post-fit residuals in right ascension of Pic du Midi Observatory observations. |
| In the text | |
 |
Fig. B. 26 Post-fit residuals in declination of Pic du Midi Observatory observations. |
| In the text | |
 |
Fig. B. 27 Post-fit residuals in right ascension of stellar occultations. |
| In the text | |
 |
Fig. B. 28 Post-fit residuals in declination of stellar occultations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


