| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220604 | |
| Published online | 16 May 2013 | |
The electron density structure and kinematics of the supernova remnant N 49⋆
1 Laboratório de Análise Numérica e Astrofísica, Departamento de Matemática, e Programa de Pós-Graduação em Física, Universidade Federal de Santa Maria, 97119-900 Santa Maria, RS, Brazil
e-mail: igorcancela@gmail.com; mvfcopetti@gmail.com
2 LUTH, Observatoire de Paris-Meudon, 92190 Meudon, France
Received: 21 October 2012
Accepted: 14 February 2013
Context. Supernova remnants commonly display strong internal inhomogeneities in physical properties; however, most of the observational studies found in the literature are limited to integrated data for extragalactic objects or data from very specific parts of the galactic objects. Thus, important information may be lost.
Aims. We studied the spatial variation of the electron density and the kinematics of N 49, the brightest supernova remnant in the Large Magellanic Cloud, based on spatial resolve observations sampling the whole object.
Methods. We acquired long-slit spectrophotometric data of high signal-to-noise from twelve locations equally spaced in declination. We extracted 1D spectra in the range 5950 to 6750 Å from 312 different regions each 2.3″ × 2″ in angular size. The electron density was derived from the line ratio [S ii] λ6717/λ6731. The radial velocity and velocity dispersion were obtained from the Hα profile.
Results. The map of the electron density presents a strong gradient with the density increasing from west to east. The densest areas, with Ne ≥ 2000 cm-3, are found on the east border of the nebula, near but not exactly coinciding with the brightest areas in the optical. The dense area at the south-east border is on the edge of the bright ridge of filaments associated with the peak of the emission from the nebula at different frequencies. However, the dense zone at the north-east borders is in an area of low brightness. From the Hα total flux, we estimate a mass of 207 ± 66 M⊙ for N 49. The maps of the radial velocities of the blue and red shifted components of Hα and of the velocity dispersion at 3σ showed a rough radial symmetry that can be interpreted as the projection effect of a expanding spherical shell. However, the kinematic centre of symmetry is far from the centre of the X-ray or radio images, although it is near the centre of the optical image of N 49.
Conclusions. The detected gradient in density confirmed a previous inference based on the decrease in the brightness ratio between the X-ray and radio emission from east and west and is consistent with the presence of a molecular cloud on the south-east border. We were able to fit the radial profile of the near side velocity using a self-similar solution of a blast wave travelling through a non-homogeneous medium characterized by a power-law density distribution.
Key words: ISM: supernova remnants / planetary nebulae: individual: N49 / ISM: kinematics and dynamics / ISM: structure
Maps (as FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A104
© ESO, 2013
1. Introduction
Supernova remnants may display strong internal inhomogeneities in physical properties. However, most of the observational studies found in the literature are limited to integrated data for extragalactic objects or data from very specific parts of the galactic objects. Thus, important information may be lost. The Magellanic Clouds provide us with an excellent sample of supernova remnants, with sizes small enough to fit the field of view of the usual detectors, but large enough to be observed with reasonable spatial resolution.
In the optical range, N 49 (=LHA 120-N 49, SNR B0525-66.1, DEM L 190) is the brightest supernova remnant (SNR) in the Large Magellanic Cloud (LMC; Dopita 1979). Because it is so bright, it was one of the first extragalactic SNR confirmed by measurements of emission-line intensity ratios (Westerlund & Mathewson 1966). N 49 is also one of the brightest SNR in X-rays (Long et al. 1981), infrared, and radio bands (Dickel & Milne 1998) in the LMC. Its images in optical and infrared emission lines (e.g. Hα, [Fe ii] 1.64 μm) are similarly rich in filaments and display an open and irregular shell structure of about 65 arcsec in diameter (≈16 pc) that is broken in the north-west direction (Dickel et al. 1995). In contrast, the X-ray and radio continuum emission exhibits a complete and more symmetric shell shape with no prominent filamentary structures, which extends farther to the west by 30 arcsec (Dickel et al. 1995; Vancura et al. 1992). N 49 presents an increase in brightness towards the south-east border in all spectral bands, but with different intensities. The ratio in brightness between the south-east and the north-west borders is 9/1 in X-rays and 3/1 in radio (Dickel & Milne 1998). A CO-emission mapping around the object revealed the presence of a molecular cloud towards the south-east and with a similar radial velocity of the SNR (Banas et al. 1997). This molecular cloud is most probably responsible for the distorted optical morphology of N 49.
In this paper, we present a study of the spatial variation in the electron density and of the kinematics of N 49, based on optical spectrophotometric observations sampling the whole object. In the next section, we describe the observational, and data reduction procedures. In Sect. 3, bi-dimensional maps of electron density, radial velocity, and velocity dispersion constructed from the observations are presented and discussed. A brief summary of the results is given in Sect. 4.
2. Observations and data reduction
Long-slit spectrophotometric data were obtained on November 2009, using the Cassegrain spectrograph attached to the 1.6 m telescope at the Observatório do Pico dos Dias, Brasópolis, Brazil1. The detector used was an SITe CCD of 2048 × 2048 pixels. A spectral dispersion of 0.5 Å pixel-1 was obtained with a grating of 1200 grooves mm-1, and the spectra covered the range between 5950 Å and 6750 Å with a spectral resolution of 3.0 Å. The spatial scale was 0.5″ pixel-1.
The slit was aligned along the east-west direction and had an entrance on the plane of sky of 360″× 2″. The slit was positioned at 12 different and equally spaced declinations separated by 5″, from Δδ = −20″ to Δδ = + 35″ from the reference star 2MASS 0525522-6605074 (α = 05 25 05.22, δ = −66 05 00.74, epoch = J2000). To limit the effects of cosmic rays, an exposure time of 20 min was chosen. A journal of the observations is given in Table 1. Several bias and dome flat-field exposures were taken to perform CCD corrections. The spectrophotometric standard stars HR 3454 and HR 9087 were observed for flux calibration.
Journal of observations.
The standard data reduction procedures (bias correction, flat-fielding, cosmic rays cleaning, wavelength and flux calibration, 1D spectrum extraction) were performed using IRAF2 software. From each two-dimensional spectrum, 110 one-dimensional spectra were extracted from adjacent apertures of 2.3″ in length along the slit, resulting in a total of 1320 one-dimensional spectra, 312 of them containing nebular emission from N 49. To extract the 1D spectra from the same right ascension bands, we first defined a fiducial position on the slit axis, by measuring on each 2D spectra the positions along the slit of the detected star and comparing them with coordinates obtained from direct images of the region.
The wavelength was calibrated based on the comparison with the spectra of He-Ar lamps taken before and after each object exposure. After that, the telluric Hα component was measured and a third-order polynomial was fitted to its wavelength shift at different positions along the slit. This function was used to refine the initial wavelength calibration. Subsequently, the sky background contamination was removed with the skysub routine. A mean spectra for each slit position was then obtained by combining the exposures referring to a same offset.
The emission lines fluxes were determined by a Gaussian fit over the line profile. Two Gaussians were fitted in the cases of line with two components. The fitting procedure was realized with the splot routine. In the case of double components of the [S ii] λλ6717, 6731 lines, the profiles of the lines were fitted by a sum of two pairs of Gaussians. For each pair, the full width at half maximum (FWHM) of both lines of the doublet was assumed to be the same, and the wavelength separation was fixed to 14.38 Å. This fitting procedure was carried out using the nfit1d routine using the output of the splot routine as initial solution. A typical one-dimensional spectra of N 49 with emission lines with double components is shown in Fig. 1.
 |
Fig. 1 Typical one-dimensional spectra of N 49 with double-peaked emission lines. |
3. Results and discussion
3.1. Electron density
In this section, maps of electron density, radial velocity and velocity dispersion will be presented and discussed. Figure 3a shows the Hα flux map. A minimum flux in Hα of 1.5 × 10-15 erg cm-2 s-1 which corresponds to 1% of the peak value, was adopted to define the limits of the nebula and to filter low signal-to-noise spectra. This selection criterion was extended to the other maps. From a total of 312 one-dimensional spectra that passed the selection criterion, 130 exhibited double-peak line profiles. In these cases, the flux was calculated by the sum of the flux associated to the bluer and redder Hα components (hereafter designated as components 1 and 2, respectively). The Hα flux map shows a typical horseshoe shape.
The ratio [S ii] λ6717/λ6731 was used to determine the electron density Ne by numerically solving the equilibrium equation for the n-level approximation (n = 8) of [S ii] with the temden routine of the nebular package of the STSDAS/IRAF. This line ratio is weakly dependent on the electron temperature and a value of Te = 10 000 K was adopted.
 |
Fig. 2 Histogram of the electron density measurements. |
A histogram of the electron density measurements determined from the individual components of the double-peaked lines or from the single lines is displayed in Fig. 2. The median value of the density distribution is 1280 cm-3, 50% of the values are found in the range of 925–1850 cm-3, and a few areas present electron density higher than 3500 cm-3.
 |
Fig. 3 Maps in Hα and of the electron density for N 49 displayed on a linear colour scale. The horizontal axis displays the right ascension coordinate and the vertical axis shows the declination offset from the reference star 2MASS 05255225-6605074. The pixel size is 2.3″ in right ascension and 5″ in declination. Panels: a) the Hα flux map; b) the mean electron density map from the sum of the Gaussian components of each line of the [S ii] doublet; c) electron density map from component 1 (blue); d) electron density map from component 2 (red). |
Figure 3 presents the electron density maps determined from different components of the [S ii] lines. In Fig. 3b, the electron density was given by the flux-weighted average of the values of the two components in the case of double-peaked lines. One can note a strong density gradient between the eastern and western borders. The mean electron density varies from 600 cm-3 in the west to 2000 cm-3 in the east. This result is in accordance with the study of Dickel & Milne (1998) that predicted a density variation by a factor of three by comparing the X-ray and radio contrast between the eastern and western edges of N 49.
Vancura et al. (1992) have measured the electron density from the [S ii] ratio based on long-slit spectrophotometric observations at three different positions. They found average densities of 1000 and 1800 cm-3 in their LS2 and LS1 regions that cover the north-west and south-east borders of N 49, respectively. Their LS1 region contains the higher density structure seen to the east on map 3b, where electron densities around 2000 cm-3 were observed. The mean electron density measured along their LS2 region is compatible with the values of map 3b, which revealed electron densities in the range 600–1200 cm-3 in this region. At these two slit positions, they observed a small variation in the electron density (correponding to less than 10% in the [S ii] ratio). The authors, however, do not specify the aperture size, and probably this conclusion was obtained because the dense filaments appears smoothed in their data. On the other hand, they found an increase in density by a factor of two from north-west to south-east from the data obtained with the slit positioned along roughly a diameter of the nebula (PA = 120°). This conclusion is compatible with the gradient observed in the electron density maps displayed in Fig. 3.
The density increase in the east direction can be due to the interaction of the SNR with the CO molecular cloud detected by Banas et al. (1997). The maps presented here should be compared with their Fig. 5, where an X-ray image of N 49 was overlaid with velocity-integrated CO emission contours. They found that N 49 and the molecular cloud have similar radial velocities, and claimed that the two systems are physically associated. The density structures seen in Fig. 3c support this assertion. At the south-east border, an aromatic feature at 3.3 μm was detected for the first time in SNRs (Seok et al. 2012). Furthermore, Park et al. (2003) found evidence that this portion of N 49 is reheated by a reverse shock that arises from the interaction with the molecular cloud.
Two dense areas with Ne ≥ 2000 cm-3 are found on the eastern border of the nebula, near but not exactly coinciding with the brightest areas in the optical. The dense area on the south-east border is on the edge of the bright ridge of filaments associated with the peak of the emission of the nebula in different frequencies. See the Hubble Space Telescope high resolution images in different emission lines presented by Bilikova et al. (2007). However, the dense zone on the north-east borders is in an area of low brightness. The low brightness in Hα of an area of high density can be produced by a net of dense but sparse filaments or by a dense sheet of material seen perpendicularly. The contour map of N 49 in H2 emission at 2.12 μm presented by Dickel et al. (1995) shows no molecular emission at this area.
The two main velocity components show, in general, a similar spatial density distributions, with the density increasing from west to east. The local differences between them can be associated to the bright filaments seen in the Hα image. For example, the bright filamentary structure crossing from south-east to north of the nebula does show especially high densities from the red components of the [S ii] doublet, while from the blue components the density towards this structure is lower than in the neighbourhood. This indicates that this structure is on the far side of the nebula.
3.2. Nebular mass and filling factor
The observed Hα flux was F(Hα) = 9.85 × 10-11 erg cm-2 s-1 (after a correction by a factor of 5/2, since the slit had a width of 2″ and the offset between the slit position was 5″). A reddening-corrected flux of Fc(Hα) = 2.86 × 10-10 erg cm-2 s-1 was calculated by adopting E(B − V) = 0.37, which is the mean value determined by Vancura et al. (1992). In many SNRs, it has been observed that most of the emission comes from the near side of the remnant due to an internal extinction (Milisavljevic et al. 2010). In the case of N 49, the Hα fluxes of the blue and red components are similar, indicating that the internal extinction is negligible.
Adopting a distance for the LMC of d = 49 kpc (Feast 1991) and a mean electron density of Ne = 1300 cm-3, a mass of ionized hydrogen of MH+ = 148 ± 47 M⊙ was estimated using the expression 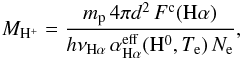 (1)where mp is the proton mass, hνHα is the energy of the Hα photon,
(1)where mp is the proton mass, hνHα is the energy of the Hα photon, 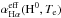 is the effective recombination coefficient for Hα (from Osterbrock & Ferland (2006) for a 10 000 K gas). The error was estimated assuming an uncertainty of 5% in the measured Hα flux, 10% in the LMC distance, and 10% in the extinction coefficient and electron temperature between 8000 and 12 000 K. Assuming an abundance of He:H of 10% (in number of atoms), which is typical of the interstellar medium of the LMC, we estimate a total mass of 207 ± 66 M⊙. Hughes et al. (1998) obtained a mass of 210 M⊙ by estimating the quantity of X-ray emitting plasma from a Sedov model fits over a X-ray spectrum of N 49. A more uncertain estimate of 60 M⊙ for N 49 was given by Westerlund & Mathewson (1966). This value was obtained by applying a modified Shklovsky method to a sample of SNRs with known distances.
is the effective recombination coefficient for Hα (from Osterbrock & Ferland (2006) for a 10 000 K gas). The error was estimated assuming an uncertainty of 5% in the measured Hα flux, 10% in the LMC distance, and 10% in the extinction coefficient and electron temperature between 8000 and 12 000 K. Assuming an abundance of He:H of 10% (in number of atoms), which is typical of the interstellar medium of the LMC, we estimate a total mass of 207 ± 66 M⊙. Hughes et al. (1998) obtained a mass of 210 M⊙ by estimating the quantity of X-ray emitting plasma from a Sedov model fits over a X-ray spectrum of N 49. A more uncertain estimate of 60 M⊙ for N 49 was given by Westerlund & Mathewson (1966). This value was obtained by applying a modified Shklovsky method to a sample of SNRs with known distances.
An rms electron density of ⟨ Ne ⟩ = 60 cm-3 was estimated from the reddening corrected Hα flux, assuming spherical symmetry and a radius of 8 pc (Vancura et al. 1992) for the nebula. From this value and the mean electron density from the [S ii] ratio, a filling factor of 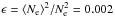 was obtained. The rms density estimated here for the whole nebula is between the values given by Bilikova et al. (2007) of ⟨ Ne ⟩ ≈ 10 cm-3 for areas with a diffuse Hα emission and ⟨ Ne ⟩ ≈ 70 − 310 cm-3 for the filaments.
was obtained. The rms density estimated here for the whole nebula is between the values given by Bilikova et al. (2007) of ⟨ Ne ⟩ ≈ 10 cm-3 for areas with a diffuse Hα emission and ⟨ Ne ⟩ ≈ 70 − 310 cm-3 for the filaments.
3.3. Kinematics
 |
Fig. 4 Radial velocity and velocity dispersion maps of N 49. Panels: a) mask for the adopted limits of N 49 (black for discarded pixels) and for the areas with double-peak (white) or single (red) lines; b) radial velocity of component 1 (blue); c) radial velocity of component 2 (red); d) 3σv velocity dispersion. |
Although our data do not have the high spectral and spatial resolutions of some previous observations of the radial velocity field in N 49 (e.g. Shull 1983; Bilikova et al. 2007), we have a full coverage of the nebula that allows us to draw an overall picture of the kinematics of this supernova remnant.
A narrow Hα emission was detected throughout the object and beyond its western border. This emission has a constant velocity of ≈295 km s-1 over the area and has been detected by several authors. Bilikova et al. (2007), Shull (1983), and Vancura et al. (1992) have argued that this emission comes from a gas ionized by the UV precursor of SNR shocks. On the other hand, Chu & Kennicutt (1988) claimed that this emission comes from an H ii region located on the western edge of N 49. This Hα component was left out in this study.
Figure 4a presents a mask representing the spatial distribution of spectra with single and double-peak lines. As can be seen in this figure, points further from the centre tend to detect just a single Hα component. Figures 4b,c display the maps of the LSR (local standard of rest) radial velocities obtained from the Doppler shifts of components 1 (blue) and 2 (red) of Hα, respectively.
The velocity dispersion was determined from the Gaussian fitting of the Hα line profile (with one or two components). Instrumental broadening effects were removed by subtracting quadratically the FWHM of lines of the comparison lamp spectra extracted from the same windows along the slit. The two components of Hα may have very different flux values. As a result, we use a 3σv velocity dispersion, which corresponds to a full-width of a line at 1% of the peak intensity, calculated (in velocity units) by 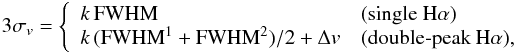 (2)where
(2)where 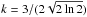 , the superscripts 1 and 2 refer to the two main Hα components, and Δv is the velocity difference between the centroids of the two Hα components. This criterion makes a comparison possible between the values of velocity dispersion of regions that exhibit one and two Hα components, and it corresponds to a practical calculation of a full width at zero intensity of the line in velocity units. The 3σv velocity dispersion map is shown in Fig. 4d. This map is a clear indication of the expanding shell structure of N 49.
, the superscripts 1 and 2 refer to the two main Hα components, and Δv is the velocity difference between the centroids of the two Hα components. This criterion makes a comparison possible between the values of velocity dispersion of regions that exhibit one and two Hα components, and it corresponds to a practical calculation of a full width at zero intensity of the line in velocity units. The 3σv velocity dispersion map is shown in Fig. 4d. This map is a clear indication of the expanding shell structure of N 49.
Radial velocity and velocity dispersion statistics.
Figures 4a,b,d exhibit a rough radial symmetry that can be interpreted as a projection effect if we assume that N 49 is an expanding spherical shell. In fact, the maps of the difference between the radial velocities from blue and the red components of Hα and of the 3σv radial velocity dispersion have a peak nearly at the centre of the image, and at the borders of the maps these components could not be resolved. However, it is surprising that, although near the centre of the optical image of N 49, this kinematic centre of symmetry is far from the centre of the X-ray or radio images. In fact, the eastern border of the nebula almost coincides in all frequencies, but the radio continuum and X-ray emissions extend farther to the west by 30 arcsec (see Fig. 2 in Dickel et al. 1995).
A statistical summary of the measurements of the radial velocity (from the two main components of Hα (c1 and c2) and from the single Hα (s)) and of the 3σv velocity dispersion is given in Table 2. Figure 5a shows the histograms of the radial velocities of components 1 and 2. The two distributions present a similar dispersion of ≈60 km. The velocity difference between the peaks of the distributions is ≈180 km s-1, which indicates a lower limit to the expansion velocity of 90 km s-1. An upper limit of 250 km s-1 can be set by the difference between the maximum and the minimum values measured (at different positions) for the velocity of ≈510 km s-1. The histogram of the velocity difference between components 1 and 2 is shown in Fig. 5b. The maximum velocity difference between the Hα components is ≈270 km s-1, and it is attained at the centre of the image. These histograms, as well the asymmetry of the optical morphology, show that N 49 is far from being an spherical and thin expanding shell. In that case, the velocity histograms would be more asymmetric with the peaks occurring close to the maximum and minimum values. A wide range of velocities is found in each of the Hα components.
Previous kinematical studies of N 49 based on high spectral resolution echelle observations (Shull 1983; Chu & Kennicutt 1988; Vancura et al. 1992; Bilikova et al. 2007) have shown that the echellograms of Hα and other emission lines of this object are dominated by distinct clumps with large internal velocity dispersions. Different interpretations are possible, but all authors agree that the kinematics and the structure of N 49 are the consequence of its expansion in an inhomogeneous interstellar medium. Bilikova et al. (2007) attribute the filaments to long ribbon-like structures and argue against the existence of an expanding shell based on the lack of a clear bow-shaped line in their echellograms. However, we observe that these clumps seen in all echellograms, which are in fact associated to the conspicuous filaments of the remnant, are located inside a fainter bow-shaped envelope. Our low spatial resolution maps of velocity and velocity dispersion smooth out the filamentary structures and show the overall kinematics of an expanding shell, as does the drifted-scanned integrated echelle spectrum presented by Shull (1983).
 |
Fig. 5 Histograms of a) the radial velocities of components 1 (red) and 2 (blue) and of b) the radial velocity difference between these components. |
3.3.1. Analysis of the radial velocity profile of the near side of the shell
In this section, we discuss a quantitative model for the spatial profile of the radial velocities on the near side of the shell, measured from component 1 of Hα. Figure 6 shows the mean value of the radial velocity inside a set of concentric annuli centred on the position of the peak of the difference between the velocities of components 1 and 2 against the projected distance to this point. The form of the relationship between the radial velocity and the radius observed in N 49 cannot be explained by a simple projection effect, as we show by means of simplified models. In the case of a thin spherical shell of radius R, at a position on the near hemisphere with a projected (on the plane of the sky) distance to the centre of γR, the radial velocity is 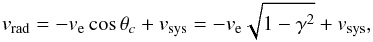 (3)where θc is the angle between the line of sight and the axis of the sphere (or the direction of expansion) at that point, ve is the expansion velocity, and vsys is the systemic velocity of the shell. For a homogeneous sphere of radius R with a velocity field following
(3)where θc is the angle between the line of sight and the axis of the sphere (or the direction of expansion) at that point, ve is the expansion velocity, and vsys is the systemic velocity of the shell. For a homogeneous sphere of radius R with a velocity field following 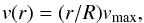 (4)we would find that
(4)we would find that 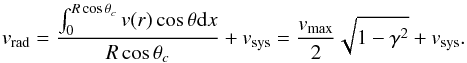 (5)The functional dependence of the radial velocity with γ is exactly the same in both Eqs. (3) and (5), and it is not appropriate to describe the observed radial velocity profile, because the concavities are opposite. To illustrate, in Fig. 6 we plot Eq. (3) with ve = 100 km s-1 and vsys = 260 km s-1, which is the LMC radial velocity (van der Marel et al. 2002).
(5)The functional dependence of the radial velocity with γ is exactly the same in both Eqs. (3) and (5), and it is not appropriate to describe the observed radial velocity profile, because the concavities are opposite. To illustrate, in Fig. 6 we plot Eq. (3) with ve = 100 km s-1 and vsys = 260 km s-1, which is the LMC radial velocity (van der Marel et al. 2002).
 |
Fig. 6 Mean radial velocity versus projected radius for the near-side of N 49. The non-dimensional variable γ is defined as the ratio between the projected distance from the centre and the radius of the remnant. The blue line shows that the functional dependence with γ of Eq. (3) is unsuitable for fitting the data. The green line is the best fitting of Eq. (8). |
For the self similar solution developed by Sedov (1959) for the adiabatic expansion of a blast wave in a homogeneous medium, the dependence of the radial velocity with γ is similar of that of Eq. (3) or (5), since the predicted velocity field follows closely Eq. (4), and about 80% of the mass is concentrated next to the shock front within a thin shell of thickness 0.1R (Chevalier 1976). The observed radial velocity profile indicates that N 49 is not a thin shell, and its internal velocity field cannot be describe by a simple law as Eq. (4). The velocity projection effect alone would not explain the kinematic data.
3.3.2. Sedov solution in a non-uniform medium
A circumstellar power-law density profile ρ(r) ∝ r− ω prior to the explosion may arise by the action of the stellar wind of the supernova progenitor. If a constant mass loss rate is assumed, then ω = 2. Other values for ω can be reached with variable mass loss rate or stellar wind velocity. To describe the dynamics of SN 1993, van Dyk et al. (1994) inferred ω = 1.5. They argued that this density distribution may be caused by a decrease in the mass loss rate or, alternatively, by an increase in the stellar wind velocity prior to the explosion. N 49 is probably the result of the explosion of a massive star. The main evidence is the association between the remnant and the soft gamma-ray repeater 0526-66 (Evans et al. 1980). The mass of its progenitor is estimated to be at least 20 M⊙ by assuming it was a member of the nearby stellar association LH 53 (Hill et al. 1995; Klose et al. 2004). Alternatively, a similar power-law density distribution may be produced at the moment of the explosion. According to the model of McKee & Ostriker (1977), the radiation pulse emitted in the explosion evaporates the cloudy component of the medium around the star, leading to a power-law density distribution with ω = 5/3.
The Sedov similarity solution for a medium whose density varies as ρ(r) = Ar− ω states that the kinematics of a monoatomic gas with adiabatic index 5/3 that lies behind the blast wave front is described by 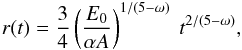 (6)where t is the time after the explosion, E0 is the released energy, and α is a constant. This equation implies that gas velocity v(r) satisfies
(6)where t is the time after the explosion, E0 is the released energy, and α is a constant. This equation implies that gas velocity v(r) satisfies 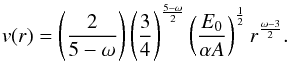 (7)Integrating v(r) as on the lefthand of Eq. (5), we find that the mean radial velocity along the line-of-sight is given by
(7)Integrating v(r) as on the lefthand of Eq. (5), we find that the mean radial velocity along the line-of-sight is given by 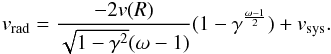 (8)The negative sign of the first term reflects that we are only dealing with blue-shifted velocities relative to the systemic velocity of the nebula. This equation fits the mean radial velocity profile of Fig. 6 very well. The best-fit parameters are vsys = 275 km s-1, ω = 1.1, and v(R) = 75 km s-1. The vsys value is close to the LMC systemic radial velocity of ≈260 km s-1 (van der Marel et al. 2002).
(8)The negative sign of the first term reflects that we are only dealing with blue-shifted velocities relative to the systemic velocity of the nebula. This equation fits the mean radial velocity profile of Fig. 6 very well. The best-fit parameters are vsys = 275 km s-1, ω = 1.1, and v(R) = 75 km s-1. The vsys value is close to the LMC systemic radial velocity of ≈260 km s-1 (van der Marel et al. 2002).
The optical spectra of N 49 obtained by Vancura et al. (1992) were reproduced well by the radiative shock model of Raymond (1979) by assuming a power-law shock velocity distribution. They found that, for an area A covered by shocks with velocity v, the relation A(v) ∝ v-2.2 holds for 40 km s-1 ≤ v ≤ 270 km s-1. From our model, we found that v(r) ∝ r-0.9. If we assume that A(r) ∝ r2, then A(v) ∝ v-2.2, which is in perfect agreement with the work of Vancura et al. (1992). This is remarkable since our description is based only on kinematic data of N 49, while these authors obtained the same result by modelling its observed spectrum.
4. Conclusions
From long-slit spectrophotometric data obtained over twelve distinct declinations separated by steps of 5′′, we have extracted 1D spectra in the range 5950 to 6750 Å from 312 different area of 2.3″ × 2″ over N 49 to study the spatial variation of the electron density and the kinematics of this supernova remnant. The main results are the following.
-
1.
We constructed a map of the electron density from the line ratio[S ii] λ6717/λ6731 that revealed a strong gradient with the density increasing from west to east, which can be attributed to the interaction of N 49 with a molecular cloud detected on the south-east border. The densest areas, with Ne ≥ 2000 cm-3, are found on the east border of the nebula, near but not exactly coinciding with the brightest areas in the optical. The dense area on the south-east border is on the edge of the bright ridge of filaments associated with the peak of the emission of the nebula in different frequencies. However, the dense zone on the north-east borders is in an area of low brightness.
-
2.
From the reddening corrected Hα flux, we inferred a hydrogen nebular mass of 148 ± 47 M⊙. Assuming an He:H abundance of 10%, we estimated a total mass of 207 ± 66 M⊙. An rms density of ⟨ Ne ⟩ = 60 cm-3 was obtained from the surface brightness in Hα. We estimated a filling factor of about 0.002 by comparing this rms density with the mean electron density of 1300 cm-3 derived from [S ii] ratio.
-
3.
The radial velocity and the velocity dispersion were obtained from Gaussian fitting of the Hα line. In many positions, specially at the centre of the optical image, the emission lines are double-peaked. Maps of the radial velocities of the blue and red shifted components of Hα and of the velocity dispersion at 3σ, which is essentially equivalent to na FWZI (in velocity units), showed a rough radial symmetry that can be interpreted as the projection effect of an expanding spherical shell. However, although near the centre of the optical image of N 49, the kinematic centre of symmetry is far from centre of the X-ray or radio images.
-
4.
We verified that the velocity field of the near side of the object cannot be understood as a simple projection effect of a thin expanding shell as predicted by the Sedov solution for an adiabatic expansion in a homogeneous medium. Instead, we were able to fit the the radial profile of the near-side velocity using a self-similar solution of a blast wave travelling through a medium characterized by a power-law density distribution.
The spectrophotometric data are available in electronic form at the OPD data bank on http://www.lna.br/databank/databank.html, and the fits files of the maps of Figs. 3 and 4 are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5)
Acknowledgments
This work was supported by the Brazilian agency CAPES.
References
- Banas, K. R., Hughes, J. P., Bronfman, L., & Nyman, L.-A. 1997, ApJ, 480, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Bilikova, J., Williams, R. N. M., Chu, Y.-H., Gruendl, R. A., & Lundgren, B. F. 2007, AJ, 134, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1976, ApJ, 207, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Chu, Y.-H., & Kennicutt, R. C. Jr. 1988, AJ, 95, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Dickel, J. R., & Milne, D. K. 1998, AJ, 115, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Dickel, J. R., Chu, Y.-H., Gelino, C., et al. 1995, ApJ, 448, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A. 1979, ApJS, 40, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, W. D., Klebesadel, R. W., Laros, J. G., et al. 1980, ApJ, 237, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W. 1991, in The Magellanic Clouds, eds. R. Haynes, & D. Milne, IAU Symp., 148, 1 [Google Scholar]
- Hill, R. S., Cheng, K.-P., Bohlin, R. C., et al. 1995, ApJ, 446, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J. P., Hayashi, I., & Koyama, K. 1998, ApJ, 505, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Klose, S., Henden, A. A., Geppert, U., et al. 2004, ApJ, 609, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Helfand, D. J., & Grabelsky, D. A. 1981, ApJ, 248, 925 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Milisavljevic, D., Fesen, R. A., Gerardy, C. L., Kirshner, R. P., & Challis, P. 2010, ApJ, 709, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd edn. (University Science Books) [Google Scholar]
- Park, S., Burrows, D. N., Garmire, G. P., et al. 2003, ApJ, 586, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J. C. 1979, ApJS, 39, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Seok, J. Y., Koo, B.-C., & Onaka, T. 2012, ApJ, 744, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, P. Jr. 1983, ApJ, 275, 611 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- van Dyk, S. D., Weiler, K. W., Sramek, R. A., Rupen, M. P., & Panagia, N. 1994, ApJ, 432, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Vancura, O., Blair, W. P., Long, K. S., & Raymond, J. C. 1992, ApJ, 394, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Westerlund, B. E., & Mathewson, D. S. 1966, MNRAS, 131, 371 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Typical one-dimensional spectra of N 49 with double-peaked emission lines. |
| In the text | |
 |
Fig. 2 Histogram of the electron density measurements. |
| In the text | |
 |
Fig. 3 Maps in Hα and of the electron density for N 49 displayed on a linear colour scale. The horizontal axis displays the right ascension coordinate and the vertical axis shows the declination offset from the reference star 2MASS 05255225-6605074. The pixel size is 2.3″ in right ascension and 5″ in declination. Panels: a) the Hα flux map; b) the mean electron density map from the sum of the Gaussian components of each line of the [S ii] doublet; c) electron density map from component 1 (blue); d) electron density map from component 2 (red). |
| In the text | |
 |
Fig. 4 Radial velocity and velocity dispersion maps of N 49. Panels: a) mask for the adopted limits of N 49 (black for discarded pixels) and for the areas with double-peak (white) or single (red) lines; b) radial velocity of component 1 (blue); c) radial velocity of component 2 (red); d) 3σv velocity dispersion. |
| In the text | |
 |
Fig. 5 Histograms of a) the radial velocities of components 1 (red) and 2 (blue) and of b) the radial velocity difference between these components. |
| In the text | |
 |
Fig. 6 Mean radial velocity versus projected radius for the near-side of N 49. The non-dimensional variable γ is defined as the ratio between the projected distance from the centre and the radius of the remnant. The blue line shows that the functional dependence with γ of Eq. (3) is unsuitable for fitting the data. The green line is the best fitting of Eq. (8). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


