| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220568 | |
| Published online | 07 May 2013 | |
The production of craters on the mid-sized Saturnian satellites by Centaur objects
1
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La
Plata,
1900
La Plata,
Argentina
e-mail:
romina@fcaglp.unlp.edu.ar
2
Instituto de Astrofísica de La Plata, CCT La Plata-CONICET-UNLP Paseo del Bosque S/N
(1900), La Plata,
Argentina
Received:
15
October
2012
Accepted:
11
February
2013
Context. The Saturnian satellite system has been observed in detail by the Cassini-Huygens mission. These satellites present different surface features, including impact craters caused by small objects probably coming from the trans-Neptunian region.
Aims. In this paper we calculate the production of craters on the mid-sized Saturnian satellites produced by Centaurs from the scattered disk (SD) and plutinos in order to determine this contribution, and we compare our estimations with the Cassini observations.
Methods. We used a method developed in a previous paper that uses a numerical investigation of the dynamical evolution of Centaur objects to calculate the production of craters. We used a size-frequency distribution (SFD) of scattered disk objects (SDOs) as a power law with a break at diameters d = 60 km considering two cases for the differential power-law index: s2 = 2.5 and s2 = 3.5 for d < 60 km.
Results. We calculated the number of craters, the greatest crater produced by Centaurs from the SD and plutinos, and the present cratering rate on each of the mid-sized satellites, for both cases of the SFD of SDOs considered. The contribution of plutinos is negligible compared to SDOs. From our calculations and the comparison with observations we note that the calculated number of craters for s2 = 3.5 is in general nearer the observed number. However, in general for smaller craters, the observed number is less than the calculated one. This trend can be explained by at least two mechanisms. On the one hand, this could be caused by an erasing process that gradually buries the craters, which does not affect large craters. On the other hand, the comparison of the calculated and observed crater size-frequency distribution for different size ranges implies that for d < 60 km, the SFD of SDOs is consistent with the assumed index s2 = 3.5, for d ≳ 0.2−1.4 km and for d ≲ 0.2−1.4 km, it is consistent with s2 = 2.5. Then in the range d ~ 0.2−1.4 km, the SFD of SDOs could have a new break. This change of slope could explain the reduction of small craters, at least for some cases.
Conclusions. We found a good agreement when comparing our results with observations. However, independent determination of surface ages and geological processes are needed to determine if there is a new break on the SFD of SDOs, if there is a planetocentric source of craters in the Saturnian system, and which craters are primordial.
Key words: methods: numerical / Kuiper belt: general / planets and satellites: surfaces
© ESO, 2013
1. Introduction
The arrival of the Cassini-Huygens spacecraft at the Saturn system in June 2004 allowed a detailed observation of all the Saturn satellites and even the discovery of new small satellites orbiting the planet. The Saturnian satellites present a diversity of surfaces and sizes; some of them are very small (km-tens of km), others are mid-sized (hundreds of km), and we have the largest satellite, Titan. Every satellite is a unique world that presents new challenges and prospects for planetary studies in general, and also for the study of new physical, dynamical, chemical, and even biological processes in completely new lands and habitats.
The mid-sized icy satellites of Saturn are Mimas, Enceladus, Tethys, Dione, Rhea, and Iapetus. All of them are regular satellites that orbit Saturn in quasi-circular and low-inclination orbits. Thomas (2010) updated the shape information of the Saturnian satellites and the related interpretations of measurements from the Cassini imaging data and the previous calculations. The mean radius and densities obtained by Thomas (2010) are shown in Table 1. Jacobson et al. (2006) reports on the gravity field of the Saturnian system, calculating the superficial gravity based on data acquired from all of the spacecraft that have visited the system up to mid-2006. In Table 1 we summarize all the physical data of the satellites, as well as the orbital semimajor axis and mean orbital velocity. The mid-sized satellites of Saturn are mainly composed of water ice and present cratered surfaces, but some of them have young surfaces associated with recent geological processes. Cassini observations of the Saturnian system provide high-resolution images that allowed the Cassini team to obtain impact cratering records on their surfaces. Kirchoff & Schenk (2009) and (2010) (KS09 and KS10 in the following) analyzed Cassini images and obtained the number and size-frequency distribution of craters for the mid-sized icy satellites. Although the counts are not from the complete surface (Kirchoff, priv. comm.), we will use these papers in order to compare and analyze our results.
It was proposed in the Voyager era, based on the cratering data, that the satellites were struck by two different impactor populations. Population I were heliocentric objects and Population II were planetocentric impactors, such as small planetocentric debris. Many giant planetary satellites exhibit irregular shapes and features related to past catastrophic events. These events injected fragments into planetocentric orbits that became planetocentric projectiles for the satellites in the system. There are a number of papers that address the source and fate of planetocentric objects. Marchi et al. (2001) analyzed the possible transfer of mass from a satellite after a catastrophic collision onto another satellite. In particular for the Saturn system, these papers show that Hyperion was the most likely source of fragments for Titan, and a transfer from Phoebe to Iapetus was also possible. Dobrovolskis & Lissauer (2004) studied the ejecta from Hyperion and suggested that it contributed to Population II craters on the inner satellites of Saturn. They suggested that those projectiles struck with less speed than heliocentric impactors and so could be distinguished by crater morphology. The high resolution of Cassini images and more analysis on the production of craters will help to determine the origin of the craters, and if one or two populations have contributed to crater the system. Beyond this, the heliocentric population that is now the source of craters on the satellites of the giant planets are Centaurs. Centaur objects are small bodies that have orbits mainly in the giant planetary zone, and cross orbits with the giant planets and then with their satellites. They come mainly from the scattered disk (SD) in the trans-Neptunian zone (Di Sisto & Brunini 2007). The scattered disk objects (SDOs) are bodies with perihelion distances q greater than 30 AU and smaller than ~39 AU that can cross the orbit of Neptune and eventually move into the giant planetary zone. When they enter this zone they are called Centaurs and they can cross the orbits of the planets and of their satellites (Di Sisto & Brunini 2007; Levison & Duncan 1997). The secondary source of Centaurs are escaped plutinos and the low-eccentricity trans-Neptunian objects (Di Sisto et al. 2010; Levison & Duncan 1997). In short, Centaurs are small body objects capable of crossing the orbits of the giant planet’s satellites hitting them and producing craters.
In this paper, we study the production of craters on the mid-sized satellites of Saturn caused by Centaur objects coming from the SD and plutinos. In a recent paper Di Sisto & Brunini (2011) (hereafter DB11) studied the craters on Phoebe produced by Centaurs from SDOs and plutinos. We use the same method described in that paper for each of the mid-sized Saturnian satellites. We will compare our results with the crater counts from the Cassini images in order to determine for each satellite the contribution of the present Centaur population, the origin of craters and special features.
Satellite data.
2. Method
In this section we describe the population of impactors, the method, and the cratering law that we will use to evaluate the production of craters on the mid-sized satellites of Saturn.
2.1. The impactor population
The cratering rate and number of craters on a solar system body depend on the number and
size of the impactor populations. Here, we will consider as impactors the Centaur objects
that come mainly from SDOs and less often from escaped plutinos. As mentioned, SDOs are
trans-Neptunian bodies with perihelion distances
30 < q < 39 AU that can
cross the orbit of Neptune and eventually move into the giant planetary zone where they
are called Centaurs. DB11 analyzed the size-frequency distribution (SFD) of SDOs based on
new estimations of the maximum number of distant populations by Parker & Kavelaars
(2010a,b) and considered that it has a break at
diameters d ~ 60 km (Bernstein et al. 2004; Gil Hutton et al. 2009; Fraser
& Kavelaars 2009; Fuentes & Holman
2008; Fuentes et al. 2009). The differential power-law indexes of the SFD has been given the
value s1 = 4.7 for
d > 60 km (Elliot et al. 2005) and given two values for s2 = 2.5 and
3.5 for d < 60 km given the uncertainty of the
SFD for small objects. Then the cumulative number of SDOs with diameter greater than
d is given by 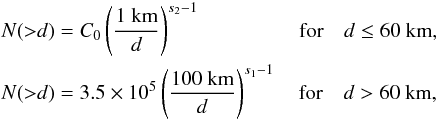 (1)where
C0 = 3.5 × 105100s1−1(60)s2 − s1
by continuity for d = 60 km.
(1)where
C0 = 3.5 × 105100s1−1(60)s2 − s1
by continuity for d = 60 km.
A secondary source of Centaurs considered here is the plutino population. We will also
consider the number of plutinos from the analysis made by DB11. The present cumulative
number of plutinos is given by 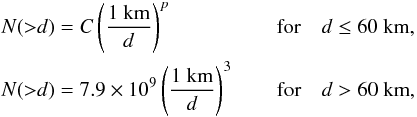 (2)where
C = 7.9 × 109 (60)p−3 by
continuity for d = 60 km and the cumulative power-law index
p has the two values 2.5 and 1.5
(p = s − 1), as in the case of the SFD of SDOs.
(2)where
C = 7.9 × 109 (60)p−3 by
continuity for d = 60 km and the cumulative power-law index
p has the two values 2.5 and 1.5
(p = s − 1), as in the case of the SFD of SDOs.
2.2. Calculation of collisions
In order to study the collisions of Centaurs on the satellites of Saturn, we used the results of the numerical simulation of SDOs by Di Sisto & Brunini (2007) and the numerical simulation of plutinos by Di Sisto et al. (2010). These simulations were done considering the present configuration of the solar system and a time span of 4.5 Gyr. Furthermore, we used the method described in DB11. In this previous work, DB11 used the output files of the encounters of SDOs and plutinos with Saturn to calculate the collisions of Centaurs (from SDOs and plutinos) with the satellites using a particle-in-a-box approximation. It is generally accepted that the initial mass of the trans-Neptunian region was ~100 times greater than its present mass and decayed to nearly its present value in at most 1 Gyr. This scale of time depends on the model of formation and evolution of the early solar system. The initial mass depletion produced a heavy bombardment of minor bodies on the planets and their satellites known as the late heavy bombardment (LHB), approximately 3.8 Gyr ago (see e.g. Morbidelli 2008). The model of DB11 does not consider what happened at early times of the solar system and begins after this initial mass depletion when the solar system began to stabilize. Our model applies to the present configuration of the solar system, as mentioned, and therefore does not take into account the LHB and earlier times. When we refer to Centaurs in the following, we are always talking of “present Centaurs”, i.e., Centaurs that come from the SD after the initial mass depletion, and then our model should be a good approximation for the post-LHB time, namely ≲4 Gyr.
From the method described in DB11, the cumulative number of collisions of Centaurs with
the satellites in the present configuration of the solar system depending on the diameter
is given by 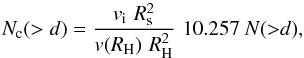 (3)where
vi is the relative collision velocity on each satellite,
Rs is the satellite radius, and
v(RH) is the mean relative encounter
velocity of the Centaurs when they enter the Hill sphere (of radius
RH) of the planet. All the velocities were calculated from
our outputs in the mentioned simulations. The number of Centaurs
N(>d) is given by Eqs.
(1) and (2) according to the corresponding source population. From that equation
we can calculate the number of collisions on a given satellite, and since we have
considered that the SFD of SDOs and plutinos have a break in d ~ 60 km,
the results will be expressed in terms of the two exponents
(s2 = 2.5 and 3.5).
(3)where
vi is the relative collision velocity on each satellite,
Rs is the satellite radius, and
v(RH) is the mean relative encounter
velocity of the Centaurs when they enter the Hill sphere (of radius
RH) of the planet. All the velocities were calculated from
our outputs in the mentioned simulations. The number of Centaurs
N(>d) is given by Eqs.
(1) and (2) according to the corresponding source population. From that equation
we can calculate the number of collisions on a given satellite, and since we have
considered that the SFD of SDOs and plutinos have a break in d ~ 60 km,
the results will be expressed in terms of the two exponents
(s2 = 2.5 and 3.5).
2.3. Cratering law
The size of a crater on a body depends on the size of the impactor through an empirical law that is obtained in general from laboratory experiments. This law depends on the composition of the target, among other factors. The surfaces of the satellites of Saturn are mainly composed of ice. The densities of the mid-sized satellites are also similar to the density of water ice (see Table 1). So we will use the cratering law for icy surfaces for all satellites.
Kraus et al. (2011) present calculations of
scaling laws for final crater size for impacts onto H2O ice. They used recent
simulations from Senft and Stewart (2011) of the
full cratering process on Ganymede to derive the crater size scaling relations for impacts
on cold ice. They consider the gravity regime, vertical impacts, impactor, and target of
the same density and found that the empirical form for the relationship between the
non-dimensionalized diameter of the transient crater πD and
the parameter π2 is 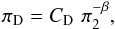 (4)where
(4)where 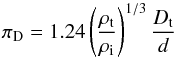 (5)and
the inverse of the Froude number π2 is defined as
(5)and
the inverse of the Froude number π2 is defined as
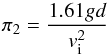 (6)with
ρt the target density, ρi the
impactor density, Dt the apparent transient crater diameter,
vi the impactor velocity, d the impactor
diameter, and g the surface gravity of the target. Kraus et al. (2011) found that the best coefficients in Eq. (4) for 150 K ice are
CD = 2.5 and β = 0.16, which are
intermediate between water and sand and below rock. From these equations and
considerations, the diameter of the transient crater in the gravity regime is then given
by
(6)with
ρt the target density, ρi the
impactor density, Dt the apparent transient crater diameter,
vi the impactor velocity, d the impactor
diameter, and g the surface gravity of the target. Kraus et al. (2011) found that the best coefficients in Eq. (4) for 150 K ice are
CD = 2.5 and β = 0.16, which are
intermediate between water and sand and below rock. From these equations and
considerations, the diameter of the transient crater in the gravity regime is then given
by 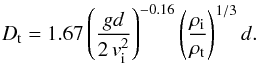 (7)In order to applicate the
size scaling law for the icy satellites of Saturn, it is important to take into account
the whole law that includes the gravitational regime and also the strength regime. Then we
consider the whole form of the cratering law from Holsapple & Housen (2007) that is a convenient empirical smoothing function
to span the transition between the gravity regime and the strength regime, but we take
into account the parameters CD and β for ice
obtained by Kraus et al. (2011) for the gravity
regime.
(7)In order to applicate the
size scaling law for the icy satellites of Saturn, it is important to take into account
the whole law that includes the gravitational regime and also the strength regime. Then we
consider the whole form of the cratering law from Holsapple & Housen (2007) that is a convenient empirical smoothing function
to span the transition between the gravity regime and the strength regime, but we take
into account the parameters CD and β for ice
obtained by Kraus et al. (2011) for the gravity
regime.
Transition diameters and largest impactor and crater.
Then, from Holsapple & Housen (2007)
![\begin{equation} D_{\rm t} = K_1 \left[ \left(\frac{g d}{ 2 v_{\rm i}^2}\right) \left(\frac{\rho_{\rm t}}{\rho_{\rm i}}\right) ^{\frac{2 \nu}{ \mu}} + K_2 \left(\frac{ Y}{\rho_{\rm t} v_{\rm i}^2}\right)^{\frac{2+\mu}{2}} \left(\frac{\rho_{\rm t}}{\rho_{\rm i}}\right)^{\frac{\nu (2+\mu)}{\mu}} \right ]^{-\frac{\mu}{2+\mu}} d, \label{rtt} \end{equation}](/articles/aa/full_html/2013/05/aa20568-12/aa20568-12-eq63.png) (8)where the two exponents
μ and ν and the constant
K1 characterize different materials. The first term is a
measure of the gravity of the target at the time of craterization and the second term
indicates the importance of the strength of the target. Thus, if the first term is larger
in value than the second term, the crater is under the gravity regime, instead if the
second term is larger, we have the strength regime. The partition between the two size
scales of impacts depends on the size of the event (Holsapple 1993). When the two terms are equal we have the transition impactor
diameter (dl) between the strength regime and the gravity
regime. From Eq. (8) we can calculate the
crater diameter produced by dl
(Dl) that is shown in Table 2.
(8)where the two exponents
μ and ν and the constant
K1 characterize different materials. The first term is a
measure of the gravity of the target at the time of craterization and the second term
indicates the importance of the strength of the target. Thus, if the first term is larger
in value than the second term, the crater is under the gravity regime, instead if the
second term is larger, we have the strength regime. The partition between the two size
scales of impacts depends on the size of the event (Holsapple 1993). When the two terms are equal we have the transition impactor
diameter (dl) between the strength regime and the gravity
regime. From Eq. (8) we can calculate the
crater diameter produced by dl
(Dl) that is shown in Table 2.
In order to obtain the appropriate coefficients for the whole cratering law for ices, we take only the first term of Eq. (8) (neglecting the second term). This is the term corresponding to the gravity regime, and equal to the result of Eq. (7). We then obtain the values of K1, μ, and ν in terms of CD and β given in Kraus et al. (2011). The parameters of the complete law are then μ = 0.38, ν = 0.397, and K1 = 1.67. For the strength Y and the constant K2 we use here the values for cold ice from (Holsapple 2011)1, i.e., K2 = 0.351 and Y = 1.5 × 105 dyn/cm2. Kraus et al. (2011) consider that the effect of the impact angle can be taken into account by multiplying the impact velocity by the sine of the angle of impact θ. Then we will consider in Eq. (8) the most probable impact angle θ = 45°.
From Eq. (8) we determine the transient
radius of a crater for an impactor of diameter d on an icy surface; this
is a simple crater. But above a certain threshold size (which depends on the target), a
simple crater collapses because of gravitational forces, leading ultimately to
complex craters with central peaks, terraced walls, and circular rings.
Then, to obtain the final crater diameter we follow the treatment in Kraus et al. (2011) where the simple-to-complex transition diameter
is given by 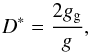 (9)where
gg is the surface gravity of Ganymede, and the final crater
diameter Df for
Dt > D∗
is given by
(9)where
gg is the surface gravity of Ganymede, and the final crater
diameter Df for
Dt > D∗
is given by 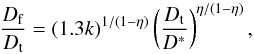 (10)where
k = 1.19 and η = 0.04. Then the final crater size can be
obtained by
(10)where
k = 1.19 and η = 0.04. Then the final crater size can be
obtained by 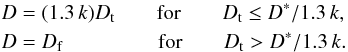 (11)We
have used here the factor 1.3 k, from transient to final simple
craters, and the factor
(1.3 k)1/(1 − η) to
have continuity in the transition from simple to complex craters, according to Marchi et
al. (2011).
(11)We
have used here the factor 1.3 k, from transient to final simple
craters, and the factor
(1.3 k)1/(1 − η) to
have continuity in the transition from simple to complex craters, according to Marchi et
al. (2011).
As can be seen from Eq. (8), the cratering law depends also on the impactor density. The trans-Neptuniana objects (TNO) calculated densities have a wide range of values from ~0.5 to ~3 gr/cm3 (Mc Kinnon et al. 2008). Then we take as the impactor density ρi = 1 gr/cm3 as a typical value of TNO densities.
Equation (3) gives the cumulative number of collisions of Centaurs with the satellites in the present configuration of the solar system, depending on the diameter of the impactor. By combining Eq. (3) with Eqs. (8) and (10), it is possible to calculate the number of craters on each satellite according to the diameter of the crater.
3. Results
First we will show general results obtained from the method described in Sect. 2. We show the results for the production of craters by Centaurs from the SD since the contribution of plutinos is negligible with respect to SDOs. In Table 2 we show the transition crater diameter between the strength regime and the gravity regime (Dl), between simple and complex crater s (D∗), and the largest impactor and crater diameter depending on the SFD index for small impactors (s2) as mentioned in Sect. 2.1. The value of Dl is in general small for all satellites and we see that km-sized craters are produced under the gravity regime.
By combining Eq. (3) with Eqs. (8) and (10), we calculate the total number of craters on each satellite produced by Centaurs according to the diameter of the crater. As already mentioned, this corresponds to the cratering contribution of Centaurs at the post-LHB time. The calculated cumulative number of craters on all mid-sized icy satellites is shown in Fig. 1. Each color represents each satellite, the upper lines correspond to the number of craters obtained using the differential power-law index s2 = 3.5 and the lower lines correspond to s2 = 2.5.
From Eq. (8), we have
D ∝ d for craters with diameters
D < Dl, and then the
cumulative number of craters
(Nc(>D)) will
follow the same power-law relation given for d (Eq. (1)). In the strength regime this is,
N(>D) ∝ D1 − s2.
In the gravity regime, when
D > Dl, the relation
between D and d is no longer linear and it can be obtained
from Eq. (8) neglecting the second term. This
is why the behavior of
Nc(>D) with
D in Fig. 1 is almost equal for all
the satellites. The very small differences between the upper and lower curves are due to the
different values of Dl and the smoothing of the general crater
law near Dl. Then from Eqs. (8) and (1), we can derive
a power-law dependence of
Nc(>D) with
D for all satellites considering both cratering regimes in order to
compare them with the observed distributions. Then for s2 = 2.5
![\begin{eqnarray} &&N_{\rm c}({>}D) \propto D^{-1.5} \hspace*{0.95cm} \text{for} \qquad D < D_{\rm l}, \nonumber \\[2mm] \label{nd1} && N_{\rm c}({>}D) \propto D^{-1.786} \qquad \text{for}\qquad D > D_{\rm l}, \end{eqnarray}](/articles/aa/full_html/2013/05/aa20568-12/aa20568-12-eq97.png) (12)and
for s2 = 3.5
(12)and
for s2 = 3.5 ![\begin{eqnarray} &&N_{\rm c}({>}D) \propto D^{-2.5} \hspace*{0.95cm} \text{for} \qquad D < D_{\rm l}, \nonumber \\[2mm] \label{nd2} &&N_{\rm c}({>}D) \propto D^{-2.976} \qquad \text{for} \qquad D > D_{\rm l}. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20568-12/aa20568-12-eq98.png) (13)We
will compare with observations and analyze this separately for each satellite.
(13)We
will compare with observations and analyze this separately for each satellite.
 |
Fig. 1 Cumulative number of craters with diameters greater than D produced by Centaurs from SDOs. The upper lines correspond to the differential power-law index s2 = 3.5, the lower lines to s2 = 2.5. |
DB11 calculated the present normalized rate of encounters of SDOs with Saturn per year as Ḟ = 7.1 × 10-11 yr-1. This rate represents the rate of encounters in the present solar system since it was obtained by fitting a linear relation for the past 3.5 Gyrs to the fraction of encounters of SDOs with Saturn, (see Fig. 3 in that paper) when the rate of encounters begins to stabilize and to be significant. Then Ḟ represents the rate of encounters (or collisions) in the present configuration of the solar system where our model applies. As already mentioned we have not modeled the early times of the solar system when it was forming. We would need to know the actual initial scenario of formation of the solar system and in particular of SDOs to know the real primordial contribution and the period of time of this process. The craterization of the satellites at these early times had to be important, and might still be visible in some satellite surfaces, but our model cannot calculate this.
We follow here the same argumentation given in DB11 to obtain the present rate of
collisions (or cratering) on each satellite. Since, from the method described in DB11, the
number of collisions is proportional to the number of encounters, the temporal dependence of
collisions is the same as the temporal dependence of encounters (see Eqs. (2)–(7) in DB11).
So the current rate of collisions
(Ċ(>D)) onto each satellite
can be obtained by multiplying Ḟ by
Nc(>D) (obtained
from Eqs. (3), (8), and (1), or Fig. 1). Then the present cratering rate can be obtained by
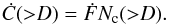 (14)In Table 3, we show the values of our calculated current rate, the
cratering rates calculated by Zahnle et al. (2003),
and the current cratering rates obtained by Smith et al. (1982 ), all for craters with D > 10 km
and for each satellite. Zahnle et al. (2003) consider
two cases for the initial population of impactors based on the relative abundance of small
comets at Jupiter (Case A) and at Neptune (Case B). They also obtained the SFDs of impactors
by inverting crater counts from Europa, Ganymede, Callisto, and Triton. Their estimations of
cratering rates have an uncertainty factor of 4. Although we can see the Zahnle et al.
(2003) calculations for case A are in agreement
with our calculation for the case where s2 = 3.5, taking into
account their uncertainty factor. The values of the current cratering rates calculated by
Smith et al. (1982) from the Voyager observations are
between our values of the current cratering rates for s2 = 2.5
and s2 = 3.5.
(14)In Table 3, we show the values of our calculated current rate, the
cratering rates calculated by Zahnle et al. (2003),
and the current cratering rates obtained by Smith et al. (1982 ), all for craters with D > 10 km
and for each satellite. Zahnle et al. (2003) consider
two cases for the initial population of impactors based on the relative abundance of small
comets at Jupiter (Case A) and at Neptune (Case B). They also obtained the SFDs of impactors
by inverting crater counts from Europa, Ganymede, Callisto, and Triton. Their estimations of
cratering rates have an uncertainty factor of 4. Although we can see the Zahnle et al.
(2003) calculations for case A are in agreement
with our calculation for the case where s2 = 3.5, taking into
account their uncertainty factor. The values of the current cratering rates calculated by
Smith et al. (1982) from the Voyager observations are
between our values of the current cratering rates for s2 = 2.5
and s2 = 3.5.
Kirchoff & Schenk (2009, 2010), presented the cumulative number of craters of different sizes (No(>D)) per 106 km2 for selected areas on each satellite. We take the data from their Figs. 6 and S1 in order to compare these observations with our calculated number of craters. We assume isotropy for the impacts to calculate the number of craters produced on an area Si = 106 km2 of the satellite.
Every mid-size satellite of Saturn is a unique world with different surface characteristics. So we will discuss our results for the craters, distribution of craters, comparison with observations and terrain characteristics in separate subsections. We have also calculated the contribution of craters by escaped plutinos following the same ideas used for Centaurs from the SD and find that they are a negligible fraction of the production by Centaurs from the SD, so we omit its contribution.
3.1. Mimas
Mimas is the smallest and innermost of the mid-sized Saturnian satellites. The surface is composed of water ice. It is heavily cratered and has the large impact crater known as Herschel (130 km) on its leading hemisphere. From our calculations, the largest crater produced by Centaurs on Mimas has a diameter of 113 km (for s2 = 3.5), which is on the order of the crater Herschel. Kirchoff & Schenk (2010), used suitable resolution images from Cassini that recorded impact craters of half of Mimas’s surface. They suggested that the impactor population may be lacking in large objects. Furthermore, they found that the crater size-frequency distribution for Mimas and Dione are very similar. Both surfaces have a high density of craters with diameters ~10 < D < 30 km. Buratti et al. (2011), analyzed spectroscopic observations of Mimas to search for plume activity in the satellite, but they did not find a measurable activity. This suggests that any possible geologic activity at Mimas, if there is any, is at a low level. Kirchoff & Schenk (2009, 2010) present counts of craters on Mimas. In Fig. 2 we plot the observed cumulative number of craters from KS09 (Fig. S1), together with our calculated cumulative number of craters for both indices s2 = 2.5 and s2 = 3.5 of the impactor SFD. We can see that the observed curve is near our calculated curve for s2 = 3.5, and for D ≲ 15 km the observed number of craters (No) is less than the calculated one (Nc). The number of craters for s2 = 2.5 is much less than the observed values. Kirchoff & Schenk (2009) obtained the cumulative crater size-frequency distribution for certain diameter ranges. For 4 km < D < 10 km the cumulative slope is −1.548, for 10 km < D < 20 km it is −2.12, and for 20 km < D < 70 km it is −3.0. From our calculations for Mimas, these craters are produced under the gravity regime, and then from Eqs. (12) and (13) the cumulative slope of the crater size-frequency distribution is −1.786 for s2 = 2.5 and −2.976 for s2 = 3.5. We can see that smaller craters have a SFD more similar to the case where s2 = 2.5, but for D > 20 km craters that correspond to d > 0.6 km-impactors the cumulative slope is very similar to the case where s2 = 3.5. If the only source of the observed craters were present Centaurs on Mimas, it would be possible for the impactor SFD to have a break near d ~ 0.6 km. If this were the case, Nc would nearly fit No. However, if there were a geologic activity at Mimas, it could be that small craters could have been erased and would be the reason for No < Nc for D ≲ 15 km.
 |
Fig. 2 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
3.2. Enceladus
The Cassini spacecraft completed three close flybys of Enceladus between February and July 2005, the closest one on July 14, 2005 down to 168 km from the surface. This encounter reveals interesting details of the surface of the satellite. Enceladus is covered in almost pure water ice except near its south pole where traces of CO2 ice and simple organics have been found (Brown et al. 2006). At the south pole a hot spot was found that is 20 K hotter than expected from models (Spencer et al. 2006), and a group of cracks on the surface called “tiger stripes” (Porco et al. 2006). Furthermore, the Cassini Spectrograph detected a plume of water vapor and micron-sized water ice particles emanating from the south pole region (Porco et al. 2006). The extra heat at the south pole seems to be associated to the tiger-stripe cracks (Spencer et al. 2006). Newman et al. (2008) analyzed the distribution of crystalline and amorphous ices on Enceladus through photometric and spectral data from Cassini. They show that the surface of Enceladus is mostly crystalline, but at the tiger-stripe cracks a higher degree of crystallinity and amorphous ice was found between these cracks. This result implies geological activity at the tiger-stripe cracks and the production of amorphous ice at the south pole either through radiation damage, cryovolcanic flash-freezing, or rapid condensation of water vapor at the Enceladus surface (Newman et al. 2008). All this suggests an active, evolving surface. Kirchoff & Schenk (2009), used Cassini images of Enceladus to count and analyze the craters on the surface and related the results with the satellite geological history. They analyzed separately different types of terrain according to variations in crater density and geological features and obtained the crater counts and size distributions. They obtained a variation of crater density with latitude, the north and south mid-latitude being more densely cratered than the region restricted to the equator. They suggest that this distribution can be explained by burial of material from Saturn’s E ring. The regions and areas analyzed by KS09 (see Fig. 4) are cratered plains: cp-eq and cp-mid, and regions:
 In Figs. 3 and 4 we plot the
observed cumulative number of craters from KS09 (Fig. 6), together with our calculated
cumulative number of craters for both indices s2 = 2.5 and
s2 = 3.5 of the impactor SFD. We can see that the observed
curves for cp are nearer our calculated curve for s2 = 3.5,
although
No < Nc
for all plotted values of D. All the observed curves are below the
calculated curves for s2 = 3.5. The number of craters for
s2 = 2.5 is much lower than the observed values.
In Figs. 3 and 4 we plot the
observed cumulative number of craters from KS09 (Fig. 6), together with our calculated
cumulative number of craters for both indices s2 = 2.5 and
s2 = 3.5 of the impactor SFD. We can see that the observed
curves for cp are nearer our calculated curve for s2 = 3.5,
although
No < Nc
for all plotted values of D. All the observed curves are below the
calculated curves for s2 = 3.5. The number of craters for
s2 = 2.5 is much lower than the observed values.
 |
Fig. 3 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
 |
Fig. 4 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
Kirchoff & Schenk (2009) calculated the cumulative and differential size-frequency distribution of craters and found that the slope values vary with diameter within each terrain studied, so the distribution cannot be represented by a simple power law for the entire surface of Enceladus. All the crater sizes analyzed by KS09 are greater than the value of Dl and so are produced under the gravity regime. Then our calculated cumulative slope of the crater size-frequency distribution is −1.786 for s2 = 2.5 and −2.976 for s2 = 3.5. The values obtained by KS09 for the crater plain are compatible with −1.786 for D ≲ 4 km, and for greater diameters it is smaller; in particular, for cp-mid for 7 km <D < 30 km the slope is −2.99, compatible with our case for s2 = 3.5. For the other six terrains analyzed by KS09, the slopes are variable and we cannot make a general comparison or confirm any trend. However, for all terrains and for all the observed crater sizes No < Nc, if Centaurs are the main present source of craters on Enceladus, there are craters that must be erased. This is obviously compatible with the very young and evolving surface that strongly erases the Enceladus craters. Besides, we can see that the rp1 region, a very active region near the tiger stripes, is the youngest region, and rp6 is the oldest one as was already noted by KS09.
3.3. Tethys
The Cassini spacecraft performed several flybys of Tethys that allowed the detection of the spectral properties of its surface. It is heavily cratered and has two predominant features. One of them is a large impact crater known as Odysseus (400 km in diameter) and the other one is a very large fracture called Ithaca Chasma whose extension is about 2000 km. Emery et al. (2005) performed spectral measurements and found that there is no component other than H2O. Kirchoff & Schenk (2010) used high resolution images from Cassini and developed a count of craters. They analyzed different terrains, the heavily cratered plains, and the zone inside of Odysseus. The cratered plains are probably older than the zone inside Odysseus, which could be much younger. They concluded that the differences between both terrains concerning the size distribution and different ages suggests that the impactor population might have changed in time.
In Fig. 5 we plot the observed cumulative number of craters from KS09 (Fig. S1), together with our calculated cumulative number of craters for both indices s2 = 2.5 and s2 = 3.5. We can see that the observed curve is near our calculated curve for s2 = 3.5, and for D ≲ 10 km the observed counts becomes smaller than the calculated ones. The number of craters for s2 = 2.5 is much lower than the observed values.
Kirchoff & Schenk (2009, 2010) calculated the cumulative slopes for the size-frequency distribution. For 0.2 km < D < 10 km the cumulative slope is −1.728, and for 10 km <D < 60 km is −2.2. From our calculations, craters greater than 0.2 km are produced under gravity regime, so the cumulative slope is −1.786 for s2 = 2.5, and −2.976 for s2 = 3.5. Our results with s2 = 2.5 are near the observed slope for 0.2 km <D < 10 km, while for 10 km < D < 60 km the observed slope is in the range of our calculated ones for both indices. So it is possible that the impactor SFD could have a break near d ~ 0.3 km which produces a crater of D ~ 10 km. If this were the case, Nc will nearly fit No.
Buratti et al. (2011) performed a spectroscopic analysis on Tethys to search for plume activity, without success. Cassini spectroscopic observations does not show evidence for plumes at least at the threshold of detection. So current geological activity cannot be excluded. The Buratti et al. (2011) results suggest that any possible geological activity could be at a low level. So if this activity exists, it could be the reason for No < Nc for D ≲ 10 km.
 |
Fig. 5 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
3.4. Dione
The Cassini spacecraft performed several flybys of Dione, the closest one going down to 99 km from the surface, whose main goal was to determine its internal structure2. These encounters provide details of the surface allowing us to know its history. Clark et al. (2008) found that Dione’s surface is composed mainly of water ice and it also has a dark component whose spectral characteristics are similar to those found in the spectra of Iapetus, Phoebe, and in the F ring. Moreover, they suggested a possible detection of activity. In fact, their observations might indicate ejection of water ice and methane, but this needs to be confirmed. Buratti et al. (2011) searched for plume activity in the satellite through spectroscopy, but they did not find a measurable activity. Stephan et al. (2010) performed a study of geological properties and spectral analysis of Dione. Their results show that Dione’s surface is dominated by at least one global process. Although they have not observed geologically active regions, high spatial resolution images show clean water ice implying that tectonic processes could have continued in more recent times. Kirchoff & Schenk (2009, 2010) used high resolution images from Cassini to record impact craters in the surface of Dione. The analysis was based on two types of terrains, the heavily cratered plains (cp) and the smooth plains (sp). They suggested that the cratered terrains are very old because they are a record of an ancient bombardment, while the smooth plains are younger.
In Fig. 6 we plot the observed cumulative number of craters from KS09 (Fig. S1), together with our calculated cumulative number of craters for both indices s2 = 2.5 and s2 = 3.5. We can see that for s2 = 3.5 the No of cp-terrain is somewhat greater than our calculated number of craters for D ≳ 5 km. For D ≲ 5 km, the observed counts for cp begin to be fewer in number than the calculated ones. The number of craters for s2 = 2.5 is much lower than the observed values. The observed sp curve is very near the calculated one for s2 = 3.5 indicating that those craters may have been produced by present Centaurs from the SD. However, there are no observations of craters less than 4 km, and then we cannot compare with our calculations for these sizes.
Kirchoff & Schenk (2010) obtained the cumulative crater size-frequency distribution from the observations. For cratered plains for 0.25 km < D < 4 km the cumulative slope is b = −1.640, for 4 km < D < 10 km, b = −1.166, for 10 km <D <30 km b = −2.31, and for 30 km <D < 150 km is −2.9. For the smooth plains for 5 km <D < 10 km, b = −2.21, and for 10 km <D < 45 km is −2.57. These crater sizes are produced under the gravity regime in Dione and so our calculated values of b are −1.786 for s2 = 2.5 and −2.976 for s2 = 3.5. For both terrains, smaller craters have a SFD more similar to the case s2 = 2.5, and for larger craters, the observed cumulative slope corresponds better to the case s2 = 3.5. So, for craters with D ~ 10−30 km which corresponds to an impactor size d ~ 0.4−1.4 km, the SFD of impactors could have a break from a power-law index of the differential SFD of 3.5 for larger craters to 2.5 for smaller ones. However, if geological activity exists, as suggested by Clark et al. (2008), this could be the reason for No < Nc for D ≲ 5 km.
 |
Fig. 6 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
3.5. Rhea
Rhea was imaged and studied in detailed by Cassini from numerous flybys. Its surface has a high albedo, suggesting a composition of water ice. Determinations of the density and the axial moment of inertia indicate that Rhea is a non-differentiated body, almost homogeneously composed of 75% of ice water and 25% of rock (Anderson & Shubert 2007). Wagner et al. (2008) observed that large craters and basins are abundant with diameters of up to 500 km, but heavily degraded. They also observed smoother areas with a paucity of smaller craters, but no clear evidence for cryovolcanic resurfacing. The homogeneous interior proposed for Rhea implies that cryovolcanism as an endogenous process of resurfacing is improbable. Stephan et al. (2012) presented the analysis of the spectral characteristics of Rhea from data obtained by the Visual and Infrared Spectrometer of Cassini. They concluded that the major process that affects the surface properties of Rhea is the interaction between the surface material and the space environment that includes the impacts of energetic particles from the magnetospheric plasma. They also concluded that this process could be responsible for the concentration of dark material on the trailing hemisphere. So, this is an exogenous process that erodes the surface of Rhea. The spectral study by Stephan et al. (2012) of different surface structures like fresh impact craters and tectonic scarps implied the crust of Rhea is composed of clean water ice. Teolis et al. (2010) detected from measurements on a Rhea flyby, a tenuous atmosphere of oxygen and carbon dioxide that appears to be sustained by the chemical decomposition of the surface water ice under the irradiation from Saturn’s magnetospheric plasma. An outstanding feature on Rhea is a fresh ray impact crater of ~50 km in diameter with an estimated age of ~280 Myr or ~8 Myr (Wagner et al. 2008). From our calculations of the cratering rate and the number of craters produced by Centaurs, we can estimate the age of that crater. The total number of craters greater than 50 km produced by Centaurs from the SD on Rhea is Nc(>50) = 33 (with s2 = 3.5). From Eq. (1), the current rate of production of craters greater than 50 km on Rhea is Ċ(>50) = 2.34 × 10-9 craters per year. So the youngest crater produced by Centaurs has an age of 426 My. This age can be considered in agreement with the previous age estimates.
 |
Fig. 7 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
Kirchoff & Schenk (2009, 2010) present counts of craters for a ~22% of the total area of the satellite. In Fig. (7) we plot the observed cumulative number of craters from KS09 (Fig. 6), together with our calculated cumulative number of craters for both indices s2 = 2.5 and s2 = 3.5. We can see, that for s2 = 3.5, No of is somewhat greater than our calculated number of craters for D ≳ 5 km. For D ≲ 5 km, the observed counts begins to be less than the calculated ones. The number of craters for s2 = 2.5 is much lower than the observed values. All this is very similar to the analysis for Dione.
Kirchoff & Schenk (2009, 2010), obtained the cumulative crater size-frequency distribution for certain diameter ranges. For 0.14 km < D < 10 km the cumulative slope is −1.44 and for 10 km < D < 80 km is −2.024. From our calculations for Rhea, craters greater than 0.1 km are produced under the gravity regime and then we obtained from Eqs. (12) and (13) that the cumulative slope of the crater size-frequency distribution is −1.786 for s2 = 2.5 and −2.976 for s2 = 3.5. Our values for s2 = 2.5 are near the observed values. However, the calculation of the number of craters with s2 = 3.5 is closer to the observations of KS09 and KS10. The fact that No is less than Nc for D ≲ 5 km, could be explained by the above mentioned exogenous process that gradually erodes the surface of Rhea, thus erasing smaller craters first, but which does not bury the largest craters. Moreover, since the Nc > No for D > 5 km, there would be registers of a primordial crater contribution and/or another main source of craters might exist.
3.6. Iapetus
Images of Iapetus were obtained by Cassini during its orbits and flybys. The most striking surface property is its unique albedo dichotomy; the leading hemisphere is dark with a redder color and an albedo of ~0.04 (named “Cassini Regio”) and the trailing hemisphere and poles are bright with an albedo of ~0.6. The other relevant feature on the Iapetus surface is a near equatorial ridge system of aligned peaks that rise more than 20 km above the surroundings plains and have in some sections three nearly parallel ridges (Porco et al. 2005). This ridge seems to be an old feature since it is cut by impact craters in some parts. Iapetus is heavily cratered implying that its surface is globally ancient (Denk et al. 2010). Kirchoff & Schenk (2010) compile crater distributions on both the bright and dark terrain of Iapetus. They show counts for craters with D > 5 km which are greater than our calculated values for both areas. This is consistent with the observed high density of craters associated with an old surface. Also KS10 obtained the cumulative crater size-frequency distribution for certain diameter ranges. On the dark terrain, for 0.2 km < D < 4 km the cumulative slope is −1.308, and for 4 km < D < 80 km is −2.666. On the bright terrain, for 4 km < D < 65 km, the cumulative slope is −1.7. These crater sizes are produced under the gravity regime in Iapetus and so from Eqs. (12) and (13), the cumulative slope of the crater size-frequency distribution is −1.786 for s2 = 2.5 and −2.976 for s2 = 3.5. So for the dark terrain smaller craters have a SFD more similar to the case where s2 = 2.5, but for D > 4 km-craters that correspond to d > ~ 0.2 km-impactors, the cumulative slope is very similar to the case s2 = 3.5. If the only source of the observed craters were the present Centaurs, then the impactor SFD could have a break near d ~ 0.2 km. For the bright terrain the cumulative slope of the crater SFD is very similar to the case where s2 = 2.5. However, as mentioned the Iapetus surface seems to have preserved old craters and so it is not clear if this break corresponds to the present source of craters.
4. Discussion and conclusions
In this paper we have studied the production of craters on the mid-sized Saturnian satellites. We calculated the number of craters on the mid-sized satellites produced by Centaurs from the SD and by plutinos. We used previous numerical simulations of Centaurs, in particular the encounters output files of the simulation that, together with a method developed for the calculation of craters, allows us to calculate the production of craters on the satellites. We assumed a population of SDOs with a break at a diameter d = 60 km (following the literature) such that for d < 60 km two exponents of the differential SFD, s2 = 2.5 and s2 = 3.5, were considered. In the section of results we showed the maximum crater sizes and the number of craters on each satellite. The contribution of plutinos is negligible and we made all calculations with the contribution of Centaurs from the SD. The other heliocentric source of craters could be escaped Jupiter and Neptune trojans. But at first we can say that it may probably be a second-order contribution.
We also assumed a cratering law corresponding to water ice for all the satellites considering both the gravitational and strength regime. Then we obtained the cumulative crater size-frequency distribution of craters for both regimes and also for both exponents of the SFD used for the impactor population. It was possible to calculate the current cratering rate for each satellite, and it is shown in Table 3. Through the comparison of our results with observation by Cassini it was possible to obtain very interesting results. Since each satellite is a unique world, we have made the comparison and analysis for each satellite in each of the previous subsections. However, it is possible to make a general analysis here. Comparing the number of craters, we noted that the calculated number of craters for s2 = 3.5 is in general closer to the observed number of craters. The number of craters obtained for s2 = 2.5 is very small and inconsistent with observations. However, one cannot lose sight of the fact that we are assuming that the only and most important source of craters are Centaurs from SD.
In general, comparing the observed number of craters with the calculated number for s2 = 3.5, we found for smaller craters, that the observed number is less than the calculated one. This trend can be explained by two mechanisms. On the one hand, this could be caused by an erasing process that gradually buries the craters, but does not affect large craters, the size limit depends on the satellite. For craters greater than this size limit, for Dione and Rhea the observed number is greater than the calculated one. This could mean that there are primordial craters and/or another main source of craters might exist. There are papers that have analyzed planetocentric populations that can hit the satellites, as mention in the introduction, but we cannot distinguish with our method and results if the other source of large craters is this population or if they are primordial. This could be answerd if we knew the geological process acting on each satellite surface. On the other hand, we also noticed when comparing the calculated and observed crater size-frequency distribution for different size ranges, that in general the size distribution index of SDOs (the impactors) for d < 60 km is consistent with the assumed index s2 = 3.5 for d ≳ 0.2−1.4 km and for d ≲ 0.2−1.4 km, it is consistent with s2 = 2.5. So in the range d ~ 0.2−1.4 km the SFD of SDOs could have a new break from s2 = 3.5 to s2 = 2.5. This change of slope could explain the reduction of small craters, at least for some cases. Particularly for Enceladus, in all the observed terrains the calculated number is less than the observed number, implying very young surfaces. On the contrary, for Iapetus our results are in agreement with an old surface.
Although we found a good agreement when comparing our results with observations, all our calculations are strongly dependent on the number and size distribution of the initial impactor population. So, it would be very useful to count on independent determination of geological processes that could erode the satellite surfaces to determine if there is a new break on the SFD of SDOs, if there is really a planetocentric source of craters on the Saturnian system, and which craters are primordial.
Web page http://keith.aa.washington.edu/craterdata/scaling/index.htm. Accessed December, 2011
Acknowledgments
We would like to thank Michelle Kirchoff for kindly providing us the areas of the crater count zones. We also acknowledge an anonymous referee for valuable comments and suggestions that helped us to improve the manuscript.
References
- Anderson, J. D., & Schubert, G. 2007, Geophys. Res. Lett., 34, L02202 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. H., Clark, R. N., Buratti, B., et al. 2006, Science, 311, 1425 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Buratti, B. J., Faulk, S. P., Mosher, J., et al. 2011, Icarus, 214, 534540 [CrossRef] [Google Scholar]
- Clark, R. N., Curchin, J. M., Jaumann, R., et al. 2008, Icarus, 193, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Denk, T., Neukum, G., Roatsch, T., et al. 2010, Science, 327 435 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Di Sisto, R. P., & Brunini, A. 2007, Icarus, 190, 224 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Sisto, R. P., & Brunini, A. 2011, A&A, 534, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Sisto, R. P., Brunini, A., & de Elía, G. C. 2010, A&A, 519, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrovolskis, A. R., & Lissauer, J. J. 2004, Icarus, 169, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Dones, L., Chapman, C. R., McKinnon, W. B., et al. 2009, in Saturn from Cassini-Huygens, eds. M. K. Dougherty, L. W. Esposito, & S. M. Krimigis, 613 [Google Scholar]
- Emery, J. P., Burr, D. M., Cruikshank, D. P., et al. 2005, A&A, 435, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elliot, J. L., Kern, S. D., Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, W. C., & Kavelaars, J. J. 2009, AJ, 137, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes, C. I., & Holman, M. J. 2008, AJ, 136, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes, C. I., George, M. R., & Holman, M. J. 2009, ApJ, 696, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Hutton, R., Licandro, J., Pinilla-Alonso, N., et al. 2009, A&A, 500, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holsapple, K. A. 1993, Annu. Rev. Earth Planet Sci., 21, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Holsapple, K. A., & Housen, K. R. 2007, Icarus, 187, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A., Antreasian, P. G., Bordi, J. J., et al. 2006, AJ, 132, 2520 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchoff, M. R., & Schenk, P. 2009, Icarus, 202, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchoff, M. R., & Schenk, P. 2010, Icarus, 206, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, R. G., Senft, L. E., & Stewart, S. T. 2011, Icarus, 214, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H., & Duncan, M. 1997, Icarus, 127, 13 [Google Scholar]
- Marchi, S., Dell‘Oro, A., Paolicchi, P., & Barbieri, C. 2001, A&A, 374, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchi, S., Massironi, M., Cremonese, G., et al. 2011, Planet. Space Sci., 59, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, W. B., Prialnik, D., Stern, S. A., & Coradini, A. 2008, In The Solar System Beyond Neptune, eds. M. A. Barucci, et al. (Tucson, USA: University of Arizona Press), 213 [Google Scholar]
- Morbidelli, A., Levison, H. F., & Gomes, R. 2008, In The Solar System Beyond Neptune, eds. M. A. Barucci, et al. (Tucson, USA: Univ. of Arizona Press), 275 [Google Scholar]
- Newman, S. F., Buratti, B. J., Brown, R. H., et al. 2008, Icarus, 193, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2010a, PASP, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2010b, Icarus, 209, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Baker, E., Barbara, J., et al. 2005, Science, 307, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Helfenstein, P., Thomas, P. C., et al. 2006, Science, 311, 1393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Smith, B. A., Soderblom, L., Batson, R., et al. 1982, Science, 215, 504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Senft, L. E., & Stewart, S. T. 2011, Icarus, 214, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Pearl, J. C., Segura, M., et al. 2006, Science, 311, 1401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stephan, K., Jaumann, R., Wagner, R., et al. 2010, Icarus, 206, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Stephan, K., Jaumann, R., Wagner, R., et al. 2012, Planet. Space Sci., 61, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Teolis, B. D., Jones, G. H., Miles, P. F., et al. 2012, Science, 330, 181 [Google Scholar]
- Thomas, P. C. 2010, Icarus, 208, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, R. J., Neukum, G., Giese, B., et al. 2008, In Lunar Planet. Sci. XXXIX, 39, 1930 [NASA ADS] [Google Scholar]
- Zahnle, K., Schenk, P., Levison, H., & Dones, L. 2003, Icarus, 163, 263 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cumulative number of craters with diameters greater than D produced by Centaurs from SDOs. The upper lines correspond to the differential power-law index s2 = 3.5, the lower lines to s2 = 2.5. |
| In the text | |
 |
Fig. 2 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
| In the text | |
 |
Fig. 3 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
| In the text | |
 |
Fig. 4 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
| In the text | |
 |
Fig. 5 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
| In the text | |
 |
Fig. 6 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. S1 of KS09. |
| In the text | |
 |
Fig. 7 Cumulative number of craters calculated from our model with the two values of the differential power-law index s2 and the observed cumulative number of craters taken from Fig. 6 of KS09. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


