| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220601 | |
| Published online | 15 April 2013 | |
Formation of giant planets and brown dwarfs on wide orbits
1
University of Vienna, Institute of Astrophysics,
1180
Vienna,
Austria
e-mail: eduard.vorobiev@univie.ac.at
2
Research Institute of Physics, Southern Federal University,
Stachki Ave. 194,
344090
Rostov-on-Don,
Russia
Received:
20
October
2012
Accepted:
6
February
2013
Aims. We numerically studied the formation of giant planet (GP) and brown dwarf (BD) embryos in gravitationally unstable protostellar disks and compared our findings with the directly imaged, wide-orbit (≳50 AU) companions that are known to-date. The viability of the disk fragmentation scenario for the formation of wide-orbit companions in protostellar disks around (sub-)solar mass stars was investigated. We focused on the likelihood of survival of GP/BD embryos formed via disk gravitational fragmentation.
Methods. We used numerical hydrodynamics simulations of disk formation and evolution with an accurate treatment of disk thermodynamics. Using the thin-disk limit allowed us to probe the long-term evolution of protostellar disks, starting from the gravitational collapse of a pre-stellar core and ending in the T Tauri phase after at least 1.0 Myr of disk evolution. We focused on models that produced wide-orbit GP/BD embryos that opened a gap in the disk and showed radial migration timescales similar to or longer than the typical disk lifetime.
Results. While most models showed disk fragmentation, only 6 models out of 60 revealed the formation of quasi-stable, wide-orbit GP/BD embryos. The low probability for the fragment survival is caused by efficient inward migration/ejection/dispersal mechanisms that operate in the embedded phase of star formation. We found that only massive and extended protostellar disks (≳0.2 M⊙), which experience gravitational fragmentation not only in the embedded but also in the T Tauri phases of star formation, can form wide-orbit companions. Disk fragmentation produced GP/BD embryos with masses in the 3.5–43 MJ range, covering the whole mass spectrum of directly imaged, wide-orbit companions to (sub-)solar mass stars. On the other hand, our modeling failed to produce embryos on orbital distances ≲170 AU, whereas several directly imaged companions were found at smaller orbits down to a few AU. Disk fragmentation also failed to produce wide-orbit companions around stars with mass ≲0.7 M⊙, in disagreement with observations.
Conclusions. Disk fragmentation is unlikely to explain the whole observed spectrum of wide-orbit companions to (sub-)solar-mass stars and other formation mechanisms, for instance, dynamical scattering of closely packed companions onto wide orbits, should be invoked to account for companions at orbital distance from a few tens to ≈150 AU and wide-orbit companions with masses of the host star ≤ 0.7 M⊙. Definite measurements of orbit eccentricities and a wider sample of numerical models are needed to distinguish between the formation scenarios of GP/BD on wide orbits.
Key words: protoplanetary disks / planets and satellites: formation / stars: formation / hydrodynamics / stars: protostars
© ESO, 2013
1. Introduction
With the detection of giant planets (GPs) and brown dwarfs (BDs) on orbital distances on the order of tens to hundreds AU (e.g. Marois et al. 2008; Kalas 2008; Lafreniére 2010; Schmidt et al. 2008), gravitational instability and fragmentation of protostellar disks has gained renewed interest as one of the likely mechanisms that can explain the formation of wide-orbit companions (e.g. Boss 2003, 2011; Stamatellos & Whitworth 2009a; Boley 2009; Dodson-Robinson et al. 2009; Kratter et al. 2010a,b; Vorobyov & Basu 2010b). Measurements of disk masses in the T Tauri phase of stellar evolution yielded a few candidates with disks masses as massive as 0.1–0.5 M⊙ (Eisner et al. 2008; Andrews et al. 2009; Isella et al. 2009). These massive disks are expected to be more frequent in the earlier, embedded phase of star formation (e.g. Eisner et al. 2005; Jorgensen et al. 2009; Vorobyov 2011b; Eisner 2012), which makes disk fragmentation at least in this early evolutionary stage more likely.
Numerical hydrodynamics simulations and semi-analytical studies seem to converge on the view that disk fragmentation is feasible at distances greater than a few tens of AU from the central star (Mayer et al. 2007; Boley 2009; Rice et al. 2010; Vorobyov & Basu 2010a; Zhu et al. 2012), where the cooling time becomes shorter than the local dynamical timescale (Gammie 2001; Johnson & Gammie 2003; Rice et al. 2003). Although the exact distance beyond which disk fragmentation may operate is still under debate (Rafikov 2005; Nero & Bjorkman 2009; Meru & Bate 2011, 2012), it now becomes evident that parental cores must have enough mass and angular momentum to form extended disks with mass sufficient to drive the local Toomre Q-parameter below unity (e.g. Vorobyov & Basu 2010a; Vorobyov 2011b).
It has recently become evident that the formation of massive fragments via disk gravitational fragmentation does not guarantee that the fragments will ultimately evolve into GPs/BDs on wide orbits. Gravitational instability in the embedded phase of star formation is strong, fuelled with a continuing infall of gas from a parent cloud core, and resulting gravitational and tidal torques from spiral arms are rampant. As a consequence, the majority of the fragments are torqued into the inner disk regions, probably producing a population of close-in terrestrial and icy giants due to tidal disruption/tidal downsizing (Nayakshin 2010; Boley et al. 2010; Cha & Nayakshin 2011), or driven directly onto the star, triggering intense accretion and luminosity bursts similar in magnitude to FU Orionis eruptions (Vorobyov & Basu 2006, 2010a). Some of the fragments are dispersed by tidal torques exerted by the spiral arms before they can dissociate molecular hydrogen in their interiors and contract to planetary-sized objects (Boley et al. 2010; Vorobyov 2011a; Nayakshin et al. 2011). A few fragments may be scattered away from the disk via many-body gravitational interaction with outer fragments or fully formed sub-stellar objects, producing freely floating sub-stellar objects (Stamatellos & Whitworth 2009a; Basu & Vorobyov 2012).
Therefore, the question of whether fragments can settle into stable orbits at distances where they form, from several tens to hundreds AU, remains to be open. Baruteau et al. (2011) studied planet migration in graviturbulent disks with mass 0.4 M⊙ and argued that Jupiter-mass planets (or higher) initially placed at 100 AU migrate inward on timescales of 104 yr and are unlikely to stay on wide orbits. Michael et al. (2011) found even faster migration timescales of 103 yr for a Jupiter-mass planet in a 0.14 M⊙ disk, though the planet may stall near the inner Lindblad resonance of the dominant spiral mode. Other numerical hydrodynamics simulations (Vorobyov & Basu 2006, 2010a; Cha & Nayakshin 2011; Machida et al. 2011) also revealed fast inward migration of the forming fragments in the disk. On the other hand, Vorobyov & Basu (2010b) studied the long-term (~several Myr) evolution of fragmenting protostellar disks in the thin-disk limit and found that while most disks indeed fail to produce stable companions on wide orbits, in agreement with previous studies, a small subset of models can form GPs at distances on the order of tens to hundreds AU. The authors concluded that only the fragments that happen to form in the late embedded phase, when gravitational instability and associated torques are getting weaker, may open a gap in the disk and mature into GPs on wide orbits. The low probability for survival of the fragments formed via disk gravitational fragmentation was also confirmed by Zhu et al. (2012), who numerically studied two-dimensional disks subject to mass loading and found that only 3 fragments out of 13 became massive enough to open a gap in the disk and essentially stopped migrating.
In this paper, we improve the model of Vorobyov & Basu (2010b) by including a detailed thermal balance in the protostellar disk, thus removing the barotropic relation closure adopted in Vorobyov & Basu (2010b), which is known to overpredict the number of fragments (e.g. Bate 2009; Stamatellos & Whitworth 2009b). In our numerical hydrodynamics simulations, we form disks self-consistently during the gravitational collapse of pre-stellar cores and do not introduce them artificially. This allows us to determine the range of masses and angular momenta in prestellar cores for which disk fragmentation and formation of wide-orbit companions can take place. We also avoid replacing fragments with point sink particles, i.e., we study the evolution of GP/BD embryos rather than fully formed planetary- or sub-stellar objects. We chose to do this to avoid a premature introduction of sink particles, whose effect can influence the number of surviving fragments through the essential indestructibility of point-sized objects. On the other hand, the formation of planetary/sub-stellar-sized objects is not resolved in the current approach, which may affect the short-term survivability of the fragments. We focus on models that produce planetary- or sub-stellar-mass embryos on quasi-stable orbits at radial distances where disk fragmentation takes place (≳50 AU).
The organization of this paper is as follows. A brief description of the numerical model is provided in Sect. 2. The parameter-space study of disk fragmentation and fragment survival is provided in Sect. 3. The formation of GP and BD embryos in wide orbits is presented in Sects. 4 and 5, respectively. We discuss the likelihood that multiple companions are formed in wide orbits in Sect. 6. We compare the numerical results with observed sub-stellar objects in wide orbits in Sect. 7. The main results are summarized in Sect. 8.
2. Model description
Our numerical model is described in detail in Vorobyov & Basu (2010b) and is briefly reviewed below. We use numerical hydrodynamics simulations in the thin-disk approximation to compute the gravitational collapse of pre-stellar cores of various initial mass and angular momentum. This approximation is an excellent means to calculate the evolution for many orbital periods and many model parameters, and its justification is provided in Vorobyov & Basu (2010a). To avoid too small time steps, we introduce a “sink cell” at rsc = 6 AU and impose a free boundary condition so that the matter is allowed to flow out of the computational domain but is prevented from flowing in. The sink cell is dynamically inactive; it contributes only to the total gravitational potential and secures a smooth behavior of the gravity force down to the stellar surface. We monitor the gas surface density in the sink cell, and when its value exceeds a critical one for the transition from isothermal to adiabatic evolution, we introduce a central point-mass object.
The simulations continue into the embedded phase of star formation, during which a protostellar disk is formed. In this stage, the disk is subject to intense mass loading from the remnant of the initial pre-stellar core – the so-called envelope. The self-consistent disk-envelope interaction is a key feature of our model that allows us to observe repetitive episodes of disk fragmentation in some models. During the diks evolution, 90% of the gas that crosses the inner boundary is assumed to land onto the central object plus the sink cell. The other 10% of the accreted gas is assumed to be carried away with protostellar jets. The simulations are terminated in the late T Tauri phase after more than one Myr of disk evolution when nearly all envelope material has accreted onto the resulting star-plus-disk system.
Models presented in this paper are run on a polar coordinate (r,φ) grid with 512 × 512 zones. The radial points are logarithmically spaced, with the innermost cell outside the central sink having a size 0.07–0.1 AU depending on the cloud core size (i.e., the radius of the computational region). The latter varies in the 0.025–0.12 pc (5000–24 000 AU) limits. The radial and azimuthal resolution are ≲1.0 AU at a radial distance r ≲ 100 AU.
The Truelove criterion states that the local Jeans length must be resolved by at least four
numerical cells to correctly capture disk fragmentation (Truelove et al. 1998). For a circular fragment of radius
R0 with a surface density inversely proportional to radius,
Σ = Σ0R0/r, the
kinetic energy due to random motions can be expressed as
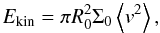 (1)where Σ0 is
the surface density at the fragment-disk interface. The velocity dispersion of a thin disk
with two translational degrees of freedom1 is
⟨ v2 ⟩ = 2ℛT0/μ,
where ℛ is the universal gas constant, μ = 2.33 is the mean molecular
weight, and T0 is the gas midplane temperature in the fragment.
(1)where Σ0 is
the surface density at the fragment-disk interface. The velocity dispersion of a thin disk
with two translational degrees of freedom1 is
⟨ v2 ⟩ = 2ℛT0/μ,
where ℛ is the universal gas constant, μ = 2.33 is the mean molecular
weight, and T0 is the gas midplane temperature in the fragment.
The corresponding gravitational energy of the fragment is
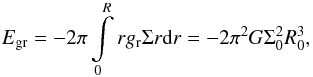 (2)where we have taken
into account that gr = πGΣ for a disk with
Σ ∝ r-1 (see Binney &
Tremaine 1987, p. 77). The resulting Jeans length RJ is
calculated from the virial theorem
2Ekin + Eg = 0 as
(2)where we have taken
into account that gr = πGΣ for a disk with
Σ ∝ r-1 (see Binney &
Tremaine 1987, p. 77). The resulting Jeans length RJ is
calculated from the virial theorem
2Ekin + Eg = 0 as 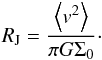 (3)Fragments usually condense
out of the densest sections of spiral arms. The typical surface densities and temperatures
in spiral arms do not exceed 100 g cm-2 and 100 K (see Figs. 2, 6, and 8 in this paper and Vorobyov
2011b). Adopting these values for Σ0 and T0,
the corresponding Jeans length is RJ ≈ 20 AU.
(3)Fragments usually condense
out of the densest sections of spiral arms. The typical surface densities and temperatures
in spiral arms do not exceed 100 g cm-2 and 100 K (see Figs. 2, 6, and 8 in this paper and Vorobyov
2011b). Adopting these values for Σ0 and T0,
the corresponding Jeans length is RJ ≈ 20 AU.
In models showing disk fragmentation, the radial and azimuthal grid resolution at r = 100 AU is ≈1.0 AU and the Jeans length is resolved by roughly 20 grid zones in each coordinate direction. On our logarithmically spaced radial grid, the Truelove criterion is expected to break only at r ≳ 500 AU where the grid resolution starts to exceed 5.0 AU. Fragmentation takes place mostly at radial distances from a few tens to a few hundred AU. Fragments that are seen in our models at larger distances are most likely scattered from the inner disk regions through gravitational interaction with other fragments2. The radii of the survived fragments (see the ninth column in Table 2) lie between 10 and 20 AU, implying that the fragments are resolved on the two-dimensional mesh by at least 30–60 grid zones in the inner 500 AU. We therefore conclude that the numerical resolution in our models is sufficient to capture disk fragmentation correctly. On the other hand, the contraction of the survived fragments to planetary-sized objects cannot be modeled in the current approach. This may have consequences for the likelihood of survival of the fragments, resulting in an increased probability of tidal destruction of AU-sized objects as compared to planetary-sized ones. Accreting sink particles are needed to correctly follow the evolution of fully formed GPs and BDs.
2.1. Basic equations
In Vorobyov & Basu (2010a), a barotropic
equation of state was used to close the equations of hydrodynamics. In this work, we
include detailed thermal physics in our model, the main concepts of which are briefly
reviewed below. The basic equations of mass, momentum, and energy transport are
![\begin{eqnarray} \label{cont} &&\frac{{\partial \Sigma }}{{\partial t}} = - \nabla_{\rm p} \cdot \left( \Sigma \bl{v}_{\rm p} \right), \\ \label{mom} &&\frac{\partial}{\partial t} \left( \Sigma \bl{v}_{\rm p} \right) + \left[ \nabla \cdot \left( \Sigma \bl{v_{\rm p}} \otimes \bl{v}_{\rm p} \right) \right]_{\rm p} = - \nabla_{\rm p} {\cal P} + \Sigma \, \bl{g}_{\rm p} + (\nabla \cdot \mathbf{\Pi})_{\rm p}, \\\label{energ} &&\frac{\partial e}{\partial t} +\nabla_{\rm p} \cdot \left( e \bl{v}_{\rm p} \right) = -{\cal P} (\nabla_{\rm p} \cdot \bl{v}_{\rm p}) -\Lambda +\Gamma + \left(\nabla \bl{v}\right)_{\rm pp^\prime}{:}\,\Pi_{\rm pp^\prime}, \end{eqnarray}](/articles/aa/full_html/2013/04/aa20601-12/aa20601-12-eq39.png) where
subscripts p and p′ refers to the planar components (r,φ) in
polar coordinates, Σ is the mass surface density, e is the internal
energy per surface area,
where
subscripts p and p′ refers to the planar components (r,φ) in
polar coordinates, Σ is the mass surface density, e is the internal
energy per surface area,  is the vertically integrated gas pressure calculated via the ideal equation of state as
is the vertically integrated gas pressure calculated via the ideal equation of state as
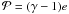 with γ = 7/5, Z is the radially and
azimuthally varying vertical scale height determined in each computational cell using an
assumption of local hydrostatic equilibrium,
with γ = 7/5, Z is the radially and
azimuthally varying vertical scale height determined in each computational cell using an
assumption of local hydrostatic equilibrium, 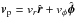 is the velocity in the disk plane,
is the velocity in the disk plane, 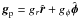 is the gravitational acceleration in the disk plane, and
is the gravitational acceleration in the disk plane, and
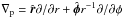 is the
gradient along the planar coordinates of the disk. We note that the adopted value of
γ neglects a possible stiffening of the equation of state at low
temperatures (<100 K) where the ratio of specific heats may
approach a value typical for a monatomic gas, γ = 5/3
(Masunaga & Inutsuka 2000). The adopted
equation of state may be important for disk gravitational instability (Boley et al. 2007), though the recent study of Zhu et al. (2012) found that fragmentation of
two-dimensional disks does not depend sensitively on γ in the range
from 7/5 to 5/3.
is the
gradient along the planar coordinates of the disk. We note that the adopted value of
γ neglects a possible stiffening of the equation of state at low
temperatures (<100 K) where the ratio of specific heats may
approach a value typical for a monatomic gas, γ = 5/3
(Masunaga & Inutsuka 2000). The adopted
equation of state may be important for disk gravitational instability (Boley et al. 2007), though the recent study of Zhu et al. (2012) found that fragmentation of
two-dimensional disks does not depend sensitively on γ in the range
from 7/5 to 5/3.
Turbulent viscosity is taken into account via the viscous stress tensor
Π expressed as 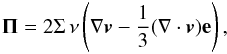 (7)where
e is the unit tensor and ∇v is
the symmetrized velocity gradient tensor. We parameterize the magnitude of kinematic
viscosity ν using a modified form of the α-prescription
(7)where
e is the unit tensor and ∇v is
the symmetrized velocity gradient tensor. We parameterize the magnitude of kinematic
viscosity ν using a modified form of the α-prescription
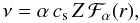 (8)where
(8)where
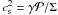 is the
square of effective sound speed calculated at each time step from the model’s known
is the
square of effective sound speed calculated at each time step from the model’s known
 and Σ. The function
ℱα(r) = 2π-1tan-1 [(rd/r)10]
is a modification of the commonly used α-prescription that guarantees
that the turbulent viscosity operates only in the disk and quickly reduces to zero beyond
the disk radius rd. We here use a spatially and temporally
uniform α, whose value is set to 5 × 10-3 to take into account
mass and angular momentum transport via mechanisms such as magnetorotational instability.
Transport of mass and angular momentum via gravitational instability is self-consistently
taken into account via solution of the Poisson equation for the gravitational potential of
the disk and envelope.
and Σ. The function
ℱα(r) = 2π-1tan-1 [(rd/r)10]
is a modification of the commonly used α-prescription that guarantees
that the turbulent viscosity operates only in the disk and quickly reduces to zero beyond
the disk radius rd. We here use a spatially and temporally
uniform α, whose value is set to 5 × 10-3 to take into account
mass and angular momentum transport via mechanisms such as magnetorotational instability.
Transport of mass and angular momentum via gravitational instability is self-consistently
taken into account via solution of the Poisson equation for the gravitational potential of
the disk and envelope.
The radiative cooling Λ in Eq. (6) is
determined using the diffusion approximation of the vertical radiation transport in a
one-zone model of the vertical disk structure (Johnson
& Gammie 2003) 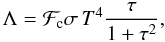 (9)where σ
is the Stefan-Boltzmann constant, T is the midplane temperature of gas,
and
ℱc = 2 + 20tan-1(τ)/(3π)
is a function that secures a correct transition between the optically thick and optically
thin regimes. We use the frequency-integrated opacities of Bell & Lin (1991). The heating function is expressed as
(9)where σ
is the Stefan-Boltzmann constant, T is the midplane temperature of gas,
and
ℱc = 2 + 20tan-1(τ)/(3π)
is a function that secures a correct transition between the optically thick and optically
thin regimes. We use the frequency-integrated opacities of Bell & Lin (1991). The heating function is expressed as
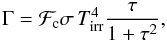 (10)where
Tirr is the irradiation temperature at the disk surface
determined by the stellar and background black-body irradiation as
(10)where
Tirr is the irradiation temperature at the disk surface
determined by the stellar and background black-body irradiation as 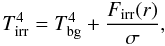 (11)where
Tbg is the uniform background temperature (in our model set
to the initial temperature of the natal cloud core
Tinit = 10 K) and
Firr(r) is the radiation flux (energy per
unit time per unit surface area) absorbed by the disk surface at radial distance
r from the central star. The latter quantity is calculated as
(11)where
Tbg is the uniform background temperature (in our model set
to the initial temperature of the natal cloud core
Tinit = 10 K) and
Firr(r) is the radiation flux (energy per
unit time per unit surface area) absorbed by the disk surface at radial distance
r from the central star. The latter quantity is calculated as
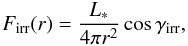 (12)where
γirr is the incidence angle of radiation arriving at the
disk surface at radial distance r.
(12)where
γirr is the incidence angle of radiation arriving at the
disk surface at radial distance r.
The stellar luminosity L∗ is the sum of the accretion luminosity L∗,acr = GM∗Ṁ/2R∗, arising from the gravitational energy of accreted gas, and the photospheric luminosity L∗,ph due to gravitational compression and deuterium burning in the stellar interior. The stellar mass M∗ and accretion rate onto the star Ṁ are determined self-consistently during numerical simulations using the amount of gas passing through the sink cell. The stellar radius R∗ is calculated using the approximation formula of Palla & Stahler (1991), modified to take into account the formation of the first molecular core. The photospheric luminosity L∗,ph is taken from the pre-main sequence tracks for the low-mass stars and BDs calculated by D’Antona & Mazitelli (1997). More details on the numerical code are given in Vorobyov & Basu (2010a).
2.2. Initial conditions in pre-stellar cores
We considered two limiting cases to describe the initial distribution of the gas surface
density Σ and angular velocity Ω in the pre-stellar cores. The first distribution, taken
from Basu (1997), is typical of pre-stellar cores
formed as a result of the slow expulsion of magnetic field through ambipolar diffusion,
with the angular momentum remaining constant during axially-symmetric core compression
![\begin{eqnarray} \Sigma&=&{r_0 \Sigma_0 \over \sqrt{r^2+r_0^2}}, \label{dens} \\ \Omega&=&2\Omega_0 \left( {r_0\over r}\right)^2 \left[\sqrt{1+\left({r\over r_0}\right)^2 } -1\right]. \label{omega} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20601-12/aa20601-12-eq86.png) Here,
Ω0 and Σ0 are the angular velocity and gas surface density at the
disk center and
Here,
Ω0 and Σ0 are the angular velocity and gas surface density at the
disk center and 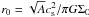 is the radius of
the central plateau, where cs is the initial sound speed in
the core. The gas surface density distribution described by Eq. (13) can be obtained (to within a factor of
unity) by integrating the three-dimensional gas density distribution characteristic of
Bonnor-Ebert spheres with a positive density-perturbation amplitude A (Dapp & Basu 2009). In all models the value of
A is set to 1.2, except for model 4, for which
A = 3.3.
is the radius of
the central plateau, where cs is the initial sound speed in
the core. The gas surface density distribution described by Eq. (13) can be obtained (to within a factor of
unity) by integrating the three-dimensional gas density distribution characteristic of
Bonnor-Ebert spheres with a positive density-perturbation amplitude A (Dapp & Basu 2009). In all models the value of
A is set to 1.2, except for model 4, for which
A = 3.3.
The second set of initial conditions described by Ω = const. and Σ = const. represents the other limiting case suggested in Boss & Hartmann (2001). Cores that can be described, to a first degree of accuracy, by spatially constant Σ and Ω can form via gravitational fragmentation of filamentary structures, which are often encountered in numerical hydrodynamics simulations of the turbulent fragmentation of giant molecular clouds. Another possible mechanism for the formation of such cores may be the planar compression of pre-stellar condensations by shocks and UV radiation of massive stars.
2.3. Tracking the fragments
Motivated by the absence of sink particles in our grid-based code, we designed a fragment-tracking algorithm that allows us to follow the trajectory of the fragments and calculate their physical parameters. The most straightforward way to identify fragments in the disk is to set a threshold gas surface density Σcrit that would help to distinguish between the fragments and the rest of the disk. We quickly found out, however, that setting a single value of Σcrit, independent of radial distance, did not work because too low a value for Σcrit might result in spiral arms in the inner disk being identified as fragments. We therefore need to define a radially varying value of Σcrit that is greater at smaller radii and vice versa.
Noting that the fragments are usually characterized by peak surface
densities that are greater than the local azimuthally averaged surface density
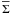 (Vorobyov 2010, 2011b), the threshold gas surface density can be defined as
(Vorobyov 2010, 2011b), the threshold gas surface density can be defined as
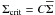 , where
C is an empirically determined constant. Numerical simulations show
that the azimuthally averaged gas surface density in gravitationally unstable disks
declines with radius as
, where
C is an empirically determined constant. Numerical simulations show
that the azimuthally averaged gas surface density in gravitationally unstable disks
declines with radius as 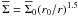 (e.g. Vorobyov 2010; Rice
et al. 2010), where
(e.g. Vorobyov 2010; Rice
et al. 2010), where 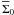 is the typical
azimuthally averaged density at r0. For gravitationally
unstable disks,
is the typical
azimuthally averaged density at r0. For gravitationally
unstable disks, 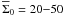 g cm-2 at
r ≈ 100 AU (Vorobyov 2011b). We
therefore chose the following expression for the threshold density
g cm-2 at
r ≈ 100 AU (Vorobyov 2011b). We
therefore chose the following expression for the threshold density 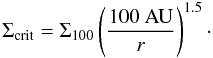 (15)The best value
for threshold surface density at r = 100 AU was found by trial-and-error
method to be Σ100 = 200 g cm-2. This value is greater than the mean
gas surface density
(15)The best value
for threshold surface density at r = 100 AU was found by trial-and-error
method to be Σ100 = 200 g cm-2. This value is greater than the mean
gas surface density 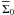 by at least a
factor of several. The local maxima in the gas surface density that exceed
Σcrit usually represent the true fragments rather than the local maxima in
the disk and/or spiral arms. Although we may occasionally miss some low-density fragments,
this does not invalidate our main conclusions.
by at least a
factor of several. The local maxima in the gas surface density that exceed
Σcrit usually represent the true fragments rather than the local maxima in
the disk and/or spiral arms. Although we may occasionally miss some low-density fragments,
this does not invalidate our main conclusions.
After the radial rc and angular
φc coordinates of the local maximum representing the center
of the fragment were identified on the computational mesh, we determined the neighboring
cells that belong to the fragment by imposing the following two conditions on the gas
pressure 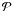 and gravitational potential Φ
and gravitational potential Φ  where
r′ = r − rc and
φ′ = φ − φc.
The first condition requires that the fragment must be pressure-supported, with a negative
pressure gradient with respect to the center of the fragment. The second condition
requires that the fragment is kept together by gravity, with the potential well being
deepest at the center of the fragment. A substantial support against gravity may be
provided by rotation, but we assume that this does not invalidate our criteria, i.e., no
fragments assume a torus shape.
where
r′ = r − rc and
φ′ = φ − φc.
The first condition requires that the fragment must be pressure-supported, with a negative
pressure gradient with respect to the center of the fragment. The second condition
requires that the fragment is kept together by gravity, with the potential well being
deepest at the center of the fragment. A substantial support against gravity may be
provided by rotation, but we assume that this does not invalidate our criteria, i.e., no
fragments assume a torus shape.
In practice, we start from the grid cell that corresponds to the center of the fragment and proceed in eight directions (along the four coordinate directions and also at median angles to them) until at least one of the above-mentioned criteria is violated in every direction. This procedure helps in identifying an approximate shape of the fragment. We then check all remaining grid cells that are encompassed by this octahedral shape and retain only those that meet both criteria (16) and (17). In addition, we filter out cells whose gas surface density is lower than that defined by Eq. (15), even if these cells still fulfil both criteria. We found that such cells are likely to belong to the circum-fragment disk and not to the fragment itself. The cells that belong to the fragment are later utilized to calculate the mass and Hill radius and also the gravitational torque exerted on the fragment, while the cell corresponding to the center of the fragment is used to calculate the trajectory of the fragment. The characteristics of the fragments thus depend somewhat on the adopted value of Σ100 = 200 g cm-2. However, this dependence is not critical and, for instance, the estimated masses of the fragments change by only about 10% if Σ100 is varied by a factor of two.
3. Fragmentation and survival of fragments
We have considered the evolution of 60 initial pre-stellar cores with masses Mc ranging from 0.1 M⊙ to 2.0 M⊙ and ratios of rotational to gravitational energy β lying between 0.27% and 2.2%. We also varied the magnitude of the initial positive density perturbation A in the 1.2–3.3 limits and considered cores with distinct initial radial profiles of Σ and Ω.
For each model we ran our fragment-tracking algorithm at various evolution times to identify models that experienced disk fragmentation. We found that most models showed disk fragmentation but at the same time failed to produce wide-orbit companions. The majority of the fragments were torqued into the inner disk region and through the sink cell (6 AU), producing mass accretion and luminosity bursts similar in magnitude to those of FU-Ori-type objects (Vorobyov & Basu 2006, 2010a), while the remaining few were ejected from the disk into the intracluster medium via many-body gravitational interaction (Basu & Vorobyov 2012) or were dispersed via tidal torques (Vorobyov 2011a; Boley et al. 2010). Boley et al. (2010) and Zhu et al. (2012) also found support for clump-driven FUor events. Only 6 models out of 60 have shown the formation of stable companions in wide orbits, with their mass ranging from 3.5 to 43 Jovian masses. Our obtained survival probability is even lower than that of Zhu et al. (2012) (3 out of 13), though these authors followed the evolution of the fragments for a significantly shorter time period.
 |
Fig. 1 Phase space of β, the initial ratio of rotational to gravitational energy, vs. core mass Mc. The solid/open circles correspond to models with/without disk fragmentation. In the black region we found formation of sub-stellar- or planetary-mass companions on wide orbits. The dark-shaded region is the region in which both fragmentation and ejection events may occur, and in the light-shaded region occur only fragmentation events. The white area marks the region without fragmentation. Arrows illustrate uncertainties associated with a coarse grid of models and indicate models in the β: Mc phase space that might have shown (with a 50% probability) disk fragmentation (ejection/companion formation) had we considered a finer grid of models. Each pair of data in parenthesis indicates the mean disk radius and mass for the corresponding model. |
 |
Fig. 2 Gas surface density distribution in model 1 shown at various times since the formation of the central protostar. Only the inner 3000 × 3000 AU box is shown, the total computational region extends to 22 000 AU. The scale bar is in log g cm-2. Note the fragment on a stable orbit in the bottom row. |
Figure 1 illustrates our findings on the phase space of β versus Mc covered in our modeling. The light-shaded area defines the region with disk fragmentation, while the dark-shaded area outlines the region where both fragmentation and ejection of the fragments may occur. The data related to disk fragmentation and fragment ejection were taken from the numerical hydrodynamics simulations of Basu & Vorobyov (2012). In the present study we added several models that revealed the survival of the fragments. We investigated 60 models, but only 16 key models (those lying at the boundary of the considered regions) are shown in Fig. 1 to avoid overcrowding.
Previous numerical and analytical studies of protostellar disk evolution demonstrated that
gravitational fragmentation is possible at distances ≳50 AU (e.g. Clarke 2009; Stamatellos &
Whitworth 2009a; Boley 2009; Rice et al. 2010) and in disks with mass
≳0.1 M⊙ (e.g. Rice
et al. 2003; Mayer et al. 2007). Disk masses
and radii in our models can be calculated by separating the disk and infalling core on the
computational mesh. This is not an easy task, however. In practice we first constructed the
azimuthally averaged gas surface density profiles 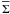 and then
applied a threshold value of
and then
applied a threshold value of 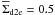 g cm-2 between the
disk and the core. We also used the radial gas velocity profile to see where the infalling
envelope lands onto the disk (see Vorobyov 2011b, for
details). The disk radius estimates are further complicated by substantial outward
excursions (or even complete ejections) of some fragments. It is not always clear whether
the fragment belongs to the circumstellar disk or if it has already detached from it and
should be treated as an external companion (see e.g. Fig. 2). We assumed that the fragment belongs to the disk if
g cm-2 between the
disk and the core. We also used the radial gas velocity profile to see where the infalling
envelope lands onto the disk (see Vorobyov 2011b, for
details). The disk radius estimates are further complicated by substantial outward
excursions (or even complete ejections) of some fragments. It is not always clear whether
the fragment belongs to the circumstellar disk or if it has already detached from it and
should be treated as an external companion (see e.g. Fig. 2). We assumed that the fragment belongs to the disk if
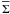 between the
fragment and the disk does not drop below 0.05 g cm-2, a typical value for the
interface between the disk and the external environment (Vorobyov 2011b). In the opposite case, the fragment is supposed to have detached
from the natal disk and is treated as a separate entity.
between the
fragment and the disk does not drop below 0.05 g cm-2, a typical value for the
interface between the disk and the external environment (Vorobyov 2011b). In the opposite case, the fragment is supposed to have detached
from the natal disk and is treated as a separate entity.
Our choice of a threshold of 0.5 g cm-2 is motivated by the fact that the resulting distribution of disk radii peaks between 102 and 103 AU; adopting a threshold lower by an order of magnitude would shift the entire distribution up by about a factor of 2–3 towards higher values. The sizes of the embedded disks are very poorly constrained by observations and are typically assumed to be on the order of 100 AU or smaller based on simple centrifugal radius arguments. In reality, however, gravitational and viscous transport of mass and angular momentum will cause disks to spread to sizes greater than the corresponding centrifugal radii. We note that there are some limited observations supporting the existence of large protostellar disks (e.g. Enoch et al. 2009; Jorgensen et al. 2009). Ultimately, the correct threshold to adopt to separate the disk and core in the simulations will remain uncertain until the masses and sizes of protostellar disks are better constrained from observations.
Each pair of data in Fig. 1 indicates the mean disk
radius and mass for the corresponding model marked with circles. The mean values are
calculated by time-averaging the instantaneous values over the duration of the Class I
phase, in which disk fragmentation is usually most vigorous. It is evident that the disk
mass and radius both have to exceed some threshold values for the disk to
fragment. In particular, models with higher β experience disk fragmentation
at lower disk masses then their low-β counterparts. The minimum mean disk
mass at which fragmentation can take place according to our modeling is
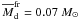 for
β ≳ 1.3%. This value may increase by about a factor of 2 for models with
lower β. We take into account here the uncertainty illustrated by the
errors in Fig. 1 associated with a coarse grid of
models. Our values of
for
β ≳ 1.3%. This value may increase by about a factor of 2 for models with
lower β. We take into account here the uncertainty illustrated by the
errors in Fig. 1 associated with a coarse grid of
models. Our values of 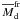 agree
reasonably well with previous estimates, 0.1 M⊙ (e.g. Rice et al. 2003; Mayer
et al. 2007). The minimum radius of a disk experiencing fragmentation in our models
is
agree
reasonably well with previous estimates, 0.1 M⊙ (e.g. Rice et al. 2003; Mayer
et al. 2007). The minimum radius of a disk experiencing fragmentation in our models
is 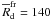 AU for
β ≈ 0.3%. This value may increase by up to a factor of 2 for models with
higher β. Our derived values of
AU for
β ≈ 0.3%. This value may increase by up to a factor of 2 for models with
higher β. Our derived values of 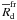 are
difficult to compare with other studies of disk fragmentation because these tend to provide
the minimum radial distance at which fragmentation can take place
(rfr) and not the minimum disk radius
(
are
difficult to compare with other studies of disk fragmentation because these tend to provide
the minimum radial distance at which fragmentation can take place
(rfr) and not the minimum disk radius
(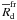 ) that
is required for disk fragmentation to occur. Obviously,
) that
is required for disk fragmentation to occur. Obviously,
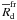 must
be grater than rfr and our simulations suggest that
must
be grater than rfr and our simulations suggest that
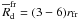 .
.
The black area in Fig. 1 marks the region where the
formation of GP and/or BD companions on wide orbits is found in the present work. None of
our models have shown the formation of wide-orbit companions for β ≳ 1.5%
but we attribute this to a rather narrow sampling of models at this region. Therefore, we
extrapolated the companion-forming domain to β ≳ 1.5% assuming the same
likelihood for the formation of wide-orbit companions as for models with lower
β. The companion-formation domain is notably narrower than both the
fragmentation and fragmentation plus ejection domains, particularly as far as the initial
core mass is concerned. It appears that Mc has to be greater
than 1.2 M⊙ and the ratio of rotational to gravitational
energy has to exceed 0.5% to enable the formation of wide-orbit companions. Moreover, the
minimum mean disk mass at which the formation of wide-orbit companions is found in our
modeling is 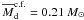 for models with
β ≳ 0.8%. The value of
for models with
β ≳ 0.8%. The value of 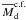 may
increase somewhat for lower-β models. The minimum mean disk radius that is
required for the formation of wide-orbit companions is
may
increase somewhat for lower-β models. The minimum mean disk radius that is
required for the formation of wide-orbit companions is
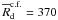 AU, and
this value increases with increasing β. Our values of the minimum disk
radius and mass both depend on the adopted threshold. For instance, adopting a density
threshold lower by a factor of five,
AU, and
this value increases with increasing β. Our values of the minimum disk
radius and mass both depend on the adopted threshold. For instance, adopting a density
threshold lower by a factor of five, 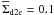 g cm-2, would yield a
factor of 1.2 greater minimum disk mass
g cm-2, would yield a
factor of 1.2 greater minimum disk mass 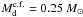 and a factor of 1.3
greater minimum disk radius
and a factor of 1.3
greater minimum disk radius 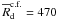 AU.
AU.
It is unclear why models with Mc < 1.2 M⊙ fail to produce wide-orbit companions. Large masses and radii of protostellar disks in companion-forming models must certainly be factors that help wide-orbit companions to survive. Another likely reason why low-Mc models fail to form wide-orbit companions is that disk fragmentation in these models is mostly confined to the embedded phase of star formation and is sustained by continuing mass-loading from an infalling envelope. A fragment may escape inward migration if the net torque exerted on it is not negative.
To a first order of accuracy, the net torque acting on the fragment in a gravitationally
unstable disk can be expressed as the sum of the gravitational torques from the inner
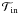 and outer
and outer 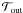 parts of the disk with respect to the current position of the fragment. Spiral arms and
other fragments are the main contributors to the total torque. Due to the trailing nature of
the spiral arms in gravitationally unstable protostellar disks,
parts of the disk with respect to the current position of the fragment. Spiral arms and
other fragments are the main contributors to the total torque. Due to the trailing nature of
the spiral arms in gravitationally unstable protostellar disks,
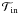 is usually positive and
is usually positive and 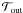 is usually negative. The condition for the fragment to avoid inward migration can then be
written as
is usually negative. The condition for the fragment to avoid inward migration can then be
written as 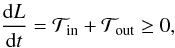 (18)where L is
the angular momentum of the fragment. Evidently, the fragment will stay in the disk for as
long as
(18)where L is
the angular momentum of the fragment. Evidently, the fragment will stay in the disk for as
long as 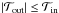 .
.
Even if the fragment forms near the disk outer edge where inequality (18) is likely to be fulfilled initially, it can
start migrating inward during the subsequent evolution due to continuing mass-loading from
the parental core. The mass infall onto the disk is a double-edged-sword effect: it promotes
disk fragmentation by increasing the disk mass (e.g. Vorobyov & Basu 2006, 2010a; Kratter et al. 2010a), but it also deposits a
sub-Keplerian material at/near the disk outer region (e.g. Visser & Dullemond 2010). This last acts to increase
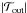 as the mass near the disk outer edge accumulates so that the fragment starts to migrate
inward when
as the mass near the disk outer edge accumulates so that the fragment starts to migrate
inward when 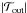 becomes greater than
becomes greater than 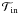 .
In addition, a sub-Keplerian material falling onto the disk can exert a torque onto the
fragment and push it in toward the star.
.
In addition, a sub-Keplerian material falling onto the disk can exert a torque onto the
fragment and push it in toward the star.
In contrast, models with Mc ≳ 1.2 M⊙ are usually characterized by disks that are sufficiently massive and large to experience fragmentation not only in the embedded phase and but also in the T Tauri phase when mass loading onto the disk diminishes (see Figs. 2 and 8). When formed at the disk outer regions where inequality (18) is fulfilled, fragments in these models have chances to open a gap in the disk and settle on quasi-stable, wide orbits. The main conclusion drawn from our parameter space study is that disk fragmentation is not sufficient to guarantee the formation of GP or BD companions on wide orbits.
We here used a spatially and temporally uniform α = 5 × 10-3. This choice is based on the work of Vorobyov & Basu (2009a,b), who found that models with α = 10-2 reproduce well the slope of the mass accretion rate to stellar mass relation for young BDs and low-mass stars (~1.0 Myr old), though they slightly overpredict the mean accretion rates. Higher values of α act to weaken the strength of gravitational instability through an overall increase in the mass transport efficiency and the corresponding decrease in the total disk mass. However, high values of α (≳10-1) destroy circumstellar disks during less than 1.0 Myr of evolution and are thus inconsistent with the mean disk lifetimes on the order of 2−3 Myr. We therefore conclude that a moderate increase in the adopted value of α (by a factor of several) can shift the fragmentation boundary in Fig. 1 toward higher values of Mc and β, but is not expected to shut completely off disk fragmentation.
Below, we present six models that have shown the formation of GP/BD embryos on wide, quasi-stable orbits via disk gravitational fragmentation. We focus on models 1–3 and provide only the main results for the other three models. The parameters of the models are listed in Table 1.
Model parameters.
4. Formation of a planetary-mass companion
In this section, we describe the formation of an 11-Jupiter-mass companion around a 1.2 M⊙ star. Figure 2 presents a series of the gas surface density images showing the evolution of the disk in model 1 starting soon after the formation of the central object (t = 0.05 Myr) and ending in the T Tauri phase (t = 2.37 Myr). The box size is 3000 AU on each side and represents a small subregion of the overall computational domain. The time elapsed after the formation the central protostar is shown in each image and the minimum gas surface density plotted in the figure is 0.06 g cm-2 or −1.2 in the log units.
The forming disk is gravitationally unstable and first fragments start to appear in the disk as early as at 50 kyr after the formation of the central star. Gravitational perturbations from spiral arms and massive fragments cause significant radial motions in the disk. As a result, the disk appears as a somewhat chaotic structure with dense filaments connecting the fragments. Nevertheless, a near-Keplerian rotation can be retrieved after azimuthal averaging. Fragmentation is predominantly concentrated in the intermediate and outer disk regions, a consequence of the mass infall and stellar irradiation, and no fragmentation is evident at r ≲ 50−100 AU.
One may notice from Fig. 2 that the number of fragments varies with time, indicating that the fragments may be tidally destroyed or otherwise lost by the disk. For instance, fragments may migrate inward onto the star (Vorobyov & Basu 2010a; Machida et al. 2011) or be ejected from the disk into the intracluster medium (Basu & Vorobyov 2012). As a result of these migration/ejection/destruction processes, only one fragment survives after 1.7 Myr of the disk evolution. The bottom row in Fig. 2 reveals the typical picture with the surviving fragment opening a gap and inducing spiral waves in the disk. The fragment itself is connected with the inner and outer disks by a wake of enhanced surface density that trails/leads the fragment outside/inside its orbit.
Figure 3 presents the number of fragments in the disk
at a given time instant. The number of fragments varies with time and a maximum value
(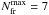 ) is reached at
t ≈ 0.2 Myr and t ≈ 0.9 Myr. Between these two maxima, a
local minimum with just two fragments in the disk occurs at t ≈ 0.5 Myr.
The disk mass at the end of the embedded phase (t = 0.65 Myr) is
≈0.3 M⊙, sufficient to sustain fragmentation in the disk
for another 0.8 Myr.
) is reached at
t ≈ 0.2 Myr and t ≈ 0.9 Myr. Between these two maxima, a
local minimum with just two fragments in the disk occurs at t ≈ 0.5 Myr.
The disk mass at the end of the embedded phase (t = 0.65 Myr) is
≈0.3 M⊙, sufficient to sustain fragmentation in the disk
for another 0.8 Myr.
 |
Fig. 3 Number of fragments vs. time in model 1. The number of fragments at a given time instant is calculated using the fragment tracking algorithm described in Sect. 2.3. An increase in the number of fragments shows recent fragmentation, and a decrease shows recent destruction/accretion of the fragments. |
Figure 4 shows four zoomed-in images of the surviving
fragment taken during a time period of 1180 yr covering just two orbital periods of the
fragment. The box size is 500 × 500 AU. The fragment is outlined by the yellow curve,
which is found using the tracking algorithm described in Sect. 2.3. The red circle represents the corresponding Hill radius of the fragment
calculated as 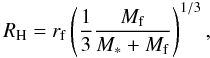 (19)where
M∗ is the stellar mass, rf is
the orbital distance of the fragment and Mf is the mass of the
fragment confined within the yellow curve. A mini-disk with a developed two-armed spiral
structure can be seen around the fragment in the lower-right image.
(19)where
M∗ is the stellar mass, rf is
the orbital distance of the fragment and Mf is the mass of the
fragment confined within the yellow curve. A mini-disk with a developed two-armed spiral
structure can be seen around the fragment in the lower-right image.
 |
Fig. 4 Zoomed-in view on the surviving fragment in model 1 at four time instances. The color image shows the gas surface density in log g cm-2, the yellow curve outlines the fragment and the red circles mark the Hill radius. |
We used our fragment-tracking algorithm to calculate physical properties of the surviving
fragment. Figure 5 presents (a) the orbital distance of
the fragment rf, (b) the mass of the fragment
Mf and the mass confined within the Hill radius
MH (solid and dashed lines, respectively), (c) the radius of
the fragment Rf and the Hill radius
RH (solid and dashed lines, respectively), and (d) the
integrated gravitational torque acting on the
fragment 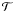 (solid line). The latter quantity is calculated as the sum of all individual torques
τ = −m(r,φ)∂Φ/∂φ
acting on the fragment, where m(r,φ) is the gas mass in a
cell with polar coordinates (r,φ) and Φ is the corresponding gravitational
potential. The dotted line marks the zero torque.
(solid line). The latter quantity is calculated as the sum of all individual torques
τ = −m(r,φ)∂Φ/∂φ
acting on the fragment, where m(r,φ) is the gas mass in a
cell with polar coordinates (r,φ) and Φ is the corresponding gravitational
potential. The dotted line marks the zero torque.
 |
Fig. 5 Characteristics of the surviving fragment in model 1: a) orbital distance, b) mass of the fragment (solid line) and mass confined within the Hill radius (dashed line), c) radius of the fragment (solid line) and the Hill radius (dashed line), and d) integrated gravitational torque acting on the fragment in units of 8.6 × 1040 g cm2 s-2. |
The orbital distance of the fragment varies in the 308−352 AU limits. The mean distance
from the central star is 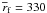 AU and
the orbit eccentricity is ϵ ≈ 0.07. These low-eccentricity orbits are
typical for companions formed by disk gravitational instability (Vorobyov & Basu 2010b; Boss
2012). The mass of the fragment varies in the 7–14 MJ
limits. This wide scatter reflects either imperfections in the fragment tracking mechanism
or continuous perturbations imposed onto the fragment by the circumfragment disk and spiral
density wake (or both effects). These perturbations, however, do not lead to the fragment
dispersal at least on the timescales of our numerical simulations. The mean mass of the
fragment calculated over two orbital periods shown in Fig. 5 is
AU and
the orbit eccentricity is ϵ ≈ 0.07. These low-eccentricity orbits are
typical for companions formed by disk gravitational instability (Vorobyov & Basu 2010b; Boss
2012). The mass of the fragment varies in the 7–14 MJ
limits. This wide scatter reflects either imperfections in the fragment tracking mechanism
or continuous perturbations imposed onto the fragment by the circumfragment disk and spiral
density wake (or both effects). These perturbations, however, do not lead to the fragment
dispersal at least on the timescales of our numerical simulations. The mean mass of the
fragment calculated over two orbital periods shown in Fig. 5 is 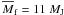 , which is still in
the planetary mass regime. However, the mean mass confined within the Hill radius is
, which is still in
the planetary mass regime. However, the mean mass confined within the Hill radius is
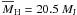 , which implies that
the fragment may accumulate some more material in the course of the evolution as it cools
and contracts into a planetary-sized object. On the other hand, if the fragment could not
get rid of angular momentum, most of the material in the Hill sphere would ultimately land
onto a circumfragment disk and the fragment may remain the planetary-mass regime.
, which implies that
the fragment may accumulate some more material in the course of the evolution as it cools
and contracts into a planetary-sized object. On the other hand, if the fragment could not
get rid of angular momentum, most of the material in the Hill sphere would ultimately land
onto a circumfragment disk and the fragment may remain the planetary-mass regime.
Figure 5c shows the radius of the fragment and the
Hill radius. The mean Hill radius 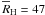 AU is
greater than mean radius of the fragment Rf = 20 AU by more than
a factor of 2. The mean scale height at the position of the planet is about
Z = 40 AU, somewhat smaller than the Hill radius. According to Crida et al. (2006) and Kley & Nelson (2012), the gap opening criterion can be written as
AU is
greater than mean radius of the fragment Rf = 20 AU by more than
a factor of 2. The mean scale height at the position of the planet is about
Z = 40 AU, somewhat smaller than the Hill radius. According to Crida et al. (2006) and Kley & Nelson (2012), the gap opening criterion can be written as
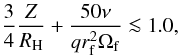 (20)where
q = MH/M∗
and Ωf is the orbital frequency of the fragment. Substituting the corresponding
mean values for RH and rf into
Eq. (20), noticing that
q = 0.017 for
M∗ = 1.2 M⊙ and
MH = 20.5 MJ, and finally
calculating ν using Eq. (8)
and mean disk temperature of 15 K at rf = 330 AU, we estimated
the left-hand side of Eq. (20) to be ≈0.9,
which marginally satisfies the gap-opening criterion. The future orbital dynamics of the
fragment can be predicted using the integrated gravitational torque acting on the fragment
from the rest of the disk,
(20)where
q = MH/M∗
and Ωf is the orbital frequency of the fragment. Substituting the corresponding
mean values for RH and rf into
Eq. (20), noticing that
q = 0.017 for
M∗ = 1.2 M⊙ and
MH = 20.5 MJ, and finally
calculating ν using Eq. (8)
and mean disk temperature of 15 K at rf = 330 AU, we estimated
the left-hand side of Eq. (20) to be ≈0.9,
which marginally satisfies the gap-opening criterion. The future orbital dynamics of the
fragment can be predicted using the integrated gravitational torque acting on the fragment
from the rest of the disk, 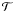 ,
shown in Fig. 5d. Evidently, the torque is mostly
positive, implying outward migration, and its mean value is
,
shown in Fig. 5d. Evidently, the torque is mostly
positive, implying outward migration, and its mean value is
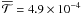 in units of 8.6 × 1040 g cm2 s-2.
in units of 8.6 × 1040 g cm2 s-2.
We estimated the characteristic migration timescale using the following simple analysis. A
(small) change of the orbital distance drf of a fragment with
mass Mf on a Keplerian orbit caused by a (small) change in the
angular momentum of the fragment dL can be written as
drf = 2 dL/Mfvf,
where
vf = (GM∗/rf)1/2
is the angular velocity of the fragment. The migration velocity of the fragment is then
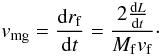 (21)Noticing that
(21)Noticing that
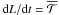 , the
characteristic migration time can be calculated as
, the
characteristic migration time can be calculated as 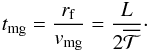 (22)Substituting the
corresponding mean values for rf, Mf
and
(22)Substituting the
corresponding mean values for rf, Mf
and 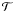 into Eq. (22), and also noticing that
M∗ = 1.2 M⊙ in model 1, we
estimated the migration timescale to be on the order of 10 Myr.
into Eq. (22), and also noticing that
M∗ = 1.2 M⊙ in model 1, we
estimated the migration timescale to be on the order of 10 Myr.
Since the fragment in model 1 opens a gap in the disk, a more appropriate estimate of the
migration timescale may be that given by the viscous diffusion time in the disk (Lin & Papaloizou 1986)
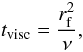 (23)which essentially yields
the same timescale of 10 Myr. The above estimates show that the fragment will remain on a
wide orbit for a time period longer than the typical disk lifetime of 2–3 Myr (Strom et al. 1989; Haisch
et al. 2001), implying that the fragment will finally turn into a massive GP or
low-mass BD on a stable orbit on the order of 400 AU from the central object.
(23)which essentially yields
the same timescale of 10 Myr. The above estimates show that the fragment will remain on a
wide orbit for a time period longer than the typical disk lifetime of 2–3 Myr (Strom et al. 1989; Haisch
et al. 2001), implying that the fragment will finally turn into a massive GP or
low-mass BD on a stable orbit on the order of 400 AU from the central object.
5. Formation of an intermediate-mass brown dwarf
In this section we describe the formation of a 43-Jupiter-mass BD around a 0.9 M⊙ star. Figure 6 shows a series of images of the gas surface density (logarithmic in g cm-2) in model 2 for the inner 1000 AU of our computational box. The time elapsed since the formation of the central protostar is indicated in each image. This model is characterized by initial gas surface density and angular velocity in the pre-stellar core that are independent of radial distance, i.e., Σ = const. and Ω = const. As a consequence, model 2 has an elevated mass infall onto the disk, stronger gravitational instability and more vigourous fragmentation in the Class 0 phase (Vorobyov 2012) than model 1, notwithstanding the fact that the prestellar core in the latter model is more massive. Gravitational instability in model 2, fueled by intense mass-loading from the envelope, is so strong that the disk has broken into massive clumps linked with each other by long and dense filaments. During the course of the evolution, most fragments have migrated onto the star due to strong torques but one massive fragment manages to survive through the initial violent stage and settles onto a quasi-stable orbit at around 0.3 Myr.
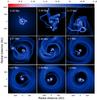 |
Fig. 6 Gas surface density distribution in model 2 shown at various times since the formation of the central protostar. Only the inner 2000 × 2000 AU box is shown, the total computational region extends to 16 000 AU. The scale bar is in log g cm-2. Note the fragment on a stable orbit in the bottom row. |
Figure 7 presents main characteristics of the
surviving fragment during approximately four orbital revolutions. The layout of the figure
is the same as that of Fig. 5. The orbital distance of
the fragment varies in the 170–185 AU limits and the mean distance is
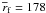 AU. The fragment is characterized
by a low-eccentricity orbit, ϵ ≈ 0.04, somewhat smaller than that of the
fragment in model 1. The mean mass of the fragment is
AU. The fragment is characterized
by a low-eccentricity orbit, ϵ ≈ 0.04, somewhat smaller than that of the
fragment in model 1. The mean mass of the fragment is
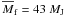 and the mean mass
contained within the Hill radius is
and the mean mass
contained within the Hill radius is 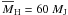 . This implies that
the fragment will ultimately form an intermediate mass BD, perhaps surrounded by its own
circum-BD disk. The mean radius of the fragment is
. This implies that
the fragment will ultimately form an intermediate mass BD, perhaps surrounded by its own
circum-BD disk. The mean radius of the fragment is 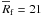 AU and
the mean Hill radius is
AU and
the mean Hill radius is 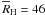 AU. The
latter value is greater than the local scale height, Z ≈ 24 AU, and the gap
opening criterion (20) is satisfied. In
general, the fragment in model 2 appears to be in a more perturbed state than that of
model 1, perhaps because the former is more massive, younger and less evolved.
AU. The
latter value is greater than the local scale height, Z ≈ 24 AU, and the gap
opening criterion (20) is satisfied. In
general, the fragment in model 2 appears to be in a more perturbed state than that of
model 1, perhaps because the former is more massive, younger and less evolved.
The integrated gravitational torque acting on the fragment in model 2 is always positive and is somewhat stronger than that of model 1, possibly due to the higher mass of the former. The migration timescale calculated using Eq. (22) is found to be on the order of 4 Myr, which is comparable to or even longer than the typical lifetime of the disk. We conclude that the fragment in model 2 has good chances to survive migration and settle on a wide orbit ultimately evolving into an intermediate-mass BD.
6. Attempted formation of multiple companions
Although the protostellar disks in models 1 and 2 exhibit multiple episodes of gravitational fragmentation, only one fragment in each model has survived after 1.0 Myr of disk evolution. This raises the question of whether gravitational fragmentation can account for the formation of multi-companion systems similar to HR 8799 (Marois et al. 2008, 2010), which has four planetary-mass objects on orbits at 15–70 AU from the central star. Below, we discuss this possibility.
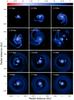 |
Fig. 8 Gas surface density distribution in model 3 shown at various times since the formation of the central protostar. Only the inner 2000 × 2000 AU box is shown, the total computational region extends to 20 000 AU. The scale bar is in log g cm-2. Note the two fragments on quasi-stable orbits in the third row of the images. One of the fragments disperses at t ≈ 1.55 Myr and the other survives to the end of numerical simulations (t = 1.8 Myr). |
Figure 8 presents a series of images of the gas surface density in model 3. The parameters of the model are listed in Table 1 and the time after the formation of the protostar is indicated in each image. The initial evolution of the disk is characterized by vigourous fragmentation and several fragments at a time are usually present in the disk. By t = 1.1 Myr only two fragments survive and settle on quasi-stable orbits with only slightly different radial distances from the star but with a 160° offset in azimuthal angle with respect to each other. However, after orbiting in unison for about 0.45 Myr, one of the fragments disperses at t ≈ 1.55 Myr. The dispersed fragments leaves a a crescent-shaped density enhancement in the disk that can still be seen in Fig. 8 at t = 1.6 Myr. The other fragment survives to the end of our numerical simulations (t = 1.8 Myr).
Figure 9 shows the main characteristics of the two surviving fragments during a time period of 1.46–1.5 Myr, i.e., before one of the fragments has dispersed. In particular, the left-hand and right-hand panels belong to fragment 1 (most massive) and fragment 2 (least massive). Panels (a) in Fig. 9 present the orbital distance of the fragments, panels (b) – masses of the fragments (solid lines) and masses contained within the Hill radii of each fragment (dashed lines), and panels (c) – radii of the fragments (solid lines) and their Hill radii (dashed lines).
 |
Fig. 9 Main characteristics of fragment 1 (left column) and fragment 2 (right column) in model 3 before the least massive of them (fragment 2) has dispersed. In particular, panel a) presents the orbital distance of the fragments, panel b) the masses of the fragments (solid lines) and masses confined within the Hill radii (dashed lines), and panel c) denotes the radii of the fragments (solid lines) and their Hill radii (dashed lines). |
The two fragments move on orbits that are less stable than those in models 1 and 2, perhaps
due to continuing gravitational perturbation exerted on the fragments by spiral density
wakes excited by both fragments in the disk. The mean orbital distances of fragment 1 and 2
are 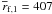 AU and
AU and
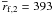 AU. The
eccentricity of the orbits also varies somewhat and the highest eccentricities for
fragments 1 and 2 are estimated to be approximately ϵ1 = 0.05
and ϵ2 = 0.1. As a result, notable radial excursions are evident
in the top panels of Fig. 9. The masses of the two
fragments stay in the planetary-mass regime, though with significant variations reflecting
their highly perturbed state, and the mean masses of fragments 1 and 2 are
AU. The
eccentricity of the orbits also varies somewhat and the highest eccentricities for
fragments 1 and 2 are estimated to be approximately ϵ1 = 0.05
and ϵ2 = 0.1. As a result, notable radial excursions are evident
in the top panels of Fig. 9. The masses of the two
fragments stay in the planetary-mass regime, though with significant variations reflecting
their highly perturbed state, and the mean masses of fragments 1 and 2 are
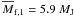 and
and
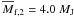 . The mean masses
contained within the Hill radii of fragment 1 and 2 are
. The mean masses
contained within the Hill radii of fragment 1 and 2 are
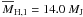 and
and
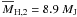 , indicating that if
both fragments had survived, they would have formed massive GPs. The mean radii of
fragments 1 and 2 are
, indicating that if
both fragments had survived, they would have formed massive GPs. The mean radii of
fragments 1 and 2 are 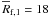 AU and
AU and
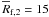 AU, and
their mean Hill radii are
AU, and
their mean Hill radii are 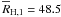 AU and
AU and
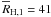 AU. Both
values are greater than the local scale hight Z ≈ 25 AU.
AU. Both
values are greater than the local scale hight Z ≈ 25 AU.
The likely reason why one of the fragments has dispersed is that this pair of fragments
violates the criterion for orbital stability between two coplanar planets on circular orbits
(Gladman 1993) 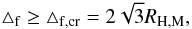 (24)where
(24)where
 AU and
RH,M is the mutual Hill radius defining the
region in which the gravitational force between two bodies is stronger than the force
exerted on them from the star
AU and
RH,M is the mutual Hill radius defining the
region in which the gravitational force between two bodies is stronger than the force
exerted on them from the star 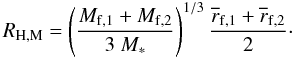 (25)Substituting the
corresponding values into Eqs. (24)
and (25), one obtains
RH,M = 56 AU,
△ f,cr = 193 AU, and
△ f ≪ △ f,cr. Evidently, the orbits of the two
fragments are unstable. Moreover, the mutual Hill radius is greater than the difference
between the mean orbital distances of the fragments, implying that the less massive fragment
might not have withstood the disturbing tidal influence from the more massive counterpart.
This effect may have been aided by the insufficient numerical resolution of our logarithmic
polar grid at a radial distance of the fragments (~400 AU). We note that the value of
△ f,cr = 193 AU is on the order of the orbital distance for
directly-imaged wide-orbit companions (see forth column in Table 3), which implies that the separation between companions in multicomponent
systems should be comparable to their orbital distances. This hinders the formation of such
wide-orbit, multicomponent systems even more. In any case, the results of this numerical
simulation and other studies (e.g. Boss 2011) have
demonstrated that gravitational fragmentation can account for the formation of multiple
fragments at a time, but the question of whether these fragments can ultimately mature into
a system with more than one companion in wide orbits is still open.
(25)Substituting the
corresponding values into Eqs. (24)
and (25), one obtains
RH,M = 56 AU,
△ f,cr = 193 AU, and
△ f ≪ △ f,cr. Evidently, the orbits of the two
fragments are unstable. Moreover, the mutual Hill radius is greater than the difference
between the mean orbital distances of the fragments, implying that the less massive fragment
might not have withstood the disturbing tidal influence from the more massive counterpart.
This effect may have been aided by the insufficient numerical resolution of our logarithmic
polar grid at a radial distance of the fragments (~400 AU). We note that the value of
△ f,cr = 193 AU is on the order of the orbital distance for
directly-imaged wide-orbit companions (see forth column in Table 3), which implies that the separation between companions in multicomponent
systems should be comparable to their orbital distances. This hinders the formation of such
wide-orbit, multicomponent systems even more. In any case, the results of this numerical
simulation and other studies (e.g. Boss 2011) have
demonstrated that gravitational fragmentation can account for the formation of multiple
fragments at a time, but the question of whether these fragments can ultimately mature into
a system with more than one companion in wide orbits is still open.
Characteristics of surviving embryos.
After the less massive fragment dispersed at t ≈ 1.55 Myr, the other
fragment settled on a quasi-stable orbit with a mean radial distance
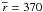 AU. The main characteristics of
the surviving fragment are shown in Fig. 10, the
layout of which is the same as that of Fig. 5. The last
surviving fragment is characterized by the mean mass
AU. The main characteristics of
the surviving fragment are shown in Fig. 10, the
layout of which is the same as that of Fig. 5. The last
surviving fragment is characterized by the mean mass 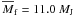 , which is similar to
the total mass of the two fragments before one of them dispersed. This suggests that the
surviving fragment has accreted most of the material released by the destroyed fragment.
Significant temporal variations in the instantaneous mass of the surviving fragment are
indicative of its highly perturbed state. The mean mass contained within the Hill radius is
, which is similar to
the total mass of the two fragments before one of them dispersed. This suggests that the
surviving fragment has accreted most of the material released by the destroyed fragment.
Significant temporal variations in the instantaneous mass of the surviving fragment are
indicative of its highly perturbed state. The mean mass contained within the Hill radius is
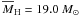 . The orbit of the
surviving fragment is characterized by rather low eccentricity, ϵ = 0.02.
The integrated torque acting on the fragment is positive and the estimated characteristic
migration time of the fragment is tmg = 6.9 Myr. We conclude
that this fragment is likely to evolve into a massive GP or low-mass BD, depending on the
amount of mass that will ultimately settle into a circumfragment disk.
. The orbit of the
surviving fragment is characterized by rather low eccentricity, ϵ = 0.02.
The integrated torque acting on the fragment is positive and the estimated characteristic
migration time of the fragment is tmg = 6.9 Myr. We conclude
that this fragment is likely to evolve into a massive GP or low-mass BD, depending on the
amount of mass that will ultimately settle into a circumfragment disk.
7. Characteristics of survived GP/BD embryos and comparison with observations
We have run 60 models with the total integration time in each model exceeding 1.0 Myr after the formation of the central protostar. Protostellar disks in most models were sufficiently massive to experience vigorous gravitational fragmentation at radial distances greater than several tens of AU during the initial several hundred thousand years. The number of the fragments amounted to more than ten at a time. However, most of the fragments have either migrated through the inner computational boundary at 6 AU or were ejected from the computational domain into the intracluster medium or were dispersed by tidal torques on timescales shorter than 1.0 Myr. Only six models out of 60 revealed the survival of one of the fragments after 1.0 Myr of evolution.
 |
Fig. 11 Gas surface density distribution in models showing the formation of quasi-stable GP/BD embryos on wide orbits. The model number and time elapsed since the formation of the central protostar is indicated in each panel. Only the inner 2000 × 2000 AU box is shown. The scale bar is in log g cm-2. |
Characteristics of known wide-orbit GPs and BDs.
Figure 11 gathers the six models that have demonstrated the formation of stable companions on wide orbits (to which we refer below as GP/BD embryos), showing for each model the gas surface density image (g cm-2 in log units) at the end of numerical simulations. The model number and time elapsed since the formation of the central protostar are indicated in each panel. Only the inner 2000 × 2000 box is shown for each model. All six embryos possess their own circum-embryo disks, whose masses are comparable to those of the parent embryos as implied by the mass contained within the Hill radius (see Table 2). In particular, circum-embryo disks in models 2 and 5 exhibit a pronounced two-armed spiral structure.
Remarkably, the survived embryos and circum-embryo disks both exhibit a retrograde rotation with respect to that of the parental protostellar disk. This contradicts expectations of prograde rotation (e.g Boley et al. 2010; Zhu et al. 2012), borne out by the fact that the specific angular momentum of a fluid element in a rotationally supported disk increases with distance as r0.5. Our numerical scheme performs well in standard numerical tests (Vorobyov & Basu 2006), including an angular momentum conservation test (Norman et al. 1980), and hence this phenomenon is unlikely to be caused by numerical reasons. However, significant local deviations from Keplerian orbits can be present in strongly gravitationally unstable disks (e.g. Vorobyov 2010), with the consequence that the specific angular momentum radial profile may not locally reflect a rotationally supported disk. A visual analysis of Figs. 2, 6, and 8 demonstrates that both the retrograde and prograde fragments are present at the initial stages of disk evolution, but the retrograde systems may be favoured for survival. For instance, type III migration strongly depends on the flow pattern near the planet (Pepliński et al. 2008). The counterrotating circum-embryo disk may additionally hinder the formation of horseshoe streamlines near the corotation, thus weakening the efficiency of type III migration. In any case, a more focused study is needed to understand the phenomenon of retrograde rotation.
Embryos in models 1–5 satisfy the gap opening criterion (20) and clear a well-defined gap in the protostellar disk. The embryo in model 6 is the least massive of all and the corresponding gap is less pronounced. We note that the gap is profoundly non-axisymmetric in models 2, 3, and 5, an effect that can in principle be used to infer the presence of massive GPs/BDs in the disk.
We present the main characteristics of surviving embryos in Table 2. In particular, Cols. 1–11 list the model number, mass of the prestellar
core Mc, the ratio of the rotational to gravitational energy in
the prestellar core β, the mass of the protostar
M∗, the mean mass of the embryo
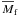 , the mean mass within
the Hill radius
, the mean mass within
the Hill radius 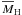 , the mean orbital
distance of the embryo
, the mean orbital
distance of the embryo 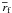 , the orbital
eccentricity ϵ, the mean radius of the embryo
, the orbital
eccentricity ϵ, the mean radius of the embryo
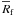 , the mean Hill radius
, the mean Hill radius
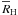 , and migration timescale
tmg. For the purpose of comparison, we also provide in
Table 3 the main characteristics of directly
imaged, wide-orbit (>50 AU) companions to stars with mass
0.08 M⊙ ≤ M∗ ≤ 2.1 M⊙.
We excluded lower-separation companions because we are interested only in GPs/BDs that can
be formed by disk gravitational fragmentation, which is likely to occur at radial distances
greater than 50 AU. In particular, Cols. 2–5 list stellar masses
M∗, masses of companions Mp,
orbital distances of companions rp, and stellar ages as compiled
by the Extrasolar Planets Encyclopedia (http://exoplanet.eu). We have ordered the
objects along in order of increasing stellar masses.
, and migration timescale
tmg. For the purpose of comparison, we also provide in
Table 3 the main characteristics of directly
imaged, wide-orbit (>50 AU) companions to stars with mass
0.08 M⊙ ≤ M∗ ≤ 2.1 M⊙.
We excluded lower-separation companions because we are interested only in GPs/BDs that can
be formed by disk gravitational fragmentation, which is likely to occur at radial distances
greater than 50 AU. In particular, Cols. 2–5 list stellar masses
M∗, masses of companions Mp,
orbital distances of companions rp, and stellar ages as compiled
by the Extrasolar Planets Encyclopedia (http://exoplanet.eu). We have ordered the
objects along in order of increasing stellar masses.
The embryo masses in our models lie in the 3.5−43 MJ limits and cover the entire range of masses found for detected wide-orbit companions. There is no clear indication that more massive cores tend to produce more massive companions, though the range of companion-forming core masses considered here (1.2−1.7 M⊙) is quite narrow. There is a hint that models with higher β tend to produce more massive companions (e.g., models 2 and 5) and that BD embryos tend to orbit less massive protostars, but these tendencies need to be confirmed with a wider sample of models. Our modeling suggests that the companion masses are likely to be determined by the disk/stellar properties rather than by the properties of parental prestellar cores. The masses contained within the Hill radius are generally a factor of 1.5–2.5 greater than those of the embryos. The final masses of the embryos are therefore expected to be somewhat higher, though the actual growth will be limited by the angular momentum of the disk gas that the embryo is trying to accrete (Boley et al. 2010).
The orbital distances of GP/BD embryos in our models are confined in the 178–415 AU limits, whereas Table 3 indicates a wider range of orbital distances for directly imaged companions, 15–1170 AU. While the upper limit on the orbital distance in our modeling (415 AU) may increase if we run higher-resolution numerical simulations (because of better resolution at large radial distances on the adopted logarithmically-spaced radial grid), the lower limit (178 AU) is not expected to change considerably given that all embryos in our models are in fact slowly migrating outward. Vorobyov & Basu (2010b) found GP embryos forming at distances of about 50 AU but their models employed a barotropic equation of state, which is known to facilitate disk fragmentation at small radial distances from the star.
The dearth of embryos at orbital distances ≲170 AU in our simulations cannot be explained by numerical resolution effects and is intriguing because it conflicts with observations. Four objects in Table 3 have companions orbiting the star at radial distances less than 170 AU (CD-35 2722, GQ Lup, HR 8799, and Fomalhaut). If disk fragmentation cannot explain these objects, then they must have been formed by dynamical scattering of closely-packed companions, leading to ejection of the least massive companion onto a wide orbit (e.g. Scharf & Menou 2009; Veras et al. 2009). The resulting orbits of these companions are expected to cover the full range of possible eccentricities, some of them may even become unbound with time (Veras et al. 2009). In addition, the probability to form wide-orbit companions via dynamical scattering declines quickly with the increasing orbital distance of the companions (Scharf & Menou 2009). The eccentricities of our formed embryos lie in the 0.02–0.07 range and the only known eccentricity of a wide-orbit companion is that of Fomalhaut b, ϵ = 0.11. Interestingly enough, the orbital distance of Fomalhaut b is 119 AU and fits into the scattering scenario for the formation of wide-orbit companions. The above analysis suggests a unified picture for the formation of wide-orbit companions, in which objects at orbital distances from several tens to ≈150 AU are preferentially formed by dynamical scattering and are characterized by a whole spectrum of eccentricities while those at greater orbital distances are mostly formed via disk fragmentation and are characterized by low eccentricities. Definite measurements of eccentricities for other wide-orbit companions are therefore expected to clarify the formation mechanism of GPs/BDs on wide orbits (see also Dodson-Robinson et al. 2009).
The minimum mass of a protostar that hosts a wide-orbit GP/BD embryo in our models is found to be M∗ = 0.75 M⊙, whereas the directly imaged wide-orbit companions have host stars with masses extending down to the brown-dwarf-mass regime (e.g., UScoCTIO 108, Bj´ar et al. 2008). It appears that protostars with mass ≲0.7 M⊙ possess protostellar disks with a mass that is insufficient to experience gravitational fragmentation in the T Tauri phase. Fragmentation episodes in these disks are mostly confined to the embedded phase and are driven by mass infall from the parental core. As discussed in Sect. 3, fragments in these disks have little chance to escape fast inward migration and are unlikely to form wide-orbit companions. We note that Boss (2011) reported the formation of companions in disks around stars with mass <0.7 M⊙, but the total integration time was limited to just 1000 yr and was insufficient to draw firm conclusions about the likelihood of survival of these companions.
If disk fragmentation cannot explain wide-orbit companions around stars with mass ≲0.7 M⊙, then a viable alternative is dynamical scattering of close-orbit companions. However, Table 3 demonstrates that most of the stars with mass <0.7 M⊙ have companions on orbital distances of about several hundred AU. Such large orbital distances are difficult to explain in the framework of dynamical scattering since the number of scattered objects quickly declines with increasing orbital distance (Scharf & Menou 2009). This inconsistency necessitates additional research into this subject.
Finally, we note that our modeling failed to produce systems with more than one stable companion. This is consistent with observations. The only known system with several wide-orbit companions is HR 8799, and even in this case only one companion has an orbital distance greater than 50 AU. The lack of multiple wide-orbit companions is likely caused by the fact that the orbital stability criterion (24) imposes strict limitations on the minimum orbital distance between two stable companions △ f,cr. For instance, in model 3, which showed an attempted formation of two companions (but one of them finally dispersed), the corresponding minimum distance was △ f,cr = 193 AU, while the actual mean radial separation between the companions was only 14 AU. Large values of △ f,cr make the disk fragmentation scenario an unlikely explanation of multi-component systems because it may require very extended and hence massive disks.
8. Conclusions
We computed the gravitational collapse of prestellar cores with masses in the range of 0.1 M⊙ < Mc ≤ 1.8 M⊙ and ratios of the rotational to gravitational energy confined within the 0.2% < β ≤ 2.2% limit. The integration time in our numerical hydrodynamics simulations extended beyond 1 Myr after the formation of the central protostar and covered the entire embedded phase and part of the T Tauri phase of stellar evolution. We focused on models that showed disk gravitational fragmentation and, in particular, on models that revealed the formation of quasi-stable, giant planet (GP) and brown dwarf (BD) embryos on orbits greater than 50 AU (referred to as wide-orbit companions). The typical migration timescales of the embryos are comparable to or greater than the lifetime of a typical disk (2–3 Myr), which allows us to conclude that they will ultimately cool and contract into fully formed GPs or BDs. Our insufficient numerical resolution did not allow us to resolve the formation of planetary-sized objects.
While most of our models showed disk fragmentation, only 6 out of 60 models revealed the formation of wide-orbit companions. We compared the characteristics of our embryos with those of fully formed GPs and BDs obtained from direct imaging (http://exoplanet.eu). The disk masses and radii provided below were calculated by time-averaging instantaneous values over the duration of the Class I phase, which is most relevant to studying disk fragmentation. Our findings can be summarized as follows:
-
Masses of wide-orbit companions lie in the 3.5−43 MJ limits and cover the entire range of masses found for directly imaged GPs and BDs on orbits greater than 50 AU. There is no clear indication that the mass of the companion depends on the mass and angular momentum in the pre-stellar core, though a wider sample of companion-forming models is needed to draw firm conclusions.
-
The orbital distances of the companions found in our modeling lie within the 178–415 AU limit. This range of orbital distances is notably narrower than that found for directly imaged companions, a few AU–1170 AU. While the upper limit (415 AU) may increase if we consider higher resolution simulations3, the lower limit (178 AU) cannot be explained by resolution effects and is intriguing because it conflicts the observations. We propose that companions at orbital separations from a few tens to 150 AU are likely to form via dynamical scattering of closely-packed companions onto wide orbits or other mechanisms (e.g. Lambrechts & Johansen 2012), while companions at larger orbital distances are predominantly formed via disk fragmentation. Definite measurement of eccentricities as a function of orbital distance is needed to clarify the formation mechanism of GPs/BDs on wide orbits, because the disk fragmentation scenario tends to produce companions on low eccentricities, ϵ ≤ 0.1.
-
Our numerical simulations did not produce multiple companions on wide orbits. Although model 3 revealed an attempted formation of two companions at orbital distances ≈190−210 AU, one of the fragments dispersed in less than 0.5 Myr. The likely reason for this failure is that the radial separation between the two companions, ≈14 AU, was much smaller than the required 190 AU according to the orbital stability criterion of Gladman (1993). The formation of multi-component systems would require very extended and hence massive disks, which are statistically rare. The only known system with several wide-orbit companions, HR 8799, has only one companion at a distance greater than 50 AU and is likely to form via dynamical scattering.
-
The minimum mass of a companion-hosting star found in our modeling is 0.75 M⊙, whereas the corresponding value for directly imaged systems extends to the BD-mass regime. It is likely that disk fragmentation in systems with stellar mass ≤ 0.7 M⊙ is mostly confined to the embedded phase of star formation, in which mechanisms causing migration/ejection/destruction of the fragments are strong and the likelihood for survival of the fragments is low.
-
Disk gravitational fragmentation does not automatically guarantee the formation of wide-orbit companions. Most of the fragments do not stay on wide orbits for more than several orbital periods. The majority are torqued into the disk inner region and through the sink cell (6 AU) by gravitational torques from spiral arms or other fragments; a few fragments may be ejected from the disk via many-body gravitational interaction (Stamatellos & Whitworth 2009a; Basu & Vorobyov 2012), and some fragments may be tidally dispersed at various radial distances in the disk (Boley et al. 2010; Nayakshin 2010; Vorobyov 2011a; Zhu et al. 2012). The fragments that pass through the sink cell may be completely destroyed and accreted onto the forming star (Vorobyov & Basu 2006, 2010a; Machida et al. 2011) or lose their gaseous envelopes and form terrestrial cores or icy giants if the dust sedimentation timescale was sufficiently short (Nayakshin 2010; Boley et al. 2010).
-
The minimum disk mass at which fragmentation can take place is found to be
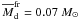 for models with
β ≳ 1.2%. The value of
for models with
β ≳ 1.2%. The value of 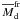 may
increase by almost a factor of 2 for disks formed from pre-stellar cores with lower
angular momentum, 0.2% ≤ β < 1.2%. Our values
of
may
increase by almost a factor of 2 for disks formed from pre-stellar cores with lower
angular momentum, 0.2% ≤ β < 1.2%. Our values
of 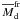 agree reasonably well with previous estimates of the critical disk mass,
≈0.1 M⊙ (Rice et al.
2003; Mayer et al. 2007).
agree reasonably well with previous estimates of the critical disk mass,
≈0.1 M⊙ (Rice et al.
2003; Mayer et al. 2007). -
The minimum disk mass that is required for the formation of wide-orbit companions is found to be
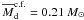 , a factor of 3
greater than the minimum disk mass for gravitational fragmentation
, a factor of 3
greater than the minimum disk mass for gravitational fragmentation
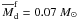 . The minimum
disk radius that is required to produce wide-orbit companions is 370 AU, more than a
factor of two greater than that required for disk fragmentation to occur.
. The minimum
disk radius that is required to produce wide-orbit companions is 370 AU, more than a
factor of two greater than that required for disk fragmentation to occur.
In the most extreme cases, some of the fragments may even be ejected from the disk into the intracluster medium (Basu & Vorobyov 2012).
Acknowledgments
The author gratefully acknowledges the referee for useful comments, which helped to improve the paper. The author also thanks Prof. Shantanu Basu for stimulating discussions. This work is supported by the RFBR grants 10-02-00278 and 11-02-92601. The simulations were performed on the Shared Hierarchical Academic Research Computing Network (SHARCNET), on the Atlantic Computational Excellence Network (ACEnet), and on the Vienna Scientific Cluster (VSC-2).
References
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Meru, F., & Paardekooper, S.-J. 2011, MNRAS, 416, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S. 1997, ApJ, 485, 240 [CrossRef] [Google Scholar]
- Basu, S., & Vorobyov, E. I. 2012, ApJ, 750, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. 2009, MNRAS, 392, 1368 [Google Scholar]
- Béjar, V. J. S., Zapatero Osorio, M. R., Pérez-Garrido, A., et al. 2008, ApJ, 673, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton Univ. Press) [Google Scholar]
- Boley, A. C. 2009, ApJ, 695, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, A. C., Hartquist, T. W., Durisen, R. H., & Michael, S. 2007, ApJ, 656, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, A. C., Hayfield, T., Mayer, L., & Durisen, R. H. 2010, Icarus, 207, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2003, ApJ, 599, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2011, ApJ, 731, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2012, MNRAS, 419, 1930 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P., & Hartmann, L. W. 2001, ApJ, 562, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P., Liu, M. C., Kraus, A. L., Mann, A. W., & Ireland, M. J. 2011, ApJ, 743, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Cha, S.-H., & Nayakshin, S. 2011, MNRAS, 415, 3319 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J. 2009, MNRAS, 396, 1066 [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- D’Antona, F., & Mazitelli, I. 1997, Mem. Soc. Astron. It., 68, 807 [Google Scholar]
- Dapp, W. B., & Basu, S. 2009, MNRAS, 395, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson-Robinson, S. E., Veras, D., Ford, E. B., & Beichman, C. A. 2009, ApJ, 707, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A. 2012, ApJ, 755, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Hillenbrand, L. A., Carpenter, J. M., & Wolf, S. 2005, ApJ, 635, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Plambeck, R. L., Carpenter, J. M., et al. 2008, ApJ, 683, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Corder, S., Dunham, M. M., & Duchêne, G. 2009, ApJ, 707, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, K. E., Jr, Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2009, ApJ, 701, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2003, ApJ, 597, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgensen, J. K., van Dishoeck, E. F., Visser, R., et al. 2009, A&A, 507, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 2011 [Google Scholar]
- Kratter, K. M., Matzner, C. D., Krumholz, M. R., & Klein, R. I. 2010a, ApJ, 708, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Kratter, K. M., Murray-Clay, R. A., & Youdin, A. N. 2010b, ApJ, 710, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Lafreniére, D., Jayawardhana, R., & van Kerkwijk, M. H. 2010, ApJ, 719, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, 32 [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S., & Matsumoto, T. 2011, ApJ, 729, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Lufkin, G., Quinn, T., & Wadsley, J. 2007, ApJ, 661, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masunaga, H., & Inutsuka, S. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Meru, F., & Bate, M. R. 2011, MNRAS, 410, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Meru, F., & Bate, M. R. 2012, MNRAS, accepted [arXiv:1209.1107] [Google Scholar]
- Michael, S., & Durisen, R. H. 2010, MNRAS, 406, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Michael, S., Durisen, R. H., & Boley, A. C. 2011, ApJ, 737, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S., 2010, MNRAS, 408, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S., Cha, S.-H., & Bridges, J. C. 2011, MNRAS, 416, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Nero, D., & Bjorkman, J. E. 2009, ApJ, 702, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Norman, M. L., Wilson, J. R., & Barton, R. T. 1980, ApJ, 239, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1991, ApJ, 375, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Pepliński, A., Artymowicz, P., & Mellema, G. 2008a, MNRAS, 386, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2005, ApJ, 621, 69 [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Bate, M. R., & Bonnell, I. A. 2003, MNRAS, 339, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Mayo, J. N., & Armitage, P. J. 2010, MNRAS, 402, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Scharf, C., & Menou, K. 2009, ApJ, 693, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, T. O. B., Neuhäuser, R., Seifahrt, A., et al. 2008, A&A, 491, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H., Tremaine, S., Adams, F. C., & Ruden, S. P. 1990, ApJ, 358, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009a, MNRAS, 392, 413 [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009b, MNRAS, 400, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1998, ApJ, 495, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., Crepp, J. R., & Ford, E. B. 2009, ApJ, 696, 1600 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., & Dullemond, C. P. 2010, A&A, 519, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I. 2010, ApJ, 723, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2011a, ApJ, 728, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2011b, ApJ, 729, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2012, Astron. Rep., 56, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2006, ApJ, 650, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2009a, MNRAS, 393, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2009b, ApJ, 703, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2010a, ApJ, 719, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2010b, ApJ, 714, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Nelson, R. P., & Gammie, C. F. 2012, ApJ, 746, 110 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Phase space of β, the initial ratio of rotational to gravitational energy, vs. core mass Mc. The solid/open circles correspond to models with/without disk fragmentation. In the black region we found formation of sub-stellar- or planetary-mass companions on wide orbits. The dark-shaded region is the region in which both fragmentation and ejection events may occur, and in the light-shaded region occur only fragmentation events. The white area marks the region without fragmentation. Arrows illustrate uncertainties associated with a coarse grid of models and indicate models in the β: Mc phase space that might have shown (with a 50% probability) disk fragmentation (ejection/companion formation) had we considered a finer grid of models. Each pair of data in parenthesis indicates the mean disk radius and mass for the corresponding model. |
| In the text | |
 |
Fig. 2 Gas surface density distribution in model 1 shown at various times since the formation of the central protostar. Only the inner 3000 × 3000 AU box is shown, the total computational region extends to 22 000 AU. The scale bar is in log g cm-2. Note the fragment on a stable orbit in the bottom row. |
| In the text | |
 |
Fig. 3 Number of fragments vs. time in model 1. The number of fragments at a given time instant is calculated using the fragment tracking algorithm described in Sect. 2.3. An increase in the number of fragments shows recent fragmentation, and a decrease shows recent destruction/accretion of the fragments. |
| In the text | |
 |
Fig. 4 Zoomed-in view on the surviving fragment in model 1 at four time instances. The color image shows the gas surface density in log g cm-2, the yellow curve outlines the fragment and the red circles mark the Hill radius. |
| In the text | |
 |
Fig. 5 Characteristics of the surviving fragment in model 1: a) orbital distance, b) mass of the fragment (solid line) and mass confined within the Hill radius (dashed line), c) radius of the fragment (solid line) and the Hill radius (dashed line), and d) integrated gravitational torque acting on the fragment in units of 8.6 × 1040 g cm2 s-2. |
| In the text | |
 |
Fig. 6 Gas surface density distribution in model 2 shown at various times since the formation of the central protostar. Only the inner 2000 × 2000 AU box is shown, the total computational region extends to 16 000 AU. The scale bar is in log g cm-2. Note the fragment on a stable orbit in the bottom row. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 but for model 2. |
| In the text | |
 |
Fig. 8 Gas surface density distribution in model 3 shown at various times since the formation of the central protostar. Only the inner 2000 × 2000 AU box is shown, the total computational region extends to 20 000 AU. The scale bar is in log g cm-2. Note the two fragments on quasi-stable orbits in the third row of the images. One of the fragments disperses at t ≈ 1.55 Myr and the other survives to the end of numerical simulations (t = 1.8 Myr). |
| In the text | |
 |
Fig. 9 Main characteristics of fragment 1 (left column) and fragment 2 (right column) in model 3 before the least massive of them (fragment 2) has dispersed. In particular, panel a) presents the orbital distance of the fragments, panel b) the masses of the fragments (solid lines) and masses confined within the Hill radii (dashed lines), and panel c) denotes the radii of the fragments (solid lines) and their Hill radii (dashed lines). |
| In the text | |
 |
Fig. 10 Same as Fig. 5 but for model 3. |
| In the text | |
 |
Fig. 11 Gas surface density distribution in models showing the formation of quasi-stable GP/BD embryos on wide orbits. The model number and time elapsed since the formation of the central protostar is indicated in each panel. Only the inner 2000 × 2000 AU box is shown. The scale bar is in log g cm-2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


