| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201220575 | |
| Published online | 29 March 2013 | |
Semiconvection: theory
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1,
85748
Garching,
Germany
e-mail: henk@mpa-garching.mpg.de
Received: 16 October 2012
Accepted: 16 February 2013
A model is developed for the transport of heat and solute in a system of double-diffusive layers under astrophysical conditions (where viscosity and solute diffusivity are low compared with the thermal diffusivity). The process of formation of the layers is not part of the model but, as observed in geophysical and laboratory settings, is assumed to be faster than the life time of the semiconvective zone. The thickness of the layers is a free parameter of the model. When the energy flux of the star is specified, the effective semiconvective diffusivities are only weakly dependent on this parameter. An estimate is given of the evolution of layer thickness with time in a semiconvective zone. The model predicts that the density ratio has a maximum for which a stationary layered state can exist, Rρ ≲ Le−1/2. Comparison of the model predictions with a grid of numerical simulations is presented in a companion paper.
Key words: convection
© ESO, 2013
1. Introduction
In stellar evolution, “semiconvection” denotes the situation where a thermally unstable stratification is stabilized against (adiabatic) overturning by a gradient in composition (called solute in the following; typically the helium concentration, increasing with depth). It was first recognized as a complication in the calculation of stellar structure by Tayler (1953). Uncertainty whether the stabilizing gradient should be ignored (“according to Schwarzschild”), included in the condition for overturning (“according to Ledoux”), or something in between has led to a number of different recipes for mixing the helium gradient. The evolution of the star subsequent to the semiconvective phase is sensitive to these differences (e.g. Weiss 1989; Langer et al. 1989; Langer 1991; Stothers & Chin 1994; Langer & Maeder 1995). The fluid mechanics encountered in geophysics in the same case of a thermally unstable stratification stabilized by a stabilizing solute is called double-diffusive or thermohaline convection.
The observations show that such a stratification forms a stack of many thin layers, called a “staircase”, each consisting of overturning convection sandwiched between stable steps in composition and temperature (Turner & Stommel 1964; Padman & Dillon 1987; Schmid et al. 2010, and references therein). Effectively, this is a “compromise between Schwarzschild and Ledoux”. Correspondingly, the net transport coefficients (of heat and solute) lie somewhere between those of convection and diffusion.
The reason for this layer formation are understood (for references, cf. Spruit 1992, hereafter S92; and Zaussinger & Spruit 2013, hereafter ZS13). The main theoretical contribution in this context has been the work of Proctor (1981), who analytically showed that a finite amplitude layered state exists for conditions when the stratification is still linearly stable: layering is the result of a subcritical instability. His analysis applies to the case of vanishing diffusivity of the solute and a Prandtl number not exceeding 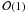 , which is the astrophysically relevant case. In this limit, layered states exist whenever the Rayleigh number exceeds the critical value for normal convection, independent of the strength of the stabilizing solute gradient. An energy argument (S92) shows that the layered state in this case can be reached with an initial perturbation of vanishing amplitude as the layer thickness decreases.
, which is the astrophysically relevant case. In this limit, layered states exist whenever the Rayleigh number exceeds the critical value for normal convection, independent of the strength of the stabilizing solute gradient. An energy argument (S92) shows that the layered state in this case can be reached with an initial perturbation of vanishing amplitude as the layer thickness decreases.
Attempts have been made to address the astrophysical problem with direct numerical simulations (Merryfield 1995; Biello 2001; Rosenblum et al. 2011). This encounters two problems: the very high thermal diffusivity in a stellar interior (very small Prandtl number) cannot be matched without some form of approximation. More importantly, the quantity of main interest, the effective mixing rate, depends on the thickness of the double-diffusive layers formed, a quantity that is not a stable outcome of the simulations.
It makes sense to divide the “semiconvection problem” into two parts: on the one hand the physics that determines the thickness of the layers, on the other, the effective mixing rate for a given layering state. This separation is especially meaningful because observations in geophysics and laboratory experiments show layer thickness to be a slowly changing function of time compared with the overturning times within the layers. In the following we concentrate on the second question; that is, the mixing rate is studied as a function layer thickness.
It turns out that the simple observation of a layer structure consisting of an overturning zone between stable zones is sufficient to derive a predictive model for the effective transport coefficients (Sect. 3). It is quantitative enough to be tested against the results of numerical simulations. The translation of the model to the astrophysical case of a compressible stratification can be done exactly in the limit where the layers are thin compared with the pressure scale height. It is given in Sect. 6, and yields an easily implemented prescription for the mixing rate.
In the present treatment, the transition in composition and temperature between neighboring layers has a finite width, as opposed to S92 (see also Zaussinger & Spruit 2010, hereafter ZS10), where it was approximated as a step. This generalization turns out to make no significant difference for practical astrophysical application, but it is essential for meaningful comparison of the theory with numerical results. Section 7 finally gives a (less quantitative) estimate of the layer thickness and its evolution in time.
The astrophysical term “semiconvection” will be used in the text interchangeably with the terms “double-diffusive” or “thermohaline” convection used in the laboratory and geophysical literature1.
2. Physics of a semiconvective layer
2.1. Notation and definitions
As in the above, we use the term “layer” for an individual double-diffusive step in the semiconvective staircase, and the term “solute” for the stabilizing component (e.g. helium in hydrogen). Such a layer consists of a zone of overturning convection between adjacent stagnant zones. In the stagnant zones overturning convection is suppressed by a stable (N2 > 0) density gradient, and transport of heat and solute takes place by diffusion.
 |
Fig. 1 Notation used, showing temperature as a function of depth through half of a semiconvective layer of thickness d, from the middle (z = 0) of the stagnant zone (of thickness ds), to the middle of the overturning zone at z = d/2. ΔT is the temperature difference across the whole layer, |
As illustrated in Fig. 1, depth through the layer is counted from the middle of a stagnant zone. The thickness of the layer as a whole is d, that of the stagnant zone ds. The temperature difference across the layer is ΔT, the solute difference ΔS. The stabilizing influence of the solute is expressed conveniently in terms of the density ratio, which is the ratio of density differences caused by temperature and solute differences ΔT and ΔS across the layer: 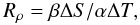 (1)where α, the thermal expansion coefficient, is the relative density decrease per unit temperature and β, called the haline contraction coefficient, is the relative density increase per unit of solute concentration. Since density increases with S and decreases with T, the density differences have the opposite sign when ΔT and ΔS both increase with depth (in the direction of gravity) as in our semiconvective case.
(1)where α, the thermal expansion coefficient, is the relative density decrease per unit temperature and β, called the haline contraction coefficient, is the relative density increase per unit of solute concentration. Since density increases with S and decreases with T, the density differences have the opposite sign when ΔT and ΔS both increase with depth (in the direction of gravity) as in our semiconvective case.
The flow in the overturning zone of the layer is driven by a temperature difference 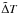 (<ΔT) and opposed by a solute difference
(<ΔT) and opposed by a solute difference  (<ΔS). Associated with these is an “internal density ratio”, related to the overall density ratio by
(<ΔS). Associated with these is an “internal density ratio”, related to the overall density ratio by 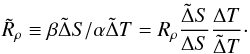 (2)Obviously, the values of
(2)Obviously, the values of 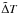 and
and  depend on where we define the boundaries between stagnant zone and overturning zone. Since the internal layer is actually convecting, the boundary has to be set at a point in the T,S profile where
depend on where we define the boundaries between stagnant zone and overturning zone. Since the internal layer is actually convecting, the boundary has to be set at a point in the T,S profile where 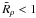 (see also Sect. 3).
(see also Sect. 3).
The overturning zone is characterized by a Rayleigh number; for convection in a layer of thickness D, with temperatures Tt and Tb at top and bottom, the Rayleigh number is 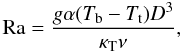 (3)where g is the acceleration of gravity, κT the thermal diffusivity, and ν the (kinematic) viscosity. In our case (Fig. 1), D has the value d − ds. The critical value for onset of convection is of the order of Rac = 1400 (for no-slip boundary conditions). If viscosity is low, (Prandtl number Pr = ν/κT ≪ 1), the heat flux at large Rayleigh number becomesindependent of viscosity (a fact that is used implicitly in the “mixing length” formalism for convection in a stellar interior). At high Ra, a more relevant quantity for characterizing the heat flux in this case is the modified Rayleigh number Ra∗:
(3)where g is the acceleration of gravity, κT the thermal diffusivity, and ν the (kinematic) viscosity. In our case (Fig. 1), D has the value d − ds. The critical value for onset of convection is of the order of Rac = 1400 (for no-slip boundary conditions). If viscosity is low, (Prandtl number Pr = ν/κT ≪ 1), the heat flux at large Rayleigh number becomesindependent of viscosity (a fact that is used implicitly in the “mixing length” formalism for convection in a stellar interior). At high Ra, a more relevant quantity for characterizing the heat flux in this case is the modified Rayleigh number Ra∗: 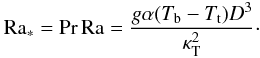 (4)Its square root can be read as the ratio of the thermal diffusion time D2/κT to the free fall time of the density contrast α(Tb − Tt) over the distance D.
(4)Its square root can be read as the ratio of the thermal diffusion time D2/κT to the free fall time of the density contrast α(Tb − Tt) over the distance D.
Let F be the (time averaged) heat flux across the layer, and Fd the flux in the absence of convection, i.e. when the temperature profile between Tb and Tt is determined by diffusion alone. The Nusselt number is then defined as 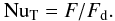 (5)Similarly, there is a Nusselt number for the solute flux FS:
(5)Similarly, there is a Nusselt number for the solute flux FS: 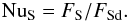 (6)In the absence of a solute, i.e. for normal (unstratified) laboratory convection, NuT is only a function of Pr and Ra (apart from boundary conditions and geometry). In the case of semiconvection, the Nusselt numbers are functions of two additional parameters characterizing the solute: the density ratio Rρ and the Lewis number Le, which is the ratio of solute diffusivity κS and thermal diffusivity κT,
(6)In the absence of a solute, i.e. for normal (unstratified) laboratory convection, NuT is only a function of Pr and Ra (apart from boundary conditions and geometry). In the case of semiconvection, the Nusselt numbers are functions of two additional parameters characterizing the solute: the density ratio Rρ and the Lewis number Le, which is the ratio of solute diffusivity κS and thermal diffusivity κT, 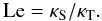 (7)
(7)
2.2. Transport coefficients: classical results
The heat flux is determined by the boundary layers at the top and bottom. As the overturning flow passes along the boundary, the temperature contrast with the boundary diffuses into the flow, and it is this temperature difference that carries the heat flux. If τ is the time during which the flow is in contact with the boundary before descending/ascending into the bulk, the depth DT over which the temperature difference penetrates is DT = (κTτ)1/2. At high Rayleigh numbers, this depth is small compared with the layer thickness d. In a simple two-dimensional view of the flow the amount of fluid carrying this difference also scales with DT. The same flow along the boundary determines how much solute contrast diffuses into the flow. The solute diffusion depth is thus DS = (κSτ)1/2, and the amount of solute flowing into the overturning zone is proportional to DS and inversely proportional to the flow speed v along the boundary.
The ratio of the convective fluxes of solute and heat is thus expected to scale as (κS/κT)1/2. On the other hand, the (diffusive) fluxes over the thickness of the overturning layer, in the absence of convection, scale as κS and κT. In terms of the Nusselt numbers, in the limit NuT, NuS ≫ 1 such that the boundary layers are thin compared with the layer thickness this implies 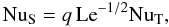 (8)where q is a numerical factor expected to be of order unity. If the heat flux is kept fixed, the effective diffusivity of the solute then scales as
(8)where q is a numerical factor expected to be of order unity. If the heat flux is kept fixed, the effective diffusivity of the solute then scales as 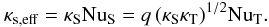 (9)These are classical scalings, as found in previous analyses of double-diffusive convection, e.g. in Turner (1980, 1985). In this form they do not address the dependence of the fluxes on the density ratio Rρ. The argument above implicitly assumes that all the density contrast in the solute boundary layer DS is carried across with the flow. In reality, only a fraction of the boundary layer can flow across, namely the fraction that is not too buoyant to be carried down by the flow, or too heavy to be carried up. Taking this into account (Spruit 1992, hereafter S92), yields a correction to (8):
(9)These are classical scalings, as found in previous analyses of double-diffusive convection, e.g. in Turner (1980, 1985). In this form they do not address the dependence of the fluxes on the density ratio Rρ. The argument above implicitly assumes that all the density contrast in the solute boundary layer DS is carried across with the flow. In reality, only a fraction of the boundary layer can flow across, namely the fraction that is not too buoyant to be carried down by the flow, or too heavy to be carried up. Taking this into account (Spruit 1992, hereafter S92), yields a correction to (8): 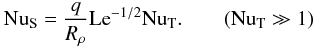 (10)This scaling applies to the overturning zone, and it would be valid for the layer as a whole only if the stagnant zone were absent. More precisely, it assumes that the thickness dS of the stagnant zone is smaller than the thickness of the boundary layers DT,DS. This is not always the case (cf. Sect. 5 below). In the following, the presence of the stagnant zone is explicitly taken into account by consistently taking the distinction between between Nusselt numbers for the overturning zone and those for the layer as a whole into account. This results in a generalization of (10).
(10)This scaling applies to the overturning zone, and it would be valid for the layer as a whole only if the stagnant zone were absent. More precisely, it assumes that the thickness dS of the stagnant zone is smaller than the thickness of the boundary layers DT,DS. This is not always the case (cf. Sect. 5 below). In the following, the presence of the stagnant zone is explicitly taken into account by consistently taking the distinction between between Nusselt numbers for the overturning zone and those for the layer as a whole into account. This results in a generalization of (10).
2.2.1. “Erosion”
To determine the numerical factor q in (10) more quantitatively than order unity, the hydrodynamic interaction of the flow with the stagnant zone has to be considered in more detail. This is somewhat beyond the scope of the model to be developed here, but we can identify a process involved, and use this to show that q is probably somewhat larger than unity. I will call q the “erosion factor”.
The unsteady flow in the overturning zone induces perturbations in the stagnant zone. Since it is stably stratified, these take the form of internal gravity waves. They can contain internal structure on length scales (perpendicular to the interface) that are less than the thickness of the stagnant zone. Diffusion of solute on these length scales increases the amount that has low enough buoyancy to be carried with the overturning flow, so we may expect q > 1. In the absence of a more detailed theory, its value can in principle be used as a fitting parameter, as long as it is not taken larger than order unity. In the following, however, I will ignore this option, and simply set 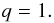 (11)For astrophysical applications, the effective solute transport will turn out to be so low that tuning the erosion factor by order unity would have little effect anyway. At low Le, this erosion process takes place well inside the thermal boundary layer. It consequently affects only the transport of the solute; its effect on the transport of heat can be neglected.
(11)For astrophysical applications, the effective solute transport will turn out to be so low that tuning the erosion factor by order unity would have little effect anyway. At low Le, this erosion process takes place well inside the thermal boundary layer. It consequently affects only the transport of the solute; its effect on the transport of heat can be neglected.
3. Model
The layer of thickness d now consists (Fig. 1) of a stagnant zone of thickness dS, and an overturning zone occupying the remainder of d. An incompressible (Boussinesq) fluid is assumed, to be generalized to the compressible astrophysical case in Sect. 6.
In the stagnant zone, we assume that the transport of heat and solute is only by diffusion (i.e. ignoring the possible “erosion” effect discussed above). In the overturning zone of the layer, the flow is approximated as convection like it would take place in the absence of a solute. The presence of the solute affects the flow somewhat, but the amount of solute carried, and hence its influence on the flow, vanishes in the limit of low solute diffusivity (S92, Schmitt 1994). Apart from the boundary conditions it sets, the stagnant zone has little effect on the flow inside the overturning zone. In the limit Le ≪ 1 considered here, the effect of the solute on the flow of heat in the overturning zone can thus be neglected.
To describe transport of heat in the overturning zone, we use a fit from laboratory measurements for the Nusselt number as a function of the temperature difference. Since the thickness and temperature difference are different from those of the layer as a whole, the Rayleigh and Nusselt numbers of the overturning zone are distinguished here with a tilde (~). With the notation 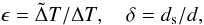 (12)they are related to Ra and NuT by (cf. Eq. (4) and the geometry sketched in Fig. 1):
(12)they are related to Ra and NuT by (cf. Eq. (4) and the geometry sketched in Fig. 1):  In the measurements of Niemela et al. (2000), at Ra up to 1017, the Nusselt number is well fit by a power law of slope 0.309 and amplitude 0.124. The Prandtl number in these experiments is of order unity, so Ra∗ and Ra are approximately the same. Combining the above, I approximate the heat flux in the overturning zone as given by
In the measurements of Niemela et al. (2000), at Ra up to 1017, the Nusselt number is well fit by a power law of slope 0.309 and amplitude 0.124. The Prandtl number in these experiments is of order unity, so Ra∗ and Ra are approximately the same. Combining the above, I approximate the heat flux in the overturning zone as given by 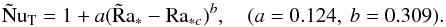 (15)Since, as argued in 2.1 the dependence on Prandtl number is expected to be weak below Pr = 1, (15) will be assumed approximately valid for all Pr ≤ 1. (This can be checked with numerical simulations, see Zaussinger & Spruit 2013, hereafter ZS13.) The constant 1 and the critical Rayleigh number have been added to better approximate the behavior at low Ra∗.
(15)Since, as argued in 2.1 the dependence on Prandtl number is expected to be weak below Pr = 1, (15) will be assumed approximately valid for all Pr ≤ 1. (This can be checked with numerical simulations, see Zaussinger & Spruit 2013, hereafter ZS13.) The constant 1 and the critical Rayleigh number have been added to better approximate the behavior at low Ra∗.
The buoyancy of the solute is opposite to that of the driving temperature difference, and the flow will only be driven by density differences of the unstable sign. This implies that the solute concentration contrast in the overturning flow, 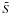 say, is limited by the temperature contrast
say, is limited by the temperature contrast 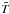 through
through 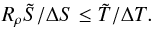 (16)At the boundary between the overturning and the diffusive zones, these contrasts are
(16)At the boundary between the overturning and the diffusive zones, these contrasts are 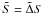 ,
, 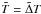 . Define the location of this boundary as the point where the equal sign holds in (16), that is, the point where the buoyancy of the solute is just low enough to be carried with the thermally driven flow in the overturning zone (cf. discussion above). This yields the relation
. Define the location of this boundary as the point where the equal sign holds in (16), that is, the point where the buoyancy of the solute is just low enough to be carried with the thermally driven flow in the overturning zone (cf. discussion above). This yields the relation 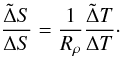 (17)In the overturning zone, the original scaling (8) applies, i.e.
(17)In the overturning zone, the original scaling (8) applies, i.e. 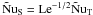 (assuming q = 1), since
(assuming q = 1), since  is the density difference that can just be carried with the flow. At low Ra,
is the density difference that can just be carried with the flow. At low Ra, 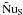 should approach unity at the same time as
should approach unity at the same time as 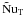 . To accomplish this I adopt a slight modification:
. To accomplish this I adopt a slight modification: 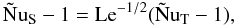 (18)which is now assumed to hold for all
(18)which is now assumed to hold for all 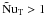 .
.
This completes the definition of the model. It defines the fluxes of heat and solute uniquely as functions of the external parameters.
4. Effective diffusivities
In a stationary state, the fluxes of heat and solute are constant with depth through the layer. The fluxes by diffusion in the stagnant zone are equal to the fluxes in the overturning zone. Expressing this in terms of the Nusselt numbers, we first need to write 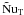 and
and 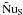 in terms of the Nusselt numbers for the layer as a whole. For temperature this is given by (14):
in terms of the Nusselt numbers for the layer as a whole. For temperature this is given by (14): 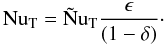 (19)The equivalent relation for the solute is
(19)The equivalent relation for the solute is 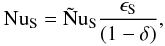 (20)where (using 17):
(20)where (using 17): 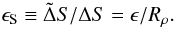 (21)The fluxes in the stagnant zone are given by
(21)The fluxes in the stagnant zone are given by  (22)(since carried by diffusion alone). With (18), Eqs. (19)−(22) yield two equations for the unknown δ and ϵ:
(22)(since carried by diffusion alone). With (18), Eqs. (19)−(22) yield two equations for the unknown δ and ϵ: 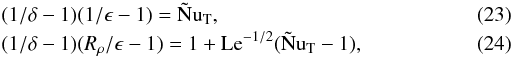 with
with 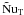 given by (15). Eliminating
given by (15). Eliminating 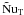 between these two yields
between these two yields 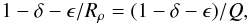 (25)where
(25)where 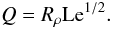 (26)Solving this for ϵ:
(26)Solving this for ϵ: 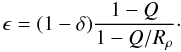 (27)Since ϵ must be a positive number, and Rρ is larger than 1 (otherwise we would not be “below Ledoux”), it follows that in a stationary state as envisaged, Q must be less than 1, or Rρ < Le−1/2. This is a necessary condition (independent of the Rayleigh number), but not sufficient. The actual, somewhat lower, value of the critical density ratio has to be determined from (19), (20) by solving for δ as well as ϵ. To see how this solution comes about, consider the left-hand and right-hand sides of (23) separately. They represent the heat flux in the stagnant and the overturning zones, respectively, and in a stationary state they are equal. Figure 2 shows the two as functions of δ, with ϵ taken from (27) and
(27)Since ϵ must be a positive number, and Rρ is larger than 1 (otherwise we would not be “below Ledoux”), it follows that in a stationary state as envisaged, Q must be less than 1, or Rρ < Le−1/2. This is a necessary condition (independent of the Rayleigh number), but not sufficient. The actual, somewhat lower, value of the critical density ratio has to be determined from (19), (20) by solving for δ as well as ϵ. To see how this solution comes about, consider the left-hand and right-hand sides of (23) separately. They represent the heat flux in the stagnant and the overturning zones, respectively, and in a stationary state they are equal. Figure 2 shows the two as functions of δ, with ϵ taken from (27) and 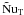 from (15).
from (15).
 |
Fig. 2 Determination of the thickness δ of the stagnant zone, (example for Ra ∗ = 107, Le = 0.01, Pr = 0.1). The steep curve shows the heat flux in the stagnant zone as a function of the assumed value of δ, the shallow curves the corresponding flux in the overturning zone. Intersection points are possible values of δ for stationary heat flow. Top: density ratio Rρ = 4. For the higher density ratio of 5.5 (bottom), there is no value of the thickness for which the two match (see text). |
The two intersection points of the curves are potential solutions for a steady state. To see which of the two is the relevant one, consider the slopes of the curves. At the equilibrium point with the lower value of δ the flux in the stagnant zone decreases more rapidly with δ than the flux in the overturning zone. A small decrease of δ away from the equilibrium would increase the flux in the stagnant zone relative to that in the overturning zone. This would result in a temperature deficit at the boundary between the two, causing the temperature to decrease there. This would reduce the heat flux in the stagnant zone again, the opposite of the assumed perturbation. This equilibrium point is thus the stable one; the intersect at the larger δ is an unstable point.
The necessary condition for existence of the layered state, Rρ < Le−1/2 also figures prominently in Proctor (1981). In his analysis it shows up as a necessary condition for its validity.
4.1. Maximum density ratio
The maximum density ratio can be determined as a function of Ra∗, it is the value for which the two curves in Fig. 2 just touch. The result is shown in Fig. 3. At large Ra∗, Rρ max (slowly) approaches the value Le−1/2. The behavior of NuT and δ near Rρ max is shown in Fig. 4 for an illustrative case.
At the critical density ratio, the value of δ is about 0.2 (cf. Fig. 2), while the Nusselt number reaches a minimum value of a few. At this density ratio, the model predicts a jump from an overturning state (NuT > 1) to a purely diffusive state NuT = 1. An example is shown in Fig. 4. The presence of this jump suggests that the behavior of the system near the maximum density ratio needs a closer look than is possible with the present model. This question is explored with numerical simulations in ZS13.
The maximum on Rρ can also be read as a minimum on the Rayleigh number. For an observed density ratio of 4 at Le = 0.01 for example, one should not expect to see double-diffusive layering with a layer thickness less than corresponds to a Ra∗ of 106 (from Fig. 3). In terms of the reference length d0 defined below (Eq. (42)), the layers must have a thickness d/d0 > 45, for this combination of Rρ and Le.
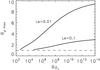 |
Fig. 3 Maximum value of the density ratio, as a function of the modified Rayleigh number of the layer, for Le = 0.01 and Le = 0.1. |
4.2. Solute flux
The net solute Nusselt number can be expressed in terms of NuT. Using (18)–(22) and (26), (27), this yields the simple expression 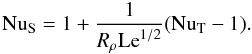 (28)The stagnant zone of finite thickness included here thus leads to the same relation between NuS and NuT as the simpler model in S92 (cf. Eq. (10) above). There is a difference, however, in the relation between NuT and Ra∗, and in the presence of a maximum density ratio (cf. Figs. 3, 4).
(28)The stagnant zone of finite thickness included here thus leads to the same relation between NuS and NuT as the simpler model in S92 (cf. Eq. (10) above). There is a difference, however, in the relation between NuT and Ra∗, and in the presence of a maximum density ratio (cf. Figs. 3, 4).
 |
Fig. 4 Dependence of Nusselt number and thickness of the stagnant zone on density ratio Rρ in a range around the critical value, for Le = 0.01, Ra ∗ = 1012 (Rρ max = 8.82). |
4.3. Asymptotic behavior
The Nusselt number is, with (19), (27), 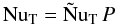 (29)where
(29)where 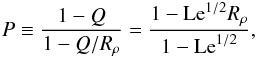 (30)and
(30)and 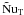 is given in terms of
is given in terms of 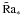 by (15). For Ra ∗ ≫ 1, and with Rρ not close to Rρ max, the stagnant zone is thin, δ ≪ 1.
by (15). For Ra ∗ ≫ 1, and with Rρ not close to Rρ max, the stagnant zone is thin, δ ≪ 1. 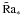 as a function of Rρ and Le is then, with (14), (27):
as a function of Rρ and Le is then, with (14), (27): 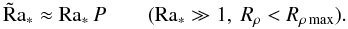 (31)The solute Nusselt number follows from (28),
(31)The solute Nusselt number follows from (28), 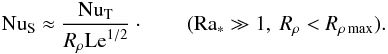 (32)It is instructive to compare δ to the thickness of the boundary layers DT, DS of the overturning zone. These can be written in terms of the Nusselt numbers NuT and NuS since at the boundaries with the stagnant zone the fluxes are carried by diffusion. For the thermal boundary layer, for example, this implies
(32)It is instructive to compare δ to the thickness of the boundary layers DT, DS of the overturning zone. These can be written in terms of the Nusselt numbers NuT and NuS since at the boundaries with the stagnant zone the fluxes are carried by diffusion. For the thermal boundary layer, for example, this implies 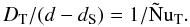 (33)Using (23), (27):
(33)Using (23), (27): 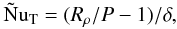 (34)hence in the limit δ ≪ 1:
(34)hence in the limit δ ≪ 1: 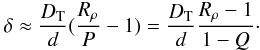 (35)Unless Q is close to unity, the width of the stagnant zone is thus of the same order of magnitude as the boundary layers of the overturning zone, and the distinction between the two becomes somewhat academic. At a high density ratio, or under the fixed heat flux conditions discussed in the next section, however, the distinction becomes more significant.
(35)Unless Q is close to unity, the width of the stagnant zone is thus of the same order of magnitude as the boundary layers of the overturning zone, and the distinction between the two becomes somewhat academic. At a high density ratio, or under the fixed heat flux conditions discussed in the next section, however, the distinction becomes more significant.
5. Fixed heat flux conditions
In laboratory situations and theoretical analyses, it is usual to consider the temperature difference or temperature gradient as given and the heat flux or Nusselt number as the object to be determined. In some natural systems, however, the conditions under which double-diffusive convection occurs are closer to ones where the heat flux is the given quantity. In the East African volcanic lakes, for example, the heat flux imposed by the influx at the bottom of the lake is probably more of a given than the temperature at the bottom of the lake. The same is the case in semiconvective zones of stars.
The temperature difference across the layers adjusts to an imposed heat flux. Since both the density ratio and the Rayleigh number depend on ΔT, neither of these can be used as control parameter any longer. This requires a change of perspective on the problem.
The stratifications of both temperature and solute change with time, under the effective transport properties of the semiconvective process. In the limit of low solute diffusivity, the time scale for changes in the solute profile is long compared with the time scale on which the temperature profile adjusts. In this thermally quasi-steady state, the solute profile can be taken as fixed. Assume therefore that the mean solute gradient dS/dz is given. As new control parameters, use the heat heat flux F and layer thickness d.
To make the imposed heat flux practical as control parameter, measure it with respect to a reference flux F0 that can be expressed in terms of the solute gradient. Take for this the diffusive heat flux that would be present in the linear temperature profile T0(z) that is just marginally stable against adiabatic overturning (“Ledoux”). If K is the thermal conductivity, the heat flux of this stratification is 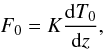 (36)and its density ratio is
(36)and its density ratio is 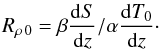 (37)Since we have assumed that the stratification is marginally stable, Rρ 0 = 1. The reference heat flux is thus
(37)Since we have assumed that the stratification is marginally stable, Rρ 0 = 1. The reference heat flux is thus 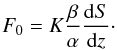 (38)The actual layered state has a Nusselt number NuT and a density ratio Rρ > 1; by definition of the Nusselt number, its heat flux is
(38)The actual layered state has a Nusselt number NuT and a density ratio Rρ > 1; by definition of the Nusselt number, its heat flux is 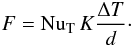 (39)With ΔS = d dS/dz,
(39)With ΔS = d dS/dz, 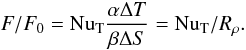 (40)To replace the Rayleigh number as control parameter, note that it can be written in terms of solute gradient and density ratio as (using 1)
(40)To replace the Rayleigh number as control parameter, note that it can be written in terms of solute gradient and density ratio as (using 1) 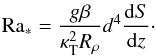 (41)The quantity
(41)The quantity 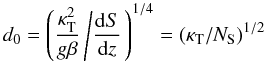 (42)is a characteristic length scale of the problem: the distance over which temperature diffuses on the buoyancy time scale of the stable solute gradient,
(42)is a characteristic length scale of the problem: the distance over which temperature diffuses on the buoyancy time scale of the stable solute gradient, 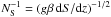 . The Rayleigh number can then be written as
. The Rayleigh number can then be written as 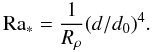 (43)The Nusselt number in Eq. (40) is a function of Rρ and Ra∗, which can be evaluated from Eqs. (15), (22), (23), (23) in Sect. 4 above. Together, Eqs. (40) and (43) thus determine Ra∗ and Rρ, and other quantities of interest, as functions of the new control parameters d/d0 and F/F0. An example of the dependence on d/d0 of Ra∗, Rρ, the Nu’s, and δ is shown in Fig. 5 for F/F0 = 1.5.
(43)The Nusselt number in Eq. (40) is a function of Rρ and Ra∗, which can be evaluated from Eqs. (15), (22), (23), (23) in Sect. 4 above. Together, Eqs. (40) and (43) thus determine Ra∗ and Rρ, and other quantities of interest, as functions of the new control parameters d/d0 and F/F0. An example of the dependence on d/d0 of Ra∗, Rρ, the Nu’s, and δ is shown in Fig. 5 for F/F0 = 1.5.
 |
Fig. 5 Dependences on layer thickness d, for fixed heat flux conditions (F/F0 = 1.5). In reading order: Rayleigh number, density ratio, Nusselt numbers (dashed for solute), and thickness of the stagnant zone. |
5.1. Asymptotic dependences for fixed heat flux
The limiting case d/d0 ≫ 1 (corresponding to Ra ∗ ≫ 1) has a pleasingly simple form. As expected from the discussion in Sect. 4 (cf. Fig. 3), the density ratio approaches its maximum value Le−1/2 in this limit. With (40) and (28) the Nusselt numbers approach the value 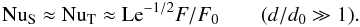 (44)For NuS, this is in fact also a good approximation at lower values of d/d0, as Fig. 5 (lower left) shows. The corresponding effective solute diffusivity becomes
(44)For NuS, this is in fact also a good approximation at lower values of d/d0, as Fig. 5 (lower left) shows. The corresponding effective solute diffusivity becomes 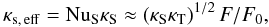 (45)in agreement with the classical “geometric mean of diffusivities” scaling. The thickness of the stagnant zone is related to NuS by Eq. (22). In the present limit, ϵS ≪ 1, hence
(45)in agreement with the classical “geometric mean of diffusivities” scaling. The thickness of the stagnant zone is related to NuS by Eq. (22). In the present limit, ϵS ≪ 1, hence 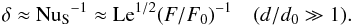 (46)The relative thickness of the stagnant zone is thus small for low Lewis numbers or at high heat flux. In the opposite case of modest Le and conditions closer to marginal, it can be a significant fraction of the layer thickness, however. This may be the explanation for the relatively large thickness of the stagnant zones observed in lake Kivu (Schmid et al. 2010). The heat flux measured there corresponds to Nusselt numbers of order 2. A stagnant zone thickness δ of order 30% is observed, larger than in other natural cases like the double-diffusive steps under the arctic ice sheet (e.g. Timmermans et al. 2008 and references therein). Though the present analysis does not apply directly to this case because the assumption Pr < 1 does not hold (Pr ≈ 7 for water), the thickness of the stagnant zones in lake Kivu may be an indication that it is actually close to the marginal state to be expected at imposed low heat flux conditions.
(46)The relative thickness of the stagnant zone is thus small for low Lewis numbers or at high heat flux. In the opposite case of modest Le and conditions closer to marginal, it can be a significant fraction of the layer thickness, however. This may be the explanation for the relatively large thickness of the stagnant zones observed in lake Kivu (Schmid et al. 2010). The heat flux measured there corresponds to Nusselt numbers of order 2. A stagnant zone thickness δ of order 30% is observed, larger than in other natural cases like the double-diffusive steps under the arctic ice sheet (e.g. Timmermans et al. 2008 and references therein). Though the present analysis does not apply directly to this case because the assumption Pr < 1 does not hold (Pr ≈ 7 for water), the thickness of the stagnant zones in lake Kivu may be an indication that it is actually close to the marginal state to be expected at imposed low heat flux conditions.
5.1.1. Thickness of the stagnant zone
As Fig. 5 shows, the density ratio approaches its maximum in the limit d/d0 ≫ 1 (cf. Sect. 4.1): 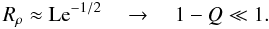 (47)The actual value of 1 − Q as a function of the parameters d/d0 and F/F0 is a somewhat complicated expression involving the coefficients a,b in (15) (it is not needed in the following).
(47)The actual value of 1 − Q as a function of the parameters d/d0 and F/F0 is a somewhat complicated expression involving the coefficients a,b in (15) (it is not needed in the following).
Comparing δ with the thermal boundary layer thickness DT of the overturning zone then yields, from (35): 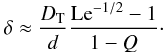 (48)In this asymptotic case with fixed heat flux, the stagnant zone is thus much wider than the boundary layers of the overturning zone (but still thin compared with the layer thickness d). Its presence manifests itself in the approximate equality of NuT and NuS (Eq. (44)) as opposed to the original estimate (8).
(48)In this asymptotic case with fixed heat flux, the stagnant zone is thus much wider than the boundary layers of the overturning zone (but still thin compared with the layer thickness d). Its presence manifests itself in the approximate equality of NuT and NuS (Eq. (44)) as opposed to the original estimate (8).
6. Astrophysical conditions
For the compressible gas in a stellar interior, an incompressible approximation (Boussinesq) can still be used for flows on length scales small compared with the pressure scale height and time scales short compared with the sound travel time over this length, provided two factors are taken into account (e.g. Massaguer & Zahn 1980). First, the adiabatic lapse rate (dT/dz)a has to be subtracted from the temperature difference driving the flows. The modified Rayleigh number for a layer of thickness d is now 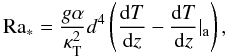 (49)where α = 1/T for the ideal gas with constant ratio of specific heats assumed here. In terms of the logarithmic gradient ∇ = dlnT/dlnp:
(49)where α = 1/T for the ideal gas with constant ratio of specific heats assumed here. In terms of the logarithmic gradient ∇ = dlnT/dlnp: 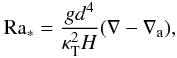 (50)where H is the scale height of the gas pressure p,
(50)where H is the scale height of the gas pressure p, 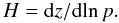 (51)This length scale is not present in the Boussinesq case. An equivalent of the quantity d0 used in Sect. 5 still plays a role as well, but in the astrophysical context H is a more conventional choice as reference length, and Ra ∗ can then be written as
(51)This length scale is not present in the Boussinesq case. An equivalent of the quantity d0 used in Sect. 5 still plays a role as well, but in the astrophysical context H is a more conventional choice as reference length, and Ra ∗ can then be written as 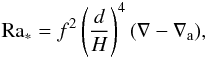 (52)where the dimensionless number f,
(52)where the dimensionless number f, 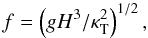 (53)typically a large number, is the ratio of the thermal diffusion and free-fall time scales over a pressure scale height. The dimensionless layer thickness d/H will be the control parameter replacing d/d0 above.
(53)typically a large number, is the ratio of the thermal diffusion and free-fall time scales over a pressure scale height. The dimensionless layer thickness d/H will be the control parameter replacing d/d0 above.
A second difference concerns the radiative heat flux, since it is driven by the temperature gradient itself rather than the potential temperature2. This affects the definition of Nusselt number, as well as the choice of control parameter specifying the heat flux. Define a thermal conduction constant k (a function of the opacity and the thermodynamic state of the gas), in terms of the the radiative heat flux Fr: 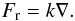 (54)Following standard notation, the total heat flux F is represented by the radiative gradient ∇r:
(54)Following standard notation, the total heat flux F is represented by the radiative gradient ∇r: 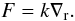 (55)∇r is the astrophysical control parameter specifying heat flux. The ratio of density changes due to composition and temperature changes upon adiabatic displacement in the stratification, i.e. the density ratio, is
(55)∇r is the astrophysical control parameter specifying heat flux. The ratio of density changes due to composition and temperature changes upon adiabatic displacement in the stratification, i.e. the density ratio, is 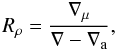 (56)where
(56)where 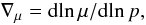 (57)and the μ the mean atomic weight per particle. Define the Nusselt number NuT through
(57)and the μ the mean atomic weight per particle. Define the Nusselt number NuT through 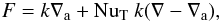 (58)so that it measures the part of the heat flux that is due to (only) the superadiabatic part of the temperature gradient, instead of the total heat flux. This has to be clearly distinguished from the ratio ∇r/∇ of heat flux to radiative heat flux in the stratification, which one might consider the more logical definition of a Nusselt number. The latter includes, however, a flux that is irrelevant for the convective flow (the radiative heat flux due to the adiabatic part of the stratification), since it would contribute even if there is no flow at all3. From (55), (56), (58) we obtain a relation between Nusselt number and density ratio for our astrophysical, imposed heat flux conditions:
(58)so that it measures the part of the heat flux that is due to (only) the superadiabatic part of the temperature gradient, instead of the total heat flux. This has to be clearly distinguished from the ratio ∇r/∇ of heat flux to radiative heat flux in the stratification, which one might consider the more logical definition of a Nusselt number. The latter includes, however, a flux that is irrelevant for the convective flow (the radiative heat flux due to the adiabatic part of the stratification), since it would contribute even if there is no flow at all3. From (55), (56), (58) we obtain a relation between Nusselt number and density ratio for our astrophysical, imposed heat flux conditions: 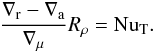 (59)To complete the model, a prescription for the Nusselt number as a function of the control parameters is needed. For this, we assume that the layer thickness d is small enough that an incompressible approximation is valid, so the results of Sect. 4 can be used. Equations (18)–(26) then determine NuT as a function of Ra ∗ and Rρ. Together with Rρ from (56) and Ra ∗ from (50), this forms a set of equations for the superadiabaticity ∇−∇a as a function of the control parameters d/H and ∇r.
(59)To complete the model, a prescription for the Nusselt number as a function of the control parameters is needed. For this, we assume that the layer thickness d is small enough that an incompressible approximation is valid, so the results of Sect. 4 can be used. Equations (18)–(26) then determine NuT as a function of Ra ∗ and Rρ. Together with Rρ from (56) and Ra ∗ from (50), this forms a set of equations for the superadiabaticity ∇−∇a as a function of the control parameters d/H and ∇r.
6.1. Asymptotic results
This is a somewhat implicit algebraic problem, but the limiting case equivalent to d/d0 ≫ 1 in Sect. 5 again has a simple form. This limit corresponds to 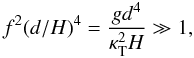 (60)or
(60)or 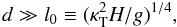 (61)i.e. d large compared to the length l0 on which the thermal diffusion time scale equals the free fall time over a scale height. As before, Rρ tends to its maximum, Rρ ≈ Le−1/2 in this limit, so that
(61)i.e. d large compared to the length l0 on which the thermal diffusion time scale equals the free fall time over a scale height. As before, Rρ tends to its maximum, Rρ ≈ Le−1/2 in this limit, so that 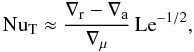 (62)while the superadiabaticity follows from (56):
(62)while the superadiabaticity follows from (56): 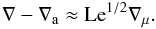 (63)The solute Nusselt number follows as in Sect. 5,
(63)The solute Nusselt number follows as in Sect. 5, 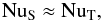 (64)so the effective solute diffusivity is
(64)so the effective solute diffusivity is 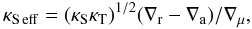 (65)the same as in the simpler model of S92 and ZS10 (apart from a factor involving radiation pressure). It is independent of the layering thickness d, within the range of validity of the approximations,
(65)the same as in the simpler model of S92 and ZS10 (apart from a factor involving radiation pressure). It is independent of the layering thickness d, within the range of validity of the approximations, 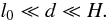 (66)The relative thickness of the stagnant zones is
(66)The relative thickness of the stagnant zones is 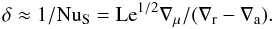 (67)For Le ≪ ∇r − ∇a the stagnant zone is thus thin compared with the layer thickness (but still significantly thicker than the boundary layers of the overturning zone, cf. Sect. 5.1.1).
(67)For Le ≪ ∇r − ∇a the stagnant zone is thus thin compared with the layer thickness (but still significantly thicker than the boundary layers of the overturning zone, cf. Sect. 5.1.1).
7. Evolution of the layer thickness
The main uncertainty of any model for semiconvection is the thickness d of the layers in the double-diffusive stack. In a stellar interior, the layer thickness has little influence on the quantities of interest (Eqs. (63), (65)), but it can become important for the structure of the star when layer thickness becomes macroscopic, i.e. comparable with the pressure scale height.
In geophysical and laboratory cases, it is observed that d evolves secularly, on a long time scale compared with the thermal diffusion time. Layer thickness is therefore a quantity that cannot be discussed independently of the history of the system. The process has not been studied very extensively (but see Wirtz & Reddy 1979; McDougall 1981; Young & Rosner 2000; Ross & Lavery 2009, and the coffee table experiment in ZS13). The layer thickness increases by a process of merging of neighboring layers. Two mechanisms are observed: vanishing contrast and drift of interface position. This is illustrated schematically in Fig. 6.
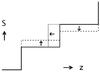 |
Fig. 6 Merging of two neighboring layers in a double-diffusive staircase. The solute concentration can change by exchange between the two until the contrast disappears (dashed), or one can grow in thickness at the expense of the other (dotted). |
Which of these two dominates, why, and at what rate the merging takes place appears to be not well understood. From the model presented here, however, an estimate for the merging rate which is independent of this uncertainty can be derived, as well as the resulting layer thickness as a function of time.
Both merging mechanisms involve the redistribution of solute between neighboring layers. For example, if an interface between two layers transmits solute somewhat faster than average, the contrast between them decreases. The time scale τ on which such changes take place is limited by the effective solute diffusivity, hence is of the order of 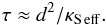 (68)The rate of merging is then
(68)The rate of merging is then 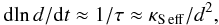 (69)so that
(69)so that 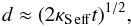 (70)if κS eff is constant in time. The layer thickness is thus predicted to increase as the square root of time. This agrees qualitatively with the dependence inferred empirically in some laboratory experiments. In most of these, however, the layering is induced by lateral heating of the solute gradient rather than vertical heating, so is not directly comparable with the astrophysical case. Wirtz & Reddy (1979) for example find an initial square-root-like dependence, which saturates when the thickness reaches the separation between the lateral boundaries.
(70)if κS eff is constant in time. The layer thickness is thus predicted to increase as the square root of time. This agrees qualitatively with the dependence inferred empirically in some laboratory experiments. In most of these, however, the layering is induced by lateral heating of the solute gradient rather than vertical heating, so is not directly comparable with the astrophysical case. Wirtz & Reddy (1979) for example find an initial square-root-like dependence, which saturates when the thickness reaches the separation between the lateral boundaries.
In terms of a merging time scale tm, (70) becomes 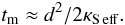 (71)For a quantitative check, compare this to the measurements from Lake Kivu, where the observed layer thicknesses are 0.3−0.5 m, the relative interface thickness δ of the order of 0.4 (Schmid et al. 2010). With the diffusivity of CO2 in water, κS = 2 10-9 m2/s, the effective solute diffusivity is
(71)For a quantitative check, compare this to the measurements from Lake Kivu, where the observed layer thicknesses are 0.3−0.5 m, the relative interface thickness δ of the order of 0.4 (Schmid et al. 2010). With the diffusivity of CO2 in water, κS = 2 10-9 m2/s, the effective solute diffusivity is 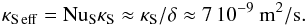 (72)For a layer of thickness 0.4 m, this predicts a merging time of the order of 8 months. This agrees with the observed time scale for changes in the layering, of the order of several months. This comparison has to be taken with a grain of salt, of course, since the present analysis is not strictly valid for the Prandtl number of water.
(72)For a layer of thickness 0.4 m, this predicts a merging time of the order of 8 months. This agrees with the observed time scale for changes in the layering, of the order of several months. This comparison has to be taken with a grain of salt, of course, since the present analysis is not strictly valid for the Prandtl number of water.
8. Summary
The theory presented here expands on the previous analyses in S92 and ZS10. It improves on these by including the effect of a stagnant zone of finite thickness, that is, the region over which heat and solute are transported by diffusion is not limited to just the boundary layers of the overturning interior of a double-diffusive step, but can in principle be an arbitrary fraction of the layer thickness. The need for this extension arose from observations of geophysical examples of thermohaline layering and results from numerical experiments.
A simple 2-zone model consisting of a stagnant and an overturning zone and using an experimental fitting formula for convective heat transport in the overturning zone produces a clear physical picture of the dependence of the effective transport properties of double-diffusive layered convection (Sect. 4). The results predict the existence of a maximum to the density ratio for which such a layered state can exist. It is Rρ max ≈ Le−1/2 = (κT/κS)1/2 and approaches this value from below with increasing Rayleigh number (or layer thickness).
Of special interest is the astrophysical case where the heat flux is given rather than a temperature difference. In this case the dependence of effective solute diffusivity on solute stratification and heat flux has the simple form (65). This is the same as before in ZS10 and S92 (except for the effect of radiation pressure on the equation of state not included here). Owing to the presence of the stagnant zone the value of the superadiabaticity (63) differs from the one in S92, ZS10. For practical conditions in a stellar interior, however, ∇−∇a is so small that its exact
functional form makes little difference for the temperature stratification. The thickness of the stagnant zone is small compared with the layer thickness, as a consequence of the low value of the Lewis number.
The main conceptual difference with respect to ZS10 and S92 is the existence of a maximum to the density ratio. In the astrophysical case of imposed heat flux it only plays a rather implicit role. The differences are more significant under more general conditions than the astrophysical limiting case. In numerical simulations, in particular, which are necessarily much closer to marginal conditions for double-diffusive layering, the stagnant zone and the maximum density ratio have a substantial influence on the results. A comparison with simulations is presented in the companion paper ZS13.
Semiconvection is only one of the potential mixing processes in stars. Rotation induced mixing and magnetic processes are likely to be relevant as well, and could actually be more effective.
Existing nomenclature is somewhat ambiguous. The opposite case of a destabilizing composition gradient in a stable thermal gradient is called “saltfingering”, but in geophysics also “thermohaline convection”, where our semiconvective case is often called “diffusive convection” (e.g. Schmitt 1994). “Double diffusive” is usually meant to cover both cases.
The significance of this distinction is not apparent in some of the numerical work on semiconvection, e.g. Biello (2001).
Acknowledgments
The author thanks F. Zaussinger for extensive discussions and suggestions, and the referee for many corrections and detailed comments. These have led to significant improvements.
References
- Biello, J. A. 2001, Ph.D. Thesis, Univ. of Chicago [Google Scholar]
- Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
- Langer, N., & Maeder, A. 1995, A&A, 295, 685 [NASA ADS] [Google Scholar]
- Langer, N., El Eid, M. F., & Baraffe, I. 1989, A&A, 224, L17 [NASA ADS] [Google Scholar]
- Massaguer, J. M., & Zahn, J.-P. 1980, A&A, 87, 315 [NASA ADS] [Google Scholar]
- McDougall, T. 1981, Prog. Oceanogr., 10, 91 [Google Scholar]
- Merryfield, W. J. 1995, ApJ, 444, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Niemela, J., Skrbek, L., Sreenivasan, K. R., & Donnelly, R. 2000, Nature, 404, 837 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Padman, L., & Dillon, T. M. 1987, J. Geophys. Res., 92, 10799 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, M. R. E. 1981, J. Fluid Mech., 105, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenblum, E., Garaud, P., Traxler, A., & Stellmach, S. 2011, ApJ, 731, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, T., & Lavery, A. 2009, Exp. Fluids, 46, 355 [Google Scholar]
- Schmid, M., Busbridge, M., & Wüst, A. 2010, Limnol. Oceanogr., 55, 225 [CrossRef] [Google Scholar]
- Schmitt, R. W. 1994, Ann. Rev. Fluid Mech., 26, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1992, A&A, 253, 131 (S92) [NASA ADS] [Google Scholar]
- Stothers, R. B., & Chin, C.-W. 1994, ApJ, 431, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1953, Doctoral Dissertation, Cambridge University [Google Scholar]
- Timmermans, M.-L., Toole, J., Krishfield, R., & Winsor, P. 2008, J. Geophys. Res., 113, C00A02 [CrossRef] [Google Scholar]
- Turner, J. S. 1980, Buoyancy Effects in Fluids (Cambridge University Press) [Google Scholar]
- Turner, J. S. 1985, Ann. Rev. Fluid Mech., 17, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. S., & Stommel, H. 1964, Proc. Nat. Acad. Sci., 52, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Young, Y., & Rosner, R. 2000, Phys. Rev. E, 61, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A. 1989, A&A, 209, 135 [NASA ADS] [Google Scholar]
- Wirtz, R. A., & Reddy, C. S. 1979, J. Fluid Mech., 91, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Zaussinger, F., & Spruit, H. C. 2010 [arXiv:1012.5851] (ZS10) [Google Scholar]
- Zaussinger, F., & Spruit, H. C. 2013, A&A, accepted (ZS13) [Google Scholar]
All Figures
 |
Fig. 1 Notation used, showing temperature as a function of depth through half of a semiconvective layer of thickness d, from the middle (z = 0) of the stagnant zone (of thickness ds), to the middle of the overturning zone at z = d/2. ΔT is the temperature difference across the whole layer, |
| In the text | |
 |
Fig. 2 Determination of the thickness δ of the stagnant zone, (example for Ra ∗ = 107, Le = 0.01, Pr = 0.1). The steep curve shows the heat flux in the stagnant zone as a function of the assumed value of δ, the shallow curves the corresponding flux in the overturning zone. Intersection points are possible values of δ for stationary heat flow. Top: density ratio Rρ = 4. For the higher density ratio of 5.5 (bottom), there is no value of the thickness for which the two match (see text). |
| In the text | |
 |
Fig. 3 Maximum value of the density ratio, as a function of the modified Rayleigh number of the layer, for Le = 0.01 and Le = 0.1. |
| In the text | |
 |
Fig. 4 Dependence of Nusselt number and thickness of the stagnant zone on density ratio Rρ in a range around the critical value, for Le = 0.01, Ra ∗ = 1012 (Rρ max = 8.82). |
| In the text | |
 |
Fig. 5 Dependences on layer thickness d, for fixed heat flux conditions (F/F0 = 1.5). In reading order: Rayleigh number, density ratio, Nusselt numbers (dashed for solute), and thickness of the stagnant zone. |
| In the text | |
 |
Fig. 6 Merging of two neighboring layers in a double-diffusive staircase. The solute concentration can change by exchange between the two until the contrast disappears (dashed), or one can grow in thickness at the expense of the other (dotted). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


