| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118719 | |
| Published online | 12 April 2013 | |
Dimethyl ether in its ground state, v = 0, and lowest two torsionally excited states, v11 = 1 and v15 = 1, in the high-mass star-forming region G327.3-0.6⋆
1
Centre for Star and Planet Formation, Natural History Museum of Denmark,
University of Copenhagen, Øster
Voldgade 5-7, 1350
Copenhagen K.,
Denmark
e-mail:
suzanne@snm.ku.dk
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
3
Centre for Star and Planet Formation, Niels Bohr
Institute, Juliane Mariesvej
30, 2100
Copenhagen Ø,
Denmark
4
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Straße 77,
50937
Köln,
Germany
Received:
22
December
2011
Accepted:
21
February
2013
Context. One of the big questions in astrochemistry is whether complex organic molecules are formed in the gas phase after evaporation of the icy mantles of interstellar dust grains or at intermediate temperatures within these icy mantles. Dimethyl ether (CH3OCH3) is one of these species that may form through either of these mechanisms, but it is yet unclear which is dominant.
Aims. The goal of this paper is to determine the respective importance of solid state vs. gas phase reactions for the formation of dimethyl ether. This is done by a detailed analysis of the excitation properties of the ground state and the torsionally excited states, ν11 = 1 and ν15 = 1, toward the high-mass star-forming region G327.3-0.6.
Methods. With the Atacama Pathfinder EXperiment 12 m submillimeter telescope, we performed a spectral line survey toward G327.3-0.6 around 1.3, 1.0, and 0.9 mm as well as at 0.43 and 0.37 mm. The observed CH3OCH3 spectrum is modeled assuming local thermal equilibrium.
Results. CH3OCH3 has been detected in the ground state, ν= 0, and in the torsionally excited states ν11 = 1 and ν15 = 1, for which lines have been detected here for the first time. The emission is modeled with an isothermal source structure as well as with a non-uniform spherical structure. In the isothermal case two components at 80 and 100 K are needed to reproduce the dimethyl ether emission, whereas an abundance jump at 85 K or a model with two abundance jumps at 70 and 100 K fit the emission equally well for the non-uniform source model. The emission from the torsionally excited states, ν11 = 1 and ν15 = 1, is very well fit by the same model as the ground state.
Conclusions. For non-uniform source models one abundance jump for dimethyl ether is sufficient to fit the emission, but two components are needed for the isothermal models. This suggests that dimethyl ether is present in an extended region of the envelope and traces a non-uniform density and temperature structure. Both types of models furthermore suggest that most dimethyl ether is present in gas that is warmer than 100 K, but a smaller fraction of 5%–28% is present at temperatures between 70 and 100 K. The dimethyl ether present in this cooler gas is likely formed in the solid state, while gas phase formation probably is dominant above 100 K. Finally, the ν11 = 1 and ν15 = 1 torsionally excited states are easily excited under the density and temperature conditions in G327.3-0.6 and will thus very likely be detectable in other hot cores as well.
Key words: astrochemistry / line: identification / methods: observational / stars: formation / ISM: abundances / ISM: molecules
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
A key stage in high-mass star-formation is the hot molecular core phase, in which high abundances of complex organic molecules are found in the inner warm regions (e.g. Rodgers & Charnley 2003). The origin of complex organic species is still debated, in particular, which species are formed by solid state reactions in the cooler stages, and which form in the gas phase after evaporation of icy grain surfaces, when the young forming high-mass star starts heating up its surroundings (Tielens & Charnley 1997; Charnley et al. 1992; Charnley 1995). CH3OCH3 (dimethyl ether) is one of these “hot core molecules” for which the exact formation mechanism is not yet clear. It has frequently been detected toward high-mass star-forming regions and has a typical abundance of 10-8–10-7 with respect to H2 (see e.g., Sutton et al. 1995; Nummelin et al. 2000; Schilke et al. 2001; Comito et al. 2005). It has been observed toward low-mass star-forming regions as well (Cazaux et al. 2003; Jørgensen et al. 2005a).
A recent discussion of CH3OCH3 formation is given by Peeters et al. (2006). Two alternative formation
mechanisms are suggested: grain surface reactions and warm gas phase chemistry. In the first
route, large quantities of CH3OCH3 may be produced by the combination
of radicals formed as the photo-dissociation products of organic molecules on the surfaces
of icy grains (Garrod et al. 2008). Since these
radicals are mobile only at intermediate ice temperatures or higher,
CH3OCH3 is formed above 30 K. It evaporates before H2O
and CH3OH, due to its inability to form hydrogen bonds. In laboratory experiments
by Öberg et al. (2009) an evaporation temperature of
85–90 K is found. However, the total number of desorbed molecules is a function of both
temperature and time. Therefore the expected evaporation temperature of
CH3OCH3 for more realistic warm-up time scales for star-forming
regions, e.g., 104–106 yr for an envelope warming up from 20 to 200 K
(Garrod et al. 2008), is expected to be around 70 K
(see e.g., Bisschop et al. 2006, where this time scale
effect is demonstrated for CO and N2). After evaporation it is destroyed and/or
protonated (Peeters et al. 2006). This results in a
decreasing abundance over time and a peak in the CH3OCH3 abundance
early in the evolution of the hot core. The second route is gas phase formation of
CH3OCH3 from CH3OH. This reaction has been measured in
the laboratory by Karpas & Mautner (1989) and
occurs in two steps. The first step is the self-alkylation of protonated methanol:
CH3OH OCH
OCH . The
second step is dissociative recombination, which leads to the neutral dimethyl ether. Hamberg et al. (2010) report that the dissociative
recombination of CD3OCD
. The
second step is dissociative recombination, which leads to the neutral dimethyl ether. Hamberg et al. (2010) report that the dissociative
recombination of CD3OCD leads to the formation of deuterated dimethyl ether in about 7% of the cases. If the same
branching ratio holds for the non-deuterated species, this means that the expected gas phase
abundance ratio CH3OCH3/CH3OH is probably not higher than
~7%. The abundance of CH3OCH3 formed in the gas phase is expected to
peak at higher temperatures compared to the grain-surface formation scenario, since
CH3OH only evaporates at around 100 K (Viti et
al. 2004). However, low abundances of two orders of magnitude less of
CH3OH are also found in the outer parts of low-mass protostars and even cold
dark clouds (Jørgensen et al. 2005b; Maret et al. 2005; Dickens et al. 2000). If this is also the case for high-mass star-forming regions,
it may also lead to the formation of a small amount of dimethyl ether at low temperatures in
the gas phase. In summary, CH3OCH3 is mainly expected to be present in
the hot core and the emission should be very well modeled with one or two temperature
components. One of the main questions we would like to answer in this paper is whether this
is indeed is the case.
leads to the formation of deuterated dimethyl ether in about 7% of the cases. If the same
branching ratio holds for the non-deuterated species, this means that the expected gas phase
abundance ratio CH3OCH3/CH3OH is probably not higher than
~7%. The abundance of CH3OCH3 formed in the gas phase is expected to
peak at higher temperatures compared to the grain-surface formation scenario, since
CH3OH only evaporates at around 100 K (Viti et
al. 2004). However, low abundances of two orders of magnitude less of
CH3OH are also found in the outer parts of low-mass protostars and even cold
dark clouds (Jørgensen et al. 2005b; Maret et al. 2005; Dickens et al. 2000). If this is also the case for high-mass star-forming regions,
it may also lead to the formation of a small amount of dimethyl ether at low temperatures in
the gas phase. In summary, CH3OCH3 is mainly expected to be present in
the hot core and the emission should be very well modeled with one or two temperature
components. One of the main questions we would like to answer in this paper is whether this
is indeed is the case.
The detailed study of CH3OCH3 is part of a larger project in which we obtained a large, unbiased, line-survey of the 230, 290, 345, 690 and 810 GHz atmospheric windows with the Atacama Pathfinder EXperiment1 (APEX) telescope for the chemically extremely rich high-mass star-forming region G327.3-0.6 (Bisschop et al., in prep.). The G327.3-0.6 hot core is located in an active region of high-mass star-formation, close to two HII regions, and its formation may have been triggered by an expanding infrared bubble (Minier et al. 2009). North of the “hot core” there is a colder cloud core detected in CO and N2H+ (Wyrowski et al. 2006). Recent observations of mid-J CO-lines by Leurini et al. (2013) show that the molecular emission is extended and suggest that smaller high density clumps are also present in the region. The aim of our large unbiased line-survey of the high-mass star-forming region G327.3-0.6 is to make an inventory of the chemical composition of the “hot core” and to compare their abundances and excitation properties to astrochemical models of gas and grain-surface chemistry (as for example shown for ethyl formate and n-propyl cyanide by Belloche et al. 2009). Hereby we aim to get a better understanding of the chemical mechanisms, e.g., which species may be formed on grain surfaces and which in the gas phase. G327.3-0.6 is very suitable for such a study since the emission lines are strong and narrow. There is relatively little line blending, which makes it possible to detect many weaker transitions. Next to the detection of dimethyl ether, a large number of other complex organic molecules have been detected in this source, such as C2H5CN and CH3C(O)CH3 (Gibb et al. 2000; Bisschop et al., in prep.). Currently, we have detected 44 molecular species in this source, 51 isotopologues and 23 vibrationally excited states of which two are detected for minor isotopologues. Papers in which the full CHAMP+ and SHeFI surveys will be presented are in preparation.
This paper is structured as follows: Sect. 2 discusses the observations, Sect. 3 presents the analysis methods, Sect. 4 describes the results of the observations, and discusses the results of radiative transfer models for the dimethyl ether emission with either an isothermal or non-uniform density and temperature structure, in Sect. 5 the isothermal and non-uniform source structure models are compared and the resulting constraints on the formation mechanisms of CH3OCH3 are discussed, and finally Sect. 6 summarizes the main conclusions.
2. Observations
Overview of the observed frequencies, half-power beam widths (HPBW) and the telescope beam efficiencies (Beff).
G327.3-0.6 was observed in 2008 in the 230, 290 and 345 GHz atmospheric windows with APEX
located in the Atacama desert in Chile (Güsten et al.
2006a,b). Additional observations were
performed in August 2009 in the 690 and 810 GHz atmospheric windows. The coordinates for the
G327.3-0.6 hot core are  2,
δJ2000 = −54°37′06.6″ and the source has a
Vlsr = −45 km s-1. We used a distance of 2.9 kpc
for G327.3-0.6 (Simpson & Rubin 1990) and a
luminosity of 1 × 105 L⊙ (Wyrowski et al. 2006). In Table 1
the precise frequency ranges that are covered are given. The front-ends used were the SHeFI
heterodyne receivers, APEX-1 for the 230 GHz window and APEX-2 for the 290 and 345 GHz
windows (Vassilev et al. 2008). The 2 times 7-pixel
dual channel heterodyne receiver array, CHAMP+ (Kasemann et al. 2006), was employed for the 690 and 810 GHz observations. The Fast
Fourier Transform Spectrometer (FFTS) was the backend for all the SHeFI observations (Klein et al. 2006). It has 8192 spectral channels divided
over two units, each of which has a bandwidth of 1 GHz with a channel spacing of 122 kHz.
The two units are spaced such that there is 100 MHz overlap, which results in a bandwidth of
1.9 GHz covered per setting. For the CHAMP+ array the Array FFTS (AFFTS) was
used. It has 2048 channels in each of its two units, both of which have a bandwidth of 1.5
GHz, a resolution of 732 kHz and an overlap between both units of 180 MHz. All observations
were done in single sideband mode. The telescope pointing was performed on the continuum of
the source itself. The pointing was checked every two hours for the SHeFI instrument and
every hour for the CHAMP+ instrument and found to be accurate within
2′′. The focus was optimized every few hours or around sun-set and sun-rise and
when large temperature changes occurred. The wobbling mode with a throw of ±100′′
was used for the observations.
2,
δJ2000 = −54°37′06.6″ and the source has a
Vlsr = −45 km s-1. We used a distance of 2.9 kpc
for G327.3-0.6 (Simpson & Rubin 1990) and a
luminosity of 1 × 105 L⊙ (Wyrowski et al. 2006). In Table 1
the precise frequency ranges that are covered are given. The front-ends used were the SHeFI
heterodyne receivers, APEX-1 for the 230 GHz window and APEX-2 for the 290 and 345 GHz
windows (Vassilev et al. 2008). The 2 times 7-pixel
dual channel heterodyne receiver array, CHAMP+ (Kasemann et al. 2006), was employed for the 690 and 810 GHz observations. The Fast
Fourier Transform Spectrometer (FFTS) was the backend for all the SHeFI observations (Klein et al. 2006). It has 8192 spectral channels divided
over two units, each of which has a bandwidth of 1 GHz with a channel spacing of 122 kHz.
The two units are spaced such that there is 100 MHz overlap, which results in a bandwidth of
1.9 GHz covered per setting. For the CHAMP+ array the Array FFTS (AFFTS) was
used. It has 2048 channels in each of its two units, both of which have a bandwidth of 1.5
GHz, a resolution of 732 kHz and an overlap between both units of 180 MHz. All observations
were done in single sideband mode. The telescope pointing was performed on the continuum of
the source itself. The pointing was checked every two hours for the SHeFI instrument and
every hour for the CHAMP+ instrument and found to be accurate within
2′′. The focus was optimized every few hours or around sun-set and sun-rise and
when large temperature changes occurred. The wobbling mode with a throw of ±100′′
was used for the observations.
The main-beam temperatures have been calculated by:
 (1)where
Feff and Beff are the forward and
the main beam efficiencies, respectively. The main beam efficiencies were based on the
measurements at a number of given frequencies: the SHeFI efficiencies are tabulated in Vassilev et al. (2008), whereas the efficiencies of the
CHAMP+ instrument for the August 2009 observing campaign are given online2 All values used in this paper are shown in Table 1. These efficiencies were scaled to the efficiencies at
the observing frequencies using the Ruze-formula. The half power beam widths (HPBW) of APEX
(Güsten et al. 2006b, 2008) are given by:
(1)where
Feff and Beff are the forward and
the main beam efficiencies, respectively. The main beam efficiencies were based on the
measurements at a number of given frequencies: the SHeFI efficiencies are tabulated in Vassilev et al. (2008), whereas the efficiencies of the
CHAMP+ instrument for the August 2009 observing campaign are given online2 All values used in this paper are shown in Table 1. These efficiencies were scaled to the efficiencies at
the observing frequencies using the Ruze-formula. The half power beam widths (HPBW) of APEX
(Güsten et al. 2006b, 2008) are given by:
 (2)The
rms noise level reached on the TMB scale at 0.244 MHz resolution
was 30–40 mK for the 230 and 290 GHz bands and 45–55 mK in the 345 GHz window. For the 690
GHz and 810 GHz windows the rms was 100–200 mK and 150–500 mK, respectively, at a resolution
of 0.732 MHz.
(2)The
rms noise level reached on the TMB scale at 0.244 MHz resolution
was 30–40 mK for the 230 and 290 GHz bands and 45–55 mK in the 345 GHz window. For the 690
GHz and 810 GHz windows the rms was 100–200 mK and 150–500 mK, respectively, at a resolution
of 0.732 MHz.
Before modeling the molecular emission of the source a zeroth order baseline was subtracted. The baseline was determined based on emission-free parts of the spectra. In general, the system temperatures calculated were averaged over the observed range of 1.8 GHz per setting. However, for the CHAMP+ spectra, there are a few frequency settings where strong atmospheric emission lines are present. These settings were recalibrated channel-by-channel off-line. In most cases this reduced the atmospheric features in the spectra and increased the overall calibration accuracy in the band. However, the calibration close to these strong atmospheric lines remains very uncertain and does thus not give reliable quantitative constraints. We have compared observations of the exact same frequency taken at different days and from this we estimate that the calibration uncertainty leads to an overall uncertainty on the line-strengths of 15–20% for the SheFI data and ~25–30% for the CHAMP+ data. At 1.3, 1.0, and 0.9 mm the confusion limit is reached for a significant fraction of the observed frequency ranges, however sufficient emission free ranges were present to determine a baseline.
3. Data analysis
This research made use of the myXCLASS program3 (Comito et al. 2005), which accesses the CDMS4 (Müller et al. 2001, 2005) and JPL5 (Pickett et al. 1998) molecular data bases. Additionally, we modeled selected emission lines of the ground state with the new radiative transfer tool LIME (Brinch & Hogerheijde 2010). The line assignments for CH3OCH3 are based on new measurements of the ground state, ν= 0, by Endres et al. (2009) as well as the lowest two torsionally excited states, ν11 = 1 and ν15 = 1 (Endres et al., in prep.). The ν11 = 1 and ν15 = 1 states lie 200 and 240 cm-1, or in temperature units 288 and 346 K above the ground state, respectively. Local thermal equilibrium (LTE) models were constructed for the emission, in which the source size θ is given in ″, column density NT in cm-2, rotational temperature Trot in K, and line width ΔV in km s-1 were varied to obtain the best-fit model by-eye. We have estimated the uncertainties by systematically varying all the parameters in the myXCLASS models. The model results are shown together with the uncertainties in Table 2. The increments with which the different parameters were varied is equal to half the uncertainty given in Table 2.
Resulting best by-eye fits for the isothermal myXCLASS model.
Although the myXCLASS models are used to derive the molecular parameters, rotational
diagrams (see Goldsmith & Langer 1999, for a
discussion of the method) were used to assess the reliability of the fits. Rotational
diagrams were constructed for the lines of the ground and torsionally excited states that
were not too severely blended, meaning that CH3OCH3 is found to be the
major contribution to the emission feature. Blending with known features of other molecules
has been corrected for by the subtraction of the model for all molecules minus dimethyl
ether from the integrated line-intensities. Under LTE conditions and assuming the emission
is optically thin the integrated line intensities,  in K km
s-1 are related to the column density in the upper energy level,
Nu in cm-1, divided by the degeneracy in the upper
energy level, gu, by:
in K km
s-1 are related to the column density in the upper energy level,
Nu in cm-1, divided by the degeneracy in the upper
energy level, gu, by:  (3)where
ν is the transition frequency in Hz, Aul is
the Einstein A-coefficient in s-1. The Einstein
A-coefficient can be calculated through:
(3)where
ν is the transition frequency in Hz, Aul is
the Einstein A-coefficient in s-1. The Einstein
A-coefficient can be calculated through:
 (4)where
μ is the dipole moment in Debye and S is the line
strength. B is the beam-filling factor and is calculated through:
(4)where
μ is the dipole moment in Debye and S is the line
strength. B is the beam-filling factor and is calculated through:
 (5)where
θG327.3−0.6 is the size (FWHM) of the source in arcsec,
which is determined from the isothermal myXCLASS model for the optically thick transitions.
If the emission for a specific transition is optically thick the integrated line intensity
additionally has to be multiplied by the correction factor
Cτ, which is given by:
(5)where
θG327.3−0.6 is the size (FWHM) of the source in arcsec,
which is determined from the isothermal myXCLASS model for the optically thick transitions.
If the emission for a specific transition is optically thick the integrated line intensity
additionally has to be multiplied by the correction factor
Cτ, which is given by:  (6)where
τ is the optical depth. Thus:
(6)where
τ is the optical depth. Thus:
 (7)In
this paper the optical depths for the emission lines are calculated with the isothermal
myXCLASS model. The total source-averaged column density
NT can then be computed from:
(7)In
this paper the optical depths for the emission lines are calculated with the isothermal
myXCLASS model. The total source-averaged column density
NT can then be computed from:  (8)where
the rotational temperature, Trot, should be equal to the kinetic
temperature of the gas under LTE conditions,
Q(Trot) is the rotational partition function,
and Eu is the upper level energy in K. Practically, this means
that Trot can be determined from the slope of the rotational
diagram (such as for example shown in Fig. 2) and
NT from the intercept with the y-axis.
(8)where
the rotational temperature, Trot, should be equal to the kinetic
temperature of the gas under LTE conditions,
Q(Trot) is the rotational partition function,
and Eu is the upper level energy in K. Practically, this means
that Trot can be determined from the slope of the rotational
diagram (such as for example shown in Fig. 2) and
NT from the intercept with the y-axis.
The fit to the data has been optimized, using an iterative approach. First we made a model that fits the data well by-eye and subsequently a rotation diagram was constructed. The results of this fit were then used as renewed input until the fit was optimal.
3.1. Critical density
One of the main assumptions in our analysis is that the emission is in LTE. In the
following we will use the critical density, ncr in
cm-3, to validate this assumption. However, it is necessary to mention that
ncr is not per definition equal to the density where the
excitation temperature is equal to the kinetic temperature. This depends on for example
the frequency of a transition, and the temperature of the gas (Evans 1999, 1989). Both higher
frequencies and higher temperatures decrease the densities at which a given transition is
effectively thermalized. At submillimeter wavelengths the thermalization density is
approximately the same as the critical density. We therefore use the critical density here
to estimate the effective thermalization density. Unfortunately it is not possible to
derive the critical density for transitions of dimethyl ether directly, since its
collisional rates are not known. However, we can attempt to estimate them, when we assume
that the rates for CH3OH are comparable within an order of magnitude. The
critical density for a transition is calculated by:  (9)Here
γ is the collisional rate in cm3 s-1. The
collisional rates for CH3OH are ~10-11−10-10
cm3 s-1 (Pottage et al.
2004). The values for the Einstein A-coefficients of
CH3OCH3 range from 10-6 s-1 up to
4.0 × 10-3 s-1 at the highest frequencies and up to
3.0 × 10-4 s-1 for frequencies below 370 GHz. This means that
ncr can be as high as 107−108
cm-3 for the lines with the highest line-strengths assuming the collisional
rate is 10-11 cm3 s-1. However, as previously mentioned
the effective density at which a transition is thermalized is likely to be different from
the critical density. Multiple effects can play a role, e.g., for transitions from
moderately to highly excited states the sum over all collisional rates from the upper
state need to be considered and not only the one corresponding to the radiative
transition. High optical depths can also lower the density at which a transition is
thermalized. Additionally, a strong infrared radiation field can thermalize the
populations to the radiation field irrespective of the density. However we do not expect
the latter to be a problem for dimethyl ether in this source (see Sect. 4.2). When effects like high optical depth or the
inclusion of all collisional rates are taken into account, the density at which the
molecular emission reflects the kinetic temperature is one or two orders of magnitude
lower than the critical density, i.e., 105−106 cm-3.
Since we used a rather conservative estimate for the collisional rate, the effective
thermalization density may be lower still. This means that most transitions should easily
be thermalized at densities of 106−107 cm-3 we expect
at temperatures from 70 K and higher from the model by Rolffs et al. (2011).
(9)Here
γ is the collisional rate in cm3 s-1. The
collisional rates for CH3OH are ~10-11−10-10
cm3 s-1 (Pottage et al.
2004). The values for the Einstein A-coefficients of
CH3OCH3 range from 10-6 s-1 up to
4.0 × 10-3 s-1 at the highest frequencies and up to
3.0 × 10-4 s-1 for frequencies below 370 GHz. This means that
ncr can be as high as 107−108
cm-3 for the lines with the highest line-strengths assuming the collisional
rate is 10-11 cm3 s-1. However, as previously mentioned
the effective density at which a transition is thermalized is likely to be different from
the critical density. Multiple effects can play a role, e.g., for transitions from
moderately to highly excited states the sum over all collisional rates from the upper
state need to be considered and not only the one corresponding to the radiative
transition. High optical depths can also lower the density at which a transition is
thermalized. Additionally, a strong infrared radiation field can thermalize the
populations to the radiation field irrespective of the density. However we do not expect
the latter to be a problem for dimethyl ether in this source (see Sect. 4.2). When effects like high optical depth or the
inclusion of all collisional rates are taken into account, the density at which the
molecular emission reflects the kinetic temperature is one or two orders of magnitude
lower than the critical density, i.e., 105−106 cm-3.
Since we used a rather conservative estimate for the collisional rate, the effective
thermalization density may be lower still. This means that most transitions should easily
be thermalized at densities of 106−107 cm-3 we expect
at temperatures from 70 K and higher from the model by Rolffs et al. (2011).
3.2. Dust optical depth
 |
Fig. 1 Selected emission lines for ground-state CH3OCH3, ν= 0, in all atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for CH3OCH3, ν= 0, in red and the myXCLASS isothermal model for all assigned species in blue. The major transitions of CH3OCH3, ν= 0, and other detected species are indicated in the plot as well as the values for Eu for the transitions of CH3OCH3, ν= 0. |
The observations described in this paper cover a large frequency range and it is
therefore important to obtain a model that is consistent over all frequencies. The LTE
models constructed with the myXCLASS software systematically overestimate the
line-strength for the CHAMP+ part of the survey. This is likely due to the dust
optical depth at higher frequencies, which absorbs part of the radiation emitted by the
molecules (Mezger et al. 1990). This can be
corrected for by estimating the total column density of hydrogen,
NH, from which the dust optical depth is calculated such
that the relative intensities over all frequencies match. NH
is given by N(H) + 2N(H2) in cm-2.
The dust optical depth, τd, is calculated by:
 (10)The
dust collisional cross section
(10)The
dust collisional cross section  is given by:
is given by:  (11)for
λ > 100 μm. The metallicity
for G327.3-0.6,
(11)for
λ > 100 μm. The metallicity
for G327.3-0.6,  ,
is assumed to be equal to that in the galactic center, i.e. 2, and b is
an adjustable factor, that takes grain properties into account. The myXCLASS program
assumes a value of 3.4 for deeply embedded IR sources where the grains are expected to be
coated with thin ice layers (Rengarajan 1984). In
comparison, a factor of 1.9 is used for grains without ice layers. The latter may be more
correct for the CH3OCH3 emission that is arising from warmer gas.
Furthermore in the myXCLASS program, dust is considered to be present in a foreground
layer and corrected for with the factor e−τd. For
consistency we use the same correction factor for the rotational diagram treatment.
However, when the dust is present in the source itself molecular line emission is expected
to be attenuated with the factor
(1−e− τd)/τd.
The combination of the effect of the dust grain properties and foreground/in situ
treatment could lead to an underestimation of the value for NH
with a factor 4–5 in addition to the uncertainty of about ~50% on the value derived from
the CHAMP+ observations with myXCLASS. However, with the additional
uncertainties on the source structure and the dust composition it is accurate enough for
our purposes. The line-intensities over the full frequency range covered in this paper are
corrected for by the factor e−τd. The optimal value for
NH is derived by assuming the model for dimethyl ether found
at the lower frequencies also to hold at the higher frequencies (see Sect. 4.1). Typical values for τd
are 0.08 (230 GHz), 0.13 (290 GHz), 0.19 (345 GHz), 0.76 (690 GHz) and 1.04 (810 GHz).
,
is assumed to be equal to that in the galactic center, i.e. 2, and b is
an adjustable factor, that takes grain properties into account. The myXCLASS program
assumes a value of 3.4 for deeply embedded IR sources where the grains are expected to be
coated with thin ice layers (Rengarajan 1984). In
comparison, a factor of 1.9 is used for grains without ice layers. The latter may be more
correct for the CH3OCH3 emission that is arising from warmer gas.
Furthermore in the myXCLASS program, dust is considered to be present in a foreground
layer and corrected for with the factor e−τd. For
consistency we use the same correction factor for the rotational diagram treatment.
However, when the dust is present in the source itself molecular line emission is expected
to be attenuated with the factor
(1−e− τd)/τd.
The combination of the effect of the dust grain properties and foreground/in situ
treatment could lead to an underestimation of the value for NH
with a factor 4–5 in addition to the uncertainty of about ~50% on the value derived from
the CHAMP+ observations with myXCLASS. However, with the additional
uncertainties on the source structure and the dust composition it is accurate enough for
our purposes. The line-intensities over the full frequency range covered in this paper are
corrected for by the factor e−τd. The optimal value for
NH is derived by assuming the model for dimethyl ether found
at the lower frequencies also to hold at the higher frequencies (see Sect. 4.1). Typical values for τd
are 0.08 (230 GHz), 0.13 (290 GHz), 0.19 (345 GHz), 0.76 (690 GHz) and 1.04 (810 GHz).
4. Results
4.1. The CH3OCH3 ground state, v = 0
Emission lines for the ground state are detected in all atmospheric windows, more specifically 337 in the SHeFI bands and 136 at the frequencies observed with CHAMP+. Examples of lines detected for each band are shown in Fig. 1. Naturally a large number of lines is blended with transitions of other species, which results in a number of 250 features, for which CH3OCH3 is the main contributor (an overview of the CH3OCH3, ν= 0 transitions is given in the appendix in Table A.1). As described in Sect. 3, the model for the emission of all other assigned features is taken into account in the isothermal myXCLASS model. The values for Eu for the detected transitions range from 21.7 to 677.5 K, and are very evenly spread in energy. The optical depths for detected transitions range from 0.056 to 26.
 |
Fig. 2 Rotational diagram for CH3OCH3, ν= 0, uncorrected for the predicted optical depth (left) and corrected for the optical depth (right), in all other aspects the data is treated in the same way, as well as that the same symbols and line-styles are used in both panels. Line-emission from other species, derived from an isothermal model of all identified species minus dimethyl ether, has been subtracted from the dimethyl ether emission in both figures. The filled squares (■) indicate the lines with Eu > 200 K and open squares (Λ) lines with Eu < 200 K, detected with SHeFI in the 230, 290 and 345 GHz windows. The open triangles (△) indicate CHAMP+ data. The solid line shows the least squares-fit to the Eu > 200 K data and the dotted line the least-square fit to the Eu < 200 K transitions. The dust absorption has been corrected for. NT for the fit to the transitions with Eu > 200 K is 5.5 × 1017 cm-2 and Trot is 105 K for a source size of 2.6′′. For the transitions with Eu < 200 K these values are 5.0 × 1017 cm-2 and 82 K, respectively for a source size of 3.2′′. |
We have attempted to fit the data with both a one-component and two-component isothermal model (see Sect. 3). In general the two components fit the data better by-eye, since it is difficult to model both the intensities of the optically thick transitions with excitation temperatures above and below 200 K accurately with only one component. The optically thick lines with the lowest excitation temperatures of ~30 K namely suggest a significantly larger source size compared to the optically thick lines of ~200 K. To get an idea of how well both models fit we have calculated a reduced χ2 for both isothermal models for the same transitions as modeled with the non-uniform density model discussed in Sect. 4.3. The parameters for both models, as well as the reduced χ2 are shown in Table 2. The two-component isothermal model has a reduced χ2 of 1.34 vs. 2.08 for the one-component model. This result may suggest that there are two physical components, but could also indicate that the dimethyl ether emission arises from a region with a non-uniform density and/or temperature structure. The same is seen in the CHAMP+ data. Here two different values for NH are needed to correct for the dust optical depth (see Sect. 3.2 for an explanation). This is also illustrated in Fig. 2, where the CHAMP+ data (shown as △) is corrected for the τd found for the highest excitation lines for a hydrogen column density of 2 × 1024 cm-2. This value is consistent within the uncertainties mentioned in Sect. 3.2 with NT > 100 K of 4.5 × 1024 cm-2 derived for the models by Rolffs et al. (2011) from the 870 μm dust emission, in particular since the value found with myXCLASS (see Sect. 3.2) likely underestimates the actual value. The CHAMP+ detections are well fit at the highest excitation energies, but the excitation levels below 200 K actually are corrected too much and lie above the fit and most of the transitions detected with SheFI (shown in Fig. 2 as Λ). These lower energy CHAMP+ detections thus seem to require a lower dust optical depth and corresponding hydrogen column density (NH = 1 × 1024 cm-2) to match the lower frequency data. This could be explained by dimethyl ether gas that is present in an extended region with a temperature and density gradient or that has two different abundance components. Both scenarios may well cause dimethyl ether to “see” different dust columns dependent on the location in the envelope of the star-forming region (see also Sect. 5).
The two-component isothermal myXCLASS model fit to the data is shown in the rotation diagram in Fig. 2 for the ground state. On the left the rotation diagram is shown without the correction for optical depth and on the right with the correction for the optical depth derived from the model. Least-square fits of the transitions are shown for both Eu values above 200 K (solid line) and below 200 K (dotted line). The column density for the fit to the transitions with Eu > 200 K is 5.5 × 1017 cm-2 and the rotational temperature is 105 K for a source size of 2.6′′. For the transitions with Eu < 200 K these values are 5.0 × 1017 cm-2 and 82 K, respectively for a source size of 3.2′′. The difference between the column densities from the rotational diagram and the two components given in Table 2 are due to the fact that the two temperature components of the isothermal model are both contributing to the emission of all transitions, and the least-square column densities are therefore higher. The comparison between the two rotation diagrams clearly shows that a large fraction of the “scatter” is due to the optical depth of the emission lines. The rotational temperature derived in the uncorrected rotational diagram is furthermore higher and the column density about an order of magnitude lower compared to that corrected for optical depth. Some scatter remains for the corrected data which is most likely due to the presence of line-blends with unidentified features, as well as uncertainties in the baseline level due to line-confusion.
As discussed in Sect. 3.1, it is possible (though not likely) that some transitions for dimethyl-ether are excited under non-LTE conditions. If we remove those lines for which this is most probable, the fit to the data is not affected significantly, and most of these transitions are very well-fit by the LTE model. Thus we conclude that LTE indeed is a good approximation for dimethyl ether in this source.
4.2. The CH3OCH3 torsionally excited states v11 = 1 and v15 = 1
 |
Fig. 3 Selected emission lines for CH3OCH3, ν11 = 1, in all atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for only CH3OCH3, ν11 = 1, in red and the model for all assigned species in blue. Transitions of CH3OCH3, ν11 = 1, and other detected species are labeled in the plot as well as the values for Eu for CH3OCH3, ν11 = 1. |
 |
Fig. 4 Selected emission lines for CH3OCH3, ν15 = 1 in four atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for only CH3OCH3, ν15 = 1, in red and the model for all assigned species in blue. Transitions of CH3OCH3, ν15 = 1, and other detected species are labeled in the plot as well as the values for Eu for CH3OCH3, ν15 = 1. |
Emission from the ν11 = 1 torsionally excited state is detected in all atmospheric windows studied here. The ν15 = 1 state is detected in all atmospheric windows except for the highest (810 GHz) window. The number of lines present in the observations for ν11 = 1 with the SHeFI receiver is 117 and 84 with the CHAMP+ receiver. For ν15 = 1 these numbers are 59 and 39, respectively. Unfortunately, some of these features are very strongly blended with transitions of other species so that there are only 101 and 42 “clean” features that can reliably be used for the analysis of ν11 = 1 and ν15 = 1, respectively (see for an overview of these assignments Tables A.2 and A.3 in the appendix). In Figs. 3 and 4 selected transitions for both states are shown for all atmospheric windows in which they are detected. The torsionally excited states states lie ~288 K (ν11 = 1) and 346 K (ν15 = 1) above the ground state. Lines with Eu up to 550 K have been detected. The smaller energy range covered compared to the ground state, means that the column densities and rotational temperatures for ν11 = 1 and ν15 = 1 lines are less well-constrained. However, their spectra are very well modeled with the same LTE model as the ground state (see Sect. 4.1). Interestingly the ν11 = 1 torsionally excited state is infrared inactive while ν15 = 1 is infrared active. If dimethyl ether would strongly interact with the infrared radiation field, a difference between the excitation of the ground state and the torsionally excited states or between the two torsionally excited states would be expected. Since this clearly is not the case, we conclude that for this specific molecule it is not necessary to include or correct for an infrared radiation field in the models.
 |
Fig. 5 Rotational diagrams for the torsionally excited states, ν11 = 1 (left) and ν15 = 1 (right), of dimethyl ether. The filled squares (■) indicate transitions detected with the SHeFI instrument, the open squares (Λ) detections with the CHAMP+ instrument. The solid line represents the fit to the torsionally excited states and the dotted line indicates the fit to the ground state transitions with Eu > 200 K. The least-square fit to the torsionally excited state, ν11 = 1 gives a resulting NT of 7.5 × 1017 cm-2 and a Trot of 95 K. For the torsionally excited state, ν15 = 1, these values are 6.3 × 1017 cm-2 and 107 K, respectively. |
In Fig. 5 the rotational diagrams are shown for the ν11 = 1 and ν15 = 1 states. The least-square fits are indicated by the solid black line and a fit to the high energy transitions of the ground state is indicated with the dotted line. The least-square fit to the torsionally excited state, ν11 = 1 gives a resulting column density of 7.5 × 1017 cm-2 and a rotational temperature of 95 K. For the torsionally excited state, ν15 = 1, these values are 6.3 × 1017 cm-2 and 107 K, respectively. The consistency between the model for the ground state and the torsionally excited states is not just clear from the isothermal model fits shown in Figs. 3 and 4, but is also apparent in these rotational diagrams (Fig. 5). Due to the lower optical depths for the transitions of the excited states one could expect that the critical densities for the lines from the ν11 = 1 and ν15 = 1 states and thus the densities where LTE is a good approximation are higher than for the ground state. Nonetheless they are very well fit by the same model, confirming our conclusion in Sect. 3.1 that LTE is a good assumption for dimethyl ether toward the G327.3-0.6 star-forming region.
The optical depths in the isothermal models for the torsionally excited states range from 0.05–0.655 and 0.038–0.387 for ν11 = 1 and ν15 = 1, respectively. The line intensities are very close to what is expected based on the ground state and no lines that are expected to be there are missing. We are therefore confident, that we have detected the ν11 = 1 and ν15 = 1 states here for the first time in space and expect that their transitions will easily be detected in other hot core sources in the future.
4.3. A non-uniform density and temperature model
In Sect. 4.1 we show that two abundance components are needed to model the dimethyl ether emission with an isothermal model. This may either be due to two physical components or to the fact that the dimethyl ether emission arises from an extended region in the envelope. We now want to test these scenarios for a spherical model for the source structure with a physically more realistic temperature and density profile.
We have used the density and temperature profile for the source G327.3-0.6 calculated by Rolffs et al. (2011) and modeled the dimethyl ether emission with the new radiative transfer tool LIME (Brinch & Hogerheijde 2010). Rolffs et al. (2011) approximate the density and temperature profile of G327.3-0.6 with a spherical model based on the 870 μm dust radial profile observed with the Large APEX Bolometer Camera (LABOCA) in the ATLASGAL project (APEX Telescope Large Area Survey of the Galaxy, Schuller et al. 2009). In the model the source has a luminosity of 7 × 104 L⊙, a temperature of 55 K at the photospheric radius (i.e., diffusion sets the temperature gradient in the inner region, and the balance between heating and cooling sets the temperature gradient in the outer region), and a density of 3.5 × 106 cm-3. The photospheric radius is derived by computing the Planck and Rosseland opacities and weighting them with the Planck function (see Rolffs et al. 2011, for the details). The model assumes the gas is static, and has a turbulent line width, FWHM, of 4 km s-1.
The dimethyl ether in the non-uniform density and temperature LIME models is assumed to be in LTE as for the isothermal myXCLASS models presented in Sect. 4.1. The dust opacity has not been taken into account in the LIME models, due to issues of its implementation into the code in combination with overlapping transitions, which for dimethyl nearly always is the case. For this reason we have chosen to use only low frequency dimethyl ether transitions (up to: 261 956 MHz) for which the dust is optically thin (see Sect. 3.2) and thus does not affect the model results significantly. Another assumption is that CH3OCH3 evaporates above 70 K and that dimethyl ether’s precursor methanol evaporates at ~100 K (see Sect. 1). The radii at which these temperatures occur are consistent with those found for the two components of the isothermal myXCLASS model described in Sect. 4.1.
To assess the accuracy of the models, we have performed a reduced χ2-analysis for the calculated emission for a set of 7 dimethyl ether transitions that span a range of temperatures and optical depths and are known to be free from emission line blends from our survey. In Table 3 we show the best reduced χ2 for the fits to the transitions shown in Figs. 6–8 for the non-uniform density and temperature models with the CH3OCH3 abundance jumping at a temperature ranging from 70 K up to 100 K. Results for the best-fit model with a jump at 70 K (light grey) and 100 K (dark grey) are also shown in Fig. 6, as well as the model with a jump at both 70 and 100 K (light grey) and a single jump at 85 K (dark grey) in Fig. 7. The reduced χ2 is calculated for a 10 km s-1 wide window around the peak position except for the blended features (second and fifth panel), where the velocity range covered is 8 km s-1 to avoid including emission from other species. Below the jump temperature the abundance is set to be negligible (1.0 × 10-15 w.r.t. H2). For each jump temperature, we first tried to identify around which abundance the reduced χ2 was lowest and afterwards ran a set of 4–6 models with abundance steps of 1–2 × 10-8 to identify the best-fit abundance.
Results of the fits to a selected number of dimethyl ether transitions for both the non-uniform density and temperature LIME models as well as the isothermal myXCLASS models.
As can be seen in Fig. 6 the LIME model, where the abundance jump for CH3OCH3 occurs at 100 K, fits most emission lines very well, but seems to over-reproduce the transitions with the highest excitation energies. In contrast, the model where there is a single jump at 70 K, has the opposite problem, that the lower excitation transitions are over-produced, when those at high energies are well fit. When there are two abundance jumps at 70 and 100 K or one at an intermediate temperature of 85 K (see Fig. 7) this systematic mismatch of low or higher excitation transitions is not observed. The difference between the model with the abundance jump at 85 K and that with a jump at both 70 and 100 K is, however, negligible. Both models fit the observed line strength and width very well. It is only in the second panel for the 22 K lines that some deviation is seen for two weaker lines, which are slightly under-produced very likely due to unknown line blends.
Due to the similarities for the non-uniform density LIME models with a single or double abundance jump no conclusion about whether there are one or two jumps in the CH3OCH3 abundance, can be drawn. Finally, the models suggest that most dimethyl ether emission arises from a region with temperatures above 100 K, but that some emission seems to arise from a region with temperatures lower than 100 K.
5. Discussion
5.1. Comparison of an isothermal source model with a non-uniform density and temperature model
In general, we can conclude that isothermal models for the dimethyl ether emission are in qualitative agreement with the models with a non-uniform source structure. This is demonstrated by the comparison of Figs. 7 and 8. There are small differences, i.e., the line wings are better fit with the isothermal model, whereas the line-centers are often better fit with the non-uniform source model. To compare the isothermal fit to the non-uniform spherical model, we have calculated a reduced χ2 for the myXCLASS models with one and two components of the same lines that are used in the LIME model. The isothermal model suggests two abundance jumps for CH3OCH3, as can be seen by the significantly lower value for χ2 for the two-component model (see Sect. 4.1). However, the non-uniform density and temperature models suggest that two separate abundance jumps are not needed. This suggests that dimethyl ether traces gas that has a temperature and density gradient. In a way our two-component isothermal model can be considered as a “simple” non-uniform density and temperature model. The non-uniform source model is therefore a useful tool for the interpretation of the emission of CH3OCH3 in the hot core of G327.3-0.6.
5.2. Implications for the formation mechanisms of CH3OCH3
The fact that CH3OCH3 is present in regions with a range of temperatures makes it difficult to separate the contribution of grain surface formation or gas phase formation and determine which is dominant. If we assume that dimethyl ether with excitation temperatures below 100 K is due to solid state formation, then it is possible to estimate the lower limit to the fraction of CH3OCH3 that is formed on icy grains. The reason we can only deduce lower limits is, that the dimethyl ether present at higher temperatures may also originate from solid state chemistry. A laboratory study by Collings et al. (2004) namely shows that many molecular species can be trapped in ices up to the H2O evaporation temperature. For species with similar binding energies as CH3OCH3, about 50% remains trapped in a mixed ice until water evaporates. This fraction is lower for layered ices, where the studied species was deposited on top of a water ice layer. Unfortunately, CH3OCH3 was not one of the species studied by Collings et al. (2004), but it is reasonable to assume that something similar would occur for dimethyl ether and that some fraction of the dimethyl ether gas at temperatures above 100 K is due to CH3OCH3 co-desorbing with H2O.
In Table 3 we show the fractional contribution of
the dimethyl ether containing gas that has a temperature between 70 and 100 K,
 .
.
 is defined as the total number of dimethyl ether molecules in the model, and is derived by
integrating over the radial density profile combined with the radial abundance dependence
for dimethyl ether.
is defined as the total number of dimethyl ether molecules in the model, and is derived by
integrating over the radial density profile combined with the radial abundance dependence
for dimethyl ether.  is calculated in a similar way, but only by integrating over the part of the envelope that
is below 100 K. If we consider the model with the abundance jump at 85 K, the fraction of
dimethyl ether present in gas between 70 and 100 K is 21%. This would suggest that at
least 21% is formed on icy grains. If we assume that the two-jump model is the most
extreme case, since, as mentioned earlier in this section, the 100 K systematically
under-reproduces all the lower excitation lines, then the models suggest that the lower
limit to the grain surface contribution is 5% and conversely, this means that the upper
limit to the gas phase contribution is 95%.
is calculated in a similar way, but only by integrating over the part of the envelope that
is below 100 K. If we consider the model with the abundance jump at 85 K, the fraction of
dimethyl ether present in gas between 70 and 100 K is 21%. This would suggest that at
least 21% is formed on icy grains. If we assume that the two-jump model is the most
extreme case, since, as mentioned earlier in this section, the 100 K systematically
under-reproduces all the lower excitation lines, then the models suggest that the lower
limit to the grain surface contribution is 5% and conversely, this means that the upper
limit to the gas phase contribution is 95%.
 |
Fig. 6 Selected emission lines for CH3OCH3, ν= 0, over-plotted with the best-fit non-uniform LIME model with a single jump of the CH3OCH3 abundance at 70 or 100 K (see Table 3). The observed spectrum is displayed in black, the model for CH3OCH3, ν= 0, with an abundance jump at 70 K in light grey and at 100 K in dark grey. The value of Eu for each transition is given in the upper right corner of each panel. |
 |
Fig. 7 Same as Fig. 6, but with two jumps of the CH3OCH3 abundance at 70 and 100 K (light grey) and a single jump of the abundance at 85 K (dark grey). The observed spectrum is displayed in black. |
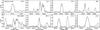 |
Fig. 8 Same as Fig. 7, but with the isothermal myXCLASS model over-plotted in grey (see Table 2 for the properties of the two isothermal components). |
An alternative formation mechanism for low-temperature gas-phase dimethyl ether is that a
small fraction of solid CH3OH evaporates from the ices at low temperatures and
gives rise to a small amount of CH3OCH3 that is formed in the cooler
gas phase. For 13CH3OH we have performed a similar analysis as
described for dimethyl ether in this paper, i.e. we modeled its emission with both
isothermal and a non-uniform density and temperature models. The best-fit abundances found
for 13CH3OH in non-uniform density and temperature models are
2(± 0.5) × 10-11 and 4.5(± 0.5) × 10-8, below and above 100 K,
respectively. When we assume the 12C/13C ratio to be 53 the average
found by Wilson & Rood (1994) for the 4 kpc
molecular ring, the CH3OH abundance below 100 K in G327.3-0.6 would be
~1 × 10-9 and ~2 × 10-6 above 100 K. This is consistent with
models of both low and high-mass star-forming regions where the abundance of
CH3OH is on the order of 10-10–10-9 below 90–100 K
(Schöier et al. 2006; Maret et al. 2005; Van der Tak et al.
2000). Since radiative dissociation experiments performed with
CD3OCD by Hamberg et al. (2010) only results in the
formation of deuterated dimethyl ether in 7% of the reactions, and not all
CH3OH will react to form
CH3OCH
by Hamberg et al. (2010) only results in the
formation of deuterated dimethyl ether in 7% of the reactions, and not all
CH3OH will react to form
CH3OCH ,
we expect the CH3OCH3/CH3OH ratio to be 0.07 at most, but
probably much lower. The gas phase abundances of dimethyl ether formed at low temperatures
is therefore likely not larger than 7 × 10-11. Additionally,
CH3OCH3 itself may also desorb directly through non-thermal
mechanisms. In theoretical models of grain-surface formation the solid state
CH3OCH3/CH3OH ratio is on the order of
10-3–10-4 (Garrod et al.
2008). The gas phase abundance of CH3OCH3 that could be due
to non-thermal desorption is thus expected to be ~10-13, which is lower than
the CH3OCH3 abundance that could be formed from non-thermally
desorbed CH3OH. Since abundances of ~10-8 for dimethyl ether are
needed in the outer regions both in the isothermal case and for the non-uniform source
models for the G327.3-0.6 high-mass star-forming region, the major contributor to cooler
dimethyl ether gas cannot be direct non-thermally desorbed CH3OCH3
or gas phase formation through the non-thermal evaporation of CH3OH.
CH3OCH3 that desorbs thermally from icy grain surfaces is
therefore most likely responsible for the CH3OCH3 emission below 100
K. Interestingly, the CH3OCH3/CH3OH ratio above 100 K is
in the 5–10% range for our non-spherical source models, which is close to the upper limit
for the ratio expected from gas phase formation mechanism, underlining that although the
data suggests that there is some grain-surface formation of dimethyl ether, the gas phase
mechanism likely is dominant.
,
we expect the CH3OCH3/CH3OH ratio to be 0.07 at most, but
probably much lower. The gas phase abundances of dimethyl ether formed at low temperatures
is therefore likely not larger than 7 × 10-11. Additionally,
CH3OCH3 itself may also desorb directly through non-thermal
mechanisms. In theoretical models of grain-surface formation the solid state
CH3OCH3/CH3OH ratio is on the order of
10-3–10-4 (Garrod et al.
2008). The gas phase abundance of CH3OCH3 that could be due
to non-thermal desorption is thus expected to be ~10-13, which is lower than
the CH3OCH3 abundance that could be formed from non-thermally
desorbed CH3OH. Since abundances of ~10-8 for dimethyl ether are
needed in the outer regions both in the isothermal case and for the non-uniform source
models for the G327.3-0.6 high-mass star-forming region, the major contributor to cooler
dimethyl ether gas cannot be direct non-thermally desorbed CH3OCH3
or gas phase formation through the non-thermal evaporation of CH3OH.
CH3OCH3 that desorbs thermally from icy grain surfaces is
therefore most likely responsible for the CH3OCH3 emission below 100
K. Interestingly, the CH3OCH3/CH3OH ratio above 100 K is
in the 5–10% range for our non-spherical source models, which is close to the upper limit
for the ratio expected from gas phase formation mechanism, underlining that although the
data suggests that there is some grain-surface formation of dimethyl ether, the gas phase
mechanism likely is dominant.
In summary, our non-uniform density and temperature LIME models of the emission of dimethyl ether, give qualitatively the same result as the isothermal myXCLASS model. They namely suggest that most emission of dimethyl ether arises from regions with temperatures of 100 K and higher, but that some fraction of dimethyl ether emission is present at lower temperatures. The most likely origin of this low temperature component is formation of dimethyl ether in the solid state.
6. Summary and conclusions
In this paper we have analyzed the rotational emission of CH3OCH3 in its ground state, ν= 0, and the torsionally excited states ν11 = 1 and ν15 = 1 for the source G327.3-0.6 observed with APEX. The data have been modeled with an isothermal model as well as a radiative transfer model with a non-uniform spherical density and temperature structure. The main conclusions are:
-
Many transitions from the ground state, ν= 0, of dimethyl ether are detected toward the high-mass star forming region G327.3-0.6. The emission can be very well described by a two-component isothermal model with two abundance jumps at 80 K and 100 K. Since dimethyl ether has both optically thin and moderately optically thick lines, it is a very suitable diagnostic for dense and fairly warm regions.
-
A variety of lines from the ν11 = 1 and ν15 = 1 torsionally excited states of dimethyl ether are detected here for the first time. The emission can be well described by the same model as for the ground state. Due to the large line-strengths these states should also easily be detectable in other line-rich hot core sources, in particular with new upcoming interferometers such as the Atacama Large Millimeter Array (ALMA).
-
Radiative transfer models with a non-uniform density and temperature structure show that the emission can be very well fit by an abundance jump in the dimethyl ether emission at either 85 K or by two abundance jumps at 70 and 100 K. In contrast two components are needed to accurately reproduce the emission with an isothermal model. We therefore conclude that the non-uniform density and temperature models suggest that dimethyl ether emission arises from an extended region with a significant density and temperature structure, but not necessarily has two abundance components. We estimate that the lower limit for the solid state vs. gas phase contribution is 5%. However, the large abundance ratio CH3OCH3/CH3OH suggest that the gas phase formation mechanism is likely the major contributor.
The presented study shows the potential for these kind of surveys to constrain the chemical structure of high-mass protostellar hot cores. The study of CH3O13CH3 could potentially give additional clues to the formation of dimethyl ether. The 12C/13C ratio namely has the potential to distinguish between grain surface formation and gas phase formation of dimethyl ether (Charnley et al. 2004). This would make it possible to not just improve our understanding of the formation routes of dimethyl ether, but also address whether isotopologues in general can be used as important tracers of the chemistry in star-forming regions.
In addition, it would be interesting to perform similar analyses for a variety of complex organic species. This will make it possible to compare different molecular species with each other as well as to astrochemical models. Specifically, a strong correlation between the abundances of different complex organic species in large sample of star-forming regions, such as performed by Bisschop et al. (2007) may tell us whether two complex organic molecules likely are chemically related. In the longer term, high resolution interferometric measurements, in particular with ALMA, are key to understanding the origin of CH3OCH3 and other complex organics in star-forming regions. The higher spatial resolution will place better constraints on the physical structure of the source and will for example show whether the emission is clumpy or non-spherical. Also, such observations will show how the absolute abundances vary with temperature and thus reveal whether a given species comes off dust grains directly at its evaporation temperature – or perhaps is formed only at even higher temperatures in the gas-phase. From this it is possible to conclude what the relative importance of solid state and gas phase formation mechanisms are and for which key reactions laboratory investigations and quantum chemical calculations are most needed.
Online material
Assignments of CH3OCH3, v = 0, v11 = 1, and v15 = 1 for G327.3-0.6 in all observed frequency windows
In this appendix we show the line parameters for all the unblended lines that have been
detected for CH3OCH3, ν= 0 (Table A.1), ν11 = 1 (Table A.2),
and ν15 = 1 (Table A.3). For questions
about the full line-list please contact the authors. For all transitions frequencies,
quantum numbers and the energies of the upper state (Eu) are
given as well as the measured integrated line intensities
(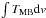 ) and model line-intensities
from the isothermal myXCLASS model for the dimethyl ether emission
(Imodel). Most features are actually composed of a set of
multiple transitions, and we therefore refer to Endres
et al. (2009) and Endres et al. (in prep.) for the values of
μ2S for the individual transitions.
) and model line-intensities
from the isothermal myXCLASS model for the dimethyl ether emission
(Imodel). Most features are actually composed of a set of
multiple transitions, and we therefore refer to Endres
et al. (2009) and Endres et al. (in prep.) for the values of
μ2S for the individual transitions.
Detections of CH3OCH3, ν= 0 toward G327.3-0.6.
Detections of CH3OCH3, ν11 = 1, transitions found to be free of emission from other species toward G327.3-0.6.
Detections of CH3OCH3, ν15 = 1, found to be free of emission from other species toward G327.3-0.6.
Acknowledgments
The research of SEB was supported by a Rubicon grant from the Netherlands Organization for Scientific Research and a grant from Instrument center for Danish Astrophysics. The research in Copenhagen was furthermore supported by Centre for Star and Planet Formation, which is funded by the Danish National Research Foundation and the University of Copenhagens program of excellence and a Junior Group Leader Fellowship to J.K.J. from the Lundbeck foundation. H.S.P.M. is very grateful to the Bundesministerium für Bildung und Forschung (BMBF) for financial support aimed at maintaining the Cologne Database for Molecular Spectroscopy, CDMS. This support has been administered by the Deutsches Zentrum für Luft- und Raumfahrt (DLR). Laboratory work on complex molecules in funded by DFG within CRC956. We would also like to thank an anonymous referee and the editor Malcolm Walmsley for constructive comments on this paper.
References
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B. 1995, Ap&SS, 224, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Millar, T. J. 1992, ApJ, 399, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., Ehrenfreund, P., Millar, T. J., et al. 2004, MNRAS, 347, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Comito, C., Schilke, P., Philips, T. G., et al. 2005, ApJ, 156, 127 [Google Scholar]
- Dickens, J. E., Irvine, W. M., Snell, R. L., et al. 2000, ApJ, 542, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Endres, C. P., Drouin, B. J., Pearson, J. C., et al. 2009, A&A, 504, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, II, N. J. 1989, Rev. Mex. Astron. Astrofis., 18, 21 [NASA ADS] [Google Scholar]
- Evans, II, N. J. 1999, ARA&A, 37, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000, ApJ, 545, 309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Booth, R. S., Cesarsky, C., et al. 2006a, in Ground-based and Airborne Telescopes, ed. L. M. Stepp, Proc. SPIE, 6267, 626714 [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006b, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Baryshev, A., Bell, A., et al. 2008, in Millimeter and Submillimeter Detectors and Instrumentation for Astronomy IV, eds. D. W. Duncan, W. S. Holland, S. Withington, & J. Zmuidzinas, Proc. SPIE, 7020, 702010 [Google Scholar]
- Hamberg, M., Österdahl, F., Thomas, R. D., et al. 2010, A&A, 514, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2005a, ApJ, 632, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2005b, A&A, 437, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karpas, Z., & Mautner, M. 1989, J. Phys. Chem., 93, 1859 [CrossRef] [Google Scholar]
- Kasemann, C., Güsten, R., Heyminck, S., et al. 2006, in Millimeter and Submillimeter Detectors and Instrumentation for Astronomy III, eds. J. Zmuidzinas, W. S. Holland, S. Withington, & W. D. Duncan, Proc. SPIE, 6275, 627509 [Google Scholar]
- Klein, B., Philipp, S. D., Krämer, I., et al. 2006, A&A, 454, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Wyrowski, F., Herpin, F., et al. 2013, A&A, 550, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maret, S., Ceccarelli, C., Tielens, A. G. G. M., et al. 2005, A&A, 442, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mezger, P. G., Zylka, R., & Wink, J. E. 1990, A&A, 228, 95 [NASA ADS] [Google Scholar]
- Minier, V., André, P., Bergman, P., et al. 2009, A&A, 501, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peeters, Z., Rodgers, S. D., Charnley, S. B., et al. 2006, A&A, 445, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectrosc. Radiat. Transfer, 60, 883 [Google Scholar]
- Pottage, J. T., Flower, D. R., & Davis, S. L. 2004, MNRAS, 352, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Rengarajan, T. N. 1984, A&A, 140, 213 [NASA ADS] [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2003, ApJ, 585, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Rolffs, R., Schilke, P., Wyrowski, F., et al. 2011, A&A, 527, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Benford, D. J., Hunter, T. R., Lis, D. C., & Phillips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., Jørgensen, J. K., Pontoppidan, K. M., & Lundgren, A. A. 2006, A&A, 454, L67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, J. P., & Rubin, R. H. 1990, ApJ, 354, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Charnley, S. B. 1997, Origins Life Evol. B., 27, 23 [Google Scholar]
- Van der Tak, F. F. S., Van Dishoeck, E. F., & Caselli, P. 2000, A&A, 361, 327 [NASA ADS] [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., McCoustra, M. R. S., & Williams, D. A. 2004, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrowski, F., Heyminck, S., Güsten, R., & Menten, K. M. 2006, A&A, 454, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Overview of the observed frequencies, half-power beam widths (HPBW) and the telescope beam efficiencies (Beff).
Results of the fits to a selected number of dimethyl ether transitions for both the non-uniform density and temperature LIME models as well as the isothermal myXCLASS models.
Detections of CH3OCH3, ν11 = 1, transitions found to be free of emission from other species toward G327.3-0.6.
Detections of CH3OCH3, ν15 = 1, found to be free of emission from other species toward G327.3-0.6.
All Figures
 |
Fig. 1 Selected emission lines for ground-state CH3OCH3, ν= 0, in all atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for CH3OCH3, ν= 0, in red and the myXCLASS isothermal model for all assigned species in blue. The major transitions of CH3OCH3, ν= 0, and other detected species are indicated in the plot as well as the values for Eu for the transitions of CH3OCH3, ν= 0. |
| In the text | |
 |
Fig. 2 Rotational diagram for CH3OCH3, ν= 0, uncorrected for the predicted optical depth (left) and corrected for the optical depth (right), in all other aspects the data is treated in the same way, as well as that the same symbols and line-styles are used in both panels. Line-emission from other species, derived from an isothermal model of all identified species minus dimethyl ether, has been subtracted from the dimethyl ether emission in both figures. The filled squares (■) indicate the lines with Eu > 200 K and open squares (Λ) lines with Eu < 200 K, detected with SHeFI in the 230, 290 and 345 GHz windows. The open triangles (△) indicate CHAMP+ data. The solid line shows the least squares-fit to the Eu > 200 K data and the dotted line the least-square fit to the Eu < 200 K transitions. The dust absorption has been corrected for. NT for the fit to the transitions with Eu > 200 K is 5.5 × 1017 cm-2 and Trot is 105 K for a source size of 2.6′′. For the transitions with Eu < 200 K these values are 5.0 × 1017 cm-2 and 82 K, respectively for a source size of 3.2′′. |
| In the text | |
 |
Fig. 3 Selected emission lines for CH3OCH3, ν11 = 1, in all atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for only CH3OCH3, ν11 = 1, in red and the model for all assigned species in blue. Transitions of CH3OCH3, ν11 = 1, and other detected species are labeled in the plot as well as the values for Eu for CH3OCH3, ν11 = 1. |
| In the text | |
 |
Fig. 4 Selected emission lines for CH3OCH3, ν15 = 1 in four atmospheric windows. The observed spectrum is displayed in black, the myXCLASS isothermal model for only CH3OCH3, ν15 = 1, in red and the model for all assigned species in blue. Transitions of CH3OCH3, ν15 = 1, and other detected species are labeled in the plot as well as the values for Eu for CH3OCH3, ν15 = 1. |
| In the text | |
 |
Fig. 5 Rotational diagrams for the torsionally excited states, ν11 = 1 (left) and ν15 = 1 (right), of dimethyl ether. The filled squares (■) indicate transitions detected with the SHeFI instrument, the open squares (Λ) detections with the CHAMP+ instrument. The solid line represents the fit to the torsionally excited states and the dotted line indicates the fit to the ground state transitions with Eu > 200 K. The least-square fit to the torsionally excited state, ν11 = 1 gives a resulting NT of 7.5 × 1017 cm-2 and a Trot of 95 K. For the torsionally excited state, ν15 = 1, these values are 6.3 × 1017 cm-2 and 107 K, respectively. |
| In the text | |
 |
Fig. 6 Selected emission lines for CH3OCH3, ν= 0, over-plotted with the best-fit non-uniform LIME model with a single jump of the CH3OCH3 abundance at 70 or 100 K (see Table 3). The observed spectrum is displayed in black, the model for CH3OCH3, ν= 0, with an abundance jump at 70 K in light grey and at 100 K in dark grey. The value of Eu for each transition is given in the upper right corner of each panel. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but with two jumps of the CH3OCH3 abundance at 70 and 100 K (light grey) and a single jump of the abundance at 85 K (dark grey). The observed spectrum is displayed in black. |
| In the text | |
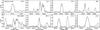 |
Fig. 8 Same as Fig. 7, but with the isothermal myXCLASS model over-plotted in grey (see Table 2 for the properties of the two isothermal components). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


