| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220719 | |
| Published online | 13 February 2013 | |
Search for very-high-energy γ-ray emission from Galactic globular clusters with H.E.S.S.
1 Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149, 22761 Hamburg, Germany
2 Laboratoire Univers et Particules de Montpellier, Université Montpellier 2, CNRS/IN2P3, CC 72, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France
3 Max-Planck-Institut für Kernphysik, PO Box 103980, 69029 Heidelberg, Germany
4 Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
5 National Academy of Sciences of the Republic of Armenia, Yerevan, Armenia
6 Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036 Yerevan, Armenia
7 Universität Erlangen-Nürnberg, Physikalisches Institut, Erwin-Rommel-Str. 1, 91058 Erlangen, Germany
e-mail: Christopher.van.Eldik@physik.uni-erlangen.de
8 University of Durham, Department of Physics, South Road, Durham DH1 3LE, UK
9 DESY, 15735 Zeuthen, Germany
10 Institut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Strasse 24/25, 14476 Potsdam, Germany
11 Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716 Warsaw, Poland
12 CEA Saclay, DSM/Irfu, 91191 Gif-Sur-Yvette Cedex, France
13 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
14 Laboratoire Leprince-Ringuet, École Polytechnique, CNRS/IN2P3, 91128 Palaiseau, France
15 Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
16 Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15, 12489 Berlin, Germany
17 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 Place Jules Janssen, 92190 Meudon, France
18 LPNHE, Université Pierre et Marie Curie Paris 6, Université Denis Diderot Paris 7, CNRS/IN2P3, 4 Place Jussieu, 75252 Paris Cedex 5, France
19 Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
20 Astronomical Observatory, The University of Warsaw, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
21 Unit for Space Physics, North-West University, 2520 Potchefstroom, South Africa
22 School of Physics, University of the Witwatersrand, 1 Jan Smuts Avenue, Braamfontein, 2050 Johannesburg, South Africa
23 Landessternwarte, Universität Heidelberg, Königstuhl, 69117 Heidelberg, Germany
24 Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center, 10691 Stockholm, Sweden
25 Université Bordeaux 1, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan, 33175 Gradignan, France
26 Funded by contract ERC-StG-259391 from the European Community ,
27 University of Namibia, Department of Physics, Private Bag 13301, Windhoek, Namibia
28 School of Chemistry & Physics, University of Adelaide, 5005 Adelaide, Australia
29 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG), UMR 5274, 38041 Grenoble, France
30 Department of Physics and Astronomy, The University of Leicester, University Road, Leicester, LE1 7RH, UK
31 Instytut Fizyki Ja¸drowej PAN, ul. Radzikowskiego 152, 31-342 Kraków, Poland
32 Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck, Austria
33 Laboratoire d’Annecy-le-Vieux de Physique des Particules, Université de Savoie, CNRS/IN2P3, 74941 Annecy-le-Vieux, France
34 Obserwatorium Astronomiczne, Uniwersytet Jagielloński, ul. Orla 171, 30-244 Kraków, Poland
35 Toruń Centre for Astronomy, Nicolaus Copernicus University, ul. Gagarina 11, 87-100 Toruń, Poland
36 Charles University, Faculty of Mathematics and Physics, Institute of Particle and Nuclear Physics, V Holešovičkách 2, 180 00 Prague 8, Czech Republic
Received: 12 November 2012
Accepted: 8 January 2013
Context. Globular clusters (GCs) are established emitters of high-energy (HE, 100 MeV < E < 100 GeV) γ-ray radiation which could originate from the cumulative emission of the numerous millisecond pulsars (msPSRs) in the clusters’ cores or from inverse Compton (IC) scattering of relativistic leptons accelerated in the GC environment. These stellar clusters could also constitute a new class of sources in the very-high-energy (VHE, E > 100 GeV) γ-ray regime, judging from the recent detection of a signal from the direction of Terzan 5 with the H.E.S.S. telescope array.
Aims. To search for VHE γ-ray sources associated with other GCs, and to put constraints on leptonic emission models, we systematically analyzed the observations towards 15 GCs taken with the H.E.S.S. array of imaging atmospheric Cherenkov telescopes.
Methods. We searched for point-like and extended VHE γ-ray emission from each GC in our sample and also performed a stacking analysis combining the data from all GCs to investigate the hypothesis of a population of faint emitters. Assuming IC emission as the origin of the VHE γ-ray signal from the direction of Terzan 5, we calculated the expected γ-ray flux from each of the 15 GCs, based on their number of millisecond pulsars, their optical brightness and the energy density of background photon fields.
Results. We did not detect significant VHE γ-ray emission from any of the 15 GCs in either of the two analyses. Given the uncertainties related to the parameter determinations, the obtained flux upper limits allow to rule out the simple IC/msPSR scaling model for NGC 6388 and NGC 7078. The upper limits derived from the stacking analyses are factors between 2 and 50 below the flux predicted by the simple leptonic scaling model, depending on the assumed source extent and the dominant target photon fields. Therefore, Terzan 5 still remains exceptional among all GCs, as the VHE γ-ray emission either arises from extra-ordinarily efficient leptonic processes, or from a recent catastrophic event, or is even unrelated to the GC itself.
Key words: globular clusters: general / radiation mechanisms: non-thermal / pulsars: general / gamma rays: general
© ESO, 2013
1. Introduction
Globular clusters (GCs) are very dense systems of stars, hosting the oldest and most evolved stellar populations of the Galaxy. The extremely high rate of close stellar encounters in the cores of GCs likely gives rise to large numbers of dynamically formed compact binary systems (Pooley & Hut 2006; Pooley et al. 2003; Hui et al. 2010) which are believed to be the progenitors of millisecond pulsars (msPSRs). Indeed, large msPSR populations have been detected in many Galactic GCs through radio observations (see Camilo & Rasio 2005; Ransom 2008).
A complementary approach to study the msPSR populations of GCs comes from high-energy (HE, 100 MeV< E < 100 GeV) γ-ray observations. Because msPSRs can be strong sources of pulsed magnetospheric emission in this energy regime (as shown by observations with Fermi/LAT, Abdo et al. 2009a), γ-ray signals are expected from GCs either due to bright individual msPSRs or due to the cumulative emission from the whole population. Up to now, 14 Galactic GCs have been detected with Fermi/LAT (Abdo et al. 2009b, 2010b; Kong et al. 2010; Tam et al. 2011), and the γ-ray spectra of most of these sources show steep cut-offs at a few GeV, very reminiscent of the spectra measured from individual msPSRs. Indeed, an individual γ-ray msPSR has recently been detected in the GC NGC 6624 with Fermi/LAT (Freire et al. 2011).
Through the observations of very-high-energy (VHE, E >100 GeV) γ-rays even the whole msPSR population might be accessible. Models predicting emission in the VHE regime rely on inverse Compton (IC) up-scattering of soft photon fields by ultra-relativistic leptons accelerated in the pulsars’ magnetospheres (Venter et al. 2009) or even re-accelerated in colliding pulsar wind nebula shocks (Bednarek & Sitarek 2007). Following Cheng et al. (2010), under certain conditions even the HE emission observed by Fermi/LAT could be explained within a pure IC scenario. In all these models, depending on the assumed diffusion timescale, the magnetic field strength and the location of the GC, the relevant target photon fields could either be the GC starlight, the cosmic microwave background (CMB) or the Galactic optical and infrared background light. In other words, if the leptons remain localized close to their sources, e.g. due to slow particle diffusion, the photon field of the GC member stars would be the dominant target for the IC process. In contrast, if the leptons propagate out of the core region of the GCs, other photon fields would become more important, because the energy density of the GC photon field rapidly decreases with the distance from the core. Thus, in this case the morphology and size of the VHE γ-ray source would be decoupled from the distribution of msPSRs as well as from the extent of the GC stellar population.
Recently, VHE γ-ray emission has been detected from the direction of the GC Terzan 5 with the H.E.S.S. telescope array (HESS J1747−248, Abramowski et al. 2011a). Should this signal indeed be associated to Terzan 5 this would establish GCs as a new class of sources in VHE γ-rays, since previous studies of GCs by H.E.S.S., MAGIC, VERITAS, and CANGAROO in this energy domain resulted only in upper limits (see e.g. Aharonian et al. 2009; Abramowski et al. 2011b; Anderhub et al. 2009; McCutcheon for the VERITAS Collaboration 2009; Kabuki et al. 2007). Even though the nature of this source is not settled yet, IC emission from leptons accelerated by the particularly large msPSR population of Terzan 5 remains a possibility. In this case also diffuse X-ray emission could be expected arising from synchrotron radiation (SR) from the same population of leptons (Venter & de Jager 2008). Interestingly, extended and diffuse non-thermal X-ray emission was detected from Terzan 5 with Chandra by Eger et al. (2010). However, the apparent offset between the X-ray and VHE γ-ray signals challenges simple (IC/SR) models. A search for diffuse X-ray emission on similar scales from other HE-detected GCs resulted only in upper limits (Eger & Domainko 2012).
As an alternative to the leptonic msPSR scenarios, a hadronic model was proposed for HESS J1747−248 by Domainko (2011). Here, it is suggested that the VHE γ-ray emission arises from the decay of neutral pions that were produced in inelastic collisions of relativistic protons with interstellar matter. These protons could have been accelerated in a remnant of a short γ-ray burst resulting from a merger of binary neutron stars. In the cores of GCs the probability for such a rare event is expected to be enhanced compared to Galactic average, due to their large binary fraction. With a rate for such rare catastrophic events of only ~10-4 yr-1 (Nakar 2007), it is unlikely that two of them can be observed at the same time and, thus, Terzan 5 may stand out as an exception among all GCs.
At this point it is thus unclear if or to what extent the X-ray, HE and VHE γ-ray signals detected from GCs are related and what the underlying radiation mechanisms are. Further studies, particularly in the X-ray and VHE γ-ray regimes are the most promising to shed new light on the high-energy processes in these systems. In this work we present a systematic search for VHE γ-ray emission from all Galactic GCs that are covered by the present observational data set of the H.E.S.S. telescope array. To increase the sensitivity for the detection of a population of individually faint emitters we also performed a stacking analysis, where we combined the number of photon candidate counts from the individual GCs to test for a statistically significant signal. We then compare the obtained results to the VHE γ-ray signal detected from Terzan 5 to investigate scenarios based on IC emission from leptons accelerated by msPSRs.
2. H.E.S.S. observations
H.E.S.S. is an array of four imaging atmospheric Cherenkov telescopes located in the Khomas Highland of Namibia. Each telescope is equipped with a tessellated mirror with a surface area of 107 m2 and a camera comprising 960 photomultiplier tubes with a total field of view (FoV) of 5°. For the reconstruction of atmospheric air showers the array works in coincidence mode requiring at least two telescopes to detect individual events. In this mode the array features a point-spread-function (PSF) with a 68% containment radius of ~007 and an energy resolution of 15% on average. The stereoscopic reconstruction provides an excellent suppression of the cosmic-ray background reducing the number of background events after all cuts by a factor of up to 104 (Benbow 2005). With modern reconstruction techniques the H.E.S.S. array has a point-source sensitivity of about 2 × 10-13 ph cm-2 s-1 (E > 200 GeV) for 25 h of observation, requiring a statistical significance of 5σ (see e.g. de Naurois & Rolland 2009; Ohm et al. 2009). Here a zenith angle of 20° and an offset of of 07 is assumed.
The GC sample studied in this work.
2.1. The globular cluster sample
We based our target selection on the GC catalog of Harris (2010, henceforth H10) from which we also took all basic parameters such as position, distance (d), core radius (rc), and central luminosity density (ρ0). To select the sample of GCs and observational data that are suited for our study with H.E.S.S. we applied the following a priori cuts on the target and observation run list:
-
1.
GC |Galactic latitude| ≥ 10;
-
2.
Run passes standard quality selection criteria and is pointed <20 offset from GC position;
-
3.
GC has at least 20 available runs passing cut 2.
The first cut is to conservatively exclude GCs towards the direction of the Galactic plane to avoid chance coincidences with unrelated sources and to prevent potential contamination from a population of faint unresolved sources and/or diffuse emission. Following the same approach as in the case of Terzan 5 (see Abramowski et al. 2011a) we find that the probability of an individual GC coinciding by chance with an unrelated Galactic source based on its latitude is less than 10-3 for all GCs in this sample. The second cut excludes GCs that were only observed at very large offset angles from the camera center, because such observation runs would only provide relatively low effective exposure. With the third cut we make sure that there is a reasonably long exposure on these potentially faint sources. In addition we excluded Terzan 5 from this study because those results were recently covered in a separate paper (see Abramowski et al. 2011a). Table 1 lists the 15 GCs passing these cuts. We note that one of the GCs, M 54, is actually not Galactic but most likely belongs to Sagittarius Dwarf Elliptical Galaxy (Ibata et al. 1994).
Most of the GC positions were either serendipitously covered in the H.E.S.S. Galactic plane survey (see Aharonian et al. 2006b; Gast et al. 2012) or lie in the same FoV as other sources observed with H.E.S.S. Therefore, the offsets of the GCs with respect to the camera center show a larger run-by-run scatter and in many cases larger mean values (see Table 1) compared to dedicated source observations. However, with a maximum allowed offset of 20 for individual runs (i.e. “cut 2”) the dataset is still in a range where the analysis is very well calibrated. Also, the H.E.S.S. observations have been carried out during a time span of about six years where the gains of the photo multipliers and the optical reflectivity of the mirrors changed. To correct for these effects we calibrate the energy scale of the instrument using the response to single muons (see Aharonian et al. 2006a).
Analysis results and model predictions.
2.2. Analysis of individual GCs
We applied the standard quality selection cuts on the H.E.S.S. observational runs to reject data affected by bad weather conditions or poor instrument performance (see Aharonian et al. 2006a). For the analysis we used the model technique where the air showers are described by a semi-analytical model. The expected camera images are then compared to the observational data based on a maximum likelihood method (see de Naurois & Rolland 2009). The model analysis yields an improved sensitivity, particularly at lower energies, and a more efficient Gamma-Hadron separation compared to the standard Hillas approach. We used standard cuts for the model analysis which include a 60 photo electron cut on the image size. With this configuration the model analysis features a PSF with a 68% containment radius of 007 on average. We cross-checked all results with an independent calibration using a Hillas analysis framework, which employs a machine-learning algorithm based on Boosted Decision Trees (Ohm et al. 2009).
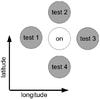 |
Fig. 1 Scheme showing the orientation of the four offset test regions with respect to the on-source region, aligned to the Galactic coordinate system. The offsets are 04 in both directions and are defined such that region “test 4" is always closer to the Galactic plane than region “test 2”. |
To search for VHE γ-ray emission from each GC we performed two different kinds of analyses where the size of the emission region was assumed to be either a) point-like (01 integration radius) or b) extended while using the nominal GC position as the center of the extraction region (see Table 1). For case b) we determined the expected intrinsic size (with the effects of the PSF removed) of the source related to each GC based on the measured extent of the VHE γ-ray source HESS J1747−248 detected from the direction of Terzan 5 (Abramowski et al. 2011a). The morphology of HESS J1747−248 was fitted with an asymmetrical 2-dimensional Gaussian with intrinsic major and minor axes of 016 and 003, respectively. Assuming that the physical size of the VHE γ-ray source is the same among all GCs, we scaled the angular size of the major axis of HESS J1747−248 with the relative distance of each individual GC (as given by H10) and Terzan 5 (dT5 = 5.9 kpc, Ferraro et al. 2009). We note here that HESS J1747−248 is not only extended but also offset by from the center of Terzan 5. Should such offsets be a general feature of VHE γ-ray emission from GCs this would also affect the regions for analysis b). However, the reason for this offset has not been attributed to any physical parameter of Terzan 5 and particularly its direction for other GCs is therefore not easily predictable. Keeping the regions centered on the nominal GC positions but increasing the radius to also account for a potential offset could increase the fraction of the emission covered by the extraction region. However, this would also heavily increase the number of background counts, thereby decreasing the sensitivity. Due to this fact, and since the offset seen from Terzan 5 is much less significant than the intrinsic extent of the signal, we decided to not include the offset in the determination of the expected source size. To define the final extraction region for analysis b) we assumed a 2-dimensional gaussian morphology with the width of the expected intrinsic size, folded with the H.E.S.S. PSF. The radius of the extraction region was then the 68% containment radius of the folded distribution. These radii are listed in Table 2. Note that for the two GCs NGC 6715 and HP 1 the calculated intrinsic size was negligible (<1% of the size of the PSF) and we therefore considered the point-like analysis results also for case b).
For the analyses we used the reflected background technique (see Berge et al. 2007), which ensures that the regions used for signal (ON) and background (OFF) extraction have the same acceptance in the FoV of the camera. In Table 2 we present the results for both analyses and for each individual GC. From none of the GCs, neither with analysis a) nor b), significant excess emission is seen above the estimated background, as the individual significances for a detection, even pre-trials, are well below the threshold of 5σ. The mean (rms) values of the significance distributions are 0.30 (1.0)σ and 0.34 (1.1)σ for analysis a) and b), respectively. Thus, the significance distributions are reasonably compatible with only background fluctuations within statistical uncertainties. We derived upper limits for the photon flux above the energy threshold (99% confidence level, following Feldman & Cousins 1998) assuming a power-law spectrum for the photon flux 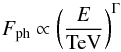 (1)with an index of Γ = −2.5, which we chose to allow for a comparison with the results obtained for Terzan 5 (ΓT5 = −2.5 ± 0.3stat ± 0.2sys, Abramowski et al. 2011a). Varying the assumed spectral index between −2.0 and −3.0 changes the upper limit by only 10% to 15%.
(1)with an index of Γ = −2.5, which we chose to allow for a comparison with the results obtained for Terzan 5 (ΓT5 = −2.5 ± 0.3stat ± 0.2sys, Abramowski et al. 2011a). Varying the assumed spectral index between −2.0 and −3.0 changes the upper limit by only 10% to 15%.
Results for on-source and offset regions.
As a cross check, we performed analyses with identical parameters for four test positions in the vicinity of each GC. These regions are offset by ±04 in Galactic coordinates (see Fig. 1). At this distance in no case a contamination from the supposed GC sources would be expected. The purpose of these test positions is to generate a sample of source-free regions with a similar distribution in Galactic coordinates as the GC positions while still using a dataset comparable to the on-source regions. Also, because the region test 4 is always closer to the Galactic plane than the other regions, particularly test 2, one can study the effects that the Galactic latitude may have on this particular population study. In Table 3 we show the parameters of the significance distributions for the on-source and the four test regions. As is evident from these results, we did not detect a significant signal from any of these regions. Even though there appears to be a slight tendency towards negative significances for the test regions, the absolute mean values are very small and nothing substantial can be concluded from that apparent shift. To estimate the background for the test regions we excluded the on-source area. Therefore, the slight shift towards negative significances for test 1 to test 4 cannot be explained by a faint signal related to the GCs, which could have otherwise led to an overestimation of the background.
2.3. Stacking analysis
Because no individual GC studied in this sample shows significant VHE γ-ray emission, we performed a stacking analysis to search for a population of faint emitters. To combine the analysis results and count-statistics from the observation runs of all GCs we applied the same method that is used to combine the results for analyses of individual sources: the total number of ON (OFF) counts is the sum over all ON (OFF) counts of the runs in the stack. We calculated the ratio between the ON and OFF exposure (α) as the weighted mean of α of all observation runs with the weight being the number of OFF counts per run. The energy-dependent effective area of the stack is calculated as the average over all runs, weighted with the livetime.
The total GC stack has an acceptance-corrected livetime of 195 h of good quality data and features an energy threshold of 0.23 TeV. We performed the stacking analysis for both the point-like and extended source analyses described in the previous section. The results are shown in Table 2. The total detection significances obtained with these stacking analyses are 1.6σ and 2.4σ, respectively, which are also very well below the threshold of 5σ required for a firm detection. Therefore, we calculated upper limits on the photon flux for the full stack, again assuming a power-law spectrum with an index of Γ = −2.5 (see Table 2).
For comparison we also performed the stacking analyses on each of the four offset test regions as defined in the previous section. The stacked significances obtained for these regions are systematically lower than for the on-source positions (see Table 3). However, the differences are not sufficiently significant to draw any firm conclusions at this point.
3. Discussion
Even though neither any individual GC nor the stack as a whole revealed a significant γ-ray signal, the resulting upper limits on the photon flux can still be used to investigate models based on IC emission from leptons accelerated by msPSRs. All statements below rely on the assumption that the size of the potential emission region is covered by either of the two analysis methods we employed for this study. Given the angular resolution of H.E.S.S., a point-like source would basically mean that the leptons are contained within a <4′ radius around the GC center. For the analyses searching for extended emission we assumed that the physical size of the emission region is the same among all GCs, using the intrinsic extent of HESS J1747−248 as a template. This would be justified if HESS J1747−248 is indeed related to the msPSR/IC scenario, if the leptons can propagate out of the half-mass region (for some smaller GCs even out of the tidal radius), and if the diffusion and energy-loss mechanisms as well as the age of the lepton population are comparable among all GCs.
Now, assuming that HESS J1747−248 is indeed related to Terzan 5 and that the msPSR/IC scenario is the dominant process for VHE γ-ray emission, the IC flux should scale as: 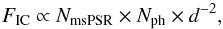 (2)with the number of msPSRs NmsPSR, the total number of available target photons in the volume occupied by relativistic leptons for the IC process Nph and the distance to the GC d (Eq. (2) is essentially the same as Eq. (8) in Venter & de Jager 2008). This simple scaling relation is of course only valid if the mechanisms for lepton production are similar among all GCs and, particularly, if the lepton energy spectra and the acceleration efficiencies of the msPSR populations are comparable. In this case the proportionality constant in Eq. (2) can be fixed using the flux of HESS J1747−248, which then allows to calculate the expected VHE γ-ray flux for the other GCs. In addition to the parameters given in Eq. (2) also the energy density of the ambient magnetic field in the emission region influences the IC flux due to the competing synchrotron radiation losses. However, this only changes our predicted IC fluxes if the magnetic field strengths (BGC) for the 15 GCs are different from the one in Terzan 5 (BT5). In this case the expected IC flux should be scaled by an additional factor of
(2)with the number of msPSRs NmsPSR, the total number of available target photons in the volume occupied by relativistic leptons for the IC process Nph and the distance to the GC d (Eq. (2) is essentially the same as Eq. (8) in Venter & de Jager 2008). This simple scaling relation is of course only valid if the mechanisms for lepton production are similar among all GCs and, particularly, if the lepton energy spectra and the acceleration efficiencies of the msPSR populations are comparable. In this case the proportionality constant in Eq. (2) can be fixed using the flux of HESS J1747−248, which then allows to calculate the expected VHE γ-ray flux for the other GCs. In addition to the parameters given in Eq. (2) also the energy density of the ambient magnetic field in the emission region influences the IC flux due to the competing synchrotron radiation losses. However, this only changes our predicted IC fluxes if the magnetic field strengths (BGC) for the 15 GCs are different from the one in Terzan 5 (BT5). In this case the expected IC flux should be scaled by an additional factor of 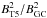 .
.
The total number of msPSRs is difficult to access directly in a homogeneous way for all 15 GCs in this study. This is mainly due to the fact that the various radio surveys feature varying or unknown degrees of completeness, which becomes a very problematic issue for such a large sample of GCs. As an alternative to the number count of detected radio msPSRs the total HE γ-rays flux measured with Fermi/LAT could also be used as a direct indicator for the msPSR population. However, the GeV measurements suffer from large statistical uncertainties and are only available for two GCs in this sample.
Here, we rely on a more indirect approach to estimate NmsPSR by using the stellar encounter rate 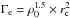 which is strongly correlated to the number of neutron star X-ray binaries, the progenitors of msPSRs (see, e.g. Pooley & Hut 2006, and references therein). Here ρ0 and rc denote the central luminosity density and the core radius of the GC, respectively. It has also been shown that Γe is correlated with the HE γ-ray flux (Abdo et al. 2010b; Hui et al. 2010). However, there might be systematic uncertainties in using Γe as a proxy for NmsPSR because the efficiency for the formation of msPSRs also depends on other parameters such as the metallicity of the GC (see e.g. Ivanova et al. 2008). Assuming that Γe is indeed proportional to NmsPSR and that the proportionality constant is the same for all GCs, Eq. (2) then reads:
which is strongly correlated to the number of neutron star X-ray binaries, the progenitors of msPSRs (see, e.g. Pooley & Hut 2006, and references therein). Here ρ0 and rc denote the central luminosity density and the core radius of the GC, respectively. It has also been shown that Γe is correlated with the HE γ-ray flux (Abdo et al. 2010b; Hui et al. 2010). However, there might be systematic uncertainties in using Γe as a proxy for NmsPSR because the efficiency for the formation of msPSRs also depends on other parameters such as the metallicity of the GC (see e.g. Ivanova et al. 2008). Assuming that Γe is indeed proportional to NmsPSR and that the proportionality constant is the same for all GCs, Eq. (2) then reads: 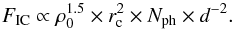 (3)To calculate FIC we used the values for ρ0, d and rc (converted to units of pc using d) as given by H10. For Nph we used four different target photon fields: 1) the optical light from the GC stars, 2) the Galactic infrared and 3) the Galactic optical background photon fields (as used in GALPROP1, Porter & Strong 2005) at the location of the GC (as given by H10), and finally 4) the CMB. The number of photons in case 1) is approximately proportional to the V-band luminosity of the globular cluster, which we chose for Nph using the values given in H10. For cases 2), 3) and 4) Nph is proportional to the energy density of the respective radiation fields. To compare the expected IC flux with the upper limits we first calculated for each GC the VHE γ-ray flux of HESS J1747−248 above the respective energy threshold, using the published results (Abramowski et al. 2011a): flux normalization at 1 TeV: (5.2 ± 1.1) × 10-13 cm-2 s-1 TeV-1, and power-law spectral index: −2.5 ± 0.3stat ± 0.2sys. We then used this flux to determine the proportionality constant in Eq. (3), which in turn yields the expected IC flux for the respective GC. Here we considered two extreme cases, namely that the leptons are either confined within the core region where the GC starlight is the dominant target photon field, or that the particles have propagated far away from the core where the Galactic background fields and the CMB become the most important components. In the latter case we used the sum of the energy densities of the three photon fields as a proxy for Nph. The ratio between the flux upper limits and the expected IC flux are given for both cases in the last two columns of Table 2.
(3)To calculate FIC we used the values for ρ0, d and rc (converted to units of pc using d) as given by H10. For Nph we used four different target photon fields: 1) the optical light from the GC stars, 2) the Galactic infrared and 3) the Galactic optical background photon fields (as used in GALPROP1, Porter & Strong 2005) at the location of the GC (as given by H10), and finally 4) the CMB. The number of photons in case 1) is approximately proportional to the V-band luminosity of the globular cluster, which we chose for Nph using the values given in H10. For cases 2), 3) and 4) Nph is proportional to the energy density of the respective radiation fields. To compare the expected IC flux with the upper limits we first calculated for each GC the VHE γ-ray flux of HESS J1747−248 above the respective energy threshold, using the published results (Abramowski et al. 2011a): flux normalization at 1 TeV: (5.2 ± 1.1) × 10-13 cm-2 s-1 TeV-1, and power-law spectral index: −2.5 ± 0.3stat ± 0.2sys. We then used this flux to determine the proportionality constant in Eq. (3), which in turn yields the expected IC flux for the respective GC. Here we considered two extreme cases, namely that the leptons are either confined within the core region where the GC starlight is the dominant target photon field, or that the particles have propagated far away from the core where the Galactic background fields and the CMB become the most important components. In the latter case we used the sum of the energy densities of the three photon fields as a proxy for Nph. The ratio between the flux upper limits and the expected IC flux are given for both cases in the last two columns of Table 2.
In the simple scaling approach (Eq. (3)) to estimate the IC flux we assumed that the lepton spectral shapes as well as the acceleration efficiencies of the msPSR populations are comparable among all GCs, which might not be the case. Potential deviations could arise from different energy-loss and diffusion timescales, differences in particle (re-)acceleration mechanisms or the spectral shapes of the injection spectra. Those and other issues would need to be addressed by more detailed models for each individual GC. Apart from the systematics mentioned above, the parameters that are directly used in Eq. (3) are also subject to uncertainties, which are discussed below. The most impact by far for potential uncertainties comes from the distance d because FIC itself depends inverse-quadratically on d; also the values of ρ0 as well as rc are less strongly dependent on d. Unfortunately, the uncertainties of d are perhaps the most difficult to quantify because there are several different methods for distance determinations of GCs, each suffering from other systematic issues. Therefore, we decided here to use the distances quoted by H10 for all of the GCs studied in this work, to only rely on one method. Assuming an error margin for d of a factor of two (based on typical variations between different distance estimation methods) yields an uncertainty of a about a factor of five in the expected IC flux. Additionally, the confidence intervals of the spectral parameters of HESS J1747−248 (Abramowski et al. 2011a) introduce further uncertainties in the expected IC flux of about 20%, yielding a total error margin of a factor of ~5. To estimate the uncertainties of the predicted model flux from the full stacks, we assumed a factor of 5 uncertainty for each individual GC and propagated the errors. We show the resulting uncertainty band for the stacking analyses in the last two columns of Table 2.
With the optical light of the GC member stars as the target photon field, the flux upper limits for point-like emission from the two GCs NGC 6388 and NGC 7078 lie about one order of magnitude below the expected IC flux (see Table 2). This is mainly due to the fact that Terzan 5 is relatively faint in the V-band compared to many other GCs, which yields large expected IC fluxes for GCs with a similar or even larger stellar encounter rate Γe. Among all GCs studied here, given the uncertainties related to the predictions, only in these two cases the simple scaling model is challenged by our observational results. However, the fact that HESS J1747−248 is extended and offset beyond the half-mass-radius of Terzan 5 could point towards fast diffusion and long energy-loss timescales of the lepton population in Terzan 5. If this is indeed the case, then other target photon fields would be dominant over the GC starlight. Therefore, the results of the point-like analyses are better suited to be compared to the predictions with the GC starlight as target photon fields, whereas the results from the extended analyses are more relevant for the predictions based on Galactic background photons. We note here that for some GCs the Galactic background could still make a contribution to the IC flux even for regions close to the GC cores, an issue that is not taken into account in our scaling model. Looking at the results for the infrared and optical background photon fields, the upper limits do not allow for similarly strong constraints as in some cases when considering the GC starlight. Given the uncertainties related to the parameters in Eq. (3), the msPSR/IC scaling model cannot be ruled out for any of the GCs assuming Galactic background photons as IC target.
To make a statement about the GC sample as a whole, we derived the expected IC flux from the total stack by calculating the weighted mean flux from all GCs. As weights we used the acceptance-corrected livetimes of the individual clusters. The upper limits for the stack are about two orders of magnitude below the expectation for the GC starlight and at a level of ~50% for the external target photon fields (see bottom section of Table 2). In the first case, even considering the uncertainties, this seems to be quite a strong constraint on the simple msPSR/IC scaling model. Therefore, either the IC flux from GCs does not scale as expected, or the VHE γ-ray source near Terzan 5 is not related to msPSRs. However, for the second case, i.e. assuming background photon fields as the dominant IC target, the upper limits for the stack are compatible with expected fluxes, and therefore do not allow to put similarly strong constraints on the model.
There are many possibilities why Terzan 5 may stand out among the general GC population. In the msPSR/IC model the confinement of leptons in the emission region might be stronger in Terzan 5 compared to other GCs, which would lead to an accumulation of particles from earlier epochs that would therefore enhance the observed IC flux per msPSR. However, because HESS J1747−248 is extended and offset from the core, the trapping mechanism is required to work on similarly large spatial scales. A high interstellar magnetic field strength in the vicinity of Terzan 5 could provide such a trapping mechanism, but would also increase the synchrotron losses and therefore decrease the expected IC flux. These competing effects would need to be modeled in detail for each individual GC, and the results presented in this paper might yield interesting constraints.
As already mentioned in Sect. 1 there are also models that are not related to the msPSR/IC scenario which suggest that the VHE γ-ray emission is due to hadronic processes in a short gamma-ray burst remnant (Domainko 2011). Due to the extremely low rates of these catastrophic events of only ~10-4 yr-1 (Nakar 2007) it could be easily explained why only one GC stands out among the whole population.
4. Conclusions
Judging from recent HE and VHE γ-ray observations, GCs could feature interesting high-energy processes, and, in particular, could constitute a new class of sources in the VHE γ-ray regime, if the recently detected source HESS J1747−248 is indeed related to the GC Terzan 5.
To test the validity of the msPSR/IC scenario for VHE γ-ray emission, we analyzed the H.E.S.S. data of 15 Galactic GCs. According to our observations, neither any individual GC nor the stacking analyses show significant excess emission above the estimated background. Based on a simple model for IC emission and the measured VHE γ-ray flux of HESS J1747−248 we calculated predictions for the fluxes for each individual GC and compared them with the derived upper limits.
The non-detections of the two GCs NGC 6388 and NGC 7078 challenge the simple IC scaling model when assuming the GC starlight as the dominant target photon field. However, when searching for VHE γ-ray emission from a larger scale, comparable to what is seen from Terzan 5, and considering Galactic optical, infrared and CMB photons as the dominant IC target, no clear constraints can be put on our simple msPSR/IC scaling model. The upper limits derived from the stacking analyses are about two orders of magnitude below the expected cumulative IC flux from the whole GC sample when assuming the GC starlight as the dominant target photon field. Taking the uncertainties of those parameters into account that directly influence our flux predictions, these results still exclude the simple msPSR/IC scaling model for this case. But, as mentioned in Sect. 3, there are several caveats to the simple scaling model applied here that would have to be considered in more elaborate and custom-tailored models for each individual GC. Also, there is still the possibility that the VHE γ-ray signal from Terzan 5 might not be related to the msPSRs at all and arises from hadronic or other processes.
Further studies of GCs are still ongoing and future deep observations with Cherenkov telescopes and X-ray observatories of the most promising candidates will increase the strength of the derived upper limits, or might even facilitate another detection next to Terzan 5.
Acknowledgments
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the U.K. Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, Science, 325, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, A&A, 187, 460 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, A&A, 524, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. (H.E.S.S. Collaboration) 2011a, A&A, 531, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. (H.E.S.S. Collaboration) 2011b, ApJ, 735, 12 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H.E.S.S. Collaboration) 2006a, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H.E.S.S. Collaboration) 2006b, ApJ, 636, 777 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. (H.E.S.S. Collaboration) 2009, A&A, 499, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderhub, H., Antonelli, L. A., Antoranz, P., et al. 2009, ApJ, 702, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., & Sitarek, J. 2007, MNRAS, 377, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Benbow, W. 2005, in High Energy Gamma-Ray Astronomy, eds. F. A. Aharonian, H. J. Völk, & D. Horns, AIP Conf. Ser., 745, 611 [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [Google Scholar]
- Camilo, F., & Rasio, F. A. 2005, in Binary Radio Pulsars, eds. F. A. Rasio &. I. H. Stairs, ASP. Conf. Ser., 328, 147 [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., Hui, C. Y., & Kong, A. K. H. 2010, ApJ, 723, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- de Naurois, M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Domainko, W. F. 2011, A&A, 533, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eger, P., & Domainko, W. 2012, A&A, 540, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eger, P., Domainko, W., & Clapson, A.-C. 2010, A&A, 513, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
- Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Freire, P. C. C., Abdo, A. A., Ajello, M., et al. 2011, Science, 334, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Gast, H. et al. (H.E.S.S. Collaboration) 2012, ICRC 2011 [Google Scholar]
- Harris, W. E. 2010, [arXiv:1012.3224] (H10) [Google Scholar]
- Hillas, A. M. 1985, in International Cosmic Ray Conf. 3, ed. F. C. Jones, 445 [Google Scholar]
- Hui, C. Y., Cheng, K. S., & Taam, R. E. 2010, ApJ, 714, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Heinke, C. O., Rasio, F. A., Belczynski, K., & Fregeau, J. M. 2008, MNRAS, 386, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kabuki, S., Enomoto, R., Bicknell, G. V., et al. 2007, ApJ, 668, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., Hui, C. Y., & Cheng, K. S. 2010, ApJ, 712, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- McCutcheon for the VERITAS Collaboration 2009, ICRC 2009 [Google Scholar]
- Nakar, E. 2007, Phys. Rep., 442, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Ohm, S., van Eldik, C., & Egberts, K. 2009, Astropart. Phys., 31, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., & Hut, P. 2006, ApJ, 646, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., Lewin, W. H. G., Anderson, S. F., et al. 2003, ApJ, 591, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., & Strong, A. W. 2005, in ICRC, 4, 77 [Google Scholar]
- Ransom, S. M. 2008, Dynamical Evolution of Dense Stellar Systems, 246, 291 [NASA ADS] [Google Scholar]
- Tam, P. H. T., Kong, A. K. H., Hui, C. Y., et al. 2011, ApJ, 729, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Venter, C., & de Jager, O. C. 2008, in AIP Conf. Ser. 1085, eds. F. A. Aharonian, W. Hofmann, & F. Rieger, 277 [Google Scholar]
- Venter, C., de Jager, O. C., & Clapson, A. C. 2009, ApJ, 696, L52 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Scheme showing the orientation of the four offset test regions with respect to the on-source region, aligned to the Galactic coordinate system. The offsets are 04 in both directions and are defined such that region “test 4" is always closer to the Galactic plane than region “test 2”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


