| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220697 | |
| Published online | 22 February 2013 | |
Maximum mass of neutron stars and strange neutron-star cores
N. Copernicus Astronomical Center, Polish Academy of Sciences,
Bartycka 18,
00-716
Warszawa,
Poland
e-mail: jlz@camk.edu.pl; haensel@camk.edu.pl
Received:
6
November
2012
Accepted:
15
January
2013
Context. The recent measurement of mass of PSR J1614-2230 rules out most existing models of the equation of state (EOS) of dense matter with high-density softening due to hyperonization that were based on the recent hyperon-nucleon and hyperon-hyperon interactions, which leads to a “hyperon puzzle”.
Aims. We study a specific solution of this hyperon puzzle that consists of replacing a too soft hyperon core by a sufficiently stiff quark core. In terms of the quark structure of the matter, one replaces a strangeness-carrying baryon phase of confined quark triplets, some of them involving s quarks, by a quark plasma of deconfined u, d, and s quarks.
Methods. We constructed an analytic approximation that fits modern EOSs of the two flavor (2SC) and the color-flavor-locked (CFL) color-superconducting phases of quark matter very well. Then, we used it to generate a continuum of EOSs of quark matter. This allowed us to simulate continua of sequences of first-order phase transitions at prescribed pressures, from hadronic matter to the 2SC and then to the CFL state of color-superconducting quark matter.
Results. We obtain constraints in the parameter space of the EOS of superconducting quark cores, EOS.Q, resulting from Mmax > 2 M⊙. These constraints depend on the assumed EOS of baryon phase, EOS.B. We also derive constraints that would result from significantly higher measured masses. For 2.4 M⊙ the required stiffness of the CFL quark core is close to the causality limit while the density jump at the phase transition is very small.
Conclusions. The condition Mmax > 2 M⊙ puts strong constraints on the EOSs of the 2SC and CFL phases of quark matter. Density jumps at the phase transitions have to be sufficiently small and sound speeds in quark matter sufficiently large. The condition of thermodynamic stability of the quark phase results in a maximum mass of hybrid stars similar to that of purely baryon stars. This is due to the phase transition of quark matter back to the baryon phase (reconfinement) that we find for both EOS.B. Therefore, to obtain Mmax > 2 M⊙ for hybrid stars, both sufficiently strong additional hyperon repulsion at high-density baryon matter and a sufficiently stiff EOS of quark matter would be needed. However, we think that the high-density instability, which results in the reconfinement of quark matter, indicates actually the inadequacy of the point-particle model of baryons in dense matter at ρ ≳ 5 ÷ 8ρ0. We expect that reconfinement can be removed by a sufficient stiffening of the baryon phase, resulting from the repulsive finite size contribution for baryons to the EOS.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2013
1. Introduction
The mass of PSR J1614-2230, 1.97 ± 0.04 M⊙ (Demorest et al. 2010), puts a constraint on the equation of state (EOS) of dense matter in neutron star (NS) cores. This is that the maximum allowable mass calculated using an acceptable EOS, Mmax(EOS), should be greater than 2.0 M⊙. This proves to be of crucial importance for strong interactions in NS cores: their repulsive effect triples the value of Mmax compared to that obtained for non-interacting Fermi gas of neutrons, 0.7 M⊙.
The observational constraint
Mmax(EOS) > 2.0 M⊙
is easy to satisfy if NS cores contain nucleons only, and realistic nuclear forces are used,
from which we derive  for many realistic
nucleon interaction models (Lattimer 2011). However,
nuclear interaction models, consistent with experimental data on hypernuclei, predict the
presence of hyperons at densities exceeding 2−3ρ0, where the
normal nuclear density is
ρ0 = 2.7 × 1014 g cm-3 (baryon number
density n0 = 0.16 fm-3). Hyperonization of the
matter implies a softening of the EOS through replacement of most energetic neutrons by
massive, slowly moving hyperons. For realistic models of baryon interactions one obtains
for many realistic
nucleon interaction models (Lattimer 2011). However,
nuclear interaction models, consistent with experimental data on hypernuclei, predict the
presence of hyperons at densities exceeding 2−3ρ0, where the
normal nuclear density is
ρ0 = 2.7 × 1014 g cm-3 (baryon number
density n0 = 0.16 fm-3). Hyperonization of the
matter implies a softening of the EOS through replacement of most energetic neutrons by
massive, slowly moving hyperons. For realistic models of baryon interactions one obtains
 (see, e.g. Burgio et al. 2011; Vidana
et al. 2011; Schulze & Rijken 2011,
and references therein). Such a low Mmax is only marginally
consistent with 1.44 M⊙ of the Hulse-Taylor pulsar, but was
contradicted by 1.67 ± 0.04 M⊙ of PSR J1903-0327 (Champion et al. 2008; a more precise value has been
recently obtained by Freire et al. 2011).
(see, e.g. Burgio et al. 2011; Vidana
et al. 2011; Schulze & Rijken 2011,
and references therein). Such a low Mmax is only marginally
consistent with 1.44 M⊙ of the Hulse-Taylor pulsar, but was
contradicted by 1.67 ± 0.04 M⊙ of PSR J1903-0327 (Champion et al. 2008; a more precise value has been
recently obtained by Freire et al. 2011).
Two solutions of the problem of a too low  have been proposed after the discovery of a 2 M⊙ pulsar.
have been proposed after the discovery of a 2 M⊙ pulsar.
Strong hyperon repulsion at high density. It has been suggested that adding a new component to the hyperon-hyperon interaction, important for ρ ≳ 5ρ0, can stiffen the high-density EOS.B sufficiently to yield Mmax > 2.0 M⊙. Repulsive interaction between baryons is supplied by the exchange of vector mesons (spin = 1). Hyperon repulsion due to an exchange of vector φ mesons allows for Mmax > 2.0 M⊙, without spoiling the agreement with nuclear and hyper-nuclear data (Bednarek et al. 2012; Weissenborn et al. 2012a,b; Łastowiecki et al. 2012). Dexheimer & Schramm (2008) give an earlier general discussion of vector-meson contribution to EOS. An additional increase of Mmax (above 2.1−2.2 M⊙) can be obtained via some breaking of the SU(6) symmetry, which is usually applied to generate vector-meson – hyperon coupling constants from the nucleon one (Weissenborn et al. 2012b). Hyperon repulsion at high density is limited by the condition of thermodynamic stability (Bednarek et al. 2012).
Stiff quark cores in NS. From the point of view of quantum chromodynamics (QCD), the appearance of hyperons in dense matter is associated with the presence of the s-quarks, in addition to the u and d quarks confined in nucleons. Some authors suggested that the hyperon core in NS could actually be replaced by a core of the u-d-s quark matter (Baldo et al. 2006 and references in Schulze & Rijken 2011). We denote the EOS of the u-d-s quark matter by EOS.Q. To yield Mmax > 2.0 M⊙, quark matter needs to have two important (necessary) features: (1) a significant overall quark repulsion resulting in a stiff EOS.Q; (2) a strong attraction in a particular channel, resulting in a strong color superconductivity, which is needed to make the deconfined Q-phase energetically preferred over the confined B(baryon) phase. After the announcement of the discovery of a 2 M⊙ pulsar, several models of quark cores of NS (hybrid stars), with the necessary properties to yield Mmax > 2.0 M⊙, have been proposed (Özel et al. 2010; Weissenborn et al. 2011; Klaehn et al. 2012; Bonanno & Sedrakian 2012; Łastowiecki et al. 2012; Lenzi & Lugones 2012). The EOS of the hybrid baryon-quark (BQ) stars (EOS.BQ) was constructed using a two-phase model of B→Q transition, with different underlining theories of the B and Q phases.
There exist many models of color-superconducting quark matter states (see, e.g., Alford et al. 2008). The two basic states are the two-flavor color-superconducting (2SC) state and the color-flavor-locked (CFL) superconducting state. In the 2SC state only light u and d quarks are paired. The 2SC state is predicted to be the ground state of quark matter at nb ≲ 4n0. On the other hand, the CFL superconductor, in which all three flavors are paired, is predicted to prevail at high density, nb ≳ 4n0. Hybrid stars with a double phase transition B→Q.2SC→Q.CFL were first considered by Pagliara & Schaffner-Bielich (2008). Other superconducting quark-matter states, different from 2SC and CFL, were also predicted (Alford et al. 2008), but they will not be considered here.
In the present paper we derive constraints on the EOS.BQ using an analytical description of EOS.Q. This allows us to consider a continuum of the EOS.Q models, or, for a given EOS.B, a continuum of the EOS.BQ models. As other authors, we use a two-phase description of first-order phase transitions (no mixed-phase state; neglecting possibility of a mixed-phase state does not influence the value of Mmax much, see, e.g., Alford et al. 2005). We also discuss the thermodynamic stability of the Q phase in stiff quark cores and its impact on Mmax (this problem has been mentioned previously in Łastowiecki et al. 2012).
The EOSs of baryon matter used in our work are described in Sect. 2. In Sect. 3 we construct an
analytic approximation of the EOS of quark matter, and we show that it gives a precise
approximation of several existing models of color-superconducting quark cores in NS. Our
analytic approximation is then used to construct a continuum of EOS.Q, suitable for
constructing an EOS.BQ with phase transitions at prescribed pressures, for a given EOS.B. In
Sect. 3.2 we construct continua of the EOS.BQ models
for two models of EOS.B: a soft one that significantly violates a
2.0 M⊙ bound, and a stiff one that satisfies this bound.
Constraints on EOS.Q, resulting from  , are derived in
Sect. 4. We then study in Sect. 5 the thermodynamic stability of a stiff high-density quark matter.
Finally, in Sect. 6 we summarize and discuss our
results, and point out the weak points of our models.
, are derived in
Sect. 4. We then study in Sect. 5 the thermodynamic stability of a stiff high-density quark matter.
Finally, in Sect. 6 we summarize and discuss our
results, and point out the weak points of our models.
Preliminary results of our work were presented at the ERPM Pulsar Conference, Zielona Góra, Poland, 24th–27th April, 2012.
2. EOSs of baryon matter
There are two types of existing EOS.B, which lead to Mmax < 2 M⊙ and Mmax > 2 M⊙, respectively. They will be hereafter referred to as soft-baryon EOS and stiff-baryon EOS. We will select one EOS belonging to each of these two groups and use them to illustrate the features characteristic of the two types of EOS.B.
2.1. Soft-baryon EOS
Most existing EOS.Bs yield an  significantly lower than 2 M⊙. Replacing a soft hyperon core
by a stiff quark one seems to be the only way to obtain
Mmax > 2 M⊙1. As an example, we consider the very recent EOS.B of
Schulze & Rijken (2011). This EOS was
obtained using the Brueckner-Hartree-Fock many-body approach and a realistic up-to-date
baryon interaction. In the nucleon sector, an Argonne V18 nucleon-nucleon
potential (Wiringa et al. 1995) was used,
supplemented with a phenomenological three-body force (Li
et al. 2008). The hyperon-nucleon and hyperon-hyperon potentials were Nijmegen
ESC08 (Rijken et al. 2010a,b). This EOS.B gives a low
significantly lower than 2 M⊙. Replacing a soft hyperon core
by a stiff quark one seems to be the only way to obtain
Mmax > 2 M⊙1. As an example, we consider the very recent EOS.B of
Schulze & Rijken (2011). This EOS was
obtained using the Brueckner-Hartree-Fock many-body approach and a realistic up-to-date
baryon interaction. In the nucleon sector, an Argonne V18 nucleon-nucleon
potential (Wiringa et al. 1995) was used,
supplemented with a phenomenological three-body force (Li
et al. 2008). The hyperon-nucleon and hyperon-hyperon potentials were Nijmegen
ESC08 (Rijken et al. 2010a,b). This EOS.B gives a low  (Schulze & Rijken 2011). It will hereafter be referred to as SR
one.
(Schulze & Rijken 2011). It will hereafter be referred to as SR
one.
2.2. Stiff-baryon EOS
The number of EOS.B that satisfy
Mmax > 2 M⊙
started to increase steadily after the discovery of a 2 M⊙
pulsar. We selected the BM165 EOS.B of Bednarek et al.
(2012). This EOS was obtained using a non-linear relativistic mean field model
involving the baryon octet coupled to meson fields. The effective Lagrangian includes, in
addition to scalar and vector-meson terms, also terms involving a hidden-strangeness
scalar and a vector-meson coupled to hyperons only. For this EOS.B we obtain
 . It will hereafter be
referred to as BM165.
. It will hereafter be
referred to as BM165.
3. Quark-matter cores and their EOS
We consider electrically neutral u-d-s quark matter in beta equilibrium and at
T = 0. The baryon number density is
 , the
energy density is denoted ℰ, the matter density
ρ = ℰ/c2, and the baryon
chemical potential
μb = dℰ/dnb. An
important relation is
nb = dP/dμb.
The phase transitions under consideration are assumed to be first-order transitions.
Therefore, they occur at a specific (sharp) value of pressure, and are accompanied by a
density jump from ρ1 to ρ2. This is
a good approximation for the B→Q phase transition in cold dense matter, because the
smoothing effect of the mixed B-Q state is weak and can be neglected (Endo et al. 2006, and references therein). An important parameter
characterizing the density jump at the interface between the two phases is
λ = ρ2/ρ1.
Indeed, as we mentioned in Sect. 1, including of a
mixed-phase state does not change, to a very good approximation, the value of
Mmax (Alford et al.
2005).
, the
energy density is denoted ℰ, the matter density
ρ = ℰ/c2, and the baryon
chemical potential
μb = dℰ/dnb. An
important relation is
nb = dP/dμb.
The phase transitions under consideration are assumed to be first-order transitions.
Therefore, they occur at a specific (sharp) value of pressure, and are accompanied by a
density jump from ρ1 to ρ2. This is
a good approximation for the B→Q phase transition in cold dense matter, because the
smoothing effect of the mixed B-Q state is weak and can be neglected (Endo et al. 2006, and references therein). An important parameter
characterizing the density jump at the interface between the two phases is
λ = ρ2/ρ1.
Indeed, as we mentioned in Sect. 1, including of a
mixed-phase state does not change, to a very good approximation, the value of
Mmax (Alford et al.
2005).
3.1. Analytical approximation – 2SC and CFL phases
Our method is based on the observation that starting from a simple linear formula one is
able to obtain a very precise analytic representation of modern
EOS.Q( )
in a phase
)
in a phase  = 2SC,CFL, of color-superconducting quark matter under conditions prevailing in NS cores.
In what follows, we omit for simplicity the phase label
= 2SC,CFL, of color-superconducting quark matter under conditions prevailing in NS cores.
In what follows, we omit for simplicity the phase label
 unless noted otherwise.
unless noted otherwise.
A linear EOS (P being a linear function of ρ) is characteristic of the simplest bag model of quark matter that assumes massless quarks, but it also holds with very high accuracy for a more realistic bag model with massive s-quarks (Zdunik 2000).
The linear EOS is determined by three parameters: a, ℰ∗, and
n∗, where a is the square of the sound
velocity in the units of c, and ℰ∗ and
n∗ are the energy and baryon number density at zero
pressure, respectively. We obtain then ![\begin{equation} \begin{array}{lcl} P({\cal E})&=&a ({\cal E}-{\cal E}_\ast)~,\\ \mu(P)&=&\mu_\ast\cdot\left[1+ (1+a)P/(a{\cal E}_\ast)\right]^{a/(1+a)}~,\\ n(P)&=&n_\ast\cdot\left[1+ (1+a)P/(a{\cal E}_\ast)\right]^{1/(1+a)}=n_\ast\left({\mu}/{\mu_\ast}\right)^{1/a},\end{array} \label{eq:lin} \end{equation}](/articles/aa/full_html/2013/03/aa20697-12/aa20697-12-eq49.png) (1)where
μ∗ = ℰ∗/n∗
is the baryon chemical potential at zero pressure. The stiffness of the matter is
described by the parameter
a = dP/dℰ = (vsound/c)2.
Special cases of linear EOSs with a = 1 and
a = 1/3 were recently considered by Chamel et al. (2012) in their study of exotic cores in
NS.
(1)where
μ∗ = ℰ∗/n∗
is the baryon chemical potential at zero pressure. The stiffness of the matter is
described by the parameter
a = dP/dℰ = (vsound/c)2.
Special cases of linear EOSs with a = 1 and
a = 1/3 were recently considered by Chamel et al. (2012) in their study of exotic cores in
NS.
Numerical results for a quark matter EOS are usually given as points in the P − μb plane (Agrawal 2010; Blaschke et al. 2010). These variables are very convenient to study the microscopic stability of matter and to determine the phase transition, which corresponds to the crossing point of the P(μ) relations for different phases. The density jump at phase transition is then described by the change of the slope of the P(μ) function through the relations n = dP/dμ and ℰ = nμ − P (see, e.g., Fig. 2).
We assume that the linear EOS, Eq. (1), accurately describes quark matter cores in NS, corresponding to the baryon density range 2n0 ≲ nb ≲ 10n0 We stress that the use of linear dependence, Eq. (1), is restricted to 2n0 − 10n0 (or 300 MeV fm-3 < ℰ < 1500 MeV fm-3, or 30 MeV fm-3 < P < 300 MeV fm-3), and by no means is claimed to be valid outside the neutron-star core regime.
We introduce dimensionless quantities:  and
and
 . We can then use
Eq. (1) to derive P as a
function of
. We can then use
Eq. (1) to derive P as a
function of  ,
,  (2)where
ν ≡ (1 + a)/a.
Then an analytical approximation for
(2)where
ν ≡ (1 + a)/a.
Then an analytical approximation for  reads
reads
 (3)The
determination of the value of n∗ deserves an additional
comment. It can be taken from original numerical calculations if available. If not
directly available, it can be calculated from the original plot of
P(calc)(μb) using
n∗ = (dP(calc)/dμb)μ∗.
(3)The
determination of the value of n∗ deserves an additional
comment. It can be taken from original numerical calculations if available. If not
directly available, it can be calculated from the original plot of
P(calc)(μb) using
n∗ = (dP(calc)/dμb)μ∗.
 |
Fig. 1 Calculated points of EOS of color-superconducting quark matter in the P − μb plane (Agrawal 2010) and their approximation by our analytical formula. See the text for additional details. (This figure is available in color in the electronic form.) |
 |
Fig. 2 Calculated points of EOS of color-superconducting quark matter in the P − μb plane (Blaschke et al. 2010) and their approximation by our analytical formula. See the text for additional details. (This figure is available in color in the electronic form.) |
We now pass to the specific cases of  = 2SC, CFL. The least-squares fit method results in the curves presented in Figs. 1 and 2. This fit
works very well and can also be checked by comparing the values of
n = dP/dμ with
exact results (if available, like in Agrawal 2010).
= 2SC, CFL. The least-squares fit method results in the curves presented in Figs. 1 and 2. This fit
works very well and can also be checked by comparing the values of
n = dP/dμ with
exact results (if available, like in Agrawal 2010).
2SC. In view of its intermediate-density range, 2n0 ≲ nb ≲ 4n0, the 2SC state is less important for Mmax than the high-density CFL state realized for nb > 4n0. However, as we will show, the softening caused by the density jump at the B-Q(2SC) transition has a significant indirect effect on the 2 M⊙ constraint imposed on the EOS of the CFL phase. We considered two numerical EOS.Q(2SC)s, calculated by Agrawal (2010) and two of Blaschke et al. (2010). All these EOSs were calculated using the Nambu – Jona-Lasinio (NJL) model of quark matter and color superconductivity. The NJL model is a non-perturbative low-energy approximation to QCD. As seen in Figs. 1 and 2, our analytic formulae fit the numerical results very precisely. It should be stressed that these analytical formulae also reproduce numerically calculated points in the P − nb plane very well, whenever these points are available, e.g., in Agrawal (2010). Our approximation in this case gives the value of parameter ν = 4.1 ÷ 4.6, which corresponds to a = 0.25 ÷ 0.33.
 |
Fig. 3 Examples of EOS.BQ from a continuum { EOS.BQ } emerging from a soft SR EOS. Hadronic EOSs are plotted as dashed lines: N – nucleon EOS; B – nucleons and hyperons. The phase transition B→Q(2SC) takes place at P1 = 31 MeV fm-3, and Q(2SC)→Q(CFL) at P2 = 45 MeV fm-3. The 2SC phase has a2SC = 0.302. Three examples of B → Q(2SC)→Q(CFL) are shown corresponding to following choices of { λ2SC,λCFL,aCFL }: { 1.05,1.2,0.57 }, { 1.15,1.1,0.58 }, { 1.3,1.1,0.7 }. In all these cases the maximum mass is equal to 2 M⊙, i.e., parameters { λ2SC,λCFL,aCFL } lie on the bounding curves in Fig. 7. (This figure is available in color in the electronic form.) |
 |
Fig. 4 Examples of EOS.BQ from a continuum { EOS.BQ } emerging from a stiff MB165 EOS. Hadronic EOSs are plotted as dashed lines: N – nucleon EOS (black); B – nucleons and hyperons (red). The phase transition B →Q(2SC) takes place at P1 = 47 MeV fm-3, a2SC = 0.302 and λ2SC = 1.3. EOS.Q(2SC) is plotted as a blue line. Two examples of Q(2SC)→Q(CFL) at P2 = 69 MeV fm-3 are shown, corresponding to a stiffer CFL phase (aCFL = 0.6, λ2SC = 1.3) and a softer phase (aCFL = 0.35, λ2SC = 1.5). The EOS.Q(CFL)s are plotted as green solid lines. (This figure is available in color in the electronic form.) |
CFL. The baryon density interval
4n0 ≲ nb ≲ 10n0
is crucial for the value of Mmax. Therefore, it is the EOS in
the CFL state that is decisive for the value of  . We
considered five numerical EOS of CFL superconducting quark matter, three models from Agrawal (2010) and two models from Blaschke et al. (2010). All of them were based on the NJL model. As we
see in Figs. 1 and 2, our analytical formulae are very precise. Similarly as for the 2SC phase,
these formulae also reproduce numerically calculated points in the
P − nb plane very well. The CFL phase is
stiffer than that of the 2SC phase: the values of a range within 0.3 and
0.4 (ν = 3.5 ÷ 4.3).
. We
considered five numerical EOS of CFL superconducting quark matter, three models from Agrawal (2010) and two models from Blaschke et al. (2010). All of them were based on the NJL model. As we
see in Figs. 1 and 2, our analytical formulae are very precise. Similarly as for the 2SC phase,
these formulae also reproduce numerically calculated points in the
P − nb plane very well. The CFL phase is
stiffer than that of the 2SC phase: the values of a range within 0.3 and
0.4 (ν = 3.5 ÷ 4.3).
3.2. A family of analytical models of EOS.BQ
We generalize now discrete sets  into a continuum of
three-parameter models
into a continuum of
three-parameter models  ,
within a region of parameter space determined by appropriate constraints on these
parameters. We assume that
0.2 < a < 0.8, while
2n0 < n < 10n0
and
10 MeV fm-3 < P < 300 MeV fm-3.
,
within a region of parameter space determined by appropriate constraints on these
parameters. We assume that
0.2 < a < 0.8, while
2n0 < n < 10n0
and
10 MeV fm-3 < P < 300 MeV fm-3.
After constructing a continuum of the EOS.Q( )
models, we are able to simulate, for a given EOS.B, a sequence of phase transition
B→Q(2SC)→Q(CFL).
)
models, we are able to simulate, for a given EOS.B, a sequence of phase transition
B→Q(2SC)→Q(CFL).
Transition from B to Q(2SC). We assume that B→Q(2SC) takes place at
P = P1. Three parameters of an EOS.Q(2SC)
taken from our family are then interrelated by two conditions at the B→Q(2SC) phase
transition point: the continuity of the baryon chemical potential, and the continuity of
the pressure,  (4)Upper
indices (B) and (2SC) refer to the baryon phase and the 2SC quark phase, respectively.
Now, we fix the EOS of baryon matter, EOS.B. Models of the phase transition to the 2SC
quark matter are then labeled by
P1 = P(B)(ℰ1) and the
relative density jump
λ2SC = ℰ2/ℰ1,
with thermodynamical parameters
(n1,n2,ℰ1,ℰ2)
satisfying Eqs. (4). Here, the index 1
refers to the B phase, and 2 to the 2SC phase.
(4)Upper
indices (B) and (2SC) refer to the baryon phase and the 2SC quark phase, respectively.
Now, we fix the EOS of baryon matter, EOS.B. Models of the phase transition to the 2SC
quark matter are then labeled by
P1 = P(B)(ℰ1) and the
relative density jump
λ2SC = ℰ2/ℰ1,
with thermodynamical parameters
(n1,n2,ℰ1,ℰ2)
satisfying Eqs. (4). Here, the index 1
refers to the B phase, and 2 to the 2SC phase.
Transition from Q(2SC) to Q(CFL). We now choose the pressure at which
the 2SC→CFL transition occurs, P = P2.
Using conditions of continuity of the pressure and of the baryon chemical potential at
P = P2, we obtain a one-parameter family
{ EOS.Q(CFL) } attached to a specific EOS.Q(2SC) from the previously
constructed { EOS.BQ(2SC) } family. A continuous parameter within
{ EOS.Q(CFL) } can be  or
or
 .
This completes the second step in the procedure of constructing a general family
{ EOS.BQ } with B→Q(2SC)→Q(CFL) phase transitions at prescribed
pressures P1 and P2, respectively.
.
This completes the second step in the procedure of constructing a general family
{ EOS.BQ } with B→Q(2SC)→Q(CFL) phase transitions at prescribed
pressures P1 and P2, respectively.
To have a “reference one-phase quark core” we also consider EOS.BQ(CFL), with a phase
transition from B directly to the CFL phase of quark matter, at pressure
 and
density
and
density  .
.
Direct transition from B to Q(CFL) at
 .
For
P1 < PCFL < P2
this EOS can be either softer or stiffer than in the case of B→2SC→CFL, depending on
the softness of the hyperonic EOS. This is illustrated in Fig. 3 where the “middle” model of the B→2SC transition (with
λ2SC = 1.15) gives a mean stiffness similar to
that of the hyperon (B) phase (i.e., pressures and densities at the bottom of CFL core are
almost the same in both cases).
.
For
P1 < PCFL < P2
this EOS can be either softer or stiffer than in the case of B→2SC→CFL, depending on
the softness of the hyperonic EOS. This is illustrated in Fig. 3 where the “middle” model of the B→2SC transition (with
λ2SC = 1.15) gives a mean stiffness similar to
that of the hyperon (B) phase (i.e., pressures and densities at the bottom of CFL core are
almost the same in both cases).
Several examples of EOS.BQ constructed following the procedure described above are shown in Figs. 3 and 4.
For two considered EOS.B, i.e., SR and BM165, we used two different choices of transition pressures P1 and P2. Here, P1 corresponds to the pressure at which in original models hyperons start to appear. For SR EOS P1 ≃ 30 MeV fm-3, while for BM165 EOS P1 ≃ 50 MeV fm-3. The thickness of the 2SC phase layer corresponds to ΔP = P2 − P1 ≈ 20 MeV fm-3. In both cases the pressure P1 corresponds to nb ≈ 2n0.
Strictly speaking, ΔP is an additional parameter of our model. In presenting the results in Figs. 3–7 we restricted ourselves to a ΔP similar to that of Agrawal (2010) and Blaschke et al. (2010). Lowering P2, which corresponds to replacing the 2SC phase by the CFL phase, results in a weaker constraint for aCFL implied by a 2 M⊙ pulsar. This tendency is visualized in Fig. 5 where we assume a direct transition B→CFL corresponding to ΔP = 0, and in Figs. 6 and 7 by the relative positions of the dashed and dotted curves.
4. Constraints on EOS.Q in the a− λ plane
 |
Fig. 5 Constraints on the a − λ plane, resulting from
Mmax > 2 M⊙,
obtained assuming SR EOS of baryon matter, and for purely CFL cores (no 2SC layer)
starting at
ρCFL = 1.7ρ0,...,4.0ρ0.
Densities 2.3ρ0 and 3.0ρ0
correspond to P1 and P2,
relevant for the boundaries of the 2SC layer in a 2SC+CFL core. Each line is an upper
boundary of the region of
(aCFL,λCFL)
consistent with
Mmax > 2 M⊙.
These lines are labeled by the density |
A first-order phase transition in the NS core affects the EOS in two ways. First, it softens it because λ > 1 implies some density range with dP/dρ = 0. Second, a new phase is either stiffer or softer than the less dense phase, the stiffness of the quark phase being determined by a. The condition Mmax > 2 M⊙ therefore imposes a condition in the a − λ plane. In what follows, we start with a case of a purely CFL quark core and then consider the quark core composed of an outer 2SC layer and an inner CFL core. Our results are illustrated by examples presented in Figs. 5–7. As in the preceding sections, we considered two EOS of baryon matter, a soft SR EOS, and a stiff BM165 EOS.
Pure CFL core. We consider EOS.BQ(CFL), with a quark core edge at
P = PCFL. We calculate a locus of
points in the
aCFL − λCFL
plane corresponding to Mmax = 2 M⊙.
This locus is a line  such that points
(a,λ) below it generate Q-cores that satisfy
Mmax > 2 M⊙,
while those above it violate this condition. We can alternatively call this locus line
such that points
(a,λ) below it generate Q-cores that satisfy
Mmax > 2 M⊙,
while those above it violate this condition. We can alternatively call this locus line
 . Of course the location of
lines
aCFL − λCFL
depends on the value of the pressure
. Of course the location of
lines
aCFL − λCFL
depends on the value of the pressure  (density
(density
 ) at which
the phase transition to the quark core (CFL) occurs. This dependence is presented in Fig.
5.
) at which
the phase transition to the quark core (CFL) occurs. This dependence is presented in Fig.
5.
2SC+CFL core, effect of a 2SC layer: general procedure.
We replace an outer layer of the matter in the B phase that contains hyperons (or a
layer of the CFL core with pressures
PCFL < P < P2),
with a layer of the 2SC phase. The effect of this additional layer of the 2SC phase depends
on the value of  . If
PCFL = P1, we replace
an outer layer of the CFL core with the quark matter in the 2SC phase. This will result in a
softening of the quark core since the 2SC phase is thought to be softer than the CFL phase
(due to a much smaller superfluid gap), and also because of an additional density jump
. If
PCFL = P1, we replace
an outer layer of the CFL core with the quark matter in the 2SC phase. This will result in a
softening of the quark core since the 2SC phase is thought to be softer than the CFL phase
(due to a much smaller superfluid gap), and also because of an additional density jump
 .
Even if
.
Even if  is very close to one, we obtain
is very close to one, we obtain  . However, the effect of the
2SC phase on the value of
. However, the effect of the
2SC phase on the value of  is then quite weak. With an increasing value of
is then quite weak. With an increasing value of  ,
the effect of softening increases, and an allowed region of
(aCFL,λCFL)
shrinks. In the limit of PCFL = P2
we replace baryon matter with the 2SC phase and the net effect depends on the relative
stiffness of these two phases (see Fig. 3 and the
discussion at the end of Sect. 3.2).
,
the effect of softening increases, and an allowed region of
(aCFL,λCFL)
shrinks. In the limit of PCFL = P2
we replace baryon matter with the 2SC phase and the net effect depends on the relative
stiffness of these two phases (see Fig. 3 and the
discussion at the end of Sect. 3.2).
 |
Fig. 6 Constraints on the a − λ plane, resulting from Mmax > 2 M⊙, obtained assuming a BM165 EOS of baryon matter and a quark core starting at P1 = 47 MeV fm-3. Each line is an upper boundary of the region of (aCFL,λCFL) consistent with Mmax > 2 M⊙. Solid lines are obtained for quark cores composed of a 2SC layer (P1 < P < P2) and a CFL core starting at P2 = 69 MeV fm-3. These lines are labeled by the density jump at the B-2SC interface λ2SC = 1.05,1.15,1.30. We used a2SC = 0.3 (Agrawal 2010). The dashed line is obtained for purely CFL cores (no 2SC layer) starting at P2, and the dotted line corresponds to purely CFL cores starting at P1, i.e., replacing the 2SC with the CFL phase. (This figure is available in color in the electronic form.) |
 |
Fig. 7 Constraints on the a − λ plane, resulting from Mmax > 2 M⊙, obtained assuming an SR EOS of baryon matter and a quark core starting at P1 = 31 MeV fm-3. Each line is an upper boundary of the region of (aCFL,λCFL) consistent with Mmax > 2 M⊙. The solid lines are obtained for quark cores composed of a 2SC layer (P1 < P < P2) and a CFL core starting at P2 = 45 MeV fm-3. These lines are labeled by the density jump at the B-2SC interface λ2SC = 1.05,1.15,1.30. We used a2SC = 0.3 (Agrawal 2010). The dashed line is obtained for purely CFL cores (no 2SC layer) starting at P2 = 45 MeV fm-3, and the dotted line corresponds to purely CFL cores starting at P1, i.e., replacing the 2SC with the CFL phase. Open circles correspond to EOSs presented in Fig. 3. (This figure is available in color in the electronic form.) |
Stiff EOS.B, 2SC+CFL core. The loci
 are shown in Fig. 6. Although the mass fraction contained in the 2SC layer is
small, its effect on the size of the allowed
(aCFL,λCFL)
region is strong. For
λCFL > 1.2, the required
are shown in Fig. 6. Although the mass fraction contained in the 2SC layer is
small, its effect on the size of the allowed
(aCFL,λCFL)
region is strong. For
λCFL > 1.2, the required
 has to be
significantly higher than the values obtained in (Blaschke et
al. 2010; Agrawal 2010). Simultaneously, at
aCFL ≈ 0.5 the density jump caused by the
2SC→CFL transition is constrained to values significantly below the ones obtained in
Blaschke et al. (2010) and Agrawal (2010).
has to be
significantly higher than the values obtained in (Blaschke et
al. 2010; Agrawal 2010). Simultaneously, at
aCFL ≈ 0.5 the density jump caused by the
2SC→CFL transition is constrained to values significantly below the ones obtained in
Blaschke et al. (2010) and Agrawal (2010).
Soft EOS.B, 2SC+CFL core. The loci
 are shown in Fig. 7. Even for a very low density jump
λ2SC = 1.05, we obtain
aCFL > 0.4, which is
rather stringent. In our case, the result obtained for B→Q(CFL) at
PCFL = P2 is very
similar to that of B→Q(2SC)→Q(CFL) with λ2SC = 1.15 (the
dashed line is very close to the solid one).
are shown in Fig. 7. Even for a very low density jump
λ2SC = 1.05, we obtain
aCFL > 0.4, which is
rather stringent. In our case, the result obtained for B→Q(CFL) at
PCFL = P2 is very
similar to that of B→Q(2SC)→Q(CFL) with λ2SC = 1.15 (the
dashed line is very close to the solid one).
 |
Fig. 8 Mass M vs. radius R for non-rotating NS models
calculated using different assumptions concerning the structure of dense matter for
ρ > 2ρ0. Dotted
segments of M(R) curves: configurations unstable
with respect to small radial perturbations. N – nucleon matter, Argonne
V18+TBF nucleon interaction (Schulze
& Rijken 2011). B – baryon matter, EOS calculated using
hyperon-nucleon and hyperon-hyperon potentials Nijmegen ESC08 (Rijken et al. 2010a,b). Open
circles – configurations of maximum allowable mass, with central density given in
units of ρ0. BQ – hybrid stars with quark cores, when
reconfinement is not allowed. |
 |
Fig. 9 Same notations as in Fig. 8, but for BM165 EOS of nucleon and baryon matter (Bednarek et al. 2012). Analytical EOS of quark matter and EOS.Q(CFL) with ρ2 = 2.5ρ0, aCFL = 0.5, λCFL = 1.2. (This figure is available in color in the electronic form.) |
5. Stability of quark cores and Mmax
Up to now, we did not consider in detail the high-density thermodynamical stability
of a stiff quark core in a hybrid (BQ) star. A stiffening of the EOS is necessarily
associated with the increase of the baryon chemical potential (see an example in Bednarek et al. 2012). In particular, it may lead to the
thermodynamical instability of the stiff (Q) phase with respect to the re-conversion into
the (B) one. This instability results from the violation, above a certain pressure, of the
condition 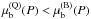 . Assuming a complete
thermodynamical equilibrium, we are dealing there with a first-order phase transition back
to the (B) phase that one can call reconfinement (cf., Łastowiecki et al. 2012). A corresponding EOS is denoted
EOS.
. Assuming a complete
thermodynamical equilibrium, we are dealing there with a first-order phase transition back
to the (B) phase that one can call reconfinement (cf., Łastowiecki et al. 2012). A corresponding EOS is denoted
EOS. and the
M(R) branch based on this EOS is labeled
and the
M(R) branch based on this EOS is labeled
 . Examples of
the N, B, BQ and
. Examples of
the N, B, BQ and  branches in
the M − R plane, obtained for a soft SR EOS of baryon
matter, are presented in Fig. 8. The reconversion
Q− → B strongly limits the size of the quark core in hybrid stars and results in the value
of
branches in
the M − R plane, obtained for a soft SR EOS of baryon
matter, are presented in Fig. 8. The reconversion
Q− → B strongly limits the size of the quark core in hybrid stars and results in the value
of  (Fig. 8)
(Fig. 8)
For the BM165 EOS.B we derive  . Replacing hyperon cores
by stiff quark ones can additionally increase the value of Mmax.
An example is shown in Fig. 9, where we obtain
. Replacing hyperon cores
by stiff quark ones can additionally increase the value of Mmax.
An example is shown in Fig. 9, where we obtain
 . However, if complete
thermodynamic equilibrium is imposed, the Q→B transition back to the B phase takes place
and one derives a maximum allowable mass
. However, if complete
thermodynamic equilibrium is imposed, the Q→B transition back to the B phase takes place
and one derives a maximum allowable mass  .
.
6. Summary, discussion, and conclusions
The existence of a 2 M⊙ pulsar is a challenge for neutron star models with strangeness-carrying cores. Strangeness is associated with s quarks, either confined to hyperons or moving in a (deconfined) quark plasma.
The threshold density for the appearance of hyperons, predicted by realistic models of dense matter consistent with nuclear and hypernuclear data, is ~2ρ0 − 3ρ0. Realistic baryon interactions lead to Mmax, for NS with hyperon cores starting at this density, this is significantly below M = 2.0 M⊙. This contradiction can be removed by a hypothetical strong high-density repulsion acting between hyperons. As discussed in several papers, this strong high-density repulsion could result from the exchange of a vector meson φ coupled only to hyperons.
 |
Fig. 10 Constraints in the a − λ plane resulting from three
different values of maximum measured mass |
Howewer, it has also been considered that massive NS could actually be hybrid stars with stiff quark-matter cores that allow for M > 2 M⊙. Strong overall repulsion between quarks should be accompanied by a strong attraction (pairing) in a specific two-quark state, corresponding to a strong color superconductivity with a superfluid gap ~100 MeV.
In the present paper we performed a general study of the possibility for hybrid NS with quark cores to reach M > 2 M⊙. We considered a continuum of parameterized EOS of quark matter, including several existing models. This allowed us to consider the general case of quark cores coexisting with baryonic matter at a prescribed pressure. We determined necessary features of a baryon – quark-matter phase transition. First, the density at which the first-order phase transition to quark phase occurs should be similar to the threshold density for hyperons, ~2ρ0 − 3ρ0. Second, the relative density jump at the baryon-quark matter phase transition should be below 30%. Third, the quark matter should be sufficiently stiff, which can be expressed as a condition on the sound speed in quark plasma.
The measured 2.0 M⊙ is a lower bound to a true
 . The
upper bound, resulting in the condition of the speed of sound less than c
combined with our confidence in the theoretical nucleon EOS for
ρ < 2ρ0, is
3.0 M⊙ (see, e.g., Haensel et
al. 2007, and references therein).
. The
upper bound, resulting in the condition of the speed of sound less than c
combined with our confidence in the theoretical nucleon EOS for
ρ < 2ρ0, is
3.0 M⊙ (see, e.g., Haensel et
al. 2007, and references therein).  lies
therefore between 2 M⊙ and 3 M⊙.
Obviously, NS masses higher than 2.0 M⊙ have to be
contemplated. The question is, how much higher? The mass of a “black widow” pulsar could be
as high as 2.4 M⊙, but the present uncertainty is too large for
this number to be used as an observational constraint (see, e.g., Lattimer 2011).
lies
therefore between 2 M⊙ and 3 M⊙.
Obviously, NS masses higher than 2.0 M⊙ have to be
contemplated. The question is, how much higher? The mass of a “black widow” pulsar could be
as high as 2.4 M⊙, but the present uncertainty is too large for
this number to be used as an observational constraint (see, e.g., Lattimer 2011).
To discuss the possibility that masses significantly larger than
2.0 M⊙ could be reached, we plotted in Fig. 10 the bounding lines for
 and
and
 . As we see in Fig. 10, to fulfill condition
. As we see in Fig. 10, to fulfill condition
 , we have to assume very
stiff quark matter, quite close to the causality limit a = 1.
, we have to assume very
stiff quark matter, quite close to the causality limit a = 1.
The situation becomes even more difficult if we require a strict stability of quark cores.
As a result of the high stiffness of quark matter that is necessary for
 (and a fortiori for
higher lower bounds
(and a fortiori for
higher lower bounds  ), the
quark phase turns out to be unstable, beyond some pressure, with respect to hadronization.
Assuming complete thermodynamic equilibrium, we derived very similar
Mmax for stars with hyperon and quark cores. Consequently, the
transition to quark matter could not yield
Mmax > 2 M⊙
if NS with hyperonic cores had
), the
quark phase turns out to be unstable, beyond some pressure, with respect to hadronization.
Assuming complete thermodynamic equilibrium, we derived very similar
Mmax for stars with hyperon and quark cores. Consequently, the
transition to quark matter could not yield
Mmax > 2 M⊙
if NS with hyperonic cores had  (significantly) below 2 M⊙. This is true also for
(significantly) below 2 M⊙. This is true also for
 . Therefore, provided our
picture of dense matter is valid, we find that a strong hyperon repulsion at high density is
mandatory in general.
. Therefore, provided our
picture of dense matter is valid, we find that a strong hyperon repulsion at high density is
mandatory in general.
The high-density thermodynamic instability of the quark phase and its consequences for Mmax should be taken with a grain of salt. Our models of dense baryonic matter assume point particles. This assumption may be expected to break down at ρ ~ 5 ÷ 8ρ0. Therefore, the “reconfinement” of the quark phase is, in our opinion, likely to indicate the inadequacy of point-particle baryonic phase models (see also Łastowiecki et al. 2012). A similar “reconfinement” was encountered in the numerical modeling of the phase diagram of hot and dense hadron gas specific to relativistic heavy-ion collisions (see Satarov et al. 2009). A proposed solution consisted in introducing the finite-size corrections for hadrons within the excluded volume approximation in the confined (hadronic) phase (Satarov et al. 2009). We will use this approximation to re-calculate EOS.B in our forthcoming paper on strange cores in massive NS.
There is another weak point in the commonly used models of quark cores in NS, characteristic also of the present paper: this is a two-phase approach, with each phase, baryon and quark, treated using basically different descriptions. In principle, both phases and the transition between them should have been treated using a unified approach based on the QCD, so that that the influence of the dense medium on the baryon structure and baryon interactions are taken into account in a consistent way. This approach is beyond the reach of the present-day theory of dense matter. However, a phenomenological modeling of baryon structure in dense matter is possible, e.g., within a quark-meson coupling model (for references, see Whittenbury et al. 2012). A more complete description of neutron-star quark cores, going beyond the two-phase approximation, can hopefully be achieved in the future.
In this paper we were considering non-rotating configurations. Pulsar PSR J1614-2230 rotates with a frequency f = 1/P = 317 Hz and the effect for maximum mass is on the order of ≃0.01 M⊙ (Bednarek et al. 2012), much weaker than the accuracy of the mass measurement. However, it should be noted that for a NS that rotates with a maximum observed frequency of 716 Hz, the effect of rotation would be about five times stronger.
It seems that such a possibility was first considered in Baldo et al. (2006); we are grateful to David Blaschke for calling our attention to this paper.
Acknowledgments
We thank David Blaschke and Rafał Łastowiecki for sharing their numerical results on the sound speed in quark matter. We are grateful to David Blaschke for reading the manuscript and calling our attention to several papers relevant to our work. We also thank Nicolas Chamel for reading the manuscript and helpful remarks. We express our gratitude to an anonymous referee, for constructive critical remarks, useful comments, and for calling our attention to several papers relevant to our work that were missing in our initial list of references. This work was partially supported by the Polish MNiSW research grant No. N N203 512838.
References
- Agrawal, B. K. 2010, Phys. Rev. D., 81, 023009 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Braby, M., Paris, M., & Reddy, S. 2005, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Schmitt, A., Rajagopal, K. I., & Schaefer, T. 2008, Rev. Mod. Phys., 80, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Burgio, F., & Schulze, H.-J. 2006, in Superdense QCD Matter and Compact Stars, eds. D. Blaschke, & D. Sedrakian (Springer), 113 [Google Scholar]
- Bednarek, I., Haensel, P., Zdunik, J. L., Bejger, M., & Mańka, R. 2012, A&A, 543, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaschke, D., Klaehn, T., Lastowiecki, R., & Sandin, F. 2010, J. Phys. G: Nucl. Part. Phys., 37, 094063 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, L., & Sedrakian, A. 2012, A&A, 539, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgio, G. F., Schulze, H.-J., & Li, A. 2011, Phys. Rev. C, 83, 025804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2012, [arXiv:1205.0983] [Google Scholar]
- Champion, D. J., Ransom, S. M., Lazarus, P., et al. 2008, Science, 320, 1309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dexheimer, V., & Schramm, S. 2008, ApJ, 683, 943 [Google Scholar]
- Endo, T., Maruyama, T., Chiba, S., & Tatsumi, T., 2006, Prog. Theor. Phys., 115, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Bassa, C. G., Wex, N., et al. 2011, MNRAS, 412, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1. Equation of State and Structure (New York: Springer) [Google Scholar]
- Klahn, T., Blaschke, D., & Łastowiecki, R. 2012, Acta Phys. Pol. B Proc. Suppl., 5, 757 [CrossRef] [Google Scholar]
- Lattimer, J. M. 2011, Ap&SS, 336, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. H., Lombardo, U., Schulze, H.-J., & Zuo, W. 2008, Phys. Rev. C, 77, 034316 [NASA ADS] [CrossRef] [Google Scholar]
- Lastowiecki, R., Blaschke, D., Grigorian, H., & Typel, S. 2012, Acta Phys. Pol. B Proc. Suppl., 5, 535 [Google Scholar]
- Lenzi, C. H., & Lugones, G. 2012, ApJ, 759, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., Psaltis, D., Ransom, S., Demorest, P., & Alford, M. 2010, ApJ, 724, L199 [Google Scholar]
- Pagliara, G., & Schaffner-Bielich, J. 2008, Phys. Rev. D, 77, 063004 [NASA ADS] [CrossRef] [Google Scholar]
- Rijken, T., Nagels, M., & Yamamoto, Y. 2010a, Nucl. Phys. A, 835, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Rijken, T., Nagels, M., & Yamamoto, Y. 2010b, Prog. Theor. Phys. Suppl., 185, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Satarov, L. M., Dmitriev, M. N., & Mishustin, I. N. 2009, Phys. Atom. Nucl., 72, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, H.-J., & Rijken, T. 2011, Phys. Rev. C, 84, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Vidana, I., Logoteta, D., Providencia, C., & Bombaci, I. 2011, Europhys. Lett., 94, 11002 [Google Scholar]
- Weissenborn, S., Sagert, I., Pagliara, G., Hempel, M., & Schaeffner-Bielich, J. 2011, ApJ, 740, L14 [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaeffner-Bielich, J. 2012a, Nucl. Phys. A, 881, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaeffner-Bielich, J. 2012b, Phys. Rev. C, 85, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Whittenbury, D. L., Carroll, J. D., Thomas, A. W., Tsushima, K., & Stone, J. R. 2012 [arXiv:1204.2614v1] [Google Scholar]
- Wiringa, R. B., Stoks, V. G. J., & Schiavilla, R. 1995, Phys. Rev. C, 51, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L. 2000, A&A, 359, 311 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Calculated points of EOS of color-superconducting quark matter in the P − μb plane (Agrawal 2010) and their approximation by our analytical formula. See the text for additional details. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 2 Calculated points of EOS of color-superconducting quark matter in the P − μb plane (Blaschke et al. 2010) and their approximation by our analytical formula. See the text for additional details. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 3 Examples of EOS.BQ from a continuum { EOS.BQ } emerging from a soft SR EOS. Hadronic EOSs are plotted as dashed lines: N – nucleon EOS; B – nucleons and hyperons. The phase transition B→Q(2SC) takes place at P1 = 31 MeV fm-3, and Q(2SC)→Q(CFL) at P2 = 45 MeV fm-3. The 2SC phase has a2SC = 0.302. Three examples of B → Q(2SC)→Q(CFL) are shown corresponding to following choices of { λ2SC,λCFL,aCFL }: { 1.05,1.2,0.57 }, { 1.15,1.1,0.58 }, { 1.3,1.1,0.7 }. In all these cases the maximum mass is equal to 2 M⊙, i.e., parameters { λ2SC,λCFL,aCFL } lie on the bounding curves in Fig. 7. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 4 Examples of EOS.BQ from a continuum { EOS.BQ } emerging from a stiff MB165 EOS. Hadronic EOSs are plotted as dashed lines: N – nucleon EOS (black); B – nucleons and hyperons (red). The phase transition B →Q(2SC) takes place at P1 = 47 MeV fm-3, a2SC = 0.302 and λ2SC = 1.3. EOS.Q(2SC) is plotted as a blue line. Two examples of Q(2SC)→Q(CFL) at P2 = 69 MeV fm-3 are shown, corresponding to a stiffer CFL phase (aCFL = 0.6, λ2SC = 1.3) and a softer phase (aCFL = 0.35, λ2SC = 1.5). The EOS.Q(CFL)s are plotted as green solid lines. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 5 Constraints on the a − λ plane, resulting from
Mmax > 2 M⊙,
obtained assuming SR EOS of baryon matter, and for purely CFL cores (no 2SC layer)
starting at
ρCFL = 1.7ρ0,...,4.0ρ0.
Densities 2.3ρ0 and 3.0ρ0
correspond to P1 and P2,
relevant for the boundaries of the 2SC layer in a 2SC+CFL core. Each line is an upper
boundary of the region of
(aCFL,λCFL)
consistent with
Mmax > 2 M⊙.
These lines are labeled by the density |
| In the text | |
 |
Fig. 6 Constraints on the a − λ plane, resulting from Mmax > 2 M⊙, obtained assuming a BM165 EOS of baryon matter and a quark core starting at P1 = 47 MeV fm-3. Each line is an upper boundary of the region of (aCFL,λCFL) consistent with Mmax > 2 M⊙. Solid lines are obtained for quark cores composed of a 2SC layer (P1 < P < P2) and a CFL core starting at P2 = 69 MeV fm-3. These lines are labeled by the density jump at the B-2SC interface λ2SC = 1.05,1.15,1.30. We used a2SC = 0.3 (Agrawal 2010). The dashed line is obtained for purely CFL cores (no 2SC layer) starting at P2, and the dotted line corresponds to purely CFL cores starting at P1, i.e., replacing the 2SC with the CFL phase. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 7 Constraints on the a − λ plane, resulting from Mmax > 2 M⊙, obtained assuming an SR EOS of baryon matter and a quark core starting at P1 = 31 MeV fm-3. Each line is an upper boundary of the region of (aCFL,λCFL) consistent with Mmax > 2 M⊙. The solid lines are obtained for quark cores composed of a 2SC layer (P1 < P < P2) and a CFL core starting at P2 = 45 MeV fm-3. These lines are labeled by the density jump at the B-2SC interface λ2SC = 1.05,1.15,1.30. We used a2SC = 0.3 (Agrawal 2010). The dashed line is obtained for purely CFL cores (no 2SC layer) starting at P2 = 45 MeV fm-3, and the dotted line corresponds to purely CFL cores starting at P1, i.e., replacing the 2SC with the CFL phase. Open circles correspond to EOSs presented in Fig. 3. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 8 Mass M vs. radius R for non-rotating NS models
calculated using different assumptions concerning the structure of dense matter for
ρ > 2ρ0. Dotted
segments of M(R) curves: configurations unstable
with respect to small radial perturbations. N – nucleon matter, Argonne
V18+TBF nucleon interaction (Schulze
& Rijken 2011). B – baryon matter, EOS calculated using
hyperon-nucleon and hyperon-hyperon potentials Nijmegen ESC08 (Rijken et al. 2010a,b). Open
circles – configurations of maximum allowable mass, with central density given in
units of ρ0. BQ – hybrid stars with quark cores, when
reconfinement is not allowed. |
| In the text | |
 |
Fig. 9 Same notations as in Fig. 8, but for BM165 EOS of nucleon and baryon matter (Bednarek et al. 2012). Analytical EOS of quark matter and EOS.Q(CFL) with ρ2 = 2.5ρ0, aCFL = 0.5, λCFL = 1.2. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 10 Constraints in the a − λ plane resulting from three
different values of maximum measured mass |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




