| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220589 | |
| Published online | 12 February 2013 | |
Unraveling the high-energy emission components of gamma-ray binaries
1
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117
Heidelberg,
Germany
e-mail:
Victor.Zabalza@mpi-hd.mpg.de
2
Departament d’Astronomia i Meteorologia, Institut de Ciències del
Cosmos (ICC), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028
Barcelona,
Spain
3
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place, Dublin 2,
Ireland
4
Institute of Space and Astronautical Science/JAXA,
3-1-1 Yoshinodai, Chuo-ku,
Sagamihara, 252-5210
Kanagawa,
Japan
Received: 18 October 2012
Accepted: 24 December 2012
Context. The high and very high energy spectrum of gamma-ray binaries has become a challenge for all theoretical explanations since the detection of powerful, persistent GeV emission from LS 5039 and LS I +61 303 by Fermi/LAT. The spectral cutoff at a few GeV indicates that the GeV component and the fainter, hard TeV emission above 100 GeV are not directly related.
Aims. We explore the possible origins of these two emission components in the framework of a young, non-accreting pulsar orbiting the massive star, and initiating the non-thermal emission through the interaction of the stellar and pulsar winds.
Methods. The pulsar/stellar wind interaction in a compact-orbit binary gives rise to two potential locations for particle acceleration: the shocks at the head-on collision of the winds and the termination shock caused by Coriolis forces on scales larger than the binary separation. We explore the suitability of these two locations to host the GeV and TeV emitters, respectively, through the study of their non-thermal emission along the orbit. We focus on the application of this model to LS 5039 given its well-determined stellar wind with respect to other gamma-ray binaries.
Results. The application of the proposed model to LS 5039 indicates that these two potential emitter locations provide the necessary conditions for reproduction of the two-component high-energy gamma-ray spectrum of LS 5039. In addition, the ambient postshock conditions required at each of the locations are consistent with recent hydrodynamical simulations.
Conclusions. The scenario based on the interaction of the stellar and pulsar winds is compatible with the GeV and TeV emission observed from gamma-ray binaries with unknown compact objects, such as LS 5039 and LS I +61 303.
Key words: radiation mechanisms: non-thermal / gamma rays: stars / binaries: general
© ESO, 2013
1. Introduction
Gamma-ray binaries are compact binary systems composed of a massive star and a compact object, either a black hole or a neutron star. They exhibit non-thermal emission from radio to high-energy (HE, >100 MeV) and very high energy (VHE, >100 GeV) gamma rays, which is typically modulated with the orbital period, and most of their energy output is emitted in the MeV to TeV range. Four gamma-ray binaries have been confirmed to emit at VHE: LS 5039 (Aharonian et al. 2005a), PSR B1259−63 (Aharonian et al. 2005b), LS I +61 303 (Albert et al. 2006), and HESS J0632+057 (Skilton et al. 2009). The Fermi/LAT source 1FGL J1018.6−5856 (Ackermann et al. 2012) appears to have a binary origin as well, but its candidate VHE counterpart is still not clearly associated (Abramowski et al. 2012). PSR B1259−63 is known to host a young, non-accreting pulsar (Johnston et al. 1992), but the nature of the compact objects in all other gamma-ray binaries remains unknown. Flaring HE or VHE gamma-ray emission has also been detected from the X-ray binaries Cyg X-1 (Albert et al. 2007) and Cyg X-3 (Abdo et al. 2009b; Tavani et al. 2009), but this emission is neither dominant nor persistent as is the case for the gamma-ray binaries mentioned above.
Two different scenarios have been extensively proposed in the literature to account for the non-thermal emission from LS I +61 303 and LS 5039, probably the most-studied gamma-ray binaries along with PSR B1259−63: a microquasar scenario, with relativistic jet formation through matter accretion onto the compact object (see, e.g., Bosch-Ramon & Khangulyan 2009, for a review), and the pulsar wind shock (PWS) scenario, with particle acceleration being the result of the interaction between the pulsar and stellar winds, first proposed by Maraschi & Treves (1981). LS 5039 is the best gamma-ray binary to test wind interaction models because of its radial, well-determined stellar wind, as compared to LS I +61 303, PSR B1259−63 and HESS J0632+057, which all contain Be stars. We will therefore focus the present work on this system.
LS 5039 is a system with a O6.5V(f) main star and a compact object within a mildly eccentric ~3.9 day orbit (Casares et al. 2005; Sarty et al. 2011). The source shows periodic X-ray emission with a peak around the inferior conjunction (Takahashi et al. 2009), a modulation practically mirrored by its VHE emission (Aharonian et al. 2005a, 2006a). The X-ray and VHE fluxes have a minimum at orbital phases φ = 0.0–0.3 and a maximum at φ = 0.6–0.9, where φ = 0 is the periastron phase and the inferior and superior conjunctions take place at φ ≈ 0.06 and φ ≈ 0.65, respectively.
The observation of LS 5039 with Fermi/LAT starting from 2008 provided a wealth of new data but also new challenges for the understanding of its nature. It was shown that LS 5039 exhibits extremely powerful emission at GeV energies with a spectral shape consistent with a powerlaw and an exponential cutoff at energies of a few GeV (Abdo et al. 2009a). Long-term observations confirm that the emission is modulated with the orbital period, with flux variations of a factor three along the orbit, but the spectral cutoff energy appears to remain constant (Hadasch et al. 2012). The apparent similarity of the GeV spectrum with that of magnetospheric pulsar emission (hard powerlaw with an exponential cutoff at a few GeV), prompted the consideration of the latter as an origin for the gamma-ray emission of LS 5039 (Abdo et al. 2009a). However, the clear modulation with the orbital period and the lack of pulsations are hard to reconcile with a magnetospheric origin. A way to overcome these limitations has been explored in the IC emission of the unshocked pulsar wind by invoking the striped pulsar wind model (Pétri & Dubus 2011), but this approach would result in a lightcurve modulation amplitude of a factor ~3 larger than the observations show. Bednarek (2011) considered electron acceleration in the stellar wind termination shock as a mechanism to obtain a cutoff around a few GeV, but the stellar wind energetics is hardly enough to explain the GeV luminosity. In addition, both approaches continue to consider the TeV emission as arising from a region close to the apex of the contact discontinuity between the two winds, where pair creation absorption is extremely strong in orbital phase ranges with clear VHE detections (Bosch-Ramon et al. 2008b).
The complex spectral characteristics exhibited by LS 5039 are not compatible with the predictions from electromagnetic cascading models, an effect that would result in a pileup of emitted energy just below the photon-photon pair production threshold at ~100 GeV (see Bosch-Ramon et al. 2008b; Cerutti et al. 2010, and references therein). The combined effects of adiabatic losses, synchrotron and IC cooling, and anisotropic IC emission applied to a single particle population with a powerlaw energy distribution are also unable to reproduce a cutoff at a few GeV while accounting for the hard spectrum from 10 GeV to 1 TeV (Khangulyan et al. 2008a; Dubus et al. 2008, see also Zabalza et al. 2011b for LS I +61 303). Therefore, present evidence points towards the presence of at least two particle populations that give rise to the GeV and TeV components in the high-energy spectrum of LS 5039.
In this paper we propose a model that assumes two different locations for the production of the observed GeV and TeV components of gamma-ray emission. These two components arise naturally from the orbital motion of a compact pulsar wind nebula around a massive star. We propose the apex of the contact discontinuity as the candidate location for the GeV emitter, and a pulsar wind termination shock in the direction opposite of the star, which appears because of the orbital motion, as the candidate location for the TeV emitter.
2. Dynamical model
The interaction of the pulsar and stellar winds gives rise to an interface between the two winds defined by the so-called contact discontinuity (CD), a surface where the perpendicular velocities of both winds are null. The CD is bounded on either side by the shocked winds of the pulsar and the star. Considering a static binary system, the shape of the CD can be analytically computed by approximating it as the location where the ram pressures of the winds are in balance (Zabalza et al. 2011a, and references therein). In this scenario, the shape is defined by the ratio of the ram pressures of the pulsar and stellar winds ηw ≡ (Lsd/c)/(Ṁvw). However, the orbital motion in gamma-ray binaries is bound to modify the shape of the interaction between the two winds.
Close to the pulsar, the effect of the orbital motion is not significant for the currently known gamma-ray binaries. At the location of the apex of the CD, the orbital motion manifests itself in the aberration of the CD, with an angle given by tanμ = vorb/vw, where vorb is the orbital velocity and vw is the speed of the slowest wind (i.e., the stellar wind). For the case of LS 5039, the aberration angle reaches a maximum of 23° at periastron, an angle small enough for the scenario to remain essentially unchanged from an stationary CD. The location of the apex of the CD, or wind standoff distance, can be computed from the balance of the ram pressures of the stellar and pulsar winds as 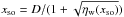 , where D is the orbital separation and ηw(xso) is the pulsar-to-stellar wind ram pressure ratio at a distance xso from the star. When considering a β-law for the velocity profile of the stellar wind, as expected from hot, young stars (Pauldrach et al. 1986), xso must be obtained numerically.
, where D is the orbital separation and ηw(xso) is the pulsar-to-stellar wind ram pressure ratio at a distance xso from the star. When considering a β-law for the velocity profile of the stellar wind, as expected from hot, young stars (Pauldrach et al. 1986), xso must be obtained numerically.
Hydrodynamical simulations of stellar and pulsar wind interaction indicate that the shocked pulsar wind flows roughly parallel to the CD and is accelerated up to high bulk Lorentz factors within the binary system (Bogovalov et al. 2008). This implies that significant Doppler boosting of the emission from the pulsar wind shocked in the inner part of the system may be at play (Khangulyan et al. 2008b; Dubus et al. 2010). At larger distances from the apex, the flow is disturbed by hydrodynamical instabilities and gas mixing between the two winds becomes significant (Bosch-Ramon et al. 2012). Observational confirmation of the morphology of the interaction between the stellar and pulsar winds has been obtained in at least one case of a binary system known to contain a pulsar. Moldón et al. (2011) resolved the variable radio nebula of PSR B1259−63 and deemed it to be compatible with the emission from cooled electrons originated in the interaction of the stellar and pulsar winds.
On scales larger than the binary separation the wind interaction region undergoes dramatic changes with respect to the stationary scenario. The CD is distorted by the sideways asymmetric interaction with the stellar wind and results in a bending that would mix the stellar and pulsar winds, eventually becoming an expanding disrupted structure interacting with the interstellar medium (Bosch-Ramon & Barkov 2011). Given this orbital effect, the pulsar wind is expected to be shocked even in the direction opposite from the star, as was predicted for pulsar binary systems by Bosch-Ramon & Barkov (2011) and later confirmed through hydrodynamical simulations in Bosch-Ramon et al. (2012). Following Bosch-Ramon & Barkov (2011) we can obtain an analytical estimate of the location of the pulsar wind termination shock as the location for which the ram pressure of the stellar wind owing to Coriolis forces and the ram pressure of the pulsar wind are in balance, obtaining the following approximate expression for locations outside of the binary system 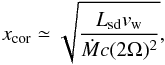 (1)where Ω is the angular velocity of the compact object around the star. Owing to Kepler’s second law, Ω ∝ D-2, where D is the orbital separation, and therefore xcor ∝ D2 for eccentric orbits and constant stellar and pulsar wind properties. Thus, the balance position xcor will be closer to the pulsar at periastron and farther at apastron. In spite of the approximate nature of Eq. (1), it is consistent with the location of the shock in the simulations of Bosch-Ramon et al. (2012), and will therefore be used throughout this work.
(1)where Ω is the angular velocity of the compact object around the star. Owing to Kepler’s second law, Ω ∝ D-2, where D is the orbital separation, and therefore xcor ∝ D2 for eccentric orbits and constant stellar and pulsar wind properties. Thus, the balance position xcor will be closer to the pulsar at periastron and farther at apastron. In spite of the approximate nature of Eq. (1), it is consistent with the location of the shock in the simulations of Bosch-Ramon et al. (2012), and will therefore be used throughout this work.
The presence and properties of this quasi-perpendicular strong shock at the Coriolis turnover location sets apart the characteristics of the interaction of stellar and pulsar wind with respect to that of binary stellar systems. The non-relativistic stellar wind in binary stellar systems can be smoothly deflected by sound waves, as found in the simulations of Lamberts et al. (2012). However, sound wave deflection would not affect an already trans-sonic relativistic pulsar wind, leading to the formation of a quasi-perpendicular strong shock because of structure bending. We note that this approach may not be valid for ηw ≲ 1.2 × 10-2, as numerical simulations indicate that a reconfinement shock, with different characteristics to those explored above, will develop in the pulsar wind for those cases where the stellar wind vastly overpowers the pulsar wind (Bogovalov et al. 2008).
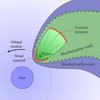 |
Fig. 1 Sketch of the proposed scenario at the periastron of a close-orbit system similar to LS 5039. The region of the CD where significant turbulence, and therefore wind mixing, are expected to take place is indicated with a wavy line. The red regions indicate the two proposed emitter locations. |
3. Location and properties of the non-thermal emitters
A sketch of the system, as described in the previous section, can be found in Fig. 1. The influence of the orbital motion on the shape of the pulsar wind zone gives rise to two distinct regions where most of the energy of the pulsar wind is deposited in quasi-parallel shocks: the wind standoff and Coriolis turnover locations. The intermediate regions of PWS, i.e., those not marked in red in Fig. 1, are not expected to contribute significantly to the non-thermal emission of the system given the high obliquity of the impact of the pulsar wind and correspondingly low energy transfer into non-thermal particles.
The pulsar wind termination region close to the wind standoff location has been generally considered as the preferred location for acceleration of electrons up to ultrarelativistic energies, which would give rise to the observed non-thermal broadband emission through synchrotron and IC processes (e.g., Dubus 2006). However, the intense stellar photon field at this location, and corresponding high opacities owing to photon-photon pair production, precludes VHE gamma-rays above ~40 GeV from reaching the observer for some orbital phases with clear VHE detections (Khangulyan et al. 2008a). On the other hand, an emitter with constant particle injection located at the wind standoff is compatible with the phenomenology exhibited by the source at GeV energies. The modulation is mainly driven by the change in the IC interaction angle, with enhanced (reduced) emission at superior (inferior) conjunction. For the allowed orbital inclination angles (20°–60°, Casares et al. 2005), the modulation is too strong to reproduce the Fermi lightcurve, but this effect may be mitigated by Doppler boosting. As a proxy for the complex hydrodynamical properties of the flow (Bogovalov et al. 2008), we have considered an effective bulk flow velocity of 0.15 c in the direction of the axis of symmetry of the CD apex, which changes along the orbit (see CD aberration in Sect. 2) but is always close to the radial direction. The bulk flow velocity of 0.15 c used here applies exclusively to the Doppler effect averaged over the CD cone and with respect to the observer line-of-sight. Therefore, it is still possible, and, given the simulations of Bogovalov et al. (2008), probable, that the intrinsic bulk flow velocity of the shocked pulsar wind is higher.
The pulsar wind termination shock at the Coriolis turnover location is a good candidate for the VHE emitter. The reduced stellar photon field density implies pair production absorption characteristics consistent with the observed spectra at VHE. For scenarios in which the stellar wind ram pressure is dominant, the pulsar wind solid angle subtended by the Coriolis turnover shock is much lower than that of the apex region. This is consistent with the reduced emission power of the TeV component with respect to the GeV component.
The magnetic field of the shocked pulsar wind is generally well known in plerions from observations (e.g., Kennel & Coroniti 1984), but the so-called sigma problem precludes one from deriving it theoretically. The situation in gamma-ray binaries is even more complex, as there might be a reduction of the post shock magnetic field strength owing to the reacceleration of the flow (Bogovalov et al. 2012). Since knowledge of the post-shock magnetic field could only be obtained via a magnetohydrodynamical simulation of the system, we have chosen to parametrize the magnetic field energy density as a fraction ξ of the pre-shock equipartition magnetic field. We define the latter at the balance of the magnetic field energy density and the kinetic energy density of the pulsar wind at the shock. Therefore, for a constant value of ξ, the post-shock magnetic field strength will behave along the orbit as B ∝ 1/rp, where rp is the distance of the shock to the pulsar.
3.1. Maximum electron energy
A distinct feature of the GeV and TeV spectra of LS 5039 are the cutoffs present at a few GeV and above 10 TeV, respectively. The former is apparently constant along the orbit, whereas owing to the softer TeV spectrum during superior conjunction the latter has only been detected clearly during inferior conjunction. These spectral cutoffs can be directly related to the maximum energy of the electrons in the respective particle populations. The maximum energy that can be reached in any acceleration process can be determined by the balance of the acceleration rate with the energy losses owing to radiative processes. The acceleration timescale is characterized as tacc = ηaccrL/c, where rL is the Larmor radius, and ηacc ≥ 1 parametrizes the efficiency of the acceleration process (see Sect. 5.1 below for a discussion of ηacc). For electrons accelerated close to the binary system, the dominant radiative losses will be related to synchrotron and IC emission. A study of LS 5039 led Khangulyan et al. (2008a) to the conclusion that the production of the HESS spectrum required ηacc ≲ 10 for emitters close to the binary system. The wind standoff location will present both higher seed photon density and magnetic field, owing to its proximity to the star and the denser preshock pulsar wind, and the higher energy losses will lead to a lower maximum electron energy compared to the location outside the binary system.
The highest energy particles in the Coriolis turnover location may be used to gain information on its magnetic field. The maximum electron energies obtained under dominant synchrotron or IC losses in the Klein-Nishina regime depend differently on the magnetic field: Ee,max(syn) ∝ B− 1/2, and Ee,max(IC,KN) ∝ B3.3 (Khangulyan et al. 2008a). For a given ηacc, the highest maximum energies will be obtained for a narrow range of magnetic field strengths where synchrotron losses are only slightly dominant over IC losses.
3.2. Emission model
As a first approximation, we will simplify the scenario mentioned above by considering the two emitting regions as point-like, homogeneous emitters located at the wind standoff and Coriolis turnover locations. They are located on the axis of symmetry of the system, and corotate with the pulsar around the star.
At each of the two positions, we consider an injection in accelerated electrons with a total luminosity as a fraction of the pulsar spindown luminosity, which may be different for the two locations but constant along the orbit. Given the short cooling timescales with respect to the dynamical timescales of the system, a steady state approach to computing the evolved particle spectrum can be taken (Khangulyan et al. 2007; Zabalza et al. 2011b). Radiative losses through synchrotron and IC cooling are considered, as well as non-radiative adiabatic losses. Adiabatic expansion losses can be approximated as tad ≃ R/vexp, where R is the characteristic size of the expanding emitter and vexp the expansion velocity. For our two emitters, we have approximated the characteristic size as the distance to the pulsar and the expansion velocity as c/3. Nevertheless, under these approximations adiabatic losses are not dominant in any electron energy range.
The resulting emission spectra is then computed for each of the two positions. The anisotropic nature of IC is of utmost relevance in gamma-ray binaries (Khangulyan et al. 2008a; Dubus et al. 2008), and is taken into account using the simple analytical presentation of the differential cross-sections for anisotropic inverse Compton scattering of Aharonian & Atoyan (1981) and considering the black body radiation from the star as the seed photon field. The pair production absorption along the line of sight to the observer is then computed and applied to the intrinsic spectrum. To compare with spectral observations spanning significant fractions of the orbit, we computed the average of the emission along the observation period from a sampling of 100 points along the orbit.
4. Application to LS 5039
 |
Fig. 2 Spectral energy distribution of LS 5039. The computed emission and observational data during the inferior conjunction (0.45 < φ < 0.9) is shown in red and during the superior conjunction (0.9 < φ < 0.45) in blue. The emission components from the wind standoff and Coriolis turnover locations are indicated with a dotted and dashed line, respectively. |
The stellar mass-loss rate and pulsar spin-down luminosity of LS 5039 have been constrained into a relatively narrow range by a variety of studies of the system. The lack of orbital variability of the photoelectric soft X-ray absorption places an upper limit on the stellar mass-loss rate of 5 × 10-8 M⊙ yr-1 for a point-like X-ray emitter (Bosch-Ramon et al. 2007) and of 1.5 × 10-7 M⊙ yr-1 for an extended emitter, as expected in a PWS scenario (Szostek & Dubus 2011). Note, however, that for these calculations an emitter located at the position of the compact object was assumed. If the X-ray emitter is located outside the orbit of the compact object, in a position similar to the Coriolis turnover location mentioned above, these constrains would likely be relaxed. A direct measure through Hα line measurements yields 3.7 to 4.8 × 10-7 M⊙ yr-1 (Sarty et al. 2011), but this method could overpredict mass-loss rates by a factor of two if there is clumping present in the stellar wind (Markova et al. 2004). The non-detection of thermal X-ray emission from the shocked stellar wind in the X-ray spectra of LS 5039 places a robust upper limit on the pulsar spin-down luminosity of ~6 × 1036 erg s-1 (Zabalza et al. 2011a).
In the application of the model to LS 5039 we considered a stellar wind with a mass-loss rate of Ṁ = 10-7 M⊙ yr-1, a terminal wind velocity of vw = 2400 km s-1, and a pulsar spin-down luminosity of Lsd = 5 × 1036 erg s-1, which results in a ram pressure ratio of ηw,∞ ≃ 0.1. Under these conditions the distance of the wind standoff emitter to the star varies between half and two thirds of the orbital separation for periastron and apastron, respectively. In order to match the powerful observed GeV emission, a non-thermal electron injection power of 3.5 × 1035 erg s-1 is required at this location, corresponding to 7% of the pulsar spin-down luminosity. In spite of the strong radiative losses owing to the intense stellar photon field, a relatively low acceleration efficiency of ηacc ~ 2000 is required to reproduce the spectral cutoff at a few GeV. The spectral shape of the GeV component is qualitatively well reproduced during the inferior and superior conjunctions (Fig. 2), and its orbital lightcurve agrees well with the observational data (Fig. 3). The computed emission is lower than the observed one only during inferior conjunction, which could be related to uncertainties in the Doppler boosting direction. While here we have considered a single quasi-radial direction for the entire emission from the shocked pulsar wind, a wider spread in the direction of the different parts of the post-shock flow (as seen in the simulation results of Bosch-Ramon et al. 2012) could mean that certain parts are boosted in a direction closer to the observer line-of-sight, which would lead to increased emission.
The emitter located at the Coriolis turnover region requires a lower injection energy of 5 × 1034 erg s-1, or 1% of the pulsar spindown luminosity, which is consistent with the lower solid angle subtended by this region. The lower magnetic field and larger distance to the star, resulting in lower synchrotron and IC losses, favor the acceleration of particles up to very high energies at this location. However, a very efficient accelerator, with ηacc < 20, is still required to obtain the multi TeV electrons that give rise to the gamma-ray emission up to ~10 TeV detected by HESS. The requirement for such energetic particles also constrains the magnetic field in the emitter (see Sect. 3.1), to a fraction ξ = 0.025 of the equipartition preshock magnetic field, resulting in magnetic fields that vary along the orbit in the range from 0.2 to 0.4 G. The computed emission provides a very good spectral match to observed data during inferior conjunction, with a flat spectrum up to the spectral cutoff around 10 TeV, as can be seen in Fig. 2. At superior conjunction the computed spectra has the characteristic shape of pair-production absorption, with a minimum around a few hundred GeV, whereas the observed spectrum is closer to a powerlaw. Additionally, the overall flux around periastron and superior conjunction is underestimated, as seen in Fig. 3, bottom. Possible reasons for this discrepancy are discussed below in Sect. 5.3. Under the assumption of a constant ξ = 0.025 for all PWSs, the resulting magnetic field of the wind standoff postshock material is between 0.6 and 0.9 G.
 |
Fig. 3 Top: Fermi/LAT orbital lightcurve of LS 5039 in the energy range 100 MeV to 30 GeV, along with the computed gamma-ray emission. Bottom: HESS orbital lightcurve in the range 0.2 to 5 TeV. Two orbital periods are shown for clarity. |
The inclination of the orbital system has a strong effect on the orbital modulation of the IC emission, both because of the emission angular dependency (affecting both the HE and VHE light curves) and because of the variation in pair-production opacity along the orbit with inclination (affecting the VHE light curve). We found that the value of the inclination angle that best leverages the influence of these two effects in reproducing the HE and VHE gamma ray light curves is i = 45°. Taking the mass function f(m) ≈ 0.0049 ± 0.0006 M⊙ measured by Sarty et al. (2011) and a primary star mass of 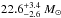 , this inclination results in a lower limit to the mass of the compact object of ~2 M⊙.
, this inclination results in a lower limit to the mass of the compact object of ~2 M⊙.
5. Discussion
5.1. Acceleration efficiencies
In Sect. 4 we showed that significantly different acceleration efficiencies are required in our model for the two emitter locations. It is beyond the scope of this paper to study the specific acceleration mechanisms present in the PWS, but a few insights can be gained through the acceleration efficiency requirements of the two locations.
Given the ultrarelativistic velocity of the pulsar wind, the PWSs will necessarily be relativistic. The detailed physics of realistic particle acceleration in astrophysical relativistic shocks is currently not well characterized, even though significant progress has been made in the last decade (see, e.g., Lemoine & Pelletier 2012, for a review). One of the key points that has resulted from these developments is that particle acceleration efficiency, and therefore electron maximum energy, depends strongly on magnetic turbulence around the shock and on the size of the shock. The different acceleration efficiencies at the wind standoff and Coriolis turnover could be considered an indication of the level of magnetic turbulence present around the relativistic shocks, and in particular in the postshock regions. The lower density and the influence of turbulent flow from the outer regions of the CD may give rise to a significantly higher magnetic field inhomogeneity in the Coriolis turnover postshock material with respect to the wind standoff location. In addition, the two shocks have significantly different sizes, with characteristic dimensions of ~0.1D and ~5D for the wind standoff and Coriolis turnover shocks, respectively. The shock size is key in determining how long a particle can be retained close to the shock, and therefore how much energy can be transfered to it. These two effects, magnetic tubulence and shock size, could work together and result in the required ηacc of ~20 and ~2000 for the Coriolis turnover and wind standoff locations, respectively.
5.2. X-ray emission
The model presented here does not aim to explain the whole broadband spectrum of gamma-ray binaries, but is limited to the HE and VHE gamma-ray bands. However, the X-ray emission of LS 5039 deserves discussion owing to the resemblance of its orbital modulation to that of VHE emission, as well as the significant fraction of energetic output of the system it represents. Takahashi et al. (2009) proposed a common origin of the X-ray and VHE emission, the orbital modulation of both arising from dominant adiabatic losses. In order to obtain the observed high X-ray fluxes through synchrotron emission, the emitter magnetic field was required to be on the order of 3 G. In Sect. 4 we have shown, however, that to reproduce the observed TeV spectrum from the Coriolis turnover location a magnetic field on the order of 0.2 to 0.4 G is required. A stronger magnetic field would lead to a dominance of synchrotron cooling over Klein-Nishina IC for the highest energy particles and, as a result, a softening of the spectrum above 100 GeV that would be in contradiction with the observed inferior conjunction spectrum (see Fig. 2). Even considering dominant adiabatic losses, as done by Takahashi et al. (2009), results in a spectrum above 5 TeV that is too soft compared to the observations. Nevertheless, it is clear that a magnetic field strength of 0.2 to 0.4 G is insufficient to produce the observed X-ray fluxes. The 0.3 to 10 keV X-ray flux observed by Suzaku varies in the range 5–12 × 10-12 erg cm-2 s-1, whereas the fluxes computed through the proposed model are more than an order of magnitude fainter at around 3 × 10-13 erg cm-2 s-1.
The two magnetic field requirements, however, need not be in contradiction. The turbulence present in the postshock flow at the Coriolis turnover location results in strong fluctuations in the magnetic field. Close to the shock, these could be lower and result in effective magnetic field strengths of ~0.5 G, as required to account for the observed TeV emission. As particles flow downstream, they might encounter stronger magnetic field turbulence with local magnetic field strengths on the order of or higher than 3 G, resulting in stronger synchrotron emission. However, the process through which this emission may be modulated along the orbit is still unclear.
The electron population accelerated at the wind standoff location does not contribute significantly to the X-ray emission of the system. Even though the magnetic field at this location is higher (between 0.6 and 0.9 G) owing to its proximity to the pulsar, electrons are not energetic enough to radiate synchrotron in the X-ray band, displaying a spectral cutoff at around 100 eV. In addition, because of the higher stellar photon field density, the IC emission channel is more efficient than the synchrotron, resulting in a low synchrotron-to-IC-luminosity ratio.
5.3. TeV emission at superior conjunction
The most significant deviation between the computed fluxes of the proposed model and the observed phenomenology of the source is the behavior of TeV emission around superior conjunction. As seen in Sect. 4, the predicted integrated flux above 200 GeV is below the observed flux (Fig. 3) and the predicted spectrum shape presents the characteristic pair-production absorption features instead of a powerlaw spectrum (Fig. 2).
A simple reason for this discrepancy could be our simplification of the emitter as a point-source instead of as an extended source where part of the emitter would be above the orbital plane and could be significantly less absorbed (see, e.g., Khangulyan et al. 2008a, for a study of the optical depth of various locations around the binary system). It must be noted that the Coriolis turnover shock would be compressed in the tangential direction by Coriolis forces, but not in the direction perpendicular to the orbital plane. Therefore, it would rise above the plane following an opening angle of θ ≃ 28.6°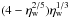 (Bogovalov et al. 2008), resulting in heights between 2 and 5 × 1012 cm above the orbital plane at periastron and apastron, respectively. Additionally, the energy absorbed through pair production is bound to be reemitted by secondary electrons (Bosch-Ramon et al. 2008a), and, for certain values of magnetic field and photon density, by efficient pair cascades (e.g., Aharonian et al. 2006b; Bednarek 2007; Cerutti et al. 2010). However, in an electromagnetic cascade scenario a significant part of the absorbed energy would also end up being emitted as ~10 GeV photons, just below the threshold for γγ pair production on stellar photons, an excess that would be in contradiction with the relatively low flux spectral point detected by Fermi/LAT at ~10 GeV.
(Bogovalov et al. 2008), resulting in heights between 2 and 5 × 1012 cm above the orbital plane at periastron and apastron, respectively. Additionally, the energy absorbed through pair production is bound to be reemitted by secondary electrons (Bosch-Ramon et al. 2008a), and, for certain values of magnetic field and photon density, by efficient pair cascades (e.g., Aharonian et al. 2006b; Bednarek 2007; Cerutti et al. 2010). However, in an electromagnetic cascade scenario a significant part of the absorbed energy would also end up being emitted as ~10 GeV photons, just below the threshold for γγ pair production on stellar photons, an excess that would be in contradiction with the relatively low flux spectral point detected by Fermi/LAT at ~10 GeV.
5.4. Application to other gamma-ray binaries
LS 5039 is an ideal system to test wind interaction models because of its radial, well-determined stellar wind. The rest of the currently known gamma-ray binaries present a harder challenge either because the stellar wind structure is significantly more complex or because our current phenomenological knowledge of them is rather limited. The former applies to PSR B1259−63, LS I +61 303 and HESS J0632+057, which contain a Be star with a dense equatorial near-Keplerian disk, whereas the latter is the case for 1FGL J1018.6−5856. The extremely large orbital separation of PSR B1259−63 sets it apart from the other gamma-ray binaries, as radiative processes in the wind interaction region are only significant during a short period of time around periastron. During this time, the interaction of the pulsar wind with the stellar equatorial disk gives rise to broadband non-thermal emission with a rich phenomenology (e.g., Aharonian et al. 2005b; Chernyakova et al. 2009; Abdo et al. 2011). Given the presence of the dense equatorial disk during the compact object passage, the model presented here is not applicable. For the other two gamma-ray binaries with Be stars, LS I +61 303 and HESS J0632+057, the situation is different as most of their emission takes place away from periastron and therefore far from the equatorial disk. Additionally, the compact orbit of LS I +61 303 means that the stellar disk is probably disrupted by the compact object passage (Romero et al. 2007). These two systems have a wider orbit than LS 5039, and their radial component of the stellar wind is less powerful, resulting in a Coriolis turnover location farther from the system. Our model, however, provides a plausible explanation for the orbit-to-orbit instability of VHE and X-ray emission from LS I +61 303. The wind standoff region is quite stable under wind irregularities, so that GeV emission is expected to be more stable, but the shock properties at the Coriolis turnover location are much more dependent on the turbulence generated along the CD, which is in turn strongly affected by wind irregularities. This could mean that for certain wind interaction regimes this shock might even disappear, leading to the VHE/X-ray instability of LS I +61 303.
1FGL J1018.6−5856 is the only other gamma-ray binary, along with LS 5039, to host an O-type star. Its similar-sized orbit makes it also a good candidate to apply our model and further our understanding of the source. The HE gamma-ray spectrum indeed agrees well with the prediction from a wind standoff location emitter (Ackermann et al. 2012). However, its detection at VHE is still not clear, as it is in confusion with a nearby extended source and no flux variability has been detected yet (Abramowski et al. 2012). In addition, the orbital parameters of the system are currently unknown, making any theoretical predictions highly uncertain. However, the general observational features appear to be similar to LS 5039 and as such could be consistent with the framework presented by our model.
6. Conclusion
The results presented here show that the two-emitter model for the GeV-TeV emission of LS 5039 provides a new explanation to the non-trivial problem of the origin of the HE and VHE spectral components of gamma-ray binaries. These two locations arise naturally from the interaction of the stellar and pulsar winds in an orbiting system.
However, the development of this model and comparison with the increasingly better-quality observations at GeV and TeV showcases the intrinsic difficulty in understanding the processes responsible for non-thermal emission in gamma-ray binaries. The compound effects of acceleration, (magneto)hydrodynamical, and radiation processes are impossible to disentangle and require a comprehensive approach to the problem. Even though the best method to unveil the workings of gamma-ray binaries would be radiation-coupled magnetohydrodynamical simulations, the large amount of unknown quantities that would be required for such simulations still make simpler approaches, like the one presented in this paper, a safer, more confident way to advance in our understanding.
Acknowledgments
The authors thank the referee, Guillaume Dubus, for his thorough review and helpful comments on the manuscript. We thank D. Hadasch for providing the Fermi/LAT observational data. V.Z. acknowledges support by the Generalitat de Catalunya through the Beatriu de Pinós program, the Max-Planck-Gesellschaft, and the Spanish MICINN under grant AYA2010-21782-C03-01. V.B.-R. acknowledges support by the Spanish Ministerio de Ciencia e Innovación (MICINN) under grants AYA2010-21782-C03-01 and FPA2010-22056-C06-02. V.B.-R. acknowledges financial support from MINECO through a Ramón y Cajal fellowship.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 706, 56 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, Science, 326, 1512 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, 11 [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 541, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ackermann, M., Ajello, M., Ballet, J., et al. 2012, Science, 335, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1981, Ap&SS, 79, 321 [NASA ADS] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005a, Science, 309, 746 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005b, A&A, 442, 1 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, A&A, 460, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Anchordoqui, L., Khangulyan, D., & Montaruli, T. 2006b, J. Phys. Conf. Ser., 39, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, Science, 312, 1771 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 665, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 2007, A&A, 464, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bednarek, W. 2011, MNRAS, 418, L49 [NASA ADS] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D. V., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2008, MNRAS, 387, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2012, MNRAS, 419, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Barkov, M. V. 2011, A&A, 535, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2009, IJMPD, 18, 347 [Google Scholar]
- Bosch-Ramon, V., Motch, C., Ribó, M., et al. 2007, A&A, 473, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Khangulyan, D., & Aharonian, F. A. 2008a, A&A, 482, 397 [Google Scholar]
- Bosch-Ramon, V., Khangulyan, D., & Aharonian, F. A. 2008b, A&A, 489, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Barkov, M. V., Khangulyan, D., & Perucho, M. 2012, A&A, 544, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribó, M., Ribas, I., et al. 2005, MNRAS, 364, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Cerutti, B., Malzac, J., Dubus, G., & Henri, G. 2010, A&A, 519, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernyakova, M., Neronov, A., Aharonian, F., Uchiyama, Y., & Takahashi, T. 2009, MNRAS, 397, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G., Cerutti, B., & Henri, G. 2008, A&A, 477, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G., Cerutti, B., & Henri, G. 2010, A&A, 516, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadasch, D., Torres, D. F., Tanaka, T., et al. 2012, ApJ, 749, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., Manchester, R. N., Lyne, A. G., et al. 1992, ApJ, 387, 37 [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Hnatic, S., Aharonian, F., & Bogovalov, S. 2007, MNRAS, 380, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F., & Bosch-Ramon, V. 2008a, MNRAS, 383, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D. V., Aharonian, F. A., Bogovalov, S. V., Koldoba, A. V., & Ustyugova, G. V. 2008b, IJMPD, 17, 1909 [Google Scholar]
- Lamberts, A., Dubus, G., Lesur, G., & Fromang, S. 2012, A&A, 546, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemoine, M., & Pelletier, G. 2012, in AIPC, eds. P.-L. Sulem, & M. Mond, 1439, 194 [Google Scholar]
- Maraschi, L., & Treves, A. 1981, MNRAS, 194, 1 [Google Scholar]
- Markova, N., Puls, J., Repolust, T., & Markov, H. 2004, A&A, 413, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moldón, J., Johnston, S., Ribó, M., Paredes, J. M., & Deller, A. T. 2011, ApJ, 732, 10 [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Pétri, J., & Dubus, G. 2011, MNRAS, 417, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarty, G. E., Szalai, T., Kiss, L. L., et al. 2011, MNRAS, 411, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Skilton, J. L., Pandey-Pommier, M., Hinton, J. A., et al. 2009, MNRAS, 399, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Szostek, A., & Dubus, G. 2011, MNRAS, 411, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Kishishita, T., Uchiyama, Y., et al. 2009, ApJ, 697, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., Bulgarelli, A., Piano, G., et al. 2009, Nature, 462, 620 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zabalza, V., Bosch-Ramon, V., & Paredes, J. M. 2011a, ApJ, 743, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V., Paredes, J. M., & Bosch-Ramon, V. 2011b, A&A, 527, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the proposed scenario at the periastron of a close-orbit system similar to LS 5039. The region of the CD where significant turbulence, and therefore wind mixing, are expected to take place is indicated with a wavy line. The red regions indicate the two proposed emitter locations. |
| In the text | |
 |
Fig. 2 Spectral energy distribution of LS 5039. The computed emission and observational data during the inferior conjunction (0.45 < φ < 0.9) is shown in red and during the superior conjunction (0.9 < φ < 0.45) in blue. The emission components from the wind standoff and Coriolis turnover locations are indicated with a dotted and dashed line, respectively. |
| In the text | |
 |
Fig. 3 Top: Fermi/LAT orbital lightcurve of LS 5039 in the energy range 100 MeV to 30 GeV, along with the computed gamma-ray emission. Bottom: HESS orbital lightcurve in the range 0.2 to 5 TeV. Two orbital periods are shown for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


