| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220424 | |
| Published online | 01 March 2013 | |
Chandra LETGS observation of the variable NLS1 galaxy Ark 564⋆
Centro de Física, Instituto Venezolano de Investigaciones Científicas
(IVIC), PO Box 025304, Caracas 1020A, Venezuela
e-mail:
josem@ivic.gob.ve
Received:
21
September
2012
Accepted:
18
January
2013
We present an analysis of the 100 ks X-ray spectrum of the narrow-line Seyfert 1 Galaxy Ark 564, taken with the Low Energy Transmission Grating Spectrometer (LETGS) on board Chandra. Using χ2 statistics, several continuum models of the time-averaged spectrum of this object are compared, obtaining a semi-empirical solution for the description of the intrinsic emission continuum and a physical solution for the intrinsic absorption of the system. We find that the 0.1−10 keV spectrum can be well described by a power law plus two thermal components that account for the soft step. We are also able to detect and measure several narrow, unresolved absorption lines arising from highly ionized species of C, N, O, and Fe. The material seems to have a velocity consistent with the systemic velocity of the galaxy. This piece of evidence, in addition to the very low observed column density of NH ~ 1020 cm-2, is in good agreement with the scenario of a transverse biconical outflow with a gas density of n ≲ 3 × 1012 cm-3 at distances beyond the broad-line region r ≳ 10 lt-days, but a dust torus origin cannot be ruled out.
Key words: galaxies: Seyfert / line: identification / quasars: absorption lines
The reduced spectrum is only available in electronic form at the CDS via anonymous ftp to http://cdsarc.u-strasbg.fr(130.79.128.5) or via cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A95
© ESO, 2013
1. Introduction
Narrow-line Seyfert 1 galaxies (NLS1s) are a subclass of the “normal” Seyfert 1 galaxies that exhibit in their optical spectra Hβ lines with full width at half maximum FWHM ≲ 2000 km s-1 (Osterbrock & Pogge 1985) and strong Fe II emission (Boroson & Green 1992). X-ray observations of these objects reveal extreme spectral and temporal properties, Ark 564 being the most representative and observed Seyfert of this category. Firstly, NLS1s show a “soft X-ray excess emission” which has been the subject of an extensive debate for at least two decades. Pounds et al. (1995) proposed that this soft excess might be produced by an optically thick emission from the accretion disk. However, the temperature of this optically thick region (kT ~ 0.1−0.15 keV) is too hot for a disk around a supermassive black hole (SBH). If described as a thermal component, the temperature of this soft excess is exceptionally constant (~0.1−0.2 keV) for a wide range of SBH masses (Czerny et al. 2003; Gierliński & Done 2004; Crummy et al. 2006). Instead, Gierliński & Done (2004) propose that the inflexion point or soft step seen around ~0.7−0.8 keV is the result of the atomic physics, showing that a strongly smeared, partially ionized absorption edge can reproduce the XMM-Newton EPIC soft X-ray spectra of a sample of Palomar Green quasars. The other explanation for the soft X-ray step, also related to the atomic physics, is that this partially ionized material is shown in reflection (Fabian et al. 2002).
Secondly, NLS1s usually show rapid and large amplitude variability (Boller et al. 1996; Turner et al. 1999), with changes of up to a factor of 100 in timescales of days (e.g., Forster & Halpern 1996; Boller et al. 1997), but also of smaller factors in shorter timescales (e.g., Leighly 1999; Edelson et al. 2002; Dewangan et al. 2007). Using ROSAT observations (Boller et al. 1996; Wang et al. 1996), it is nowadays commonly accepted that the slope differences of the soft X-ray spectra of NLS1s and BLS1s (broad line Seyfert 1, FWHM ≳ 2000 km s-1) are due to differences in their black-hole masses and accretion rates (e.g., Pounds et al. 1995; Puchnarewicz et al. 2001) and Eddington luminosities (e.g., Grupe et al. 2004; Shemmer et al. 2008; Grupe et al. 2010).
The galaxy Ark 564 (IRAS 22403+2927, MCG+05-53-012) at redshift z = 0.02468 (Huchra et al. 1999) and V = 14.6 (de Vaucouleurs et al. 1991) is one of the brightest NLS1s. With a 2−10 keV luminosity L2−10 keV ~ 2 × 1043 erg s-1 (Turner et al. 2001), it has been observed in almost every band of the electromagnetic spectrum by space-based missions, namely ROSAT (Brandt et al. 1994), ASCA (Pounds et al. 2001; Edelson et al. 2002), Hubble Space Telescope (HST, Crenshaw et al. 2002), Far-Ultraviolet Spectroscopic Explorer (FUSE, Romano et al. 2002), BeppoSAX (Comastri et al. 2001), and ground-based observatories in optical long-term (1999−2010) campaigns (e.g., Shapovalova et al. 2012).
Detailed power density spectrum (PDS) analysis using RXTE data (Pounds et al. 2001) and ASCA monitoring observations (e.g., Papadakis et al. 2002) further support the picture that Ark 564 may have a relatively small black-hole mass and a high accretion rate. Dewangan et al. (2007) find evidence of a 4−10 keV band lag behind the 0.2−0.5 keV band of ≈1.8 ks, thus concluding (for Ark 564) that the soft excess cannot be the reprocessed emission of the primary X-ray spectrum. They then propose two coronae: an optically thick one for the soft excess, and a hot one for the power law component.
Making use of the Chandra High Energy Transmission Grating Spectrometer (HETGS), Matsumoto et al. (2004) report that the spectrum of Ark 564 above 2 keV can be modeled by a power law with a photon index of Γ = 2.56 ± 0.06. They are able to fit a black body to account for the soft excess, its best-fit temperature being kT = 0.124 keV. They also detect an edge-like feature at 0.712 keV that is interpreted as the product of a warm absorber with ξ ~ 1 and NW ~ 1021 cm-2, which includes the rest-frame O VII edge at 0.739 keV as part of the complex. Their data also allow the identification of a second warm absorber at log ξ ~ 2 and NW ~ 1021 cm-2 in order to produce the narrow absorption lines of O VII, O VIII, Ne IX, Ne X, and Mg XI observed in the spectrum.
Analyzing the 100 ks XMM-Newton time-averaged spectrum of Ark 564, Papadakis et al. (2007) propose that the spectrum below ~2 keV can be modeled either by two black bodies (2BB, kT ~ 0.07−0.15 keV) or a single black body plus reflection. They also detect a shallow flux deficit ~0.65−0.85 keV which is associated with the so-called unresolved transition array (UTA), but neither a strong absorption edge at 0.7 keV nor an emission line at ~1 keV are reported.
Recently, using the XMM-Newton Reflection Grating Spectrometer (RGS), Smith et al. (2008) present a characterization of the high-resolution X-ray spectrum of Ark 564, and find that it can be reproduced by a three-phase photoionization model with ionization parameters log ξ = −0.86, 0.87 and 2.56, and column densities NW = (0.89,2.41,6.03) × 1020 cm-2, which are able to predict the O VIII Lα, O VII(f), N VII Lα, N VI(i), and C VI Lα lines detected in the spectrum.
It may be appreciated that the X-ray spectrum of this extreme Seyfert galaxy is far from being described by a simple power law, but rather by a range of reprocessed features such as absorption edges, emission and absorption lines, thermal components, reflection, etc. (e.g., Turner & Miller 2009). The aim of the present work is thus to explore in detail several of these features, using both semi-empirical models, e.g., a power law plus black bodies, put-by-hand absorption edges, and sophisticated photoionization models so as to find an interpretation for the “X-ray soft step” in Ark 564 that could be extrapolated to other NLS1s. Throughout the text, we use the following cosmological parameters: H0 = 70 km s-1 Mpc-1, ΩM = 0.3 and Ωλ = 0.7, and a luminosity distance of DL = 107.7 Mpc.
2. Observation and data reduction
We obtained an observation1 of Ark 564 in April 2008 with the Low Energy Transmission Grating Spectrometer (LETGS, Brinkman et al. 2000) on board Chandra (sequence number 701 593, ObsID 09151, 100 ks exposure time). The spectrum was obtained by reducing the data with the Chandra Interactive Analysis of Observation (CIAO2, version 4.2) and following the standard Science Threads3 for extraction of LETG/HRC-S grating spectra.
We used the default spectral extraction region (i.e., a bow-tie shaped region). When the Low Energy Transmission Grating (LETG) is used with the High Resolution Camera (HRC-S) detector, this comprises a central rectangle abutted to outer regions whose widths increase with the dispersion distance. The background region is taken from above and below the dispersed spectra. The region shape for both source and background, negative and positive orders is given precisely in a file4 that can be accessed from the LETGS calibration webpage5.
Having properly extracted both source and background spectra from each arm, we merged them to increase the signal-to-noise ratio (S/N) of the final spectrum, and the analysis in the present work is based on this co-added spectrum. The effective areas (EA) for orders 2−10 used in fitting procedures were built using the standard CIAO task mkgarf and fullgarf. For the first order we used the corrected EA of Beuermann et al. (2006); EA orders 1−10 (positive and negative orders) were added to be used with the corresponding co-added spectrum.
3. X-ray light curve and source extent
We show the background-subtracted LETGS ±1 order light curve in the upper panel of Fig. 1. The soft source average count rate in the 0.3−1 keV band is ≈1.2 counts s-1. In the middle panel we show the count rate of the hard band 2−10 keV, with ≈0.05 counts s-1. To check background flaring, we extracted event photons from a source-free region defined by four circles with radii of 25′′ equidistantly distributed from the center of the zeroth-order image. This is carried out in order to avoid contamination from events associated with the dispersion and cross-dispersion directions. The background average count rate was practically constant over the whole exposure, and the source clearly exhibited flux variability.
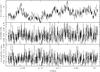 |
Fig. 1 Upper panel: background-substracted LETGS ± 1 order light curve of Ark 564 binned at 200 s. The light curve shows 0.3−1 keV flux variation. The shortest (detectable) timescale is ~1.2 ks. The min/max amplitude change ΔC (Cmin at ~38 ks to Cmax at ~70 ks from the start of the observation), is ~60%. See text for more details. Middle panel: the light curve shows the hard band 2−10 keV flux variation. Bottom panel: the hardness ratio hard/soft band shows no important variation. |
Basic properties of the light curve can be highlighted from some of our preliminary results. The variation of the hard energy X-ray band (2−10 keV) is weak. The strongest variation comes from the “soft” 0.3−1 keV energy band with a fractional variability amplitude frms,soft ~ 16%. Therefore, no important correlation is found between these two bands, i.e., no variation in the hardness ratio (see bottom panel in Fig. 1). This is different from the XMM-Newton PDS analysis presented by Dewangan et al. (2007), who find that the 4−10 keV band lags behind that of 0.2−0.5 keV by τlag ≈ 1.8 ks. Our result is also different from the hard-band variability reported by Papadakis et al. (2007) in the 100 ks XMM-Newton observation of Ark 564. Having found no correlation, it implies that during this epoch (April 2008) the soft emission is not reprocessed hard X-ray emission. The shortest (detectable) timescale is ~1.2 ks. The min/max amplitude change ΔC (Cmin at ~38 ks to Cmax at ~68 ks from the start of the observation) is ~60%. There are several intervals of detectable count changes of ~5 ks. The time interval between the two highest peaks is ~50 ks.
Although Ark 564 is classified as a compact steep-spectrum (CSS) radio source (Gaskell et al. 2004), it has a radio luminosity at 400 MHz of νLν = (2.8 ± 0.8) × 105 L⊙ (Colla et al. 1970). For this reason we checked for evidence of spatial extent of the source or the presence of other possible X-ray sources, e.g., jets close to Ark 564. We extracted events within a stack of concentric annuli with radii ~0.1−1.3′′ from the zeroth-order image, and fit a β-model to the surface brightness flux profile resulting from that extraction centered at the target center. The best fit model gives core radius r0 ~ 0.5′′ and β ~ 1.1. The core radius is consistent with the point-spread function (PSF) FWHM of the HRC (~0.4′′). We conclude that no evidence of appreciable source extent is found in this observation and we treat it as a point-like source. We also checked for angular dependence in the X-ray image, and found that the emission of the object is symmetrically distributed.
4. Time-average spectral analysis
In this section we present a time-averaged spectral analysis of the spectrum of Ark 564. All the models considered in this section are multiplied by an absorption column of gas (phabs model in XSPEC6) with NH = 5.34 × 1020 cm-2 to describe the Galactic absorption toward Ark 564 (Kalberla et al. 2005). Thanks to our interest in the global picture of the spectrum, the co-added LETGS spectrum of Ark 564 has been binned as follows: above 0.33 keV, the data are uniformly binned by a factor of 8 (i.e., bin width of 0.1 Å). This ensures that the detected narrow features actually come from the data and are not artifacts created by the requirement that a certain amount of counts per bin are necessary. In either case, the data are of sufficient quality to have more than 70 counts per bin using this rebinning mode. Between 0.33 and 0.15 keV, the spectrum is adaptively binned to have at least 1000 counts per bin. Finally, below 0.15 keV the spectrum is adaptively binned to have at least 2500 counts per bin. The result is a high-quality (large number of counts per resolution element) spectrum distributed in 443 PHA bins which optimize the use of the full band (0.1−10 keV) of the spectrometer, and this is the spectrum used for the next analysis. The spectral fit analysis has been performed with the XSPEC v11.3 package. The parameters are reported with 90% confidence intervals.
4.1. X-Ray fluxes and luminosities
The high quality of the LETGS X-ray spectrum of Ark 564 allows us to report fluxes and
luminosities with high precision for different X-ray bands. Papadakis et al. (2007), using the 100 ks XMM-Newton
spectrum of Ark 564 do not report fluxes and luminosities in the 0.1−0.3 keV band. The
only observation with reliable data in this band is precisely the one we are reporting
here. To highlight the magnitude of the luminosity in the 0.1−0.3 keV band, we report the
intrinsic luminosity 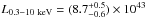 erg
s-1. This is about the same X-ray luminosity of
L0.3−10 keV = 6.5 × 1043 erg s-1
reported by Papadakis et al. (2007) using the 100
ks XMM-Newton spectrum of Ark 564. However, the luminosity in the 0.1−0.3
keV band is about three times higher, measured thanks to the high sensitivity of the LETGS
in this band7. For the hard 2−10 keV band, we
computed a 2−10 keV flux of
erg
s-1. This is about the same X-ray luminosity of
L0.3−10 keV = 6.5 × 1043 erg s-1
reported by Papadakis et al. (2007) using the 100
ks XMM-Newton spectrum of Ark 564. However, the luminosity in the 0.1−0.3
keV band is about three times higher, measured thanks to the high sensitivity of the LETGS
in this band7. For the hard 2−10 keV band, we
computed a 2−10 keV flux of 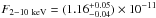 ergs cm-2 s-1. The finding is that during this epoch (April 2008)
Ark 564 was fainter than previous observations in the hard band (2−10 keV). Papadakis et al. (2007) reported
F2−10 keV = 1.5 × 10-11 ergs cm-2
s-1. It was also lower by a factor of two than the 2−10 keV ASCA flux of
F2−10 keV = 2 × 10-11 ergs cm-2
s-1 reported by Turner et al. (2001).
ergs cm-2 s-1. The finding is that during this epoch (April 2008)
Ark 564 was fainter than previous observations in the hard band (2−10 keV). Papadakis et al. (2007) reported
F2−10 keV = 1.5 × 10-11 ergs cm-2
s-1. It was also lower by a factor of two than the 2−10 keV ASCA flux of
F2−10 keV = 2 × 10-11 ergs cm-2
s-1 reported by Turner et al. (2001).
4.2. The hard LETGS spectrum
In order to investigate in detail the soft excess or soft step, we started by fitting a
simple power law to the hard (2−10 keV) band of the spectrum. The best-fit photon index is
Γhard = 2.5 ± 0.1 and normalization
normhard = (9.8 ± 1.5) × 10-3 photons
keV-1 cm-2 s-1 at 1 keV, resulting in an acceptable fit
to this band with χ2 = 24.94 for 46 degrees of freedom
(d.o.f.). The photon index of the power law is consistent with previous values found in
spectral analysis for this band in this object. An example is the
Γ2−10 keV ≈ 2.5 found by Vignali et al.
(2004) in the 2000 June XMM-Newton observation. Comastri et al. (2001) also found
Γ2−10 keV ≈ 2.4 in the BeppoSAX observation of Ark 564,
similar to the Γhard = 2.34−2.44 found by Papadakis et al. (2007) in the ~100 ks XMM-Newton
observation of the same object with the EPIC-pn (European Photon Imaging Camera with the
pn CCDs) and EPIC-MOS (European Photon Imaging Camera with the Metal Oxide Semi-conductor
CCD arrays) cameras. The ASCA observation of Ark 564 also shows
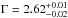 (Turner et al. 1999) and the Suzaku observation
Γ = 2.52 ± 0.01 (Walton et al. 2012). Therefore, we
adopt this value of Γhard for the analysis in the next section.
(Turner et al. 1999) and the Suzaku observation
Γ = 2.52 ± 0.01 (Walton et al. 2012). Therefore, we
adopt this value of Γhard for the analysis in the next section.
4.3. Broad-band spectrum and the soft excess or soft step?
In this section we present a spectral analysis of the soft step (0.8 keV) seen in the spectrum of Ark 564. All the measurements below are in the rest frame. Figure 2 shows the extrapolation of the best-fit hard-power-law model to low energies, where an emission excess is clearly seen to be quantitatively similar to the soft excess found by Comastri et al. (2001), Vignali et al. (2004) and Papadakis et al. (2007). In order to investigate the nature of this soft excess or soft step (it is still in debate, e.g., Done & Nayakshin 2007), we have added to the hard power law (i.e., PLhard with fixed parameters as “baseline”) several other components to describe the soft band8. The extra components are 1) single black body (BB); 2) two black bodies (2BB); 3) a soft power law (PLsoft), where we set the power law (i.e., PLhard) to vary freely and consider only absorption models; 4) single edge (Ed); 5) two edges (2Ed); 6) a single partial covering (Cov); and 7) two-partial-covering (2Cov).
 |
Fig. 2 Background-substracted LETGS ± 1 0.1−10 keV spectrum of Ark 564. Extrapolation of the best-fit hard power law to low energies to demonstrate the soft excess. The upper panel shows the data with the convolved model in red (black and white [BW] as a solid line). Below, the ratio data/model. |
The temperature of a single black body when it is added to the PLhard results in kT = 120 ± 1 eV9. This temperature is consistent with best-fit temperatures found in others X-ray observations of Ark 564 (e.g., Vignali et al. 2004; Comastri et al. 2001), usually attributed to a thermal component produced by the high-energy tail of the accretion disk in NLS1 (e.g., Soria & Puchnarewicz 2002).
Motivated by the finding that the two black body components describe relatively well the
EPIC-pn and EPIC-MOS spectra of this object (Papadakis et
al. 2007), we add a second black body to our single-black-body model. Using the
values reported by Papadakis et al. (2007) of
kT1 = 0.15 and
kT2 = 0.07 keV as initial estimates of the
fitting procedure, we were able to find a statistically significant improvement of the 2BB
(over BB) model to our data at higher than 99.99% (according to an F-test). The
temperatures of the two-black-body component are 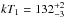 eV
and kT2 = 39 ± 2 eV, with
χ2/d.o.f. = 583.38/439.
They match those reported by Papadakis et al.
(2007) remarkably well, making this model interesting for further
examination10. These are, nevertheless, not well
constrained by Papadakis et al. (2007) and they
were thus reported without error estimates. This is not surprising since some of the
authors failed to use the EPIC-pn and EPIC-MOSes 0.1−0.3 keV band of that
XMM-Newton observation. However, the temperature of the first black
body is different from the hot component found by Pounds
et al. (2004) (~270 eV) in the high-flux state of NGC 4051. Figure 3 shows the model quality in fitting the data.
eV
and kT2 = 39 ± 2 eV, with
χ2/d.o.f. = 583.38/439.
They match those reported by Papadakis et al.
(2007) remarkably well, making this model interesting for further
examination10. These are, nevertheless, not well
constrained by Papadakis et al. (2007) and they
were thus reported without error estimates. This is not surprising since some of the
authors failed to use the EPIC-pn and EPIC-MOSes 0.1−0.3 keV band of that
XMM-Newton observation. However, the temperature of the first black
body is different from the hot component found by Pounds
et al. (2004) (~270 eV) in the high-flux state of NGC 4051. Figure 3 shows the model quality in fitting the data.
 |
Fig. 3 Background-substracted LETGS ± 1 0.1−10 keV spectrum of Ark 564, with the best-fit hard power law and the addition of two black bodies (the PLhard+2BB model). The upper panel shows the data with the convolved model in red (BW v. as a solid line). Below, the ratio data/model. The lower panel shows the flux spectrum with the composed physical model (and its components separately) as a solid line. |
We then add a PLsoft to the baseline; as expected, compared to the PLhard alone, this addition gives a better fit with a photon index Γsoft ~ 3.6 and normalization normsoft ~ 3.3 × 10-3 photons keV-1 cm-2 s-1 at 1 keV, which helps to describe the soft band of the spectrum, although it remains statistically unacceptable with χ2/d.o.f. = 1177.23/44111.
Even when reaching a “good” global description of the spectrum, for instance with the PLhard+2BB model, we easily see edge- and narrow-line-like structures in the range ~0.5−2 keV. We begin the search for absorption-like structures with a global power law modified by an edge, namely the PL+Ed model.
The initial estimate of the edge energy (in the fitting procedure) is set at 0.739 keV (rest frame), motivated by the detection of an edge-like feature in the HETGS observation of this object by Matsumoto et al. (2004), and interpreted by these authors as a combination of the O VII K edge and a number of L-absorption iron lines. However, in our PL+Ed model the best-fit edge energy is Eedge = 1263 ± 6 eV and the optical depth τ = 0.25 ± 0.03, with χ2/d.o.f. = 739.41/439. We also tried fixing the edge energy at the theoretical value of the O VII K edge, but it results in a worse χ2 of 891.43 for 440 d.o.f. and a negligible optical depth. We conclude that there is no clear evidence for an edge-like structure at ~0.7 keV in the LETGS spectrum of Ark 564. A similar conclusion is reached by Papadakis et al. (2007) using the ~100 ks XMM-Newton observation of this object, but different from the ≈0.73 keV feature (O VII edge) reported by Vignali et al. (2004) in the 2000 June XMM-Newton observation of Ark 564 and also found by Matsumoto et al. (2004) in the HETGS spectrum. We will return to this point in the high-resolution analysis (i.e., finer binning of 25 mÅ) presented in Sect 5.
The realization that the material surrounding the central black hole in active galactic
nuclei (AGN) absorbs/reprocesses part of the continuum radiation which affects the
observed spectrum, gives rise to unresolved issues on the location of the medium,
ionization, and clumpiness of the material. Here we explore how the partial coverage
affects the final spectrum and how it compares to simple absorption models such as PL+Ed
and PL+2Ed. We start with a simple power law modified by a single partial coverage,
PL+Cov. The best-fit photon index is Γ ~ 2.9, best-fit column density of the
material 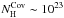 cm-2, and
the covering factor f ~ 0.4 with
χ2/d.o.f. = 856.21/439.
It is comparable to PLfree + PLsoft, but not superior to any of the
following models: PL+BB, PL+2BB, PL+Ed, or PL+2Ed. For this reason we added a second
partial coverage, PL+2Cov. It gives best-fit values of
cm-2, and
the covering factor f ~ 0.4 with
χ2/d.o.f. = 856.21/439.
It is comparable to PLfree + PLsoft, but not superior to any of the
following models: PL+BB, PL+2BB, PL+Ed, or PL+2Ed. For this reason we added a second
partial coverage, PL+2Cov. It gives best-fit values of
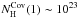 cm-2,
f1 ~ 0.4,
cm-2,
f1 ~ 0.4, 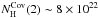 cm-2, and f2 ~ 0.2, but it does not
improve the data fit relative to PL+Cov with
χ2/d.o.f. ~ 856/437,
and thus we do not consider it further. Then we tried the case where PL+BB is partially
coverage (i.e., the covering material modify the PL+BB model giving the PL+BB+Cov model).
In this case we have a statistical improvement at the 99.9% level (according to an F-test)
with respect to PL+BB and the following best-fit parameters: Γ ~ 3.2,
kT=175 eV,
cm-2, and f2 ~ 0.2, but it does not
improve the data fit relative to PL+Cov with
χ2/d.o.f. ~ 856/437,
and thus we do not consider it further. Then we tried the case where PL+BB is partially
coverage (i.e., the covering material modify the PL+BB model giving the PL+BB+Cov model).
In this case we have a statistical improvement at the 99.9% level (according to an F-test)
with respect to PL+BB and the following best-fit parameters: Γ ~ 3.2,
kT=175 eV,
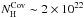 cm-2,
f ~ 0.7, and
χ2/d.o.f. = 615/437.
Again, adding a second partial coverage does not improve the fit relative to the PL+BB+Cov
model. Finally, we verified if the same single partial coverage improves the PL+2BB in a
statistical sense but no important improvement is found, although well constrained
parameters on the covering material can be assigned with
cm-2,
f ~ 0.7, and
χ2/d.o.f. = 615/437.
Again, adding a second partial coverage does not improve the fit relative to the PL+BB+Cov
model. Finally, we verified if the same single partial coverage improves the PL+2BB in a
statistical sense but no important improvement is found, although well constrained
parameters on the covering material can be assigned with
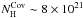 and
f ~ 0.8 (see Table 1
for errors). We conclude that there is weak evidence that a partial coverage ranging
between
and
f ~ 0.8 (see Table 1
for errors). We conclude that there is weak evidence that a partial coverage ranging
between 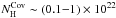 cm-2 and
f ~ 0.1−0.8 may be accommodated as an additional element in
some of our model fits; however, it is not superior to the (simplified) absorption edge
(or 2Ed) model.
cm-2 and
f ~ 0.1−0.8 may be accommodated as an additional element in
some of our model fits; however, it is not superior to the (simplified) absorption edge
(or 2Ed) model.
Fit results of continuum models of Ark 564.
4.4. Photoionization modeling on the coarse binned spectrum
We have so far tried to explain the soft X-ray excess seen in the spectrum of Ark 564
using several emission (PL or BB) and simple-absorption (only photoelectric edges) models.
It is, however, well known that complex absorption − in addition to primary (and/or
reflection) emission − might play a role in the explanation of what we see as an excess in
emission (e.g., Chevallier et al. 2006). For this
reason we build a grid of photoionization models to describe the complex absorption in the
X-ray spectrum of Ark 564. To describe the state of the absorbing gas, we assume
ionization and thermal equilibrium. Under conditions of ionization equilibrium, the state
of the gas depends mostly (apart from nH, abundances, and
column density) upon the shape of the ionizing spectrum and the ionization parameter
ξ that we define as in Tarter et al.
(1969)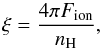 (1)where
Fion is the total ionizing flux
(Fion = Lion/ [4πr2],
see below for definition of Lion) and
nH is the gas density. We have carried out all the
photoionization calculations using the XSTAR12 code
with the atomic data of Bautista & Kallman
(2001). The code includes all the relevant atomic processes (including
inner-shell processes) and computes the emissivities and optical depths of the most
prominent X-ray and UV lines identified in AGN spectra. Our models are based on spherical
shells illuminated by a point-like X-ray continuum source. The input parameters are the
source spectrum, the gas composition, the gas density nH, the
column density and the ionization parameter. The source spectrum is described by the
spectral luminosity
Lϵ = Lionfϵ,
where Lion is the integrated luminosity from 1 to 1000 Ryd,
and
(1)where
Fion is the total ionizing flux
(Fion = Lion/ [4πr2],
see below for definition of Lion) and
nH is the gas density. We have carried out all the
photoionization calculations using the XSTAR12 code
with the atomic data of Bautista & Kallman
(2001). The code includes all the relevant atomic processes (including
inner-shell processes) and computes the emissivities and optical depths of the most
prominent X-ray and UV lines identified in AGN spectra. Our models are based on spherical
shells illuminated by a point-like X-ray continuum source. The input parameters are the
source spectrum, the gas composition, the gas density nH, the
column density and the ionization parameter. The source spectrum is described by the
spectral luminosity
Lϵ = Lionfϵ,
where Lion is the integrated luminosity from 1 to 1000 Ryd,
and 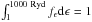 . The
spectral function is taken to be the ionizing spectrum of Leighly (2004). The gas consists of the following elements: H, He, C, N, O, Ne,
Mg, Si, S, Ar, Ca and Fe. We use the abundances of Grevesse et al. (1996) in all our models and use the term solar
for these abundances. We adopt a turbulent velocity of 200 km s-1 and
a gas density nH = 1010 cm-3.
. The
spectral function is taken to be the ionizing spectrum of Leighly (2004). The gas consists of the following elements: H, He, C, N, O, Ne,
Mg, Si, S, Ar, Ca and Fe. We use the abundances of Grevesse et al. (1996) in all our models and use the term solar
for these abundances. We adopt a turbulent velocity of 200 km s-1 and
a gas density nH = 1010 cm-3.
We are finally ready to fit the global spectrum of Ark 564 with self-consistent photoionization models, and characterize its warm absorber with and without the thermal components. However, there is a point we must discuss first. After an exhaustive investigation (and in the light of the obvious residual left by virtually every continuum model we fit on the spectrum), we have come to realize that the strong feature at ~0.53 keV might be the Galactic atomic oxygen absorption lines (Garcia et al. 2011). This is the reason for modeling this feature with two Gaussians fixing the energies at EG1 = 0.527 keV and EG2 = 0.531 keV and the width (σ) at the spectrometer resolution FWHM = 0.05 Å. These two features have also been identified in the XMM-Newton RGS analysis of this object by Smith et al. (2008), as well as along the line of sight of Mrk 421, a blazar with similar redshift (z ~ 0.03 the LETGS spectrum reported by Nicastro et al. 2005). Therefore, all the global photoionization models include these Gaussian features due to Galactic oxygen absorption. If we try to model the X-ray spectrum of Ark 564 with only a power law modified by a warm absorber (PL+WA), the best-fit column density is low (NWA ~ 1019 cm-2), which reflects weak narrow spectral features (if at all) and an ionization parameter of log ξ ~ 1, the quality of the fit being as “bad” as the PLhard + PLsoft with the same d.o.f. (i.e., χ2/(d.o.f.) ~ 1120/439).
It is worth noting the low residual at 0.53 keV thanks to our inclusion of the Galactic
oxygen absorption. Then we verified whether additional modification by partial coverage
improves the fit. It gives a better fit by
Δχ2 ~ −20 for two less d.o.f.13. We subsequently added a black body (PL+BB+WA) to the PL+WA which
is required at a significant level of 99.99% (according to an F-test) resulting in
log ξ = 1.0 ± 0.3, 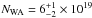 cm-2 and
cm-2 and
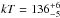 eV
with
χ2/(d.o.f.) = 600/437.
Again, we checked whether additional covering material improves the fit in any respect.
This time the fit is better with Δχ2 ~ −45 over the
PL+BB+WA, with similar values of the physical parameters of the ionized absorber, covering
column density
eV
with
χ2/(d.o.f.) = 600/437.
Again, we checked whether additional covering material improves the fit in any respect.
This time the fit is better with Δχ2 ~ −45 over the
PL+BB+WA, with similar values of the physical parameters of the ionized absorber, covering
column density 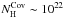 cm-2 and
covering factor f ~ 0.6. Our purpose now is to find a “good”
global continuum which, after being modified by a slab of ionized gas, would account for
the spectral features seen in the spectrum. This was managed with the model PL+2BB+WA
(power law + 2 black bodies + warm absorber). The column density, ionization parameter,
and temperature of the first black body remain almost identical to that found in the
PL+BB+WA model, and the second black body gives a temperature
kT2 ~ 35 eV. This model has two
important statistical properties: 1) the addition of the second black body gives a
statistically significant improvement of 99.99% (according to an F-test) over the
PL+BB+WA, and 2) it gives a better fit by Δχ2 ~ −50
over the PL+BB+WA+Cov. Formally, we finish with a solution that includes a power law plus
a soft excess represented by two black bodies with temperatures
kT1 = 137 and
kT2 = 34 eV and a warm-absorber with column
density NWA = 6 × 1019 cm-2 at a
physical state given by log ξ = 1 (PL+2BB+WA). This model represents the
best mathematical solution to the 0.1−10 keV spectrum of Ark 564 with a reduced
cm-2 and
covering factor f ~ 0.6. Our purpose now is to find a “good”
global continuum which, after being modified by a slab of ionized gas, would account for
the spectral features seen in the spectrum. This was managed with the model PL+2BB+WA
(power law + 2 black bodies + warm absorber). The column density, ionization parameter,
and temperature of the first black body remain almost identical to that found in the
PL+BB+WA model, and the second black body gives a temperature
kT2 ~ 35 eV. This model has two
important statistical properties: 1) the addition of the second black body gives a
statistically significant improvement of 99.99% (according to an F-test) over the
PL+BB+WA, and 2) it gives a better fit by Δχ2 ~ −50
over the PL+BB+WA+Cov. Formally, we finish with a solution that includes a power law plus
a soft excess represented by two black bodies with temperatures
kT1 = 137 and
kT2 = 34 eV and a warm-absorber with column
density NWA = 6 × 1019 cm-2 at a
physical state given by log ξ = 1 (PL+2BB+WA). This model represents the
best mathematical solution to the 0.1−10 keV spectrum of Ark 564 with a reduced
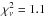 (for
435 d.o.f.). Tables 1 and 2 give values for the model parameters discussed in this section with
and without photoionization. A closer evaluation of this solution along with its physical
implications is given in the next section.
(for
435 d.o.f.). Tables 1 and 2 give values for the model parameters discussed in this section with
and without photoionization. A closer evaluation of this solution along with its physical
implications is given in the next section.
Warm-absorber fit results on the broad-band spectrum of Ark 564.
5. High-resolution spectral analysis
The fitting of the coarsely-binned spectrum (bin size of 0.1 Å) with our photoionization model points to a semi-empirical solution composed by a power law plus two black bodies and a single warm absorber modifying this continuum in our line-of-sight (PL+2BB+WA). This is already a sophisticated solution for the representation of the soft X-ray spectrum of Ark 564, and is as good as the best solution (BASELINE+2BBs, the name the authors gave to their best-fit model, see Table 2 of their paper) found for the time-average spectrum of this object in the analysis of Papadakis et al. (2007), using the EPIC (pn, MOS1, and MOS2) cameras on board XMM-Newton. It has been found, however, in the finer version of the spectrum, i.e., in the RGS spectrum analysis made by Smith et al. (2008), that the absorption might be more complex than just a single photoionized cloud in the line of sight. Smith et al. (2008) find it appropriate to describe the 0.35−2 keV spectrum of Ark 564 with three separated phases of photoionized X-ray absorbing gas with ionization parameters log (ξ) = −0.86,0.87,2.56, and column densities NWA = (0.89,2.41,6.03) × 1020 cm-2, respectively. Matsumoto et al. (2004), using a ~50 ks Chandra HETGS observation of the same object, were also able to detect two phases of absorption by photoionized gas: Phase 1 (log (ξ) ~ 1 and NWA = 1021 cm-2), and Phase 2 (log (ξ) ~ 2 and NWA = 1021 cm-2). For this reason we investigate in more detail the possibility that the LETGS spectrum of Ark 564 is reproduced by more than one absorption component. For the analysis of this section we take the coadded-LETGS spectrum of Ark 564 and bin it as follows. Above 0.33 keV, the data is uniformly binned by a factor of 2 (i.e., bin width of 25 mÅ). Each bin has at least ~20 counts which allows the use of χ2-statistic to evaluate goodness-of-fit. This gives full resolution to the spectrum in order to study in detail the narrow features. Between 0.33 and 0.15 keV, the spectrum is adaptively binned to have at least 1000 counts per bin. Finally below 0.15 keV the spectrum is adaptively binned to have at least 2500 counts per bin. The result is a high-quality spectrum distributed in 1533 PHA bins which optimizes the use of the full band (0.1−10 keV). We model the Galactic absorption in the same fashion as in the coarse version analysis, using a phabs (XSPEC) model with a column of gas NH = 5.34 × 1020 cm-2 (Kalberla et al. 2005).
5.1. Photoionization modeling
Figure 4 shows the high-resolution (bin size 25 mÅ),
background-subtracted, coadded-LETGS spectrum (from ~5 to 37 Å) of Ark 564
together with our best solution (PL+2BB+WA) denoted by a solid blue line. We have taken
only the best-fit physical parameters − namely Γ = 2.52,
kT1 = 133, and
kT2 = 37 eV, with
NWA = 6 × 1019 cm-2, and
log [ξ] = 1.1 − found in the previous section and fixed them,
thus reproducing the associated physical model. The goodness of the fit is given by
χ2/d.o.f. = 1440/1530.
The model matches several of the predicted wavelengths of the narrow features arising from
highly ionized species of Ne, Fe, O, C, and N. The O VII Heβ
at λ18.63 Å and the O VIII Lyα at
λ18.97 Å are predicted in the 17−21 Å portion of the spectrum. These
lines also appear to be observed in the RGS (Smith et al.
2008) and the HETGS (Matsumoto et al.
2004) spectra of Ark 564. If the ionized gas has solar abundances, oxygen
absorption features are expected and have been detected in several AGNs with warm
absorbers (e.g., Kaastra et al. 2000; Sako et al. 2001; Lee
et al. 2001; Blustin et al. 2003; Krongold et al. 2003; Netzer et al. 2003; Fields et al. 2007;
Costantini et al. 2007; Krongold et al. 2007). However, only a few of them have well-measured
column densities. This implies a high-ionization state for the absorbing material in our
line of sight with possibly complex structure, e.g., multi-component, and we therefore
investigate this possibility. Adding a second component improves the fit significatively
at 99.99% (according to an F-test). The column density of the second absorber is
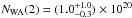 cm-2
and has a ionization parameter of log [ξ] (2) = 3.2 ± 0.2 giving
χ2/d.o.f. = 1404/1528.
We plot (in red) these two WA models where it can be seen that the second component seems
to be improving the narrow spectral bands, including the region around 1) the O VIII
Lyα 2) the Ne IX Kα, and 3)
several L and M Fe lines (in addition to a few oxygen lines) in the range
~15−17 Å.
cm-2
and has a ionization parameter of log [ξ] (2) = 3.2 ± 0.2 giving
χ2/d.o.f. = 1404/1528.
We plot (in red) these two WA models where it can be seen that the second component seems
to be improving the narrow spectral bands, including the region around 1) the O VIII
Lyα 2) the Ne IX Kα, and 3)
several L and M Fe lines (in addition to a few oxygen lines) in the range
~15−17 Å.
 |
Fig. 4 High-resolution (bin size 25 mÅ) background-substracted coadded-LETGS spectrum (5−37 Å) of Ark 564. Solid blue line: single-XSTAR photoionization model (PL+2BB+WA). Red solid line: two-XSTAR photoionization model (PL+2BB+2WA). Theoretical prediction of absorption lines coming from highly ionized species of C, N, O, and Fe are labeled above the data. The Galactic oxygen absorption is marked. |
Parameters of the narrow absorption lines from Gaussian fits.
5.2. Absorption spectral features
In this section we investigate the narrow absorption features. Our continuum is estimated in the following way: 1) we take the best-fit continuum model PL+2BB found in Sect. 4.3; 2) we remove small spectral bands which deviate ≳2σ from that continuum; 3) we then interpolate with a spline function in the regions removed and re-fit. In this way we obtain a new best-fit continuum. The resulting continuum is shown in Fig. 4 as a blue dashed line.
Table 3 gives measurements of the strongest
absorption lines seen in the spectrum along with their atomic transition identifications.
We can see an Fe L-shell line, highly ionized species of oxygen from O v to O
viii, and the C vi Lyα, β
lines that belong to intrinsic absorption in the frame of the galaxy. All these are
unresolved lines with only upper limits in their equivalent widths (EW). The two
exceptions are the Fe xvii and O vii Kβ
lines, with 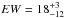 and
32 ± 8 mÅ, respectively. Using these two ions, it is possible to make a direct comparison
of the physical parameters of the absorbing material detected in previous observations of
Ark 564 with the present. First, Matsumoto et al.
(2004) report a 3σ detection of the Fe
xviiλ13.89 Å line, produced by the inner-shell
2p6−2s2p63p transition, with an
EW [Fe XVII inner] of
and
32 ± 8 mÅ, respectively. Using these two ions, it is possible to make a direct comparison
of the physical parameters of the absorbing material detected in previous observations of
Ark 564 with the present. First, Matsumoto et al.
(2004) report a 3σ detection of the Fe
xviiλ13.89 Å line, produced by the inner-shell
2p6−2s2p63p transition, with an
EW [Fe XVII inner] of 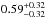 eV in the MEG ± 1 spectrum of Ark 564. Its oscillator strength is relatively low,
fij [Fe XVII inner] ~ 0.032,
which means that, even at Fe+16 peak abundance, the hydrogen column density of
the absorbing slab must be large, i.e., NH ≳ 1022
cm-2, in order to make it detectable. On the other hand, the LETGS spectrum
of Ark 564 seems to point to a rather weak Fe xviiλ13.89 Å line
with an EW [Fe XVII inner] ~ 0, as is in fact predicted by
our theoretical model. This would imply a change in Fe+16 column density
between the HETGS and LETGS epochs.
eV in the MEG ± 1 spectrum of Ark 564. Its oscillator strength is relatively low,
fij [Fe XVII inner] ~ 0.032,
which means that, even at Fe+16 peak abundance, the hydrogen column density of
the absorbing slab must be large, i.e., NH ≳ 1022
cm-2, in order to make it detectable. On the other hand, the LETGS spectrum
of Ark 564 seems to point to a rather weak Fe xviiλ13.89 Å line
with an EW [Fe XVII inner] ~ 0, as is in fact predicted by
our theoretical model. This would imply a change in Fe+16 column density
between the HETGS and LETGS epochs.
Instead, what Matsumoto et al. (2004) identify as an Fe xvii line at ~0.82 keV rest-frame (with an exclamation mark in their Fig. 5), we believe is the line associated with the atomic transition Fe xvii 2p6−2p53d with oscillator strength ~ two order of magnitudes larger than fij [Fe XVII inner], i.e., fij [2p6−2p53d] ~ 2.7, and which we identify at ≳2σ level. Our photoionization model predicts this line to be strong and detectable at the high ionization parameter log (ξ) ~ 3, as is suggested by the second component of our two-WA model.
6. Discussion
6.1. Physical conditions of the ionized material
Our discussion of the physical conditions of the absorbing material begins by comparing
the number of components (or phases) found in previous X-ray analyses of Ark 564 with the
present findings. Smith et al. (2008) find three
components in the analysis of the high resolution RGS spectrum of Ark 564 – referred to as
Phases 1, 2, and 3 – with respective ionization parameters of
log ξ = −0.86,0.87 and 2.56 and column densities
NH = (0.89,2.41,6.03) × 1020 cm-2.
However, they conclude that, because of the low flow velocity of the warm-absorber phases,
it is possible that the low ionization phases belong to the interstellar gas. Phases 2 and
3 roughly match the ionization states given by our photoionization (XSTAR-based) best-fit
model of the LETGS spectrum. Apart from the very low component found by Smith et al. (2008) with
log (ξ) = −0.86, Matsumoto et al.
(2004) also find a two-component photoionization model that reproduces
satisfactorily the narrow absorption features seen in the HETGS spectrum of Ark 564, with
log (ξ) ~ 0 and log (ξ) ~ 2, and
column density NH ~ 1021 cm-2
in both cases. These two ionization states, log (ξ)1
~ 0−1 and log (ξ)2 ~ 2−3, represent
highly ionized states of the material in the line of sight very well, producing absorption
lines from highly ionized species of C, N, O, Mg, Ne, and Fe. For instance, the O vii
Kβ line (atomic transition 1s2−1s3p) is
present in the three spectra of HETGS, RGS, and LETGS with measured equivalent widths
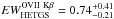 eV (~22 mÅ) and
eV (~22 mÅ) and 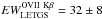 mÅ. Smith et al. (2008) model the line with a photoionization model (see
Fig. 4 of their paper), but do not report an individual measurement of the line. Our
theoretical prediction for a slab of ionized gas with
NH ~ 1019 cm-2 at
log (ξ) ~ 1.1 and the equivalent width of the O vii
Kβ line is
mÅ. Smith et al. (2008) model the line with a photoionization model (see
Fig. 4 of their paper), but do not report an individual measurement of the line. Our
theoretical prediction for a slab of ionized gas with
NH ~ 1019 cm-2 at
log (ξ) ~ 1.1 and the equivalent width of the O vii
Kβ line is 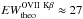 mÅ, compatible with what we
observe. In order to reproduce conditions with
NH ~ 1021 cm-2,
log (ξ) must be ≈0.
mÅ, compatible with what we
observe. In order to reproduce conditions with
NH ~ 1021 cm-2,
log (ξ) must be ≈0.
We tried to fit a third photoionization component in the LETGS spectrum of Ark 564, but no statistical evidence was found. Matsumoto et al. (2004) also base their estimate of the column density of the absorbing material NH ~ 1021 cm-2 on the detection of very low ionization species of Fe, i.e., Fe v-vii, which we do not detect at a significant level. Our total average column density of NH ~ 1020 cm-2 is more in agreement with Smith et al. (2008), who report X-ray column densities NH ~ 1020 cm-2 for this object. We conclude that our best-fit Phase 1 with log (ξ) ~ 1 agrees with previous X-ray observations. It also agrees with UV absorption previously detected and reported by Crenshaw et al. (2002) and Romano et al. (2002), who are able to identify UV absorbers with log (ξ) ~ 1.2 and column density NH ~ 1021 cm-2. Our best-fit Phase 2 with log (ξ) ~ 3 and NH ~ 1020 cm-2 is too highly ionized to be detected in the optical or UV bands, but it also agrees with the Phase 2 of Matsumoto et al. (2004) and the Phase 3 of Smith et al. (2008). This phase was required in order to match the strength of the lines produced by Fe in the 16−17 Å band pertaining to the unresolved transition array of Fe xvii-xx and few oxygen lines (Behar et al. 2001), also clearly observed and detected in the quasar MR 2251−178 (Ramírez et al. 2008). Two-component photoionization models have been successfully applied to other Seyfert galaxies and quasars: NGC 4051 (Krongold et al. 2007), NGC 3783 (Krongold et al. 2003; Netzer et al. 2003), MR 2251−178 (Kaspi et al. 2004), NGC 985 (Krongold et al. 2009), and at least one highly red-shifted quasar APM 08279+5255 (Chartas et al. 2002; Ramírez 2008; Chartas et al. 2009; Saez et al. 2009; Saez & Chartas 2011). We conclude that our Phase 2 with log (ξ) ~ 3 and NH ~ 1020 cm-2 is real, and we estimate the following column densities of ionized species (assuming solar abundances): NMgX ~ 1015 cm-2, NNeIX ~ 1016 cm-2, NOVII ~ 1016 cm-2, NOVIII ~ 1016 cm-2, NCVI ~ 1016 cm-2, and NNVII ~ 1017 cm-2.
6.2. Spatial location of the X-ray absorber in Ark 564
Here we discuss how we might obtain an estimate of the location of the X-ray absorbing
material. It is based on the use of the O v K-shell lines as a density diagnostic
tool (Kaastra et al. 2004). In principle the
distance r from the central source to the absorbing material is connected
to the ionization parameter ξ by
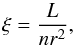 (2)where L
is the ionizing luminosity of the central X-ray source and n is the gas
density of the absorber. Since L and ξ can be directly
measured from the observed spectrum, the product of the two unobservable
nr2 is then known; therefore, having either
n or r, we can compute the other. The ion O v
is known to have metastable levels that are density dependent, and by measuring the
absorption line properties of it, we are able to estimate the gas density and thus
distances through the use of the ionization parameter. Since we only have an upper limit
on the EW of the O v Kα line, we will only obtain a
lower limit on the distance. After a careful inspection of the technique by Kaastra et al. (2004), we were able to constrain the
density by using our measurement of EW[O v] in the LETGS spectrum of Ark 564, and
compared it with the EW[O v] found in the LETGS spectrum of the Seyfert 1 galaxy
Mrk 279. We took the upper limit of the EW measurement of the O v line arising
from the transition 1s22s2−1s2s22p
1P1, i.e.,
(2)where L
is the ionizing luminosity of the central X-ray source and n is the gas
density of the absorber. Since L and ξ can be directly
measured from the observed spectrum, the product of the two unobservable
nr2 is then known; therefore, having either
n or r, we can compute the other. The ion O v
is known to have metastable levels that are density dependent, and by measuring the
absorption line properties of it, we are able to estimate the gas density and thus
distances through the use of the ionization parameter. Since we only have an upper limit
on the EW of the O v Kα line, we will only obtain a
lower limit on the distance. After a careful inspection of the technique by Kaastra et al. (2004), we were able to constrain the
density by using our measurement of EW[O v] in the LETGS spectrum of Ark 564, and
compared it with the EW[O v] found in the LETGS spectrum of the Seyfert 1 galaxy
Mrk 279. We took the upper limit of the EW measurement of the O v line arising
from the transition 1s22s2−1s2s22p
1P1, i.e., ![\hbox{$EW_{\rm OV}^{\rm upper}[Kaastra]=24$}](/articles/aa/full_html/2013/03/aa20424-12/aa20424-12-eq384.png) mÅ. This is actually
comparable to our value of
mÅ. This is actually
comparable to our value of ![\hbox{$EW_{\rm OV}^{\rm upper}[our]=25$}](/articles/aa/full_html/2013/03/aa20424-12/aa20424-12-eq385.png) mÅ. Thus, using the velocity
broadening σv = 50 km s-1
(appropriate for this system), we obtained the upper limit of the column density for O
v in its ground state of
NOV ≲ 3.8 × 1016 cm-2. This is roughly
consistent with the upper limit of the O v column density estimated by Krongold et al. (2009) in NGC 985 using
XMM-Newton data. Assuming that the density for conditions at
NOV ≈ 3.8 × 1016 cm-2are similar to
NOV ≈ 1.5 × 1016 cm-2(only different
by a small factor) and using Table 7 of Kaastra et al.
(2004), either we estimated a lower distance
r ≳ 2.3 × 1015 cm, or the material is beyond 0.9 light
day (lt-day). This lower r limit is ~10 times smaller than the
lower limit set by Smith et al. (2008)on their warm
absorber Phases 1 and 2, if we use arguments that involve the computation of the size of
the Hβ emitting region using the FWHM of the UV and optical
emission lines (Romano et al. 2004). However, if we
carefully inspect our spectrum, we see that the emission lines are rather weak or
non-existent. Using this piece of evidence, and because of the assumption that absorption
takes place beyond the emitting region, we place the X-ray warm absorber beyond our lower
limit plus the size of the Hβ Broad line
Region in Ark 564 (Romano et al. 2004), i.e.,
r ≳ 2.7 × 1016 cm, or beyond 10.4 lt-day. Also, our estimate
of NOV allows us to constrain the size of the absorbing slab.
Assuming solar abundances, Δr ≳ 9.4 × 106 cm. We would like to
emphasize, however, that the estimate of the X-ray gas density depends on several modeling
factors, e.g., the assumption of additional heating processes occurring in the absorbing
region, well described in Kaastra et al. (2004),
and so, will not be discussed further.
mÅ. Thus, using the velocity
broadening σv = 50 km s-1
(appropriate for this system), we obtained the upper limit of the column density for O
v in its ground state of
NOV ≲ 3.8 × 1016 cm-2. This is roughly
consistent with the upper limit of the O v column density estimated by Krongold et al. (2009) in NGC 985 using
XMM-Newton data. Assuming that the density for conditions at
NOV ≈ 3.8 × 1016 cm-2are similar to
NOV ≈ 1.5 × 1016 cm-2(only different
by a small factor) and using Table 7 of Kaastra et al.
(2004), either we estimated a lower distance
r ≳ 2.3 × 1015 cm, or the material is beyond 0.9 light
day (lt-day). This lower r limit is ~10 times smaller than the
lower limit set by Smith et al. (2008)on their warm
absorber Phases 1 and 2, if we use arguments that involve the computation of the size of
the Hβ emitting region using the FWHM of the UV and optical
emission lines (Romano et al. 2004). However, if we
carefully inspect our spectrum, we see that the emission lines are rather weak or
non-existent. Using this piece of evidence, and because of the assumption that absorption
takes place beyond the emitting region, we place the X-ray warm absorber beyond our lower
limit plus the size of the Hβ Broad line
Region in Ark 564 (Romano et al. 2004), i.e.,
r ≳ 2.7 × 1016 cm, or beyond 10.4 lt-day. Also, our estimate
of NOV allows us to constrain the size of the absorbing slab.
Assuming solar abundances, Δr ≳ 9.4 × 106 cm. We would like to
emphasize, however, that the estimate of the X-ray gas density depends on several modeling
factors, e.g., the assumption of additional heating processes occurring in the absorbing
region, well described in Kaastra et al. (2004),
and so, will not be discussed further.
6.3. On the low observed outflow velocity and geometry
Table 3 shows measurements of the strongest (≳2σ) absorption lines detected in the LETGS spectrum of Ark 564. The fifth column gives the velocity (with error bars) of the measured line centroids. We can see velocities from v ~ −50 km s-1 associated to the Fe xvii line up to v ~ −800 km s-1 associated to the O vi line. An outflow of this nature can be characterized as a low-velocity outflow since our data do not allow us to claim a velocity different from zero within the error bars.
A plausible location for a low velocity outflow (v ~ 50−800 km s-1) is in the base of a radiatively accelerated wind which originates in the accretion disk of an AGN (Elvis 2000; Krongold et al. 2007; Murray et al. 1995; Proga et al. 2000; Ramírez & Tombesi 2012). For instance, Elvis (2000) try to explain phenomenologically the kinematics seen in Seyfert galaxies and quasars through a geometric effect given by a biconal wind. If we observe the flow transversely through the base of the wind, we will only see low column densities NH ~ 1020−1021 and low velocities v ~ 0−1000 km s-1, totally compatible with what we observe in Ark 564. Large column densities NH ~ 1022−1024 and large blueshifted velocities from v ~ a few thousand km s-1 up to 0.2 c would be detected in the spectra only if we are observing the system along the flow, which is clearly not the case for Ark 564, and we thus rule out line of sight in the direction of the flow for this system. Krongold et al. (2007) are able to put tight constraints on the location and geometry of the X-ray absorbing wind in NGC 4051, a Seyfert 1 galaxy with general temporal and spectral properties similar to those observed in Ark 564. They locate their two absorbing systems (LIP and HIP in their notation) close to the supermassive black hole at r ~ (0.5−4) lt-days, and find an appropriate angle between the disk and the observer’s line of sight of δ ≈ 30° (see Fig. 12 of their paper for the exact geometry). Assuming that our system has geometric properties similar to those in NGC 4051, we tend to infer an angle of δ ≲ 30° since the measured v ~ 500 km s-1 for that system would rather be an upper limit for the average velocity observed in Ark 564. This very small angle would locate our observed column density of NH ~ 1020 cm-2 within the right order of magnitude for the transverse outflow column density found to work in Elvis (2000). On the other hand, because of their contribution to the UV spectrum, Smith’s Phases 1 and 2 are more probably connected with spatial regions well beyond the narrow line region (NLR), eliminating an accretion disk origin. Nevertheless, Smith’s Phase 3 could easily be linked to the NLR, and therefore display a radiative wind origin as suggested by our results.
There have been, however, reports of strong and fast outflows observed in NLS1 galaxies,
i.e., NGC 4051 Ogle et al. (2004) and MCG-6-30-15
Sako et al. (2003), which would imply
non-base-disk origins. Another location for the wind could be at the edge of the molecular
torus that faces the intense radiation coming from the center of the system (Krolik & Kriss 2001). The minimum distance for
a system of this kind would be the sublimination radius
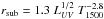 pc. For Ark 564, we use
LUV = 1045.2 erg s-1,
and assume a grain sublimination temperature of 1500 K (Barvainis 1987) and rsub = 0.56 pc well beyond the
lower limit we estimated in the previous section. We conclude that we cannot rule out the
torus origin of the X-ray absorbing system seen in the LETGS time-averaged spectrum of Ark
564. Tighter constraints might be applied through the use of variability arguments which
are beyond the scope of this paper.
pc. For Ark 564, we use
LUV = 1045.2 erg s-1,
and assume a grain sublimination temperature of 1500 K (Barvainis 1987) and rsub = 0.56 pc well beyond the
lower limit we estimated in the previous section. We conclude that we cannot rule out the
torus origin of the X-ray absorbing system seen in the LETGS time-averaged spectrum of Ark
564. Tighter constraints might be applied through the use of variability arguments which
are beyond the scope of this paper.
Finally, we discuss discrete components vs. continuous flow models. It has been suggested that the soft X-ray absorption features seen in the spectra of Seyfert galaxies are caused by the flow of ionized material covering a continuous range in ionization parameters, i.e., up to three orders of magnitude (Steenbrugge et al. 2003; Ogle et al. 2004). For a proposal of a continuous flow using high resolution, high S/N ratio (NGC 3783), see Ramírez et al. (2005) and Ramírez (2011). The high data quality in the LETGS spectrum of Ark 564, allows us to find statistical improvements when we go from single- to two-component photoionization models. However, this is strictly not the case when we go from two- to three-component models (only an improvement of Δχ2 ≈ 3). We also do not see the need to include a third component in order to reproduce narrow features in the spectrum, even if there is no global improvement in the fit. This case is different from Krongold et al. (2009), where they do actually find statistical evidence of a third component to be required in the X-ray spectrum of NGC 985, but no identification of discrete, individual features was possible, and as a result it was not implemented as part of the solution. In the case of the LETGS spectrum of Ark 564, it is not required. Smith et al. (2008) also try to model a continuous-flow in the XMM-Newton high-resolution spectrum version of Ark 564 using the warm component instead of xabs, finding that their discrete three-component model fits their data better than the continuous flow model. In the case of the LETGS spectrum of Ark 564, we cannot add a third component, and have concluded that a continuous flow is likely ruled out.
7. Summary
We have presented a detailed spectral analysis of the LETGS time-average 100 ks X-ray spectrum of Ark 564. We applied several continuum models, and investigated the possible semi-empirical solutions for the soft X-ray spectrum seen in this Seyfert galaxy.
We find that a power law plus two black bodies modified by a two-WA model ([PL+2BB]x2WA) give a statistically acceptable data fit. The photon index is Γ ≈ 2.5, the temperature of the thermal components kT1 ≈ 133 eV and kT2 ≈ 37 eV, and the properties of the absorbing material log ξ1 ~ 1 and log ξ2 ~ 3 with column densities NH ~ 1020 cm-2 in both cases. This two-component model reproduces very well the theoretical prediction and the several observed narrow and unresolved absorption lines arising from highly ionized species of C, N, O, and Fe. These features seem to indicate a low velocity flow. This piece of evidence, in addition to the very low column density of NH ~ 1020 cm-2 observed, is in good agreement with the scenario of a transverse biconical outflow originating in the accretion disk. However, we cannot rule out other locations for the absorbing material, e.g., the inner edge of the putative torus of the system. We estimate an upper limit of the gas density of n ≲ 3 × 1012 cm-3 and a distance beyond the broad-line region at r ≳ 10 lt-days. The detection of two inner shell oxygen lines (O v and O vi) implies that, if metastable levels are sufficiently populated, UV lines should be in principle detectable, as observed in previous UV analyses of this object. This gives evidence, therefore, for a possible relationship between the material absorbing X-ray and that absorbing UV.
http://heasarc.nasa.gov/docs/xanadu/xspec/manual. The abundances are solar from Anders & Grevesse (1989).
The 0.1−0.3 keV unabsorbed flux of 10-10 ergs cm-2 s-1 can be compared with the F0.2−2 keV = 9.79 × 10-11 ergs cm-2 s-1, measured with ROSAT 18 years ago (Brandt et al. 1994).
Interestingly, we have also checked the model where the second black body is not modified (or absorbed) by the Galactic medium. It gives temperatures kT1 ~ 170 and kT2 ~ 100 eV with χ2/d.o.f. = 682.11/439 that are better than the BB model, but statistically inferior to 2BB. The model where the two black bodies are not absorbed is of no interest with χ2/d.o.f. = 985.79/439, and thus we will not consider it further.
Acknowledgments
The author would like to thank the referee for useful and constructive comments and Dr. C. Mendoza for extensively revising the manuscript. The data were taken during the author’s stay at MPE sponsored by the Chandra GTO program. He is indebted to Drs. P. Predehl, Vadim Burwitz, and Stefanie Komossa for internally supporting the proposal of this observation. The great efforts of all the members of the Chandra team are kindly acknowledged.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A., & Kallman, T. R. 2001, ApJS, 134, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., Sako, M., & Kahn, S. M. 2001, ApJ, 563, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Burwitz, V., & Rauch, T. 2006, A&A, 458, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blustin, A. J., Branduardi-Raymont, G., Behar, E., et al. 2003, A&A, 403, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53 [NASA ADS] [Google Scholar]
- Boller, T., Brandt, W. N., Fabian, A. C., & Fink, H. H. 1997, MNRAS, 289, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Fabian, A. C., Nandra, K., Reynolds, C. S., & Brinkmann, W. 1994, MNRAS, 271, 958 [NASA ADS] [Google Scholar]
- Brinkman, B. C., Gunsing, T., Kaastra, J. S., et al. 2000, in X-Ray Optics, Instruments, and Missions III, eds. J. E. Truemper, & B. Aschenbach, Proc. SPIE, 4012, 81 [Google Scholar]
- Chartas, G., Brandt, W. N., Gallagher, S. C., & Garmire, G. P. 2002, ApJ, 579, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Chartas, G., Saez, C., Brandt, W. N., Giustini, M., & Garmire, G. P. 2009, ApJ, 706, 644 [Google Scholar]
- Chevallier, L., Collin, S., Dumont, A.-M., et al. 2006, A&A, 449, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colla, G., Fanti, C., Ficarra, A., et al. 1970, A&AS, 1, 281 [NASA ADS] [Google Scholar]
- Comastri, A., Stirpe, G. M., Vignali, C., et al. 2001, A&A, 365, 400 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costantini, E., Kaastra, J. S., Arav, N., et al. 2007, A&A, 461, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Turner, T. J., et al. 2002, ApJ, 566, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., Nikołajuk, M., Różańska, A., et al. 2003, A&A, 412, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Berlin Heidelberg, Springer-Verlag), 2069, 7 [Google Scholar]
- Dewangan, G. C., Griffiths, R. E., Dasgupta, S., & Rao, A. R. 2007, ApJ, 671, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., & Nayakshin, S. 2007, MNRAS, 377, L59 [NASA ADS] [Google Scholar]
- Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Ballantyne, D. R., Merloni, A., et al. 2002, MNRAS, 331, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, D. L., Mathur, S., Krongold, Y., Williams, R., & Nicastro, F. 2007, ApJ, 666, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Forster, K., & Halpern, J. P. 1996, ApJ, 468, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., Goosmann, R. W., Antonucci, R. R. J., & Whysong, D. H. 2004, ApJ, 616, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., & Done, C. 2004, MNRAS, 349, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, ASP Conf. Ser., 117 [Google Scholar]
- Grupe, D., Wills, B. J., Leighly, K. M., & Meusinger, H. 2004, AJ, 127, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Vogeley, M. S., & Geller, M. J. 1999, ApJS, 121, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., Mewe, R., Liedahl, D. A., Komossa, S., & Brinkman, A. C. 2000, A&A, 354, L83 [NASA ADS] [Google Scholar]
- Kaastra, J. S., Raassen, A. J. J., Mewe, R., et al. 2004, A&A, 428, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Netzer, H., Chelouche, D., et al. 2004, ApJ, 611, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Kriss, G. A. 2001, ApJ, 561, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Brickhouse, N. S., et al. 2003, ApJ, 597, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Elvis, M., et al. 2007, ApJ, 659, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Jiménez-Bailón, E., Santos-Lleo, M., et al. 2009, ApJ, 690, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Ogle, P. M., Canizares, C. R., et al. 2001, ApJ, 554, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Leighly, K. M. 1999, ApJS, 125, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Leighly, K. M. 2004, ApJ, 611, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, C., Leighly, K. M., & Marshall, H. L. 2004, ApJ, 603, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Chiang, J., Grossman, S. A., & Voit, G. M. 1995, ApJ, 451, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., Kaspi, S., Behar, E., et al. 2003, ApJ, 599, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Mathur, S., Elvis, M., et al. 2005, ApJ, 629, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Ogle, P. M., Mason, K. O., Page, M. J., et al. 2004, ApJ, 606, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Negoro, H., & Gliozzi, M. 2002, A&A, 382, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Page, M. J., McHardy, I., & Uttley, P. 2007, A&A, 461, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pounds, K. A., Done, C., & Osborne, J. P. 1995, MNRAS, 277, L5 [NASA ADS] [Google Scholar]
- Pounds, K., Edelson, R., Markowitz, A., & Vaughan, S. 2001, ApJ, 550, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Reeves, J. N., King, A. R., & Page, K. L. 2004, MNRAS, 350, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Pradhan, A. K., Chen, G. X., Delahaye, F., Nahar, S. N., & Oelgoetz, J. 2003, MNRAS, 341, 1268 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Proga, D., Stone, J. M., & Kallman, T. R. 2000, ApJ, 543, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Puchnarewicz, E. M., Mason, K. O., Siemiginowska, A., et al. 2001, ApJ, 550, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, J. M. 2008, A&A, 489, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, J. M. 2011, Rev. Mex. Astron. Astrofis., 47, 385 [NASA ADS] [Google Scholar]
- Ramírez, J. M., & Tombesi, F. 2012, MNRAS, 419, L64 [NASA ADS] [Google Scholar]
- Ramírez, J. M., Bautista, M., & Kallman, T. 2005, ApJ, 627, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, J. M., Komossa, S., Burwitz, V., & Mathur, S. 2008, ApJ, 681, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Mathur, S., Pogge, R. W., Peterson, B. M., & Kuraszkiewicz, J. 2002, ApJ, 578, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Mathur, S., Turner, T. J., et al. 2004, ApJ, 602, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Saez, C., & Chartas, G. 2011, ApJ, 737, 91 [Google Scholar]
- Saez, C., Chartas, G., & Brandt, W. N. 2009, ApJ, 697, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Kahn, S. M., Behar, E., et al. 2001, A&A, 365, L168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sako, M., Kahn, S. M., Branduardi-Raymont, G., et al. 2003, ApJ, 596, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Shapovalova, A. I., Popović, L. Č., Burenkov, A. N., et al. 2012, ApJS, 202, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2008, ApJ, 682, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. A. N., Page, M. J., & Branduardi-Raymont, G. 2008, A&A, 490, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soria, R., & Puchnarewicz, E. M. 2002, MNRAS, 329, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbrugge, K. C., Kaastra, J. S., de Vries, C. P., & Edelson, R. 2003, A&A, 402, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., & Miller, L. 2009, A&ARv, 17, 47 [Google Scholar]
- Turner, T. J., George, I. M., & Netzer, H. 1999, ApJ, 526, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., Romano, P., George, I. M., et al. 2001, ApJ, 561, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., Boller, T., Fabian, A. C., & Vaughan, S. 2004, MNRAS, 347, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2012, ArXiv e-prints [Google Scholar]
- Wang, T., Brinkmann, W., & Bergeron, J. 1996, A&A, 309, 81 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: background-substracted LETGS ± 1 order light curve of Ark 564 binned at 200 s. The light curve shows 0.3−1 keV flux variation. The shortest (detectable) timescale is ~1.2 ks. The min/max amplitude change ΔC (Cmin at ~38 ks to Cmax at ~70 ks from the start of the observation), is ~60%. See text for more details. Middle panel: the light curve shows the hard band 2−10 keV flux variation. Bottom panel: the hardness ratio hard/soft band shows no important variation. |
| In the text | |
 |
Fig. 2 Background-substracted LETGS ± 1 0.1−10 keV spectrum of Ark 564. Extrapolation of the best-fit hard power law to low energies to demonstrate the soft excess. The upper panel shows the data with the convolved model in red (black and white [BW] as a solid line). Below, the ratio data/model. |
| In the text | |
 |
Fig. 3 Background-substracted LETGS ± 1 0.1−10 keV spectrum of Ark 564, with the best-fit hard power law and the addition of two black bodies (the PLhard+2BB model). The upper panel shows the data with the convolved model in red (BW v. as a solid line). Below, the ratio data/model. The lower panel shows the flux spectrum with the composed physical model (and its components separately) as a solid line. |
| In the text | |
 |
Fig. 4 High-resolution (bin size 25 mÅ) background-substracted coadded-LETGS spectrum (5−37 Å) of Ark 564. Solid blue line: single-XSTAR photoionization model (PL+2BB+WA). Red solid line: two-XSTAR photoionization model (PL+2BB+2WA). Theoretical prediction of absorption lines coming from highly ionized species of C, N, O, and Fe are labeled above the data. The Galactic oxygen absorption is marked. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


