EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 551 (March 2013) A&A, 551 (2013) A123 Full HTML
Free Access
Issue
A&A
Volume 551, March 2013
Article Number A123
Number of page(s) 7
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201220401
Published online 05 March 2013

© ESO, 2013

1. Introduction

Galactic chemical evolution predicts how chemical elements are formed and distributed in galaxies. In particular, it follows the evolution of chemical abundances in the interstellar medium (ISM) is space and time. Chemical evolution is determined by the history of star formation, the stellar yields, and gas flows. In particular, most chemical evolution models deal with the infall and outflow of gas in galaxies but very few models have taken the effects of radial flows into account, and even less the effects of galactic fountains on the chemical evolution. Galactic fountains are created by supernova (SN) explosions in the disk of a galaxy: the gas ejected by multiple SN explosions occurring in OB associations reaches a certain height above the galactic plane and then, due to the potential well of the galaxy, it falls back onto the disk.

Bregman (1980) first modeled this process by assuming that the gas falls back ballistically. Spitoni et al. (2008, 2009) followed this approach and computed the effects of fountains on the chemical evolution of the Galactic disk and concluded that they are negligible; in fact, the gas ejected from the disk is likely to land very close to the place where it escaped. Moreover, the time delay with which the enriched supernova material is coming back into the ISM (~100 Myr) does not substantially influence the chemical enrichment process. Gas infall is an important ingredient in the build-up of galactic disks and it produces radial gas flows, as shown first by Mayor & Vigroux (1981). In fact, the infalling gas has a lower angular momentum than the circular motions in the disk, and mixing with the gas in the disk induces a net radial inflow.

Lacey & Fall (1985) computed a chemical model with radial flows and estimated that the gas inflow velocity is up to a few km s-1. Later, Goetz & Köppen (1992) studied numerical and analytical models including radial flows. Chemical models with radial flows have been studied more recently by Portinari & Chiosi (2000), Schönrich & Binney (2009), and Spitoni & Matteucci (2011), among others. In particular, Spitoni & Matteucci (2011) concluded that models assuming no inside-out formation of the Galactic disk need the presence of radial flows to explain the existence of abundance gradients. On the other hand, an inside-out formation of the disk coupled with a threshold in the star formation, could equally reproduce the observed gradients, although less steep ones than in the case of radial flows. Since the inside-out formation of disks seems to be observed at high redshift (Munoz-Mateos et al. 2007), the more reasonable conclusion was that both the inside-out process and radial flows should be at work in the Milky Way.

Here, we plan to compute the chemical evolution of the disk of M 31 including both the effects of galactic fountains and radial gas flows. We start by adopting the model of chemical evolution of M 31 developed by Marcon-Uchida et al. (2010) including inside-out formation of the disk but neither fountains nor radial flows. The paper is organized as follows: in Sect. 2 we describe the model of Spitoni et al. (2008) used to compute the fountains in M 31 and in Sect. 3 the results of this model are described. In Sect. 4 the Marcon-Uchida et al. (2010) model and the implementation of radial flows in it are described. In Sect. 5 the results for the abundance gradients in M 31 are shown. In Sect. 6 some conclusions are drawn.

2. The Galactic fountain model of Spitoni et al. (2008)

To study galactic fountains, Spitoni et al. (2008) followed the evolution of a superbubble driven by supernova explosions in the Galactic disk. They describe the superbubble evolution using the Kompaneets (1960) approximation. Here we do not enter into the details of this model and only recall that Kompaneets (1960) founds analytical expressions for the shape of the bubble during its expansion in an exponential atmosphere with density: 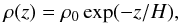(1)where ρ0 and H are the disk density and scale height, respectively.

In Spitoni et al. (2008) we showed that the total time necessary for the growth of instabilities and for the fragmentation of the superbubble in terms of ρ0, H, and the luminosity of the system L0 is 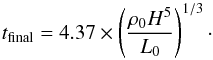(2)Once the top of the supershell reaches the height above the Galactic plane related to the time tfinal (see Eq. (2)), the thin shell can leave the stellar disk and move towards the extraplanar gas. Ballistic models describe the gas as an inhomogeneous collection of clouds, subject only to the gravitational potential of the Galaxy. The way we consider the galactic fountain for M 31 is identical to the model described in Spitoni et al. (2008), therefore we address the reader to that paper for all the details.

2.1. The galactic potential and the OB associations of M 31

The potential well of M 31 is assumed to be the sum of three components as suggested by Howley et al. (2008): a dark matter halo, a bulge, and a disk. The dark matter halo gravitational potential is assumed to follow the Navarro et al. (1996) profile: (3)where δc is a dimensionless density parameter, ρc is today’s critical density with Hubble constant h = 0.71 in units of 100 km s-1 Mpc-1, and rh the halo scale radius (Navarro et al. 1996). The bulge gravitational potential is given by (Hernquist 1990): 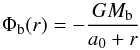(4)where a0 is the scale radius, and Mb is the bulge mass.

For the disk potential we have chosen the axisymmetrical Miyamoto & Nagai (1975) model, which provides results that are comparable to those from the exponential disk used by Geehan et al. (2006). In cylindrical coordinates (R,z) can be written as 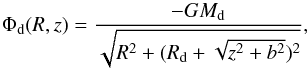(5)where Rd is the disk scale length and b the vertical scale factor.

As done in Howley et al. (2008) we use the “Best-fit Model” values derived by Geehan et al. (2006) to describe the various parameters of M 31, with the sole exception of b, the vertical scale factor, which was not a reported parameter. For b we use the vertical scale height of the dust at a value of 0.1 kpc (Hatano et al. 1997). The values reported by Geehan et al. (2006) include the bulge mass, with Mb = 3.3 × 1010  M⊙, the bulge scale factor with a0 = rb = 0.61 kpc, the disk central surface density with Σ0 = 4.6 × 108  M⊙ kpc-2, the disk scale radius with Rd = 5.4 kpc, and the halo scale radius with rh = 8.18 kpc.

For the interstellar medium (ISM) z-density profile we used Eq. (1) where ρ0 = n0μmp is the density in the disk plane, mp is the proton mass and μ mean molecular weight for the disk (assumed to be 0.61). At 8 kpc we fix n0 = 1. In Banerjee & Jog (2008) it is shown that in the external regions of M 31, the H values range between 300 and 400 pc. Then we tested at 8 kpc two scale heights: H = 200 pc and H = 300 pc.

In our models we vary the number of SNeII in the OB association (SNe). We consider four possible OB associations containing 50, 100, 250, and 500 SNe. Assuming an explosion energy of 1051 erg, the luminosities L0 of these OB associations are 5 × 1037, 1038, 2.5 × 1038, and 5 × 1038 erg s-1, respectively. These numbers of massive stars in OB associations are consistent with observations of Magnier et al. (1994), who showed that the average number of massive stars in an OB association in M 31 is ≃250.

3. Results for the galactic fountains in M 31

In this section we report the results concerning the fragmentation of the superbubble, the formation of the cloud, and the study of the orbits of the galactic fountains in the cases of 8 kpc and 18 kpc. In Figs. 1 and 2 we report our results at 8 kpc for OB associations that can give rise to 250 SNeII, differing only in the height scale of the ISM: H = 200 pc and H = 300 pc respectively. Figure 3 explores the case of 250 SNeII at 18 kpc with H = 300. In Table 1 we report the ejection velocities for 50, 100, 250, and 500 SNeII at 8 kpc.

thumbnail Fig. 1

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (8 kpc, 636 pc). The red filled circle on the R axis is the average falling radial coordinate.

thumbnail Fig. 2

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (8 kpc, 955 pc). The red filled circle on the R axis is the average falling radial coordinate.

thumbnail Fig. 3

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (18 kpc, 955 pc). The red filled circle on the R axis is the average falling radial coordinate.

Table 1

Ejection velocities of our clouds as a function of the number of SNeII and the height scale, when the superbubble is fixed at 8 kpc.

3.1. R0 = 8 kpc, H = 200 pc

We computed the model with an OB association composed of 250 SNeII at 8 kpc, and the ISM height scale is 200 pc. Using the Kompaneets approximation we found that the superbubble is already fragmented in clouds when its top reaches zL = 636 pc (≃3H as found in Spitoni et al. 2008; Mac Low 1994). This phase lasts 11.7 Myr. In Fig. 1 we followed the orbit of our fountains. The initial velocity in this model is 63 km s-1, and our main result is that the clouds are generally thrown outward, but the average landing coordinate is 8.29 kpc (only ΔR = 0.29 kpc). The average orbit time is 42.7 Myr.

3.2. R0 = 8 kpc, H = 300 pc

Then we considered the model with the ISM medium height scale equal to 300 pc. The superbubble is already fragmented in clouds when its top reaches zL = 955 pc (≃3H). This phase lasts 22.9 Myr. In Fig. 2 we followed the orbit of the fountains with an initial velocity of 47 km s-1, and our main result is that the clouds are generally thrown outward, but the average landing coordinate is 8.15 kpc (only ΔR = 0.15 kpc). The average orbit time is 39.6 Myr.

3.3. R0 = 18 kpc, H = 300 pc

In Fig. 3 we followed the orbit of fountains with an initial velocity of 47 km s-1 and initial radial coordinate fixed at 18 kpc. Also the clouds are generally thrown outward in this case and the average landing coordinate is 18.89 kpc (ΔR = 0.89 kpc). The average orbit time is 147.1 Myr.

Because the average landing coordinate differs for the throwing one for a value always less than 1 kpc, we conclude that the effects of galactic fountains cannot directly affect the chemical evolution of M 31, as we found for the Milky Way in Spitoni et al. (2008). Even if we consider the delay in the chemical evolution enrichment, because the clouds originating in the galactic fountain processes take a finite time to orbit the galaxy and fall back onto the disk, we find that this effect is negligible, since the delays are the same as found in Spitoni et al. (2010) for the Milky Way (~100 Myr). These delays have been proven not to have any substantial effects on the process of chemical evolution.

However, the infalling gas onto the disk, created by the galactic fountain, can be affected by the loss of angular momentum (Lacey & Fall 1985), in the same way as for the primordial infall of gas. Therefore, this fountain gas can participate to the radial inflow toward the galactic center, as we show in the next sections.

Concerning galactic fountains, we also recall that in the MaGICC (Brook et al. 2012a,b,c; Pilkington et al. 2012b) program, where hydrodynamical simulation in a cosmological context are presented, fountains can be an important process during the galactic evolution. First of all, in Brook et al. (2012a) it was shown that the majority of gas that loses angular momentum and falls into the central region of the galaxy during the merging epoch is blown back into the hot halo, with much of it returning later to form stars in the disk. They propose that this mechanism of redistribution of angular momentum via a galactic fountain can solve the angular momentum/bulgeless disk problem of the cold dark matter paradigm. It was shown that this redistribution of angular momentum via large-scale galactic fountains can lead to forming of massive disk galaxies that do not have classical bulges.

The MaGICC program has also found that a extensive and significant mixing of fountain material throughout the disk can have a strong impact on the disk’s chemistry. In fact, Brook et al. (2012c) shows that disk stars are dominated by smoothly accreted gas but a significant amount of gas that feeds the thin disk does come from gas-rich mergers. Much of this is recycled to the disk via the hot halo, after being ejected from the star forming regions of the galaxy during starbursts. This large-scale galactic fountain process allows the recycled gas to gain angular momentum and aids in suppressing of the ubiquitous G-dwarf problem (Pilkington et al. 2012b).

The importance of strong feedback in securing correct scaling relations for disks and the correct coronal gas abundances in a cosmological context is discussed in Brook et al. (2012a,b,c) and Stinson et al. (2012). It is shown that the scale of outflows invoked in models matches the observed absorption line features of local galaxies (Prochaska et al. 2011; Tumlinson et al. 2011).

4. The chemical evolution model of M 31

4.1. Our reference model for M 31

To reproduce the chemical evolution of the M 31 disk, we started from the one-infall chemical evolution model presented by Marcon-Uchida et al. (2010), where the details can be found, and then we introduced radial flows in the same way as in Spitoni & Matteucci (2011, see Sect. 4.1). In the starting model, the galactic disk is divided into several concentric rings that evolve independently without any exchange of matter.

The disk is built up in an “inside-out” scenario that is a necessary condition for reproducing the radial abundance gradients when no radial gas flows are considered (Colavitti et al. 2008). For the star formation rate (SFR) a Schmidt law was used: 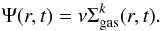(6)The star formation efficiency ν is assumed to vary with the galactocentric distance in the following way: 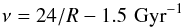(7)until it reaches a minimum value of 0.5 Gyr-1 and then is assumed to be constant.

This is suggested by the best model of Marcon-Uchida et al. (2010) meant to reproduce the present day gas profile of M 31. This gas profile is different relative to that of the Milky Way: the gas increases with decreasing galactic radius, and after reaching a peak (at around 12 kpc) it decreases steeply towards the center, thus suggesting a different scenario. This trend is probably the signature of a very prominent spiral arm that is detectable in M 31.

4.2. The chemical evolution models of M 31 in the literature

Several studies in the past have addressed the modeling of the chemical evolution of M 31. Here we compare our reference model of Marcon-Uchida et al. (2010) model of M 31 with some of them.

As in Marcon-Uchida et al. (2010), the chemical evolution of M 31 in comparison with the Milky Way has been discussed by Renda et al. (2005) and Yin et al. (2009). The former conclude that while the evolution of the Milky Way and M 31 share some properties, differences in the formation history of these two galaxies are required to explain the observations in detail. In particular, they find that the observed higher metallicity in the M 31 halo can be explained by either higher halo star formation efficiency, or a larger reservoir of infalling halo gas with a longer halo formation phase, which would lead to younger stellar populations in the M 31 halo. Both pictures result in a more massive stellar halo in M 31, which suggests a possible correlation between the halo metallicity and its stellar mass. Yin et al. (2009) conclude that M 31 must have been more active in the past than the Milky Way although its current SFR is lower than in the Milky Way. They also concluded that the star formation efficiency in M 31 must have been higher by a factor of two than in the Galaxy. However, by adopting the same SFR as in the Milky Way they failed to reproduce the observed radial profile of the star formation and of the gas, and suggest that possible dynamical interactions could explain these distributions. The main difference between the best model of M 31 in Renda et al. (2005) and the model M 31B of Marcon-Uchida et al. (2010) is the absence of any threshold in the star formation in the previous one.

In Yin et al. (2009) the infall prescription is the one presented by Boissier & Prantzos (2000), according to which the infall timescale is assumed to be correlated with the flat rotational velocity for the galaxy disk. In this work the star formation efficiency is proportional to ΣgasΩ, where Ω is the rotation speed of the gas. In this model it was also not consider a threshold in the star formation.

Carigi et al. (2012) presented a model of the chemical evolution of M 31 also computing the galactic habitable zones (GHZs) for this galaxy. We want to underline that they adopted the instantaneous recycling approximation, and therefore they can study only elements produced mainly by massive stars, such as oxygen.

4.3. The implementation of the radial inflow on M 31 chemical evolution model

Table 2

Model parameters.

In Spitoni et al. (2011) we considered the case of radial inflow of gas for the Milky Way disk . Here we have followed the same procedure to include radial gas flows in the disk of M 31.

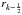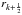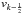We define the kth shell in terms of the galactocentric radius rk, its inner and outer edge being labeled as and . Through these edges, gas inflow occurs with velocity and 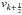, respectively. The flow velocities are assumed to be positive outward and negative inward.

The radial flow term to be added into the chemical evolution equation is (8)where βk and γk are, respectively,

where σA(k + 1) and σAk are the actual density profile at the radii rk + 1 and rk, respectively.

thumbnail Fig. 4

Oxygen abundances observed in the HII Regions of M 31. Data taken by Galarza et al. (1999), Trundle et al. (2002), Blair et al. (1982), and Dennefeld & Kunth (1981).

In our implementation of the radial inflow of gas in M 31, only the gas that resides inside the galactic disk within the radius of 22 kpc can move inward by radial inflow, and as boundary condition we impose that there is no flow of gas from regions outside the ring centered at 22 kpc.

5. Radial flows results

We computed the oxygen gradient along the disk of M 31 and compared it to the available data. In particular, we adopted the same data as in Marcon-Uchida et al. (2010). In Fig. 4 we report the whole collection of the data that we used in this paper: Galarza et al. (1999) (HII regions), Trundle et al. (2002) (OB stars), Blair et al. (1982), and Dennefeld & Kunth (1981) (supernova remnants and HII regions).

thumbnail Fig. 5

Radial oxygen abundance gradient. The blue dotted line refers to the model M 31B of Marcon-Uchida et al. (2010), the black dashed line to the M 31N model with a constant SF efficiency, fixed at the value of 2 Gyr-1, and without threshold, the red solid line refers to the best fit model M 31R with a radial inflow of gas. The filled circles and relative error bars are the observed values from HII regions.

To better understand the trend in the data, we divided the data into six bins as functions of the galactocentric distance. In each bin, we computed the mean value and the standard deviations for the studied element, and relatives errors in Fig. 5. We are aware that there are some severe systematic uncertainties in each study that might justify larger error bars. In Fig. 5 we also plot the M 31B model of Marcon-Uchida et al. (2010) without radial flows and we note that the model fits the average trend in the data well. In Table 2 we show the parameters of all the models we considered in this work: in particular, in Col. 2 there is the assumed inside-out law, in Col. 3 the assumed efficiency of star formation, and in Col. 3 the presence or absence of radial flows. Model M 31B is the best model adopted by Marcon-Uchida et al. (2010). This model contains an inside-out formation of the disk, coupled with variable efficiency of star formation and a threshold in the gas density, and it can reproduce the data without invoking radial flows. However, the existence of a threshold in the star formation process has been questioned by several GALEX studies (e.g. Boissier et al. 2007). Without such a threshold the model would not reproduce the external parts of the disk of M 31 so well. In addition, the hypothesis of variable star formation efficiency is not proven and with constant star formation efficiency, the gradient would look much flatter. Therefore, we can conclude, as Spitoni & Matteucci (2011) did for the Milky Way disk, that radial gas flows can in principle be very important for reproducing the gradients along M 31 disk, since all these processes are probably at work. To decide which of these processes is the most important in the formation of the disk, we will need more detailed data on the abundance, gas, and star formation rate gradients, as well as data on high-redshift disks.

thumbnail Fig. 6

Evolution of the radial oxygen abundance gradient for the model M 31R (the best model in this study) as a function of the redshifts z = 0, 0.5, 1, 1.5.

thumbnail Fig. 7

Oxygen abundance gradient, d[O/H]/dr, computed between 4–8 kpc, 4–14 kpc, and 4–22 kpc for the model M 31R (best model), as a function of redshift.

The first model we computed is M 31N. It has constant star formation efficiency, fixed at the value of 2 Gyr-1, it does not assume a star formation threshold or radial flows. The abundance gradient obtained with this model is shown in Fig. 5. We see that this model fails to reproduce the gradient in the outer M 31 regions.

Then we assumed the same parameters as in M 31N, but we included the radial flows with a variable velocity. In particular, we used a linear relation between the radial inflow velocity and galactocentric distance, as done in Spitoni & Matteucci (2011) for the disk of the Milky Way. In Fig. 5 we label the M 31R model. The radial inflow velocity pattern requested to reproduce the data follows this linear relation: 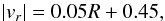(11)and spans the range of velocities between 1.55 and 0.65 km s-1. This model fits the O abundance gradient in the disk of M 31 very well, so we consider it our best model.

In Fig. 6 we report the abundance gradient evolution for oxygen as a function of the redshift for the our best model M 31R. Pilkington et al. (2012a) show the time evolution of the metallicity gradients dZ/dr [dex/ kpc] using a suite of disk galaxy hydrodynamical simulations and comparing it to the chemical evolution models of Chiappini et al. (2001) and Molla & Diaz (2005). We computed the gradient d[O/H]/dR for the model M 31R at redshifts z = 0,0.5,1,1.5. In Fig. 7 we show the gradients for oxygen computed in the ranges 4–8 kpc, 4–14 kpc, and 4–22 kpc. We conclude that for the model M 31R, where a variable gas inflow velocity is considered, a constant star formation efficiency, inside-out formation, and no threshold in the star formation are assumed, the abundance gradient steepens with time, in accordance with the Chiappini et al. (2001) model.

The temporal evolution of the abundance gradients within cosmological hydrodynamical simulations has been shown to be sensitive to the spatial scale on which energy feedback operates (Pilkington et al. 2012a). Conventional feedback schemes with “localized” energy feedback result in steep gradients at high redshift, which flatten with time towards redshift zero; conversely, conventional schemes that distribute energy more “globally” and/or enhanced feedback schemes that drive significant outflows, circulation of the ISM, and radial gas flows result in flat gradients at high redshift, which evolve little with time. In this sense, the models presented here are entirely consistent with these enhanced feedback models (and vice versa).

6. Conclusions

In this paper we have studied the effects of galactic fountains and radial inflows of gas on the predictions of a detailed chemical evolution model for M 31. Our main conclusions can be summarized as follows:

  • Considering the average number of massive stars in an OB association in M 31, the range of the cloud orbits is quite narrow. The clouds are generally directed outwards, but the average landing coordinates differ from the throwing coordinates by values less than 1 kpc. Because of this fact, we conclude that galactic fountains cannot affect the chemical evolution of M 31, as we found for the Milky Way in Spitoni et al. (2008). The reason is that inside 1 kpc, such as in the solar neighborhood, the gas is well mixed.

  • The average time delay produced by a galactic fountain generated by an OB association in M 31 is ≃100 Myr. As we suggested for the Milky Way in Spitoni et al. (2009), such a short delay time has a negligible effect on the abundance gradients in the galactic disk.

  • We started by adopting the best chemical evolution model of Marcon-Uchida et al. (2010) for the disk of M 31. To reproduce the observed abundance gradient, this model needs to assume a threshold in the star formation and an inside-out formation plus star formation efficiency varying with the galactocentric distance. However, the existence of a threshold in the star formation has been questioned and the variable efficiency of star formation with galactocentric distance is not very physically motivated. On the other hand, a moderate inside-out formation for galactic disks seems to be observed at high redshift (Munoz-Mateos et al. 2007).

  • The radial gas-flow velocity, which we found to be the most consistent with the data, varies linearly with the galactocentric distance and spans a range between 0.65 and 1.55 km s-1. This conclusion holds for the M 31 chemical evolution model with inside-out formation, without threshold, and a constant star formation efficiency fixed at 2 Gyr-1.

  • We showed that the abundance gradient d(O/H)/dr steepens with time for our best model, which assumes no gas threshold in the star formation, an inside-out formation of the disk, constant star formation efficiency along the disk and radial gas flows.

Finally, we concluded, in agreement with Spitoni & Matteucci (2011), that also for M 31 the radial gas flows can be very important for reproducing the gradients along the disk, although an inside-out formation coupled with variable efficiency of star formation and a threshold in gas density can also closely reproduce the data without radial flows.

To decide which of these processes are the most relevant in the formation of the disk, we will need more detailed and precise data on the abundance, gas, and star formation rate gradients in M 31, as well as more data on high redshift disks.

Acknowledgments

We thank the referee B. K. Gibson for his suggestions which have improved the paper. E. Spitoni acknowledges financial support from the Portuguese Science Foundation (FCT) by post-doctoral grant SFRH/BPD/78953/2011. F. Matteucci aknowledges financial support from PRIN MIUR 2010-2011, project “The Chemical and dynamical Evolution of the Milky Way and Local Group Galaxies”, prot. 2010LY5N2T. M. M. Marcon-Uchida acknowledges financial support from FAPESP (2010/17142-4).

References

  1. Banerjee, A., & Jog, C. J. 2008, ApJ, 685, 254 [NASA ADS] [CrossRef] [Google Scholar]
  2. Blair, W. P., Kirshner, R. P., & Chevalier, R. A. 1982, ApJ, 254, 50 [NASA ADS] [CrossRef] [Google Scholar]
  3. Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] [Google Scholar]
  4. Boissier, S., Gil de Paz, A., Boselli, A., et al. 2007, ApJS, 173, 524 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bregman, J. N. 1980, ApJ, 365, 544 [Google Scholar]
  6. Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012a, MNRAS, 419, 771 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012b, MNRAS, 424, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012c, MNRAS, 426, 690 [NASA ADS] [CrossRef] [Google Scholar]
  9. Carigi, L., Meneses-Goytia, S., & Garcia-Rojas, J. 2012, Rev. Mex. Astron. Astrofis., submitted [arXiv:1208.4198] [Google Scholar]
  10. Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  11. Colavitti, E., Matteucci, F., & Murante, G. 2008, A&A, 483, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Dennefeld, M., & Kunth, D. 1981, AJ, 86, 989 [NASA ADS] [CrossRef] [Google Scholar]
  13. Galarza, V. C., Walterbos, R. A. M., & Braun, R. 1999, AJ, 118, 2775 [NASA ADS] [CrossRef] [Google Scholar]
  14. Geehan, J. J., Fardal, M. A., Babul, A., & Guhathakurta, P. 2006, MNRAS, 366, 996 [NASA ADS] [CrossRef] [Google Scholar]
  15. Goetz, M., & Koeppen, J. 1992, A&A, 262, 455 [NASA ADS] [Google Scholar]
  16. Kompaneets, A. S. 1960, Soviet Phys. Dokl., 5, 46 [Google Scholar]
  17. Hatano, K., Branch, D., Fisher, A., & Starrfield, S. 1997, AJ, 487, L45 [Google Scholar]
  18. Hernquist, L. 1990, AJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
  19. Howley, K. M., Geha, M., Guhathakurta, P., et al. 2008, ApJ, 683, 722 [NASA ADS] [CrossRef] [Google Scholar]
  20. Lacey, C. G., & Fall, M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef] [Google Scholar]
  21. Magnier, E., Prins, S., Haiman, Z., et al. 1994, ESOC, 51, 904 [Google Scholar]
  22. Marcon-Uchida, M. M., Matteucci, F., & Costa, R. D. D. 2010, A&A, 520, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Mayor, M., & Vigroux, L. 1981, A&A, 98, 1 [NASA ADS] [Google Scholar]
  24. Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
  25. Molla, M., Ferrini, F., & Diaz, A. I. 1997, ApJ, 425, 519 [NASA ADS] [CrossRef] [Google Scholar]
  26. Munoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2007, ApJ, 658, 1006 [NASA ADS] [CrossRef] [Google Scholar]
  27. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
  28. Pilkington, K., Few, C. G., Gibson, B. K., et al. 2012a, A&A, 540, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Pilkington, K., Gibson, B. K., Brook, C. B., et al. 2012b, MNRAS, 425, 969 [NASA ADS] [CrossRef] [Google Scholar]
  30. Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
  31. Prochaska, J. X., Weiner, B., Chen, H.-W., Mulchaey, J., & Cooksey, K. 2011, ApJ, 740, 91 [NASA ADS] [CrossRef] [Google Scholar]
  32. Renda, A., Kawata, D., Fenner, Y., & Gibson, B. K. 2005, MNRAS, 356, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  33. Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
  34. Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Spitoni, E., Recchi, S., & Matteucci, F. 2008, A&A, 484, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Spitoni, E., Matteucci, F., Recchi, S., Cescutti, G., & Pipino, A. 2009, A&A, 504, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Stinson, G. S., Brook, C., Prochaska, J. X., et al. 2011, MNRAS, 425, 1270 [Google Scholar]
  38. Trundle, C., Dufton, P. L., Lennon, D. J., Smartt, S. J., & Urbaneja, M. A. 2002, A&A, 395, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Tumlinson, J., Thom, C., Werk, J. K., et al. 2011, Science, 334, 948 [NASA ADS] [CrossRef] [Google Scholar]
  40. Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Ejection velocities of our clouds as a function of the number of SNeII and the height scale, when the superbubble is fixed at 8 kpc.

In the text
Table 2

Model parameters.

In the text

All Figures

thumbnail Fig. 1

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (8 kpc, 636 pc). The red filled circle on the R axis is the average falling radial coordinate.
In the text
thumbnail Fig. 2

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (8 kpc, 955 pc). The red filled circle on the R axis is the average falling radial coordinate.
In the text
thumbnail Fig. 3

Galactic fountains reported in the meridional plane with the spatial initial conditions: (R,z) = (18 kpc, 955 pc). The red filled circle on the R axis is the average falling radial coordinate.
In the text
thumbnail Fig. 4

Oxygen abundances observed in the HII Regions of M 31. Data taken by Galarza et al. (1999), Trundle et al. (2002), Blair et al. (1982), and Dennefeld & Kunth (1981).
In the text
thumbnail Fig. 5

Radial oxygen abundance gradient. The blue dotted line refers to the model M 31B of Marcon-Uchida et al. (2010), the black dashed line to the M 31N model with a constant SF efficiency, fixed at the value of 2 Gyr-1, and without threshold, the red solid line refers to the best fit model M 31R with a radial inflow of gas. The filled circles and relative error bars are the observed values from HII regions.
In the text
thumbnail Fig. 6

Evolution of the radial oxygen abundance gradient for the model M 31R (the best model in this study) as a function of the redshifts z = 0, 0.5, 1, 1.5.
In the text
thumbnail Fig. 7

Oxygen abundance gradient, d[O/H]/dr, computed between 4–8 kpc, 4–14 kpc, and 4–22 kpc for the model M 31R (best model), as a function of redshift.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.