| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220379 | |
| Published online | 14 February 2013 | |
Luminosity function from dedicated SDSS-III and MMT data of quasars in 0.7 < z < 4.0 selected with a new approach
1 CEACentre de Saclay, Irfu/SPP, 91191 Gif-sur-Yvette, France
e-mail: nathalie.palanque-delabrouille@cea.fr
2 Department of Physics and Astronomy, University of Wyoming, Laramie, WY 82071, USA
3 Max-Planck-Institut fürAstronomie, Königstuhl 17, 69117 Heidelberg, Germany
4 Université Paris 6, Institut d’Astrophysique de Paris, CNRS UMR 7095, 98bis Bd Arago, 75014 Paris, France
5 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
6 APC, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
7 Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
8 National Optical Astronomy Observatory, Tucson, AZ 85726-6732, USA
9 Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
10 Apache Point Observatory, PO Box 59, Sunspot, NM 88349-0059, USA
11 University of Utah, Dept. of Physics & Astronomy, 115 S 1400 E, Salt Lake City, UT 84112, USA
12 Department of Astronomy, University of Florida, 211 Bryant Space Science Center, PO Box 112055, Gainesville, FL 32611, USA
13 Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
14 Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
15 Brookhaven National Laboratory, Bldg 510, Upton, NY 11973, USA
16 Center for Cosmology and Particle Physics, New York University, New York, NY 10003, USA
Received: 13 September 2012
Accepted: 23 December 2012
We present a measurement of the quasar luminosity function in the range 0.68 < z < 4 down to extinction corrected magnitude gdered = 22.5, using a simple and well understood target selection technique based on the time-variability of quasars. The completeness of our sample was derived directly from a control sample of quasars, without requiring complex simulations of quasar light-curves or colors. A total of 1877 quasar spectra were obtained from dedicated programs on the Sloan telescope (as part of the SDSS-III/BOSS survey) and on the Multiple Mirror Telescope. They allowed us to derive the quasar luminosity function. It agrees well with results previously published in the redshift range 0.68 < z < 2.6. Our deeper data allow us to extend the measurement to z = 4. We measured quasar densities to gdered < 22.5, obtaining 30 QSO per deg2 at z < 1, 99 QSO per deg2 for 1 < z < 2.15, and 47 QSO per deg2 at z > 2.15. Using pure luminosity evolution models, we fitted our LF measurements and predicted quasar number counts as a function of redshift and observed magnitude. These predictions are useful inputs for future cosmology surveys such as those relying on the observation of quasars to measure baryon acoustic oscillations.
Key words: quasars: general / dark energy / surveys
© ESO, 2013
1. Introduction
The measurement of the baryon acoustic oscillation (BAO) scale (Eisenstein et al. 2005; Eisenstein 2007) relies on large samples of objects selected with an unbiased method. To probe the distant Universe, quasars appear to be one of the sources of choice, since they are both among the brightest extragalactic objects, and expected to be present at sufficiently high density.
The selection of quasars to redshift z ~ 4 and magnitude g ~ 23, which is the objective of current and future cosmology projects dedicated to BAO studies in the distant Universe, is a major challenge. Traditional selections relying on quasar colors for several broad optical bands (Schmidt & Green 1983; Croom et al. 2001; Richards et al. 2002, 2004, 2009; Croom et al. 2009; Bovy et al. 2011a,b, 2012) present serious drawbacks for the selection of quasars at redshifts near z ~ 2.7, which occupy similar regions of ugriz color-space as the more numerous white dwarfs and blue halo stars (Fan 1999; Richards et al. 2002; Worseck & Prochaska 2011). To circumvent this difficulty, Palanque-Delabrouille et al. (2011) developed a selection algorithm relying on the time variability of quasar fluxes. This technique was tested in 2010 as part of the BOSS survey (Ross et al. 2012). It was shown to increase by 20 to 30% the density of identified quasars, and, in particular, to effectively recover additional quasars in the redshift range 2.5 < z < 3.5.
Here we use this variability-based selection to measure the quasar luminosity function to extinction-corrected magnitude gdered = 22.5 and redshift z = 4 from two sets of dedicated observations. For the first set of data, we took advantage of the re-observation, as part of the SDSS-III/BOSS survey (Eisenstein et al. 2011; Dawson et al. 2012), of a 14.5 deg2 region in Stripe 82 (the SDSS Southern equatorial stripe). The second set of data used the Hectospec multi-object spectrograph (Fabricant et al. 2005) on the Multiple Mirror Telescope (MMT) and covered 4.7 deg2. The quasar samples being selected with only minimal color constrains, they are expected to be highly complete and do not suffer from the usual biases in their redshift distribution induced by color selections. The selection algorithms of both samples are well understood, and can be applied to large control samples of already identified quasars in order to compute the completeness of the method. With this strategy, all corrections can be derived from the data themselves and do not require any modeling of quasar light curves or colors.
The outline of the paper is as follows. In Sect. 2 we explain the strategy for the selection of the targets and its specific application to the BOSS and the MMT observations. In Sect. 3, we describe the different contributions to the global completeness correction for both sets of data and present the quasar control sample used to derive them. The raw and the completeness-corrected quasar number counts are given in Sect. 4, where we also present several cross-checks of the results obtained. The quasar luminosity function in g derived from these data is given in Sect. 5.
2. Target selection
While the basis of the target selection algorithm is the same for the two components of our program, it was applied with different thresholds to obtain the targets for the BOSS and the MMT observations. The BOSS component was indeed designed to identify a large number of quasars to a magnitude limit g ~ 22.5 corresponding to the limit of BOSS spectroscopy at typical exposure times. The MMT data were primarily designed to complete the sample to fainter magnitudes (g ~ 23), since the telescope has a 6.5 m primary mirror compared to the 2.5 m primary of the Sloan telescope. In addition, the BOSS sample was restricted to point sources, while the MMT sample was also used to recover quasars lying in extended sources.
2.1. Target selection algorithm
As a detailed description of the variability selection can be found in Palanque-Delabrouille et al. (2011), we only summarize here the major steps of our algorithm.
For each source, lightcurves were computed from the data collected by SDSS using the dedicated Sloan Foundation 2.5 m telescope (Gunn et al. 2006). A mosaic CCD camera (Gunn et al. 1998) imaged the sky in the ugriz bandpasses (Fukugita et al. 1996). The imaging data were processed through a series of pipelines (Stoughton et al. 2002) which performed astrometric calibration, photometric reduction and photometric calibration.
The starting source list was built from images that resulted from the co-addition (Annis et al. 2012) of SDSS single-epoch images1. The completeness of the coadd catalog reaches 50% at a magnitude g = 24.6 for stars and g = 23.5 for galaxies. The g magnitude mentioned throughout the paper results from a PSF-fit on the coadd images, and effectively represents the mean magnitude of a variable source. The source morphology (point-like or extended) is also determined from these coadds.
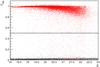 |
Fig. 1 Output of the variability Neural Network as a function of g magnitude for a sample of known stars (small black dots near yNN = 0) and for known quasars (larger red dots at yNN ~ 1). BOSS targets and the MMT point-source targets are required to pass the criterion yNN > 0.5. |
The lightcurves of our sources contained on average 52 individual epochs spread over 7 years. They were used to compute two sets of parameters that characterize the source variability. These parameters are:
-
the five χ2s for the fit of the lightcurvein each of the ugriz filters by a constant (
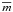 ),
),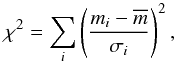 (1)where the sum runs over all observations i;
(1)where the sum runs over all observations i; two parameters, an amplitude A and a power γ as introduced by Schmidt et al. (2010), that characterized the variability structure function
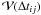 , i.e. the change in magnitude Δmij as a function of time lag Δtij for any pair ij of observations, with
, i.e. the change in magnitude Δmij as a function of time lag Δtij for any pair ij of observations, with 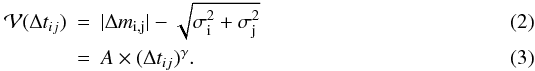
This technique has been applied by BOSS for the selection of z > 2.2 quasars in Stripe 82, down to g ~ 22 (Palanque-Delabrouille et al. 2011). As was clearly illustrated by this study, this approach presents the advantage of being highly complete (the selection reached the unprecedented quasar completeness of 90%), even for a sample purity of 92%, higher than for typical selections based on quasar colors. In addition, this variability-based selection was shown to overcome the drawbacks of color-based methods and to recover quasars near redshift z ~ 3 that are systematically missed with traditional selections (Richards et al. 2002).
Here, we applied this technique to fainter magnitudes, with the aim of detecting quasars to g ~ 23. The magnitude dependence of the output of the variability neural network is illustrated in Fig. 1. Requiring an output yNN > 0.5 selects 95% of the sample of known quasars with 18 < g < 23 (cf. the description of this control sample in Sect. 3.1). Even when restricting to faint quasars with a magnitude g > 22, 88% of them still pass this threshold.
In addition to the variability-based selection, a loose color constraint was used to reject a region of color-space mostly populated by stars, in order to reduce the fraction of stellar contaminants in the target list. The cut consisted in requiring c3 < a − c1/3, where c1 and c3 are defined as in Fan (1999) by 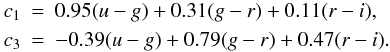 (4)The parameter a can take either of two values: a = 1.0 for a very loose color cut, or a = 0.6 for a tighter color constraint (cf. Fig. 2). About 100% of z < 2.2 and 98% of z > 2.2 known quasars (resp. 95% and 93%) pass the condition with a = 1.0 (resp. a = 0.6).
(4)The parameter a can take either of two values: a = 1.0 for a very loose color cut, or a = 0.6 for a tighter color constraint (cf. Fig. 2). About 100% of z < 2.2 and 98% of z > 2.2 known quasars (resp. 95% and 93%) pass the condition with a = 1.0 (resp. a = 0.6).
 |
Fig. 2 Locus of stars (upper blue contours), z < 2.2 quasars (lower left green contours) and z > 2.2 quasars (lower right red contours) in the c3 vs. c1 color–color plane. The upper solid line corresponds to the color cut c3 < 1.0 − c1/3 (loose, for point sources) and the lower dashed line to c3 < 0.6 − c1/3 (strict, for extended sources). |
2.2. The BOSS sample
The BOSS fields dedicated to this high density quasar survey were part of Stripe 82 and located at 317° < αJ2000 < 330° and 0° < δJ2000 < 1.25°.
The starting source list consisted of all point sources in this area passing the usual BOSS quality cuts (on photometry, pixel saturation, source blending etc.) as described in the Appendix of Ross et al. (2012), as well as the loose color cut (with a = 1.0) mentioned in the previous section, yielding about 5200 objects per deg2.
All objects passing yNN > 0.5 were selected as targets. The resulting list contained ~270 targets per deg2. To increase the identification rate of new targets, we removed from this list all targets that had already been observed by BOSS (Ahn et al. 2012). They consisted almost exclusively of spectroscopically identified quasars with redshifts between 0 and 5, totaling a density of ~30 quasars per square degree. This reduced the list to ~240 objects per deg2.
In case of fiber collisions during the tiling procedure, priorities were set on the targets according to their magnitude, giving higher priority to the brightest objects since these are more likely to obtain an accurate identification. An identical maximal priority was attributed to all targets with g < 22.7 (not corrected for extinction as the quantity of interest here is the actual observed flux of the object), and lesser priorities for fainter magnitudes.
Seven partially overlapping BOSS half-plates were allocated to the project (numbered 5141 to 5147 from low to high αJ2000), covering a total of 14.5 deg2. The other plate halves were used for the standard BOSS survey and are not included in this analysis. Plate 5141 was exposed for over 2 h (i.e. twice the normal time), without significant increase in the number of quasars identified. The subsequent plates were thus exposed for 1 h. All seven plates were observed during July and September 2011.
2.3. The MMT sample
For the sake of completeness, the starting list for the MMT sample was built from all SDSS sources in the area of the previous BOSS sample, whether point-like or extended and whether or not they passed the standard BOSS quality cuts, and passing the loose color cut with a = 1.0 described in Sect. 2.1. This initial list consisted of ~11 300 deg-2 objects, 60% of which were resolved (i.e. “extended”, like galaxies), and 40% of which were unresolved (i.e. “point-like”, like stars). As for the BOSS sample, all objects that have already obtained spectra with SDSS-III/BOSS were removed from the target list. These were again mostly quasars. In addition, we rejected targets with g < 22 that were simultaneously selected for the BOSS sample, since the redshift determination efficiency of BOSS is close to unity at least to that magnitude.
Most quasars are expected to be significantly more luminous than their host galaxy, making them appear point-like. We thus expect less quasars in the “extended” sub-sample. The fraction of random objects artificially drifting into the region of large yNN values being independent of the source morphology, however, the ratio of the number of quasars to the total number of selected targets is therefore smaller for extended sources. To counteract the effect of a more liberal morphological selection, extended sources were therefore subject to tighter constraints on both color and variability. They were also given a lesser priority than the MMT point-like targets.
The highest priority (priority A) was given to point-like targets with observed magnitude g < 23.0, yNN > 0.5 and c3 < 1.0 − 0.33c1, leading to ~130 deg-2 targets.
Priority B was given to extended objects with g < 23.0, yNN > 0.8 and c3 < 0.6 − 0.33 × c1. This led to 140 deg-2 additional targets.
Priority C (respectively D) was given to objects with 23.0 < g < 23.2 passing the same conditions as the priority A (resp. B) targets, leading to 40 deg-2 (resp. 30 deg-2) additional targets.
A total of 6 non-overlapping circular fields of 1 deg in diameter were observed with MMT/Hectospec in the last trimester of 2011, with exposure times of 150 min each. The fields were located within the coverage of the BOSS sample of Sect. 2.2, in the area farthest from the Galactic plane, which is least contaminated by Galactic stars. The region 326.5° < αJ2000 < 328° was avoided because of a higher Galactic extinction on average (Ag ~ 0.4) than for the other MMT fields (Ag ~ 0.2 for 322° < αJ2000 < 326.5° and Ag ~ 0.3 for 328° < αJ2000 < 330°), where the extinctions come from the maps of Schlegel et al. (1998).
Because of weather conditions, only five MMT fields (all but the field with lowest Right Ascencion) produced usable data. This resulted in a total sky coverage of 3.92 deg2.
Figure 3 illustrates the locations of the BOSS and MMT fields dedicated to the present study.
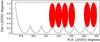 |
Fig. 3 Footprint of the BOSS half-plates (black contours) and of the MMT fields (filled red disks) dedicated to the present study. BOSS plates were attributed the numbers 5141 to 5147 from left to right. MMT fields were labeled 0 to 5 with increasing Right Ascension. |
2.4. Impact of source morphology
While most quasars, whatever their redshift, appear point-like on single-epoch SDSS images, this is no longer the case on co-added frames, which result from the superposition, at the image level, of about 56 Stripe 82 scans, thus reaching a depth about 2 mag fainter than individual scans. In the BOSS sample, we thus rejected a large fraction of low-redshift quasars by only considering point-like objects. Figure 4 shows the fraction of quasars classified as point-like on the co-added images, for several bins in redshift.
 |
Fig. 4 Fraction of known quasars identified as point-like in co-added images, as a function of magnitude, for several bins in redshift (rising redshift from bottom to top). The asymptotic red histogram is the fraction of stars that are identified as point-like. |
Figure 4 also displays the fraction of point-like objects on a single-epoch image of excellent seeing (most of these objects are indeed stars) that are classified as stars on the co-added frame. While all stars with magnitudes g < 22 appear point-like in the deep frame, up to 16% of them appear extended at g = 23, possibly due to small misalignments in the co-addition procedure that affect the object morphology at faint magnitudes, or to noise that starts to contribute significantly in the wings of the PSF, thus smearing it out. High redshift (z > 3) quasars follow the same trend as stars, therefore suffering from the same technical drawbacks. In contrast, as the redshift decreases, more and more quasars appear extended on the co-added frame, pointing towards a physical effect that cannot be explained with the previous arguments. Even the curves for 2.0 < z < 3.0 quasars are significantly lower than that obtained for stars, our control sample of point-like objects. There is a clear step at a redshift z ~ 0.8, where 60 to 80% of the quasars, even bright (g < 20) ones, appear extended.
These results are consistent with the host galaxy becoming detectable in the co-added images, making the quasar appear extended. Figure 4 thus indicates a statistical detection of the host galaxy of quasars, even at redshifts as large as z ~ 2. The brightest (g < 19) quasars, however, still sufficiently outshine their host galaxy to remain point-like, except in the lowest redshift bin where the host galaxy is resolved.
3. Completeness corrections
To estimate quasar densities and the luminosity function from raw quasar counts, the data have to be corrected for instrument-related losses and for biases introduced by the cuts applied to select the targets. The completeness-corrected number of quasars is determined as 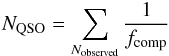 (5)where fcomp is the fraction of recovered quasars based on the product of various selection effects. The analysis-related completeness corrections are computed from control samples of known quasars, while the instrument-related ones are computed from the data.
(5)where fcomp is the fraction of recovered quasars based on the product of various selection effects. The analysis-related completeness corrections are computed from control samples of known quasars, while the instrument-related ones are computed from the data.
The different contributions to the completeness corrections are detailed in the following sections, and a summary of the magnitude dependence of the corrections for BOSS and the MMT is illustrated in Fig. 5.
 |
Fig. 5 Magnitude dependence of the contributions to the total completeness correction for the different samples. Upper left: the new quasars identified in the BOSS sample. Upper right: the known quasars that were intentionally removed from the target lists. Lower left (resp. right): the quasars identified in the MMT sample and that appeared point-like (resp. extended) in the coadded SDSS frame. These corrections are computed from all quasars contained in either sample. |
3.1. Control sample of known quasars
The analysis-related completeness corrections are determined using a list of 19 215 spectroscopically confirmed quasars in Stripe 82 obtained from the 2dF quasar catalog (2QZ; Croom et al. 2004), the 2dF-SDSS LRG and Quasar Survey 2SLAQ (Croom et al. 2009), the SDSS-DR7 spectroscopic database (Abazajian et al. 2009), the SDSS-DR7 quasar catalog (Schneider et al. 2010) and BOSS observations up to July 2011 (Ahn et al. 2012; Pâris et al. 2012). About 48% of the quasars (over 90% of the z > 2.2 quasars and 25% of the z < 2.2 quasars) come from BOSS, 40% from SDSS-DR7 and 10% from 2SLAQ. Note that BOSS re-observed all the z > 2.2 quasars identified in previous surveys that fell in its footprint. As shown in Fig. 6, these quasars have redshifts in the range 0 ≤ z ≤ 5 and g magnitudes in the range 17 ≤ g ≤ 23 (Galactic-extinction corrected) with 212 quasars having a magnitude fainter than g = 22.5. The irregular shape of the distributions results from the use of several surveys with different redshift goals and selection algorithms. At z > 2, most of the quasars come from color-selection with the standard BOSS survey (Yèche et al. 2010; Kirkpatrick et al. 2011; Bovy et al. 2011a,b; Ross et al. 2012).
The incompleteness of the control sample is not an issue for this analysis since it is used to compute ratios and not absolute numbers of quasars. The only hypothesis is that it covers in an unbiased way the full range of quasar parameters (such as colors, magnitudes, morphologies, or time sampling of the lightcurves) that the various selections depend upon.
For each of these known quasars, lightcurves in all 5 SDSS filters were built as described in Sect. 2. We used all matching single-epoch data that passed quality criteria on the photometry described in Appendix A.1 of Ross et al. (2012). Requiring at least one valid epoch on the lightcurve removed approximately 2% of the objects, reducing the sample to 18 910 quasars. The variability parameters of Eqs. (1) and (3) were computed for these quasars and used to determine completeness corrections.
3.2. Analysis-related completeness corrections
The analysis-related corrections arise from two contributions that affect the BOSS and the MMT samples differently: a quality factor ϵqual and a selection factor ϵsel. These corrections depend on the source morphology (point-like or extended), the redshift z and the magnitude g uncorrected for extinction (since we are here sensitive to the observed and not to the intrinsic quasar magnitude). For the sake of clarity, the magnitude corrected for Galactic extinction will henceforth be denoted gdered.
Quality completeness ϵqual(g):
This contribution is related to the quality cuts described in the Appendix A of Ross et al. (2012) that were applied to obtain the initial list of the sources from which the selection was made. It only affects BOSS data as no quality cut was applied to build the list of sources for the MMT sample (see Sects. 2.2 and 2.3). The mean quality factor over the BOSS data of the present study is 0.89, with a plateau at 0.90 for all bright sources with g < 22, dropping to 0.70 at g = 23 (see blue curve in upper two plots of Fig. 5).
Target selection completeness ϵsel (g, z, source morphology):
This contribution is related to the variability-based and color-based selection algorithms, as described in Sect. 2. It depends on the telescope that the target list is designed for, because of the different thresholds that were set on the selection variables.
BOSS targets were selected from an initial list limited to point-sources. To take into account the incompleteness due to the exclusion of extended sources, ϵsel BOSS was computed from the ratio, in the control sample, of the point-like quasars that passed the selection cuts to the total number of quasars. This yielded the correction table shown in Fig. 7 as a function of magnitude g and redshift z. The mean completeness correction for the selection step, over the BOSS sample, is 0.78.
 |
Fig. 6 Distributions in redshift (top plot) and extinction-corrected magnitude (bottom plot) for the sample of quasars from previous quasar surveys covering Stripe 82. |
 |
Fig. 7 Selection completeness ϵsel BOSS(g, z) for the quasars in the BOSS program. The significant drop at low redshift is due to the fact that many quasars with z < 1 appear as extended sources in coadded frames and were thus not considered in the initial source list. We also observe the expected efficiency drop at faint magnitudes. Bins left unfilled (white) are bereft of quasars. |
For the MMT data, the completeness correction for the selection step was computed separately for point-like sources and for extended ones. For each source morphology, ϵsel MMT(g, z) was determined from the control sample as the fraction of quasars of a given morphology that passed the relevant selection criteria (cf. Sect. 2.3). The mean selection completeness correction over the MMT sample of quasars is 0.76 (0.82 for the point-like sources and 0.57 for the extended ones).
3.3. Instrument-related completeness corrections
These corrections come from two contributions: a tiling factor ϵtiling quantifying whether a target could indeed have been observed, and a spectrograph factor ϵspectro quantifying the probability of obtaining a secure identification and redshift for a given target. These depend on the source morphology (point-like or extended) through the target priority, and on the observed magnitude g.
Tiling completeness ϵtiling(priority):
This contribution is related to the tiling procedure (Dawson et al. 2012), taking into account the density of allocated fibers and the target priorities in case of fiber collisions. This correction just represents the fraction of targets that were assigned fibers. It entirely depends on the instrumental configuration and thus must be computed specifically for BOSS and the MMT. As explained in Sect. 2, the target priority varies with magnitude for BOSS targets, and with both magnitude and source morphology (point-like or extended) for MMT targets. In the case of BOSS, however, the fraction of spectra that can be correctly identified drops significantly beyond g ~ 22.5 and only the first priority bin was used for the present analysis (cf. Sect. 4.3). The mean tiling completeness correction is 0.95 (respectively 0.84) for the quasars recovered from the BOSS (resp. the MMT) data and selected for our measurement of the Quasar Luminosity Function. Corrections per priority bin, numbers of observed targets and of selected quasars are given in Table 1.
Tiling completeness correction for BOSS (unique priority level) and the MMT (priorities A through D).
Spectrograph completeness ϵspectro(g):
Some spectra did not produce a reliable identification of the source, either because the extraction procedure had failed (yielding flat and useless spectra hereafter labeled “bad”) or because the spectrum had too low a signal-to-noise ratio (S/N) for adequate identification (hereafter “?”). Details on the classification of the spectra can be found in Pâris et al. (2012). Figure 8 illustrates the rate of the “bad” spectra as a function of magnitude g for the BOSS (filled black dots) and the MMT (open red circles) spectra. The overlaid dashed curves are fits to the data. The fraction of “bad” spectra reaches 15% at g = 23.15 for the MMT and g = 22.9 for BOSS. The upper blue dotted curve illustrates the total loss 1 − ϵspectro(g), similar for both instruments, when considering both the “bad” and the “?” spectra. This total fraction of inconclusive spectra is negligible for g < 22, it reaches 15% at g = 22.8, and 30% at g = 23.1.
 |
Fig. 8 Fraction of inconclusive spectra (declared so after visual inspection) as a function of observed g magnitude. The curves are fits to the data. In our analysis, we use the upper blue curve to correct for the total fraction of inconclusive spectra. |
 |
Fig. 9 Quasar number counts per deg2 as a function of observed g magnitude (top) and redshift (bottom). The black (resp. red) line is for quasars measured by BOSS (resp. MMT). The BOSS histograms include the already identified quasars in the area that were removed from the target list. |
4. Results
BOSS data were taken on the dedicated Sloan Foundation 2.5 m telescope (Gunn et al. 2006) using the BOSS spectrograph (Smee et al. 2012). The BOSS spectra were reduced with the standard BOSS pipeline (Bolton et al. 2012; Dawson et al. 2012; see also Bolton & Schlegel 2010) which also provides an automated determination of the target classification and redshift. A manual inspection was performed on all the spectra of this program, as for all quasar targets of the main BOSS survey (Pâris et al. 2012). The MMT spectra were reduced with a customized pipeline based heavily on the E-SPECROAD package2. All the spectra were checked visually to produce final identifications and redshifts. The spectra were classified as quasi stellar object (“QSO”) for secure quasars with reliable redshift, “QSO?” for secure quasars but uncertain redshift, “Star”, “Galaxy” or “Inconclusive”. The latter case encompasses the “bad” and the “?” spectra of the previous section. In our analysis, we use all spectra that were identified as “QSO” or “QSO?”, where we call “quasar” an object with a luminosity Mi [z = 2] < − 20.5 and either displaying at least one emission line with FWHM greater than 500 km s-1 or, if not, having interesting/complex absorption features.
4.1. Raw counts for the BOSS and MMT samples
We identified 1179 new quasars with BOSS (hereafter referred to as “New BOSS” or simply “BOSS”) and 262 ones with the MMT. To these, we add the 436 previously identified quasars in our area of interest that were explicitly removed from the target lists and hereafter referred to as “Known”. Our survey data cover 14.5 deg2, among which 3.92 deg2 with both BOSS and MMT.
Figure 9 shows the distributions of the redshift and observed magnitude in the g band for our sample of confirmed quasars. While the redshift distributions of the BOSS and MMT samples are similar in shape, the MMT sample reaches more than half a magnitude deeper than the BOSS sample. The typical quasar magnitude of each of the two samples is ⟨ g ⟩ MMT = 22.2 and ⟨ g ⟩ BOSS = 21.5. The sample of previously known quasars that were not included in the target lists have a mean magnitude ⟨ g ⟩ Known = 21.0.
As explained in Sect. 2.3, the MMT targets at g < 22 only consisted of the selected objects that were not included in the BOSS sample, i.e., either those did not pass the quality criteria or that appeared as extended in the source catalog. This led to 69 quasars with g < 22 in the MMT sample. For g > 22, the MMT sample included 116 quasars in common with BOSS, plus 77 additional ones.
Table 2 summarizes the raw quasar counts in the BOSS and MMT samples.
4.2. Identification cross-checks
Raw number counts for the different samples in several g magnitude bins.
Cross-identification between BOSS and MMT spectra for the 344 targets with g > 22 that were observed by both telescopes.
We have intentionally observed some targets with both instruments in the g > 22 mag regime where we expect the BOSS identification to become less secure. Table 3 summarizes the cross-identification of the 344 common targets, among which 116 quasars identified as such from both instruments. There are very few changes in identification. The most notable feature is that, as expected in this faint magnitude regime and compared with BOSS, MMT observations allow more quasars to be identified and given a secure redshift: 19 “QSO?” BOSS targets were confirmed as “QSO” with MMT, as well as 9 targets classified as “bad” in BOSS. It is noteworthy that even at these faint magnitudes, there were almost no false quasar detections in BOSS: only 1 “QSO?” BOSS target was identified as a star from the MMT spectrum; all others were confirmed as quasars.
At brighter magnitudes (22 < g < 22.5), Table 4 suggests excellent consistency in the identification by either telescope. Out of a total of 66 targets for which a secure identification is available from the MMT spectra, 59 were correctly identified by BOSS, 5 had too low S/N, and 2 were misidentified. There are no false quasar detections.
From the set of targets with an identification in both samples (i.e., not considering those declared “unknown” in either case), and assuming the true identification to be the one from the MMT spectrum, we can estimate the identification reliability with BOSS to be of order 237/251 = 94 ± 2% at g > 22 and of order 59/61 = 97 ± 2% over the magnitude range 22 < g < 22.5.
4.3. Corrected counts
To study quasar number counts, we use the quasars identified in the BOSS sample to g < 22.5 and in the MMT sample to g < 23.0. The depth of the observations is insufficient to use identified quasars with g > 23.0. The spectra are too low signal-to-noise and the spectrograph incompleteness corrections too large to yield reliable corrected counts. All fields suffer from relatively high Galactic extinction: ⟨ Ag ⟩ = 0.27 (rms of 0.10) ranging from 0.15 to 0.75 in the BOSS fields and ⟨ Ag ⟩ = 0.25 (rms of 0.04), ranging from 0.15 to 0.35, in the MMT fields. The previous limitations on observed magnitude therefore result in the following effective bounds on the extinction-corrected magnitude, equal to gmax − Ag, min: gdered < 22.35 for BOSS and gdered < 22.85 for the MMT.
Cross-identification between BOSS and MMT spectra for the 68 targets with 22 < g < 22.5 that were observed by both telescopes.
To compute completeness-corrected quasar counts, we defined three mutually exclusive samples, based on observed g magnitude and sky coverage:
-
g < 22.0: use of the BOSS sample over the entire 14.5 deg2 area (691 BOSS and 346 known, for a total of 1037 quasars);
-
22 < g < 22.5: use of the MMT sample over its 3.9 deg2 coverage (88 quasars); and of the BOSS sample for the remaining 10.6 deg2 area (169 quasars), completed by 47 known quasars
-
22.5 < g < 23.0 use of the MMT sample over its 3.9 deg2 coverage (105 MMT and 3 known quasars).
This division ensures, for each magnitude range, the use of the data with best redshift reliability (cf. Sect. 4.2) and maximal statistical significance. This also prevents us from double-counting quasars that were observed both with BOSS and the MMT. The data that did not explicitly enter the computation of the corrected counts or quasar luminosity function were used for cross-checks (cf. Sects. 4.2 and 4.4).
Data from the BOSS sample were corrected for selection (ϵsel) and quality (ϵqual) incompleteness. In addition, tiling (ϵtiling) and spectrograph (ϵspectro) completeness corrections were applied to the quasars that were identified from this deep program. The previously identified quasars in the area were only corrected by ϵsel and ϵqual since they were removed from the list prior to the tiling procedure.
 |
Fig. 10 Quasar number counts per deg2 as a function of redshift (Δz = 0.2). Blue is for the new sample of quasars identified with our BOSS deep program, green for the previously known BOSS sample, red is for the MMT sample and black for the total. The blue, green and red curves use mutually exclusive samples and correspond to the zones defined in Sect. 4.3. |
Data from the MMT sample were corrected for spectrograph (ϵspectro) incompleteness, and for the relevant ϵtiling and ϵsel that, for the MMT sample, depended on the target morphology.
The completeness-corrected number of quasars is thus computed from the following equation: 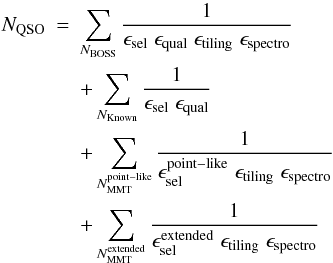 (6)where the completeness corrections are 2D functions of the quasar magnitude g and redshift z, and where the BOSS and MMT quasars entering the summations are those selected according to the 3 mutually exclusive samples defined previously.
(6)where the completeness corrections are 2D functions of the quasar magnitude g and redshift z, and where the BOSS and MMT quasars entering the summations are those selected according to the 3 mutually exclusive samples defined previously.
Figure 10 illustrates the completeness-corrected quasar number counts as a function of redshift for 3 mag limits: gdered < 22 as in the BOSS survey (Schlegel et al. 2009), gdered < 22.5 as required for the eBOSS project3, and gdered < 23 as required for BigBOSS4. As explained above, however, the last set of histograms are only complete to at most gdered < 22.85 and thus represent lower limits for gdered < 23. On average over the quasars of this project, total completeness corrections are at the level of 80% to g < 20, and drop smoothly to 50% at g ~ 22.5. Table 5 summarizes the total quasar number counts for various ranges in corrected g magnitude and redshift.
4.4. Counting cross-checks
Because we had overlapping data in terms of magnitude range or sky coverage from two different programs, several counting cross-checks can be performed. Every single quasar observed was therefore used to compute the luminosity function or for cross-checks, and some for both.
Density comparison in 22 < g < 22.5
The magnitude range 22 < g < 22.5 was accessible to both the MMT and the BOSS samples. Because of the different constraints on source morphology and quality, however, and since the MMT zone only covers a portion of the BOSS zone, the quasars observed in the two cases were not the same. The completeness-corrected quasar number counts derived from either sample over 22 < g < 22.5 are given in Table 6. The last column indicates the number of identified quasars used to make the measurement. The quasar densities derived from BOSS or the MMT over this magnitude range are in excellent agreement.
Number counts (quasars per deg2) for several ranges in extinction-corrected magnitude gdered and redshift z.
Efficiency-corrected number counts for the BOSS and MMT samples (including, in both cases, the BOSS standard QSOs that were selected but not re-observed) over the magnitude range 22 < g < 22.5 accessible to both samples.
Cross-check of ϵqual using MMT point-like targets at g < 22
The sample of quasars selected for the MMT observations from point-like sources in the magnitude range g < 22 should allow recovery of the quasars that were not selected in the BOSS target list because of the constraints on source quality. They can therefore be used to verify the estimated ϵqual. This concerned N = 22 MMT quasars, with a mean tiling correction (corresponding to priority level A) ϵtiling = 0.903. Given a survey area S = 3.9 deg2, the density of point-like sources observed with MMT at g < 22 is therefore N/ϵtiling/S = 6.2 ± 1.3 deg-2.
In the same magnitude range, the BOSS sample consisted of N = 691 quasars, with a mean tiling correction ϵtiling = 0.945 and a mean source quality completeness correction ϵqual = 0.897. Given a survey area S = 14.5 deg2, the estimated density of quasars not included in the sample because of the quality constraint is thus N/ϵtiling/ϵqual × (1 − ϵqual)/S = 5.8 ± 0.2 deg-2, in agreement within 1σ with what was estimated from the MMT sample.
Cross-check of ϵsel using MMT extended targets at g < 22.5
Finally, the quasars selected for the MMT observations from extended sources at g < 22.5 should allow recovery of the quasars that were not selected in BOSS because of constraints on the source morphology. This can be checked by comparing the density of extended quasars in the MMT survey to the number of quasars that were not selected in BOSS for this same reason, estimated from the observed number of point-like quasars and the morphology-part of the selection completeness correction.
Quantitatively, we compute the following two quantities, in the g < 22.5 mag range. On the one hand, the density of extended quasars identified in MMT: 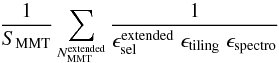 and on the other hand, the density of unselected extended quasars in BOSS:
and on the other hand, the density of unselected extended quasars in BOSS: 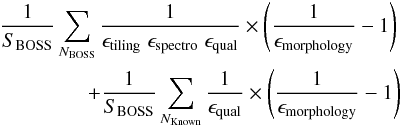 where SMMT and SBOSS are respectively the areas of the MMT and the BOSS programs, and ϵmorphology is the fraction of the targets that are point-like (as a function of magnitude and redshift). This correction is the part of ϵsel that does not include the effect of the target selection based on its color and time variability. These two densities are illustrated in Fig. 11. They are clearly in agreement.
where SMMT and SBOSS are respectively the areas of the MMT and the BOSS programs, and ϵmorphology is the fraction of the targets that are point-like (as a function of magnitude and redshift). This correction is the part of ϵsel that does not include the effect of the target selection based on its color and time variability. These two densities are illustrated in Fig. 11. They are clearly in agreement.
 |
Fig. 11 Comparison of the number of “extended” quasars estimated from BOSS data and completeness corrections (blue curve) or observed in the MMT sample (purple points). |
5. Luminosity function in g
We compute the quasar luminosity function (LF) from the corrected number counts derived above, and considering our completeness limit at gdered < 22.5. The distance modulus dM(z) is computed using the standard flat ΛCDM model with the cosmological parameters of Larson et al. (2011): ΩM = 0.267, ΩΛ = 0.734 and h = 0.71.
5.1. K-corrections
Selection for this survey was performed in the g-band, and for the majority of the data this band provides the highest S/N. We define the K-correction in terms of the observed g magnitude and follow Croom et al. (2009, hereafter C09) in applying the correction relative to z = 2, which is near the median redshift of our quasar sample (see also Richards et al. 2009). The absolute magnitude normalized to z = 2 is given by: ![\begin{equation} M_g(z=2)=g_c-d_M(z)-[K(z)-K(z=2)]\;. \end{equation}](/articles/aa/full_html/2013/03/aa20379-12/aa20379-12-eq181.png) (7)Hereafter we will use Mg as a shorthand for the redshift-corrected Mg(z = 2). The K-correction as a function of redshift is derived from model quasar spectra in a similar fashion to Richards et al. (2009). The quasar model includes a broken power law continuum with αν = −0.5 at λ > 1100 Å and αν = −1.5 at λ ≤ 1100 Å (Telfer et al. 2002). Strong quasar emission lines are included, where the equivalent width is a function of luminosity according to the well-known Baldwin Effect (Baldwin 1977); thus, the K-correction is a function not only of redshift but also luminosity (or equivalently, observed g-magnitude). The model also includes Fe emission using the template of Vestergaard & Wilkes (2001) and Lyman-α forest absorption using the prescription of Worseck & Prochaska (2011). The forest model is particularly relevant here, as for z ≳ 2.5 the g-band K-correction necessarily includes a component due to forest absorption; our K-correction accounts for the mean value but for high redshift objects the uncertainty in individual K-corrections is increased by line-of-sight fluctuations in the amount of forest absorption within the g-band. The models used to derive the K-corrections will be described in fuller detail in McGreer et al. (2013). In general, as shown in Fig. 12, the values are very similar to those used by C09 (e.g., their Fig. 1), but are extended to z = 4. At z ~ 2 − 3, our use of a luminosity-dependent K-correction introduces a spread in K-correction values of ~ 0.25 mag across the luminosity range of the quasars in our sample, as the Lyman-α and C IV lines are within the g-band and contribute substantially to the flux within the bandpass.
(7)Hereafter we will use Mg as a shorthand for the redshift-corrected Mg(z = 2). The K-correction as a function of redshift is derived from model quasar spectra in a similar fashion to Richards et al. (2009). The quasar model includes a broken power law continuum with αν = −0.5 at λ > 1100 Å and αν = −1.5 at λ ≤ 1100 Å (Telfer et al. 2002). Strong quasar emission lines are included, where the equivalent width is a function of luminosity according to the well-known Baldwin Effect (Baldwin 1977); thus, the K-correction is a function not only of redshift but also luminosity (or equivalently, observed g-magnitude). The model also includes Fe emission using the template of Vestergaard & Wilkes (2001) and Lyman-α forest absorption using the prescription of Worseck & Prochaska (2011). The forest model is particularly relevant here, as for z ≳ 2.5 the g-band K-correction necessarily includes a component due to forest absorption; our K-correction accounts for the mean value but for high redshift objects the uncertainty in individual K-corrections is increased by line-of-sight fluctuations in the amount of forest absorption within the g-band. The models used to derive the K-corrections will be described in fuller detail in McGreer et al. (2013). In general, as shown in Fig. 12, the values are very similar to those used by C09 (e.g., their Fig. 1), but are extended to z = 4. At z ~ 2 − 3, our use of a luminosity-dependent K-correction introduces a spread in K-correction values of ~ 0.25 mag across the luminosity range of the quasars in our sample, as the Lyman-α and C IV lines are within the g-band and contribute substantially to the flux within the bandpass.
 |
Fig. 12 K-corrections as a function of redshift. The spread illustrates the variation over the luminosity range of the quasars in our sample. The red curve shows for comparison the parameterization K(z) = −2.5(1 + να)log 10(1 + z) introduced in C09, with να = −0.5 and normalized to z = 2. |
5.2. Luminosity function determination
We define eight redshift bins: the first five are the same redshift intervals as in C09, with limits 0.68, 1.06, 1.44, 1.82, 2.2, 2.6; the last three are specific to our analysis and have the limits 2.6, 3.0, 3.5, 4.0.
For our quasar sample, we calculate the binned LF using the model-weighted estimator Φ suggested by Miyaji et al (2001), which presents the advantage of not having to assume a uniform distribution across each bin, unlike 1/V estimators. Instead, it models the unbinned LF data and uses it to correct for the variation of the LF and for the completeness within each bin, which is here particularly critical at the faint end of the LF where the latter is incompletely sampled. This estimator gives the binned LF as 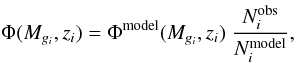 (8)where Mgi and zi are, respectively, the absolute magnitude and the redshift at the center of bin i, Φmodel is the model LF estimated at the center of the bin,
(8)where Mgi and zi are, respectively, the absolute magnitude and the redshift at the center of bin i, Φmodel is the model LF estimated at the center of the bin, 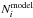 is the number of quasars with gdered < 22.5 estimated from the model in the bin and
is the number of quasars with gdered < 22.5 estimated from the model in the bin and 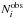 is the observed number of quasars in the bin. A drawback of this estimator is that it is model-dependent, but Miyaji et al (2001) show that the uncertainties due to the model dependence are practically negligible.
is the observed number of quasars in the bin. A drawback of this estimator is that it is model-dependent, but Miyaji et al (2001) show that the uncertainties due to the model dependence are practically negligible.
We assume the LF to be appropriately described by a standard double power-law of the form (Boyle et al. 2000): 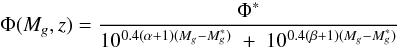 (9)where Φ is the quasar comoving space density. For our Φmodel, we follow the pure luminosity evolution model of C09, where a redshift dependence is introduced through an evolution in
(9)where Φ is the quasar comoving space density. For our Φmodel, we follow the pure luminosity evolution model of C09, where a redshift dependence is introduced through an evolution in 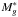 described by
described by 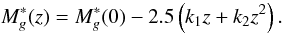 (10)Systematics on our LF measurements are computed by estimating the uncertainty on the completeness corrections of Sect. 3 using Monte Carlo simulations in which the selected and total number of quasars follow Poisson distributions centered on the observed means. The error bars on each measurement include both our statistical and systematic uncertainties, added in quadrature.
(10)Systematics on our LF measurements are computed by estimating the uncertainty on the completeness corrections of Sect. 3 using Monte Carlo simulations in which the selected and total number of quasars follow Poisson distributions centered on the observed means. The error bars on each measurement include both our statistical and systematic uncertainties, added in quadrature.
5.3. Comparison to luminosity function of Croom et al. (2009)
In a first step, we keep all 6 parameters (Φ ∗ , α, β, 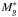 , k1 and k2) of the LF fixed. We impose, for our model Φmodel, the values fitted by C09 for the 0.4 < z < 2.6 redshift range and given in their Table 2, i.e.
, k1 and k2) of the LF fixed. We impose, for our model Φmodel, the values fitted by C09 for the 0.4 < z < 2.6 redshift range and given in their Table 2, i.e. 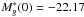 , k1 = 1.46 and k2 = −0.328, and we compare our data to this luminosity function. Figure 13 illustrates our LF measurements (black circles). The blue open circles are the LF measurements from C09 and the blue dashed curve is their best-fit Φmodel.
, k1 = 1.46 and k2 = −0.328, and we compare our data to this luminosity function. Figure 13 illustrates our LF measurements (black circles). The blue open circles are the LF measurements from C09 and the blue dashed curve is their best-fit Φmodel.
 |
Fig. 13 Quasar luminosity function measurements (black circles) compared to the C09 data (blue open circles at 0.68 < z < 2.6). The blue dashed curve is the LF of C09 and the best-fit model of this analysis is shown as the red curve. The green curves are best fits to COSMOS data (Masters et al. 2012) at z ~ 3.2 (plain curve) and z ~ 4.0 (dashed curve). The cyan line is the best fit, with fixed-α, to binned LF data from SWIRE and SDSS at z ~ 3.2 (Siana et al. 2008). |
The data presented in this work from dedicated BOSS and MMT surveys cover the redshift range from z = 0.68 to z = 4, allowing 3 additional redshift bins beyond those of C09. Over the 0.68 < z < 2.6 redshift range common to both studies, our data and the C09 points are in good agreement. The extrapolation of the C09 model to z = 4 is also in reasonable agreement with our data points. Two discrepancies, however, are worth being noted. In the 3.5 < z < 4.0 redshift bin, our measured LF points are all above the extrapolated curve. The low number of quasars with z > 3.5 in our control sample, however, yields large uncertainties in the completeness corrections that result in systematic uncertainties on our LF measurements in this redshift regime. Moreover, the statistical uncertainties on the measured LF are also very large and the trend needs to be confirmed with improved statistics. In the 2.2 < z < 2.6 bin, the C09 LF measurements are all systematically below the best-fit C09 model and this trend is corroborated by our data in the same redshift bin, confirming the hypothesis that the feature is real and not related to a redshift limitation of the sample since ours extends significantly beyond z = 2.6. This disagreement was already noted by C09 who observed a significant improvement of the fit when reducing the upper limit in redshift to z < 2.1.
5.4. Luminosity function fit
In a second step, since the data from our analysis and from C09 are independent, we included both samples to constrain the luminosity function in larger redshift and magnitude ranges than either data set alone. In the fitting procedure, we let all parameters of the model free and do a least-squares-fit, using the MINUIT package (James & Roos 1975), to determine the best fit values and their errors. Since our LF measurements depend on the fitted Φmodel, iterative fitting is performed to determine the luminosity function of our sample from Eq. (8), until parameter convergence is reached. Up to z ~ 2.6, the choice of model used in this procedure only changes the last magnitude bin since it’s the only one affected by the gdered cut. Above z ~ 2.6, the cut on gdered typically affects the last two magnitude bins, where the LF measurement and its error can change by up to a factor of 3.
Fitting the model defined in Eqs. (9) and (10) to the combined LF does not significantly change the result from the best-fit model of C09. In particular, Eqs. (9) and (10) do not provide sufficient freedom to solve the discrepancies mentioned above.
Predicted number of quasars over 15.5 < g < 25 and 0 < z < 6 for a survey covering 10 000 deg2, based on our best-fit luminosity function.
We therefore defined a new model, based on the same equations as before but allowing the redshift evolution parameters (k1 and k2) and the model slopes (α and β) to be different on either side of a pivot redshift zp = 2.2. The model is thus described by Eq. (9) where α and β now have subscripts l for z < zp and h for z > zp, and an evolution in 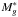 characterized by
characterized by ![\begin{equation} M_g^*(z)=M_g^*(z_{\rm p})-2.5\left[k_1(z-z_{\rm p})+k_2(z-z_{\rm p})^2\right], \label{eq:mg2} \end{equation}](/articles/aa/full_html/2013/03/aa20379-12/aa20379-12-eq251.png) (11)where k1 and k2 are again to be considered separately for low (subscript l) and high (subscript h) redshifts w.r.t. zp. This more general form of our model now contains 10 parameters that are all let free.
(11)where k1 and k2 are again to be considered separately for low (subscript l) and high (subscript h) redshifts w.r.t. zp. This more general form of our model now contains 10 parameters that are all let free.
The best-fit parameters are reported in Table 7, and the resulting luminosity function is illustrated in Fig. 13 as the red curve. The high redshift parameters result from a fit to the data at z > zp = 2.2. The faint end slope βh is well constrained by the 2.2 < z < 2.6 data points. Given the large error bars on the data at z > 3, however, the redshift evolution is much less constrained, as reflected by the large error bars on k1h and k2h. The best fit has a χ2 of 324 for 162 degrees of freedom. For the sake of comparison, we also provide the parameters of C09, translated into the parameters defined in Eq. (11) with a pivot redshift zp = 2.2 instead of zp = 0 in the original work of C09. We provide, in Appendix A, the measured luminosity function values and associated uncertainties, where the measurements were corrected using the estimator described in Sect. 5.2 and considering the best-fit model.
In the redshift bins from z = 0.68 to z < 2.2 where the data from C09 are the most constraining, the best-fit model shows negligible difference with that of C09. It starts to deviate at redshifts z > 2.2, with a significantly flatter faint luminosity slope (smaller | β | ) than observed at low redshift. Our data, however, only constrain the faint luminosity slope to z ~ 2.6, as the 2.6 < z < 3.0 redshift bin has only 2 points beyond the knee, and the following bins have none with small error bars. Deeper data should be used for a secure measurement of the high-redshift faint-luminosity slope. A similar trend, however, was observed by Siana et al. (2008) at z = 3.2, where the authors noted that estimates at high redshift that were derived at low redshift and normalized using bright high-redshift QSOs resulted in a factor of about 2 overestimate at z ~ 3.
Further discussions on the quasar luminosity function can be found in Ross et al. (2013), where the BOSS data of this analysis are combined with the full data set from the DR9 release of the SDSS-III/BOSS survey. The quasar selection there requires models of quasar colors to determine the selection completeness, but the statistics are increased by over an order of magnitude, thus allowing better constrains on the LF model in the high redshift bins.
Binned luminosity function using the model weighted estimator.
Using our best-fit parameters of the quasar luminosity function, we provide, in Table 8, an estimate of the number of quasars in the redshift-magnitude plane for an hypothetical survey covering 10 000 deg2. Integrated to g = 23 as expected for instance for the future BigBOSS survey, these counts indicate a ~ 10% reduction compared to the extrapolation of the Hopkins et al. (2007) luminosity function that was used to predict quasar number counts in the LSST science book5 (Abell et al. 2009).
6. Conclusions
We have designed dedicated observations to measure the quasar luminosity function to z = 4. The targets were selected with a technique relying on optical variability of the quasars, which allows both high completeness and a simple estimation of the incompleteness corrections. These include inefficiencies related to the selection technique, which we compute using a control sample of almost 20 000 known quasars, as well as instrument-related inefficiencies that we compute from the data. The targets were shared between two instruments, the Sloan telescope (though an ancillary SDSS-III/BOSS program) and the MMT. They yielded a total of 1877 quasars, divided into 436 previously known quasars, 1179 new quasars identified with BOSS and 262 with the MMT. Cross-checks between the results from the two instruments indicate that the identification of the spectra is reliable to observed magnitudes g ~ 23. We have also verified that we obtained compatible number counts from BOSS and the MMT, in magnitude regimes where we had data observed with both instruments.
These dedicated data allow us to compute reliable quasar counts and to derive the quasar luminosity function to the limiting magnitude gdered = 22.5. Relatively high Galactic extinction in the fields prevent us from reaching fainter magnitudes.
The quasar number counts we measure at z < 2 are in agreement with previous estimates from Hopkins et al. (2007) or Croom et al. (2009). At higher redshifts, we observe of order 10% less quasars than assumed in Abell et al. (2009). This trend is shown by the luminosity function that we fit to our data, corrected for incompleteness in the faintest magnitude bins using the model weighted estimator of Miyaji et al (2001). While our best-fit model is in good agreement with that of Croom et al. (2009) over the common range in redshift 0.68 < z < 2.6, our fainter and deeper data indicate a flatter faint luminosity slope than what is predicted from the extrapolation of their model. This trend was already visible in the the last redshift bin (2.2 < z < 2.6) of Croom et al. (2009), and has been confirmed with the present work. Siana et al. (2008) also note a reduction in the number counts at z ~ 3.2 compared to LF extrapolations from low-redshift data. At 3.5 < z < 4.0, our best-fit model indicates an excess of bright quasars compared to the best-fit model of Croom et al. (2009). This result, however, is in a redshift regime where both statistical and systematic uncertainties are large. It would benefit from observations in less extincted regions of the sky, in order to reach fainter magnitudes and increased statistics.
Appendix
Table 9 provides the binned luminosity function (LF) for the data of our analysis using the model weighted estimator described in Sect. 5, as plotted in Fig. 13. We give the value of log Φ in 8 redshift intervals from z = 0.68 to z = 4.00, and for ΔMg = 0.40 magnitude bins from Mg = −29 to Mg = −21 to. We also give the number of quasars (NQ) contributing to the LF in the bin and the error (Δlog Φ).
We used the Catalog Archive Server (CAS) interface (http://casjobs.sdss.org) to recover both the Stripe 82 coadd and the single epoch information.
Acknowledgments
The observations reported here were obtained in part at the MMT Observatory, a facility operated jointly by the Smithsonian Institution and the University of Arizona. The other observations were obtained as part of the SDSS-III/BOSS project. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. The French Participation Group to SDSS-III is supported by the Agence Nationale de la Recherche under grant ANR-08-BLAN-0222. N.P.-D. and Ch.Y. acknowledge support from grant ANR-11-JS04-011-01. A.D.M. is a research fellow of the Alexander von Humboldt Foundation of Germany. X.F. and I.D.M. acknowledge supports from a David and Lucile Packard Fellowship, and NSF Grants AST 08-06861 and AST 11-07682.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abell, P. A., Allison, J., Anderson, S. F., et al. 2009, LSST science book [arXiv:0912.0201] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Annis, J., Soares-Santos, M., Strauss, M. A., et al. 2012, ApJ, submitted [arXiv:1111.6619A] [Google Scholar]
- Baldwin, J. A. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., & Schlegel, D. J. 2010, PASP, 122, 248 [NASA ADS] [Google Scholar]
- Bolton, A. S., Schlegel, D. J., & Aubourg, É. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A.S., Schlegel, D. J., Aubourg, É., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Hennawi, J. F., Hogg, D. W., et al. 2011a, ApJ, 729, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Myers, A. D., Hennawi, J. F., et al. 2011b, ApJ, 729, 41 [Google Scholar]
- Boyle, B. J., Shanks, T., Croom, S. M., et al. 2000, MNRAS, 317, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., Shanks, T., & Croom, S. M. 2012, ApJ, 749, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Smith, R. J., Boyle, B. J., et al. 2001, MNRAS, 322, 29 [Google Scholar]
- Croom, S. M., Smith, R. J., Boyle, B. J., et al. 2004, MNRAS, 349, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Richards, G. T., Shanks, T., et al. 2009, MNRAS, 392, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K., et al. 2012, AJ, 145, 10 [Google Scholar]
- Eisenstein, D. J. 2007, Am. Astron. Soc. Meet. Abstracts, 210, #47.01 [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Fabricant, D., Fata, R., Roll, J., et al. 2005, PASP 117, 1411 [Google Scholar]
- Fan, X. 1999, AJ, 117, 2528 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Richards, G. T., Hernquist, L., et al. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- James, F., & Roos, M. 1975, Comput. Phys. Commun., 10, 343 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kirkpatrick, J. A., Schlegel, D. J., Ross, N. P., et al. 2011, ApJ, 743, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D., Capak, P., Salvato, M., et al. 2012, ApJ, 755, 169 [NASA ADS] [CrossRef] [Google Scholar]
- McGreer, I. D., Jiang, L., Fan, X., et al. 2013, ApJ, submitted [arXiv:1212.4493] [Google Scholar]
- Miyaji, T., Hasinger, G., & Schmidt, M. 2001, A&A, 369, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palanque-Delabrouille, N., Yeche, Ch., Myers, A. D., et al. 2011, A&A, 530, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2012, A&A, 548, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, G. T., Fan, X., Newberg, H. J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Nichol, R. C., Gray, A. G., et al. 2004, AJS, 155, 257 [Google Scholar]
- Richards, G. T., Strauss, M. A., Fan, X., et al. 2006, AJ, 131, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Myers, A. D., Gray, A. G., et al. 2009, AJS, 180, 67 [Google Scholar]
- Ross, N. P., Myers, A. D., Sheldon, E. S., et al. 2012, ApJS, 199, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., McGreer, I. D., White, M., et al. 2013, ApJ, submitted [arXiv:1210.6389] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D., White, M., & Eisenstein, D., Astro2010, The Astronomy and Astrophysics Decadal Survey, Science White Papers 314 [arXiv:0902.4680] [Google Scholar]
- Schmidt, M., & Green, R. F. 1983, ApJ, 269, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, K. B., Marshall, P. J., Rix, Hans-Walter, et al. 2010, ApJ, 714, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Siana, B., Polletta, M., Smith, H. E., et al. 2008, ApJ, 675, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Smee, S., James, E. G., Alan U., et al. 2012, AJ [arXiv:1208.2233] [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., et al. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., & Prochaska, J. X. 2011, ApJ, 728, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Yèche, Ch., Petitjean, P., Rich, J., et al. 2010, A&A, 523, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Tiling completeness correction for BOSS (unique priority level) and the MMT (priorities A through D).
Cross-identification between BOSS and MMT spectra for the 344 targets with g > 22 that were observed by both telescopes.
Cross-identification between BOSS and MMT spectra for the 68 targets with 22 < g < 22.5 that were observed by both telescopes.
Number counts (quasars per deg2) for several ranges in extinction-corrected magnitude gdered and redshift z.
Efficiency-corrected number counts for the BOSS and MMT samples (including, in both cases, the BOSS standard QSOs that were selected but not re-observed) over the magnitude range 22 < g < 22.5 accessible to both samples.
Predicted number of quasars over 15.5 < g < 25 and 0 < z < 6 for a survey covering 10 000 deg2, based on our best-fit luminosity function.
All Figures
 |
Fig. 1 Output of the variability Neural Network as a function of g magnitude for a sample of known stars (small black dots near yNN = 0) and for known quasars (larger red dots at yNN ~ 1). BOSS targets and the MMT point-source targets are required to pass the criterion yNN > 0.5. |
| In the text | |
 |
Fig. 2 Locus of stars (upper blue contours), z < 2.2 quasars (lower left green contours) and z > 2.2 quasars (lower right red contours) in the c3 vs. c1 color–color plane. The upper solid line corresponds to the color cut c3 < 1.0 − c1/3 (loose, for point sources) and the lower dashed line to c3 < 0.6 − c1/3 (strict, for extended sources). |
| In the text | |
 |
Fig. 3 Footprint of the BOSS half-plates (black contours) and of the MMT fields (filled red disks) dedicated to the present study. BOSS plates were attributed the numbers 5141 to 5147 from left to right. MMT fields were labeled 0 to 5 with increasing Right Ascension. |
| In the text | |
 |
Fig. 4 Fraction of known quasars identified as point-like in co-added images, as a function of magnitude, for several bins in redshift (rising redshift from bottom to top). The asymptotic red histogram is the fraction of stars that are identified as point-like. |
| In the text | |
 |
Fig. 5 Magnitude dependence of the contributions to the total completeness correction for the different samples. Upper left: the new quasars identified in the BOSS sample. Upper right: the known quasars that were intentionally removed from the target lists. Lower left (resp. right): the quasars identified in the MMT sample and that appeared point-like (resp. extended) in the coadded SDSS frame. These corrections are computed from all quasars contained in either sample. |
| In the text | |
 |
Fig. 6 Distributions in redshift (top plot) and extinction-corrected magnitude (bottom plot) for the sample of quasars from previous quasar surveys covering Stripe 82. |
| In the text | |
 |
Fig. 7 Selection completeness ϵsel BOSS(g, z) for the quasars in the BOSS program. The significant drop at low redshift is due to the fact that many quasars with z < 1 appear as extended sources in coadded frames and were thus not considered in the initial source list. We also observe the expected efficiency drop at faint magnitudes. Bins left unfilled (white) are bereft of quasars. |
| In the text | |
 |
Fig. 8 Fraction of inconclusive spectra (declared so after visual inspection) as a function of observed g magnitude. The curves are fits to the data. In our analysis, we use the upper blue curve to correct for the total fraction of inconclusive spectra. |
| In the text | |
 |
Fig. 9 Quasar number counts per deg2 as a function of observed g magnitude (top) and redshift (bottom). The black (resp. red) line is for quasars measured by BOSS (resp. MMT). The BOSS histograms include the already identified quasars in the area that were removed from the target list. |
| In the text | |
 |
Fig. 10 Quasar number counts per deg2 as a function of redshift (Δz = 0.2). Blue is for the new sample of quasars identified with our BOSS deep program, green for the previously known BOSS sample, red is for the MMT sample and black for the total. The blue, green and red curves use mutually exclusive samples and correspond to the zones defined in Sect. 4.3. |
| In the text | |
 |
Fig. 11 Comparison of the number of “extended” quasars estimated from BOSS data and completeness corrections (blue curve) or observed in the MMT sample (purple points). |
| In the text | |
 |
Fig. 12 K-corrections as a function of redshift. The spread illustrates the variation over the luminosity range of the quasars in our sample. The red curve shows for comparison the parameterization K(z) = −2.5(1 + να)log 10(1 + z) introduced in C09, with να = −0.5 and normalized to z = 2. |
| In the text | |
 |
Fig. 13 Quasar luminosity function measurements (black circles) compared to the C09 data (blue open circles at 0.68 < z < 2.6). The blue dashed curve is the LF of C09 and the best-fit model of this analysis is shown as the red curve. The green curves are best fits to COSMOS data (Masters et al. 2012) at z ~ 3.2 (plain curve) and z ~ 4.0 (dashed curve). The cyan line is the best fit, with fixed-α, to binned LF data from SWIRE and SDSS at z ~ 3.2 (Siana et al. 2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


