| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 3 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201220150 | |
| Published online | 22 February 2013 | |
Research Note
Coronal ejection and heating in variable X-ray sources
Nicolaus Copernicus Astronomical Center, ul. Bartycka 18,
00-716
Warszawa,
Poland
e-mail:
wlodek@camk.edu.pl
Received:
1
August
2012
Accepted:
16
December
2012
A sudden increase in stellar luminosity may lead to the ejection of a large part of any optically thin gas orbiting the star. Test particles in circular orbits will become unbound and will escape to infinity (if radiation drag is neglected) when the luminosity changes from zero to at least one half the Eddington value, or more generally, from L to (LEdd + L)/2 or more. Conversely, a decrease in luminosity will lead to the tightening of orbits of optically thin fluid. Even a modest fluctuation of luminosity of accreting neutron stars or black holes is expected to lead to substantial coronal heating. Luminosity fluctuations may thus account for the high temperatures of the X-ray corona in accreting black hole and neutron star systems.
Key words: accretion, accretion disks / scattering / X-rays: binaries / stars: winds, outflows / stars: neutron
© ESO, 2013
1. Introduction
Low mass X-ray binaries (LMXBs) are bright X-ray sources whose luminosity is thought to be powered by accretion from a binary companion onto a neutron star or a black hole. Typically, each source can be found in one of two or more distinct spectral states, some of which include a hard X-ray power-law component interpeted as radiation from a hot (~102 keV) corona above the accretion disk (e.g., Done et al. 2007). Each state has an associated characteristic variability on many timescales. Nearly all sources exhibit quasi-random excursions of luminosity. In this paper, I examine some of the consequences of rapid variations of luminosity, particularly for optically thin Keplerian flow which I identify with the X-ray corona.
Since the paper of 3 it is understood that high luminosity of an accreting neutron star will be associated with removal of angular momentum from the optically thin flow via the Poynting-Robertson drag. Many workers seem to assume that the primary effect of high luminosity is to bring matter down from its nearly-circular orbits towards the inner parts of the accretion disk and perhaps even onto the stellar surface. This is indeed true for optically thin flow in a steady radiation field. However, a rapid change in luminosity may have the opposite effect and, as I show below in a Newtonian calculation, under certain conditions may lead to ejection of the optically thin matter.
An even more important effect will occur when the luminosity undergoes a small but rapid change. The optically thin fluid will then continue its orbital motion in very nearly the same circular orbits, but will undergo strong heating caused by dissipation of excess kinetic energy. This may explain the presence of hot X-ray coronae in some spectral states of LMXBs.
The system under consideration is a standard thin accretion disk. The term “corona” is meant to signify the optically thin plasma “above the surface” of the disk. It is assumed that the dissipative processes responsible for angular momentum transport within the disk, and hence for accretion, occur in the optically thick regions “below the surface” of the disk. It is recognized that in some sources the optically thin plasma is much hotter than the body of the disk: spectral fits to the observed X-rays require the presence of a power-law component in addition to the multi-color thermal disk emission. The presence of such a hot corona is usually explained by magnetic heating, by analogy with the solar corona. However, I will not invoke the presence of magnetic fields to heat the corona. Instead, the heating will be related to the changes in luminosity that are assumed to occur, as observed in numerous X-ray binaries.
2. Luminosity effects
Consider orbits in the spherically symmetric Newtonian potential of a non-rotating star of
mass M. If the star is radiating isotropically, optically thin hydrogen
plasma suffers radiation pressure forces proportional to the Thomson cross-section and the
radiative flux. At Eddington luminosity LEdd, the radiative
force balances gravity exactly. At lower luminosity, the presence of radiation pressure is
equivalent to a proportional reduction of the gravitational mass by irradiation, so that the
potential may be taken to be
V(r) = −GM(1 − λ)/r,
with
λ ≡ L/LEdd.
Hence, the eccentricity of a test-particle orbit is 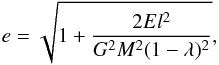 (1)where E
and l are the specific (per unit mass) energy and angular momentum of the
orbiting particle. The specific kinetic energy in circular orbit at
r0 for a source with luminosity L and true
gravitational mass M is
(1)where E
and l are the specific (per unit mass) energy and angular momentum of the
orbiting particle. The specific kinetic energy in circular orbit at
r0 for a source with luminosity L and true
gravitational mass M is
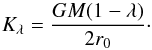 (2)Upon an impulsive change of
stellar luminosity from zero to L, a particle that has been traveling in
circular orbit at r0 would conserve its kinetic energy and
angular momentum so that its new orbit would be described by the following specific energy
and angular momentum
(2)Upon an impulsive change of
stellar luminosity from zero to L, a particle that has been traveling in
circular orbit at r0 would conserve its kinetic energy and
angular momentum so that its new orbit would be described by the following specific energy
and angular momentum 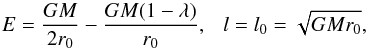 (3)and because of the mismatch
between energy and angular momentum values this orbit would no longer be circular. The
eccentricity of the orbit would be, from Eq. (1),
(3)and because of the mismatch
between energy and angular momentum values this orbit would no longer be circular. The
eccentricity of the orbit would be, from Eq. (1), 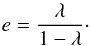 (4)In particular,
λ ≥ 1/2 ⇒ e ≥ 1, i.e., if the
luminosity is now one half of the Eddington value, or greater, the particle is in an unbound
orbit. If, on the other hand, the increase was from zero to less than one half of the
Eddington luminosity,
λ < 1/2 ⇒ e < 1,
the particle remains in a bound elliptic orbit with an increased semi-major axis
a = r0(1−λ)/(1−2λ).
(4)In particular,
λ ≥ 1/2 ⇒ e ≥ 1, i.e., if the
luminosity is now one half of the Eddington value, or greater, the particle is in an unbound
orbit. If, on the other hand, the increase was from zero to less than one half of the
Eddington luminosity,
λ < 1/2 ⇒ e < 1,
the particle remains in a bound elliptic orbit with an increased semi-major axis
a = r0(1−λ)/(1−2λ).
3. Coronal ejection
In reality, the fluctuations of luminosity in LMXBs do not occur between
L = 0 and L ≠ 0, but rather between some initial
L1 ≠ 0 and some final value L ≠ 0.
Generalizing the derivation from the previous section, we start with circular orbits at
luminosity L1, with
λ1 ≡ L1/LEdd,
the specific kinetic energy and angular momentum in circular orbits in the optically thin
region being given by 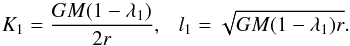 (5)Following an impulsive
change of luminosity to L, the new orbits are defined by a new potential
and the same values of kinetic energy and angular momentum
(5)Following an impulsive
change of luminosity to L, the new orbits are defined by a new potential
and the same values of kinetic energy and angular momentum
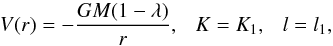 (6)where, as before,
λ ≡ L/LEdd.
The eccentricity of the new orbits is
(6)where, as before,
λ ≡ L/LEdd.
The eccentricity of the new orbits is
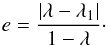 (7)The condition for an
unbound trajectory (e ≥ 1) now becomes
(7)The condition for an
unbound trajectory (e ≥ 1) now becomes
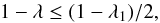 (8)i.e.,
(8)i.e.,
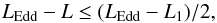 (9)or
(9)or  (10)So far, we have been
considering test particles. However, the condition applies also to optically thin plasma.
Since the wavefront of increased radiative flux travels at the speed of light, all elements
of the plasma become unbound before any collisons on the outbound trajectories take place.
The hot coronal plasma is assumed to be radiatively inefficient so any rarefaction or
compression waves in an unbound medium cannot bind the bulk of it to the star (the total
energy of the plasma is positive).
(10)So far, we have been
considering test particles. However, the condition applies also to optically thin plasma.
Since the wavefront of increased radiative flux travels at the speed of light, all elements
of the plasma become unbound before any collisons on the outbound trajectories take place.
The hot coronal plasma is assumed to be radiatively inefficient so any rarefaction or
compression waves in an unbound medium cannot bind the bulk of it to the star (the total
energy of the plasma is positive).
Identifying the corona with the optically thin region, the condition for its ejection would then be that the luminosity reduces its distance to the Eddington value by at least a factor of two. Clearly, the closer the initial value L1 is to LEdd, the lower the fractional value of luminosity increase needs to be for the corona to be ejected; e.g., an increase from 0.8LEdd to 0.9LEdd (corresponding to a fluctuation of less than 13%) is sufficient to clear out the corona.
4. Coronal heating
Now we turn to changes of luminosity that do not lead to coronal ejection. This could be
because the luminosity has increased from L1 by less than
(LEdd − L1)/2,
thus violating Condition 10, or because the
luminosity has decreased. In any case, the new test particle orbit is an ellipse with
semi-major axis r0(1 − λ)/
|1 + λ1 − 2λ | in the notation of the
previous sections. The periastron is at radius r0 for
λ > λ1 and at
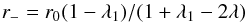 (11)for
λ < λ1. For a small
decrease of luminosity, the latter value becomes
r− ≈ r0 [1−2(λ1 − λ)/(1 − λ1)].
(11)for
λ < λ1. For a small
decrease of luminosity, the latter value becomes
r− ≈ r0 [1−2(λ1 − λ)/(1 − λ1)].
Naturally, the state of the corona cannot be described by test particle orbits, as those of different particles would intersect. It is clear that some energy will be dissipated and the fluid orbits will circularize. The ultimate outcome is difficult to predict, because redistribution of angular momentum may occur. However, it seems clear that the dissipated energy will be on the order of (λ1 − λ)2 times the virial energy of the corona.
Consider the evolution of a geometrically thin annulus initially orbiting at
r0, under a small impulsive change of luminosity of the
central star
| δλ| ≡ |λ − λ1| ≪ 1,
and a subsequent dissipation of energy. If the annulus conserves its angular momentum, it
will settle down in a circular orbit at
r1 = r0(1−λ1)/(1−λ)
after dissipating an amount of specific energy equal to
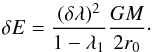 (12)
(12)
5. Discussion
The observed accreting neutron stars and black holes are usually quite luminous and are typically variable in time. It seems important to explore the consequences of rapid changes of luminosity whose magnitude may be a large fraction of the Eddington value.
The relevance of Poynting-Robertson drag to neutron stars was first pointed out by 3. While there is no doubt that high luminosity is accompanied by radiation drag, which at least in the optically thin regime in a steady source will eventually remove kinetic energy and angular momentum of orbiting matter, this process takes time. If the luminosity undergoes a rapid change, the first and immediate response of orbiting matter is to change its trajectory.
I have assumed that the luminosity changes are either caused by changes in the mass-accretion flux that are unrelated to the state of the corona, or by a change of the state of the star, e.g., an X-ray burst. The opposite case, when the luminosity changes reflect accretion of the optically thin fluid, could correspond to oscillatory behavior and has been considered by 4.
By considering Newtonian orbital mechanics, I have shown that an impulsive increase of central luminosity of sufficiently high magnitude L − L1 > (LEdd − L1)/2 may lead to an ejection of the optically thin corona on a dynamical timescale. This may have an application to X-ray spectral-state changes of black holes and neutron stars (e.g., Fender et al. 2005), and may be of some importance in X-ray bursts. Inclusion of radiation drag requires numerical computations, and will be postponed until another paper, where a fully general relativistic discussion will be presented (Stahl et al., in prep.).
The coronal response to small changes in luminosity was considered in Sect. 4. It seems inevitable that relatively minor changes in the luminosity of the central source lead to substantial energy dissipation. This could be the as yet unexplained mechanism of coronal heating. The estimated magnitude of the effect is surprisingly large. The dissipated energy at 50 Schwarzschild radii caused by a single excursion in luminosity of 10% Eddington (0.1LEdd) is on the order of 10-4 of the coronal rest mass, i.e., it corresponds to a temperature of ~100 keV. At 5 Schwarzschild radii the same result will be obtained by a fluctuation of only 3% Eddington luminosity.
In passing, we note that for a steady source of luminosity λ in Eddington
units, the orbital frequency in the optically thin regime is modified by a factor of
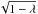 .
Care must be taken to
.
Care must be taken to
account for this effect when interpreting the redshift/blueshift of any spectral features in terms of orbital motion.
Acknowledgments
The anonymous referee is thanked for helpful comments that allowed a clarification of certain points.
References
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fender, R., Belloni, T., & Gallo, E. 2005, Ap&SS, 300, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. A., & Mészáros, P. 1989, ApJ, 346, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Wielgus, M., Stahl, A., Abramowicz, M., & Kluźniak, W. 2012, A&A, 545, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


