EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 551 (March 2013) A&A, 551 (2013) A124 Full HTML
Free Access
Issue
A&A
Volume 551, March 2013
Article Number A124
Number of page(s) 11
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201220023
Published online 05 March 2013

© ESO, 2013

1. Introduction

The first gamma-ray burst (GRB) spectra were obtained by the gamma and X-ray spectrometers on board the IMP-6 satellite and the Apollo 16 spacecraft (Cline et al. 1973; Metzger et al. 1974). These early observations were complemented by the large sample of 143 spectra collected by the Konus experiments on the Venera probes from 1978 to 1980 (Mazets et al. 1981). It was shown that these spectra could be fitted by a power law with an exponential cutoff or a broken power law (Cline & Desai 1975), and various physical processes were invoked to explain this shape, such as optically-thin thermal bremsstrahlung (Gilman et al. 1980), Compton scattering of soft photons by non-thermal electrons (Zdziarski & Lamb 1986) or synchrotron emission by thermal or non-thermal electrons (Brainerd & Lamb 1987). Following the launch of the Compton Gamma-Ray Observatory, the Burst and Transient Source Experiment (BATSE) provided the first solid indications that GRBs were located at cosmological distances and confirmed the broken power law shape of the spectra that was represented by the phenomenological Band function (Band et al. 1993). Possible cyclotron or annihilation lines found by previous experiments were not seen by BATSE.

In the context of the cosmological models that were developed hereafter, the spectra were generally interpreted in terms of synchrotron emission from shock accelerated electrons (see e.g. Piran 1999) and therefore believed to be mostly non-thermal. The possibility that a thermal contribution could also be present was, however, considered by Mészáros et al. (2002), and was supported by several observational indications. The first one came from the very hard low-energy spectral slopes that are found in some BATSE bursts during at least part of the evolution (Preece et al. 1998; Ghirlanda et al. 2003). While the commonly observed value of the low-energy spectral index is α ~ −1, it reaches 0.5 to 1 in these events, suggesting the presence of a Rayleigh-Jeans contribution. Then Ryde (2004, 2005) proposed to fit all GRB spectra in the BATSE range with the combination of a thermal and a power law component. Using a time resolved analysis, he showed that during a pulse the temperature first stays approximately constant before decaying as a power law of temporal index close to −2/3.

In the previous examples the identified thermal component represented a major contribution responsible for the peak of the E2N(E) spectrum. A different result was obtained by Guiriec et al. (2011) who found a sub-dominant thermal component in the Fermi-Gamma-ray Burst Monitor (GBM) spectrum of GRB 100724B, accounting for a few percents of the energy released by the burst. The evolution of the temperature was not correlated to the peak energy of the non-thermal component, fitted by a Band function. Similar results have been found in other bright GBM bursts, such as GRB 110721A (Ryde et al. 2012), GRB 081207, and GRB 110920 (McGlynn et al. 2012). This improved characterisation of thermal components in the prompt emission of GRBs is allowed by the larger spectral coverage of GBM (8 keV–40 MeV) compared to BATSE (20 keV–2 MeV), leading to a better quality of the spectral fits.

On the theoretical side, a thermal emission originating from the photosphere is a natural prediction of most models based on the generic fireball scenario (Paczynski 1986; Goodman 1986; Shemi & Piran 1990; Mészáros et al. 1993). Moreover, if the acceleration of the outflow has a thermal origin (as would be the case if it was powered at its basis by neutrino-antineutrino annihilation), this photospheric emission would be very bright, outshining the non-thermal emission produced by internal shocks in the 100 keV–1 MeV spectral range (Daigne & Mochkovitch 2002). One is therefore faced with the following alternative: either most of the emission we observe is indeed this thermal component, but it has been Comptonised to produce a power law tail in the spectrum at high energy (see e.g. Thompson 1994; Rees & Mészáros 2005; Giannios & Spruit 2007; Beloborodov 2010) and complemented at low energy by additional processes (e.g. Pe’er et al. 2006; Vurm et al. 2011), or the acceleration has a magnetic origin (see e.g. Begelman & Li 1994; Daigne & Drenkhahn 2002; Vlahakis & Königl 2003; Komissarov et al. 2009; Tchekhovskoy et al. 2010; Komissarov et al. 2010; Granot et al. 2011) and the fraction ϵth of thermal energy in the flow is much smaller than unity.

In this work we explore the consequences of this second possibility. We self-consistently compute the photospheric thermal emission and the non-thermal emission from internal shocks. If the internal dissipation is dominated by magnetic reconnection rather than internal shocks, we get the non-thermal spectrum in a very simple parametrised way. We discuss the conditions for the thermal emission to show up or, on the contrary, to be hidden. The paper is organised as follows: in Sect. 2 we describe the geometry and thermodynamics of the flow and explain our method to compute the photospheric and non-thermal emissions; our results are presented in Sect. 3 and discussed in Sect. 4. Finally, Sect. 5 is the conclusion.

2. Model description

2.1. Geometry and thermodynamics of the flow

We consider a schematic model where the flow that emerges from the central engine is accelerated by the conversion of thermal and/or magnetic energy to kinetic energy. We do not specify the initial geometry of the flow (which can be largely governed by magnetic forces), but we assume that beyond a radius Rsph it becomes spherically symmetric within a cone of half opening angle θ. We also define the radius Rsat, where the acceleration is essentially complete and suppose that Rsph < Rsat. The total injected power in the flow is Ė, with a fraction ϵth in thermal form. 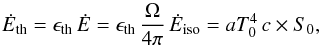The temperature T0 at the origin of the flow can then be obtained from Ėth=ϵth Ė=ϵth Ω4π Ėiso=aT04 c×S0,\begin{equation} \label{eqn_eth} {\dot E}_{\rm th}=\epsilon_{\rm th}\,{\dot E}=\epsilon_{\rm th}\,{\Omega\over 4\pi}\,{\dot E}_{\rm iso} =a T_0^4\,c\times S_0 , \end{equation}(1)where Ėiso and S0 = πℓ2 are, respectively, the isotropic injected power and the section of the flow at the origin (see Fig. 1). 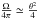The fraction of solid angle is Ω4π≃θ24\hbox{${\Omega\over 4\pi}\simeq {\theta^2\over 4}$} (we count only one jet to be consistent with the definition of S0) and a is the radiation constant. 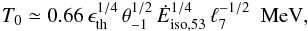We finally get T0≃0.66 ϵth1/4 θ-11/2 Ėiso,531/4 ℓ7−1/2MeV,\begin{equation} \label{eqn_t0} T_0\simeq 0.66\,\epsilon_{\rm th}^{1/4}\,\theta_{-1}^{1/2}\,{\dot E}_{{\rm iso},53}^{1/4}\,{\ell}_7^{-1/2}\ \ {\rm MeV} , \end{equation}(2)with the opening angle, injected power, and radius of the jet in units of 0.1 rad, 1053 erg s-1, and 107 cm, respectively.

We obtain the flow equations assuming that no dissipation takes place below the photosphere (so that the emerging spectrum at transparency will be thermal only). Mass and entropy conservation then lead to βΓ ρ S=Cst,Tρ1/3=Cst,\begin{eqnarray} \label{eqn_cons_mass} \beta \Gamma\,\rho\,S=Cst ,\\ \label{eqn_adia} {T\over \rho^{1/3}}=Cst , \end{eqnarray}where ρ is the comoving density, S the surface perpendicular to the flow, β = v/c, and Γ = (1 − β2)−1/2. From Eqs. 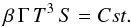(3), (4) we get β Γ T3 S=Cst.\begin{equation} \label{eqn_adia_mass} \beta \,\Gamma\,T^3\,S=Cst . \end{equation}(5)Using Eq. (5) we can obtain the temperature at any radius R > Rsph even if we ignore the details of the geometry from the basis of the flow up to Rsph. 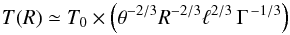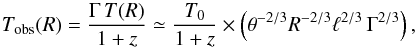With S(R) = π   θ2   R2 and assuming that β ~ 1 already close to the origin we have T(R)≃T0×(θ−2/3R−2/3ℓ2/3 Γ −1/3)\begin{equation} T(R)\simeq T_0\times \left(\theta^{-2/3}R^{-2/3}{\ell}^{2/3}\,\Gamma^{\,-1/3}\right) \end{equation}(6)so that, in the observer frame Tobs(R)=Γ T(R)1+z≃T01+z×(θ−2/3R−2/3ℓ2/3 Γ2/3),\begin{equation} \label{eqn_tobs} T_{\rm obs}(R)={\Gamma\,T(R)\over 1+z}\simeq {T_0\over 1+z}\times \left(\theta^{-2/3}R^{-2/3}{\ell}^{2/3}\,\Gamma^{2/3}\right) , \end{equation}(7)where z is the burst redshift.

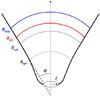thumbnail Fig. 1

Schematic view of the problem geometry. The flow emerges from the central engine through a “circular opening” of radius ℓ. Beyond a radius Rsph it expands radially within a cone of half opening θ. The acceleration is completed at Rsat. The photosphere is located at Rph and dissipation of kinetic and/or magnetic energy takes place at Rdiss.

At the photospheric radius Rph (supposed to lie beyond Rsph) the thermal luminosity is given by 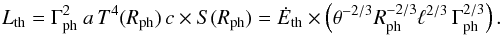Lth=Γph2a T4(Rph) c×S(Rph)=Ėth×(θ−2/3Rph−2/3ℓ2/3 Γph2/3).\begin{equation} \label{eqn_lth} L_{\rm th}=\Gamma_{\rm ph}^2\ a\,T^4(R_{\rm ph})\,c\times S(R_{\rm ph})={\dot E}_{\rm th}\times \left(\theta^{-2/3}R_{\rm ph}^{-2/3}{\ell}^{2/3}\,\Gamma_{\rm ph}^{2/3}\right) . \end{equation}(8)Equations (7) and (8) correspond to the usual scaling of the fireball scenario (Mészáros & Rees 2000; Mészáros et al. 2002; Daigne & Mochkovitch 2002) with, however, a modified normalisation that takes into account both the geometry and the mixed energy content of the outflow. Conversely, including sub-photospheric dissipation as in Giannios (2012) would change the scaling.

To estimate the photospheric radius we assume that most of the acceleration is completed at Rph1. This is, for example, the case in the simulations made by Tchekhovskoy et al. (2010), where the Lorentz factor sharply increases beyond the stellar radius, when the flow suddenly becomes unconfined. Then, in a first approximation, the photospheric radius of a given shell writes (e.g. Piran 1999; Mészáros & Rees 2000; Daigne & Mochkovitch 2002) 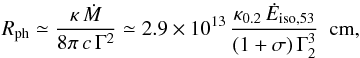Rph≃κ Ṁ8π c Γ2≃2.9×1013 κ0.2 Ėiso,53(1+σ) Γ23cm,\begin{equation} \label{eqn_rph} R_{\rm ph} \simeq {\kappa\,{\dot M}\over 8\pi\,c\,\Gamma^2} \simeq 2.9 \times10^{13}\,{\kappa_{0.2}\,{\dot E}_{\rm iso,53}\over (1+\sigma)\,\Gamma_2^3}\ \ {\rm cm} , \end{equation}(9)where κ (κ0.2 in units of 0.2 cm2 g-1) is the material opacity and Γ (Γ2 in units of 100) the Lorentz factor of the shell. The flow keeps a magnetisation σ at the end of acceleration so that Ė/(1 + σ) is the injected kinetic power ĖK. In the case of a passive magnetic field that is carried by the outflow without contributing to its acceleration (Spruit et al. 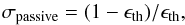2001), the magnetisation σ equals σpassive=(1−ϵth)/ϵth,\begin{equation} \sigma_{\rm passive} = (1-\epsilon_{\rm th})/\epsilon_{\rm th} , \label{eq:signa_passive} \end{equation}(10)corresponding to a pure and complete thermal acceleration. Efficient magnetic acceleration leads to σ < σpassive, whereas σ > σpassive corresponds to an inefficient magnetic acceleration, for instance with no conversion of magnetic into kinetic energy and some conversion of thermal into magnetic energy.

When the shell reaches the photospheric radius, it releases its thermal energy content while a fraction of the remaining energy (kinetic or magnetic) can be dissipated farther away at a radius Rdiss by internal shocks for σ ≲ 0.1−1, or reconnection for higher magnetisation, contributing to the non-thermal emission of the burst. It is therefore expected, on theoretical grounds, that thermal and non-thermal components both contribute to the observed emission (Mészáros et al. 2002; Daigne & Mochkovitch 2002). As mentioned in the introduction, this was already supported by BATSE results, with new evidence now coming from Fermi (Guiriec et al. 2011; Zhang et al. 2011). In Sect. 3 we present synthetic bursts showing both contributions. We explain below our method to compute the thermal and non-thermal emission.

2.2. Thermal emission

The thermal emission can be computed from Eqs. (1), (2), (7), (8), and (9), for a given set of central engine parameters ϵth, σ, ℓ, θ, Ėiso, and a distribution of the Lorentz factor in the flow. Both the thermal luminosity and observed temperature are related to the injected power and temperature at the origin of the flow via the same factor 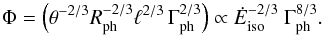Φ=(θ−2/3Rph−2/3ℓ2/3 Γph2/3)∝Ėiso−2/3Γph8/3.\begin{equation} \label{eqn_phi} \Phi=\left(\theta^{-2/3}R_{\rm ph}^{-2/3}{\ell}^{2/3}\,\Gamma_{\rm ph}^{2/3}\right)\propto {\dot E_{\rm iso}}^{-2/3}\ \Gamma_{\rm ph}^{8/3} . \end{equation}(11)If a constant Ėiso is assumed, the luminosity and temperature directly trace the distribution of the Lorentz factor Γ(s), where the Lagrangian coordinate s is the distance to the front of the flow at the end of the acceleration stage (s/c is the ejection time of the shell). The expanding flow becomes progressively transparent (starting from the front) and the contribution of a shell located at s is approximately received at an observer time tobs = (1 + z)s/c (Daigne & Mochkovitch 2002). 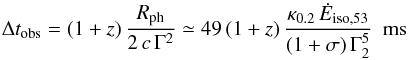However, since the different parts of the flow do not become transparent at the same radius (because Rph ∝ Γ-3), additional differences in arrival time of the order of Δtobs=(1+z) Rph2 c Γ2≃49 (1+z) κ0.2 Ėiso,53(1+σ) Γ25ms\begin{equation} \label{dtobs_ph} \Delta t_{\rm obs}=(1+z)\,{R_{\rm ph}\over 2\,c\,\Gamma^2}\simeq 49\,(1+z)\,{\kappa_{0.2}\,{\dot E}_{{\rm iso},53}\over (1+\sigma)\,\Gamma_2^5}\ \ {\rm ms} \end{equation}(12)should be included. They are, however, negligible as long as Δtobs < tvar, the typical variability time scale of the Lorentz factor.

The value of Δtobs also gives the time scale of the luminosity decline after the last shell of the flow (emitted by the source at a time τ) has reached the transparency radius (high-latitude emission). Unless the Lorentz factor of this shell is small or the burst has a very short duration, the drop in luminosity for tobs > (1 + z)τ is very steep, having initially a temporal decay index (see e.g. Sect. 6 in Beloborodov 2011) 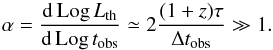α=d Log Lthd Log tobs≃2(1+z)τΔtobs≫1.\begin{equation} \alpha={{\rm d}\,{\rm Log}\,L_{\rm th}\over {\rm d}\,{\rm Log}\,t_{\rm obs}}\simeq 2{(1+z)\tau \over \Delta t_{\rm obs}}\gg 1 . \end{equation}(13)This shows that in models where the prompt emission comes from a Comptonised photosphere, the early decay of index α ~ 3−5 observed in X-rays cannot be explained by the high latitude emission and should instead be related to an effective decline of the central engine (Hascoët et al. 2012).

The expected count rate in a given spectral range and the resulting spectrum are obtained from the luminosity and temperature evolution (Eqs. (7) and (8)). However, we do not use a true Planck function for the elementary spectrum corresponding to a given temperature. As discussed in Goodman (1986) and Beloborodov (2010), geometrical effects at the photosphere lead to a low-energy spectral index close to α =  +0.4 instead of α =  +1 for a Raleigh-Jeans spectrum (see also Pe’er 2008). We therefore adopt a “modified Planck function” having the modified spectral slope at low energy, an exponential cutoff at high energy, peaking at ≃3.9 × kT as a Planck function in νFν, and carrying the same total energy.

2.3. Non-thermal emission

We first estimate the non-thermal emission assuming that it comes from internal shocks (Rees & Meszaros 1994). For a given distribution of the Lorentz factor, we obtain light curves and spectra using the simplified model of Daigne & Mochkovitch (1998), where the outflow is represented by a large number of shells that interact by direct collisions only (see also Kobayashi et al. 1997). The elementary spectrum for each collision is a broken power law with the break at the synchrotron energy. The adopted values for the two spectral indices at low and high energy respectively are α = −1 and β = −2.25. The expected value for α in the fast cooling regime should normally be −1.5 (see e.g. Sari et al. 1998; Ghisellini et al. 2000), but detailed radiative models including inverse Compton scattering in Klein-Nishina regime tend to produce harder α slopes (Derishev et al. 2001; Bošnjak et al. 2009; Nakar et al. 2009; Daigne et al. 2011), close to the typical observed value α ≃ −1 (Preece et al. 2000; Kaneko et al. 2006; Nava et al. 2011; Goldstein et al. 2012). The global efficiency of internal shocks is given by the product 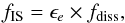fIS=ϵe×fdiss,\begin{equation} \label{eqn_efficiency_is} f_{\rm IS}=\epsilon_e\times f_{\rm diss} , \end{equation}(14)where fdiss is the efficiency for the dissipation of energy in shocks and ϵe the fraction of the dissipated energy transferred to electrons and eventually radiated. Typical values of fIS do not exceed a few percents. We used this approach to compute non-thermal light curves and spectra in Sect. 3.1 for the case of a low magnetisation σ ≲ 0.1−1.

The presence of magnetic fields reduces shock efficiency and may even prevent shock formation for σ ≳ 1 (Mimica & Aloy 2010; Narayan et al. 2011). Then for σ ≳ 1, the magnetic field cannot be ignored, and energy must be extracted by magnetic reconnection (e.g. Thompson 1994; Spruit et al. 2001), possibly triggered by internal shocks (Zhang & Yan 2011). Our limited understanding of the relevant processes does not allow a reliable description of the resulting emission. Considering these difficulties, we have adopted in Sect. 3.2 a very basic and simple point of view. We do not try to predict the burst profile and obtain the spectrum in the following way: we suppose that a fraction f  Nth of the total injected energy eventually goes into non-thermal emission with a spectrum represented by a Band function with low- and high-energy spectral indices α = −1 and β = −2.25, and a peak energy obtained from the Amati relation (Amati et al. 2002) Ep≃130 [f Nth Eiso1052erg]0.55keV,\begin{equation} \label{eqn_amati} E_{\rm p}\simeq 130\,\left[f_{\rm \,Nth}\,{E}_{\rm iso}\over 10^{52}\ {\rm erg}\right]^{0.55}\ \ {\rm keV} , \end{equation}(15)where the exponent and normalisation values are taken from Nava et al. (2012). The validity of the Amati relation is strongly debated (see e.g. Nakar & Piran 2005; Band & Preece 2005; Kocevski 2012; Collazzi et al. 2012; Ghirlanda et al. 2012). It is not clear if it corresponds to an intrinsic property of GRBs or if the relation results from a complex chain of selection effects (threshold for burst detection, and various conditions for the measure of the redshift and peak energy). For the purpose of the present study we do not address this issue and use Eq. (15) simply because it is approximately satisfied by the sample of long bursts for which the peak energy and isotropic radiated energy have been measured.

thumbnail Fig. 2

Thermal and non-thermal emission from a variable outflow – internal shock framework. Top left: initial distribution of the Lorentz factor in the flow. Top right: thermal (red), non-thermal (blue), and total (black) photon flux in the 8 keV–40 MeV spectral range. Bottom left: thermal (red), non-thermal (blue), and total (black) time-integrated spectra. Bottom right: instant temperature (red) of the photospheric emission and instant peak energy (blue) of the internal shock emission. The dotted and dashed lines correspond to the temperature and peak energy averaged over time intervals of 2 and 4 s, respectively. The adopted flow parameters are Ėiso = 1053 erg s-1, ϵth = 0.03, σ = 0.1, ℓ = 3 × 106 cm, and θ = 0.1 rad; a redshift z = 1 is assumed.

thumbnail Fig. 3

Thermal and non-thermal emission from a variable outflow – internal shock framework: impact of the outflow parameters. Starting from the reference case shown in Fig. 2 (with a redshift z = 1) we first change the thermal fraction ϵth to 0.3 (top left panel) and 0.003 (bottom left); then the isotropic power Ėiso to 1054  erg  s-1 (top middle) and 1052  erg  s-1 (bottom middle); and finally the Lorentz factor is multiplied (top right) and divided (bottom right) by a factor of 2. Each time we vary a parameter, all the others keep the value corresponding to the reference case.

3. Results

3.1. Non-thermal emission from internal shocks

To study the relative intensities of the thermal and non-thermal emission components we have considered as an example a flow ejected by a central source active for a duration stot/c = 10 s, where the Lorentz factor takes the form Γ(s)=333{1+23cos[5 π(1−sstot)] }×exp(−s2stot)·\begin{equation} \label{eqn_gp_complex} \Gamma(s)=333 \left\lbrace 1+\frac{2}{3} \ {\rm cos}\left[5\,\pi \left( 1-{s\over s_{\rm tot}}\right)\right]\,\right\rbrace\times \exp{\left(-{s\over 2 s_{\rm tot}}\right)} \cdot \end{equation}(16)This distribution is arbitrary (see other possible examples in Daigne & Mochkovitch 1998) and was adopted simply to produce a burst made of three pulses, i.e. not too simple and not too complex. It is is shown in Fig. 2 (top left panel) together with the non-thermal light curve (between 8 keV and 40 MeV; top right panel) resulting from internal shocks. The related photospheric emission is shown in the same energy range for ϵth = 0.03. We adopt a constant Ėiso = 1053 erg s-1, σ = 0.1, ℓ = 3 × 106 cm and θ = 0.1 rad (i.e. l/θ = 300 km). We also represent in the bottom left and bottom right panels the spectrum (thermal, non-thermal, and global) and the temporal evolution of the instantaneous peak energy and temperature of the non-thermal and thermal emissions. As the thermal spectrum is a superposition of elementary modified Planck functions at different temperatures, its average spectral slope α (with N(E) ∝ Eα) below the peak is close to −1. The asymptotic value α =  +0.4 is recovered only below a few keV, which corresponds to the photospheric contribution with the lowest temperature.

It can be seen in Fig. 2 (top right panel) that the emission is initially only thermal as it takes a time 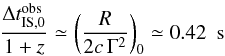ΔtIS,0obs1+z≃(R2c Γ2)0≃0.42s\begin{equation} \label{eqn_shiftb} \frac{\Delta t_{\rm IS, 0}^{\rm obs}}{1+z}\simeq \left({R\over 2c\,\Gamma^2}\right)_0\simeq 0.42\ \ {\rm s} \end{equation}(17)for the first signal from internal shocks to arrive at the observer. In Eq. (17) the subscript “0” refers to the radius and Lorentz factor of the first shocked shell that contributes to the non-thermal emission. At late times the situation is just the opposite: the photospheric emission abruptly stops at tobs = 20 s, while the emission from late internal shocks (both on- and off-axis) still contribute for about 10 s (observer frame). The spectrum (Fig. 2, bottom left) is the sum of the thermal and non-thermal contributions. They peak at 200/(1 + z) and 1000/(1 + z) keV, respectively. Finally the plot of the temperature and of the peak energy of the non-thermal spectrum as a function of observer time shows (Fig. 2, bottom right panel) that the former is more sensitive than the latter to the fluctuations of the Lorentz factor (since Tobs ∝ Γ8/3).

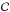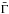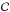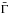We now check how these results change when we vary the model parameters. We divide these parameters into three groups describing respectively the geometry (θ, l); the energetics and flow-acceleration mechanism (Ėisoϵth, σ); and the ejecta structure (stot, \hbox{${\cal C}$}, \hbox{${\bar \Gamma}$}), where \hbox{${\cal C}$} and \hbox{$\bar \Gamma$} are the contrast (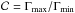\hbox{${\cal C}=\Gamma_{\rm max}/\Gamma_{\rm min}$}) and average of the Lorentz factor distribution.

The geometry only affects the thermal emission (for a fixed Ėiso). The dependence of Tobs and Lth,   iso on θ and ℓ is weak. From Eqs. (2), (7), and (8) we get Tobs ∝ θ−1/6ℓ1/6 and Lth,   iso ∝ θ−2/3ℓ2/3. Similarly, changing the magnetisation has a moderate effect on the previous results, as long as σ < 1. As explained above, for σ ≳ 1 the whole theoretical framework adopted to compute the non-thermal emission probably becomes invalid.

The consequence of increasing or decreasing the thermal fraction ϵth is illustrated in Fig. 3 (left panels). With ϵth = 0.3 the thermal spectrum overtakes the non-thermal spectrum between 20/(1 + z) and 500/(1 + z) keV, and the thermal component represents about one third of the total in the light curve. Conversely, with ϵth = 0.003 the contribution of the thermal component to the global spectrum and the light curve is barely visible.

The dependence of the temperature and thermal luminosity on the injected isotropic power Ėiso and average Lorentz factor 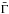\hbox{${\bar \Gamma}$} can be also obtained from Eqs. (2), (7), and (8) yielding Tobs∝Ėiso−5/12 Γ̅8/3,Lth, iso∝Ėiso1/3 Γ̅8/3.\begin{eqnarray} \label{eqn_tobs_depend} &T_{\rm obs} \propto {\dot E}_{\rm iso}^{-5/12}\,{\bar \Gamma}^{8/3} , \\[4mm] \label{eqn_lth_depend} &L_{\rm th, \,iso} \propto {\dot E}_{\rm iso}^{1/3}\,{\bar \Gamma}^{8/3} . \end{eqnarray}For the non-thermal component, the relation of the peak energy and luminosity to the model parameters can be found using the simplest possible description of internal shocks that only considers the interaction of two shells of equal mass (Barraud et al. 2005). 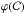One gets Ep∝Ė1/2Kϕ(𝒞) Γ̅-2tvar-1,LNth, iso∝fIS Ėiso,\begin{eqnarray} &E_{\rm p} \propto \dot{E}_{\rm K}^{1/2}\varphi({\cal C})\, \bar{\Gamma}^{-2}\ t_{\rm var}^{-1} , \\[4mm] &L_{\rm Nth, \,iso} \propto f_{\rm IS}\,{\dot E}_{\rm iso} , \end{eqnarray}where tvar is of the order of one pulse duration, \hbox{$\varphi({\cal C})$} depends on 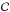\hbox{${\cal C}$} only, and fIS, defined by Eq. 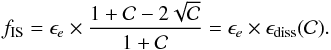(14), is given by fIS=ϵe×1+𝒞−2𝒞1+𝒞=ϵe×ϵdiss(𝒞).\begin{equation} f_{\rm IS}=\epsilon_e\times {1+{\cal C}-2\sqrt{\cal C}\over 1+\cal C}=\epsilon_e\times \epsilon_{\rm diss}({\cal C}) . \label{eqn_efficiency_nth} \end{equation}(22)It can be seen that the thermal and non-thermal components behave quite differently when the injected power and average Lorentz factor are changed. This is illustrated in Fig. 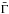3 where we increase or decrease Ėiso and \hbox{${\bar \Gamma}$} by respective factors of 10 and 2, compared to the reference case shown in Fig. 2.

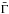It appears that for a given value of ϵth (ϵth = 0.03 in Fig. 3, middle and right panels) the thermal component becomes more visible when Ėiso is decreased and \hbox{${\bar \Gamma}$} increased. This is a direct consequence of Eqs. 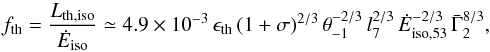(18) and (19) above, which can be made even more explicit by defining the global thermal efficiency (assuming κ = 0.2  cm2  g-1) fth=Lth,isoĖiso≃4.9×10-3 ϵth (1+σ)2/3 θ-1−2/3 l72/3 Ėiso,53−2/3 Γ̅28/3,\begin{equation} \label{eqn_efficiency_th} f_{\rm th} = {L_{\rm th,iso}\over {\dot E}_{\rm iso}} \simeq 4.9 \times 10^{-3}\, \epsilon_{\rm th}\, (1+\sigma)^{2/3} \, \theta_{-1}^{-2/3}\, l_7^{2/3}\,{\dot E}_{\rm iso, 53}^{-2/3}\,{\bar \Gamma}_2^{8/3} , \end{equation}(23)to be compared to the non-thermal efficiency fNth = fIS approximated by Eq. (22). 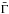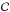While changing Ėiso and \hbox{${\bar \Gamma}$} affects only the thermal efficiency, the opposite is true for the contrast in Lorentz factor \hbox{${\cal C}$}. 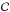Reducing \hbox{${\cal C}$} makes internal shocks much less efficient and considerably softens the emitted non-thermal spectrum. 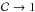In the limit where \hbox{${\cal C} \rightarrow 1$} (and moreover if the Lorentz factor is increasing outwards in the ejecta) there will be no internal shocks and the emission will only be thermal in the absence of an alternative dissipation process.

3.2. Non-thermal emission from magnetic dissipation

If the non-thermal emission is produced by reconnection in a magnetised outflow, the problem becomes very difficult, with no simple way to accurately follow the process in time and compute a light curve (see e.g. Spruit et al. 2001; Lyutikov & Blandford 2003; Giannios 2008; Zhang & Yan 2011; McKinney & Uzdensky 2012). As explained in Sect. 2.3 above, we adopted a very simple assumption to obtain the non-thermal spectrum: a Band function carrying a fraction fNth of the injected energy with the peak of E2N(E) obtained from the Amati relation. Several examples of the thermal and non-thermal spectra are represented in the left panel of Fig. 4, with the thermal component still being computed with the distribution of Lorentz factor given by Eq. (16). The results are shown for several values of ϵth and σ, and a fixed value of the isotropic magnetic power at the photosphere σĖ/(1 + σ) = 1053   erg  s-1. As expected, the detection of the photospheric component in the spectrum is favored by a high ϵth, a low fNth, and a high Γ. The specific dependency on the magnetisation is discussed in the next section.

thumbnail Fig. 4

Thermal and non-thermal emission from a variable outflow – magnetic reconnection framework. In each panel we show a sequence of thermal (red) and non-thermal (blue), spectra (the source redshift is z = 1). The Lorentz factor distribution adopted for the calculation of the thermal emission is the same as in Fig. 2 (left panel) or the same but with Γ divided by 2 (right panel). The thermal emission is computed using the formalism developed in Sect. 2.2, using five values of ϵth: 0.01, 0.03, 0.10, 0.30, and 0.5. The non-thermal spectrum is simply parametrised by a Band function, with the peak energy being given by the Amati relation (see text) and using five values of the efficiency of the magnetic reconnection, frec = fNth(1 + σ)/σ: 0.01, 0.03, 0.10, 0.30, and 0.5. In all cases, the isotropic magnetic power at the photosphere is fixed to σĖiso/(1 + σ) = 1053   erg  s-1. Finally, the magnetisation σ at large distance is either σ = 1 (solid lines) or 10 (dashed lines).

4. Discussion

4.1. Relative intensity of the thermal component in GRBs

Depending on the mechanism responsible for the acceleration of the outflow in GRBs, the consequences regarding the photospheric emission are very different. In a pure fireball (ϵth = 1) powered by neutrino-antineutrino annihilation (see e.g. Popham et al. 1999; Zalamea & Beloborodov 2011), the predicted thermal emission is very bright (Daigne & Mochkovitch 2002). To agree with the current data, the spectrum should then be Comptonised at high energy (as a result of some dissipative process below the photosphere, e.g. Rees & Mészáros 2005; Pe’er et al. 2006; Giannios 2008; Beloborodov 2010; Lazzati & Begelman 2010) to produce a power law tail and softened at low energy to decrease the spectral index α from a positive value to a negative one (possibly by the presence of an additional non-thermal component, e.g. Pe’er et al. 2006; Vurm et al. 2011). An alternative is to suppose that the flow is initially magnetically dominated (ϵth ≲ 0.1). A thermal component is still expected to be released at the photosphere, but it will now be sub-dominant compared to non-thermal processes such as internal shocks or magnetic reconnection.

We have explored this second possibility in the present paper, making the following assumptions: (i) we supposed that the flow evolves adiabatically from the origin to the photosphere, i.e. we did not include possible sources of heating below Rph; (ii) if the remaining magnetisation σ at the end of acceleration is weak and does not prevent the formation of internal shocks, we computed their contribution to the emitted radiation as if σ = 0; (iii) when σ > 1 we limited ourselves to a very simple parametrised study where we assumed that a fraction fNth of the injected power goes into the non-thermal component.

Regarding the light curve and spectrum of the thermal emission we obtained the following results:

  • Both the photosphere luminosity and temperature depend on thesame factor Φ given by Eq. (11), which directly traces the evolution of the Lorentz factor if the injected power stays constant.

  • The duration of the photospheric emission corresponds to the duration τ of production of the relativistic wind. For t > τ the luminosity drops rapidly on a time scale 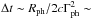Δt~Rph/2cΓph2~\hbox{$\Delta t\sim R_{\rm ph}/2 c \Gamma_{\rm ph}^2\sim$} a few ms for typical values of the burst parameters.

  • The global spectrum of the thermal emission is a composite of many elementary contributions at different temperatures. Before asymptotically reaching a slope α =  +0.4 at low energy it can be much softer below the peak as shown in Fig. 2. A time resolved spectrum will resemble more closely the “modified Planck function” adopted for each elementary collision.

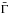If the non-thermal emission comes from internal shocks, its light curve and spectrum have been computed using the simplified approach described in Sect. 2.3. We have varied several of the model parameters: fraction ϵth of thermal energy at the origin of the flow, isotropic injected power Ėiso, and average \hbox{$\bar \Gamma$} to see under which conditions the thermal component would appear in the observed spectrum, in the internal shock scenario for σ ≲ 0.1−1 (Fig. 3) or in the magnetic reconnection scenario for σ ≳ 1 (Fig. 4). 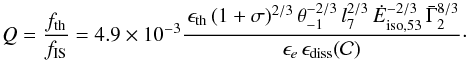In the internal shock framework, assuming κ = 0.2  cm2   g-1, the ratio Q of the thermal to non-thermal efficiency is given by Q=fthfIS=4.9×10-3 ϵth (1+σ)2/3 θ-1−2/3 l72/3 Ėiso,53−2/3 Γ̅28/3ϵe ϵdiss(𝒞)·\begin{equation} \label{eqn_ratio_thnth} Q={f_{\rm th}\over f_{\rm IS}}=4.9 \times10^{-3} \frac{\, \epsilon_{\rm th}\, (1+\sigma)^{2/3} \, \theta_{-1}^{-2/3}\, l_7^{2/3}\,{\dot E}_{\rm iso, 53}^{-2/3}\,{\bar \Gamma}_2^{8/3}} {\epsilon_e\,\epsilon_{\rm diss}({\cal C})} \cdot \end{equation}(24)As illustrated by this formula and in Fig. 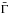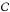3, increasing ϵth, but also increasing \hbox{$\bar \Gamma$} or reducing Ėiso or \hbox{$\cal C$} will make the thermal component more visible. The magnetisation σ has a low impact as 1 + σ ≃ 1 in this scenario. In the examples shown in Fig. 3, the model parameters are taken from the reference case used in Fig. 2 and equal l7 = 0.3, θ-1 = 1, ϵe = 1/3, and σ = 0.1. The effective constrast corresponding to the initial distribution of the Lorentz factor plotted in the upper left panel of Fig. 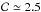2 is \hbox{${\cal C}\simeq 2.5$}. Then Eq. 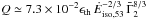(24) leads to Q≃7.3×10-2ϵth Ėiso,53−2/3 Γ̅28/3\hbox{$Q \simeq 7.3 \times10^{-2} \epsilon_{\rm th}\, {\dot E}_{\rm iso, 53}^{-2/3}\, {\bar \Gamma}_2^{8/3} $}, in reasonable agreement with Fig. 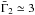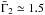3: for instance, the upper left panel corresponds to ϵth = 0.3, Ėiso,53 = 1, \hbox{$\bar{\Gamma}_2\simeq 3$}, and Q ≃ 0.4, and the bottom right panel corresponds to ϵth = 0.03, Ėiso,53 = 1, \hbox{$\bar{\Gamma}_2 \simeq 1.5$}, and Q ≃ 0.006. Note that in the E2N(E) spectrum, the ratio of the maxima of the two components is expected to be slightly higher than Q because the photospheric component has a narrower spectrum than the non-thermal one.

In the case of magnetic reconnection, the non-thermal emission is simply parametrised by its global efficiency fNth, and we have 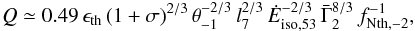Q≃0.49 ϵth (1+σ)2/3 θ-1−2/3 l72/3 Ėiso,53−2/3 Γ̅28/3 fNth,−2-1,\begin{equation} Q \simeq 0.49 \, \epsilon_{\rm th}\, (1+\sigma)^{2/3} \, \theta_{-1}^{-2/3}\, l_7^{2/3}\,{\dot E}_{\rm iso, 53}^{-2/3}\,{\bar \Gamma}_2^{8/3}\,f_{\rm Nth,-2}^{-1} , \label{eq_Qmag} \end{equation}(25)in good agreement with Fig. 4 (fNth, −2 being the non-thermal efficiency in %). Especially, Eq. (25) shows that the ratio Q increases with the magnetisation σ, which seems counter-intuitive. For a fixed value of Ė, increasing σ reduces ĖK, and therefore decreases the photospheric radius Rph (see Eq. (9)). Therefore, for a given value of ϵth, the luminosity and temperature of the photosphere increase. However, for a given acceleration mechanism, one would expect an increase of σ to be associated with a decrease of ϵth, which may affect the dependency of the ratio Q on the magnetisation σ. For instance, in the case of a passive magnetic field, including σ = σpassive in Eq. 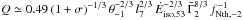(25) leads to Q≃0.49 (1+σ)−1/3 θ-1−2/3 l72/3 Ėiso,53−2/3 Γ̅28/3 fNth,−2-1\hbox{$ Q \simeq 0.49 \, (1+\sigma)^{-1/3} \, \theta_{-1}^{-2/3}\, l_7^{2/3}\,{\dot E}_{\rm iso, 53}^{-2/3}\,{\bar \Gamma}_2^{8/3}\,f_{\rm Nth,-2}^{-1} $}, i.e. a decreasing ratio for an increasing magnetisation. Since increasing the final magnetisation σ tends to decrease the photospheric radius, it should also be noted that the acceleration of the flow may well be incomplete at the photosphere in high σ scenarios. As discussed in Appendix A, this will also reduce the photospheric emission.

4.2. Comparison to observations

We now check how these results compare to the various observational indications of the presence of a thermal component in GRB spectra.

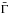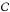One first indirect indication comes from the very hard spectral slopes α > 0 that are sometimes observed during burst evolution (e.g. Ghirlanda et al. 2003; Bosnjak et al. 2006; Abdo et al. 2009). Indeed, our results allow the thermal over non-thermal ratio (Eq. (24)) to vary with time. A locally large \hbox{$\bar \Gamma$} will boost the thermal component while a low contrast \hbox{$\cal C$} will reduce the non-thermal component (under the condition that the non-thermal emission comes from internal shocks). This can explain an erratic behaviour of the α slope, but observations often show a regular shift of α from positive to negative values during a single pulse. As explained in Sect. 3.1 a thermal start and a non-thermal ending are predicted by our models, but the fraction of time during which the emission is thermal is generally smaller than observed in the few bursts where the measured α slope is positive. It remains possible to adopt a distribution of the Lorentz factor that would extend the duration of the thermal emission but smoothly connecting the thermal and non-thermal components may not be easy.

thumbnail Fig. 5

Constraints on the thermal and non-thermal emission in GRB 090902B and GRB 100724B. Top: for a given thermal fraction ϵth = 10-2, 10-1.5, 10-1, 10-0.5, and 1, the radius R0 = ℓ/θ at the base of the flow is plotted as a function of the non-thermal efficiency fNth. The corresponding thermal efficiency fth is also shown (top x-axis). Bottom: for a given magnetisation σ = 10-1, 10-0.5, 1, 100.5, 101, 101.5, and 102 at the end of acceleration phase, the Lorentz factor of the flow is plotted as a function of fNth (the unmagnetised case σ = 0 cannot be distinguished from the case σ = 0.1). Sets of parameters representative of the different classes of scenarios discussed in the paper are indicated: F (ϵth = 1, σ = 0) (standard fireball), M,is1 (log ϵth = −0.5, σ = 0,) and M,is2 (log ϵth = −1.5, σ = 0) (efficient magnetic acceleration: magnetisation is low above the photosphere and the dominant non-thermal mechanism is internal shocks), M,rec1 (log ϵth = −0.5, σ = 10), and M,rec2 (log ϵth = −1.5, σ = 10) (magnetised flow at large distance, the dominant non-thermal mechanism is magnetic reconnection). The initial radius is fixed to R0 = 300   km, a typical value for long GRBs. The observational data (thermal flux, temperature, ratio of the thermal over the total flux) used for the calculation (see text) are taken from Abdo et al. (2009); Pe’er et al. (2012) for GRB 090902B (left column), and from Guiriec et al. (2011) for GRB 100724B (right column).

A second indication comes from the recent detection of possible thermal components in a few Fermi GRBs. GRB 090902B is a very peculiar case of a burst showing a spectrum best fitted by a Band function with a hard low-energy photon index, or a multi-colour black body, together with an additional sub-dominant power law (Abdo et al. 2009; Ryde et al. 2010). A first possibility is to interpret this burst as photospheric emission with additional dissipative processes affecting the spectrum by Comptonisation and possibly other non-thermal processes. Conversely, using the formalism presented here, we can also derive constraints on the burst parameters for alternative scenarios where the Band component is interpreted as the thermal emission produced at the photosphere without sub-photospheric dissipation, and the power law as non-thermal emission produced above the photosphere in the optically thin regime. From the analysis made by Abdo et al. (2009) and Pe’er et al. (2012), the implied thermal luminosity and temperature are large, Lth ≃ 4.6 × 1053   erg   s-1 and Tobs ≃ 168   keV. The thermal luminosity represents 53% of the total luminosity. Then, for a given ϵth, σ, and fNth, one can deduce from Eqs. (7)–(9) the isotropic power Ėiso, the size R0 = ℓ/θ of the region at the base of the outflow (see Fig. 5, top-left panel), and the Lorentz factor Γ (see Fig. 5, bottom-left panel). This is a similar approach to the one proposed by Pe’er et al. (2007), but within the more general framework defined in this paper, which allows us to consider several scenarios for the acceleration of the outflow. As GRB 090902B is very bright, this leads to huge values of Ėiso, the minimum being obtained for ϵth ≃ 1, which would make GRB 090902B a peculiar burst associated to a situation close to a pure fireball. For instance, for ϵth = 1, l7 = 0.3, θ-1 = 1 (i.e. R0 = 300   km), and σ ≪ 1 we get an isotropic power Ėiso ~ 2.6 × 1054   erg   s-1 and a Lorentz factor Γ ~ 1160. The efficiency of the photospheric emission in this case is fth ≃ 0.18 and the efficiency of the non-thermal emission above the photosphere is fNth ≃ 0.16, marginally compatible with internal shocks. This case is labelled as F in Fig. 5 (left column) and is in good agreement with the analysis made by Pe’er et al. (2012).

As most GRBs do not show such a bright thermal component, they usually require much lower values of ϵth, as illustrated below with GRB 100724B. Then, it is worth studying the possibility to model GRB 090902B with ϵth < 1, which would correspond to an initially magnetised outflow. Reducing ϵth in this burst has several consequences. As illustrated in Fig. 5 (left column), it implies a general decrease of the efficiency, except if the initial size R0 = ℓ/θ is very large (R0 ≫ 3000 km), which is not expected for most models of the central engine of long GRBs, because of their short timescale (~1–10 ms) variability. For instance, for ϵth = 10-0.5 (case labelled as M,is1, where we keep R0 = 300 km and σ ≪ 1), the thermal and non-thermal efficiencies are reduced to fth = 0.06 and fNth = 0.05, leading to an isotropic equivalent power Ėiso = 9.4 × 1054   erg   s-1. It also leads to an increase of the Lorentz factor, which was already quite high for the pure fireball scenario (see Fig. 5, bottom-left panel). Therefore, ϵth ≃ 0.3−0.5 seems a reasonable lower limit for GRB 090902B. Note that a decrease of ϵth compared to the standard fireball leads in this case to a reduced non-thermal efficiency fth in good agreement with the expected value for internal shocks. For higher values of ϵth, magnetic reconnection, which is supposed to have a higher efficiency, is a better candidate, as illustrated in Fig. 5 (left column). In addition, for a fixed value of ϵth, increasing the magnetisation σ at the end of acceleration always reduces the constraint on the Lorentz factor (bottom left panel). A more detailed modelling of GRB 090902B would be necessary to distinguish between these different possibilities.

Conversely, the results of Guiriec et al. (2011) indicating the presence of a sub-dominant thermal component in GRB 100724B, representing about 4% of the total flux, point towards low values of ϵth and, therefore, a magnetic acceleration. As shown in Fig. 5, it is difficult to interpret GRB 100724B within the standard fireball scenario (thermal acceleration) that would imply either fNth > 1 or R0 < 120   km (and even R0 < 40   km if fNth < 0.5 is required). This is obtained assuming a redshift z = 1, but we checked that our conclusions are unchanged for larger redshifts. Then a low thermal fraction ϵth ≲ 0.01−0.1 is required in GRB 100724B, whose spectral properties are much more representative of the bulk GRB population than in the unusual case of GRB 090902B. A similar conclusion was obtained by Zhang & Pe’er (2009) in the case of the very energetic burst GRB 080916C where no bright thermal component was detected. Assuming a passive magnetic field below the photosphere, they obtain the constraint σpassive ≳ 15−20, which leads to the more general condition ϵth ≲ 0.05, from Eq. (10).

If magnetic acceleration is common in GRBs, several scenarios can be discussed. In scenarios where magnetic acceleration is efficient, implying a low magnetisation at large radius and a dominant role of internal shocks, the thermal fraction should not be much larger than a few percents to avoid an unrealistic efficiency fNth. For instance in the case of GRB 100724B, for z = 1, ϵth = 10-1.5, ℓ7 = 0.3, θ-1 = 1 (i.e. R0 = 300   km), and σ ≪ 1 (case labelled as M,is2 in Fig. 5 right column), we get a non-thermal efficiency fNth ≃ 0.06 and a thermal efficiency fth ≃ 2 × 10-3. The isotropic kinetic power and the Lorentz factor in this case are Ėiso ≃ 5.6 × 1053   erg   s-1 and Γ ≃ 660. Alternative scenarios – where the flow is still magnetised at large radius and magnetic reconnection is the dominant mechanism to produce non-thermal emission – are less constrained, because of the uncertainties in the underlying physics. As illustrated in Fig. 5, for a fixed ϵth, increasing σ tends to reduce Γ, which is already in the typical range of a few hundreds for σ = 0. High values of the non-thermal efficiency fNth ≳ 0.1−0.5 (as usually expected for magnetic reconnection, see e.g. Zhang & Yan 2011; McKinney & Uzdensky 2012) also require high values of the thermal fraction ϵth ≳ 0.1−0.3, which does not seem natural in such scenarios of highly magnetised outflows.

As illustrated in Sect. 3, spectra with non-thermal and thermal components resembling those found by Guiriec et al. (2011) are easily obtained with our model, either for a photospheric + internal shocks scenario in a case of efficient magnetic acceleration, or for a photospheric + reconnection scenario if the magnetisation at large distance is still large. A potential issue for the internal shock scenario is the moderate variation of the temperature (within a factor of 2) found in the time-resolved analysis. To be efficient, internal shocks require large fluctuations of the Lorentz factors that are even amplified in the observed temperature (Tobs ∝ Γ8/3, see Fig. 2). This may suggest that the non-thermal emission in GRB 100724B comes from magnetic reconnection. This is unfortunately difficult to test in absence of theoretical predictions for the spectral evolution in this case. It should however be noted that when the temperature drops, the luminosity also drops so that, in practice, the temperature can be determined only when it is high enough. Depending on the time scale for the Lorentz factor fluctuations and the temporal resolution of the analysis, this may artificially reduce the amplitude of the measured variations of temperature. This is illustrated in Fig. 2 where dotted and dashed lines show the temperature (and peak energy of the non-thermal spectrum) averaged over intervals of 2 and 4 s, respectively. It remains to be tested if this smoothing effect can account for GRB 100724B evolution in the photospheric + internal shocks scenario.

5. Conclusion

We have explored in detail GRB scenarios with two episodes of emission: thermal emission from the photosphere without sub-photospheric dissipation, and non-thermal emission from internal dissipation above the photosphere. Our results can be used to interpret the data and obtain constraints on the burst parameters or acceleration mechanism. But one faces the difficulty arising from the diversity of the proposed evidence for the presence of a thermal component in GRB spectra. In some cases this thermal component represents a major contribution to the global spectrum (with additional non-thermal contributions) while in others it is always sub-dominant, most of the emission having a non-thermal origin. These different situations seem to imply quite different magnetic over thermal energy ratios at the origin of the flow. However the lack of bright thermal components in most GRBs clearly points towards magnetic acceleration, with ϵth ≲ 0.01 in most cases, and ϵth ≃ 0.01−0.1 in less frequent cases such as GRB 100724B. GRB 090902B with ϵth ≃ 0.3−1 remains an exception2.

More generally, one may wonder what would be the best conditions for the thermal emission to show up. Apart from the obvious requirement that ϵth should be as large as possible, Eq. (24) may suggest looking for events with a low Ėiso and/or a large average Lorentz factor. This, however, supposes that these two quantities are independent. Having 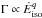Γ∝Ėqiso\hbox{$\Gamma\propto \dot{E}_{\rm iso}^{q}$} and q > 1/4 would favor both a large Ėiso and Γ while the opposite is true for q < 1/4. Finally, if the non-thermal emission comes from internal shocks, a pure thermal spectrum can be possible even if the distribution of the Lorentz factor has a low contrast or if Γ is increasing outwards.

The observation of a burst with an unambiguous photospheric signature in its spectrum would greatly help to clarify several issues in GRB physics: (i) estimating the value of ϵth would provide insight on the acceleration mechanism of the flow; (ii) obtaining the temperature and thermal luminosity evolution would constrain the distribution of Lorentz factor and injected power; and (iii) measuring the level of temperature fluctuations with a high temporal resolution would help to discriminate between internal shocks and magnetic reconnection for the non-thermal emission. Isolating the photospheric component in the available data is, however, not an easy task: it is generally one among other spectral components and possibly sub-dominant, and does not have a simple blackbody spectrum.

1

See Appendix A for a short discussion of the case where Rsat > Rph.

2

An intermediate case between GRB 100724B and 090902B has been recently found in the short GRB 120323A (Guiriec et al. 2012).

Acknowledgments

The authors thank the referee for constructive comments helping us to clarify the formulation of the paper. This work is partially supported by a grant from the French Space Agency (CNES). R.H.’s PhD work is funded by a Fondation CFM-JP Aguilar grant.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L138 [NASA ADS] [CrossRef] [Google Scholar]
  2. Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Band, D. L., & Preece, R. D. 2005, ApJ, 627, 319 [NASA ADS] [CrossRef] [Google Scholar]
  4. Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barraud, C., Daigne, F., Mochkovitch, R., & Atteia, J. L. 2005, A&A, 440, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Begelman, M. C., & Li, Z.-Y. 1994, ApJ, 426, 269 [NASA ADS] [CrossRef] [Google Scholar]
  7. Beloborodov, A. M. 2010, MNRAS, 407, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beloborodov, A. M. 2011, ApJ, 737, 68 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bosnjak, Z., Celotti, A., & Ghirlanda, G. 2006, MNRAS, 370, L33 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bošnjak, Ž., Daigne, F., & Dubus, G. 2009, A&A, 498, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Brainerd, J. J., & Lamb, D. Q. 1987, ApJ, 313, 231 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cline, T. L., & Desai, U. D. 1975, ApJ, 196, L43 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cline, T. L., Desai, U. D., Klebesadel, R. W., & Strong, I. B. 1973, ApJ, 185, L1 [NASA ADS] [CrossRef] [Google Scholar]
  14. Collazzi, A. C., Schaefer, B. E., Goldstein, A., & Preece, R. D. 2012, ApJ, 747, 39 [NASA ADS] [CrossRef] [Google Scholar]
  15. Daigne, F., & Drenkhahn, G. 2002, A&A, 381, 1066 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275 [NASA ADS] [CrossRef] [Google Scholar]
  17. Daigne, F., & Mochkovitch, R. 2002, MNRAS, 336, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  18. Daigne, F., Bošnjak, Ž., & Dubus, G. 2011, A&A, 526, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Derishev, E. V., Kocharovsky, V. V., & Kocharovsky, V. V. 2001, A&A, 372, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Ghirlanda, G., Celotti, A., & Ghisellini, G. 2003, A&A, 406, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Ghirlanda, G., Ghisellini, G., Nava, L., et al. 2012, MNRAS, 422, 2553 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313, L1 [NASA ADS] [CrossRef] [Google Scholar]
  23. Giannios, D. 2008, A&A, 480, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Giannios, D. 2012, MNRAS, 422, 3092 [NASA ADS] [CrossRef] [Google Scholar]
  25. Giannios, D., & Spruit, H. C. 2007, A&A, 469, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gilman, D., Metzger, A. E., Parker, R. H., Evans, L. G., & Trombka, J. I. 1980, ApJ, 236, 951 [Google Scholar]
  27. Goldstein, A., Burgess, J. M., Preece, R. D., et al. 2012, ApJS, 199, 19 [NASA ADS] [CrossRef] [Google Scholar]
  28. Goodman, J. 1986, ApJ, 308, L47 [NASA ADS] [CrossRef] [Google Scholar]
  29. Granot, J., Komissarov, S. S., & Spitkovsky, A. 2011, MNRAS, 411, 1323 [Google Scholar]
  30. Guiriec, S., Connaughton, V., Briggs, M. S., et al. 2011, ApJ, 727, L33 [NASA ADS] [CrossRef] [Google Scholar]
  31. Guiriec, S., Daigne, F., Hascoët, R., et al. 2012, ApJ, submitted [arXiv:1210.7252] [Google Scholar]
  32. Hascoët, R., Daigne, F., & Mochkovitch, R. 2012, A&A, 542, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Kaneko, Y., Preece, R. D., Briggs, M. S., et al. 2006, ApJS, 166, 298 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kocevski, D. 2012, ApJ, 747, 146 [NASA ADS] [CrossRef] [Google Scholar]
  36. Komissarov, S. S., Vlahakis, N., Königl, A., & Barkov, M. V. 2009, MNRAS, 394, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  37. Komissarov, S. S., Vlahakis, N., & Königl, A. 2010, MNRAS, 407, 17 [NASA ADS] [CrossRef] [Google Scholar]
  38. Lazzati, D., & Begelman, M. C. 2010, ApJ, 725, 1137 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lyutikov, M., & Blandford, R. 2003, unpublished [arXiv:astro-ph/0312347] [Google Scholar]
  40. Mazets, E. P., Golenetskii, S. V., Ilinskii, V. N., et al. 1981, Ap&SS, 80, 3 [Google Scholar]
  41. McGlynn, S., Goldstein, A., Burgess, J. M., et al. 2012, in Gamma-Ray Burst 2012, Munich, May 7–11, eds. A. Rau, & J. Greiner, PoS(GRB 2012)[012] [Google Scholar]
  42. McKinney, J. C., & Uzdensky, D. A. 2012, MNRAS, 419, 573 [Google Scholar]
  43. Mészáros, P., & Rees, M. J. 2000, ApJ, 530, 292 [NASA ADS] [CrossRef] [Google Scholar]
  44. Mészáros, P., Laguna, P., & Rees, M. J. 1993, ApJ, 415, 181 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mészáros, P., Ramirez-Ruiz, E., Rees, M. J., & Zhang, B. 2002, ApJ, 578, 812 [NASA ADS] [CrossRef] [Google Scholar]
  46. Metzger, A. E., Parker, R. H., Gilman, D., Peterson, L. E., & Trombka, J. I. 1974, ApJ, 194, L19 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mimica, P., & Aloy, M. A. 2010, MNRAS, 401, 525 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nakar, E., & Piran, T. 2005, MNRAS, 360, L73 [NASA ADS] [CrossRef] [Google Scholar]
  49. Nakar, E., Ando, S., & Sari, R. 2009, ApJ, 703, 675 [NASA ADS] [CrossRef] [Google Scholar]
  50. Narayan, R., Kumar, P., & Tchekhovskoy, A. 2011, MNRAS, 416, 2193 [NASA ADS] [CrossRef] [Google Scholar]
  51. Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Nava, L., Salvaterra, R., Ghirlanda, G., et al. 2012, MNRAS, 421, 1256 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  53. Paczynski, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef] [Google Scholar]
  54. Pe’er, A. 2008, ApJ, 682, 463 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pe’er, A., Mészáros, P., & Rees, M. J. 2006, ApJ, 642, 995 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pe’er, A., Ryde, F., Wijers, R. A. M. J., Mészáros, P., & Rees, M. J. 2007, ApJ, 664, L1 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pe’er, A., Zhang, B.-B., Ryde, F., et al. 2012, MNRAS, 420, 468 [NASA ADS] [CrossRef] [Google Scholar]
  58. Piran, T. 1999, Phys. Rep., 314, 575 [NASA ADS] [CrossRef] [Google Scholar]
  59. Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
  60. Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 1998, ApJ, 506, L23 [NASA ADS] [CrossRef] [Google Scholar]
  61. Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 2000, ApJS, 126, 19 [NASA ADS] [CrossRef] [Google Scholar]
  62. Rees, M. J., & Meszaros, P. 1994, ApJ, 430, L93 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rees, M. J., & Mészáros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ryde, F. 2004, ApJ, 614, 827 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ryde, F. 2005, ApJ, 625, L95 [NASA ADS] [CrossRef] [Google Scholar]
  66. Ryde, F., Axelsson, M., Zhang, B. B., et al. 2010, ApJ, 709, L172 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ryde, F. et al. 2012, in Gamma-Ray Burst 2012, Munich, May 7–11, eds. A. Rau, & J. Greiner, PoS(GRB 2012)[011] [Google Scholar]
  68. Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
  69. Shemi, A., & Piran, T. 1990, ApJ, 365, L55 [NASA ADS] [CrossRef] [Google Scholar]
  70. Spruit, H. C., Daigne, F., & Drenkhahn, G. 2001, A&A, 369, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2010, New A, 15, 749 [Google Scholar]
  72. Thompson, C. 1994, MNRAS, 270, 480 [NASA ADS] [CrossRef] [Google Scholar]
  73. Vlahakis, N., & Königl, A. 2003, ApJ, 596, 1080 [NASA ADS] [CrossRef] [Google Scholar]
  74. Vurm, I., Beloborodov, A. M., & Poutanen, J. 2011, ApJ, 738, 77 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zalamea, I., & Beloborodov, A. M. 2011, MNRAS, 410, 2302 [NASA ADS] [CrossRef] [Google Scholar]
  76. Zdziarski, A. A., & Lamb, D. Q. 1986, ApJ, 309, L79 [NASA ADS] [CrossRef] [Google Scholar]
  77. Zhang, B., & Pe’er, A. 2009, ApJ, 700, L65 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zhang, B., & Yan, H. 2011, ApJ, 726, 90 [NASA ADS] [CrossRef] [Google Scholar]
  79. Zhang, B.-B., Zhang, B., Liang, E.-W., et al. 2011, ApJ, 730, 141 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: incomplete acceleration at the photosphere

In the case where the flow is still accelerating at the photosphere, the expressions for the photospheric radius, observed temperature, and thermal luminosity will depend both on the Lorentz factor at the photosphere and on its value at the end of acceleration Γ∞. 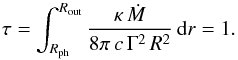To obtain the new expressions for Rph, Tobs, and Lth we write that the optical depth seen by a photon produced at Rph and leaving the flow at Rout is equal to unity τ=∫RphRoutκ Ṁ8π c Γ2 R2 dr=1.\appendix \setcounter{section}{1} \begin{equation} \tau=\int_{R_{\rm ph}}^{R_{\rm out}} {\kappa\,{\dot M}\over 8\pi\,c\,\Gamma^2\,R^2}\,{\rm d}r=1 . \end{equation}(A.1)For simplicity we suppose in this Appendix that the flow is stationary, i.e. that Ṁ is constant and that Γ∞ is identical for all the shells. 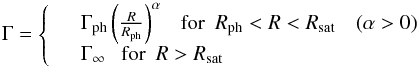Then, adopting a simple parametrisation for the Lorentz factor Γ={Γph(RRph)αforRph<R<Rsat(α>0)Γ∞forR>Rsat\appendix \setcounter{section}{1} \begin{equation} \Gamma = \left\lbrace\begin{array}{cl} & \Gamma_{\rm ph}\left({R\over R_{\rm ph}}\right)^{\alpha}\ \ \ {\rm for}\ \ R_{\rm ph}<R<R_\mathrm{sat}\ \ \ \ (\alpha>0)\\ & \Gamma_{\infty}\ \ \ {\rm for}\ \ R>R_\mathrm{sat}\\ \end{array}\right. 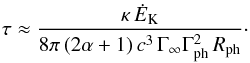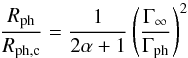\end{equation}(A.2)and with Ṁ = ĖK/Γ∞   c2 we get (neglecting terms of the order of (Rph/Rsat)2α + 1) τ≈κ ĖK8π (2α+1) c3 Γ∞Γph2 Rph·\appendix \setcounter{section}{1} \begin{equation} \tau\approx {\kappa\,{\dot E}_{\rm K}\over 8\pi\,(2\alpha+1)\,c^3\,\Gamma_{\infty}\Gamma_{\rm ph}^2\,R_{\rm ph}}\cdot \end{equation}(A.3)This finally leads to RphRph,c=12α+1(Γ∞Γph)2\appendix \setcounter{section}{1} \begin{equation} {R_{\rm ph}\over R_{\rm ph,c}}={1\over 2\alpha+1}\left({\Gamma_{\infty}\over \Gamma_{\rm ph}}\right)^2 \end{equation}(A.4)and TobsTobs,c=LthLth,c=(2α+1)2/3(ΓphΓ∞)2=(2α+1)2/3(RphRsat)2α,\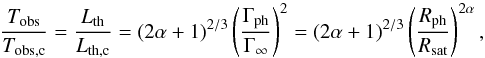appendix \setcounter{section}{1} \begin{equation} {T_{\rm obs}\over T_{\rm obs,c}}={L_{\rm th}\over L_{\rm th,c}}= ({2\alpha+1})^{2/3}\left({\Gamma_{\rm ph}\over \Gamma_{\infty}}\right)^2= ({2\alpha+1})^{2/3}\left({R_{\rm ph}\over R_\mathrm{sat}}\right)^{2\alpha}, \end{equation}(A.5)where the index c refers to the case where the acceleration is essentially complete at the photosphere. It can be seen that an incomplete acceleration can substantially reduce the thermal contribution.

All Figures

thumbnail Fig. 1

Schematic view of the problem geometry. The flow emerges from the central engine through a “circular opening” of radius ℓ. Beyond a radius Rsph it expands radially within a cone of half opening θ. The acceleration is completed at Rsat. The photosphere is located at Rph and dissipation of kinetic and/or magnetic energy takes place at Rdiss.

In the text
thumbnail Fig. 2

Thermal and non-thermal emission from a variable outflow – internal shock framework. Top left: initial distribution of the Lorentz factor in the flow. Top right: thermal (red), non-thermal (blue), and total (black) photon flux in the 8 keV–40 MeV spectral range. Bottom left: thermal (red), non-thermal (blue), and total (black) time-integrated spectra. Bottom right: instant temperature (red) of the photospheric emission and instant peak energy (blue) of the internal shock emission. The dotted and dashed lines correspond to the temperature and peak energy averaged over time intervals of 2 and 4 s, respectively. The adopted flow parameters are Ėiso = 1053 erg s-1, ϵth = 0.03, σ = 0.1, ℓ = 3 × 106 cm, and θ = 0.1 rad; a redshift z = 1 is assumed.
In the text
thumbnail Fig. 3

Thermal and non-thermal emission from a variable outflow – internal shock framework: impact of the outflow parameters. Starting from the reference case shown in Fig. 2 (with a redshift z = 1) we first change the thermal fraction ϵth to 0.3 (top left panel) and 0.003 (bottom left); then the isotropic power Ėiso to 1054  erg  s-1 (top middle) and 1052  erg  s-1 (bottom middle); and finally the Lorentz factor is multiplied (top right) and divided (bottom right) by a factor of 2. Each time we vary a parameter, all the others keep the value corresponding to the reference case.

In the text
thumbnail Fig. 4

Thermal and non-thermal emission from a variable outflow – magnetic reconnection framework. In each panel we show a sequence of thermal (red) and non-thermal (blue), spectra (the source redshift is z = 1). The Lorentz factor distribution adopted for the calculation of the thermal emission is the same as in Fig. 2 (left panel) or the same but with Γ divided by 2 (right panel). The thermal emission is computed using the formalism developed in Sect. 2.2, using five values of ϵth: 0.01, 0.03, 0.10, 0.30, and 0.5. The non-thermal spectrum is simply parametrised by a Band function, with the peak energy being given by the Amati relation (see text) and using five values of the efficiency of the magnetic reconnection, frec = fNth(1 + σ)/σ: 0.01, 0.03, 0.10, 0.30, and 0.5. In all cases, the isotropic magnetic power at the photosphere is fixed to σĖiso/(1 + σ) = 1053   erg  s-1. Finally, the magnetisation σ at large distance is either σ = 1 (solid lines) or 10 (dashed lines).

In the text
thumbnail Fig. 5

Constraints on the thermal and non-thermal emission in GRB 090902B and GRB 100724B. Top: for a given thermal fraction ϵth = 10-2, 10-1.5, 10-1, 10-0.5, and 1, the radius R0 = ℓ/θ at the base of the flow is plotted as a function of the non-thermal efficiency fNth. The corresponding thermal efficiency fth is also shown (top x-axis). Bottom: for a given magnetisation σ = 10-1, 10-0.5, 1, 100.5, 101, 101.5, and 102 at the end of acceleration phase, the Lorentz factor of the flow is plotted as a function of fNth (the unmagnetised case σ = 0 cannot be distinguished from the case σ = 0.1). Sets of parameters representative of the different classes of scenarios discussed in the paper are indicated: F (ϵth = 1, σ = 0) (standard fireball), M,is1 (log ϵth = −0.5, σ = 0,) and M,is2 (log ϵth = −1.5, σ = 0) (efficient magnetic acceleration: magnetisation is low above the photosphere and the dominant non-thermal mechanism is internal shocks), M,rec1 (log ϵth = −0.5, σ = 10), and M,rec2 (log ϵth = −1.5, σ = 10) (magnetised flow at large distance, the dominant non-thermal mechanism is magnetic reconnection). The initial radius is fixed to R0 = 300   km, a typical value for long GRBs. The observational data (thermal flux, temperature, ratio of the thermal over the total flux) used for the calculation (see text) are taken from Abdo et al. (2009); Pe’er et al. (2012) for GRB 090902B (left column), and from Guiriec et al. (2011) for GRB 100724B (right column).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.