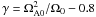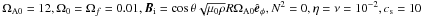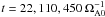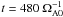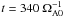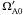| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220262 | |
| Published online | 31 January 2013 | |
Nonlinear simulations explaining Ap star magnetic fields by instability remnants
1 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: rarlt@aip.de
2 Institute of Fundamental Technological Problems PAS, Pawińskiego 5b, 02-106 Warsaw, Poland
Received: 20 August 2012
Accepted: 12 December 2012
The question of the origin of magnetic fields of Ap/Bp stars is still regarded as an interesting puzzle of stellar astrophysics. We investigate the possibility that the randomness and relative complexity of these fields are remnants of a magnetic instability. In the studied scenario it is assumed a priori that the surface of an Ap star is slowed down in its early evolutionary stage more than its analogous A star. This leads to a significant differential rotation in its interior, making it possible to generate a strong toroidal magnetic field in the radiative zone. Under such circumstances the kink-type Tayler instability is likely to set in. The presented numerical simulations in a compressible, spherical domain show that the instability can produce large surface magnetic fields, even of the order of 0.01 − 1 of the internal toroidal component (depending on the setup). The resulting magnetic fields can then serve as “initial conditions” evolving into a stable magnetic configuration (however, the matter of long-term stability is not addressed here). This theory naturally supports the fact that Ap stars rotate typically slower than normal A stars (the Tayler instability is suppressed when rotation is too fast), it also qualitatively explains the dependence of the apparent obliquity of the main magnetic axis on the rotation period, as well as the existence of the minimum field threshold (no Ap stars have been observed with fields weaker than ≈ 102 G). Given that the generation of the initial differential rotation and initial poloidal fields are not discussed here, the results have a speculative nature and can be viewed as a possible step toward a full understanding of Ap star magnetism.
Key words: stars: magnetic field / stars: chemically peculiar / magnetohydrodynamics (MHD) / instabilities
© ESO, 2013
1. Introduction
A few percent of all intermediate-mass (1.5 − 8 M⊙), near-main sequence A and B stars are known to be chemically peculiar – they are usually referred to as Ap/Bp stars and a majority of them host detectable magnetic fields. Moreover, these are the only intermediate-mass stars for which magnetic fields have been observed. Up to now, there also have been reports concerning the detection of magnetic fields in more massive stars (young Herbig Ae/Be and early B and O stars). Such fields have strengths and structures alike as in Ap/Bp stars and it is possible that they arise as a result of a similar mechanism (Donati & Landstreet 2009).
In low-mass stars, the observed magnetic fields are common and are thought to be generated by a dynamo action in the convection zone. They are characterized by a complex topology and high variability. On the other hand, Ap magnetism is not only limited to a small fraction of A stars but also has some specific properties. The fields reconstructed with oblique rotator model are shown to have relatively simple large-scale topology which resembles a dipole or a multipole of lower order, often inclined to the rotational axis. They also remain essentially unchanged on long timescales (as long as the main sequence lifetime) and the magnetic strengths are not correlated with the stellar rotation rates. These arguments are not in favor of an explanation of Ap magnetism by a dynamo. Such stars actually possess deeply buried convective zones (apart from thin convective shells close to the surface). The dynamo can only be fed by the motions deep in there, and one needs to come up with a mechanism that transports the generated strong fields from the convective core to the stellar surface. The buoyant rise of magnetic flux-tubes was considered to be too slow by Moss (1989) and was studied in a more elaborate analysis by MacGregor & Cassinelli (2003). The latter investigation resulted in quick rise times of < 106 yr through most of the radiative envelope, but in slow rise through the upper 5 − 10% of the stellar radius. The shortest total rise times obtained are 10 Myr for a 5 × 105 G flux-tube which is too long for explaining fields present early on the main sequence. Rising flux from a core dynamo would also result in more variable surface fields than the ones observed. Variations on a timescale of decades should have been noted by now.
Another characteristic feature of Ap stars is the fact that they typically rotate more slowly than their nonmagnetic counterparts. Rotation periods are usually smaller by a factor of 5 − 10, however, extremely slow rotators have been identified with periods Prot as low as of order 103 days. There is also a difference in distributions of the obliquity angles between the rotational and magnetic axes for slower and faster rotators. Faster rotators with periods of 100 days and less tend to have larger inclination angles, slower ones seem to have both axes aligned (Landstreet & Mathys 2000). However, recent results by Mathys (2008) suggest that for the extremely slowly rotating stars (Prot ≈ 103 days), the trend is reversed and the inclination angles are again large (as for the “fast” rotators, Prot < 100 days).
Since most observations are limited to detecting the largest-scale contributions to the magnetic-field topology, it is difficult to infer any dependence of the field complexity on the ages or rotation periods of the stars. Weak evidence for more complex fields at faster rotation comes from the statistics in Bagnulo et al. (2002) where the ratio of the quadrupolar to the dipolar component appears to decrease with rotation period.
One of the most striking observational facts about Ap stars is the existence of a lower threshold of the magnetic field. The sample analyzed by Aurière et al. (2007) shows that there are no stars with fields smaller than about 300 G, although such detection should in principle be possible. Last but not least, Ap stars are rarely members of close binary systems.
The currently favoured option for the origin of Ap star magnetism is the fossil field hypothesis. It is assumed that the fields originate from the interstellar medium and are amplified and advected as clouds collapse into protostars. Then the fields evolve into stable configurations. The question whether such configurations exist is for a long time one of the most important matters in the subject. No purely analytical solutions are known, see however Duez & Mathis (2010); Duez et al. (2010). By means of numerical methods, Braithwaite & Nordlund (2006) have demonstrated that in their setup, using a specific rescaling technique, indeed it was possible to find such solutions (having roughly equal poloidal and toroidal field strengths). According to their calculations, in order to observe fields with 103 G, the initial fossil fields should be rather large – of order of 106 G. Braithwaite (2009) extended this study to generate predominantly nonaxisymmetric stable solutions arising from a field spectrum mimicking the left-over state of pre-main-sequence convection, using the same field-replenishment technique as in Braithwaite & Nordlund (2006).
Although peculiar A/B stars are the objects outside Solar System for which magnetic fields have been relatively well observed and studied, little is known about small-scale details. Even quite sophisticated models involving combinations of a nonaligned dipole, quadrupole and higher terms seem to be too limited to provide reliable information about details (e.g. Bagnulo et al. 2001; Bagnulo 2001). At present, one is left with a situation where only rather general features of the magnetic fields should be considered, but the knowledge is quickly improving.
Since A/B stars have large radiative zones, it is plausible to assume that there is no significant turbulent magnetic diffusion. That implies that weak initial poloidal magnetic fields will be wound up by any differential rotation resulting in a significant toroidal component. In the absence of convection, the toroidal field may become very large and eventually unstable. The instability that is the most likely to act in such scenario is the kink-type instability, often referred to as the Tayler instability (TI – Vandakurov 1972; Tayler 1973; Acheson 1978).
In a radiative zone any radial motions are strongly suppressed by buoyancy. The TI is an instability of toroidal fields that can grow on almost horizontal displacements and therefore is probably the most relevant one in the considered circumstances. For a sufficiently large amplitude (depending on the radial profile of the field), the toroidal field becomes unstable to nonaxisymmetric disturbances. However, uniform rotation is a highly stabilizing factor for the TI (Pitts & Tayler 1985). The rotation frequency Ω is compared with the Alfvén frequency, 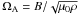 , where μ0 is the magnetic permeability and ρ is the density of the conducting medium. In particular, in the rapidly rotating regime with Ω ≫ ΩA, the system is always stable.
, where μ0 is the magnetic permeability and ρ is the density of the conducting medium. In particular, in the rapidly rotating regime with Ω ≫ ΩA, the system is always stable.
Wade et al. (2007) suggested that the existence of the lower field threshold can be related to the TI in the sense, that initially weak poloidal field of fossil origin can be too small to suppress differential rotation. Such fields become unstable and large-scale long-term stable structures cannot develop. On the other hand, if the initial field is large enough, the differential rotation is inhibited leading to a weaker, stable toroidal component enabling development of stable configurations.
Here, however, we consider an exactly opposite scenario in which the strong surface fields are actually a result of the instability. When the toroidal field becomes unstable, the TI would be responsible for “converting” the energy of differential rotation into strong surface fields. Then such fields can evolve into stable solutions or, in the initial phase, be constantly “fueled” by the instability as long as the differential rotation is large enough to wind up the toroidal field. The conditions acting in favor of the TI are the strong differential rotation and slow overall rotation – both of these can arise as a result of the process of losing angular momentum at the star surface.
The mechanism for taking away the angular momentum of a star is not discussed here and assumed to exist a priori. The issue was addressed for example in the studies by Stȩpień (2000) and Stȩpień & Landstreet (2002), where it was shown that magnetized winds can slow down a star (its surface) by orders of magnitude. From the point of view of the theory considered here, the fundamental difference between A and Ap takes place at this stage of evolution – Ap stars are, for some reason, slowed down (even a little) more than the normal A stars. This can lead to increased differential rotation (stronger toroidal fields) and slower overall rotation – both in favor of the TI. We do not have to assume the presence of a primordial field – it is possible that the fields of a convective dynamo in the first 0.2–2 Myr provide the magnetism required for spin-down. The convection zones recedes toward the surface, and according to what is known about stellar dynamos, these fields will be axisymmetric. We will come back to this issue in Sect. 5.
A similar scenario has been discussed in the studies by Arlt & Rüdiger (2011a) and Arlt & Rüdiger (2011b). While they based their simulations on the Boussinesq approximation, we present results for a fully compressible flow in the present paper. We also observe a clear exponential growth of small initial noise-like disturbances. In other works devoted to nonlinear numerical simulations of the TI, it is often assumed that some constant (in time) external fields exist, usually a toroidal field of some form (e.g. Arlt et al. 2007). Here the problem is treated as an initial-value one – all the components of the velocity or the magnetic field are evolved in time.
The paper is organized as follows:
-
Section 2 describes the numerical model.
-
Section 3 is devoted to the evolution of initially unstable toroidal fields under various circumstances. We show there how rotation and an additional poloidal magnetic field stabilize the TI, and also discuss how rotation impacts on the geometrical properties of the surface radial magnetic fields.
-
Section 4 deals with the question of the stability of a toroidal field that is created consistently by differential rotation.
-
Section 5 further discusses the application to Ap/Bp stars.
2. Numerical model
The model mimics a radiative envelope of a typical A/Ap star, which is represented as a shell with the radius r spanning Rin ≤ r ≤ Rout in the spherical coordinate system with unit vectors 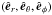 . The evolution is governed by the MHD equations together with the isothermal equation of state for the ideal gas,
. The evolution is governed by the MHD equations together with the isothermal equation of state for the ideal gas, ![\begin{eqnarray*} &&\partial_t \rho = -\grad \cdot (\rho \vec{u}), \\ &&\partial_t \vec{u} + \vec{u} \grad \cdot \vec{u} = -\frac{\grad P}{\rho} + \frac{1}{\perm \rho}(\rot{\vec{B}}) \times \vec{B} - g \er + \vec{f}\nonumber\\ && \hspace{2.15cm}+\,\nabla\cdot\left[\visc\left(\nabla\vec{u}+(\nabla\vec{u})^{\sf T} -\frac{2}{3}(\nabla\cdot\vec{u}){\rm I}\right)\right], \\ &&\partial_t \vec{B} = \grad \times (\vec{u} \times \vec{B}) + \diff \nablasq \vec{B}, \\ &&P = \rho R_{\rm gas} T_{\rm iso} / \mu, \end{eqnarray*}](/articles/aa/full_html/2013/02/aa20262-12/aa20262-12-eq20.png) \arraycolsep1.75ptwhere u,B,g,f,ρ,ν,η,μ0 represent respectively the velocity, the magnetic field, the radial gravitational force, the external body force, the density, the kinematic viscosity, the magnetic diffusivity, and the permeability. P is the pressure, Tiso the isothermal temperature, and Rgas,μ are the gas constant and the molecular weight. However, from now on, the capital R will simply denote the distance from the rotation axis, R = rsinθ. Some of the important parameters characterizing the system are: the speed of sound
\arraycolsep1.75ptwhere u,B,g,f,ρ,ν,η,μ0 represent respectively the velocity, the magnetic field, the radial gravitational force, the external body force, the density, the kinematic viscosity, the magnetic diffusivity, and the permeability. P is the pressure, Tiso the isothermal temperature, and Rgas,μ are the gas constant and the molecular weight. However, from now on, the capital R will simply denote the distance from the rotation axis, R = rsinθ. Some of the important parameters characterizing the system are: the speed of sound 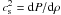 , the Alfvén speed
, the Alfvén speed 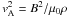 , the hydrodynamic Reynolds number defined as Re = Rin(Rout − Rin)Ωin/ν, the magnetic Prandtl number Pm = ν/η, the radial Brunt-Väisälä frequency N2 = −(g/ρ)∂rρ. In all the calculations presented here we assume Pm = 1 implying that Re = Rm, Rm being the magnetic Reynolds number, Rm = Rin(Rout − Rin)Ωin/η.
, the hydrodynamic Reynolds number defined as Re = Rin(Rout − Rin)Ωin/ν, the magnetic Prandtl number Pm = ν/η, the radial Brunt-Väisälä frequency N2 = −(g/ρ)∂rρ. In all the calculations presented here we assume Pm = 1 implying that Re = Rm, Rm being the magnetic Reynolds number, Rm = Rin(Rout − Rin)Ωin/η.
As mentioned in the introduction, we treat the problem as an initial-value one. That is, starting from an initial state (denoted by ui,Ωi,Bi,ρi), the system is evolved in time without any external magnetic background field or force. The only exceptions (optional, explicitly mentioned) are the constant radial gravity when g ≠ 0 or the additional forcing term f ≠ 0 used in Sects. 3.3 and 4.3. All calculations are done with the use of NIRVANA code (see e.g. Ziegler 1998, 2008) on a curvilinear, spherical grid (Ziegler 2011) matching the problem geometry. The calculation domain also includes the poles, 0 ≤ θ ≤ π,0 ≤ φ < 2π. The time stepping is done in normalized units, assuming rin = 1, rout = 2, ρ ~ 1, and ν = η = 10 − 2,..., − 3 representing considerably larger values than numerical viscosity and resistivity of the code (if not explicitly stated, all the plots are in the normalized units). Due to the constrained-transport ansatz for the induction equation, the divergence-free condition is fulfilled up to machine accuracy. To diminish oscillations of the compressible medium, ρ is initially always adjusted so that the gas is in the hydrostatic equilibrium with the gravity g and the centrifugal force (although not with the magnetic field which is always not force-free). Including the poles in the domain is considerably time-demanding, however we find that it gives superior accuracy when compared with “star in a box” Cartesian simulations. Consequently, the resolution in all the presented 3D runs was limited to 643. In some runs, the radial, latitudinal, and azimuthal resolutions were 64,64,128 respectively, which gave essentially the same results as the runs with smaller resolution with the same parameters (particularly, the values of the growth rates measured were independent of the resolution used). Moreover, all axisymmetric results were reproduced by means of 2D simulations and compared with a higher resolution of 2562. No significant differences were found in these cases either.
The radial boundary conditions (BCs) for the velocity are stress-free. This means that the normal component un = 0 and the tangential shear stress components Srθ = Srφ = 0 which leads to ur = 0, ∂r(uθ/r) = 0, ∂r(uφ/r) = 0. The BCs for magnetic field can be either perfectly conducting or insulating. The former require vanishing normal component of the magnetic field and the transverse components of the electric field, Br = Eφ = Eθ = 0 – in the code this is realized by setting Br to be antisymmetric and Bφ,Bθ to be symmetric. The insulating BCs are implemented as unphysical, local approximation, sometimes referred as to “pseudo-vacuum”. It is assumed that the tangential components of the field are zero, and the normal component is left unconstrained. Such BCs are utilized in the code in the way that Bφ,Bθ are antisymmetric and Br in the ghost zones is simply copied from the last cell adjacent to the boundary. Such approach significantly reduces calculation time while still allowing one to obtain surface fields of a star. We can justify this procedure by the fact that it has been shown that it does not lead to any spurious results and it has even successfully reproduced a few laboratory MHD experiments (e.g. Szklarski & Rüdiger 2007; Stefani et al. 2009; Rüdiger et al. 2012). When these “pseudo-vacuum” BCs are used in our simulations, as the initial large-scale poloidal field we choose to use B of the form of 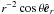 . This is somehow related to a dipolar field but is compatible with the defined BCs (since Bθ = 0). The BCs in θ and φ for all variables are periodic.
. This is somehow related to a dipolar field but is compatible with the defined BCs (since Bθ = 0). The BCs in θ and φ for all variables are periodic.
In all the cases presented below, the instability manifests itself as an exponential growth of the disturbances which in the beginning consist simply of noise in the magnetic field. The noise is essentially composed of magnetic waves in all spatial directions with random amplitudes which are smaller by a factor of about 105 than the initial large-scale field.
In the cases where differential rotation is imposed, we use initial velocity profiles as the ones in previous studies on this subject (e.g., Arlt & Rüdiger 2011a,b), namely ui = (0,0,RΩD) with 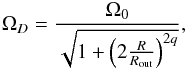 (1)Rout = 2, q ≤ 2 are subcritical to the Rayleigh instability (the Rayleigh criterion for hydrodynamical stability yields ∂RR2Ω ≥ 0).
(1)Rout = 2, q ≤ 2 are subcritical to the Rayleigh instability (the Rayleigh criterion for hydrodynamical stability yields ∂RR2Ω ≥ 0).
Obviously, the azimuthal velocity changes during the evolution. It is therefore practical to define a measure that tells us the average amplitude of the differential rotation at any instance of time. For a dimensionless measure of the differential rotation we use 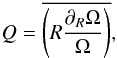 (2)where the overbar denotes volume averaging, and ∂R = sinθ∂r + r-1cosθ∂θ. Note that an initial q = 2 corresponds to Q ≈ 1.3. In some of the previous works on the subject, as the measure of the differential rotation q′, fitted to Eq. (1)at the equator was used. Since there is no particular reason why the rotational profile (1)should be maintained throughout the simulations, especially when a relatively large meridional circulation is present, we find the averaged value Q more appropriate for the diagnostics of the calculations presented below.
(2)where the overbar denotes volume averaging, and ∂R = sinθ∂r + r-1cosθ∂θ. Note that an initial q = 2 corresponds to Q ≈ 1.3. In some of the previous works on the subject, as the measure of the differential rotation q′, fitted to Eq. (1)at the equator was used. Since there is no particular reason why the rotational profile (1)should be maintained throughout the simulations, especially when a relatively large meridional circulation is present, we find the averaged value Q more appropriate for the diagnostics of the calculations presented below.
As recalled above, the criterion introduced by Pitts & Tayler (1985) requires 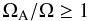 (3)for the TI to overcome the rotation. In the following, as to estimate whether the instability sets in we use the locally defined Alfvén frequency
(3)for the TI to overcome the rotation. In the following, as to estimate whether the instability sets in we use the locally defined Alfvén frequency 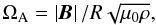 (4)and the global average w defined as
(4)and the global average w defined as 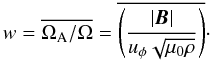 (5)The ratio w defined above takes into account variations in density which are particularly important when initially density stratified models are evolved. In such cases, in our simulations, the initial magnetic field is calculated from the potential being proportional to the density, so that the Lorentz force is independent of the density stratification. In other words, for the stratified case the magnetic field is calculated in the way that at each point the Lorentz force is the same as in a constant density ρ0 setup. When relating stratified and unstratified models, it is assumed that for the former ρ(r = Rin,θ = π/2) = ρ0. Consequently, when one wants to compare, e.g., growth rates for cases with different initial stratifications, special care needs to be taken to choose conditions giving the same w. For example, when we are interested in studying the field of the form of
(5)The ratio w defined above takes into account variations in density which are particularly important when initially density stratified models are evolved. In such cases, in our simulations, the initial magnetic field is calculated from the potential being proportional to the density, so that the Lorentz force is independent of the density stratification. In other words, for the stratified case the magnetic field is calculated in the way that at each point the Lorentz force is the same as in a constant density ρ0 setup. When relating stratified and unstratified models, it is assumed that for the former ρ(r = Rin,θ = π/2) = ρ0. Consequently, when one wants to compare, e.g., growth rates for cases with different initial stratifications, special care needs to be taken to choose conditions giving the same w. For example, when we are interested in studying the field of the form of 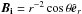 , it means
, it means 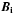 should be calculated using the potential Aφ = [ρ(r,θ)/ρ0] 1/2sinθ/2r (note that the variations in density in any case were not larger than about 30%). In the remaining part of the paper we give formulae for the initial magnetic field which are formally applied only for the models with the constant initial density ρ0. When the initial ρ(R,θ) is not constant,
should be calculated using the potential Aφ = [ρ(r,θ)/ρ0] 1/2sinθ/2r (note that the variations in density in any case were not larger than about 30%). In the remaining part of the paper we give formulae for the initial magnetic field which are formally applied only for the models with the constant initial density ρ0. When the initial ρ(R,θ) is not constant, 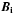 is calculated using the appropriate potential.
is calculated using the appropriate potential.
It is not entirely clear what values of Ω0 should be chosen for runs with varied degree of differential rotation, i.e. q in Eq. (1). To assure a somehow more objective comparison for each case, Ω0 is therefore adjusted so that the compared runs are characterized by the same average parameter w. We find it more informative in the sense that geometrical properties of the magnetic field and the differential rotation are both taken into account.
3. Initially unstable toroidal magnetic fields
This entire section focuses on initially unstable configurations to learn about the properties of the Tayler instability in a fully compressible, spherical domain. The initial velocity ui and initial magnetic field Bi are chosen in a way that w ≳ 1. Following Rüdiger & Kitchatinov (2010; hereafter RK10), the rotation is rigid, Ωi = Ω0, and the magnetic toroidal field is parameterized by 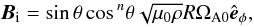 (6)with n being either 0 or 1. The first one represents a single magnetic belt symmetric with respect to the equator, the second a dipolar field antisymmetric w.r.t. the equator (two belts with opposite signs). Note that using (6)with n = 0 and rigid rotation Ω0 one gets from (5)w = ΩA0/Ω0 and
(6)with n being either 0 or 1. The first one represents a single magnetic belt symmetric with respect to the equator, the second a dipolar field antisymmetric w.r.t. the equator (two belts with opposite signs). Note that using (6)with n = 0 and rigid rotation Ω0 one gets from (5)w = ΩA0/Ω0 and 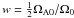 for n = 1.
for n = 1.
RK10 studied the influence of the thermal diffusion on the stability of the system (though for a much smaller Pm ≈ 10-3 than here). They have shown that such diffusion alters the criterion (3)so that the instability sets in for as low values as ΩA0/Ω ≳ 10-3. However, the growth rates γ become significantly smaller and drop quadratically with decreasing magnetic field when ΩA0/Ω < 1. In the isothermal limit the TI does not set in for ΩA0/Ω < 1 in the case if n = 0. Remarkably, the situation is different if n = 1, then the criterion for instability in such limit becomes 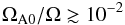 (7)(with accordingly small growth rates, e.g., for ΩA/Ω = 0.01,γ ≈ 10-5Ω; cf. Figs. 2 and 3 from RK10). If the rotation is sub-Alfvénic, the TI is always very fast – ΩA/Ω ≳ 1 gives γ ≃ ΩA.
(7)(with accordingly small growth rates, e.g., for ΩA/Ω = 0.01,γ ≈ 10-5Ω; cf. Figs. 2 and 3 from RK10). If the rotation is sub-Alfvénic, the TI is always very fast – ΩA/Ω ≳ 1 gives γ ≃ ΩA.
Figures 1 and 2 depict a nonlinear 3D simulation with growing nonaxisymmetric modes for n = 0 and w = 2 (i.e., ΩA0/Ω0 = 2). The m = 1 mode grows first and roughly exponentially. The magnetic BCs are conducting as to be compatible with the field (6).
We stress here that one of the main problems in numerical modeling of TI in a stellar context, are the small growth rates for ΩA < Ω. For example, as it will be shown later, it is fairly easy to produce toroidal fields by differential rotation which should be unstable according to (7). However, in order to reach a saturated state, it is necessary to perform simulations for a very large number of rotations. In practice it is a formidable task. In reality, 105 rotations are only about one thousand years and are so short compared to the life-time of the stars that there is no practical chance of observing a star in the process of developing instability.
 |
Fig. 1 Kinetic (Ek) and magnetic (Em) energies demonstrate a typical growth of the nonaxisymmetric m = 1 mode of the Tayler instability up to the saturated state. The initial field is of the form of a single belt, Eq. (6)with n = 0, rotation is initially rigid, Ω0 = 1,w = 2,Re = 1000,cs = 10,g = 0, and perfectly conducting radial boundaries are used. The growth rate of the m = 1 mode is γ ≈ 0.8ΩA0. |
 |
Fig. 2 Evolution of kinetic (Ek) and magnetic (Em) energies in the r,θ,φ components of the same simulation as shown in Fig. 1. Note the increased meridional flow induced by the initially not force-free magnetic field. |
One of the questions that we wanted to address in the compressible study of the TI was the influence of sonic waves on the growth rates. We performed simulations analogously to Fig. 1 with varied sound speed and radial gravity. The variation of the sound speed and the subadiabaticity of the stratification led to the growth rates shown in Fig. 3. The growth rates of the instability remain unchanged when compared to the nonstratified cases. As mentioned earlier, the magnetic potential has been multiplied for the stratified cases by the density ratio ρ(r,θ)/ρ0 so that the averaged quantity w = 2 in all the cases.
If the flow is adiabatic (vanishing thermal diffusivity κ), the stratification is highly stabilizing since the instability must work against the buoyancy forces. If non-zero thermal diffusion is included, the stabilizing effect of buoyancy is reduced on the length scales increasing with κ. Consequently, as expected, the simulations show that in the isothermal limit the stratification has no impact on the growth of the TI and the stabilizing effect of gravity does not exists. Nonetheless, in the majority of our simulations g is not zero in order to maintain, the radial dependence of the density to a certain degree (otherwise centrifugal forces would create higher density regions close to the outer shell).
 |
Fig. 3 Magnetic energy of the m = 1 mode versus time for the same initial conditions as in Fig. 1 but for various sound speeds cs as well as different magnitudes of radial gravity (expressed in terms of the square of the buoyancy frequency N2; the first four lines are for g = 0). |
3.1. Stabilization by rotation or poloidal field
Fast rotation or the additional presence of poloidal magnetic fields can suppress the Tayler instability discussed here. The stabilization due to rotation is demonstrated in Fig. 4a) where fast rotation is in the left part and slow rotation is in the right part of the diagram. For simulations the growth rates are calculated by fitting the appropriate exponential function to the values of the square root of energy in the Br-component for the m = 1 mode. For TI, for slow rotation, Ω0 ≪ ΩA0, the growth rate γ scales as γ ∝ ΩA (being proportional to the toroidal field strength), while it is 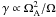 in the other case. These two scaling regimes are plotted as b) and c) on the figure.
in the other case. These two scaling regimes are plotted as b) and c) on the figure.
 |
Fig. 4 Normalized growth rate γ of the m = 1 mode (energy of Br). a) The initial magnetic field is as in Eq. (6), n = 0,ΩA0 = 2 and the rotation Ω0 is varied as to change w = ΩA0/Ω0. b) The dotted line is |
It is known that combinations of poloidal and toroidal fields are more stable than purely toroidal or purely poloidal configurations. In fact, all stable fields known in spherical geometry consist of both components. Rüdiger et al. (2011) studied a problem that is somehow analogous to the one discussed here, however, in a cylindrical geometry. As a measure of toroidal/poloidal magnetic field ratio let us use β defined as 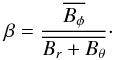 In this paper the initial large-scale poloidal field is of the form (due to the specific magnetic BCs discussed in Sect. 2):
In this paper the initial large-scale poloidal field is of the form (due to the specific magnetic BCs discussed in Sect. 2): 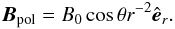 (8)Figure 5 depicts how the additional large-scale poloidal field (8)reduces the growth rate of the instability. Note that the solid line does not correspond to β → ∞ due to the non-zero initial magnetic noise which contains all components of B. The stabilization by poloidal fields is evidently a strong effect and has to be taken into account when one is interested in exciting the TI by winding up a poloidal component. It is necessary that | Btor | is significantly larger than | Bpol | . The linear calculations of Rüdiger et al. (2011) for the cylindrical case show that for β ≲ 10 there is an exponential increase (with decreasing β) of the magnetic field strength necessary to trigger the TI. Also nonaxisymmetric modes m > 1 start to dominate1.
(8)Figure 5 depicts how the additional large-scale poloidal field (8)reduces the growth rate of the instability. Note that the solid line does not correspond to β → ∞ due to the non-zero initial magnetic noise which contains all components of B. The stabilization by poloidal fields is evidently a strong effect and has to be taken into account when one is interested in exciting the TI by winding up a poloidal component. It is necessary that | Btor | is significantly larger than | Bpol | . The linear calculations of Rüdiger et al. (2011) for the cylindrical case show that for β ≲ 10 there is an exponential increase (with decreasing β) of the magnetic field strength necessary to trigger the TI. Also nonaxisymmetric modes m > 1 start to dominate1.
 |
Fig. 5 Growth of the TI for n = 0, rigid rotation Ω0 = 1,w = 2,Re = 1000,cs = 10,g = 0. The solid line is for a purely toroidal field (and some magnetic noise). The other lines correspond to the evolution with a non-zero initial large-scale poloidal field. |
3.2. Differential rotation
One of the aspects addressed in RK10 was the influence of differential rotation on the development of TI. Since the most unstable modes are nonaxisymmetric, one might anticipate that the differential rotation will tend to stabilize TI. Indeed, such effect is present in their calculation (although it is not very large).
Here we test the stability of our model for various degrees of differential rotation by adjusting the parameter q. Figure 6 shows growth of the m = 1 mode along with mean values Q. Apparently, such strong Bφ, in terms of w = 2, is enough to overcome the “smoothing” of m = 1 modes by the differential rotation and the instability develops. However, it might be not the case for w ≪ 1 where rotation itself becomes dominant. Notice that the differential rotation is maintained throughout the entire exponential growing process, i.e. Q is roughly preserved.
Figures 4, 6 and 7 demonstrate that in the parameter regime of interest here (w ≈ 1), the differential rotation does not play any significant role w.r.t. the onset of the instability and its growth rates. The horizontal shift between the curves a), d), e), f) in Fig. 4 for various q is likely just the result of our definition for the averaged quantity w. Additionally, the run denoted by an asterisk in this figure refers to a situation where initially 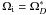 was increasing with R,
was increasing with R, 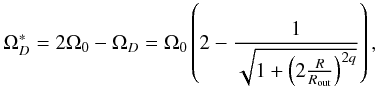 q = 2. This test assures us that the system is not yet in the regime of the azimuthal magneto-rotational instability (AMRI). No AMRI should occur in this case since the angular velocity increases outwards.
q = 2. This test assures us that the system is not yet in the regime of the azimuthal magneto-rotational instability (AMRI). No AMRI should occur in this case since the angular velocity increases outwards.
 |
Fig. 6 Magnetic energy for m = 1 (solid lines, left axis) and the measure of the mean differential rotation Q for the scenario where the gas was initially differentially rotating Ωi = ΩD. For different values q = (0,0.5,1,2), Ω0 was calculated to be (1,1.5,1.64,2.11) respectively so that all the models have w = 2. |
 |
Fig. 7 Growth rates γ in dependence on the differential rotation parameter q for various field-to-rotation ratios w. |
 |
Fig. 8 Temporal evolution of the surface magnetic field Br in the large-field limit with w = 600. |
 |
Fig. 9 Snapshots depicting the surface field Br at the time |
3.3. Influence of rotation on the geometry of the surface magnetic fields
A full study of the influence of the instability on the shape of the surface magnetic field would require a proper treatment of the radial magnetic boundary conditions (preferably including the atmosphere) and an analysis of magnetic configurations that are stable over timescales much longer than the ones considered here (as in e.g. Braithwaite & Nordlund 2006). At this stage of research this is not our main concern. However, we find it interesting to see how the resulting fields differ between models of slow and fast rotation soon after the saturation is reached, especially for the two regimes ΩA/Ω > 1 and ΩA/Ω ≲ 1. Up to this point we considered models with conducting boundary conditions that were consistent with the initial field, Eq. (6), but obviously could not provide any information about the poloidal field at the stellar surface, r = Rout. From now on, all the calculations are done with vacuum-like BCs defined in Sect. 2 which, on the other hand, can reproduce only the radial component of the magnetic field Br at the surface. Also, the initial field Bi from Eq. (6)is in such case not compatible with BCs (this is not a real problem, since the field quickly adjusts itself so the BCs are fulfilled).
In the following, we use the antisymmetric, azimuthal field Bi defined by (6)with n = 1. This configuration resembles a situation that is much more likely to exist inside the radiative envelope: two magnetic “belts” of Bφ antisymmetric w.r.t. the equator arise when a dipole-like poloidal field acts together with some differential rotation.
As discussed earlier, one of the unresolved issues concerning Ap stars is the problem of explaining the observed dependence of the obliquity on the rotation. We have performed a series of simulations with a forcing term that ensures maintaining the desired rotational profile Ωf throughout the whole simulation. We do this in order to follow the evolution of the magnetic field in the presence of the given angular velocity. Without the forcing term, maintaining the profile Ωf for timescales of our interest (couple of hundreds of Alfvén crossing times) would not be possible (see the next section).
The forcing term added to the momentum equation is 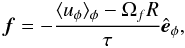 (9) ⟨ · ⟩ φ denoting an azimuthal average here, τ the timescale at which all axisymmetric deviations from the desired rotation profile will be smoothed out (in this section we use τ = 120/ΩA0). Note that with such definition of f, all the nonaxisymmetric disturbances can develop freely. The meridional flow – axisymmetric as well as nonaxisymmetric – is left unconstrained.
(9) ⟨ · ⟩ φ denoting an azimuthal average here, τ the timescale at which all axisymmetric deviations from the desired rotation profile will be smoothed out (in this section we use τ = 120/ΩA0). Note that with such definition of f, all the nonaxisymmetric disturbances can develop freely. The meridional flow – axisymmetric as well as nonaxisymmetric – is left unconstrained.
In the ΩA ≫ Ω limit, one expects that the rotation (and of course the degree of differential rotation) has no effect on the temporal evolution of the initially unstable magnetic field. Indeed, various tests showed that for w ≳ 102 the initial field with n = 1 evolves into apparently stable configurations, see Fig. 8. In the beginning of the simulation, as it is typical for this current instability, the fastest growing m = 1 disturbances are concentrated close to the axis. However, eventually, the resulting field somehow resembles a dipole inclined by 90° to the rotation axis. This structure, which we interpret as the large-scale manifestation of the m = 1 mode, decays on the magnetic diffusion timescale (which was chosen to be an order of magnitude larger than in the simulations for the previous section, ν = η = 10-2 so this diffusive decay could be easily identified). Note that in this figure and all other surface maps as well, Br is not plotted directly but rather scaled by the volume-averaged azimuthal field, 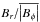 .
.
As will be discussed in Sect. 4, it is rather unrealistic to expect that the toroidal fields will reach ΩA ≫ Ω under the assumed circumstances. This is due to the fact that strong fields will reduce the shear before it produces large enough Bφ. Therefore it is more plausible to consider a scenario in which ΩA/Ω ≲ 1. In such a case one should expect that the rotation can have a significant impact on the generated surface fields, especially when the differential rotation comes into play since it can smooth out any nonaxisymmetric features.
Figures 9 and 10 show the surface fields Br for several values of w for rigid and differential rotation profiles enforced by Ωf (all the snapshots are plotted for the same time t). The rigid rotation does not prevent the existence of the already developed nonaxisymmetric poloidal fields and the nonaxisymmetric surface structure remains. On the other hand, the differential rotation has a large influence on the radial fields by diminishing the nonaxisymmetric part. After the saturated state is reached in the simulations, the toroidal component is too weak to drive any instability and, under the considered circumstances, Bφ cannot be rebuilt from poloidal fields by the differential rotation.
The energies of the m = 1 modes of the radial magnetic field Br are plotted in Fig. 12 for various parameters. As discussed earlier, the differential rotation does not prevent the TI from setting in, however, it clearly reduces the energy in the m = 1 modes at later stages of the evolution. Naturally, after the TI ceases to operate, in contrast to the poloidal fields, the toroidal field is much less affected by the differential rotation and its evolution is rather independent of q.
 |
Fig. 10 As in Fig. 9 but for various rates of differential rotation Ωf = ΩD with q = 2 and ΩD chosen so that, again, w = 60,6,1.5 (from the top). |
 |
Fig. 11 Radial surface field at |
4. The instability due to wound up Bφ
This section deals with the generation of unstable magnetic fields and the subsequent Tayler instability. In the previous Section, we considered magnetic fields with a strong initial toroidal component which triggers the TI. These are very unlikely to be present ab initio, and large Bφ must somehow be generated, preferably by poloidal fields and differential rotation as the most likely candidate in the stellar context. In the following scenarios we start with an initial Bφ = 0 (however, the magnetic noise is always added for all the components).
The interplay of poloidal magnetic fields and differential rotation is a subject widely discussed in the context of stellar evolution. In particular, the important question is how the fields influence differential rotation over time. Already fields much weaker than what a turbulent dynamo would generate are sufficient to enforce uniform rotation in various contexts such as the radiative envelopes of intermediate mass stars (e.g. Moss 1992) or the solar radiative interior (e.g. Mestel & Weiss 1987; Rüdiger & Kitchatinov 1997; Sule et al. 2005).
4.1. Winding up Bφ by differential rotation
Consider a differentially rotating gas with ΩD(r,θ) in the presence of an axisymmetric, poloidal magnetic field, Bpol = (Br,Bθ,0). Neglecting magnetic diffusion and meridional circulation, we get from the induction equation that ∂tBr = ∂tBθ = 0 and Bφ is wound up according to 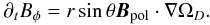 (10)This toroidal component together with Bpol reacts back on the azimuthal component of the velocity by a Lorentz force ∝ BrBφ leading to harmonic oscillations with period roughly equal to the period of a magneto-hydrodynamic wave along the lines of force,
(10)This toroidal component together with Bpol reacts back on the azimuthal component of the velocity by a Lorentz force ∝ BrBφ leading to harmonic oscillations with period roughly equal to the period of a magneto-hydrodynamic wave along the lines of force, 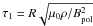 (e.g. Mestel 1953). This means that after a time ≈ τ1, the torque due to the produced Bφ will significantly affect the rotational velocity. For a typical star, an initial field of the order of μG is sufficient to generate forces that will influence the internal differential rotation of the star during its lifetime (Rüdiger & Kitchatinov 1997; Spruit 1999).
(e.g. Mestel 1953). This means that after a time ≈ τ1, the torque due to the produced Bφ will significantly affect the rotational velocity. For a typical star, an initial field of the order of μG is sufficient to generate forces that will influence the internal differential rotation of the star during its lifetime (Rüdiger & Kitchatinov 1997; Spruit 1999).
Let as assume that the differential rotation amplifies Bφ linearly. According to the local approximation by Spruit (1999) which takes into account rotation and magnetic diffusion, the time at which the instability sets in can be estimated as 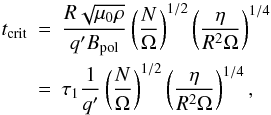 q′ being a dimensionless measure of the differential rotation, q′ = RBpol·∇ΩD/Ω | Bpol | . For a typical A star, tcrit is a very short time: in CGS N = 10-3,R = 1011,η = 103,Ω = 10-6,Bpol = 1 and q′ = 0.1 give a τcrit = 0.18τ1 or ≈ 103 years. In reality, the amplification by differential rotation diminishes when Lorentz forces start to become important, so the actual τcrit may be of similar value as τ1. It all depends on the steepness of the differential rotation whether the fields become Tayler unstable before ceased differential rotation provides no more amplification.
q′ being a dimensionless measure of the differential rotation, q′ = RBpol·∇ΩD/Ω | Bpol | . For a typical A star, tcrit is a very short time: in CGS N = 10-3,R = 1011,η = 103,Ω = 10-6,Bpol = 1 and q′ = 0.1 give a τcrit = 0.18τ1 or ≈ 103 years. In reality, the amplification by differential rotation diminishes when Lorentz forces start to become important, so the actual τcrit may be of similar value as τ1. It all depends on the steepness of the differential rotation whether the fields become Tayler unstable before ceased differential rotation provides no more amplification.
A detailed discussion concerning the initial rotational profile, and therefore the estimation of the value of q′, lies beyond the scope of this paper. We speculate that the difference between a normal A star and an Ap star lies especially in the steepness of the differential rotation. In such case an Ap star would be characterized by larger q′ than its normal counterpart.
 |
Fig. 12 Decay of nonaxisymmetric m = 1 modes of Br for various w and q. For rigid rotation, q = 0, the decay takes place at the magnetic diffusion timescale. |
The effect of initially nonaxisymmetric fields is not so obvious. As discussed by Mestel (2012, and references therein) in his Chapter 9, oblique poloidal fields are likely to be destroyed rather than acting toward uniform rotation. Since it is an interplay between wind-up, diffusion and instability, it is not straightforward to draw clear conclusions for real stars. For the scope of this paper we assume initially oblique poloidal fields are negligible in the angular-momentum transport.
From the point of view of numerical modeling of the TI due to azimuthal magnetic fields produced by differential rotation, one may think that it is crucial to reach the ratio ΩA/Ω ≳ 1 giving a growth rate of the instability of the order of the rotation period. As discussed above, calculations by RK10 show that for a dipolar magnetic geometry and ΩA/Ω = 0.01, the growth rate γ ≈ 10-5Ω. Such value can easily lead to an instability during a stellar lifetime, however, it is impossible to simulate numerically such large number of rotations of a differentially rotating body in order to obtain a saturated state.
Assuming Ω being constant in time and initially Bφ = 0, we can roughly estimate that the Bφ should be largest at the time τ1 (and much larger than the poloidal component). From Eq. (10) we obtain the upper limit 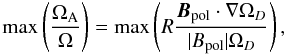 (11)which depends solely on the geometry of the initial poloidal field and the rate of differential rotation (in these considerations ΩA refers to the Alfvén frequency of the toroidal field only). For example, using the Eqs. (1)and (8)one obtains max(ΩA/Ω) = 4qqsinθ(R/Rout)2q/(1 + 4q(R/Rout)2q) giving max(ΩA/Ω) = 0.33,0.8,1.9,2.9, and 3.9 for q = 0.5,1,2,3, and 4, respectively. However, these values are significantly overestimated since the above formula does not take into account that the growth of Bφ is no longer linear when ∇ΩD gets reduced.
(11)which depends solely on the geometry of the initial poloidal field and the rate of differential rotation (in these considerations ΩA refers to the Alfvén frequency of the toroidal field only). For example, using the Eqs. (1)and (8)one obtains max(ΩA/Ω) = 4qqsinθ(R/Rout)2q/(1 + 4q(R/Rout)2q) giving max(ΩA/Ω) = 0.33,0.8,1.9,2.9, and 3.9 for q = 0.5,1,2,3, and 4, respectively. However, these values are significantly overestimated since the above formula does not take into account that the growth of Bφ is no longer linear when ∇ΩD gets reduced.
A crude approximation that does not neglect such feedback can be derived from the momentum and the induction equations assuming a linear change of ∂rΩ in time from its initial value ∂rΩi to 0 (mimicking the point where |Bφ| reaches its maximum). Neglecting some less important terms, ![\begin{eqnarray*} B_\phi(t) &=& \int\limits_0^t r B_r \sin{\theta}(\partial_r \Omegai)(1-t'/t_1) {\rm d}{t'} \\[-2mm] \Omega(t) &=& \int\limits_0^t \frac{B_r B_\phi(t')}{r^2 \sin{\theta}} {\rm d}{t'} + \Omegai \end{eqnarray*}](/articles/aa/full_html/2013/02/aa20262-12/aa20262-12-eq204.png) and setting ∂rΩ(t = t1) = 0 one can find that
and setting ∂rΩ(t = t1) = 0 one can find that ![\begin{equation} \begin{array}{l} \displaystyle{ \max{\left(\frac{\Omegaa}{\Omega}\right)} = \frac{r B_r \partial_r \Omegaz}{2\Omegaz}} \\ \phantom{\max{\left(\frac{\Omegaa}{\Omega}\right)}}\times \displaystyle{\sqrt{\frac{3 \partial_r \Omegaz} {B_r[-2r\partial_r B_r \partial_r \Omegaz + B_r(\partial_r \Omegaz - r \partial_{rr} \Omegaz)]}}}\cdot \\ \end{array}\label{eq:estmaxoma} \end{equation}](/articles/aa/full_html/2013/02/aa20262-12/aa20262-12-eq206.png) (12)Substituting our profile for the differential rotation (1)and the initial field (8)into the above equation, we get maximum values of ΩA/Ω to be 0.17, 0.32, 0.61, 0.86, and 1.1 for q = 0.5,1,2,3, and 4, respectively (in the domain r ∈ [0,∞),θ ∈ [0,π/2)). Note that already q = 3 in ΩD is hydrodynamically unstable according to the Rayleigh criterion and will probably halt the growth of Bφ much earlier.
(12)Substituting our profile for the differential rotation (1)and the initial field (8)into the above equation, we get maximum values of ΩA/Ω to be 0.17, 0.32, 0.61, 0.86, and 1.1 for q = 0.5,1,2,3, and 4, respectively (in the domain r ∈ [0,∞),θ ∈ [0,π/2)). Note that already q = 3 in ΩD is hydrodynamically unstable according to the Rayleigh criterion and will probably halt the growth of Bφ much earlier.
 |
Fig. 13 A 2D simulation demonstrating the process of winding up of Bφ by the differential rotation, Ω0 = 1,cs = 10,g = 0,q = 2,Br0 = 0.1, a) unconstrained flow; b) the meridional circulation was canceled ur = uθ = 0; c) constant background velocity field, ∂tu = 0; Bφ eventually decaying due to the magnetic diffusion; d) smaller initial magnetic field, Br0 = 0.05. |
These rough calculations show that a differential rotation and an initially weak poloidal component cannot easily produce an azimuthal magnetic field that is strong enough to excite the TI which will grow on reasonably short timescales suitable for a numerical simulation. According to the above assumptions, even for q = 2 one can get at most γ = 10-2Ω which is still rather small from the numerical point of view. This is of special importance when one deals with stress-free radial boundaries where differential rotation decays by means of hydrodynamical transport (of course, the situation would look different if a boundary driven or a forced flow would be considered).
The above discussion assumed initially axisymmetric fields. This can be justified due to the process of rotational smoothing, which in a star smears out any weak nonaxisymmetric field on a short timescale (see e.g. Spruit 1999). Neglecting the meridional flow is a simplification that has no dramatic effect, but we should keep in mind that it also reduces the differential rotation on the long term thus further reducing the maximally possible ΩA/Ω.
Figure 13 depicts the process of winding up Bφ by the differential rotation from the poloidal field of the form from Eq. (8)in an axisymmetric 2D simulation. Various conditions are considered – an unconstrained flow with stress-free boundary conditions for two different strengths of the initial poloidal field, a flow for which the meridional circulation was canceled, uθ = ur = 0, and a flow with the constant velocity background, ∂tu = 0. The small discontinuities for a) and b) are due to the fact that the actual locations of the maximum change with time. As predicted, the maximum of ΩA/Ω is independent of the strength of the initial poloidal field. For the case with constant u, the growth of Bφ is limited only by the magnetic diffusion.
 |
Fig. 14 Dependence of max(ΩA/Ω) and max(w) on the differential rotation parameter q, as obtained from 2D simulations (parameters other than q are as in Fig. 13). The dashed line was calculated by Eq. (12). |
Figure 14 shows the three quantities characterizing the wound-up Bφ as a function of q: max(ΩA/Ω),max(w), and the value calculated using Eq. (12). For various q, Ω0 was chosen so that in all these cases the initial kinetic energy is equal. One can see that for the largest q = 2 (which is close to the hydrodynamical instability according to the Rayleigh criterion), the maximum value of the averaged quantity max(w) is about 0.1 (max(ΩA/Ω) ≈ 0.4, see Fig. 13). This is a rather small value bearing in mind the growth rates of the TI. Naturally, the growth of Bφ is so much limited due to the decrease in the differential rotation. This is shown in Fig. 15 where one can see that the mean degree of differential rotation Q is significantly reduced even after couple of turns. Also note that in the purely hydrodynamical case – the solid line – for the considered Re ≈ 103, Q decreases by about 50% after 10 rotations by means of viscous and hydrodynamical-transport effects.
We conclude that the wound-up Bφ does not guarantee that the TI will be triggered in our numerical model. In the fact we were unable to “observe” the instability in any freely evolving scenario (i.e. stress-free BCs, no external magnetic fields or forcing) using initial conditions having subcritical toroidal field. One shall also keep in mind that the TI does not only require large Bφ but also Bφ ≫ Bpol since the presence of relatively strong poloidal field suppresses the instability, cf. Sect. 3.1. In the end, we are left in a situation where some numerical tricks are necessary in order to obtain the exponential growth of the TI by winding up an initially weak poloidal component.
 |
Fig. 15 Suppression of the differential rotation by the poloidal field, Eq. (8), with various amplitudes. The other parameters are as in Fig. 13. |
 |
Fig. 16 Shape of the toroidal magnetic field produced by the constant velocity field (0,0,ΩDR),q = 2. The solid (dashed) lines represent positive (negative) Bφ, the arrows illustrate the poloidal component. Initially the magnetic field was: Bi = Bpol from Eq. (8)(left) and the random noise for all the components (right). Of course, in the latter case, the polarity with respect to the equator can be arbitrary. |
4.2. Winding up Bφ using a constant velocity field
In this section, we wish to obtain numerical states that are TI unstable due to the wound up Bφ. We achieve this here by dividing simulations into two stages:
- i)
Initial weak poloidal field (of the form as in Eq. (8)or just the random noise) is wound up by the time-independent differential rotation, ∂tu = 0, meaning that the momentum equation is not evolved. In such case the growth of Bφ is limited only by the magnetic diffusion and its strength is determined by the time of winding (ΩD is the same for all simulations in this section).
- ii)
When the toroidal field becomes strong enough (in terms of w ≳ 1), the constraints on the velocity are removed and the system is let to freely evolve (with stress-free and vacuum BCs).
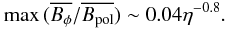 (13)This sets a limit for the magnetic diffusivity – if it would be too large, the magnetic fields would actually start to be dissipated before Bφ ≫ Bpol is achieved. In particular, for the value of η = 10-3 one obtains
(13)This sets a limit for the magnetic diffusivity – if it would be too large, the magnetic fields would actually start to be dissipated before Bφ ≫ Bpol is achieved. In particular, for the value of η = 10-3 one obtains 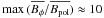 which is enough to overcome the stabilizing effect of the poloidal component. Of course, this issue is important only from the numerical point of view – the microscopic magnetic diffusivity in stars is believed to be much smaller so that the diffusive time-scale is longer than a stellar life time. Scaling the equations to physical units corresponding to a typical A star, one obtains
which is enough to overcome the stabilizing effect of the poloidal component. Of course, this issue is important only from the numerical point of view – the microscopic magnetic diffusivity in stars is believed to be much smaller so that the diffusive time-scale is longer than a stellar life time. Scaling the equations to physical units corresponding to a typical A star, one obtains 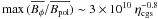 giving
giving 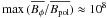 for ηcgs = 103 cm2 s-1.
for ηcgs = 103 cm2 s-1.
Figure 17 shows the evolution of the energies in different components of u and B for a typical simulation of step (ii). It is understood that the field created in step (i) is by no means force-free. Consequently, at the beginning of the unconstrained stage the system is far from an equilibrium and a highly dynamical process takes place. The energy of the meridional flow quickly increases from zero to values comparable to the energy of the toroidal magnetic field. Nonetheless, the instability sets in and the energy of m = 1 as well as the energy of the poloidal magnetic field grows by many orders of magnitude.
Note that at t = 0, the radial field is practically zero at the surface (the initial magnetic noise is constructed in a way which satisfies Br = 0 at r = Rin,r = Rout). Therefore, the relatively large surface fields visible in Fig. 18 arise solely due to the TI. The maximum surface fields reach about 10% of the mean interior Bφ. In Fig. 19 we plot the surface-averaged |Br| scaled by the volume-averaged |Bφ| in dependence on the initial w (that is w which is calculated for a flow at the end of step (i)). The threshold values for w that lead to significant surface fields is larger than unity though. We explain this by the fact that an increased Bφ is required due to the mentioned transfer of magnetic energy into kinetic energy. Nonetheless, it can be concluded that the instability is responsible for producing average surface fields being of the order of 1% of the volume-averaged toroidal field in this scenario.
 |
Fig. 17 A typical simulation of step (ii) from the procedure described in Sect. 4.2. The initial Bφ has been wound up from the magnetic noise eventually reaching a configuration as in Fig. 16 with w = 100. At the time corresponding to t = 0 in the plot, the constraints on the velocity were removed and the system could evolve freely, cs = 100,N2 ≈ 104. |
 |
Fig. 18 Map of the surface magnetic field at t = 0.3 [2π/Ω0] (this t is not shown in Fig. 17) after removing the constraints on the velocity at the moment when w reached 100 in step (i), Sect. 4.2. |
4.3. Forced slow-down of the rotation
Another way of obtaining the TI unstable states that are accessible to numerical studies is to start a simulation without any constraints and then, at some arbitrarily chosen time t′, take away the kinetic energy of the azimuthal rotation so that ΩA/Ω becomes supercritical. One can understand this as a braking process in the pre-main-sequence evolution of the star that leads to the relatively long rotation periods of Ap stars. In the model described below we start with 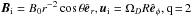 and, around the time t′, we apply a forcing that brings down the flow to the desired regime where w ≳ 1. The forcing has the form of a smooth transition
and, around the time t′, we apply a forcing that brings down the flow to the desired regime where w ≳ 1. The forcing has the form of a smooth transition 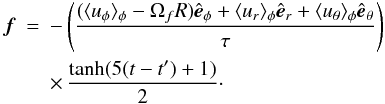 (14)Figure 20 depicts kinetic and magnetic energies for a simulation with Ωf = 0.03Ω0, t′ chosen to be about 15 rotations, t′ = 15 [2π/Ω0] and τ = 400 [2π/Ω0] . After reaching this time, the forcing term is responsible for taking away the angular momentum and ensuring rigid rotation with Ωf. While changing the azimuthal rotation, there is a very significant increase of the meridional circulation which can lead to spurious results due to the hydrodynamical mechanisms only. To get rid of this effect, the analogous forcing is applied also for the ur and uθ components (unlike in the case discussed in Sect. 3.3). This means that the axially averaged meridional circulation is significantly reduced. The exponential growth of m = 1 mode visible in the figure, clearly indicates that taking the azimuthal energy from the system leads to the fast growth of the TI.
(14)Figure 20 depicts kinetic and magnetic energies for a simulation with Ωf = 0.03Ω0, t′ chosen to be about 15 rotations, t′ = 15 [2π/Ω0] and τ = 400 [2π/Ω0] . After reaching this time, the forcing term is responsible for taking away the angular momentum and ensuring rigid rotation with Ωf. While changing the azimuthal rotation, there is a very significant increase of the meridional circulation which can lead to spurious results due to the hydrodynamical mechanisms only. To get rid of this effect, the analogous forcing is applied also for the ur and uθ components (unlike in the case discussed in Sect. 3.3). This means that the axially averaged meridional circulation is significantly reduced. The exponential growth of m = 1 mode visible in the figure, clearly indicates that taking the azimuthal energy from the system leads to the fast growth of the TI.
Note that, unlike in the simulations presented in the previous section, initially the radial component of magnetic field is not negligibly small. At the moment of the onset of the TI, it is one or two orders of magnitude smaller than Bφ. In particular, close to the critical w the structure of surface radial field is determined by the initial conditions and essentially does not change even when the saturation is reached, Fig. 21, top (w corresponds to the square in Fig. 22). Only for slower rotation (smaller Ωf), one can observe the complex structures overtaking the initial Br, Fig. 21, bottom (the triangle in Fig. 22).
For the considered scenario, the important question is the dependence of the growth rate of the TI on the ratio Ωf/Ω0 characterizing the amount of angular momentum taken from a star. From the results plotted in Fig. 22 one concludes that it is enough to slow down the differentially rotating flow by ≈ 10% in order to trigger the instability. In the figure, the growth rate γ is scaled with the Alfvén frequency 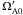 which is calculated at the time t′.
which is calculated at the time t′.
5. Discussion
We have considered the possibility that the Ap/Bp star phenomenon can be a result of the current-driven Tayler instability. In the depicted scenario, a differentially rotating star produces strong toroidal fields in its radiative zone, and is then spun down. The braking allows the TI to set in. This provides a mechanism for transporting the energy of the toroidal field into a large poloidal component at the star’s surface. Our study aims at using differential rotation for the consistent generation of the fields leading to the surface patterns. Braithwaite (2009) used a turbulent initial field as to represent the remnants of a convective phase of the star to reach nonaxisymmetric surface patterns. The actual evolution of the magnetic-field fluctuations is apparently not too different in these two studies, but the origins of the fluctuations differ. We added rotation as a discriminating parameter between unstable and stable configurations and may therefore have a handle on separating normal A stars from Ap stars.
As shown in Sect. 3.3, the problem of explaining the correlation between the rotational and the magnetic axes, would be replaced by a question about a mechanism that relates rotation rates and the degree of internal differential rotation. In particular, fast rotating stars would have to be characterized by a much weaker differential rotation. Alternatively, they would have to have the differential rotation reduced much sooner than slow rotators.
This view is naturally supported by theories explaining the loss of angular momentum in the pre-main-sequence phase by magnetized winds (Stȩpień 2000; Stȩpień & Landstreet 2002). It is reasonable to assume that slower rotators which were slowed down due to some surface effects will posses respectively stronger internal differential rotation, while faster rotators will spin less differentially. This would result in smoothing the nonaxisymmetric poloidal field for the slowly rotating Ap stars, leading to a dipolar field with small obliquity, while the faster among the Ap stars may keep their nonaxisymmetric fields emerging at the surface. Obviously, addressing these question in more details is only possible when an actual scenario responsible for slowing down a star is incorporated into the model (especially including its influence on the internal rotation). In the present paper, all these effects were parameterized with q, Ωf/Ω0, t′, etc., leaving the integration with real pre-main-sequence braking models for further studies.
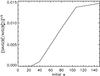 |
Fig. 19 Surface-averaged Br scaled by the volume-averaged Bφ in dependence on the strength of the initial toroidal field (represented by w which is determined by the time of winding up the field in step (i), Sect. 4.2). The values of Br and Bφ were calculated for the flow soon after saturation, at t = 0.1 [2π/Ω0] (corresponding to the rightmost side of Fig. 17). |
Also note that in the presented simulations the decay of the m = 1 mode is extremely fast when differential rotation is maintained by the forcing term. One of the key matters that is going to be addressed in further studies is what is the role of the instability on the reduction of differential rotation. The shear is certainly not reduced solely by the gas viscosity over the stellar life-time. The TI or other magnetic instabilities provide an efficient mechanism for transporting angular momentum from the stellar interior to the surface. One candidate is the magneto-rotational instability (Arlt et al. 2003).
As mentioned in the introduction, some recent observations (Mathys 2008) indicate that the obliquity angles are large for very slowly rotating Ap stars (Prot ≳ 103 days). This fact can be explained in the framework of the theory presented here as follows: stars that are spun down so significantly will posses large ΩA/Ω and rotation, differential or not, will have little impact on the large-scale fields produced by the instability. Consequently, the fields will have a tendency to build up the configuration depicted in Fig. 8. The surface fields obtained are all dominated by the l = 1, m = 1 mode. We cannot exclude that on the long term, secondary effects like thermodynamically driven flows will favour other especially higher-l modes. If observations eventually show that fields emerge as m > 1 modes, one should look into the conditions for the TI to excite larger m, or the proposed scenario may render invalid. There was no reliable statistics of observed field complexity versus stellar age or versus rotation rate available at the time of writing this paper.
 |
Fig. 20 Differentially rotating flow with Ω0 = 55,q = 2,cs = 100,N2 ≈ 104 winds up Bφ from a weak poloidal field of the form of Eq. (8). After about 15 rotations, the forcing term starts to operate, slowing down the flow to a rigid rotation with Ωf = 0.03Ω0 which leads to instability. |
We should stress that in the presented calculations we were not able to obtain a definitive stable magnetic configuration after the instability ceases to operate. Although the results (e.g. Fig. 8 and later) appear to by rather stable over hundreds of Alfvén crossing times, there is no guarantee that these structures are stable on very long (e.g. magnetic-diffusive) timescales. Treating the problem of stability of such fields is numerically uncertain and rather impossible without introducing some numerical tricks. Nonetheless, it seems plausible to assume that the TI-generated “initial conditions” can have a significant impact on the configuration of the long-term stable fields.
 |
Fig. 21 Surface radial magnetic fields for Ωf/Ω = 0.2 (top) and Ωf/Ω = 0.03 at the same time t = 50 [2π/Ω0] . At the top, only the remnant of the relatively large initial Br can be seen. |
One of the aspects of Ap/Bp magnetism that is naturally explained by the presented approach is the existence of the lower-field threshold. The observed minimal surface magnetic field is simply related to the strength of toroidal fields, that is, to the amount of internal differential rotation. To estimate this threshold, let us assume that the ratio of the Alfvén frequency to the rotational frequency in a star ΩA ∗ /Ω ∗ is similar as in the above calculations, 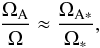 then, using the result that the averaged radial surface field is of the order of 1% of the averaged Bφ (Fig. 19), from the definition of w we obtain
then, using the result that the averaged radial surface field is of the order of 1% of the averaged Bφ (Fig. 19), from the definition of w we obtain 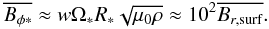 For a 2.5 M⊙ star with R = 1.5 R⊙, ρ = 0.015 g/cm3, a rotation period of 10 days, and a critical w ≈ 0.1 (Fig. 22), one gets
For a 2.5 M⊙ star with R = 1.5 R⊙, ρ = 0.015 g/cm3, a rotation period of 10 days, and a critical w ≈ 0.1 (Fig. 22), one gets 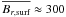 G. This is basically what is observed, so one can assume that our results are roughly of the right order of magnitude.
G. This is basically what is observed, so one can assume that our results are roughly of the right order of magnitude.
 |
Fig. 22 Growth rate γ as a function of the slow-down ratio Ωf/Ω. |
The spin-down of the stars relies on the presence of magnetic fields in the first place, during their pre-main-sequence evolution. Since fossil fields are not considered in our scenario, these fields must be generated in the convective dynamo of the early Ap star. A convective shell is present for about 0.6 to 5 Myr in 4-solar-mass and 2-solar-mass stars, respectively, assuming solar metallicity. As the convective shell recedes toward the surface, the dynamo will cease eventually, and the remaining convection destroys most of the fields by turbulent diffusion. Fields remaining in or pumped into the increasing radiative interior will persist, however, and may be considered the initial fields for our simulations.
In summary, we have shown that it is possible to trigger the current-driven kink-type instability – or Tayler instability – by a parameterized spin-down of a flow in a compressible spherical shell resembling the radiative zone of Ap/Bp stars. The TI will convert the large-scale toroidal field generated by differential rotation into relatively strong surface radial fields. The presented approach explains qualitatively the observed relation between obliquity and rotation; why slow rotators are preferred among such stars; and, more quantitatively, the existence of a minimum surface magnetic field. Undoubtedly, before accepting this scenario as a possible mechanism for Ap/Bp magnetism, it is necessary to consider the evolution of rotation/differential rotation and the interaction with a protostellar disk in a more detailed manner.
In order to qualitatively compare with the βcyl from (Rüdiger et al. 2011), for the cylindrical case we have, assuming μB = 2,η = 0.5 in their notation, 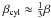 .
.
References
- Acheson, D. J. 1978, Roy. Soc. London Philos. Trans. Ser. A, 289, 459 [CrossRef] [Google Scholar]
- Arlt, R., & Rüdiger, G. 2011a, AN, 332, 70 [Google Scholar]
- Arlt, R., & Rüdiger, G. 2011b, MNRAS, 412, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Arlt, R., Hollerbach, R., & Rüdiger, G. 2003, A&A, 401, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlt, R., Sule, A., & Rüdiger, G. 2007, A&A, 461, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S. 2001, Geometrical structure of Ap and Bp star magnetic fields, in Magnetic Fields Across the Hertzsprung-Russell Diagram, eds. D. T. Wickramasinghe, G. Mathys, & S. K. Solanki, ASP Conf. Ser., 248, 287 [Google Scholar]
- Bagnulo, S., Wade, G. A., Donati, J.-F., et al. 2001, A&A, 369, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landi Degl’Innocenti, M., Landolfi, M., & Mathys, G. 2002, A&A, 394, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J. 2009, MNRAS, 386, 1947 [Google Scholar]
- Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Duez, V., & Mathis, S. 2010, A&A, 517, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duez, V., Braithwaite, J., & Mathis, S. 2010, ApJ, 724, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., & Mathys, G. G. 2000, A&A, 359, 213 [NASA ADS] [Google Scholar]
- MacGregor, K. B., & Cassinelli, J. P. 2003, ApJ, 586, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Mathys, G. 2008, Cont. Astron. Obs. Skalnate Pleso, 38, 217 [NASA ADS] [Google Scholar]
- Mestel, L. 1953, MNRAS, 113, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 2012, Stellar magnetism (Clarendon, Oxford) [Google Scholar]
- Mestel, L., & Weiss, N. O. 1987, MNRAS, 226, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1989, MNRAS, 236, 629 [NASA ADS] [Google Scholar]
- Moss, D. 1992, MNRAS, 257, 593 [NASA ADS] [Google Scholar]
- Pitts, E., & Tayler, R. J. 1985, MNRAS, 216, 139 [Google Scholar]
- Rüdiger, G., & Kitchatinov, L. L. 1997, AN, 318, 273 [Google Scholar]
- Rüdiger, G., & Kitchatinov, L. L. 2010, Geophys. Astrophys. Fluid Dyn., 104, 73 [Google Scholar]
- Rüdiger, G., Schultz, M., & Elstner, D. 2011, A&A, 530, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüdiger, G., Gellert, & M. Schultz, et al. 2012, ApJ, accepted [arXive:1201.2318] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Stȩpień, K. 2000, A&A, 353, 227 [NASA ADS] [Google Scholar]
- Stȩpień, K., & Landstreet, J. D. 2002, A&A, 384, 554 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stefani, F., Gerbeth, G., Gundrum, T., et al. 2009, Phys. Rev. E, 80, 066303 [NASA ADS] [CrossRef] [Google Scholar]
- Sule, A., Rüdiger, G., & Arlt, R. 2005, A&A, 437, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szklarski, J., & Rüdiger, G. 2007, Phys. Rev. E, 76, 066308 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Vandakurov, Y. V. 1972, SvA, 16, 265 [NASA ADS] [Google Scholar]
- Wade, G. A., Silvester, J., & Bale, K., et al. 2007, in Solar Polarization 5, eds. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 499 [Google Scholar]
- Ziegler, U. 1998, Comput. Phys. Commun., 109, 111 [Google Scholar]
- Ziegler, U. 2008, Comput. Phys. Commun., 179, 227 [Google Scholar]
- Ziegler, U. 2011, J. Comput. Phys., 230, 1035 [Google Scholar]
All Figures
 |
Fig. 1 Kinetic (Ek) and magnetic (Em) energies demonstrate a typical growth of the nonaxisymmetric m = 1 mode of the Tayler instability up to the saturated state. The initial field is of the form of a single belt, Eq. (6)with n = 0, rotation is initially rigid, Ω0 = 1,w = 2,Re = 1000,cs = 10,g = 0, and perfectly conducting radial boundaries are used. The growth rate of the m = 1 mode is γ ≈ 0.8ΩA0. |
| In the text | |
 |
Fig. 2 Evolution of kinetic (Ek) and magnetic (Em) energies in the r,θ,φ components of the same simulation as shown in Fig. 1. Note the increased meridional flow induced by the initially not force-free magnetic field. |
| In the text | |
 |
Fig. 3 Magnetic energy of the m = 1 mode versus time for the same initial conditions as in Fig. 1 but for various sound speeds cs as well as different magnitudes of radial gravity (expressed in terms of the square of the buoyancy frequency N2; the first four lines are for g = 0). |
| In the text | |
 |
Fig. 4 Normalized growth rate γ of the m = 1 mode (energy of Br). a) The initial magnetic field is as in Eq. (6), n = 0,ΩA0 = 2 and the rotation Ω0 is varied as to change w = ΩA0/Ω0. b) The dotted line is |
| In the text | |
 |
Fig. 5 Growth of the TI for n = 0, rigid rotation Ω0 = 1,w = 2,Re = 1000,cs = 10,g = 0. The solid line is for a purely toroidal field (and some magnetic noise). The other lines correspond to the evolution with a non-zero initial large-scale poloidal field. |
| In the text | |
 |
Fig. 6 Magnetic energy for m = 1 (solid lines, left axis) and the measure of the mean differential rotation Q for the scenario where the gas was initially differentially rotating Ωi = ΩD. For different values q = (0,0.5,1,2), Ω0 was calculated to be (1,1.5,1.64,2.11) respectively so that all the models have w = 2. |
| In the text | |
 |
Fig. 7 Growth rates γ in dependence on the differential rotation parameter q for various field-to-rotation ratios w. |
| In the text | |
 |
Fig. 8 Temporal evolution of the surface magnetic field Br in the large-field limit with w = 600. |
| In the text | |
 |
Fig. 9 Snapshots depicting the surface field Br at the time |
| In the text | |
 |
Fig. 10 As in Fig. 9 but for various rates of differential rotation Ωf = ΩD with q = 2 and ΩD chosen so that, again, w = 60,6,1.5 (from the top). |
| In the text | |
 |
Fig. 11 Radial surface field at |
| In the text | |
 |
Fig. 12 Decay of nonaxisymmetric m = 1 modes of Br for various w and q. For rigid rotation, q = 0, the decay takes place at the magnetic diffusion timescale. |
| In the text | |
 |
Fig. 13 A 2D simulation demonstrating the process of winding up of Bφ by the differential rotation, Ω0 = 1,cs = 10,g = 0,q = 2,Br0 = 0.1, a) unconstrained flow; b) the meridional circulation was canceled ur = uθ = 0; c) constant background velocity field, ∂tu = 0; Bφ eventually decaying due to the magnetic diffusion; d) smaller initial magnetic field, Br0 = 0.05. |
| In the text | |
 |
Fig. 14 Dependence of max(ΩA/Ω) and max(w) on the differential rotation parameter q, as obtained from 2D simulations (parameters other than q are as in Fig. 13). The dashed line was calculated by Eq. (12). |
| In the text | |
 |
Fig. 15 Suppression of the differential rotation by the poloidal field, Eq. (8), with various amplitudes. The other parameters are as in Fig. 13. |
| In the text | |
 |
Fig. 16 Shape of the toroidal magnetic field produced by the constant velocity field (0,0,ΩDR),q = 2. The solid (dashed) lines represent positive (negative) Bφ, the arrows illustrate the poloidal component. Initially the magnetic field was: Bi = Bpol from Eq. (8)(left) and the random noise for all the components (right). Of course, in the latter case, the polarity with respect to the equator can be arbitrary. |
| In the text | |
 |
Fig. 17 A typical simulation of step (ii) from the procedure described in Sect. 4.2. The initial Bφ has been wound up from the magnetic noise eventually reaching a configuration as in Fig. 16 with w = 100. At the time corresponding to t = 0 in the plot, the constraints on the velocity were removed and the system could evolve freely, cs = 100,N2 ≈ 104. |
| In the text | |
 |
Fig. 18 Map of the surface magnetic field at t = 0.3 [2π/Ω0] (this t is not shown in Fig. 17) after removing the constraints on the velocity at the moment when w reached 100 in step (i), Sect. 4.2. |
| In the text | |
 |
Fig. 19 Surface-averaged Br scaled by the volume-averaged Bφ in dependence on the strength of the initial toroidal field (represented by w which is determined by the time of winding up the field in step (i), Sect. 4.2). The values of Br and Bφ were calculated for the flow soon after saturation, at t = 0.1 [2π/Ω0] (corresponding to the rightmost side of Fig. 17). |
| In the text | |
 |
Fig. 20 Differentially rotating flow with Ω0 = 55,q = 2,cs = 100,N2 ≈ 104 winds up Bφ from a weak poloidal field of the form of Eq. (8). After about 15 rotations, the forcing term starts to operate, slowing down the flow to a rigid rotation with Ωf = 0.03Ω0 which leads to instability. |
| In the text | |
 |
Fig. 21 Surface radial magnetic fields for Ωf/Ω = 0.2 (top) and Ωf/Ω = 0.03 at the same time t = 50 [2π/Ω0] . At the top, only the remnant of the relatively large initial Br can be seen. |
| In the text | |
 |
Fig. 22 Growth rate γ as a function of the slow-down ratio Ωf/Ω. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.