| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220650 | |
| Published online | 06 December 2012 | |
Aluminium oxide in the optical spectrum of VY Canis Majoris⋆
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: kaminski@mpifr.de
2
Nicolaus Copernicus Astronomical Center, Polish Academy of
Sciences, Rabiańska
8, 87-100
Toruń,
Poland
Received: 29 October 2012
Accepted: 12 November 2012
We report the first identification of the optical bands of the B 2Σ + –X 2Σ + system of AlO in the red supergiant VY CMa. In addition to TiO, VO, ScO, and YO, which were recognized in the optical spectrum of the star long time ago, AlO is another refractory molecule which displays strong emission bands in this peculiar star. Simulating the bands of AlO, we derive a rotational temperature of the circumstellar gas of Trot = 700 K. By resolving individual rotational components of the bands, we derive the kinematical characteristics of the gas, finding that the emission is centred at the stellar radial velocity and its intrinsic width is 13.5 km s-1 (full width at half maximum). It is the narrowest emission among all (thermal) features observed in VY CMa so far. The temperature and line widths suggest that the emission arises in gas located within ~20 stellar radii, where the outflow is still being accelerated. This result contradicts equilibrium-chemistry models which predict substantial AlO abundances only to within a few stellar radii. We argue that non-equilibrium models involving propagation of shocks are needed to explain the observations.
Key words: astrochemistry / stars: winds, outflows / circumstellar matter / stars: individual: VY Canis Majoris / line: identification
© ESO, 2012
1. Introduction
VY Canis Majoris (VY CMa) is a peculiar red supergiant with a very high luminosity of 3 × 105 L⊙, an effective temperature, Teff, of 3200–3500 K, and an enormous size which may be up to 3000 R⊙ (Wittkowski et al. 2012). It is thought to be an evolved massive star with initial mass of 25 ± 10 M⊙ (Wittkowski et al. 2012). That mass was reduced to the current 17 ± 8 M⊙ (Wittkowski et al. 2012) due to mass-loss phenomena that occurred at different stages of its evolution. The current mass-loss rate of the order of 10-4 M⊙ yr-1 (Danchi et al. 1994) is probably the highest in VY CMa’s history and resulted in an extended (~7″) reflection and emission nebula that partially obscures the object (Smith et al. 2001; Humphreys et al. 2005). So far unknown remains the mechanism that elevates matter high enough above the stellar surface to cool it down to temperatures at which dust grains can condense. Once dust is formed, radiation pressure on grains can drive the powerful circumstellar outflow, but such a “standard” scenario alone does not explain all the observed features of the VY CMa’s outflow (Smith et al. 2001). It has been suggested that the highly complex structure of the nebula may be related to huge convective cells on the surface of the enormous star (e.g. Smith et al. 2001; see also Schwarzschild 1975).
Due to its extreme parameters and the possibility that it will explode as a core collapse supernova, VY CMa has been a subject of considerable astrophysical interest. This has recently intensified due to detections of new molecules in its cold circumstellar environment. While the first radio detections of oxides OH, H2O, SiO date back to late-1960s/early-1970s (Eliasson & Bartlett 1969; Knowles et al. 1969; Buhl et al. 1974), it is the recent developments in millimeter and submillimeter astronomy that have allowed to discover the rich molecular spectrum of VY CMa at radio wavelengths. Line surveys (i.e. systematic observations of substantial frequency ranges) like those of Ziurys et al. (2007) and Tenenbaum et al. (2010; see also Royer et al. 2010) allowed to fully explore the radio spectrum yielding 23 different molecular species (plus isotopologues) presently known. To date, the radio spectrum of VY CMa is the finest example of molecular richness in oxygen-rich gas around an evolved massive star.
Optical observers have realised the uniqueness of the spectrum of VY CMa much sooner (Joy 1942; Herbig 1970) than radio-astronomers and it is the unusual optical spectrum that have triggered much of the attention garnered by this object for more than a half a century. In addition to strong atomic emission lines, whose presence is a rare phenomenon by itself, VY CMa displays strong optical emission in molecular bands. Such molecular emission so far has been identified in electronic bands of TiO, VO, ScO and YO (Hyland et al. 1969; Wallerstein 1986, 1971; Herbig 1974). It indicates the presence of warm (a few hundred K) circumstellar material close to the star. All the oxides that are seen in emission in VY CMa are also those refractory molecules which are most often observed in absorption in the photospheres of cool stars. Another such refractory molecule, AlO, has never been reported in emission (nor in absorption) in the optical spectrum of VY CMa.
However, pure rotational emission from the AlO radical has been recently detected in VY CMa at millimeter wavelengths (Tenenbaum & Ziurys 2009). Being a refractory and also a relatively abundant molecule, AlO is of special astrochemical interest. It proceeds the formation of Al2O3 which is thought to be the first molecule to condense in an outflow of a late-type star like VY CMa (e.g. Sharp & Huebner 1990). Its observations bear the potential of gaining our understanding of dust condensation in outflows of cool stars, in particular of the formation of alumina dust. Due to an unresolved fine and hyperfine splitting of the pure rotation lines, the small number of detected transitions, and the poor angular resolution of the available radio data (Tenenbaum & Ziurys 2009), the origin of AlO emission in VY CMa remains poorly understood. A potential detection of AlO at shorter wavelengths (i.e. in the infrared or in the optical regimes) can help to better establish how the molecule is formed and what its role is in dust formation.
In an archival spectrum of VY CMa from 2001, we found strong emission features which undoubtedly belong to the B 2Σ + –X 2Σ + system of AlO. We describe the observations and the overall spectrum of VY CMa in Sects. 2 and 3. We characterise the AlO emission briefly in Sect. 3 and compare it to our simulations in Sect. 4, where we also give basic characteristics of the emitting gas derived in our analysis. We discuss the discovery of AlO optical emission and its implications in Sect. 5.
2. Observations and data reduction
The spectrum of VY CMa was taken with the Ultraviolet and Visual Echelle Spectrograph (UVES) at the Very Large Telescope (Paranal Observatory, Chile) on 2001 April 12. Two exposures of duration 2 and 10 s were taken. The spectrum covers three spectral ranges, i.e. 4010–5220 Å (blue), 6460–8315 Å (red), and 8430–10 300 Å (far red). The slit width of 1″ provided a spectral resolution of about R = 45 000. We acquired the spectra through the ESO archive and reduced them using the UVES pipeline1 and IRAF using standard procedures for echelle spectroscopy. With the slit length of 10″ and the slit position angle of 0°, the nebula of VY CMa filled a substantial part of the slit and a careful correction for the background was applied. The stellar spectrum was extracted within an aperture with a width of 2″. With seeing of 0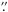 8 (full-width at half maximum, FWHM) during the observations, this aperture encloses most of the flux of the central source (the cut off was at 5% of the peak) and avoids most of the extended nebula. In this study, we focus on the blue spectrum for which the wavelength calibration is reliable to within ~0.4 km s-1 (3 rms) or better. Because no spectro-photometric standard star was observed with the spectral setup, the spectrum of VY CMa could not be properly calibrated in flux. To roughly put the final spectrum on a flux scale, we used the spectral energy distribution of VY CMa from Massey et al. (2006), which is based on observations five years after those with UVES. As we checked at the visual light curve by American Association of Variable Star Observers2, within uncertainties of 0.4 mag, VY CMa had the same brightness on the date of the UVES observations and those of Massey et al. (2006).
8 (full-width at half maximum, FWHM) during the observations, this aperture encloses most of the flux of the central source (the cut off was at 5% of the peak) and avoids most of the extended nebula. In this study, we focus on the blue spectrum for which the wavelength calibration is reliable to within ~0.4 km s-1 (3 rms) or better. Because no spectro-photometric standard star was observed with the spectral setup, the spectrum of VY CMa could not be properly calibrated in flux. To roughly put the final spectrum on a flux scale, we used the spectral energy distribution of VY CMa from Massey et al. (2006), which is based on observations five years after those with UVES. As we checked at the visual light curve by American Association of Variable Star Observers2, within uncertainties of 0.4 mag, VY CMa had the same brightness on the date of the UVES observations and those of Massey et al. (2006).
3. The optical spectrum of VY CMa
The extraordinary appearance of the optical spectrum of VY CMa has been extensively described in the literature (e.g. Hyland et al. 1969; Wallerstein 1971, 1986; Humphreys et al. 2005). In particular, a spectrum obtained a year before the UVES observations, at a similar resolution, and covering the range 5175–9140 Å was described in detail by Wallerstein & Gonzalez (2001). We find no significant differences in both spectra in the overlapping region, and therefore here outline only briefly the main spectral features. The photospheric (absorption) spectrum is dominated by molecular bands of TiO as expected for an early to intermediate type M-type star. On top of this photospheric spectrum, VY CMa displays a great variety of emission features which include atomic lines and molecular bands. The atomic emission is dominated by neutral atoms with lines of Ba II being the only known exception. Strongest is emission from resonance lines of K I, Na I, Ca I, and Rb I that form classical P-Cyg profiles. Many of the weaker emission features (e.g. from Ti I, Cr I, V I, and Fe I), exhibit inverse P-Cyg profiles or appear as pure emission lines. The spectrum contains also broad (non-photospheric) atomic absorption lines, which may be partially filled with emission.
The UVES spectrum contains strong and numerous emission bands of TiO and at least one band of VO (at 7867 Å) which all appear unchanged when compared to the spectrum of Wallerstein & Gonzalez (2001). Unfortunately, our spectrum does not cover the strongest bands of ScO and YO, which were present in the spectrum of Wallerstein & Gonzalez (2001), and there is no evidence for emission of these molecules within our coverage.
The optical spectrum of VY CMa short-ward of about 5100 Å, which is partially covered by the UVES spectrum, has not been explored by observers at high resolution. Between around 4800 and 5600 Å, we found strong emission features with a well recognizable “wavy” pattern indicating a molecular rotation spectrum. We have identified these features as belonging to the B 2Σ + –X 2Σ + (blue–green) system of AlO. A careful inspection of the spectrum revealed the presence of the Δν = −1, 0, 1, 2 sequences. The other well known sequence Δν = –2 with the main head above 5335 Å is not covered by the UVES spectrum and is too weak to be seen in the spectrum of Wallerstein & Gonzalez (2001). The UVES spectrum also does not reach the A–X system of AlO, which is located above 1.05 μm and we do not know any published spectrum that covers this range. In Fig. 1, we compare the sections of the spectrum containing the AlO emission with our best simulation of the bands (see below). The Δν = + 2 sequence is hardly recognisable and essentially appears only in two band-heads, i.e. (ν′′,ν′) = (2, 0) and (3, 1), that look similar to atomic emission features. Each of the lower overtones with Δν = −1, 0, 1 exhibits three to four unambiguously recognizable heads (i.e. with ν′′ ≤ 3 and ν′ ≤ 4) and the molecular emission can be traced in individual rotational components even up to ~100 Å from the main head. The head of the (0, 0) band, which reaches a flux level of 2.5 times the local continuum, is the most prominent emission feature in the blue part of the UVES spectrum.
 |
Fig. 1 The simulation of the B–X system of AlO (red line) is compared to the spectrum of VY CMa (blue line). The simulation was obtained for Trot = 700 K and Tvib = 2200 K. A rescaled spectrum of Betelgeuse is also shown (grey line) to illustrate the contribution of photospheric (and circumstellar) features that have not been included in the simulation. From top to bottom, the panels contain sections of the spectrum dominated by the Δν = 2, 1, 0, and –1 sequences. The positions of AlO band-heads are indicated with red markers and labels (giving ν′′ and ν′), while some of the strongest features in the stellar spectra are indicated by grey markings. |
4. Analysis of the AlO B – X system in emission
We simulated the emission in the B–X system of AlO using analogues procedures as in Kamiński et al. (2010). We assumed that the emission comes from a volume of homogeneous gas with no velocity gradient and that upper levels are populated by absorption of photons from a central source. The pumping to upper levels is less effective for optically thick lines, because of the reduction of flux from the central source, and this effect was taken into account allowing a derivation of gas optical thickness in the radial direction. The emitting gas is parametrised by vibrational and rotational temperatures (their meanings are explained later), column density in the direction to the star, and micro-turbulence. A given value of column density determines the optical thickness of a given transition and, as described later, it is the optical-thickness effects that allow a determination of the column density. In our approach, best fit parameters do not depend directly on the flux calibration nor the dust extinction in the nebula. In order to compare the simulation results to the observations, the simulated spectrum was smoothed with a Gaussian, what may be interpreted as a convolution with a macro-turbulence profile.
The molecular data were taken from a compilation of sources: the list of lines was built from spectroscopic constants in Saksena et al. (2008); the electronic transition moment was adopted from Zenouda et al. (1999); Franck-Condon factors were taken from Coxon & Naxakis (1985); rotational line-strength factors were computed numerically following Hougen (1970) and verified by comparison to the analytical formula in Kovacs (1969). Because Al has only one stable isotope, all the analysis was performed for the single isotopologue 27Al16O.
Since we deal with a 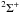 –
–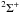 transition (Hund’s case b), each rotational level, designated by the quantum number N, is split into two sublevels, F1 and F2, with total angular momenta given by J = N+1/2 and J = N–1/2, respectively. This is known as spin- or ρ-doubling. The band is formed mainly by the doublet branches P1, P2 and R1, R2. There are also satellite branches
transition (Hund’s case b), each rotational level, designated by the quantum number N, is split into two sublevels, F1 and F2, with total angular momenta given by J = N+1/2 and J = N–1/2, respectively. This is known as spin- or ρ-doubling. The band is formed mainly by the doublet branches P1, P2 and R1, R2. There are also satellite branches 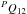 and
and 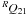 , which were included in the simulations, but their intensity drops very rapidly with increasing N and they have no practical meaning for our analysis. The ρ-doubling in the P and R branches is taken into account in our simulations following Saksena et al. (2008). Although there is some controversy in the literature on the splitting constants γ for ν′′ > 0 (see e.g. Launila & Berg 2011, for the most recent review), it does not affect our analysis.
, which were included in the simulations, but their intensity drops very rapidly with increasing N and they have no practical meaning for our analysis. The ρ-doubling in the P and R branches is taken into account in our simulations following Saksena et al. (2008). Although there is some controversy in the literature on the splitting constants γ for ν′′ > 0 (see e.g. Launila & Berg 2011, for the most recent review), it does not affect our analysis.
Figure 1 presents the results of our best simulation. The shapes of the heads, the heads-intensity ratios, and the shape of the overall rotational profile are very well reproduced by the simulation. Some minor deviations between observed and simulated spectrum are due to an imperfect spectrum normalization and a presence of photospheric and circumstellar features, which were not taken into account in the simulation. To illustrate the shape and positions of the contaminating features, we compare the spectrum of VY CMa to a spectrum of another red supergiant (Betelgeuse = α Ori, M1 Ia) in Fig. 1. This reference spectrum was extracted form the Paranal UVES Atlas (Bagnulo et al. 2003). The match between the photospheric and circumstellar absorption features in both stars is very good except that some features are slightly stronger in Betelgeuse (e.g. Hβ) or filled with emission components3. For VY CMa, the analysed spectrum can be satisfactorily explained by the combination of a cold photosphere and the emission spectrum of AlO. We also note that from the comparison of observations to the simulation, it is apparent that the AlO emission is not affected by any underlying photospheric absorption of AlO. If VY CMa follows the trend observed in giants4, which display AlO absorption only at spectral types later than M4 (very weak at M5) (Keenan et al. 1969), AlO absorption is negligible in VY CMa, which is of spectral type M4–M5 (e.g. Wittkowski et al. 2012) or earlier (~M2, Massey et al. 2006). Because the Δν = 0 sequence is strongest and least contaminated by the photospheric and circumstellar features, it was the primary subject of the further analysis.
By obtaining a grid of simulations with variable input parameters and comparing it to the observations, we were able to constrain some physical quantities of the AlO emitting gas. The rotational temperature (Trot), which corresponds to the population of rotational levels within the vibrational states, can be derived from the overall shape of the rotational contours. Particularly useful for putting constraints on Trot is the observed position of the local maximum of the emission in the (0, 0) band (outside the main bandhead), which occurs at 4654 ± 2 Å corresponding to N = 21 ± 2 (Fig. 1). It implies Trot between 600 and 900 K. Additionally, for rotational temperatures higher than ~800 K, the emission components of the R branch are too strong at the band origin, and below ~500 K the emission of the P branches forming the tail of the band is too weak. Therefore the rotation temperature implied by the simulation of the (0, 0) band is in the range Trot = 700 ± 200 K. However, the shape and intensity of the (1, 0) and (1, 2) bands is better reproduced by simulations with a higher rotational temperature between 900 and 1100 K.
Optical-depth effects also have an influence on the shape of the rotational spectrum. Because they are particularly evident in the intensity of the band-head with respect to the rest of the band, it is possible to decouple the optical thickness effects from those of varying Trot. Our best fit resulted in optical depths of τhead = 3.0, 1.0, and 0.14 in the heads of the (0, 0), (1, 1), and (2, 2) bands, respectively. These values are equivalent to setting the AlO total column density to NAlO = 6 × 1016 cm-2. Because our simulations do not contain any realistic velocity gradient, these values are upper limits on the actual optical depths and the column density, if the emission arises in an outflow. The shape of the rotational contour is also somewhat influenced by the assumed value of micro- and macro-turbulence, but we kept those parameters constant at FWHM = 1 km s-1 (equal to thermal broadening at ~1000 K) and FWHM = 6 km s-1, respectively.
The vibrational temperature (Tvib) is indicated by the relative strengths of heads within each sequence. We found satisfactory results for a broad temperature range between 1600 K and 2800 K. Particularly good fits to data were obtained when different vibrational temperatures (but still within the specified range) were assumed for different bands. The best simulation with Trot = 700 K and Tvib = 2200 K is shown in Figs. 1 and 3.
By comparing the simulation to observations, we were able to derive the bulk velocity of the AlO gas. Using the cross-correlation method implemented in IRAF’s task fxcor, we derived heliocentric radial velocity of Vhelio = 41 ± 1 km s-1 (or equivalently VLSR = 21 ± 1 km s-1 with respect of the local standard of rest). This velocity is confirmed when peaks of individual rotational components are compared to their rest wavelengths. Moreover, we do not see any systematic shift in peak positions with increasing excitation energy of the rotational components.
 |
Fig. 2 Rotational components of the B–X (0, 0) band of AlO as observed in VY CMa (blue histogram) and in our simulation (red line). The individual lines are unresolved doublets of members of the P1 and P2 branches. Their peaks are designated by rotational quantum numbers. Much fainter rotational components of the R branch can be seen in the simulation (only two were marked in the figure). |
 |
Fig. 3 The P(23) rotational component of the B–X (0, 0) band of AlO in the simulation (red line) and in the observed spectrum of VY CMa (blue histogram). The velocity is given with respect to the average wavelength of the doublet, whose splitting is 4.2 km s-1. The positions of the doublet components are shown by the two dashed lines in the upper part of the figure. Lines in the lower part show the hyperfine splitting in both components (from Launila & Berg 2011). |
Because of the good separation of the rotational components and their low optical thickness at high N (usually τ ≪ 1), we can examine the shape of individual lines for the kinematical profile of the AlO-bearing gas. The measured FWHM of lines between P(20) and P(30) of the (0, 0) band is 14.4 ± 1.2 km s-1. This value is however affected by several splitting effects. The nuclear hyperfine splitting due to nuclear spin of I = 5/2, which was not included in the simulation, is known to be very small (about 1.5 km s-1 at P(23); Launila & Berg 2011), i.e. smaller than our spectral resolution. Additionally, each rotational line is a blend of two components belonging the P1 and P2 branches separated due to the ρ-splitting, which is very well known for the (0, 0) band. Its magnitude changes linearly with rotational number and is negligible at low N (e.g. 0.3 km s-1 at N = 2), but significant at high rotational numbers (e.g. 6 km s-1 at N = 33). Correcting the measured widths for ρ-doubling gives a typical FWHM of 13.5 ± 1.5 km s-1. To illustrate the different splitting effects on the line profile we show them graphically in Fig. 3 for the P(23) line for which the hyperfine structure is known from Launila & Berg (2011).
A comparison of the individual profiles to the simulation in Fig. 2 reveals a small asymmetry of the observed profiles, i.e. the red wing is more extended (by ~2 km s-1). Although there is some uncertainty in the molecular data which we used in the simulation, we believe this effect is real. Additionally, on the blue side of each rotational component, a very weak absorption can be seen (it is more apparent when the spectrum is compared to the simulation – see Figs. 2 and 3). This and the profile asymmetry suggest that each rotational component may have a P-Cyg type profile. Some absorption can be also seen next to each of the strong band-heads (Fig. 1), what supports this interpretation. The absorption is however very weak and the P-Cyg shape is claimed here only as a tentative result.
5. Discussion
5.1. Interpretation of the emission properties
The central velocity of the optical AlO emission (VLSR = 21 ± 1 km s-1) is consistent with the velocity of the AlO millimetre lines (25 ± 6 km s-1) and is in excellent agreement with the stellar systemic velocity known from optical and radio/(sub-)millimetre observations (VLSR = 21.0 ± 1.5 km s-1) (e.g. Smith 2004, and references therein). Although, the central velocity of the AlO emission is much more accurately measured in the optical (where splitting effects are smaller and a large number of rotational transitions at high signal-to-noise ratio is observed simultaneously), the centres of optical emission lines may be red-shifted due to scattering on dust grains in the thick and expanding nebula (van Blerkom & van Blerkom 1978; Romanik & Leung 1981); this effect might have been observed in some absorption and emission features from the outer nebula of VY CMa (Humphreys et al. 2005). However, since the position of radio and optical lines of AlO are consistent within the uncertainties, this scattering effect must be very small in our case (≲3 km s-1), i.e. certainly much smaller than suggested theoretically by van Blerkom & van Blerkom (1978) for photospheric absorption lines in VY CMa.
The outflow of VY CMa observed in millimetre emission lines has been ascribed to at least three distinct kinematical components (Tenenbaum et al. 2010) with the fastest material moving at expansion velocity of at least 40 km s-1 producing broad lines with multiple peaks. In addition to those wide features, narrow emission lines centered approximately at the stellar systemic velocity have been detected, with the narrowest emission known arising from NaCl with FWHM = 16 ± 3 km s-1 (Milam et al. 2007); TiO is another molecule which displays such narrow features with FWHM = 18 ± 2 km s-1 (Kamiński et al. 2013). The narrowest of the pure atomic emission lines present in UVES spectrum have a FWHM of 22 km s-1. All these narrow lines are signatures of gas located within the inner outflow, perhaps even below the dust formation zone. The width of the AlO emission of 13.5 km s-1 is smallest among all detected (thermal) features in VY CMa’s circumstellar environment indicating that AlO probes deepest observed layers of the material leaving the photosphere. With the typical full-width at zero intensity of 27 ± 2 km s-1 corrected for the ρ-doubling, the AlO emission implies gas expansion velocity of Vexp = 13.5 ± 2.0 km s-1.
It should be mentioned that maser lines of SiO (and to a lesser degree of H2O) are known to exhibit even narrower emission components with widths down to 1 km s-1. These maser lines undoubtedly arise in the inner, accelerating envelope of VY CMa (within tens of mas from the star), but they usually do not trace the whole outflow, as most of thermal lines do, but rather individual clouds within the outflow. Moreover, due to a complex excitation mechanism, the SiO masers are observed in a ring-like feature surrounding the photosphere of VY CMa (e.g. Zhang et al. 2012) showing complex dynamics. Hence, the half-widths of individual lines do not correspond directly to the expansion velocity.
The slight asymmetry observed in AlO line profiles, with the red wing being more extended, is reminiscent of what is observed in the (sub-)millimetre lines of TiO (Kamiński et al. 2013). This asymmetry may suggest that even the inner wind region exhibits some degree of asymmetry. However, exactly the same type of asymmetry is expected to arise due to scattering in an expanding dusty nebula (van Blerkom & van Blerkom 1978; Romanik & Leung 1981). In addition to the optical thickness and geometry of the scattering medium, this effect is strongly dependent on the scattering properties of dust and for some dust types produces profile asymmetry without any apparent shift in line centres (Romanik & Leung 1981), which could be the case for the AlO lines. The origin of the asymmetry is not clear and requires modelling including a detailed treatment of scattering on dust. This is beyond the scope of this work. We note, however, that if the observed profiles are re-shaped by scattering, they are also slightly broadened and the intrinsic width of the AlO emission is even smaller than quoted above. The pure rotational lines of AlO observed at millimetre wavelengths by Tenenbaum & Ziurys (2009), for which scattering can be completely neglected, are severely affected by the hyperfine splitting and modest signal-to-noise ratios which complicate the profile analysis and the asymmetry cannot be verified. However, the authors were able to constrain the line widths to 10–15 km s-1 what is consistent with our analysis of the optical profiles.
The vibrational temperature we derived describes the population of vibrational levels in the upper electronic state in the sense of the Boltzmann distribution. Because the excitation is most likely radiative (the electronic state B2Σ is 29 691 K above the ground level), this approach is a crude simplification. The population of vibrational levels in B2Σ depends on the population in the ground state, the spectrum of the external radiation field, and the strengths of absorption bands populating the vibration levels. By taking Franck-Condon factors as band intensities and assuming a flat stellar spectrum, we calculated that a temperature between 1200 and 1800 K is more representative as the vibrational temperature. Taking the large uncertainties and the devious meaning of Tvib, it is of no practical value for the further discussion.
On the other hand, the rotational temperature of 700 K is expected to be close to the gas kinetic temperature, Tkin, what makes it a valuable parameter. The rotational temperature we derive is much above that found by Tenenbaum & Ziurys (2009) (Trot ~ 250 K) on the basis of a rotational-diagram analysis. Their value is however very uncertain as only three lines were measured at low signal-to-noise ratio. Our value of Trot is consistent with temperatures derived from analyses of other optical bands of refractory molecules observed in VY CMa in emission – Phillips & Davis (1987) found Trot = 600 ± 150 K from an analysis of the TiO γ′ system in emission, while Herbig (1974) found Trot = 370 and 790 K for the orange (A–X) band of ScO observed at two different dates.
5.2. The origin of the AlO emission
In the 2-dimensional UVES spectrum, the AlO emission is unresolved meaning that the emission region is smaller than 0 8 FWHM. The width of the AlO profile allows to constrain even better the size of the emitting region. By combining tangential (proper) and radial motions observed in H2O masers at three epochs, Richards et al. (1998) found expansion of the envelope within 75 to 440 mas from the star. By applying their expansion model (updated to the stellar distance of 1.2 kpc) we get a radius r = 18 ± 6 R⋆ (R⋆ = 2000 R⊙) for the AlO-emitting region.
8 FWHM. The width of the AlO profile allows to constrain even better the size of the emitting region. By combining tangential (proper) and radial motions observed in H2O masers at three epochs, Richards et al. (1998) found expansion of the envelope within 75 to 440 mas from the star. By applying their expansion model (updated to the stellar distance of 1.2 kpc) we get a radius r = 18 ± 6 R⋆ (R⋆ = 2000 R⊙) for the AlO-emitting region.
The type of observed line profiles also provides strong constraints on the dimension of the AlO emission region. If the gas was much closer to the star than the 18 R⋆ found above, say a few R⋆, the optical rotational profiles should display pronounced absorption components arising in gas seen in front of the stellar disk. Combined with a velocity gradient (which is observed in this region in SiO maser lines), such configuration should produce P-Cyg profiles with a high absorption-to-emission intensity ratio, i.e. much more pronounced than those we observe (if any absorption is present at all).
Decin et al. (2006) modelled the envelope of VY CMa with a variable mass loss and derived thermal model of the envelope with a detailed treatment of heating and cooling mechanisms. Assuming that Tkin ≈ Trot, we find that the temperature of 700 ± 200 K corresponds to a distance of 20 ± 5 R⋆ in Decin et al. (2006), which is consistent with the constraints found above. In the same model, gas of such temperature is located in the accelerating outflow. Their velocity law applied to the AlO expansion velocity (Vexp = 13.5 km s-1) indicates location within ~10 R⋆. The hydrogen density at 10–25 R⋆ in that model (corresponding to the mass-loss rate of 10-4 M⊙ yr-1) is within nH = 107–109 cm-3. Because critical densities for the observed rotational transitions of AlO are between 5 × 105 cm-3 (for N ≈ 1) and 5 × 109 cm-3 (for N ≈ 20)5, the population of rotational levels has a chance to be thermalized by collisions in this region (cf. Woitke et al. 1999), justifying our assumption that Tkin ≈ Trot. We must however note that the model of Decin et al. (2006) should be treated with caution as its parameters were constrained by observations of CO lines with the highest transition being J = 7–6 (155 K above the ground, ncrit = 4 × 105 cm-1) which does not probe well the accelerating outflow.
The above discussion suggests that the AlO emission comes from a region of a diameter of about 40 R⋆ (or 0 4). This allows us to calculate the AlO mean abundance. From our simulations, we get the AlO total column density of NAlO = 6 × 1016 cm-2. This value has a factor of a few uncertainty resulting from the uncertainties in the other simulation parameters. For the mass-loss rate of 10-4 M⊙ yr-1, the envelope extending from 1 R⋆ to 20 R⋆, the mean molecular weight of 1.3, and the mean velocity of 6 km s-1, the total hydrogen column is NH = 3 × 1024 cm-2 giving AlO mean abundance of [f] = log (NAlO/NH) ≈ −7.7. This value is uncertain by at least 1 dex.
4). This allows us to calculate the AlO mean abundance. From our simulations, we get the AlO total column density of NAlO = 6 × 1016 cm-2. This value has a factor of a few uncertainty resulting from the uncertainties in the other simulation parameters. For the mass-loss rate of 10-4 M⊙ yr-1, the envelope extending from 1 R⋆ to 20 R⋆, the mean molecular weight of 1.3, and the mean velocity of 6 km s-1, the total hydrogen column is NH = 3 × 1024 cm-2 giving AlO mean abundance of [f] = log (NAlO/NH) ≈ −7.7. This value is uncertain by at least 1 dex.
Chemical equilibrium models of circumstellar gas around evolved oxygen-rich stars predict high abundances of AlO only at relatively high temperatures. For instance, in the chemical-equilibrium model calculated by Gail & Sedlmayr (1998), the AlO abundance is expected to be higher than [f] = −9 only at temperatures between 1100 and 2000 K. Below these temperatures, the abundance of AlO drops steeply with the distance from the star (being converted to Al2O, Al2O2, and Al2O3) and at 800 K is already 6 dex below its peak value ([fmax] ≈ −8.5). Including condensation of alumina species into such models results in even stronger depletion of AlO at temperatures lower than 1800 K (Sharp & Huebner 1990). According to these models, therefore, the AlO gas should be located in a relatively thin layer a few R⋆ above the photosphere. This is strongly contradicted by our constraints on the size of the AlO emission region (see also Tenenbaum & Ziurys 2009) suggesting that the heavier alumina compounds, e.g. Al2O3, are formed less effectively than the models predict. Because Al2O3 is expected to condense to corundum, which is often thought to be the first circumstellar condensate (Sharp & Huebner 1990; Lodders 2003), this disagreement may signalize that we should revise the picture of how effectively (if at all) alumina dust is formed in oxygen-rich stars like VY CMa.
That the chemical-equilibrium models fail to explain the aluminium chemistry in the envelope of VY CMa has been already noted in Tenenbaum & Ziurys (2009). They proposed that the discrepancy may be caused by “freezing out” of the equilibrium abundances at a few R⋆ or that shocks disrupt the process of molecule formation at larger distances. “Freezing out” (McCabe et al. 1979) occurs when the time scale of chemical reactions (τchem ∝ (Kn)-1, where K is the reaction rate) becomes much longer than the dynamical scale of the outflow (τdyn ≈ r/Vexp). As long as chemical reactions are faster than the dynamical time scale, the molecular abundances are thought to be well described by equilibrium values, but – as the density drops – at some point in the outflow the reactions become inefficient and abundances do not change any more being fixed at a certain level corresponding to some equilibrium values. Following McCabe et al. (1979), we estimate that such freezing-out should occur in the outflow of VY CMa at densities of about nH = 1010 cm-3, which are expected at a distance of few R⋆ (Decin et al. 2006). Such a “freezing out” scenario in VY CMa would be supported for AlO by its abundance being close to the maximal value predicted by equilibrium models (and indeed those maximal abundances correspond to distances of a few R⋆). Whether such process can really take place in VY CMa should be verified by constructing a detailed model which would take into account the variable conditions in the outflow.
We favour the alternative scenario in which the observed over-abundance of AlO at larger radii is a result of shocks related to the stellar activity. There are strong suggestions that shocks are present in the close vicinity of VY CMa:
-
it has been proposed that the complex nebula surroundingVY CMa was produced by a violent andepisodic process that most likely involves creation of shocks (e.g.episodic mass-ejections advocated in Smithet al. 2001; and Humphreyset al. 2005, 2007).This proposal, however, is based on observations of the extendednebula, formed by at least 1000 yr of mass-losshistory, and it is not sure whether the same kind of activity iscurrently taking place near the stellar surface.
-
The presence of extended and variable emission and broad absorption of Hα (e.g. Humphreys et al. 2005) within the otherwise neutral nebula indicates the presence of a process energetic enough to ionise hydrogen (although some of the emission, especially in the outermost nebula, may arise in the nearby H II region).
-
The star is known as an irregular variable, with changes of the optical light reaching 2 mag. This variability may be partially explained by (non-radial) pulsations (Humphreys et al. 2005), which would be a potential driving source of shocks near the stellar surface.
-
As an extreme supergiant very close to its Hayashi limit (Wittkowski et al. 2012), VY CMa has huge convective cells (Schwarzschild 1975), which are expected to severely affect its circumstellar medium (Smith et al. 2001; Humphreys et al. 2005, 2007).
-
Circumstellar AlO bands are rarely observed. Their presence and erratic behaviour has been long known in Mira variables (Keenan et al. 1969) and was reported in an enigmatic object U Equ (Barnbaum et al. 1996). They have been also observed in some members of the recently recognized family of nova-like variables called “red novae”. These include V4332 Sgr, which has the optical and NIR bands of AlO in emission (Banerjee et al. 2003; Tylenda et al. 2005), and V838 Mon, which shows circumstellar absorption in those bands (Kamiński et al. 2009; Tylenda et al. 2011; Evans et al. 2003; Lynch et al. 2004). The AlO emitters seem to share one common characteristics – their circumstellar environments have been shocked by violent motions, e.g. large-amplitude pulsations in case of Miras, and explosions in case of red novae and U Equ. The presence of shocks would justify VY CMa belonging to the group of AlO-emitters.
It would be indeed very surprising if the star were not to develop shocks near its surface. As shown by Cherchneff (2006) (for asymptotic giant branch stars), propagation of shocks through material above the stellar photosphere changes its chemical content considerably with respect to what is expected in chemical equilibrium. Future models attempting to explain the chemistry in VY CMa’s envelope should explore this non-equilibrium approach. Since shocks are expected to produce transient phenomena, there is also a possibility of observational verification. Most of the previously described molecular bands seen in VY CMa in emission are variable (e.g. Wallerstein 1986; Herbig 1974), although it is not clear whether the absolute intensity or the intensity relative to the variable continuum changes. It is also not known what are the shortest time scales on which the variability occurs except that it may be shorter than years. To explore the possibility that these optical emission bands arise due to the presence of shocks, it is highly desirable to verify whether the AlO bands are variable too and whether there is any correlation with the variability of the other molecular bands and hydrogen recombination lines.
Showing AlO emission, VY CMa is, however, more similar to Mira variables, in which AlO intensity does not correlate with spectral type and is highly variable (Keenan et al. 1969).
Acknowledgments
We are very grateful to G. Wallerstein and G. Gonzalez for making available to us their optical spectrum of VY CMa. The research was supported by the PL-Grid infrastructure and partially founded from the National Science Center grant DEC-2011/01/B/ST9/02229.
References
- Banerjee, D. P. K., Varricatt, W. P., Ashok, N. M., & Launila, O. 2003, ApJ, 598, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Barnbaum, C., Omont, A., & Morris, M. 1996, A&A, 310, 259 [NASA ADS] [Google Scholar]
- Buhl, D., Snyder, L. E., Lovas, F. J., & Johnson, D. R. 1974, ApJ, 192, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I. 2006, A&A, 456, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coxon, J. A., & Naxakis, S. 1985, J. Mol. Spec., 111, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Danchi, W. C., Bester, M., Degiacomi, C. G., Greenhill, L. J., & Townes, C. H. 1994, AJ, 107, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, L., Hony, S., de Koter, A., Justtanont, K., Tielens, A. G. G. M., & Waters, L. B. F. M. 2006, A&A, 456, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eliasson, B., & Bartlett, J. F. 1969, ApJ, 155, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A., Geballe, T. R., Rushton, M. T., et al. 2003, MNRAS, 343, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1998, Faraday Discuss., 109, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1970, Mémoires of the Société Royale des Sciences de Liège, 19, 13 [Google Scholar]
- Herbig, G. H. 1974, ApJ, 188, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Hougen, J. T. 1970, The Calculation of Rotational Energy Levels and Rotational Line Intensities in Diatomic Molecules, Nat. Bur. Stand. (U.S.), Monogr., 115 [Google Scholar]
- Humphreys, R. M., Davidson, K., Ruch, G., & Wallerstein, G. 2005, AJ, 129, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., Helton, L. A., & Jones, T. J. 2007, AJ, 133, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Hyland, A. R., Becklin, E. E., Neugebauer, G., & Wallerstein, G. 1969, ApJ, 158, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, A. H. 1942, ApJ, 96, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Schmidt, M., Tylenda, R., Konacki, M., & Gromadzki, M. 2009, ApJS, 182, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Schmidt, M., & Tylenda, R. 2010, A&A, 522, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamiński, T., Gottlieb, C. A., Menten, K. M., et al. 2013, A&A, submitted [Google Scholar]
- Keenan, P. C., Deutsch, A. J., & Garrison, R. F. 1969, ApJ, 158, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, S. H., Mayer, C. H., Sullivan, W. T., III, & Cheung, A. C. 1969, Science, 166, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kovacs, I. 1969, Rotational structure in the spectra of diatomic molecules (London UK: Adam Hilger) [Google Scholar]
- Launila, O., & Berg, L.-E. 2011, J. Mol. Spec., 265, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, D. K., Rudy, R. J., Russell, R. W., et al. 2004, ApJ, 607, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Levesque, E. M., & Plez, B. 2006, ApJ, 646, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- McCabe, E. M., Smith, R. C., & Clegg, R. E. S. 1979, Nature, 281, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Apponi, A. J., Woolf, N. J., & Ziurys, L. M. 2007, ApJ, 668, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. G., & Davis, S. P. 1987, PASP, 99, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, A. M. S., Yates, J. A., & Cohen, R. J. 1998, MNRAS, 299, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Romanik, C. J., & Leung, C. M. 1981, ApJ, 246, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Royer, P., Decin, L., Wesson, R., et al. 2010, A&A, 518, L145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saksena, M. D., Deo, M. N., Sunada, K., Behere, S. H., & Londhe, C. T. 2008, J. Mol. Spec., 247, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M. 1975, ApJ, 195, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, C. M., & Huebner, W. F. 1990, ApJS, 72, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2004, MNRAS, 349, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Humphreys, R. M., Davidson, K., et al. 2001, AJ, 121, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, E. D., & Ziurys, L. M. 2009, ApJ, 694, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, E. D., Dodd, J. L., Milam, S. N., Woolf, N. J., & Ziurys, L. M. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tylenda, R., Crause, L. A., Górny, S. K., & Schmidt, M. R. 2005, A&A, 439, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., Kamiński, T., Schmidt, M., Kurtev, R., & Tomov, T. 2011, A&A, 532, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Blerkom, J., & van Blerkom, D. 1978, ApJ, 225, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G. 1971, ApJ, 169, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G. 1986, A&A, 164, 101 [NASA ADS] [Google Scholar]
- Wallerstein, G., & Gonzalez, G. 2001, PASP, 113, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Hauschildt, P. H., Arroyo-Torres, B., & Marcaide, J. M. 2012, A&A, 540, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Helling, C., Winters, J. M., & Jeong, K. S. 1999, A&A, 348, L17 [NASA ADS] [Google Scholar]
- Zenouda, C., Blottiau, P., Chambaud, G., Rosmus, P. 1999, J. Mol. Struct.-Theochem., 458, 61 [Google Scholar]
- Zhang, B., Reid, M. J., Menten, K. M., & Zheng, X. W. 2012, ApJ, 744, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., Milam, S. N., Apponi, A. J., & Woolf, N. J. 2007, Nature, 447, 1094 [Google Scholar]
All Figures
 |
Fig. 1 The simulation of the B–X system of AlO (red line) is compared to the spectrum of VY CMa (blue line). The simulation was obtained for Trot = 700 K and Tvib = 2200 K. A rescaled spectrum of Betelgeuse is also shown (grey line) to illustrate the contribution of photospheric (and circumstellar) features that have not been included in the simulation. From top to bottom, the panels contain sections of the spectrum dominated by the Δν = 2, 1, 0, and –1 sequences. The positions of AlO band-heads are indicated with red markers and labels (giving ν′′ and ν′), while some of the strongest features in the stellar spectra are indicated by grey markings. |
| In the text | |
 |
Fig. 2 Rotational components of the B–X (0, 0) band of AlO as observed in VY CMa (blue histogram) and in our simulation (red line). The individual lines are unresolved doublets of members of the P1 and P2 branches. Their peaks are designated by rotational quantum numbers. Much fainter rotational components of the R branch can be seen in the simulation (only two were marked in the figure). |
| In the text | |
 |
Fig. 3 The P(23) rotational component of the B–X (0, 0) band of AlO in the simulation (red line) and in the observed spectrum of VY CMa (blue histogram). The velocity is given with respect to the average wavelength of the doublet, whose splitting is 4.2 km s-1. The positions of the doublet components are shown by the two dashed lines in the upper part of the figure. Lines in the lower part show the hyperfine splitting in both components (from Launila & Berg 2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


