EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 549 (January 2013) A&A, 549 (2013) A108 Full HTML
Free Access
Issue
A&A
Volume 549, January 2013
Article Number A108
Number of page(s) 7
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/201220505
Published online 07 January 2013

© ESO, 2013

1. Introduction

The study of apsidal motion in eccentric eclipsing binaries (EEB) provides an important observational test of theoretical models of stellar structure and evolution. A detailed analysis of the period variations of EEB can be performed using the times of minimum light observed throughout the apsidal motion cycle, and from this, both the orbital eccentricity and the period of rotation of the periastron can be obtained with high accuracy (Giménez 1994). All eclipsing binaries analysed here have properties that make them important “astrophysical laboratories” for studying the structure and evolution of stars.

Here we analyse the observational data and rates of apsidal motion for five detached eclipsing systems. These systems are all relatively bright northern-hemisphere early-type objects known to have eccentric orbits and to exhibit apsidal motion. With the exception of V821 Cas and V398 Lac, no spectroscopic observations have been published for these binary systems. Our study is part of a series of papers on apsidal motion in eclipsing binaries (Wolf et al. 2008, 2010).

2. Observations of minimum light

Monitoring of eccentric eclipsing binaries is a long-term observational project, which requires only moderate or small telescopes equipped with a photoelectric photometer or a CCD camera. Moreover, a large amount of observing time is needed, which is unavailable presently at large telescopes but is more practical for small amateur telescopes equipped with modern detectors. During the past ten years, we have accumulated over 8000 photometric observations at selected phases during primary and secondary eclipses and derived over 50 precise times of minimum light for selected eccentric systems. New CCD photometry was obtained at several observatories in the Czech Republic:

  • Ondřejov Observatory, Czech Republic: the 0.65-m (f/3.6) reflecting telescope with the CCD cameras SBIG ST-8, Apogee AP7p or Moravian Instruments G2-3200 and BVRI photometric filters;

  • Johann Pallisa Observatory and Planetarium Ostrava, Czech Republic: 0.2-m or 0.3-m telescopes with the CCD camera SBIG ST-8XME and VRI filters;

  • Observatory and Planetarium Hradec Králové, Czech Republic: 0.4-m (f/5) reflector with the CCD camera G2-1600 and BVRI filters;

  • Observatory Valašské Meziříčí, Czech Republic: the 0.3-m Celestron Ultima telescope with the CCD camera SBIG ST-7 or G2-1600 and VRI filters;

  • Private observatory of PS at Brno, Czech Republic: 0.2-m Cassegrain telescope with the CCD camera ST-7XME and Johnson-Cousins BV(RI)c filters;

  • Private Observatory of MZ at Brno, Czech Republic: Helios 2/58 lens obscured to 0.035-m with the CCD camera G2-402 and UBVRI filters.

CCD measurements at most observatories were dark-subtracted and then flat-fielded using sky exposures taken at either dusk or dawn. Several comparison stars were chosen in the same frame as the variables. The C-Munipack1 (Motl 2007) was used to reduce most of our CCD images. Aphot, a synthetic aperture photometry and astrometry software developed by M. Velen and P. Pravec, was routinely used for data obtained at Ondřejov observatory. No correction for differential extinction was applied, because of the proximity of the comparison stars to the variable and the resulting negligible differences in air mass.

Using the Hipparcos photometry (ESA 1997) and NSVS data (Wozniak et al. 2004), we were able to derive several additional times of minimum light with less precision. The new times of primary and secondary minima and their errors were generally determined by the classical Kwee-van Woerden (1956) algorithm. In some cases (Hipparcos, NSVS or SWASP data, scattered points), the light-curve fitting by Gaussians or polynomials of the third or fourth order applied on the original and reflected curve, together with the least squares method, were used. All new times are given in Tables A.1–A.5, where epochs are calculated from the ephemeris given in Table 1, and the other columns are self-evident.

3. Apsidal motion analysis

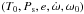The apsidal motion in all eccentric systems was studied by means of an O−C diagram analysis. For an accurate calculation of the apsidal motion rate, the method described by Giménez & García-Pelayo (1983) was routinely used. This is a weighted least-squares iterative procedure, including terms in the eccentricity up to the fifth order. There are five independent variables \hbox{$(T_0, P_{\rm s}, e, \dot{\omega}, \omega_0)$} determined in this procedure. The periastron position ω is given by the linear equation

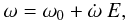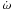ω=ω0+ω̇E,$$ \omega = \omega_0 + \dot{\omega}\ E , $$where \hbox{$\dot{\omega}$} is the rate of periastron advance, and the position of periastron for the zero epoch T0 is denoted as ω0. The relation between the sidereal and the anomalistic period, Ps and Pa, is given by

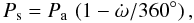Ps=Pa (1−ω̇/360◦),$$ P_{\rm s} = P_{\rm a} \,\left(1 - \dot{\omega}/360^\circ\right), $$and the period of apsidal motion by

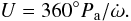U=360◦Pa/ω̇.$$ U = 360^\circ P_{\rm a}/\dot{\omega} . $$In addition, new timings are available in the literature and in the O−C Gateway2 database, maintained by Paschke and Brát, Czech Astronomical Society. All new precise CCD times of minima were used with a weight of 10 or 20 in our computation. Some of our less precise measurements were weighted by a factor of 5, while the earlier visual and photographic times (esp. the times of the mid-exposure of a photographic plate) were given a weight of one or nought because of the large scatter in these data.

3.1. V785 Cassiopeiae

thumbnail Fig. 1

The O−C diagram for the times of minimum of V785 Cas. The continuous and dashed curves represent predictions for the primary and secondary eclipses, respectively. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric or CCD measurements, which were given higher weights in the calculations.

The detached eclipsing binary V785 Cas (also BD+64°302, HIP 10173; Vmax = 9m.28; Sp. B5V) is a relatively bright binary with eccentric orbit (e = 0.09) and a short orbital period of 2.7 days. It belongs to the older photometric discoveries of the Hipparcos project (ESA 1997). The following linear light elements were derived:

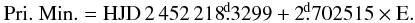Pri. Min.=HJD 2 452 218.d3299+2.d702515×E.$$ \rm Pri.~ Min. = HJD \,2\,452\,218\fd3299 + 2\fd702515 \times E. $$All photoelectric times of minimum light given in Sobotka (2007), Brát et al. (2007, 2008), and Zasche et al. (2011) were incorporated into our calculation. Using Hipparcos photometry (ESA 1997), we were able to derive additional times of minimum light using the light-curve profile fitting method. A total of 46 photoelectric times of minimum light given in Table A.1 were used in our analysis.

The computed apsidal motion parameters and their internal errors of the least-squares fit are given in Table 1. In this table, Ps denotes the sidereal period, Pa the anomalistic period, e represents the eccentricity, and 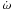\hbox{$\dot{\omega}$} is the rate of periastron advance (in degrees per cycle and in degrees per year). The zero epoch is given by T0, and the corresponding position of the periastron is represented by ω0. The O−C residuals for all times of minimum with respect to the linear part of the apsidal motion equation are shown in Fig. 1. The non-linear predictions, corresponding to the fitted parameters, are plotted for primary and secondary eclipses.

Table 1

Apsidal motion elements for V785 Cas, V821 Cas, V796 Cyg, V398 Lac, and V871 Per.

3.2. V821 Cassiopeiae

The detached and double-lined eclipsing binary V821 Cas (also HD 224557, BD+52°3571, HIP 118223; Vmax = 8m.26; Sp. A1V+A4V) is a bright eclipsing binary with an eccentric orbit (e = 0.14) and a short orbital period of 1.8 days. The eccentric orbit and apsidal motion of V821 Cas was discovered by Otero (2005) using the publicly available Hipparcos and NSVS data. The first BVR photometry and period analysis of V821 Cas were obtained by Degirmenci et al. (2003, 2007) at the Baja and Ege observatories. They confirmed the eccentric orbit and derived improved eclipse ephemeris

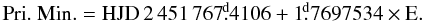Pri. Min.=HJD 2 451 767.d4106+1.d7697534×E.$$ \rm Pri.~ Min. = HJD\, 2\,451\,767\fd4106 + 1\fd7697534 \times E. $$The light curve analysis was also presented by Bulut & Demircan (2008), who obtained similar eccentricity of the system e = 0.115. Recently in their spectroscopic study, Cakirli et al. 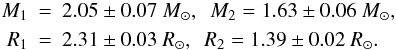(2009) determined the precise absolute parameters of the components M1=2.05±0.07 M⊙,   M2=1.63±0.06 M⊙,R1=2.31±0.03 R⊙,   R2=1.39±0.02 R⊙.\begin{eqnarray*} M_1 &=& 2.05 \pm 0.07~ M_\odot, \,\,\, M_2 = 1.63 \pm 0.06 ~ M_\odot, \\ R_1 &=& 2.31 \pm 0.03~ R_\odot, \,\,\, R_2 = 1.39 \pm 0.02 ~ R_\odot. \end{eqnarray*}They also derived the first apsidal motion period U = 118 ± 19 years and the value of internal structure constant log k2,obs = −2.56. Since the above-mentioned papers were published, new times of minima have been obtained, which allowed us to reduce the uncertainties in the derived parameters. We collected numerous times of minimum light given in Ak & Filiz (2003), Bakis et al. (2003), Bulut & Demircan (2003), Degirmenci et al. (2003, their Table 1), Degirmenci et al. (2007, their Table 3), Brát et al. (2007, 2008), Cakirli et al. (2009, their Table 2), Dvorak (2009, 2011), Diethelm (2010, 2012), and Lampens et al. (2010). These are all listed in Table A.2. Using Hipparcos photometry (ESA 1997), we were able to derive additional times of minimum light using the light-curve profile-fitting method. A total of 50 precise times of minimum light were used in our analysis including 22 secondary eclipses. 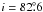The orbital inclination was adopted to be i=82.°6\hbox{$i = 82\fdg6$}, based on the analysis of Cakirli et al. (2009). The computed apsidal motion parameters are given in Table 1, the complete O−C diagram is shown in Fig. 2.

thumbnail Fig. 2

O−C residuals for the times of minimum of V821 Cas. See legend to Fig. 1.

3.3. V796 Cygni

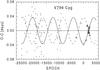thumbnail Fig. 3

O−C graph for the times of minimum of V796 Cyg. See legend to Fig. 1. Only modern data after the epoch –5000 were used for the apsidal motion solution.

The detached eclipsing binary V796 Cyg (also BV 345, S 4782, GSC 3560-0777, FL 2778; Vmax = 10m.95; Sp. A0) is a seldom studied binary system with a short orbital period (P = 1.5 d) and a slightly eccentric orbit (e = 0.07). It was discovered to be variable by Hoffmeister (1949) at Sonneberg and later independently by Strohmeier (1961) at Bamberg observatory. Busch & Haussler (1966) derived the first ephemeris with the correct orbital period:

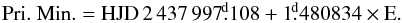Pri. Min.=HJD 2 437 997.d108+1.d480834×E.$$ \rm Pri.~ Min. = HJD\, 2\,437\,997\fd108 + 1\fd480834 \times E. $$To our knowledge no modern photometric, spectroscopic, or period study exists so far. All prevous times of minimum light are collected in the O−C Gateway database. Only those given in Table A.3 were taken into consideration, and other numerous photographic times obtained by Busch & Haussler (1966), Strohmeier (1966), and Strohmeier & Bauernfeind (1968) were not used in our analysis due to large scatter of these data. A total of 18 reliable times of minimum light were included in our analysis, with 9 secondary eclipses among them. The computed apsidal motion parameters are given in Table 1, and the O−C diagram is shown in Fig. 3.

3.4. V398 Lacertae

thumbnail Fig. 4

O−C graph of V398 Lac. See legend for Fig. 1.

The detached eclipsing binary V398 Lac (also HD 210 180, BD+51°3251, HIP 109 193; Vmax = 8m.79; Sp. A0V) is a relatively bright binary system with an eccentric orbit (e = 0.2) and longer orbital period P = 5.4 days. Its variability was discovered during the Hipparcos mission (ESA 1997). The precise absolute dimensions of components of V398 Lac were derived spectroscopically by Cakirli et al. (2007), who obtained components with similar mass and different size 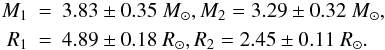M1=3.83±0.35 M⊙,M2=3.29±0.32 M⊙,R1=4.89±0.18 R⊙,R2=2.45±0.11 R⊙.\begin{eqnarray*} M_1 &=& 3.83 \pm 0.35~ M_\odot, M_2 = 3.29 \pm 0.32~ M_\odot, \\ R_1 &=& 4.89 \pm 0.18~ R_\odot, R_2 = 2.45 \pm 0.11~ R_\odot. \end{eqnarray*}In the latter paper, the following linear ephemeris is also given

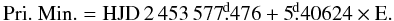Pri. Min.=HJD 2 453 577.d476+5.d40624×E.$$ \rm Pri.~ Min. = HJD\, 2\,4 53\,577\fd476 + 5\fd40624 \times E. $$The light curve analysis of V398 Lac was later presented by Bulut & Demircan (2008), who confirmed the moderate eccentricity of the system e = 0.273. Our new times of minimum light, as well as timings of previous observers (Cakirli et al. 2007; Parimucha et al. 2009; Brát et al. 2011; Zasche et al. 2011) given in Table A.4, were incorporated into our calculation. Using Hipparcos photometry (ESA 1997), we were also able to derive additional times of minimum light using the light-curve profile fitting method. Only 15 times of minimum light given in Table A.4 were used in our analysis. The orbital inclination was adopted to be 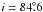i=84.°6\hbox{$i = 84\fdg6$}, based on the analysis of Cakirli et al. (2007). The resulting apsidal motion parameters are given in Table 1, and the current O−C diagram is shown in Fig. 4.

3.5. V871 Persei

thumbnail Fig. 5

O−C diagram for V871 Per. See legend to Fig. 1.

The detached eclipsing binary V871 Per (also BD+56°704, GSC 3708-1325; Vmax = 10m.89; Sp. B) is a fairly neglected binary system with a moderate eccentric orbit (e = 0.24) and a short orbital period (P ≃ 3 day). It was discovered to be an eclipsing binary by Otero et al. (2004) in the NSVS database. To our knowledge, the precise absolute parameters of the components of V871 Per are unknown. The following linear ephemeris was derived and used in the epoch calculation

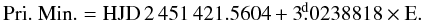Pri. Min.=HJD 2 451 421.5604+3.d0238818×E.$$ \rm Pri.~ Min. = HJD\, 2\,4 51\,421.5604 + 3\fd0238818 \times E. $$We used the times of minimum light published in the last several years by Zejda et al. (2006), Brát et al. (2007), and Diethelm (2009, 2010, 2011a,b, 2012), which are included in Table A.5. A total of 20 reliable times of minimum light were used in our analysis including nine secondary eclipses. The final apsidal motion elements are given in Table 1, and the O−C graph is shown in Fig. 5.

4. Discussion

The detection of apsidal motion in EEB provides the opportunity to test models of stellar internal structure. The internal structure constant (ISC), k2,obs, which is related to the variation in the density inside the star, can be derived using the following expression: 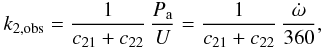k2,obs=1c21+c22 PaU=1c21+c22 ω̇360,\begin{equation} k_\mathrm{2, obs} = \frac{1}{c_{21} + c_{22}} \, \frac{P_{\rm a}}{U} = \frac{1}{c_{21} + c_{22}} \, \frac{\dot{\omega}}{360} , \end{equation}(1)where c21 and c22 are functions of the orbital eccentricity, fractional radii, the masses of the components, and the ratio between rotational velocity of the stars and Keplerian velocity (Kopal 1978). We also assume that the component stars rotate pseudosynchronously with the same angular velocity as the maximum orbital value at periastron. 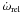In addition to the classical Newtonian contribution, the observed rate of rotation of the apses includes the contribution from General Relativity, \hbox{$\dot{\omega}_{\rm rel}$} (Giménez 1985): 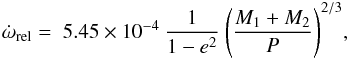ω̇rel=5.45×10-411−e2(M1+M2P)2/3,\begin{equation} \dot{\omega}_\mathrm{rel} = \; 5.45 \times 10^{-4} \: \frac{1}{1-e^2} \:\Biggl( \frac{M_1 + M_2}{P} \Biggr) ^{2/3}, \end{equation}(2)where Mi denotes the individual masses of the components in solar units and P is the orbital period in days.

Table 2

Basic physical properties of V821 Cas and V398 Lac and their internal structure constant.

The values of 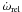\hbox{$\dot{\omega}_\mathrm{rel}$} and the resulting mean internal structure constants k2,obs for V821 Cas and V398 Lac are given in Table 2. Theoretical values k2,theo according to available theoretical models for the internal stellar structure computed by Claret (2004) for given masses of components are presented in Table 2. The chemical composition of X = 0.70 and Z = 0.02 was assumed to be in agreement with previous studies.

5. Conclusions

The apsidal motion in EEB has been used for decades to test evolutionary stellar models. This study provides accurate information on the apsidal motion rates of five main-sequence early-type binary systems: V785 Cas, V821 Cas, V796 Cyg, V398 Lac and V871 Per. With the exception of V821 Cas, the apsidal motion period has been published here for the first time. For V821 Cas we derived a longer apsidal motion period of U = 141 ± 9 years than was given in Cakirli et al. (2009). On the other hand, substantional discrepancy between the observed and theoretical ISC still remains. From the observational point of view, the apsidal motion period has not been covered satisfactorily. The index n = ΔT/U, expressing the coverage of the apsidal motion period by precise photoelectric measurements, is only 15%. For instance, the shorter apsidal motion period of 80 years could explain the difference between observed and theoretical ISC satifactorily. None of the analysed binaries presents a large relativistic contribution of up to 7% of the total apsidal motion rate.

In spite of the considerable amount of observational data collected for decades, the absolute dimensions of massive binary components are known with low accuracy. It is also highly desirable to obtain new, high-dispersion, and high-S/N spectroscopic observations, and to apply modern disentangling methods to obtain radial velocity curves of both components for these systems.

Acknowledgments

The research was supported by the Research Program MSM0021620860 Physical Study of objects and processes in the Solar System and in Astrophysics of the Ministry of Education of the Czech Republic and partially by the Czech Science Foundation, grants 205/04/2063, 205/06/0217, and in its final stage by the grant P209/10/0715. The authors would like to thank Mr. Kamil Hornoch and Mrs. Lenka Kotková, Ondřejov observatory, Mr. Tomáš Hynek, and Ms. K. Onderková, Ostrava observatory, for their important help with photometric observations. The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at the CDS, Strasbourg, France; NASA’s Astrophysics Data System Bibliographic Services; the O−C Gateway of the Czech Astronomical Society. We gratefully acknowledge very useful suggestions by the referee, Prof. Álvaro Giménez.

References

  1. Ak, H., & Filiz, N. 2003, IBVS, 5462 [Google Scholar]
  2. Bakis, V., Bakis, H., Erdem, A., et al. 2003, IBVS, 5464 [Google Scholar]
  3. Brát, L., Zejda, M., & Svoboda, P. 2007, OEJV 74, 1 [Google Scholar]
  4. Brát, L., Šmelcer, L., Kučáková, H., et al. 2008, OEJV, 94, 1 [NASA ADS] [Google Scholar]
  5. Brát, L., Trnka, J., Šmelcer, L., et al. 2011, OEJV, 137, 1 [Google Scholar]
  6. Bulut, I., & Demircan, O. 2003, IBVS, 5476 [Google Scholar]
  7. Bulut, I., & Demircan, O. 2008, New Astron., 13, 252 [NASA ADS] [CrossRef] [Google Scholar]
  8. Busch, H., & Haussler, K. 1966, IBVS, 144 [Google Scholar]
  9. Cakirli, O., Frasca, A., Ibanoglu, C., et al. 2007, AN, 328, 536 [NASA ADS] [Google Scholar]
  10. Cakirli, O., Ibanoglu, C., Bilir, S., & Sipahi, E. 2009, MNRAS, 395, 1649 [NASA ADS] [CrossRef] [Google Scholar]
  11. Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Degirmenci, O. L., Bozkurt, Z., Yakut, K., et al. 2003, IBVS, 5386 [Google Scholar]
  13. Degirmenci, O. L., Bozkurt, Z., Yakut, K., et al. 2007, New Astron., 12, 322 [NASA ADS] [CrossRef] [Google Scholar]
  14. Diethelm, R. 2009, IBVS, 5871 [Google Scholar]
  15. Diethelm, R. 2010, IBVS, 5920 [Google Scholar]
  16. Diethelm, R. 2011a, IBVS, 5960 [Google Scholar]
  17. Diethelm, R. 2011b, IBVS, 5992 [Google Scholar]
  18. Diethelm, R. 2012, IBVS, 6011 [Google Scholar]
  19. Dvorak, S. W. 2009, IBVS, 5870 [Google Scholar]
  20. Dvorak, S. W. 2011, IBVS, 5974 [Google Scholar]
  21. ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
  22. Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
  23. Giménez, A. 1994, Exp. Astron., 5, 91 [Google Scholar]
  24. Giménez, A., & García-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hanžl, D. 1991, IBVS, 3615 [Google Scholar]
  26. Hoffmeister, C. 1949, Ergaenzungshefte Astron. Nachr., 12, 1 [Google Scholar]
  27. Hübscher, J., & Lehmann, P. B. 2012, IBVS, 6026 [Google Scholar]
  28. Hübscher, J., & Monninger, G. 2011, IBVS, 5959 [Google Scholar]
  29. Hübscher, J., & Walter, F. 2007, IBVS, 5761 [Google Scholar]
  30. Hübscher, J., Lehmann, P. B., & Walter, F. 2012, IBVS, 6010 [Google Scholar]
  31. Kopal, Z. 1978, Dynamics of Close Binary Systems (Dordrecht, Holland: Reidel) [Google Scholar]
  32. Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [Google Scholar]
  33. Lampens, P., Kleidis, S., Van Cauteren, P., et al. 2010, IBVS, 5933 [Google Scholar]
  34. Nakajima, K. 2003, Var. Star Bull. Jpn, 40 [Google Scholar]
  35. Otero, S. A. 2005, IBVS, 5631 [Google Scholar]
  36. Otero, S. A., Wils, P., & Dubovsky, P. A. 2004, IBVS, 5570 [Google Scholar]
  37. Parimucha, S., Dubovsky, P., Baludansky, D., et al. 2009, IBVS, 5898 [Google Scholar]
  38. Sobotka, P. 2007, IBVS, 5809 [Google Scholar]
  39. Strohmeier, W. 1961, Bamberg Veroeffentlichungen der Remeis-Sternwarte, 5, 8 [Google Scholar]
  40. Strohmeier, W. 1966, IBVS, 145 [Google Scholar]
  41. Strohmeier, W., & Bauernfeind, H. 1968, Bamberg Veroeffentlichungen der Remeis-Sternwarte, 7, 72 [Google Scholar]
  42. Wolf, M., Zejda, M., & de Villiers, S. N. 2008, MNRAS, 388, 1836 [NASA ADS] [CrossRef] [Google Scholar]
  43. Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Wozniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
  45. Zasche, P., Uhlář, R., Kučáková, H., et al. 2011, IBVS, 6007 [Google Scholar]
  46. Zejda, M., Mikulášek, Z., & Wolf, M. 2006, IBVS, 5741 [Google Scholar]

Appendix A: Tables of minima

Table A.1

The list of minima timings of V785 Cas.

Table A.2

The list of minima timings of V821 Cas.

Table A.3

The list of minima timings of V796 Cyg.

Table A.4

The list of minima timings of V398 Lac.

Table A.5

The list of minima timings of V871 Per.

All Tables

Table 1

Apsidal motion elements for V785 Cas, V821 Cas, V796 Cyg, V398 Lac, and V871 Per.

In the text
Table 2

Basic physical properties of V821 Cas and V398 Lac and their internal structure constant.

In the text
Table A.1

The list of minima timings of V785 Cas.

In the text
Table A.2

The list of minima timings of V821 Cas.

In the text
Table A.3

The list of minima timings of V796 Cyg.

In the text
Table A.4

The list of minima timings of V398 Lac.

In the text
Table A.5

The list of minima timings of V871 Per.

In the text

All Figures

thumbnail Fig. 1

The O−C diagram for the times of minimum of V785 Cas. The continuous and dashed curves represent predictions for the primary and secondary eclipses, respectively. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric or CCD measurements, which were given higher weights in the calculations.
In the text
thumbnail Fig. 2

O−C residuals for the times of minimum of V821 Cas. See legend to Fig. 1.
In the text
thumbnail Fig. 3

O−C graph for the times of minimum of V796 Cyg. See legend to Fig. 1. Only modern data after the epoch –5000 were used for the apsidal motion solution.
In the text
thumbnail Fig. 4

O−C graph of V398 Lac. See legend for Fig. 1.
In the text
thumbnail Fig. 5

O−C diagram for V871 Per. See legend to Fig. 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.