| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220337 | |
| Published online | 16 January 2013 | |
The spectroscopic evolution of the recurrent nova T Pyxidis during its 2011 outburst⋆,⋆⋆
II. The optically thin phase and the structure of the ejecta in recurrent novae
1
Dipartimento di Fisica “Enrico Fermi”, Università di
Pisa, and INFN- Sezione Pisa, largo
B. Pontecorvo 3, 56127
Pisa,
Italy
e-mail: shore@df.unipi.it; sivan.degennaroaquino@gmail.com
2
INFN- Sezione Pisa, largo B. Pontecorvo 3,
56127
Pisa,
Italy
3
American Astronomical Society, 2000 Florida Ave NW,
Washington
DC
20009-1231,
USA
e-mail: Greg.Schwarz@aas.org
4
Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La
Palma, Santa Cruz de
Tenerife, Spain
e-mail: tau@not.iac.es
5 Department of Physics and Astronomy, Stony Brook University
Stony Brook, NY 11794-3800, USA
e-mail: frederick.walter@stonybrook.edu
6
School of Earth and Space Exploration, Arizona State
University, PO Box
871404, Tempe,
AZ
85287-1404,
USA
e-mail: sumner.starrfield@asu.edu
7
Department of Astronomy and Astrophysics, Villanova
University, 800 Lancaster
Avenue, Villanova,
PA
19085,
USA
e-mail: edward.sion@villanova.edu
Received: 4 September 2012
Accepted: 8 November 2012
Aims. We continue our study of the physical properties of the recurrent nova T Pyx, focussing on the structure of the ejecta in the nebular stage of expansion during the 2011 outburst.
Methods. The nova was observed contemporaneously with the Nordic Optical Telescope (NOT), at high resolution spectroscopic resolution (R ≈ 65 000) on 2011 Oct. 11 and 2012 Apr. 8 (without absolute flux calibration), and with the Space Telescope Imaging Spectrograph (STIS) aboard the Hubble Space Telescope (HST), at high resolution (R ≈ 30 000) on 2011 Oct. 10 and 2012 Mar. 28 (absolute fluxes). The NOT spectra cover 3800–7300 Å, the HST spectra from 2011 Oct. cover 1150–5700 Å while the 2012 Mar. spectrum covers 1150–1700 Å. We use standard plasma diagnostics (e.g. [O III] and [N II] line ratios and the Hβ line fluxes) to constrain electron densities and temperatures. Using Monte Carlo modeling of the ejecta, we derive the structure and filling factor from comparisons to the optical and ultraviolet line profiles.
Results. The ejecta can be modeled using an axisymmetric conical – bipolar – geometry with a low inclination of the axis to the line of sight, i = 15 ± 5 degrees, compatible with published results from high angular resolution optical spectro-interferometry. The structure is similar to that observed in the other short orbital period recurrent novae (e.g. CI Aql, U Sco) and RNe candidate KT Eri during their nebular stages. We show that the electron density scales as t-3 as expected from a ballistically ejected constant mass shell; there is no need to invoke a continuing mass outflow following the eruption. The derived mass for the ejecta with filling factor f ≈ 3%, Mej ≈ 2 × 10-6 M⊙ is similar to that obtained for other recurrent nova ejecta but inconsistent with the previously reported extended optically thick epoch of the explosion. We suggest that the system underwent a common envelope phase following the explosion that produced the recombination event. Implications for the dynamics of the recurrent novae are discussed.
Conclusions. The compact recurrent novae can be understood within a single phenomenological model with bipolar, although not jet-like, low mass ejecta.
Key words: novae, cataclysmic variables / stars: winds, outflows / stars: individual: T Pyx
© ESO, 2013
1. Introduction
Recurrent novae (RN) occur in binary systems where mass accretion from the companion causes a thermonuclear runaway on a white dwarf (WD). Unlike classical novae, originating in systems with very similar overall properties, the frequency of explosion and the low ejecta mass is taken to indicate that the WD is very close to the Chandrasekhar mass limit. Since the explosion is initiated by the accumulation of a hydrogen layer, and its intensity is governed by the extent of deep envelope mixing with the accreted matter, such a massive WD requires a lower accumulated mass to reach ignition conditions (see e.g. Starrfield et al. 2008). The source of the accreted material is less important than the nature of the mass gainer. Accretion is either from winds in a giant secondary in large separation systems (e.g. RS Oph, V407 Cyg, T CrB, periods > several hundred days) or Roche lobe overflow of a late type, main sequence star or a more evolved but still low mass companion in short period systems (e.g. CI Aql, V394 CrA, U Sco, periods < a few days). With an orbital period of 1.83 h (Uthlas et al. 2010), T Pyx is in the latter class of RN and has the shortest orbital of any RN. Mixed core and hydrogen rich accreted matter is violently ejected at high velocities from a few 103 to 104 km s-1. Any hydrogen not ejected from the WD continues to burn in hydrostatic equilibrium until consumed or ejected via a wind or common envelope mass ejection. It is the extremely high mass of the WD that gives RNe their characteristics of short recurrence timescales, low mass ejection (~10-6 M⊙) at large velocities, and hence rapid evolution.
The long awaited sixth historical outburst of the RN T Pyx was detected on 2011 April 14.2931 (MJD 55 665.79310) by Waagan et al. (2011). While this was not the first outburst for which spectroscopy was available, it was the first of the era of observations with linear digital detectors coupled to high resolution spectrographs providing absolute calibrations, and for which contemporaneous panchromatic ground and space based observations from γ-ray through centimeter radio were possible. In our first paper (Shore et al. 2011, hereafter Paper I) we presented high resolution optical spectra from the optically thick stage of the expansion, determined a new and larger distance, ≥3.5 kpc, and reddening, E(B − V) = 0.5, than previously thought, and discussed the diagnostics of the dynamics and structure of the ejecta. In this paper, we show the results from the late-time optical and ultraviolet high resolution observations following the transition to the nebular phase. We show that the line profiles from a range of ionizations and covering a very wide range of physical conditions provide a unified picture for the ejecta of T Pyx and, by extension, for all RN arising in compact binary systems.
Journal of NOT/FIES observations.
2. Observational data
Our optical data set, a continuation of the sequence described in Paper I, consists of spectra taken on 2011 Oct. 11 (hereafter epoch 1) and 2012 Apr. 8 (hereafter epoch 2) with the 2.6 m Nordic Optical Telescope (NOT) FIber-fed Echelle Spectrograph (FIES) with a dispersion of 0.023 Å px-1 in high-resolution mode, covering the spectral interval from 3635 to 7364 Å and 0.035 Å px-1 in medium-resolution mode, covering the spectral interval from 3680 to 7300 Å (see Table 1). Both observations were done with the high-resolution fiber The sequence was not absolutely calibrated. All NOT spectra were reduced using IRAF, FIESTool, and IDL1. Associated with these, we had two nearly simultaneous observing sequences with the Space Telescope Imaging Spectrograph (STIS) aboard the Hubble Space Telescope (HST). In the first, we obtained medium resolution echelle spectra from 1150–3100 Å and a single low resolution G430L optical spectrum from 2900–5700 Å. Note that although the first epoch observation included spectra longward of 1700 Å, the epoch 2 data used the E140M grating between 1150 and 1700 Å so we limit our discussion to the common spectral interval. A more complete description of the full NOT and STIS data sets is in preparation. The optical epoch 1 STIS spectrum was used for calibration of the nearly simultaneous NOT spectrum. The epoch 2 NOT spectrum was absolutely calibrated with a low resolution SMARTS spectrum from 2012 Apr. 2. The journal of STIS observations is given in Table 2. The dates relative to the discovery of the outburst are also listed.
Journal of HST/STIS observations.
3. Analysis
 |
Fig. 1 Hα (first row), Hβ (second row), He II 4686 Å (third row), and He I 5875 Å (bottom, left) line profiles in radial velocity (km s-1, uncorrected for LSR) epoch 1 (left) and epoch 2 (right), from the NOT spectra. Note that He I was not present in the epoch 2 spectra. |
We begin with the presentation of the profiles obtained during the two epochs. These are then used to derive the electron density and mass of the ejecta and we present a unifying model for the evolution of the profiles. The strongest lines in the optical spectrum were the Balmer and nebular forbidden lines of [O III].
3.1. Line profiles in the two epochs
The Hα and Hβ lines profiles are shown in Fig. 1. The blending of Hα with the [N II] doublet 6548, 6583 Å is more clearly seen in the epoch 2 spectrum because of the reduced flux relative to epoch 1. In contrast, the Hβ line was unblended at both epochs and we used this as the standard of comparison (see later discussion of the [O III] and [N II] lines).
He I 5875, 6678, 7065 Å were detected in epoch 1 but none were present in the epoch 2 spectrum (Fig. 1). The He II 4686 Å profile was strongly blended with the N III complex at 4640 Å but a comparison with He I 5875 Å shows that it displayed the same profile (Fig. 2). The He II 5411 Å line was not present in either spectrum. The 4686 Å line was narrow and present on the epoch 2 spectrum. The high velocity wings, with |vrad| > 1000 km s-1 were very much reduced relative to the central emission. As we will discuss in Sect. 3.3, this was a general feature of the profile development. The 4640 Å feature was still present at epoch 2 but its relative peak flux was reduced by a factor of 4 relative to He II 4686 Å.
The optical G430L STIS spectrum was used to calibrate the epoch 1 NOT observation by convolving the spectrum following median filtering to the STIS resolution (about 3 Å) and using a third order fit to the strongest lines from 3300−5700 Å. The fluxed spectrum was dereddened using E(B − V) = 0.5 (Shore et al. 2012, see Fig. 2). Despite the strong UV blend with O III] 1667 Å and the optical with the 4640 Å complex, the clear similarity of the two He II profiles is evident. The dereddened fluxes were F(He II 1640) = (5.0 ± 0.1) × 10-10 erg s-1 cm-2, F(He II 4686) = (3.0 ± 0.2) × 10-11 in the same units, so the flux ratio was ≈ 16.5 ± 0.2. The epoch 2 He II 1640 Å – line had the same narrow core as the optical forbidden lines and a low extended pedestal with |vrad,max| = 2000 km s-1. The measured flux was (6.7 ± 0.1) × 10-13 erg s-1 cm-2, the dereddened flux was 2.3 × 10-11. For the epoch 2 data, the dereddened fluxes for He II 4686 Å was (1.9 ± 0.2) × 10-12 erg s-1 cm-2. We note that the decreased flux is consistent with a constant mass ejecta. A more complete analysis, including a discussion of the He/H ratio (an open question for RN) will be presented in the next paper (Schwarz et al. 2012, in prep.).
 |
Fig. 2 Comparison of He II 1640 Å (solid) with He II 4686 Å (dot-dash) from epoch 1 (top) and epoch 2 (bottom). All spectra were dereddened with E(B − V) = 0.5. For display purposes, the optical NOT spectrum is multiplied by a factor of 40 with a boxcar smoothing to 11 points. |
 |
Fig. 3 Comparison of the N IV] 1486 Å (top) and C III] 1909 Å (bottom) profiles from the STIS epoch 1 spectrum. The C III] line was not covered in the epoch 2 STIS observation. |
 |
Fig. 4 Comparison of the simultaneous nitrogen line profiles from epoch 1 (left) and epoch 2 (right). Top: [N II] 5755 Å, bottom: N IV] 1486 Å. Note, in particular, the change in the core to wing ratio (see text for further discussion). |
As we show in Fig. 3, the epoch 1 isoelectronic ultraviolet resonance intercombination lines of C III] 1909 Å and N IV] 1486 Å had the same line profiles, essentially the same as Hβ. The N III]1751 Å, N IV] 1486 Å, and N V 1238, 1242 Å lines in the epoch 1 STIS spectrum showed the variation of the ionization in the ejecta, see Fig. 5. The N III feature is, however, a complex blend of permitted (2P-2D°) and intercombination (2P°-4P, resonance) lines. Assuming that the individual profiles are the same as the C III] 1909 Å line, the Einstein-A weighted combination profile produces a very close match to the observations. This is the same result we found for the Hα plus [N II] optical lines and highlights that we are tracing not only an ionization but also density structure. The N V UV resonance doublet is, however, quite different and cannot be reproduced by any naturally weighted combination of individual components. There appears to be a real difference on the blueshifted wing, the ionization is lower on the approaching side of the line. There was another important difference. The N V doublet showed a strong, relatively narrow peak at around 1500 km s-1 in both spectra while that component vanished on C IV 1550 Å in the epoch 2 spectrum (Fig. 5). We compare these to the Si IV/S IV] blend at 1402 Å for which we expect the dominant contributor to be from O+3. The lower ionization lines for nitrogen are shown in Fig. 4.
 |
Fig. 5 Ultraviolet resonance multiplets Si IV/S IV] 1402 AA (top), N V 1240 Å (middle) and C IV 1550 Å (bottom) for epoch 1 (left) and epoch 2 (right). The interstellar absorption components are visible on the resonance lines. For comparison the mean wavelength of the blend has been used. Note the strong change in the C IV line at about + 1300 km s-1, but note that the C IV and N V are blends with large velocity separation between the components and the variations cannot be uniquely assigned. See text for details. |
The [O III] 4363, 4959, 5007 Å nebular lines were present and strong in both spectra, as shown in Fig. 6, but displayed different profiles than the He II. The three lines show the similar profiles to Hβ for each epoch, as a contrast between Figs. 1 and 6 shows. The lines closely resembled the optical N+ transitions that are their isoelectronic analogs. In the next section, we will discuss the use of these lines to determine the electron temperature and density in the two epochs.
 |
Fig. 6 [O III] line profiles, in velocity, from epoch 1 (left) and epoch 2 (right). From the top, λ 4363 Å λ 4959 Å and λ 5007 Å. The fluxes have not been corrected for reddening and no absolute calibration was applied to the epoch 1 data for display purposes. See text for discussion. |
The high ionization [Ca V] 5309, 6086 Å lines were present in the epoch 1 spectrum and the 6086 Å line was also present at epoch 2 but the 5309 Å line was much weaker in this noisy part of the spectrum. The 6086 Å profile was similar to the He II transitions, while the 5309 Å line was asymmetric but with a FWZI about the same as the other emission lines2. The two lines are shown in Fig. 7.
 |
Fig. 7 [Ca V] 6086 Å (top) and 5309 Å line profiles for epoch 1 (left) and epoch 2 (right). |
3.2. Lyman α analysis and neutral hydrogen column density
The Lyα line was observed at both epochs. It is heavily extinguished by interstellar absorption but there appears to be a second emission line in the redward wing. To attempt an identification and to determine the extinction, we have modeled the intrinsic Lyα profile using the epoch 1 Hα line as a proxy together with a velocity shifted weighted copy. The derived wavelength for the presumed blend, 1318 Å, is roughly coincident with the intercombination resonance line O V] 1318.34 Å as shown in Fig. 83. To our knowledge, this is the first identification of this transition in a RN (it has recently been identified by Young et al. (2011) in symbiotic star spectra). It was absent in the epoch 2 spectrum. The interstellar absorption gives a column density NH = (3 ± 0.5) × 1021 cm-2 that is consistent with the reddening, E(B − V) = 0.5, proposed in Paper I. Although the continuum between 1800 and 2400 Å is weak, the strength of the 2175 Å feature is consistent with this reddening. An important feature of this simulation is the indirect verification of the transparency of the ejecta, since the model assumes the same profile for Lyα as Hα. The upper limit for the emission in the epoch 2 spectrum is compatible with the overall fading of the ultraviolet emission lines. We also note that the optical [Ca V] lines had also decreased substantially by epoch 2, consistent with this change in a high ionization species.
 |
Fig. 8 top: Epoch 1 Lyα profile model using Hα and O V] 1318.3 Å. Bottom: Epoch 1 Lyα STIS observation. |
3.3. Modeling the structure of the ejecta
Understanding the properties of the resolved ejecta of T Pyx has been a daunting task. The ejecta present an extremely fragmented appearance in almost every emission line filter. The HST images show a nearly symmetric but completely filamented ring (e.g. Shara et al. 1997). This confusion has been dramatically removed by the infrared continuum and line spectro-interferometric observations during the current outburst by Chesneau et al. (2011) using infrared CHARA and VLTI. They find that after day 28 the AMBER K-band and PIONIER-H band visibilities are consistent with a two-component bipolar plus central point source model with very low inclination. In light of the uncertainties in the orbital inclination from Uthas et al. (2010), we set our constraints based on the interferometry.
Models of nova ejecta have long included strong departures from simple expanding spheres. In her fundamental monograph, Payne-Gaposchkin (1957) highlighted examples of the variations of the line structures, invoking rings and shells to reproduce the individual components. Hutchings (1970, 1972) included polar cones and rings when modeling the profiles in HR Del 1967. The (ultimately) spatially resolved ejecta of this nova have also been studied by Solf (1983) who combined an equatorial ring with conical polar ejecta to reproduce the line profiles. This was elaborated by Hillwig (2001), using groundbased optical multifiber spectroscopy and HST/WFPC2 imaging. The HST Hα and [O III] images show strikingly different structures, Hα being more extensive and thicker while the forbidden lines show thin-walled polar cones of the sort discussed by Solf and also well known from planetary nebulae.
We used a Monte Carlo procedure to model the optically thin nebular spectra. The ejecta geometries were assumed to be either spherical or axisymmetric spheroids (prolate or oblate). The free parameters of the models were the opening conical (bipolar) angles (an inner angle θ1 ≥ 0, and an outer angle θ2 ≤ 90°), the inner radial extent, ΔR/Rmax, relative to the outer radius Rmax that is given by the maximum velocity vmax, and an inclination i to the line of sight (for the spheroidal and conical models). The position angle in the plane of the sky was fixed at o°. The velocity was assumed to be linearly dependent on the radius (a ballistic or so-called “Hubble” flow) with the density varying as r-3 (constant mass for the ejecta) and a power law density dependence for the emissivity, ρnd. In general, we assumed nd = 2 for recombination lines. This method is an extension of the procedure used in our previous studies, e.g. V1974 Cyg (Shore et al. 1993), V382 Vel (Shore et al. 2003), and V1186 Sco (Schwarz et al. 2007). A sample of line model profiles is shown in Fig. 9 and examples of the resulting images and a representative line profile are shown in Fig. 10. Gill & O’Brien (1999) presented an ensemble of computed spectra and images using ring geometries and various ellipticities for the ejecta that show many of the features we will describe. In this our efforts can be seen as an extension of the existing models but also a unification of the phenomenology. Harman & O’Brien (2003) modeled HR Del with similar assumptions. Thus, while such structures – polar ejection, rings, and shells – have been frequently suggested in the literature since the start of modern nova studies (e.g. Gill & O’Brien 1993), the novelty here is the ease of modeling provided by the Monte Carlo method and the specific dynamics.
 |
Fig. 9 Examples of simulated line profiles for θo = 5° and θi = 30°. Solid: ΔR/R = 0.4; dash: ΔR/R = 0.6; dot-dash: ΔR/R = 0.8. Top panel: i = 15°; middle panel: i = 30°; bottom panel: i = 60°. The maximum velocity was 4000 km s-1. This shows the range of profiles expected for a sample of recurrent novae with similar structure to T Pyx (see text for details). |
 |
Fig. 10 Example of a line profile and synthetic images, assuming that the lines are formed by recombination and with ballistic velocity law, constant mass bipolar ejecta for various inclinations (as noted on each frame). All models assumed vmax = 5000 km s-1, with the outer and inner angles (10, 40) and ΔR/R = 0.3. The profile shown in the upper left is for i = 20°. |
At fixed inclination, the full width at zero intensity (FWZI) and full width at half-maximum (FWHM) of the profiles depend critically on ΔR/R. In the earliest spectra, taken with the NOT during the fireball and optically thick stages (Shore et al. 2012) the maximum velocity of the P Cyg troughs on the Balmer and He I optical lines was about 4000 km s-1. Using this as the maximum velocity for the ejecta, 0.4 ≤ ΔR/R ≤ 0.5, independent of the inclination or the exponent of the intensity power law. The structure of the line peak, in contrast, has a mixed dependence on the opening angle of a polar ejection, the inner polar angle, and the inclination. Since the Balmer, [N II], and [O III] lines all display the same profiles in the spectra we discuss here, it appears that there is no particular difference between lines formed by radiative excitation (e.g. the forbidden lines) and those from recombination (Balmer, He II).
 |
Fig. 11 Composite bipolar lobe line profiles. All simulations used vmax| = 4000 km s-1, i = 20°, and ballistic, constant mass ejecta. We use the notation, here and in Fig. 12, [θ0,θ1,ΔR/R,i] for the model parameters. The broad component (consistent with the epoch 1 data) has the parameters [5, 30, 0.5, 20], and is combined with a second consistent with the [O III] profile (see Fig. 7) with [50, 90, 0.2]. The relative weights of the two contributing profiles are indicated in each frame. See text for details. |
An important clue regarding the geometry comes from the comparison of the high velocity portions of the line profiles in the two epochs. These decrease in intensity while the core to wing ratio increases. The simulations match, shown in Fig. 11 for each epoch, the line profiles shown in Fig. 1 for the Balmer and He I lines and Fig. 4 for the nitrogen transitions. The He II 1640, 4686 Å lines have much more reduced emission on the “shoulders” of the line in epoch 2 than the forbidden lines. This can be reproduced by assuming either a smaller inner fractional radius and/or changing the radial dependence of the intensity power law to mimic different ionizations without a change in the overall geometry of the ejecta. Figure 12 shows the two UV line profiles observed in both epochs, N IV] 1486 Å and He II 1640 Å. As we described, the He II UV and optical 4686 Å profiles are identical. The He+ region we find is more extensive in the ejecta, signaled by the narrower line profile, but the cone parameters are rather similar. The UV resonance intercombination lines all displayed the same profiles so we consider the match obtained here to be generic of that line forming portion of the ejecta. The major anomaly remains the N V 1240 Å and C IV 1550 Å doublets. In these doublets there seems to be a blend that is not modeled by the respective resonance lines alone. The success of the modeling for other complex lines, e.g. N III] 1751 Å, highlights this peculiarity. The relative changes in the two sides of the line appear more strongly linked to the 1548 Å component but this remains a puzzle.
Acceptable fits were obtained for a range of inclinations, depending on the assumed values for the angles. There is one very strong constraint: inclinations as low as 20° require an oblate symmetry with polar plumes for almost any angle. In general, the profiles cannot be reproduced with narrow opening angles, θ1 > 20°, 60° < θ2 ≤ 90°, because of the distinct separation of the polar ejecta in velocity. In contrast, nearly spherical ejecta – while lacking the strong central peak that is produced most easily at high inclination by the superposition of the two projected expansion velocities of the polar cones – give acceptable agreement without the central peak-shoulder structure. None of these details yield any particular value for the filling fraction, the filamentary/knotty structure of the ejecta is a natural consequence of numerical noise in the simulation. Any velocity law analogous to that from radiatively driven outflows from massive stars is ruled out by the model profiles for all inclinations.
 |
Fig. 12 N IV] 1486 Å and He II 1640 Å from the STIS 2012 Mar. spectrum with model line profiles. The parameters for the model are indicated for vmax = 4000 km s-1 and i = 20°. |
3.4. Electron density and mass of the ejecta
For epoch 1, the [O III] 4363, 4959, 5007 Å lines were strong and not severely blended with other lines. We scaled the Hβ profile to Hγ to remove the small (~10%) residual in the [O III] 4363 Å profile and calculated the electron density as a function of radial velocity by taking the ratio of the continuum subtracted resolved line profiles. The derived value depends on the electron temperature, Te. For the range 1 ≤ (Te/104 K) ≤ 4 we obtain 5.4 ≥ (ne/107 cm-3) ≥ 0.9 that is almost constant across the profile (Osterbrock & Ferland 2006). The [N II] 6583 Å line was very weak but present in the high velocity wing of Hα. Since the NOT spectrum was obtained after the transition to transparency, we used the scaled Hβ profile in an attempt to disentangle Hα and [N II] 6548, 6583 Å to have an independent estimate of the electron density (see Fig. 13). The residual emission was very weak but the ratio F(5755)/F(6583) ≤ (0.5 ± 0.1), corrected for E(B − V) = 0.5, which for the same range of Te corresponds to 4.9 ≥ (ne/106 cm-3) ≥ 1.4. No single combination of ne and Te yields both diagnostic ratios. In contrast, since for epoch 2 the [N II]/Hα ratio had significantly increased, we were able to obtain a single set of physical properties. The observed, dereddened [O III] ratio was F(4949 + 5007)/F(4363) = 8.4 ± 0.1. Using the scaled Hβ profile as before, we recovered the [N II] 6583 Å line (see Fig. 12). The 5755 Å and the recovered 6583 Å profiles are identical. The flux ratio, F(6548 + 6583)/F(5755) = 1.2 ± 0.1, is approximately constant for |vrad| < 1000 km s-1 with the exception of the narrow feature at around +600 km s-1. A single pair of parameters results from the two epoch 2 diagnostics, Te = 3.9 × 104 K and ne = 5.4 × 105 cm-3, see Fig. 14. The similarity of all profiles at this second epoch supports the picture of nearly isothermal, transparent ejecta (see Fig. 13). As a further check of the assumption of a constant mass for the ejecta for which ne ~ t-3, the density should decrease by about a factor of 10 between the two epochs (Day 170 and Day 350 after discovery). This roughly agrees with the He II 1640 Å and 4686 Å flux variations.
 |
Fig. 13 Optical N II profiles, 2012 Apr., used for the electron density analysis. Top: [N II] 5755 Å; bottom: [N II] 6583 Å (solid), composite profile with Hα before decomposition (dash). If present, [N II] 6548 Å is extremely weak. See text for details. |
 |
Fig. 14 Comparison of [N II] (dots) and [O III] (solid line) electron densities from epoch 2. The wings beyond |vrad = 1000 km s-1 are comparatively weaker in [N II] than [O III], hence the much higher noise. |
Using the electron density for epoch 2, and assuming vmax = 4000 km s-1 (based on the earliest optically thick spectra, see Paper I), the mass derived for the ejecta is approximately 5 × 10-5f M⊙ independent of the distance. The solid angle of the ejecta obtained from modeling the profiles is independent of f, which instead measures the fragmentation of the expelled gas. From the complexity of the narrow absorption features on the Balmer lines (see Paper I), we expect that f may be much less than unity so this mass is clearly an upper limit. An estimate of the filling factor can be derived from the Balmer line fluxes from the epoch 1 data. The measured Hβ flux from the G430L STIS spectrum from epoch 1 was 1.5 × 10-11 erg s-1 cm-2. Corrected for E(B − V) = 0.5, this corresponds to F(β) = 7.7 × 10-11 erg s-1 cm-2. Taking a distance ≥ 3.5 kpc gives a luminosity L(Hβ) ≥ 1.2 × 1035 erg s-1. Using the lower distance and assuming case B recombination for Te = 104 K yields an emission measure of 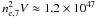 cm-3 where ne,7 is the electron density in units of 107 cm-3 for source volume V. Taking ne,7 ≈ 3 for Day 170 gives an estimate of f ≈ 0.034. This is in the range of typical values for the filling factor (see e.g. Shore (2008) and references therein). The implied ejecta mass, Mej ≈ 2 × 10-6 M⊙ is similar to that obtained for other RNe. In contrast, Schaefer et al. (2010) derived a mass for the matter that they identify with a single classical nova-like outburst of 1866, Mej ~ 3 × 10-5 M⊙. Selvelli et al. (2009) and, more recently, Evans et al. (2012) have also argued that the mass of the accumulated flotsam of previous ejections may be considerably greater, perhaps a factor of order 100, than that of a single event. Evans et al. (2012) based this on the infrared light curve of the 2011 event that they explain as a light echo from the previously ejected material5.
cm-3 where ne,7 is the electron density in units of 107 cm-3 for source volume V. Taking ne,7 ≈ 3 for Day 170 gives an estimate of f ≈ 0.034. This is in the range of typical values for the filling factor (see e.g. Shore (2008) and references therein). The implied ejecta mass, Mej ≈ 2 × 10-6 M⊙ is similar to that obtained for other RNe. In contrast, Schaefer et al. (2010) derived a mass for the matter that they identify with a single classical nova-like outburst of 1866, Mej ~ 3 × 10-5 M⊙. Selvelli et al. (2009) and, more recently, Evans et al. (2012) have also argued that the mass of the accumulated flotsam of previous ejections may be considerably greater, perhaps a factor of order 100, than that of a single event. Evans et al. (2012) based this on the infrared light curve of the 2011 event that they explain as a light echo from the previously ejected material5.
3.5. Summary of the modeling
The observed line profiles during the optically thin stages of the expansion of T Pyx can be explained by a unified model in which the ejecta have an axial (bipolar) symmetry with the expansion directed at low inclination to the line of sight. This agrees with the interferometric imaging (and perhaps also with the infrared emission described by Evans et al. 2012). The relative contributions of the inner and outer portions of the polar lobes change systematically in time. The observed line profiles for all ions, except N V 1240 and C IV 1550 – conform to this scheme. The differences between RNe is then mainly consequences of the differences in inclination of the ejecta axis to the line of sight and the thickness of the line forming region relative to the maximum velocity. The profiles are interpretable using ballistic ejection, resulting in a linear velocity law, and constant mass. While not definitively excluded, there is no need to invoke either continuing outflows, such as super-Eddington stellar winds, or multiple individual ejection events to obtain the structures in the observed line profiles during the nebular phase. By extension, this may apply to other classical novae for which similar geometries and variations have been reported in the literature. For any inclination, for ΔR/R ≥ 0.2, an outer angle of θo > 20° is not able to reproduce the profiles for any inner angle θi. The profiles are always two well separated, although not symmetric, peaks. There is general agreement in the literature that the inclination must be quite low but there is still a considerable range, from ~6° to 10° (favored by optical interferometric imaging and orbital solution) to ≤ 30° (Selvelli et al. 2009), the FWZI of the profile is uniquely determined by the ejecta thickness.
4. Discussion
The simplest way to understand the line profiles is with polar cones rather than either rings or multiple shells but these are the zones in which the emission lines are formed. They may not, however, completely delineate the mass distribution. That requires detailed photoionization modeling (e.g. Ercole et al. 2003). But on the basis of these simulations we suggest that the RN6, and by extension perhaps also classical novae, are unified by the structure observed in the profiles of the compact sources. Observations of the known RNe, e.g. CI Aql (Iijima 2012), and the RN candidate KT Eri agree morphologically with those obtained in this study of T Pyx. The main difference, aside from the photometry, is the early presence in the most compact systems, those with orbital periods less than about 0.5 days, of an optically thick stage that closely resembles classical novae during the rise to maximum visible light.
 |
Fig. 15 Comparison of the Hα line for KT Eri from 2009 Dec. 12 (Day 18), a SMARTS high resolution (3 Å) spectrum (top) with a model profile with angles (40, 60) degrees, ΔR/R = 0.35 and i = 60°. The range in i, ΔR/R, and angles is about 10%. |
As an extension of the technique, we have applied the same geometry to several other, well observed, RN. For KT Eri, the line profiles during the nebular stage obtained by the SMARTS7 (Walter et al. 2012) are almost identical to the T Pyx spectra at a similar stage in the light curve, although with a higher maximum velocity. An example of applying the modeling technique is shown in Fig. 15. This suggests that the ejecta thickness may have been slightly different between the two but the profiles are similar. The late time STIS/HST spectrum of U Sco 1999 at Hα (o5fq08010, G750M) and the spectra shown in Iijima (2002, Figs. 2 (Day 1) and 7 (Day 17)) are also quite similar once care has been taken to remove the contaminating blend with the [N II] lines.
The similarity of the T Pyx line profiles during the nebular stage to RNe of the U Sco type leaves the early long duration recombination wave event modeled in Shore et al. (2011) paradoxical. The ejecta mass is small, <10-5 M⊙, yet the spectral variations in the first two months following discovery displayed the recombination wave (Shore et al. 2011) that is expected only in optically thick gas with column densities greater than 1023 cm-2. In fact, the prolonged maximum indicates a very significant opacity in the ultraviolet, more like a classical nova for which the ejecta masses are a factor of 10 greater or even more. The low mass derived here for the T Pyx ejecta, based on the optically thin stage, is comparable to those derived for other RN. However, there is a clue. There is a very prolonged optical maximum – corresponding to an extended optically thick stage lasting nearly two months – for T Pyx, IM Nor, and CI Aql. For V394 CrA, U Sco, and the symbiotic-like RN, the early optical light curve that is dominated by the ultraviolet opacity changes in the ejecta show nothing so extended in duration. The interferometric images indicate a similar structure to the ejecta for T Pyx as many other novae, even classical types such as HR Del. The filling factors of the ionized regions are quite low. From the comparison of the line profiles of individual ionization stages we have shown that the ejecta can best be explained as bipolar structures of moderate thickness and in ballistic expansion. All indications point to a low inclination for the T Pyx orbital plane, of order 10°, while U Sco is, in contrast, an eclipsing system. The main difference seems to be the orbital period: only the compact systems with Porb less than about 0.6 days show the extended optically bright phase, based on the data discussed in Schaefer (2010). We suggest that the extended opaque phase could be due to the formation of a cool common envelope after the explosion, causing a recombination wave to move outward through the ejecta that also extinguishes the XR emission. It could then slowly clear as the WD settles into a stage of quasi-static nuclear burning and develops a supersoft source. We emphasize that this is only a hypothesis at present, current models do not permit the computation of fully three dimensional evolution of the system through this phase. It could, however, be related to the axial symmetry of the ejecta, a question yet to be explored (we thank the referee for this comment).
 |
Fig. 16 Comparison of Hβ from 2011 May 30 (top), Hβ 2011 Oct. (epoch1, middle), and [O III] 5007 Å from epoch1 (bottom). Notice the similarity of the nascent emission features in the line peak and redward portion and those in the later optically thin spectra. See text for details. |
Finally, a particularly intriguing result we are investigating is that the Balmer and metal line absorption systems described in Paper I correspond to the blueshifted peaks in the emission line profiles from months later. The last NOT spectrum from Paper I, obtained on 2011 May 30 still during the optically thick stage, shows the absorption on the Balmer lines confined to within the same velocity range as the wing of the optically thin epoch 1 profiles and the emission peak and structure on the redward portion of the Balmer lines showing similar characteristics to the later emission (see Fig. 15). This is, in our view, another strong
argument that the absorption, and the attendant “accelerations” are produced by the recombination wave within the expanding ejecta and not something arising in the circumsystem medium. The maximum absorption velocity observed before 2011 May. was −2000 km s-1, virtually identical to the limits of the emission lines, and structure appearing in the redshifted wings also mimics the later observations. This further implies that the material was confined even at the earliest stages to the narrow cone (and possibly ring) found from interferometry and our modeling. However, there is no possibility that with such a small mass, and so narrowly confined toward the periphery, that the ejecta alone could have produced the required column densities for the absorption/fluorescence spectrum and the recombination event.
URL: http://www.astro.sunysb.edu/fwalter/SMARTS/NovaAtlas/ nova survey.
Acknowledgments
We thank the referee, G. C. Anupama, for thought provoking questions, and Mike Bode, Jordi Casanova, Nye Evans, Jordi José, Tim O’Brien, Brian Warner, and Bob Williams for discussions and correspondence. We also thank Olivier Chesneau for his comments on the draft. We have made extensive use of the Astrophysics Data System (ADS), SIMBAD (CDS), and the Barbara A. Mikulski MAST archive (STScI) during this work. The STIS spectra were obtained in program GO 12200 and GO/DDT 12799. The NOT observations were obtained in Fast Track proposal 43-403.
References
- Anupama, G. C. 2008, in RS Ophiuchi (2006) and the Recurrent Nova Phenomenon, eds. A. Evans, M. F. Bode, T. J. O’Brien, & M. J. Darnley (San Francisico: ASP), ASP Conf. Ser., 401, 31 [Google Scholar]
- Bode, M., & Evans, A. 2008, The Classical Novae, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Chesneau, O. Meilland, A. Banerjee, D. P. K. Le Bouquin, J.-B., et al. 2011, A&A, 534, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., Barlow, M. J., Storey, P. J., & Liu, X.-W. 2003, MNRAS, 340, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A. N., Gehrz, R. D., Helton, L. A., et al. 2012, MNRAS, 424, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, C. D. & O’Brien, T. J. 1999, MNRAS, 307, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Harman, D. J. & O’Brien, T. J. 2003, MNRAS, 344, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Hillwig, T. C. 2001, Ph.D. Thesis (Astronomy), Indiana Univ. Bloomington [Google Scholar]
- Hjellming, R. M. 1996, ASPC, 93, 174 [NASA ADS] [Google Scholar]
- Hutchings, J. B. 1970, PDAO, 13, 347 [NASA ADS] [Google Scholar]
- Hutchings, J. B. 1972, MNRAS, 158, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Iijima, T. 2002, A&A, 387, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iijima, T. 2012, A&A, 544, A26I [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kato, M., & Hachisu, I. 2007, ApJ, 657, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, T. J., & Cohen, J. G. 1998, ApJ, 498, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Payne-Gaposchkin, C. 1957, The Galactic Novae (Amsterdam: North-Holland) [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. J., Shore, S. N., Starrfield, S., et al. 2001, MNRAS, 320, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Selvelli, P., Cassatella, A., Gilmozzi, R., & Gonzez-Riestra, R. 2008, A&A, 492, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaefer, B. 2010, ApJS, 187, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Shaefer, B., Pagnotta, A., & Shara, M. M. 2010, ApJ, 708, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Zurek, D. R., Williams, R. E., Prialnik, D., et al. 1997, AJ, 114, 2548 [Google Scholar]
- Shore, S. N. 2008, in The Classical Novae, eds. M. F. Bode, & A. N. Evans, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Shore, S. N., Augusteijn, T., Ederoclite, A., & Uthas, H. 2011, A&A, 533, L8 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solf, J. 1983, ApJ, 273, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, R. W. 2008, in The Classical Novae, eds. M. F. Bode, & A. N. Evans, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- StarrÞeld, S., Sparks, W. M., & Truran, J. W. 1985, ApJ, 291, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Uthas, H., Knigge, C., & Steeghs, D. 2010, MNRAS, 409, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Waagan, E., Linnolt, M., & Pearce, A. 2011, IAUC, 9205 [Google Scholar]
- Walter, F. M., Battisti, A., Towers, S. E., Bond, H. E., & Stringfellow, G. 2012, PASP, 124, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R., & Mason, E. 2010, Ap&SS, 327, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R., Mason, E., Della Valle, M., & Ederoclite, A. 2008, ApJ, 685, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Feldman, U., & Lobel, A. 2011, ApJS, 196, 23 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Hα (first row), Hβ (second row), He II 4686 Å (third row), and He I 5875 Å (bottom, left) line profiles in radial velocity (km s-1, uncorrected for LSR) epoch 1 (left) and epoch 2 (right), from the NOT spectra. Note that He I was not present in the epoch 2 spectra. |
| In the text | |
 |
Fig. 2 Comparison of He II 1640 Å (solid) with He II 4686 Å (dot-dash) from epoch 1 (top) and epoch 2 (bottom). All spectra were dereddened with E(B − V) = 0.5. For display purposes, the optical NOT spectrum is multiplied by a factor of 40 with a boxcar smoothing to 11 points. |
| In the text | |
 |
Fig. 3 Comparison of the N IV] 1486 Å (top) and C III] 1909 Å (bottom) profiles from the STIS epoch 1 spectrum. The C III] line was not covered in the epoch 2 STIS observation. |
| In the text | |
 |
Fig. 4 Comparison of the simultaneous nitrogen line profiles from epoch 1 (left) and epoch 2 (right). Top: [N II] 5755 Å, bottom: N IV] 1486 Å. Note, in particular, the change in the core to wing ratio (see text for further discussion). |
| In the text | |
 |
Fig. 5 Ultraviolet resonance multiplets Si IV/S IV] 1402 AA (top), N V 1240 Å (middle) and C IV 1550 Å (bottom) for epoch 1 (left) and epoch 2 (right). The interstellar absorption components are visible on the resonance lines. For comparison the mean wavelength of the blend has been used. Note the strong change in the C IV line at about + 1300 km s-1, but note that the C IV and N V are blends with large velocity separation between the components and the variations cannot be uniquely assigned. See text for details. |
| In the text | |
 |
Fig. 6 [O III] line profiles, in velocity, from epoch 1 (left) and epoch 2 (right). From the top, λ 4363 Å λ 4959 Å and λ 5007 Å. The fluxes have not been corrected for reddening and no absolute calibration was applied to the epoch 1 data for display purposes. See text for discussion. |
| In the text | |
 |
Fig. 7 [Ca V] 6086 Å (top) and 5309 Å line profiles for epoch 1 (left) and epoch 2 (right). |
| In the text | |
 |
Fig. 8 top: Epoch 1 Lyα profile model using Hα and O V] 1318.3 Å. Bottom: Epoch 1 Lyα STIS observation. |
| In the text | |
 |
Fig. 9 Examples of simulated line profiles for θo = 5° and θi = 30°. Solid: ΔR/R = 0.4; dash: ΔR/R = 0.6; dot-dash: ΔR/R = 0.8. Top panel: i = 15°; middle panel: i = 30°; bottom panel: i = 60°. The maximum velocity was 4000 km s-1. This shows the range of profiles expected for a sample of recurrent novae with similar structure to T Pyx (see text for details). |
| In the text | |
 |
Fig. 10 Example of a line profile and synthetic images, assuming that the lines are formed by recombination and with ballistic velocity law, constant mass bipolar ejecta for various inclinations (as noted on each frame). All models assumed vmax = 5000 km s-1, with the outer and inner angles (10, 40) and ΔR/R = 0.3. The profile shown in the upper left is for i = 20°. |
| In the text | |
 |
Fig. 11 Composite bipolar lobe line profiles. All simulations used vmax| = 4000 km s-1, i = 20°, and ballistic, constant mass ejecta. We use the notation, here and in Fig. 12, [θ0,θ1,ΔR/R,i] for the model parameters. The broad component (consistent with the epoch 1 data) has the parameters [5, 30, 0.5, 20], and is combined with a second consistent with the [O III] profile (see Fig. 7) with [50, 90, 0.2]. The relative weights of the two contributing profiles are indicated in each frame. See text for details. |
| In the text | |
 |
Fig. 12 N IV] 1486 Å and He II 1640 Å from the STIS 2012 Mar. spectrum with model line profiles. The parameters for the model are indicated for vmax = 4000 km s-1 and i = 20°. |
| In the text | |
 |
Fig. 13 Optical N II profiles, 2012 Apr., used for the electron density analysis. Top: [N II] 5755 Å; bottom: [N II] 6583 Å (solid), composite profile with Hα before decomposition (dash). If present, [N II] 6548 Å is extremely weak. See text for details. |
| In the text | |
 |
Fig. 14 Comparison of [N II] (dots) and [O III] (solid line) electron densities from epoch 2. The wings beyond |vrad = 1000 km s-1 are comparatively weaker in [N II] than [O III], hence the much higher noise. |
| In the text | |
 |
Fig. 15 Comparison of the Hα line for KT Eri from 2009 Dec. 12 (Day 18), a SMARTS high resolution (3 Å) spectrum (top) with a model profile with angles (40, 60) degrees, ΔR/R = 0.35 and i = 60°. The range in i, ΔR/R, and angles is about 10%. |
| In the text | |
 |
Fig. 16 Comparison of Hβ from 2011 May 30 (top), Hβ 2011 Oct. (epoch1, middle), and [O III] 5007 Å from epoch1 (bottom). Notice the similarity of the nascent emission features in the line peak and redward portion and those in the later optically thin spectra. See text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


