| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219898 | |
| Published online | 11 December 2012 | |
Infrared radiative transfer in atmospheres of Earth-like planets around F, G, K, and M stars
I. Clear-sky thermal emission spectra and weighting functions⋆
1 DLR – Deutsches Zentrum für Luft- und Raumfahrt, Institut für Methodik der Fernerkundung, Oberpfaffenhofen, 82234 Weßling, Germany
e-mail: mayte.vasquez@dlr.de
2 TUM – Technische Universität München, Lehrstuhl für Methodik der Fernerkundung, Arcisstr. 21, 80333 München, Germany
3 TUB – Technische Universität Berlin, Zentrum für Astronomie und Astrophysik, Hardenbergstr. 36, 10623 Berlin, Germany
4 DLR – Deutsches Zentrum für Luft- und Raumfahrt, Institut für Planetenforschung, Rutherfordstr. 2, 12489 Berlin, Germany
Received: 26 June 2012
Accepted: 18 October 2012
Context. The atmosphere of Earth-like extrasolar planets orbiting different types of stars is influenced by the spectral dependence of the incoming stellar radiation. The changes in structure and composition affect atmospheric radiation, hence the spectral appearance of these exoplanets.
Aims. We provide a thorough investigation of infrared radiative transfer in cloud-free exoplanets atmospheres by not only analyzing the planetary spectral appearance but also discussing the radiative processes behind the spectral features in detail and identifying the regions in the atmosphere that contribute most at a given wavelength.
Methods. Using cloud-free scenarios provided by a one-dimensional radiative-convective steady-state atmospheric model, we computed high-resolution infrared transmission and emission spectra, as well as weighting functions for exoplanets located within the habitable zone of F, G, K, and M stars by means of a line-by-line molecular absorption model and a Schwarzschild solver for the radiative transfer. The monochromatic spectra were convolved with appropriate spectral response functions to study the effects of finite instrument resolution.
Results. Spectra of the exoplanets of F, G, K, and M stars were analyzed in the 4.5 μm N2O band, the 4.3 μm and 15 μm CO2 bands, the 7.7 μm CH4 band, the 6.3 μm H2O band, and the 9.6 μm O3 band. Differences in the state of the atmosphere of the exoplanets clearly show up in the thermal infrared spectra; absorption signatures known from Earth can be transformed to emission features (and vice versa). Weighting functions show that radiation in the absorption bands of the uniformly mixed gases (CO2, CH4, N2O) and (to some extent) ozone comes from the stratosphere and upper troposphere, and also indicate that changes in the atmospheres can shift sources of thermal radiation to lower or higher altitudes. Molecular absorption and/or emission features can be identified in the high-resolution spectra of all planets and in most reduced resolution spectra.
Conclusions. Insight into radiative transfer processes is essential for analyzing exoplanet spectral observations; for instance, understanding the impact of the temperature profile (nb. non-existence of an inversion) on the CO2 bands facilitates their interpretation and can help avoid false positive or negative estimates of O3. The detailed analysis of the radiation source and sink regions could even help give an indication about the feasibility of identifying molecular signatures in cloud-covered planets, i.e. radiation mainly coming from the upper atmosphere is less likely to be hidden by clouds. Infrared radiative transfer and biomarker detectability in cloud-covered exoplanets will be presented in a companion paper.
Key words: radiative transfer / techniques: spectroscopic / planets and satellites: atmospheres / infrared: planetary systems
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The search for the potential habitability of extrasolar planets includes the study of their atmospheres. The atmospheric composition (molecules and particles) and physical conditions of extrasolar planets can be revealed and analyzed through spectroscopy, since the only quantity that can be measured from the planets is the flux. In determining the habitability of extrasolar planets, studies concentrate on Earth-like bodies since our home planet is the only available guidance in understanding planets where life may develop. For this, the modeled spectra of Earth-like planets may offer information on the atmosphere due to the influence of the different types of stars.
Several groups have studied the potential biosignatures of exoplanets in the infrared and/or visible-ultraviolet spectral regime. Schindler & Kasting (2000) modeled the longwave thermal infrared for Earth, a methane rich early Earth, Mars, and early Venus. Des Marais et al. (2002) investigated molecular bands of biomarker and greenhouse gases in order to provide wavelength regions and spectral features useful for characterizing potentially habitable exoplanets. The problem of “false-positive detection” of biosignatures with NASA’s Terrestrial Planet Finder or ESA’s Darwin has been discussed by Schindler & Kasting (2000) and Selsis et al. (2002), respectively. Segura et al. (2003, 2005) analyzed the feasibility to observe the biosignatures of Earth-like planets orbiting different main sequence stars. Complementary to Des Marais et al. providing spectra of present day Earth with different molecular abundances, Kaltenegger et al. (2007) modeled spectra for different geological epochs of Earth. Grenfell et al. (2011) assessed biosignatures and their robustness under varying conditions for early Earth’s Proterozoic epoch. Rauer et al. (2011) studied atmospheric chemistry and the resulting transmission and emission spectra of super-Earth planetary atmospheres orbiting the habitable zones of a variety of M-dwarf stars.
The presence and characteristics of clouds depends on the state of the atmosphere, and in turn clouds influence the atmosphere. In particular, clouds modify the atmospheric radiation and temperature distribution (e.g. Kitzmann et al. 2010), hence also the spectral appearance of a planet. Des Marais et al. (2002) considered clouds in the radiative transfer calculations by “inserting continuum absorbing/emitting layers at appropriate altitudes”. Clouds have not been considered in the Segura et al. (2003, 2005) studies. Kaltenegger et al. (2007) modeled radiative transfer assuming a weighted average of cloud-free, low-, medium-, and high-level clouds; however, the thermal structure of the atmosphere apparently has not been adjusted to the cloudiness. The impact of low-level water or high-level ice clouds on the low-resolution, thermal emission spectra of exoplanets orbiting F, G, K, or M stars is described by Kitzmann et al. (2011).
To study the feasibility of detecting biosignatures in cloud-contaminated exoplanet spectra based on a (physically) consistent description of atmospheres (as provided by, e.g., a one-dimensional radiative convective climate model coupled with a cloud model, Kitzmann et al. 2010) is clearly desirable. However, an assessment of the impact of clouds on the spectral signatures of exoplanets requires a profound understanding of radiative transfer and spectral appearance of cloud-free, pure gaseous atmospheres.
Accordingly, we present here a detailed description of thermal infrared emission of clear-sky atmospheres of exoplanets orbiting F, G, K, and M stars, both for “ideal” high-resolution spectra as provided by line-by-line (lbl) modeling, and for low spectral resolution (obtained by convolution of the monochromatic spectra with appropriate response functions) that could be performed by current (or planned) instruments. In addition to emission and transmission spectra, we also present weighting functions and provide a detailed discussion of the physics giving rise to the spectral patterns seen. Weighting functions, originally introduced in the context of temperature sounding for meteorology and planetary science, are a quantitative measure that describe how different altitude regimes contribute to the upwelling radiation. For our study of spectral signatures in cloud covered planets (Paper II) this information is important, because spectral regions with radiation originating from upper atmospheric layers are less likely to be affected by clouds.
The basis of this study is a lbl modeling of molecular absorption. Clearly, observed spectra of exoplanets will not deliver the high spectral resolution provided by lbl models in the foreseeable future, and the need for these computationally expensive calculations can be questioned. However, if a spectral signature of a species of interest (e.g., a biosignature) cannot be detected in the (observed) low-resolution spectra, it is unclear whether the sought-for feature does not show up because of the physics of radiative transfer, the lack of the corresponding species in the atmosphere, or other instrumental issues (“false-negative” detection). Similar care has to be taken to avoid “false-positive” detections.
Furthermore, low-resolution models typically based on band or k-distribution approaches have frequently been developed for a restricted parameter range (pressure, temperature, composition), e.g. trimmed to conditions as found in Earth’s atmosphere (e.g. Mlawer et al. 1997), and the application of these models to exoplanets spanning a wide range of atmospheric conditions should be done with care. In particular the spectral appearance as indicated by these models should be carefully checked against “benchmark” lbl spectra and low-resolution spectra obtained from them by appropriate convolution. Note that for modeling thermal emission spectra Selsis et al. (2002) and Kitzmann et al. (2011) used low-resolution band or correlated-k radiative transfer models, respectively, whereas high-resolution lbl models were used in all other studies mentioned above.
As an extension to previous investigations, we provide the first consistent treatment of all main sequence stars and the main molecular absorbers in the thermal infrared for various resolutions, and discuss the physics of infrared radiative transfer in order to understand the spectral features. In addition, the spectra have been studied with and without the presence of certain molecules at a very low-resolution in order to determine the contributing molecular species. Des Marais et al. (2002) and Kaltenegger et al. (2007) have presented spectra for Earth with varying molecular abundances or for Earth at different geological epochs. Segura et al. (2003) have discussed the low-resolution spectra of F-, G-, and K-star planets with an emphasis on ozone (CO2 and CH4 spectra have been shown, too). In addition to these three molecules, the M dwarf study of Segura et al. (2005) have also shown spectra of water. The CO2 band at 4.3 μm has not been investigated in these studies, and N2O signatures have only been considered by Des Marais et al. (2002), Grenfell et al. (2011), and Rauer et al. (2011). Kitzmann et al. (2011) have simulated thermal emission spectra for main sequence star planets only at significantly lower resolution.
This paper is organized as follows: Sect. 2 describes the atmospheric and radiative transfer models and planetary scenarios. The resulting high-resolution planetary spectra and weighting functions for cloud-free atmospheres are shown and analyzed in Sect. 3. Section 4 examines the modeled spectra at different resolutions. The results are summarized in Sect. 5. This study thus provides a starting point and reference for interpreting the infrared emission spectra of cloud-covered exoplanet atmospheres presented in a forthcoming Paper II, and might also serve as a complement to the papers cited above.
2. Modeling
2.1. Radiative transfer
Assuming a cloud-free atmosphere and local thermodynamical equilibrium, radiative transfer in the thermal infrared is described by Schwarzschild’s equation, i.e. the intensity (radiance) I at wavenumber ν seen by an observer at position s = 0 is given by the integral (e.g. Goody & Yung 1989; Zdunkowski et al. 2007) 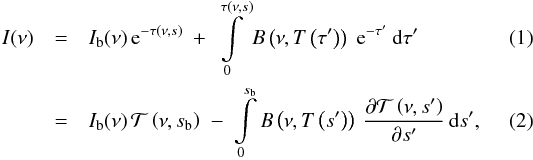 where B is the Planck function at temperature T, and Ib is a background contribution, e.g. surface emission. The transmission
where B is the Planck function at temperature T, and Ib is a background contribution, e.g. surface emission. The transmission 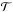 and optical depth τ are given by Beer’s law,
and optical depth τ are given by Beer’s law, ![\begin{eqnarray} \mathcal{T}(\nu,s) ~&\equiv&~ \mathrm{e}^{-\tau(\nu,s)} \\ ~&=&~ \exp{\left[ - \int_0^s \mathrm{d}s' \, \sum_m n_m\left(s'\right) \, k_m\left(\nu,p\left(s'\right),T\left(s'\right)\right) \right]} \nonumber \end{eqnarray}](/articles/aa/full_html/2013/01/aa19898-12/aa19898-12-eq20.png) (3)where p is the atmospheric pressure and nm the number density of molecule m. In high-resolution line-by-line models the absorption cross section km is given by the superposition of many lines, km(ν,p,T) = ∑ lSl(T) g(ν,p,T), each described by the product of a temperature-dependent line strength Sl and a normalized line shape function g describing the broadening mechanism(s). The combined effect of pressure broadening (corresponding to a Lorentzian line shape) and Doppler broadening (Gaussian line shape) is represented by a Voigt line profile (cf., e.g. Schreier 2011).
(3)where p is the atmospheric pressure and nm the number density of molecule m. In high-resolution line-by-line models the absorption cross section km is given by the superposition of many lines, km(ν,p,T) = ∑ lSl(T) g(ν,p,T), each described by the product of a temperature-dependent line strength Sl and a normalized line shape function g describing the broadening mechanism(s). The combined effect of pressure broadening (corresponding to a Lorentzian line shape) and Doppler broadening (Gaussian line shape) is represented by a Voigt line profile (cf., e.g. Schreier 2011).
Radiative transfer calculations were made with GARLIC (Generic Atmospheric Radiation Line-by-line Infrared Code, a modern Fortran reimplementation of the Fortran 77 code MIRART/SQuIRRL, Schreier & Schimpf 2001). MIRART/SQuIRRL has been verified in extensive intercomparisons, e.g. von Clarmann et al. (2002) and Melsheimer et al. (2005); recently, Hedelt et al. (2011) have used the code successfully to model observations of the Venus transit 2004 made by the Tenerife Vacuum Tower Telescope, and Vasquez et al. (2012) modeled near-infrared spectra of Venus observed by the SCIAMACHY instrument aboard ESA’s ENVISAT. Furthermore, it has been used for an assessment of exoplanet biosignatures by Grenfell et al. (2011); Rauer et al. (2011) and von Paris et al. (2011).
In this study, absorption cross sections for H2O, CO2, O3, CH4, and N2O were calculated using the molecular spectral line database HITRAN 2008 (Rothman et al. 2009). Continuum corrections were additionally taken into account, e.g. the CKD continuum (Clough et al. 1989) for water vapor. All spectra were convolved by applying Gaussian functions representing typical instruments of different resolutions.
The emergent flux spectra for planets around F2V, G2V, K2V, and M4.5V stars (see Table 1) were calculated by a superposition of individual radiance spectra (at appropriate angles) to account for the hemispherical integration. This integration was computed by considering beam radiances in a plane-parallel atmosphere. To check this approach, the disk-averaged outgoing fluxes were also computed for a spherical atmosphere. Only small differences were found between the fluxes. The reason behind this agreement is that the beams with zenith angles close to 0° are not very affected by the sphericity of the planet and are the main contributors to the total flux. On the other hand, spherical beam radiances close to 90° (almost parallel to the surface) differ considerably from the plane-parallel ones, but their contributions to the total flux is much less, and as a result, their impact on the flux integral turns out to be very low.
Characteristic parameters of the exoplanets and their atmospheres, surfaces, and host stars.
2.2. Scenarios
The atmospheric profiles used in the radiative transfer calculations of the different stars’ planets were calculated using a 1D steady-state, radiative-convective model. For a consistent description of the effect of clouds on the planetary spectral signatures, we decided to use the atmospheric profiles of Kitzmann et al. (2010) in both papers (i.e., only pressure, temperature, and water profiles are planet-dependent). This model can take the effect clouds produce on the atmosphere of the planet into account; however, here we only use the cloud-free atmospheric profiles, and cloud effects will be discussed in Paper II. Stellar spectra for typical F, G, K, and M stars were based on observations and/or synthetic data. The orbital distances of the planets to their central stars were scaled so that the stellar energy input at the top of the atmosphere equals the solar constant, see Table 1 (or Table 3 of Kitzmann et al. 2010). A detailed description of the model is given in Kitzmann et al. (2010).
The profiles of the major chemical species were obtained with a detailed photochemical model representing the modern Earth’s atmosphere (Grenfell et al. 2007) and are used for all model calculations. The empirical relative humidity distribution of Manabe & Wetherald (1967) is used for the relative humidity in. The radiative transfer in the atmospheric model, consists of a δ-two-stream quadrature at short wavelengths and a hemispheric mean two-stream method in the infrared (Toon et al. 1989). In the Kitzmann et al. (2010) radiative-convective model, gaseous absorption in the IR was described by the correlated-k method (Mlawer et al. 1997).
 |
Fig. 1 Pressure-temperature profiles of planets orbiting F, G, K, and M stars for clear sky conditions (see Kitzmann et al. 2010, for more details). The markers shown for the G star profile indicate the 58 pressure levels. |
 |
Fig. 2 Total transmission for a vertical path through the atmosphere of all planet types (top panel). Transmission due to water vapor (middle panel) and the other absorbers (lower panel) for an Earth atmosphere. Wavelengths are indicated at the top of the figure. |
The pressure-temperature profiles for the cloud-free atmospheres, given up to a top-of-atmosphere (ToA) pressure of pToA = 0.0755 mb, for the different planets are shown in Fig. 1. Host stars of different stellar types have a strong impact on the atmospheric conditions of their orbiting planets, as already pointed by, e.g., Segura et al. (2003). The surface temperature can differ by several tens of degrees, and the difference at the stratopause can be greater than 100 K; however, the surface temperatures of the cloud-free planets are above the freezing point of water for all planets (see the temperature profiles of the K- and M-star planets in comparison to the F-star planet).
The F- and G-star planets result in a temperature inversion in their stratospheres. The F-star planet has even higher stratospheric temperatures than its surface. The K- and M-star planet’s stratosphere is significantly different; in particular, the atmospheric temperatures decrease monotonically with increasing height throughout the K-star planet’s atmosphere. Since K and M stars are colder than the F and G stars, the amount of energy emitted in the ultraviolet (UV) and visible is considerably smaller. This UV radiation is mostly absorbed by the stratospheric O3 and, as a result, the stratosphere becomes warmer. This mechanism explains the high temperatures in the F- and G-star planets’ stratospheres. Since there is not enough energy in the UV delivered by the K and M stars, temperatures decrease further with altitude in their planet atmospheres. Strictly speaking, the K- and M-star planets do not have a stratosphere, i.e. an intermediate altitude regime of increasing temperatures; however, we use this term henceforth even for these planets to denote the mid-atmospheric altitude range, and the tropopause is considered as the upper end of the convective region.
3. Spectra at high resolution
Transmission and emission spectra, as well as weighting functions of Earth-like planets for a cloud-free atmosphere, are presented in this section. A detailed study of the spectral signatures of the main molecular absorbers found in the thermal infrared spectrum of all four planets is also presented. The G-star planet has been taken as reference in identifying the molecular bands found within the infrared region.
3.1. Transmission spectra and weighting functions
The total transmission for all planet types and the individual contributions for an Earth atmosphere are shown in Fig. 2. The atmospheric window regions 800 − 1200 cm-1 and 2500 − 3000 cm-1 are conveniently used to estimate the surface temperature; however, these estimates might be more reliable for F- or G-star planets than for K- or M-star planets due to their decreased opacity.
 |
Fig. 3 Weighting functions for the F and M star planets. Note the different color bars. Weighting functions for the G and K star planets can be found in the appendix, Fig. A.1. |
 |
Fig. 4 Location of maxima of the weighting functions for the F, G, K, and M star planets. |
 |
Fig. 5 Weighting functions for the F, G, K, and M star planets for selected wavenumbers in the regions of the CO2 (15 μm region left, 4.3 μm region right), O3, and CH4 bands. |
Differences in the state of the atmosphere have an influence on the distribution of sources and sinks of thermal radiation, which can be clearly seen by comparing of the so-called weighting functions of the F- and M-type star planets, Fig. 3. Weighting functions, defined by the partial derivatives 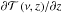 , are an important concept for nadir sounding of atmospheric temperature and are a measure of the contribution of a particular atmospheric layer to the upwelling radiation seen by a downlooking observer, see Eq. (2). In this equation, we use geometrical distance s (essentially altitude z) as integration variable. Because pressure is closely related to altitude, Schwarzschild’s equation can be easily reformulated in terms of pressure and weighting functions redefined accordingly.
, are an important concept for nadir sounding of atmospheric temperature and are a measure of the contribution of a particular atmospheric layer to the upwelling radiation seen by a downlooking observer, see Eq. (2). In this equation, we use geometrical distance s (essentially altitude z) as integration variable. Because pressure is closely related to altitude, Schwarzschild’s equation can be easily reformulated in terms of pressure and weighting functions redefined accordingly.
In the context of inverse problems and temperature sounding (e.g. Craig & Brown 1986; Hanel et al. 2003), the Schwarzschild Eq. (2) is regarded as a Fredholm integral equation where the weighting function is termed the kernel of the integral equation and the unknown B(ν,T(z)) is called the source term. Actually the unknown is the temperature profile, but Planck’s function establishes a one-to-one correspondence between B and T, i.e., T = B-1. In the case of microwave atmospheric sounding, temperature and Planck radiation are identical except for a constant, according to the Rayleigh-Jeans approximation. The properties of the kernel or its corresponding matrix representation (e.g., condition number or distribution of singular values) are crucial for an assessment of the inversion. Recently, Lee et al. (2012) have discussed a closely related quantity – the contribution function (the product of the weighting function and the Planck function, i.e., the integrand of the Schwarzschild equation) to “assess the vertical sensitivity of the emission spectrum to temperatures and molecular composition”.
As mentioned above, weighting functions are a key quantity of temperature sounding. For Earth temperature retrievals, an implicit assumption is that the amount of CO2 (for thermal infrared sounding) or O2 (for microwave sounding) is well known and independent of altitude. Clearly, the first assumption is not justified for exoplanets, whereas it is reasonable to assume a constant concentration over a wide altitude range for these long-lived species. Nevertheless, the one-to-one wavenumber (or wavelength) to altitude (or pressure) mapping as demonstrated by the weighting functions (see Figs. 3–5) will also be valid for exoplanets (for a discussion of Mars and Venus weighting functions see also Goody & Yung 1989; Hanel et al. 2003; Houghton et al. 1984). Radiation in the band center of the CO2 band (or near the line center of a microwave O2 transition, assuming O2 is present in the exoplanet atmosphere) reveals information from upper atmospheric layers, and radiation in the band wings of CO2 (or line wings of O2) reveals information from the lower atmosphere. However, the precise altitude or pressure corresponding to a given wavenumber/wavelength will certainly change; with increasing CO2 concentration, the altitude of a weighting function maximum corresponding to a given wavenumber/wavelength is shifted upwards. Note that this wavenumber-altitude mapping is valid over the troposphere and stratosphere; i.e., it is not destroyed by the temperature inversion. The one-to-one mapping of altitudes to wavenumbers/wavelengths apparent in both CO2 bands is the key to estimating atmospheric temperatures by relaxation methods, as developed by, e.g., Chahine (1968).
In the optically thick region around the 6.3 μm water band band (and in the far-infrared region), the main radiation source lies in the F- and G-star planet’s mid troposphere, whereas for the K- and M-star planets lacking temperature inversion, the main origin of radiation is shifted upwards, see Fig. 4. Likewise, in the regions of strong absorption due to CO2 or O3, the origin of radiation is shifted upwards as far as to the mid stratosphere, cf. Fig. 5. The altitudes of the weighting function maxima in the region of the 9.6 μm O3 band appear to be quite erratic at first glance; however, the position of the maxima alternates between mid stratosphere and bottom of atmosphere. Except for the F-star planet there is only a local maximum in the mid stratosphere, and the maximum lies at the bottom of the atmosphere, see middle panel of Fig. 5.
3.2. Thermal emission spectra – overview
Figure 6 illustrates the planetary spectra of planets around different host stars, calculated at a spectral resolution R ≡ λ/δλ = 3000. In the nearly transparent atmospheric window regions around 10 μm, the M-star planet shows the highest emission flux, while the F star case shows the lowest. This is consistent with the Planck radiation of a blackbody emitting at the surface temperature of these planets, assuming that the main contribution to the spectral flux comes from the surface or from atmospheric layers very close to it (but the radiance intensity is lower than the maximum atmospheric temperature, see Fig. 7). On the other hand, in regions of strong absorption, e.g. around the CO2 band at 15 μm, radiation originates mainly in the upper atmosphere (cf. Figs. 3 to 5), and the highest emission values are found for the F-star planet having the hottest stratosphere. In the case of the F-star planet, with higher stratospheric temperatures than the surface temperature, the spectral flux can exceed the Planck surface radiation. The atmospheric window between 800 and 1250 cm-1 (8 − 12 μm) gives a good estimate of the planetary surface temperature in all treated cases.
 |
Fig. 6 Thermal emission spectra for cloud-free planets around four different types of host stars. The main molecular bands are labeled. |
The shape and depth of the main molecular bands change in the spectra of the Earth-like planets around different host star types. A more detailed representation is shown next for the main molecular bands found within the thermal infrared region (CO2, N2O, H2O, CH4, and O3).
 |
Fig. 7 Spectral flux for all four different planetary cases. The black curves show blackbody emission at the corresponding surface temperature of the planet. |
3.3. Carbon dioxide
CO2 is uniformly mixed throughout the atmospheres of all the stellar type planets studied in this paper. In the context of exoplanet habitability studies, CO2 is especially important as a greenhouse gas. In the thermal infrared the dominant absorption features are due to the two fundamental bands around 4.3 and 15 μm (2200 − 2400 cm-1 and 550 − 750 cm-1, respectively). In the near infrared there are two weaker group of bands at 2.0 and 2.7 μm (cf., e.g. Goody & Yung 1989).
The band system around 4.3 μm with the ν3 fundamental, overlapping with the neighboring N2O band at 4.5 μm band, can be distinguished in all four different planetary cases. In the F-star planet, the shape of the CO2 band changes greatly compared to the rest of the planetary cases (Fig. 8a).
It is very convenient for analyzing the spectrum in brightness temperature thanks to the relevant information that it provides about the planetary atmospheres. Figure 8b is the brightness temperature counterpart of Fig. 8a. The emission at the wings of the band is produced at regions of the troposphere. On the left and right edges of the band (4.0 and 4.6 μm), the atmosphere is nearly transparent, and consequently, the spectra corresponds to the blackbody emission from the surface. In the two cases where there is a significant temperature inversion (G- and F-star planets), the tropopause is distinguishable in the brightness temperature spectra around 4.2 μm, since this one also shows the point of inflection. According to Fig. 4 the maxima at 4.2 μm are located at about 10 km for all planets. The other two cases do not present a temperature inversion at the tropopause, the temperature continues dropping along the stratosphere, and the minimum equivalent brightness temperature at 4.2 μm is not present. At the center of the 4.3 μm band, the absorption is strong (see Fig. 2) and the lower atmospheric layers are not visible. The emission at the central region (from 4.2 μm to 4.4 μm) shows a temperature range that covers the whole stratosphere. At the band center (around 4.3 μm), the brightness temperature values are found at altitudes in the upper stratosphere: see also the weighting function plots Figs. 3 to 5. This is the reason for the shape of the F-star planet spectra at 4.3 μm. This planet is the only one that presents temperatures in the upper stratosphere that are higher than the surface. Accordingly, the 4.3 μm CO2 band is present as an absorption band in all planetary cases except in the F-star planet, where it is present as an emission band.
The second dominant feature of the infrared spectrum is the ν2 fundamental absorption band at 15 μm. A similar effect to what is observed in the shape of the 4.3 μm band in the different planets is also observed in this band (Fig. 9a). Similar features, notably significantly different emission in the band center, were also shown by Segura et al. (2003, Fig. 9b) for F2V-, G2V-, and K2V-star planets, albeit at much lower resolution. In Fig. 9b, the emission at the band wings originates in the troposphere. The temperature inversion at the tropopause is also visible in the F-star planet. However, this feature is less prominent in the case of the G-star planet. The 15 μm CO2 band is wider than the 4.3 μm band (in wavelengths), but the optical depths are more than one order of magnitude smaller over the whole band except at the central peak at 15 μm. Accordingly, a larger portion of the atmosphere is seen from the top originating in the lower stratospheric regions, cf. Fig. 3. The indication of a stratosphere warmer than the surface can be seen again at the center peak of the band in the F star case. Since the stratospheric temperatures in the atmospheres of the planets around the K and M stars decrease with altitude, an inversion of the center peak appears, in contrast to the F and G star case where the stratospheric temperatures increase with altitude.
 |
Fig. 8 The atmospheric emission spectrum showing the carbon dioxide band at 4.3 μm (2500 − 2174 cm-1) is represented in spectral flux a) and in brightness temperature b) for all four planetary cases. The nitrous oxide band at 4.5 μm is also visible. |
3.4. Nitrous oxide
Owing to negligible abiotic sources N2O is considered to be an ideal biomarker molecule. Similar to CO2 and CH4, it is uniformly mixed in the troposphere (albeit with lower concentrations), and concentrations decrease by several orders of magnitude in the stratosphere. The strongest bands are the three fundamentals ν1 at 7.8 μm ≡ 1285 cm-1, ν2 at 17 μm ≈ 589 cm-1, and ν3 at 4.5 μm ≈ 2224 cm-1, cf. Goody & Yung (1989). The 4.5 μm band is affected by the CO2 band centered at 4.3 μm; nevertheless, part of the band is still visible.
At the right wing of the 4.5 μm band, the molecule absorbs up to altitudes found within the mid-troposphere (see Fig. 8). At the band center, the N2O absorption optical depth decreases considerably, the atmosphere becomes optically thin, and again one sees absorption arising from the low troposphere. According to Figs. 3 and 4„ radiation in this spectral region originates mainly in the upper troposphere/lower stratosphere, so (low level) clouds (or a significantly different water distribution) should not significantly influence the N2O spectral signature.
 |
Fig. 9 The atmospheric emission spectrum in the region of the carbon dioxide band at 15 μm (770−555 cm-1). |
 |
Fig. 10 Atmospheric emission spectra of the F star planet. a) The effect of ignoring N2O or CO2 in the radiative transfer simulation; b) the effect of ignoring H2O, N2O, or CH4 in the methane dyad region. |
The N2O molecule’s absorption features at 7.8 μm overlap with the CH4 band, cf. Fig. 2. Moreover, the N2O absorption at 17 μm is blocked by the presence of CO2. In contrast to the other molecules discussed here, the choice of the suitable spectral region for analysis of N2O appears to be controversial. Des Marais et al. (2002) have considered the 7.8 μm region and have found a detectable absorption band for enhanced N2O concentrations, whereas they have classified the ν2 band at 17 μm as unlikely to be useful. Likewise, at reduced resolution N2O can only be detected in the 7.8 μm region according to Kaltenegger et al. (2007). On the other hand, Tinetti et al. (2006) have stated that this band is hard to detect. Rauer et al. (2011) can identify the 3.8 and 4.5 μm bands in emission spectra of M dwarf planets. Grenfell et al. (2011) find clearly enhanced N2O features at 3.8 μm and 7.8 μm in the “Canfield ocean” scenario of the Proterozoic Earth atmosphere. Nevertheless, despite the interference with CO2, the 4.5 μm region appears to be the most promising because of the clearly distinguishable shape (compare Fig. 10a).
3.5. Water vapor
Besides carbon dioxide water is the most important greenhouse gas of Earth’s atmospheres, and is one of the fundamental building blocks of life as we know it. H2O has high concentrations in the low troposphere that rapidly decrease with altitude.
H2O shows significant absorption throughout the entire infrared spectral region, cf. Fig. 2b. The main features of H2O in the thermal range appear from 5 to 8 μm (1250−2000 cm-1, vibrational bands) and the rotational spectrum above 15 μm (ν < 666 cm-1). In addition to the absorption by numerous individual lines, the molecule is also associated to a smoothly varying continuum absorption (e.g. Clough et al. 1989).
 |
Fig. 11 Water vapor band at 6.3 μm (2222 − 1176 cm-1). |
The H2O strong absorption band at 6.3 μm is distinguishable in all four different stellar cases (Fig. 11a). This band presents a similar shape in all planets. Since H2O is mostly located in the troposphere and since the evolution of the temperature profiles from the surface up to the tropopause is similar for all planets (continuously decreasing), the shape of the spectra modulated by the H2O absorption is also similar. Only the absolute value is slightly different, mimicking the tropospheric temperatures of the planets. Accordingly, the M-star planet shows the highest brightness temperature and the F-star planet the lowest at this spectral region (Fig. 11b). A similar effect can be observed as well in the H2O rotational spectrum (Fig. 12).
 |
Fig. 12 Atmospheric emission spectrum in the water vapor rotational band 15 μm (666−333 cm-1): a) flux and b) brightness temperature. |
At the wings of the 6.3 μm band, the molecule absorbs energy in the low troposphere and continues absorbing till its upper levels (Fig. 3). The molecular absorption by H2O is weaker at the very center of the band, and in this region radiation arising again from lower levels in the troposphere, with higher temperatures, can be observed (note the dip around 1600 cm-1 in Fig. 4).
3.6. Methane
Methane is one of the uniformly mixed gases in terrestrial planets’ tropospheres, since concentrations decrease significantly in the stratosphere. Methane is important for planetary atmospheres both as a greenhouse gas and as a potential biomarker, although abiotic sources can be significant, too.
The CH4 spectrum is characterized by a series of so-called polyads, and in the infrared the dyad or ν4 band system produces strong absorption at 7.7 μm (1200−1400 cm-1, overlapped by weaker H2O and N2O bands, see also Fig. 2). The molecule also produces a narrower band (the pentad) at 3.3 μm, but this has a strong interference with water.
Analogous to the H2O bands previously analyzed, the 7.7 μm band spectral shape is similar for all four planets, since the absorption mostly comes from the troposphere. The F-star planet shows the lowest values in both flux and brightness-temperature spectra. Only at the main CH4 absorption peak does the optical depth increase significantly and the troposphere becomes opaque. Consequently, the radiation arises from the lower stratosphere (Fig. 13 and see also Fig. 5). The spikes in Fig. 4 around 1300 cm-1 indicating maximum contribution from altitudes at about 15 km are due to CH4, i.e., they do not show up in a methane-free atmosphere, Fig. 5c.
 |
Fig. 13 The methane vibrational band at 7.7 μm (1333 − 1282 cm-1). |
3.7. Ozone
Ozone (along with oxygen O2) is regarded as an important biomarker because no important abiotic sources of free oxygen are known (Segura et al. 2007) for Earth-like atmospheres. The O3 molecule is present in higher concentrations along the stratosphere, having relatively small abundances in the troposphere.
The O3 features at 9.6 μm also dominate the planetary spectra along with the H2O and CO2 features in the range covered in this paper. This band overlaps with the CO2 hot band at 9.5 μm, but since this last one is very weak, it does not affect much the O3 band, cf. Fig. 2.
At the center of the strong lines, in the left and right branches of the 9.6 μm band, the O3 molecule absorbs strongly in the mid-stratosphere of the planets. In the F-star planet, the band changes notably in depth compared to the rest (Fig. 14 and see also Figs. 3–5), which can also been seen (at much lower resolution) in Fig. 9a of Segura et al. (2003). It would seem as if the molecule is almost absent in the planet, but this again occurs due to the temperature inversion found in the upper atmosphere. The O3 band in this planet indicates a mid-stratosphere warmer than the rest of the planetary cases, which has comparable temperatures to those of its low troposphere.
Since the O3 optical depth is very small at the central region, around 9.6 μm, the atmosphere becomes transparent and the outgoing flux arises from levels close to the surface. These levels are at a higher temperature than the mid-stratosphere of the planet, where the molecule is emitting strongly (emission seen at the band wings). The difference in temperature to the mid-stratosphere and the small optical depth of O3 at 9.6 μm determines the peak shape at the center of the band.
The false interpretation of the absence of O3 owing to a temperature inversion in the atmosphere of the planet can be prevented by studying the CO2 bands at 4.3 and 15 μm. As shown in Figs. 8 and 9, the CO2 bands clearly give information about the behavior of the atmospheric temperatures up to the upper stratosphere. Moreover, they can be used to infer the existence of the temperature inversion also found in the mid-stratosphere, where O3 is absorbing strongly.
Ozone also shows some weaker absorption bands at 4.7 and 14 μm (cf. Fig. 2). The first one overlaps with H2O vibrational bands, and the second with the CO2 band at 15 μm, which prevents the O3 signature from being seen at 4.7 and 14 μm due to its weak intensity.
 |
Fig. 14 Atmospheric emission spectra for all planetary cases showing the ozone band at 9.6 μm (1087 − 1000 cm-1). |
4. Clear sky spectra at different resolutions
It is necessary to analyze the spectra at different resolutions, in order to study how the information given by the spectral signatures is affected. For this, spectral resolutions R ≡ λ/δλ of 10, 100, and 30 000 are compared to the 3000 case, which was used to analyze the planetary spectra in the previous section. An ideal instrument is assumed, excluding any noise-related considerations.
 |
Fig. 15 Spectra of Earth-like planets at different resolutions. Note the emission features that are present in the F star planet and absent in all other cases. |
Figure 15 illustrates the spectra at different resolutions for all planets with the spectrum at the highest resolution (30 000) in the background. All the main bands are clearly visible at a resolution of 100. At a resolution of 10, the 7.7 μm CH4 band is not separable from the interfering water vapor absorption. Actually, the contribution of H2O to the band absorption is greater than the one of CH4. However, the presence of CH4 can still be established by studying the differences between the center and the neighboring bins (see Fig. 16) with and without the CH4 molecule, respectively. Notice that the following results are only shown for the F-star planet, since it has the smallest optical depth compared to the rest of planetary cases (see Fig. 2). Difficulties arise when trying to establish that these flux differences are due to the presence of CH4 and not due to H2O. However, the impact of water vapor and methane on the spectrum is different. In case of a dry-air atmosphere, the left-side bin is strongly affected, even more than the central bin. The difference in the central to the left-side bin flux without H2O is less than with H2O. In the case of CH4 the contrary is true, since the left-side bin is not affected by CH4 absorption. This extra information can be used to assess the presence of CH4, even if this molecule is not the main absorber at 7.7 μm at resolution ten.
 |
Fig. 16 Spectra at different resolutions showing the methane band at 7.7 μm (1538 − 1111 cm-1) for a cloud-free atmosphere. Blue and green indicate spectra at resolution R = 10 modeled without methane and water, respectively. |
The 4.5 μm N2O band cannot be separated from the 4.3 μm CO2 band at a spectral resolution of ten. The same study carried out for the CH4 band can also be done to determine the presence of N2O by comparing the central and the neighboring bins. In Fig. 17a, the differences between the central and the side bins with and without N2O, are greater than for the bins with and without CO2. It happens that the average spectrum at resolution ten with and without CO2 in the central and the left bins have the same value. As one can see in Fig. 17b, the emission and absorption CO2 contributions cancel out in the first two bins. Fortunately, there is a weak CO2 band around 4.8 μm that results in the differences at the right side bin. Consequently, the presence of N2O has a distinguishably different effect than CO2 on this part of the spectrum, and its contribution can be seen.
The rest of the main molecular bands can be resolved at a spectral resolution of ten.
 |
Fig. 17 Nitrous oxide band at 4.5 μm (2860−1920 cm-1) for a cloud-free atmosphere. Blue and green indicate low resolution spectra modeled without nitrous oxide and carbon dioxide, respectively. |
5. Summary
Spectra and weighting functions of Earth-like planets around F, G, K, and M host stars have been simulated using a high-resolution, line-by-line radiative transfer code to investigate how the host star may affect the spectral bands of the various molecules present in the planets’ atmosphere. Because understanding radiation sources and sinks is crucial for any interpretation of the spectra of cloud-covered planets and for successful retrievals, we also gave a more detailed explanation of the physics of radiation processes. In this regard, weighting functions – a key concept for temperature sounding of planetary atmospheres – have helped in identifying the sources of the radiation that reaches the top of the atmosphere. Moreover, they have indicated the changes taking place in the atmospheric structure that are in the spectrum, underlining their usefulness for interpreting the observed spectra.
The atmospheric window between 8 − 12 μm gives the best estimation of the surface temperature in the different planetary cases. The CO2 bands at 4.3 μm and 15 μm show up as emission bands in the F-star planet due to the temperature inversion and because it has higher temperatures in the stratosphere than at the surface. For the planets around other types of stars, these CO2 bands are absorption bands. Assuming that the atmosphere contains CO2, the shape of these bands thus provides essential information about the upper stratospheric temperatures of the planet. In particular, for all planet types the brightness temperatures observed in the band center correspond to the upper stratospheric temperatures, in accordance with the weighting functions. Results show that the 9.6 μm O3 band for the F-star planet presents a much smaller depth than the rest, which could lead to misinterpreting the amount of O3 found in the planets’ atmosphere. However, this is because the temperatures at the O3 layer are similar to the surface temperature. Since the CO2 bands contain information from a larger part of the atmosphere, the misinterpretation of the O3 band due to the temperature inversion can be prevented by analyzing both bands. A combined analysis of several bands is also important for methane and nitrous oxide: the CH4 amount could be established from the 7.7 μm band and its neighbor regions by also determining the amount of H2O. The same is valid for N2O at 4.5 μm considering the effect of CO2 from the neighboring 4.3 μm bands. The rest of the main molecular bands could be distinguished at the lower spectral resolutions of 10 and 100.
As already indicated in the introduction, this paper had a twofold purpose. The first was to investigate the thermal radiation of cloud-free Earth-like exoplanets orbiting F, G, K, or M stars in order to facilitate the interpretation of future observations with respect to identifying biosignatures, thus continuing and complementing the discussions of several previous studies. In particular we tried to locate the sources of radiation, because biosignatures originating in upper atmospheric layers are less likely to be influenced by clouds. This study also constitutes an important preparatory step in our investigations of the infrared spectra of clouded Earth-like exoplanets. A detailed exposition of our radiative transfer modeling studies, including a description of our lbl multiple scattering approach, is the subject of the follow-up Paper (II).
Online material
Appendix A: Supplementary material
 |
Fig. A.1 Weighting functions for the G and K star planets. |
Acknowledgments
Financial support by the Helmholtz Research Alliance – Planetary Evolution and Life and within the ESA–ESTEC study ESAS-Light (Contract No. AO/1-5433/07/NL/HE) is greatly appreciated. Furthermore, we would like to thank Pascal Hedelt for helpful discussions and a critical reading of the manuscript.
References
- Chahine, M. 1968, J. Opt. Soc. Am., 58, 1634 [NASA ADS] [CrossRef] [Google Scholar]
- Clough, S., Kneizys, F., & Davies, R. 1989, Atmos. Res., 23, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I., & Brown, J. 1986, Inverse Problems in Astronomy (Bristol: A. Hilger) [Google Scholar]
- Des Marais, D. J., Harwit, M. O., Jucks, K. W., et al. 2002, Astrobiology, 2, 153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goody, R., & Yung, Y. 1989, Atmospheric Radiation – Theoretical Basis, 2nd edn. (Oxford University Press) [Google Scholar]
- Grenfell, J. L., Stracke, B., von Paris, P., et al. 2007, Planet. Space Sci., 55, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Grenfell, J., Gebauer, S., von Paris, P., et al. 2011, Icarus, 211, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Hanel, R., Conrath, B., Jennigs, D., & Samuelson, R. 2003, Exploration of the Solar System by Infrared Remote Sensing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Hedelt, P., Alonso, R., Brown, T., et al. 2011, A&A, 533, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houghton, J., Taylor, F., & Rodgers, C. 1984, Remote Sounding of Atmospheres (Cambridge University Press) [Google Scholar]
- Kaltenegger, L., Traub, W. A., & Jucks, K. W. 2007, ApJ, 658, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzmann, D., Patzer, A., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitzmann, D., Patzer, A., von Paris, P., Godolt, M., & Rauer, H. 2011, A&A, 531, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J.-M., Fletcher, L. N., & Irwin, P. G. J. 2012, MNRAS, 420, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Manabe, S., & Wetherald, R. T. 1967, J. Atmos. Sci., 24, 241 [Google Scholar]
- Melsheimer, C., Verdes, C., Bühler, S., et al. 2005, Radio Sci., 40, RS1007 [Google Scholar]
- Mlawer, E., Taubman, S., Brown, P., Iacono, M., & Clough, S. 1997, J. Geophys. Res., 102, 16663 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Gebauer, S., v.Paris, P., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spectrosc. Radiat. Transfer, 110, 533 [Google Scholar]
- Schindler, T. L., & Kasting, J. F. 2000, Icarus, 145, 262 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Schreier, F. 2011, J. Quant. Spectrosc. Radiat. Transfer, 112, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Schreier, F., & Schimpf, B. 2001, in IRS 2000: Current Problems in Atmospheric Radiation, eds. W. Smith, & Y. Timofeyev (A. Deepak Publishing), 381 [Google Scholar]
- Segura, A., Krelove, K., Kasting, J., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Segura, A., Meadows, V., Kasting, J., Crisp, D., & Cohen, M. 2007, A&A, 472, 665 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Selsis, F., Despois, D., & Parisot, J.-P. 2002, A&A, 388, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinetti, G., Meadows, V. S., Crisp, D., et al. 2006, Astrobiology, 6, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Toon, O. B., McKay, C. P., Ackerman, T. P., & Santhanam, K. 1989, J. Geophys. Res., 94, 16287 [NASA ADS] [CrossRef] [Google Scholar]
- Vasquez, M., Gottwald, M., Gimeno García, S., et al. 2012, Adv. Space Res., DOI: 10.1017/S1743921311020205, in press [Google Scholar]
- von Clarmann, T., Höpfner, M., Funke, B., et al. 2002, J. Quant. Spectrosc. Radiat. Transfer, 78, 381 [Google Scholar]
- von Paris, P., Cabrera, J., Godolt, M., et al. 2011, A&A, 534, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunkowski, W., Trautmann, T., & Bott, A. 2007, Radiation in the Atmosphere – A Course in Theoretical Meteorology (Cambridge University Press) [Google Scholar]
All Tables
Characteristic parameters of the exoplanets and their atmospheres, surfaces, and host stars.
All Figures
 |
Fig. 1 Pressure-temperature profiles of planets orbiting F, G, K, and M stars for clear sky conditions (see Kitzmann et al. 2010, for more details). The markers shown for the G star profile indicate the 58 pressure levels. |
| In the text | |
 |
Fig. 2 Total transmission for a vertical path through the atmosphere of all planet types (top panel). Transmission due to water vapor (middle panel) and the other absorbers (lower panel) for an Earth atmosphere. Wavelengths are indicated at the top of the figure. |
| In the text | |
 |
Fig. 3 Weighting functions for the F and M star planets. Note the different color bars. Weighting functions for the G and K star planets can be found in the appendix, Fig. A.1. |
| In the text | |
 |
Fig. 4 Location of maxima of the weighting functions for the F, G, K, and M star planets. |
| In the text | |
 |
Fig. 5 Weighting functions for the F, G, K, and M star planets for selected wavenumbers in the regions of the CO2 (15 μm region left, 4.3 μm region right), O3, and CH4 bands. |
| In the text | |
 |
Fig. 6 Thermal emission spectra for cloud-free planets around four different types of host stars. The main molecular bands are labeled. |
| In the text | |
 |
Fig. 7 Spectral flux for all four different planetary cases. The black curves show blackbody emission at the corresponding surface temperature of the planet. |
| In the text | |
 |
Fig. 8 The atmospheric emission spectrum showing the carbon dioxide band at 4.3 μm (2500 − 2174 cm-1) is represented in spectral flux a) and in brightness temperature b) for all four planetary cases. The nitrous oxide band at 4.5 μm is also visible. |
| In the text | |
 |
Fig. 9 The atmospheric emission spectrum in the region of the carbon dioxide band at 15 μm (770−555 cm-1). |
| In the text | |
 |
Fig. 10 Atmospheric emission spectra of the F star planet. a) The effect of ignoring N2O or CO2 in the radiative transfer simulation; b) the effect of ignoring H2O, N2O, or CH4 in the methane dyad region. |
| In the text | |
 |
Fig. 11 Water vapor band at 6.3 μm (2222 − 1176 cm-1). |
| In the text | |
 |
Fig. 12 Atmospheric emission spectrum in the water vapor rotational band 15 μm (666−333 cm-1): a) flux and b) brightness temperature. |
| In the text | |
 |
Fig. 13 The methane vibrational band at 7.7 μm (1333 − 1282 cm-1). |
| In the text | |
 |
Fig. 14 Atmospheric emission spectra for all planetary cases showing the ozone band at 9.6 μm (1087 − 1000 cm-1). |
| In the text | |
 |
Fig. 15 Spectra of Earth-like planets at different resolutions. Note the emission features that are present in the F star planet and absent in all other cases. |
| In the text | |
 |
Fig. 16 Spectra at different resolutions showing the methane band at 7.7 μm (1538 − 1111 cm-1) for a cloud-free atmosphere. Blue and green indicate spectra at resolution R = 10 modeled without methane and water, respectively. |
| In the text | |
 |
Fig. 17 Nitrous oxide band at 4.5 μm (2860−1920 cm-1) for a cloud-free atmosphere. Blue and green indicate low resolution spectra modeled without nitrous oxide and carbon dioxide, respectively. |
| In the text | |
 |
Fig. A.1 Weighting functions for the G and K star planets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


