| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 5 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220386 | |
| Published online | 14 November 2012 | |
Research Note
Recommendations for Monte Carlo nucleosynthesis sampling
1 Departament de Física i Enginyeria Nuclear, EUETIB, Universitat Politècnica de Catalunya, c/ Comte d’Urgell 187, 08036 Barcelona, Spain
e-mail: richard.longland@upc.edu
2 Institut d’Estudis Espacials de Catalunya (IEEC), Ed. Nexus-201, C/ Gran Capità 2-4, 08034 Barcelona, Spain
Received: 14 September 2012
Accepted: 16 October 2012
Context. Recent reaction rate evaluations include reaction rate uncertainties that have been determined in a statistically meaningful manner. Furthermore, reaction rate probability density distributions have been determined and published in the form of lognormal parameters with the specific goal of pursuing Monte Carlo nucleosynthesis studies.
Aims. A variety of methods is available for randomly sampling over reaction rate probability densities. The aim of this work is to investigate these methods and determine the most accurate method for estimating elemental abundance uncertainties.
Methods. Experimental Monte Carlo reaction rates are first computed for the 22Ne + α, 20Ne(p, γ)21Na, 25Mg(p, γ)26Al, and 18F(p, α)15O reactions, which are used to calculate reference nucleosynthesis yields for 16 nuclei affected by nucleosynthesis in massive stars and classical novae. Five different methods of randomly sampling over these reaction rate probability distributions are then developed, tested, and compared with the reference nucleosynthesis yields.
Results. Given that the reaction rate probability density distributions can be described accurately with a lognormal distribution, Monte Carlo nucleosynthesis variations arising from the parametrised estimates for the reaction rate variations agree remarkably well with those obtained from the true rate samples. Most significantly, the most simple parametrisation agrees within just a few percent, meaning that Monte Carlo nucleosynthesis studies can be performed reliably using lognormal parametrisations of reaction rate probability density functions.
Key words: methods: numerical / nuclear reactions, nucleosynthesis, abundances
© ESO, 2012
1. Introduction
With the growing availability of high power computers, our ability to explore the effects of nuclear physics uncertainties on nucleosynthesis has reached new levels. With post-processing calculations, for example, thousands of computations can be performed in relatively little time, thus opening new avenues for exploration. Furthermore, better treatment of reaction rate uncertainty propagation has recently lead to the publication of rates that include statistically meaningful uncertainties (Iliadis et al. 2010a,b,c; Longland et al. 2010) and include lognormal representations of the rate probability density functions1. Given that information, methods should be developed to utilise those reaction rate uncertainties and investigate their effect on nucleosynthesis.
Monte Carlo methods are one option for investigating the effects of reaction rate uncertainties on nucleosynthesis yields. These methods can either be used to investigate the effects of a single reaction, a small group of reactions, or they can be used to investigate the overall effect of all reaction rates in complex environments involving a great number of competing reactions. The general strategy in the latter case is to (i) compute a sample rate for every uncertain reaction simultaneously; (ii) compute nucleosynthesis yields using these samples in a post-processing model; and (iii) repeat many times. Correlations between abundances and reaction rates can be found in a post-analysis procedure to identify reaction rates of interest. These methods have be used previously in a number of studies (e.g., Hix et al. 2003; Parikh et al. 2008; Roberts 2006). In each of those studies, temperature independent enhancement factors were applied to the rates of all nuclear processes to investigate their effect on nucleosynthesis in novae and X-ray bursts. The enhancement factors were sampled from lognormal distributions that were chosen to represent the estimated uncertainty of the reaction rates at temperatures most important in these environments. In some studies, these estimations were arrived at by considering very general characteristics of the reaction rates such as whether they are derived purely from theoretical predictions or were measured with radioactive beams (e.g., Hix et al. 2003). Until now, however, these methods have not considered the rate uncertainties for each reaction separately.
The method of varying reaction rates by a constant factor assumes that the true, unknown, reaction rate differs from the recommended rate by that factor over all temperatures. Equivalently, this method makes the assumption that rate uncertainties are temperature-independent. However, in reality, the uncertainties of individual reaction rates are, indeed, often temperature dependent if they are based on experimental constraints, usually with larger uncertainties associated with the rate at lower temperatures. This can clearly be seen in the uncertainty bands presented by Iliadis et al. (2010b). Furthermore, by considering the way that reaction rates are computed, it is clear that the temperature dependence of a sample reaction rate should not necessarily follow the same temperature dependence as the recommended rate. For example, the rate could be higher than the recommended rate at some temperatures, while being lower at others. How important is this effect? The et al. (2000) discussed the “race against time” effect that different temperature dependencies for the 22Ne + α reaction rates might have on the s-process in massive stars. Presumably, the complex interaction and competition of reaction rates in a dynamically changing environment means that simple enhancement of reaction rates does not fully explore the nucleosynthesis variations arising from reaction rate uncertainties. More advanced methods should, therefore, be investigated to fully account for this effect in nucleosynthesis uncertainty studies. The rate probability density distributions published in Iliadis et al. (2010c) make this investigation possible, while eliminating the need for simplifying estimations of rate uncertainties based on general reaction properties.
The obvious choice for correctly performing Monte Carlo nucleosynthesis studies is to directly use Monte Carlo reaction rate samples obtained separately from the RatesMC code (Longland et al. 2010). In this case, individual samples of the nuclear physics input are used, thus accounting for all possible behaviour of the reaction rates. However, this requires a considerable amount of effort using tools that most computational astrophysicists do not have access to. The purpose of this research note, therefore, is to investigate different rate sampling schemes in comparison to the ideal case discussed above, and present the best practice with which to utilise the reaction rate uncertainties that are published in Iliadis et al. (2010c). In Sect. 2, a number of possible sampling schemes are discussed. Those schemes are tested with an example set of reaction rates (Sect. 3) and discussed in Sect. 4. Conclusions are given in Sect. 5.
2. Reaction rate sampling methods
The reactions evaluated by Iliadis et al. (2010c) involved target nuclei with masses in the A = 14−40 range, whose cross sections are usually dominated by resonant capture. For reactions that involve a large number of resonances, it is clear that a great number of possibilities exist for how a sample reaction rate could vary with respect to its recommended value. In light of this, the most consistent way to sample the reaction rates is to sample the nuclear physics input separately for each nucleosynthesis calculation. Since most computational investigations do not have access to the data necessary to perform this kind of sampling, this method is viewed as the ideal, yet unrealistically complicated standard. For the purpose of this study, the RatesMC code used by Longland et al. (2010) is used to compute this ideal case for comparison alongside the estimations considered in this work. Throughout the following discussion, rate variations obtained from samples of the nuclear physics uncertainties are referred to as the “optimum” rate samples.
In order to construct rate variation schemes, we must first evaluate the expected behaviour of the reaction rates as a function of temperature. A reaction rate per particle pair is computed by  (1)where μ is the reduced mass of the reacting particles, μ = M0M1/(M0 + M1); Mi denotes the masses of the particles; k is the Boltzmann constant; E is the centre-of-mass energy of the reacting particles; and σ(E) is the reaction cross section at energy, E. This cross section frequently consists of a collection of resonances, so the reaction rate varies according to resonance properties, such as resonance strength or energy. The convolution of these resonance cross sections with the Boltzmann distribution in Eq. (1) will always result in a smoothly varying reaction rate with temperature.
(1)where μ is the reduced mass of the reacting particles, μ = M0M1/(M0 + M1); Mi denotes the masses of the particles; k is the Boltzmann constant; E is the centre-of-mass energy of the reacting particles; and σ(E) is the reaction cross section at energy, E. This cross section frequently consists of a collection of resonances, so the reaction rate varies according to resonance properties, such as resonance strength or energy. The convolution of these resonance cross sections with the Boltzmann distribution in Eq. (1) will always result in a smoothly varying reaction rate with temperature.
To construct a rate variation scheme, first consider the available information from Iliadis et al. (2010c); information that is also included directly in the starlib library (see, for example, Iliadis et al. 2011). The tabulated rates include two parameters, μ and σ, to describe the rate probability density distribution at each temperature (see Longland et al. 2010): 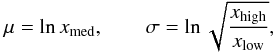 (2)where xmed, xhigh, and xlow are the recommended (median), high, and low reaction rates, respectively. The variables μ and σ here refer to the lognormal shape parameters, and are not to be confused with the more commonly used Gaussian mean and standard deviation. A reaction rate sample, x(T), at a specific temperature, T, can be represented by
(2)where xmed, xhigh, and xlow are the recommended (median), high, and low reaction rates, respectively. The variables μ and σ here refer to the lognormal shape parameters, and are not to be confused with the more commonly used Gaussian mean and standard deviation. A reaction rate sample, x(T), at a specific temperature, T, can be represented by 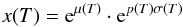 (3)where p(T) is a random variable that is normally distributed (i.e., distributed according to a Gaussian distribution with an expectation value of 0 and standard deviation of 1). The second component of Eq. (3) is dubbed as the “uncertainty factor”, and is a temperature dependent quantity. Given this information, the challenge becomes one of choosing values for p(T), recalling that these values must vary smoothly with temperature, and must be distributed normally to enforce the lognormality of reaction rate probability densities.
(3)where p(T) is a random variable that is normally distributed (i.e., distributed according to a Gaussian distribution with an expectation value of 0 and standard deviation of 1). The second component of Eq. (3) is dubbed as the “uncertainty factor”, and is a temperature dependent quantity. Given this information, the challenge becomes one of choosing values for p(T), recalling that these values must vary smoothly with temperature, and must be distributed normally to enforce the lognormality of reaction rate probability densities.
The simplest parametrisation for p(T) is determined by assuming that it is independent of temperature, i.e., p(T) = a where a is sampled from a normal distribution. This is dubbed the “flat” parametrisation in the following discussion, although it is important to emphasise that for this parametrisation, the uncertainty factor in Eq. (3) is still temperature dependent, and given by ea σ(T). This was not the case in the Monte Carlo variations of previous studies (e.g., Parikh et al. 2008). Those studies applied an uncertainty factor to the rate regardless of the uncertainty temperature dependence. Their method is equivalent to using a constant value, f, for the uncertainty factor. In this case, Eq. (3) would become x(T) = f eμ(T). As mentioned before, this is not representative of the rate uncertainty at all temperatures for experimentally constrained reaction rates. It is, however, a good approximation for reaction rates derived purely from theory.
Consider, now, the case in which the reaction rate uncertainty can be characterised in two regions. A single rate sample could, for example, be high with respect to the recommended rate at lower temperatures, while being low at higher temperatures. This situation can be reproduced by parameterising p(T) in Eq. (3) with a hyperbolic tangent function. To further generalise this parametrisation, an offset parameter can be utilised: ![\begin{equation} p(T) = \frac{1}{\sqrt{2}} \left(o + a \tanh \left[ \frac{2.94}{S}\log_{10}(T_{\rm c}/T)\right]\right), \label{eq:tanh} \end{equation}](/articles/aa/full_html/2012/12/aa20386-12/aa20386-12-eq25.png) (4)where the sampled variables a, o, S, and Tc are shown in the inset of Fig. 1 and are defined as the maximum deviation, offset, spread parameter, and cross-over temperature, respectively. The spread parameter is defined as the logarithm of the temperature range needed for p to vary from p = o + 0.9a to p = o − 0.9a. In this parametrisation scheme, a and o must be sampled from normal probability density distributions, while S and Tc can take on a range of values sampled from flat probability density functions. Here, the ranges are chosen to be 0.1 < S < 1 GK and 10-2 < Tc < 10 GK. This parametrisation is referred to as the “full” parametrisation hereafter. An example of applying this parametrisation to the 22Ne(α, n)25Mg reaction rate is shown in Fig. 1, where a = −1.5, o = −0.6, Tc = 0.1 GK, and S = 0.4 GK.
(4)where the sampled variables a, o, S, and Tc are shown in the inset of Fig. 1 and are defined as the maximum deviation, offset, spread parameter, and cross-over temperature, respectively. The spread parameter is defined as the logarithm of the temperature range needed for p to vary from p = o + 0.9a to p = o − 0.9a. In this parametrisation scheme, a and o must be sampled from normal probability density distributions, while S and Tc can take on a range of values sampled from flat probability density functions. Here, the ranges are chosen to be 0.1 < S < 1 GK and 10-2 < Tc < 10 GK. This parametrisation is referred to as the “full” parametrisation hereafter. An example of applying this parametrisation to the 22Ne(α, n)25Mg reaction rate is shown in Fig. 1, where a = −1.5, o = −0.6, Tc = 0.1 GK, and S = 0.4 GK.
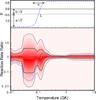 |
Fig. 1 (Colour online) Example of a single rate sample of the 22Ne(α, γ)26Mg reaction using the parametrised rate factor variations. Plotted in the lower panel is the reaction rate ratio (i.e., compared to the recommended rate). Therefore, the line at unity represents the recommended rate, while a point at 10 means that the rate is 10 times that of the recommended rate. The red density distribution represents the coverage probability of the reaction rate, with thick and thin black lines denoting the 68% and 95% uncertainties, respectively. The dashed blue line represents a single sample of the reaction rate obtained when using Eq. (3) with p(T) determined from the parametrisation in Eq. (4) and shown in the top panel. |
To further investigate the hyperbolic tangent parametrisation of the reaction rate samples, two more cases are considered. In the first case (the “no offset” case), the offset parameter is constrained to zero. This requires removing the 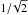 factor in Eq. (4) to ensure normality of the distribution. The parameter space for the reaction rate will be constrained for this case, in particular, the possibility that the rate has a systematic shift at all temperatures will not be accounted for. The nucleosynthesis yield uncertainties determined from this method are therefore expected to be reduced using this parametrisation. For the second case (called “fixed S and Tc”), the parameters, S and Tc are fixed at values of S = 0.2 and Tc = 0.2 GK. These values are chosen to maximise the reaction rate shape variations around 0.2 GK. This final case should help answer the question of whether the temperature dependence of the 22Ne + α reactions has a large effect on s-process yields as predicted by The et al. (2000).
factor in Eq. (4) to ensure normality of the distribution. The parameter space for the reaction rate will be constrained for this case, in particular, the possibility that the rate has a systematic shift at all temperatures will not be accounted for. The nucleosynthesis yield uncertainties determined from this method are therefore expected to be reduced using this parametrisation. For the second case (called “fixed S and Tc”), the parameters, S and Tc are fixed at values of S = 0.2 and Tc = 0.2 GK. These values are chosen to maximise the reaction rate shape variations around 0.2 GK. This final case should help answer the question of whether the temperature dependence of the 22Ne + α reactions has a large effect on s-process yields as predicted by The et al. (2000).
Finally, although we have argued that p(T) must vary smoothly with temperature, it can be illustrative to investigate the effect on nucleosynthesis when this constraint is relaxed. On a grid of temperatures, therefore, p(T) is sampled independently so that the resulting rate can fluctuate randomly from one temperature to the next. These sample rates are obtained once per Monte Carlo nucleosynthesis computation. This will be referred to as the “random” case. Another technique is to sample all reaction rates at every evaluation step within the nucleosynthesis code. In this case, the rate will change rapidly around the recommended rate over small temperature ranges, thus yielding unrealistically small nucleosynthesis uncertainties. This latter case is not investigated here.
3. Test cases
The effects of the 5 rate parametrisation schemes, in addition to the optimum rate samples calculated directly from the nuclear physics input, are investigated with respect to a test suite of reactions and scenarios. To achieve this, post-processing calculations are used to calculate Monte Carlo nucleosynthesis yields with some representative profiles and networks. To obtain a good representation of the uncertainties, 3000 Monte Carlo samples are used for each method, which are found to reproduce abundances to within 3% and uncertainties to within about 10% between runs.
The first of the test cases are the 22Ne + α reactions (i.e., 22Ne(α, γ)26Mg and 22Ne(α, n)25Mg), which are important for s-process neutron production in massive stars and asymptotic giant branch stars. For an overview of the reactions and their nuclear physics uncertainties, the reader is referred to, for example, Jaeger et al. (2001); Koehler (2002); Longland et al. (2012). A temperature-density profile corresponding to core helium burning in a 25 M⊙ massive star is used to study nucleosynthesis for these reactions, and has been discussed elsewhere by The et al. (2000) and Iliadis (2007). While helium burning occurs throughout the profile, the 22Ne + α reactions are only active towards the end when temperature and density become high enough. A nucleosynthesis network containing 583 nuclei is used, which contains nuclei around the nuclear valley of stability from A = 1 to A = 100. This network is sufficient to study the weak component of the s-process. To characterise the nucleosynthesis yield uncertainties, final abundances of 4 nuclei are considered: 26Mg, 65Cu, 70Zn, and 87Rb. These are chosen to represent nuclei that are affected by the 22Ne + α reactions.
The other three reactions considered here are important in nova nucleosynthesis. We consider a single zone temperature-density profile from the hottest hydrogen-burning zone that corresponds to a 1.25 M⊙ ONe white dwarf accreting material at a rate of 2 × 10-10 M⊙ y-1. This model is similar to the “P1” model considered by Iliadis et al. (2002) with initial abundances equal to those presented in their Table 2. A nucleosynthesis network containing 146 nuclei from A = 1 to A = 50, and linked by 1283 nuclear processes is used to integrate the system’s evolution during a single nova outburst. Two species of 26Al are used to represent the abundances of 26Al in its ground state, 26Alg, and its isomeric state, 26Alm. It was shown previously by Iliadis et al. (2002) that some important reactions for this model are 18F(p, α)15O, 20Ne(p, γ)21Na, and 25Mg(p, γ)26Al. The first of these has large uncertainties arising from ambiguities in the nuclear physics data (see, for example Beer et al. 2011), and strongly affects the final yields of oxygen and fluorine isotopes. The second reaction considered is important because at the start of the nova explosion, 20Ne comprises 25% of the material’s initial abundance. The reaction proceeds relatively slowly, thus it strongly affects abundances throughout the neon-silicon region. The final reaction considered is important because it directly affects the abundances of magnesium and 26Alg. These are important species in nova nucleosynthesis because they can be measured precisely in pre-solar grains. The uncertainties for these reactions are adopted from Iliadis et al. (2010a).
4. Results and discussion
To illustrate the final distribution of abundances that arise from the Monte Carlo nucleosynthesis calculations, the final abundances for 26Mg obtained from the optimum rate samples, the full and flat parametrisation schemes, and random sample methods are plotted using cumulative frequency plots in Fig. 2. A number of features are immediately obvious. First, the median abundances (i.e., the point at which the cumulative distribution crosses the 50% point) agree within statistical fluctuation for all methods, as is expected. This is because, provided proper sampling has been carried out, the median abundances will correspond to the median rate regardless of the parametrisation used. Secondly, the random parametrisation produces a significantly wider distribution than the results from optimum rate samples. The unphysical, rapidly changing reaction rates possible when using this method could be responsible for this, thus producing hard-to-predict nucleosynthesis results. Indeed, we find that for other reactions such as 18F(p, α)15O, the opposite effect occurs, i.e., the uncertainties resulting from this method are smaller than those obtained from optimum rate samples. We conclude, therefore, that this random sampling of rates is not only unphysical, but also unreliable for calculating accurate nucleosynthesis yield uncertainties. Thirdly, full parametrisation of the reaction rate samples using the hyperbolic tangent function in Eq. (4) agrees remarkably well with the results from using the optimum rate samples, albeit with slightly underestimated uncertainties.
 |
Fig. 2 (Colour online) Final 26Mg abundance cumulative density plots the three methods: (i) input of reaction rate samples obtained directly from RatesMC (“Optimum Samples”); (ii) full parametrisation of p from Eq. (4) (“Full”); (iii) randomly sampled reaction rates at each temperature (“Random”); and (iv) a constant value for p as a fucntion of temperature (“Flat”). |
Perhaps even more remarkable from Fig. 2 is that the uncertainties derived by using flat distributions for p(T) also agree excellently with the uncertainties derived from using optimum rate samples, and are barely distinguishable from the full parametrisation method. This finding is further enforced in Fig. 3, where the uncertainty ranges obtained for key isotopes arising from varying the four reactions described in Sect. 3 are displayed as uncertainty ratios. To obtain these ratios, uncertainties are first determined from the 16th and 84th percentiles of their respective cumulative distributions, and thus represent 1σ nucleosynthesis yield uncertainties. These ranges are then normalised to the median abundance obtained from the optimum reaction rate samples. Only the ratios for optimum samples, full parametrisation, random rate samples, and flat parametrisation are displayed. The “fixed S and Tc” and “no offset” cases are not displayed for reasons of clarity. For these two cases, the uncertainty ratios bands are only slightly smaller than those obtained from the full parametrisation for all cases considered here. This figure confirms our findings that the full and flat parametrisation schemes reproduce the uncertainties obtained from optimum rate samples. The determined uncertainties are all within a few percent of those obtained from optimum rate samples, and certainly differ by smaller amounts than the uncertainties, themselves. The random parametrisation scheme consistently performs poorly, although for some nuclei (i.e., those not directly connected to the reaction), the effect is diluted somewhat.
The only exception to these findings is the 18F(p, α)15O reaction, for which the yield uncertainties are too large by roughly a factor of two for 18O and 18F when utilising the parametrisation schemes. The random parametrisation scheme, contrary to the other reactions, yields smaller nucleosynthesis uncertainties in this case. The 18F(p, α)15O reaction presents a challenge because the current uncertainty in the rate is dominated by unknown factors in the interference effects between a number of resonances (Iliadis et al. 2010a). The reaction rate probability density distribution is, therefore, bi-modal in shape, and hence poorly represented by a lognormal distribution. This fact is reflected in the poor Anderson-Darling statistics at most relevant temperatures for this reaction. The Anderson-Darling statistic represents a measure of how well the true reaction rate distribution is reproduced by the lognormal approximation, and is discussed in detail in Longland et al. (2010). In this case, therefore, the σ parameter describing the rate uncertainty is a bad approximation, so using it to compute reaction rate uncertainties is expected to fail in reproducing the optimum sample uncertainties. However, for this case, the poor lognormal shape of the reaction rate distribution already prompts further experimental investigation. With the addition of new, more precise nuclear data, the rate will begin to approach a lognormal distribution more closely, and hence the parametrised Monte Carlo approach for this reaction will perform better.
Finally, the smallest abundance uncertainties for all nuclei considered come from using the fixed value for S and Tc parametrisation. This arises from the values adopted for the fixed parameters, which were chosen to maximise the reaction rate shape effect discussed before. Although the shape of the rates will be changing as a function of temperature, the magnitude of the rates will, on average, be closer to the recommended rate around T = 0.2 GK. We can conclude from this that, at least for the present cases, the shape of the reaction rate has little effect on nucleosynthesis yields.
 |
Fig. 3 (Colour online) The yield uncertainties computed from 3 of the parametrisation schemes investigated here compared to the individually sampled reaction rates. The final abundances for four nuclei are considered for each reaction under investigation here. Each group of vertical bars for each nucleus represents, from left to right, the abundances calculated using: (i) the “optimum” reaction rate samples; (ii) the full parametrisation; (iii) the unphysical, random, case; and (iv) constant values of p(T) = a. |
5. Conclusions
Reaction rates provided by the recent reaction rate evaluation of Iliadis et al. (2010c) included temperature dependent lognormal parameters that were found to accurately reflect the reaction rate probability densities. However, to date, no investigation has been presented that determines the most effective way to use these parameters. Past research (The et al. 2000) showed that nucleosynthesis yields can be influenced not only by reaction rate magnitudes, but also by their temperature dependence. An investigation into how best to randomly sample the reaction rates provided by Iliadis et al. (2010c) is therefore performed here. The investigation was undertaken for a range of reactions occurring in core helium burning in massive stars (22Ne + α) and in novae (20Ne(p, γ)21Na, 25Mg(p, γ)26Al, and 18F(p, α)15O).
By applying a temperature-dependent rate multiplication factor, ep(T)σ(T), to the reaction rates, the isotopic yields following post-processing of massive star helium burning and nova explosion models were investigated for a range of p(T) parametrisation schemes. These choices were compared with the yield uncertainties obtained when reaction rate samples are obtained directly from the nuclear physics input and calculated using the RatesMC reaction rate code from Longland et al. (2010).
The most significant finding was that not only can the optimum reaction rate sample uncertainties be reproduced well by using a hyperbolic tangent function for p(T), but they are approximated remarkably well by a flat function: p(T) = a. The temperature dependence of the reaction rates investigated were, therefore, found to be relatively unimportant to nucleosynthesis yields. This finding is particularly significant because it means that when performing nucleosynthesis sensitivity studies, all reaction rates can be sampled simultaneously. The sensitivity of nucleosynthesis yields to particular reactions can be characterised by plotting abundance yields against p (in a similar fashion to Fig. 8 in Parikh et al. 2008) and computing measures of correlation such as the Pearson or Spearman correlation coefficients.
For investigating the effect of single reaction rate uncertainties, or small groups of reactions where correlation coefficients are not needed, adopting either the full, or flat parametrisation schemes is recommended. Using the full parametrisation scheme is useful for investigating the effect that temperature dependence of a reaction rate has on nucleosynthesis. For rates with large uncertainties, such as those involving unstable target nuclei, this could still have an effect, and should always be considered when evaluating reaction rate uncertainties.
Note that there is no restriction that the rates obtained in Iliadis et al. (2010c) must be within the published 1σ “high” and “low” rates but rather follow a continuous probability density distribution.
Acknowledgments
This work has been partially supported by the Spanish grants AYA2010-15685 and by the ESF EUROCORES Program EuroGENESIS through the MICINN grant EUI2009-04167. I would like to thank Anuj Parikh and Jordi José for their help and recommendations for the manuscript. I would also like to thank Christian Iliadis for many informative and enlightening discussions about reaction rate uncertainties.
References
- Beer, C. E., Laird, A. M., Murphy, A. S. J., et al. 2011, Phys. Rev. C, 83, 042801 [Google Scholar]
- Hix, W., Smith, M., Starrfield, S., Mezzacappa, A., & Smith, D. 2003, Nucl. Phys. A, 718, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C. 2007, Nuclear physics of stars (Wiley-VCH) [Google Scholar]
- Iliadis, C., Champagne, A., José, J., Starrfield, S., & Tupper, P. 2002, ApJS, 142, 105 [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A. E., & Coc, A. 2010a, Nucl. Phys. A, 841, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A. E., & Coc, A. 2010b, Nucl. Phys. A, 841, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010c, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Champagne, A., Chieffi, A., & Limongi, M. 2011, ApJS, 193, 16 [Google Scholar]
- Jaeger, M., Kunz, R., Mayer, A., et al. 2001, Phys. Rev. Lett., 87, 202501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Koehler, P. E. 2002, Phys. Rev. C, 66, 055805 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Longland, R., Iliadis, C., Champagne, A. E., et al. 2010, Nucl. Phys. A, 841, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Longland, R., Iliadis, C., & Karakas, A. I. 2012, Phys. Rev. C, 85, 065809 [NASA ADS] [CrossRef] [Google Scholar]
- Parikh, A., José, J., Moreno, F., & Iliadis, C. 2008, ApJS, 178, 110 [Google Scholar]
- Roberts, L. F. 2006, in International Symposium on Nuclear Astrophysics, Nuclei in the Cosmos [Google Scholar]
- The, L., El Eid, M. F., & Meyer, B. S. 2000, ApJ, 533, 998 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 (Colour online) Example of a single rate sample of the 22Ne(α, γ)26Mg reaction using the parametrised rate factor variations. Plotted in the lower panel is the reaction rate ratio (i.e., compared to the recommended rate). Therefore, the line at unity represents the recommended rate, while a point at 10 means that the rate is 10 times that of the recommended rate. The red density distribution represents the coverage probability of the reaction rate, with thick and thin black lines denoting the 68% and 95% uncertainties, respectively. The dashed blue line represents a single sample of the reaction rate obtained when using Eq. (3) with p(T) determined from the parametrisation in Eq. (4) and shown in the top panel. |
| In the text | |
 |
Fig. 2 (Colour online) Final 26Mg abundance cumulative density plots the three methods: (i) input of reaction rate samples obtained directly from RatesMC (“Optimum Samples”); (ii) full parametrisation of p from Eq. (4) (“Full”); (iii) randomly sampled reaction rates at each temperature (“Random”); and (iv) a constant value for p as a fucntion of temperature (“Flat”). |
| In the text | |
 |
Fig. 3 (Colour online) The yield uncertainties computed from 3 of the parametrisation schemes investigated here compared to the individually sampled reaction rates. The final abundances for four nuclei are considered for each reaction under investigation here. Each group of vertical bars for each nucleus represents, from left to right, the abundances calculated using: (i) the “optimum” reaction rate samples; (ii) the full parametrisation; (iii) the unphysical, random, case; and (iv) constant values of p(T) = a. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


