| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219910 | |
| Published online | 21 November 2012 | |
A planetary system with gas giants and super-Earths around the nearby M dwarf GJ 676A
Optimizing data analysis techniques for the detection of multi-planetary systems⋆
1
Universität Göttingen, Institut für Astrophysik,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail: guillem.anglada@gmail.com
2
University of Hertfordshire, Centre for Astrophysics Research,
Science and Technology Research Institute, College Lane, AL10 9AB, Hatfield, UK
e-mail: m.tuomi@herts.ac.uk
3
University of Turku, Tuorla Observatory, Department of Physics and
Astronomy, Väisäläntie
20, 21500
Piikkiö,
Finland
e-mail: miptuom@utu.fi
Received:
28
June
2012
Accepted:
5
October
2012
Context. Several M dwarfs are targets of systematical monitoring in searches for Doppler signals caused by low-mass exoplanet companions. As a result, an emerging population of high-multiplicity planetary systems around low-mass stars are being detected as well.
Aims. We optimize classic data analysis methods and develop new ones to enhance the sensitivity towards lower amplitude planets in high-multiplicity systems. We apply these methods to the public HARPS observations of GJ 676A, a nearby and relatively quiet M dwarf with one reported gas giant companion.
Methods. We rederived Doppler measurements from public HARPS spectra using the recently developed template matching method (HARPS-TERRA software). We used refined versions of periodograms to assess the presence of additional low-mass companions. We also analysed the same dataset with Bayesian statistics tools and compared the performance of both approaches.
Results. We confirm the already reported massive gas giant candidate and a long period trend in the Doppler measurements. In addition to that, we find very secure evidence in favour of two new candidates in close-in orbits and masses in the super-Earth mass regime. Also, the increased time-span of the observations allows the detection of curvature in the long-period trend. suggesting the presence of a massive outer companion whose nature is still unclear.
Conclusions. Despite the increased sensitivity of our new periodogram tools, we find that Bayesian methods are significantly more sensitive and reliable in the early detection of candidate signals, but more work is needed to quantify their robustness against false positives. While hardware development is important in increasing the Doppler precision, development of data analysis techniques can help to reveal new results from existing data sets with significantly fewer resources. This new system holds the record of minimum-mass range (from Msini ~ 4.5 M ⊕ to 5 Mjup) and period range (from P ~ 3.6 days to more than 10 years). Although all planet candidates are substantially more massive, it is the first exoplanetary system with a general architecture similar to our solar system. GJ 676A can be happily added to the family of high-multiplicity planetary systems around M dwarfs.
Key words: techniques: radial velocities / methods: data analysis / planetary systems / stars: individual: GJ 676A
Table 6 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Doppler spectroscopy is currently the most effective method for detecting planet candidates orbiting nearby stars. The current precision enables the detection of planets of a few Earth masses in close-in orbits, especially around low-mass stars (e.g., Mayor et al. 2009). Two methods are currently used to obtain precision Doppler measurements in the visible part of the spectrum: the gas cell and the stabilized spectrograph approach. The gas cell method consists on inserting a cell containing iodine gas in the beam of the telescope which provides a very accurate method to solve for the wavelength solution, instrumental profile variability, and the Doppler changes in the stellar spectrum (Butler et al. 1996). The second approach is based on building a mechanically stable fiber-fed spectrograph calibrated with an emission lamp (Baranne et al. 1996). HARPS is the best example of a stabilized spectrograph in operation. It is installed at the 3.6 m Telescope in La Silla-ESO observatory/Chile (Pepe et al. 2003). The list of planets detected by HARPS is long and varied, as can be seen in the 35 papers of the series The HARPS search for southern extra-solar planets. Instead of citing all of them, we refer the interested reader to the latest HARPS results presented in Pepe et al. (2011), Mayor et al. (2011), and Bonfils et al. (2012). HARPS has demonstrated a radial velocity (RV) stability at the level of 1 m s-1 on time-scales of several years. Since January 2011, reduced data products derived from the HARPS data reduction software (DRS) are publicly available through a dedicated webpage in ESO1. All data used in this work have been obtained from there.
The increasing demand for higher Doppler precision has motivated a significant investment in hardware development, and a number of new stabilized spectrographs are currently under construction (e.g., Wilken et al. 2012). It is known, however, that the method employed by the HARPS-DRS to extract RV measurements (cross-correlation function) is suboptimal in exploiting the Doppler information in the stellar spectrum (Queloz 1995; Pepe et al. 2002), therefore developments in the data analysis techniques are also required to reach photon noise limited precision. We have recently developed a least-squares template matching method (HARPS-TERRA software, Anglada-Escudé & Butler 2012; Anglada-Escudé et al. 2012) that is able to derive precise RV measurements from HARPS spectra obtaining a substantial increment of precision on K and M dwarfs. In Anglada-Escudé & Butler (2012), 34 observations on the M0 dwarf GJ 676A were used to illustrate the improvement in precision of the HARPS-TERRA measurements compared to those used in the discovery paper of the massive planet candidate GJ 676Ab (Forveille et al. 2011). Additional observations on this star have recently been released through the ESO archive, and we applied HARPS-TERRA to extract new RV measurements of the full set. In a preliminary analysis using classic periodogram methods, we found tentative evidence for additional planets in the system. However, these preliminary detections did not provide convincing results. Recent developments in the Bayesian analysis methods of Doppler data (e.g., Tuomi 2012) indicate that correlation between parameters seriously affect the sensitivity of periodogram-based methods in detecting additional low-amplitude signals. Moreover, careful Bayesian analyses provide increased sensitivity to lower amplitude signals (Tuomi 2012) and seem to be less prone to false positives than methods based on sequential periodogram analyses of the residuals only (Tuomi 2011).
In this work, we develop and test data analysis methods for optimal detection of low-mass companions in multi-planetary systems and apply them to the HARPS-TERRA measurements of GJ 676A. In Sect. 2, we describe a new periodogram-based approach (recursive periodogram) and review the Bayesian analysis tools also developed to deal with multi-Keplerian fits. Section 3 reviews the stellar properties of GJ 676A, describes the observations, discusses periodicities detected in activity indices and describes the previously detected candidates (one massive gas giant and a long-period trend, Forveille et al. 2011). Section 4 analyses the RVs of GJ 676A using these tools. Both methods (recursive periodograms and Bayesian analyses) agree in the detection of two additional sub-Neptune/super-Earth mass candidates in close-in orbits. We also use the opportunity to test the sensitivity of both detection methods by applying them to a subset of observations (first 50 epochs). We find that, while the recursive periodogram approach is able to only spot one of the additional signals at low confidence, a Bayesian analysis can already recover the same candidates obtained from the full set of observations. In Sect. 5 we identify and discuss a few periodicities in some of the activity indices. Finally, in Sect. 6 we place the unique features of the planetary system around GJ 676A in the context of the currently known population of exoplanets and provide some concluding remarks.
2. Data analysis methods
2.1. Recursive periodograms
Classic least-squares periodograms and derived methods (Scargle 1982; Cumming 2004) consist of adjusting a sine-wave (equivalent to a circular orbit) to a list of test periods and plot these periods against some measure of merit. When k-periodic signals are detected in the data, the corresponding Keplerian model is subtracted from the data and a least-squares periodogram is typically applied to the residuals to assess if there is a k + 1th periodicity left. As noted by several authors (Anglada-Escudé et al. 2010; Lovis et al. 2011b; Tuomi 2012), non-trivial correlations between parameters are likely to decrease the significance of (yet undetected) low-amplitude signals. That is, as the number of the Keplerian signals in a model increase, the aliases of previously detected signals and other non-trivial correlations seriously affect the distribution of the residuals and, unless the new signal is very obvious, a periodogram of the residuals will not properly identify (even completely confuse) the next most likely periodicity left in the data.
To account for parameter correlation at the period search level, we developed a generalized version of the classic least-squares periodogram optimized for multiplanet detection that we call recursive periodogram. Instead of adjusting sine-waves to the residuals only, a recursive periodogram consists of adjusting all the parameters of the already detected signals together with the signal under investigation. Even in there are correlations, candidate periods will show prominently as long as the new solution provides a net improvement of the previous global solution. In our approach and by analogy to previous least-squares periodograms, a circular orbit (sinusoid) is always assumed for the proposed new periodicity. When no previous planets are detected, this is equivalent to the generalized least-squares periodogram discussed by Zechmeister et al. (2009), and is a natural generalization of the methods discussed by Cumming (2004) to multi-Keplerian solutions. The graphical representation of the periodogram is then obtained by plotting the obtained period for the new planet (X-axis) versus the F-ratio statistic obtained from the fit (Y-axis). The highest peak in this representation indicates, in a leasts-squares sense, the most likely periodic signal present in the data.
As with any other classic least-squares periodogram method, one has to assess if adding a
new signal is justified given the improvement of the fit. As proposed by Cumming (2004), we use the F-ratio
statistic to quantify the improvement of the fit of the new model
(k + 1 planets) compared to the null hypothesis
(k planets). The F-ratio as a function of the test
period is defined as 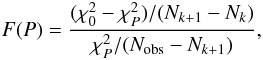 (1)where
(1)where
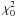 is the
chi-squared statistic for the model with k-planets (null hypothesis),
is the
chi-squared statistic for the model with k-planets (null hypothesis),
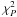 is the
chi-squared statistic at the test period P,
Nk is the number of free parameters in
the model with k-planets, and
Nk+1 is the number of free parameters in
the model including one more candidate in a circular orbit at period P.
For a circular orbit, the number of additional parameters
Nk+1 − Nk
is 2 (amplitude and phase of a sinusoid). Assuming large Nobs,
statistical independence of the observations, and Gaussian errors,
F(P) would follow a Fisher
F-distribution with
Nk+1 − Nk
and Nobs − Nk+1
degrees of freedom. The cumulative distribution (integral from 0 to the obtained
F-ratio) is then used as the confidence level c at
each P (also called single-frequency confidence level). Because the
period is a strongly nonlinear parameter, each peak in a periodogram must be treated as an
independent experiment (so-called independent frequencies). Given a dataset, the number of
independent frequencies M can be approximated
by PminΔT, where ΔT is the
time baseline of the observations and Pmin is the shortest
period (highest frequency) under consideration. Given M, the analytic
false alarm probability is finally derived as
FAP = 1 − cM.
is the
chi-squared statistic at the test period P,
Nk is the number of free parameters in
the model with k-planets, and
Nk+1 is the number of free parameters in
the model including one more candidate in a circular orbit at period P.
For a circular orbit, the number of additional parameters
Nk+1 − Nk
is 2 (amplitude and phase of a sinusoid). Assuming large Nobs,
statistical independence of the observations, and Gaussian errors,
F(P) would follow a Fisher
F-distribution with
Nk+1 − Nk
and Nobs − Nk+1
degrees of freedom. The cumulative distribution (integral from 0 to the obtained
F-ratio) is then used as the confidence level c at
each P (also called single-frequency confidence level). Because the
period is a strongly nonlinear parameter, each peak in a periodogram must be treated as an
independent experiment (so-called independent frequencies). Given a dataset, the number of
independent frequencies M can be approximated
by PminΔT, where ΔT is the
time baseline of the observations and Pmin is the shortest
period (highest frequency) under consideration. Given M, the analytic
false alarm probability is finally derived as
FAP = 1 − cM.
Since the fully Keplerian problem is very nonlinear, several iterations at each test period are necessary to ensure convergence of the solution. A typical recursive periodogram consists of testing several thousands of such solutions and, therefore, it is a time-consuming task. As a result, special care has to be taken in using a robust and numerically efficient model to predict the observables. We found that a slight modification of the parameterization given by Wright & Howard (2009) provided the best match to our needs. The only change we applied was using the initial mean anomaly M0 instead of the time of periastron T0 as a free parameter. These two quantities are related by 2πT0/P = −M0. From this expresion one can see that the replacement of T0 by M0 eliminates the non-linear coupling between T0 and P. Wright & Howard (2009) also provide the partial derivatives of the observables (radial velocity) in a numerically efficient representation. The partial derivative of the RV with respect to M0 (instead of T0) is trivially obtained as minus the partial derivative of the radial velocity with respect to the mean anomaly E (∂v/∂M0 = −∂v/∂E). Beyond this change, the adopted model is identical to the one given in Wright & Howard (2009) so, for the sake of brevity, we do not provide the full description here. To accelerate convergence at each test period, we first solve for linear parameters only. Next, we use the Levenberg-Marquardt (Levenberg 1944) method to smoothly approach the χ2 minimum and, finally, a few interations of a straight nonlinear least-squares solver (Press et al. 1992) are used to quickly converge to the final solution. Although fitting for k-planets at each test period would seem a very time-consuming effort, we are implicitly assuming that the solver is already close to the χ2 local minimum. Therefore, relatively few nonlinear iterations (between 20 and 50) are typically enough to reach the closest local minimum. Since all orbits are re-adjusted, and even though the method still suffers from some of the typical pitfalls of sequential Keplerian fitting (e.g., the solver can still become stuck on local minima), the solution at each test period always has a higher significance than a periodogram on the residuals, especially when parameters are correlated.
It is known that the assumptions required by the F-ratio tests might not be stricly satisfied by RV observations. Therefore, an empirical scheme is always desirable to better asses the FAP of a new detection. Since the recursive periodogram is a straight generalization of least-squares periodograms, we adopted the brute-force Monte Carlo method proposed by Cumming (2004) to obtain empirical estimates of the FAPs. That is, we computed recursive periodograms on synthetic datasets and counted how many times spurious peaks with higher power than the signal under investigation were obtained by an unfortunate arrangement of the noise. Each Monte Carlo trial consists of: 1) taking the residuals to the model with k-planets and randomly permutate them over the same observing epochs, 2) adding back the signal of the model with k-planets, 3) re-adjusting the solution with k-planets (new null hypothesis), 4) computing the recursive periodogram on this new synthetic dataset and, 5) recording the highest F-ratio in a file. The FAP will be the number of times we obtain an F-ratio higher than the original one divided by the number of trials.
A recursive periodogram can take a few tens of minutes depending on the number of
datapoints and number of planets in the model. While this is not a serious problem while
exploring one dataset, it becomes a problem when FAPs have to be empirically computed for
many thousands of Monte Carlo trials. As a general rule, we accept new candidates if they
show an empirical FAP lower than 1%. While this threshold is arbitrary, it guarantees that
even if some of the proposed candidates are false positives, we will not seriously
contaminate the current sample of ~700 RV detected exoplanets with spurious detections.
As a first saving measure and given that analytic FAPs are known to be over-optimistic, we
only compute empirical FAPs if the analytical FAP prediction is already lower than 1%. The
chance of obtaining a false alarm in a trial is a Poisson process and, therefore, the
uncertainty in the empirical FAP is ~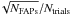 . Our aim is to
guarantee that the empirical FAP is <1% at a
4-σ level, so we designed the following strategy to minimize the the
number of Monte Carlo trials. That is, we first run 1000 trials. If no false-alarms are
detected, the candidate is accepted and the analytic FAP is used to provide an estimate of
the real one. If the number of trials generating false alarms is between 1 and 20
(estimated FAP ~ 0.1–3%), we extend the number of trials to 104. If the
updated FAP is lower than 0.5%, we stop the simulations and accept the candidate. If the
empirical FAP is still between 0.5 and 1.5%, 5 × 104 trials are obtained
and the derived FAP is used to decide if a candidate is accepted. While the computation
time for 1000 trials in a single processor is prohibitively high, the computation of many
recursive periodograms can be easily parallelized in modern multi-processor desktop
computers. For the GJ 676A dataset and a (3+1)-planet model, 103 trials would
take 2.3 days on one 2.0 GHz CPU. The same computation on 40 logical CPUs takes 1.4 h,
allowing one to obtain empirical FAP runs with 104–105 trials in
less than a week.
. Our aim is to
guarantee that the empirical FAP is <1% at a
4-σ level, so we designed the following strategy to minimize the the
number of Monte Carlo trials. That is, we first run 1000 trials. If no false-alarms are
detected, the candidate is accepted and the analytic FAP is used to provide an estimate of
the real one. If the number of trials generating false alarms is between 1 and 20
(estimated FAP ~ 0.1–3%), we extend the number of trials to 104. If the
updated FAP is lower than 0.5%, we stop the simulations and accept the candidate. If the
empirical FAP is still between 0.5 and 1.5%, 5 × 104 trials are obtained
and the derived FAP is used to decide if a candidate is accepted. While the computation
time for 1000 trials in a single processor is prohibitively high, the computation of many
recursive periodograms can be easily parallelized in modern multi-processor desktop
computers. For the GJ 676A dataset and a (3+1)-planet model, 103 trials would
take 2.3 days on one 2.0 GHz CPU. The same computation on 40 logical CPUs takes 1.4 h,
allowing one to obtain empirical FAP runs with 104–105 trials in
less than a week.
2.2. Bayesian analysis methods
As in e.g. Tuomi (2012), the Bayesian analyses of the RVs of GJ 676A were conducted using samplings of the posterior probability densities, estimation of Bayesian evidences, and the corresponding model probabilities based on these samples.
We sampled the posterior densities using the adaptive Metropolis algorithm (Haario et al. 2001), also described extensively in Tuomi (2011). Because it converges reliably and relatively rapidly to the posterior density in most situations, we performed several samplings of the parameter space of each model. Different samplings were started with different initial states to ensure that the global probability maximum of the parameter space was found for each model. If they all converged to the same solution, we could confidently conclude that the corresponding maximum was indeed the global one. This check was performed because it is possible that the Markov chains becomes stuck in a local maximum if it is sufficiently high and the initial state happens to be close to it. As a result, we could then reliably estimate the parameters using the maximum a posteriori (MAP) estimates and Bayesian credibility sets (BCSs) as uncertainty estimates (Tuomi & Kotiranta 2009).
The Bayesian evidence of each model was calculated using the one block Metropolis-Hastings (OBMH) estimate (Chib & Jeliazkov 2001). It requires a statistically representative sample from the posterior, available due to posterior samplings, and can be used to assess the evidence and the corresponding model probabilities with relatively little computational effort when determining the number of Keplerian signals in an RV data set favoured by the data (e.g. Tuomi 2011, 2012; Tuomi et al. 2011).
Using the OBMH estimates, we determined the probabilities of the models with differing numbers of Keplerian signals. However, we did not blindly choose the model with the greatest posterior probability and added it to the solution unless three detection criteria were also satisfied. We required that (1) the posterior probability of a model with k + 1 Keplerian signals was at least 150 times greater than that of a model with k signals (Kass & Raftery 1995; Tuomi 2011, 2012; Tuomi et al. 2011); (2) the RV amplitudes of every signal were significantly greater than zero (Tuomi 2012); (3) and that the periods of each signal were well-constrained from above and below because if this was not the case, we could not tell whether the corresponding signals were indeed of Keplerian nature and periodic ones. These detection criteria have been used in Tuomi (2012) and they appear to provide reliable results in terms of the most trustworthy number of signals in an RV data set. We claim a detection of a Keplerian signal in the data if the Markov chains of several samplings converge to a solution that satisfies the criteria 1−3 above.
The prior probability densities were chosen to have the same quantitative forms as in Tuomi (2012), in which e.g. the parameter space of the RV amplitude was limited to [0, 20] m s-1. However, because the RV data contain the obvious Keplerian signal of a massive candidate and a long-period trend reported by Forveille et al. (2011) with amplitudes clearly larger than 20 m s-1, the first two signals were allowed to explore a wider range of semi-major amplitudes, i.e., [0, 200] m s-1. Also, following (Tuomi 2012), we did not set the prior probabilities of different models equal but set them such that for models ℳk and ℳk+1, it holds that the prior probabilities satisfy P(ℳk) = 2P(ℳk+1) for all values of k.
Basic parameters of GJ 676A.
3. Stellar properties, observations and previous work
GJ 676 is a common proper-motion pair of M dwarfs. The primary (GJ 676A) has been classified as an M0V star (Koen et al. 2010). Using the empirical relations of Delfosse et al. (2000), the 2MASS JHK photometry (Skrutskie et al. 2006), and its trigonometric parallax (van Leeuwen 2007), we derive a mass of 0.71 M⊙ for GJ 676A. The star does not show strong evidence of activity or youth and, therefore, it is a good candidate for high-precision RV studies (Forveille et al. 2011). The basic parameters of GJ 676A are given in Table 1. The fainter member of the pair (GJ 676B) has been classified as an M3V and is currently separated 50″ from A. From its Hipparcos parallax, this corresponds to a minimum separation of 800 AU and an orbital period longer than 20 000 years. At this separation, the maximum acceleration of GJ 676A caused by GJ 676B on our line of sight is about 0.05 m s-1 yr-1.
New radial velocity measurements were obtained using the HARPS-TERRA software (Anglada-Escudé & Butler 2012) from HARPS spectra recently made public through the ESO archive. The spectra are provided extracted and wavelength calibrated by the HARPS-DRS. Each HARPS spectrum consists of 72 echelle appertures covering the visible spectrum between 3800 and 6800 Å. The average spectral resolution is λ/δλ = 110 000 and each echelle apperture consists of 4096 extracted elements (or pixels). The set of public 75 spectra have been obtained by several programmes over the years and typical exposure times vary between 300 to 900 s. The mean signal-to-noise ratio (S/N) at 6000 Å is 60 and, in a few cases, it can be as low as 22. Doppler measurements derived with HARPS-TERRA are differential against a very high S/N template spectrum generated by coadding all observations. The secular acceleration effect (Zechmeister et al. 2009) was subtracted from the RVs using the Hipparcos (van Leeuwen 2007) proper motion and parallax of the star.
One (probably two) sub-stellar companions were already reported for the system in Forveille et al. (2011). The most prominent one is a massive gas giant candidate with a period of ~1060 days and a semi-major amplitude of ~120 m s-1. Strong evidence for a second, very long period candidate was also proposed by Forveille et al. (2011) because of a strong trend detected in the residual to the one-planet fit. Forveille et al. (2011) already noted that the magnitude of this trend (~8 m s-1 yr-1) was too high to be explained by the gravitational pull of GJ 676B (max value of ~0.05 m s-1). Even after subtracting a model with one planet and a trend, Forveille et al. (2011) also noted that the rms of the residuals was significantly higher (~3.6 m s-1) than the reported uncertainties (1 to 1.5 m s-1), which was suggestive of potential additional candidates. A reanalysis of the 40 spectra available to Anglada-Escudé & Butler (2012) confirmed that, even with the increased precision derived using HARPS-TERRA (rms 3.2 m s-1), the star did show a significant excess of RV variability.
In a preliminary analysis of the new 75 HARPS-TERRA RVs, periodograms of the residuals to the two Keplerian solution (gas giant + trend) showed several tentative high peaks at 36, 59, and 3.6 days. While a solution including the 36 and 3.6-day signals provided a very extreme reduction of the rms (from 3.1 to 1.6 m s-1), the peaks in the periodograms of the residuals provided analytic FAP estimates too high to be acceptable (~5%). A preliminary Bayesian analysis of the same new RVs (methods described in Tuomi 2012), also indicated that additional candidates were strongly favoured by the data. As we will show in the analysis section, the RV measurements of GJ 676A are a textbook example where signal correlation prevents the detection of lower amplitude signals using periodogram methods based on the analysis of the residuals only.
 |
Fig. 1 Detection periodograms from most significant signal to less significant one (top to bottom). Black lines are least-squares periodograms computed on the residuals to the k-planet model. The red dots represent the refined orbital solution with k + 1-planets at each test period as obtained by the recursive periodogram. The resulting sampling of the red dots is not uniform in frequency because the tested k + 1 period is also allowed to adjust. |
4. Planetary system: new candidates
4.1. Recursive periodogram analysis
For the recursive periodogram analysis and FAP computations, a 1.0 m s-1 jitter was added in quadrature to the nominal uncertainty of each RV measurement. This value was chosen because, for any multi-planet solution we attempted, about ~1.0 m s-1 always had to be added in quadrature to match the nominal uncertainties to the rms of the residuals. As a double check of the robustness of the solution, we repeated the analysis assuming a jitter level of 0.5 m s-1, 1.5 m s-1, 2.0 m s-1 and 2.5 m s-1. The 0.5 m s-1 value is the minumum uncertainty that, according to Bonfils et al. (2012), has to be added to each measurement to acccount for the uncertainties in the wavelength solution and intra-night stability of HARPS, while 2.5 m s-1 would correspond to the random jitter on a moderately active M dwarf (e.g. GJ 433 and HIP 12961 announced in Delfosse et al. 2012; Forveille et al. 2011,respectively). The results obtained using different jitter assumptions were slightly different, but still produced the same four-planet solution. These alternative searches are briefly discussed at the end of the section.
 |
Fig. 2 Phase-folded radial velocity curves of the reported new planet candidates. Even though curvature is clearly detected (top right panel), the orbit of the of longer period companion is still poorly constrained. |
As seen in the top panel of Fig. 1, there is little doubt on the reality of the first previously reported candidate GJ676Ab (Forveille et al. 2011). As a second signal and instead of fitting a trend, we performed a recursive periodogram search for a second planet with periods between 1.1 and 50 000 days, obtaining a preferred solution of about 4000 days. As for GJ 676Ab, there is little doubt on the statistical significance of this signal/trend (analytic FAP threshold of 1% is around 15, while the signal has an F-ratio of several hundreds), and a peak at only twice the time baseline indicates the detection of significant curvature (see top-left panel in Fig. 2). As shown in the second panel of Fig. 1, the recursive periodogram (red dots) compared to the periodogram of the residuals (black line) is able to massively improve the significance of this second signal thanks to the simultaneous adjustment of the orbit of the first candidate. As discussed in the Bayesian analysis section, the period and parameters of this candidate are poorly constrained and only some nominal values are given for reference. For detection purposes only, we conservately assume that it can be adequately reproduced by a full Keplerian solution and added it to the model.
After the first two signals were included, the recursive periodogram search for a third companion revealed one additional periodicity at ~35.5 days (F-ratio ~ 17.5). The analytic FAP was 0.155%, which warranted the empirical FAP computation. In the first 1000 trials, five trials generated false alarms (FAP ~ 0.5%), meaning that more trials were necessary to securely asses if the FAP is <1%. An extended run with 104 trials produced an empirical FAP of ~0.44%, therefore the candidate was finally accepted. These candidate (GJ 676Ae) corresponded to a super-Earth/sub-Neptune mass candidate with Msini ~ 11 M ⊕ . Even though the preferred eccentricity was rather high (~0.6) quasi-circular orbits are still allowed by the data. This candidate would receive ~2.6 times more stellar radiation than the Earth receives form the Sun. According to Selsis et al. (2007), it means it would hardly be able to keep liquid water on its surface.
Again, this 35.5 day candidate was included in the models as a third full Keplerian signal and a recursive periodogram search was obtained to look for additional companions. A strong isolated peak (F-ratio 19.5, P = 3.6 days) was the next promising signal, showing an analytic FAP as low as 0.15%. Only one test over the first 1000 trials generated an spurious peak with higher power, indicating that the FAP is significantly lower than 1%, and the candidate was immediately accepted. The new candidate (GJ 676Ad) has a minimum mass of ~4.5 M ⊕ and it is certainly too close to the star to support liquid water on its surface.
The recursive periodogram search for a fifth signal showed that the next tentative periodicities have analytic FAP at the 10% or higher level, which did not satisfy our preliminary detection criteria and accordingly we stopped searching for additional candidates. Even though four planet signals might seem a lot given that only 75 RVs were used, the amplitudes of the close-in low mass companions are relatively high (2−3 m s-1, see Fig. 2) compared to the final rms of the solution (1.6 m s-1) and the nominal uncertainties.
As discussed at the begining of this section, we tested the robustness of the four-planet solution by applying the recursive periodogram approach assuming different levels of jitter. Table 2 lists the analytic FAP estimates obtained using different jitter levels. Table 2 shows that the analytic FAP for the fourth candidate becomes even lower when higher jitter levels are assumed. This is, the signals become more significant when the RV measurements are given more similar weight, which is equivalent to admitting that a significant contribution to the noise (stellar and/or instrumental) is not accounted for in the individual measurement uncertainties. In the next section, we show that once a converging solution is found, a fully Bayesian approach can consistently account for the unknown ammount of jitter and still identify the same four candidates as the most likely periodicities in the data.
Analytic false-alarm probability of planet candidates e and d as a function of assumed stellar jitter.
4.2. Bayesian analysis
As discussed, there no doubt that RV data of GJ 676A contain the signal of a massive planet (mp = 4.9 MJup) with an orbital period of roughly 1060 days (Forveille et al. 2011) and a long period trend. A model with a Keplerian signal and a linear trend was chosen as the starting point of the Bayesian analyses.
While spotting the signature of the massive planet in the RVs was trivial, we observed that instead of a linear trend, the samplings preferred a second Keplerian, indicating significant curvature. Therefore, the second model to be tested contains the trend modelled as a Keplerian. However, because the long-period signal could not be constrained, we fixed its eccentricity and period to their most probable values in the parameter space (for period, this space was the interval between 1 and 10 Tobs days, where Tobs is the baseline of the data) throughout the analyses. Because the orbit is only partially covered by the time-baseline of the observations, we could not constrain its other parameters much either, therefore only the MAP values for this candidate are given in Table 4 as a reference. Fixing period and eccentricity, however, allowed us to draw representative samples from the parameter space and to calculate reliable estimates for the Bayesian evidence of each model. The curvature in the long-period trend was so clearly present in the data that including curvature (through a fixed period-eccentricity Keplerian) increased the model probability by a factor of 1.8 × 1013 and decreased the rms of the residuals from 4.59 to 3.00 m s-1 (Table 3).
Relative posterior probabilities of models with k = 1,...,4 Keplerian signals (ℳk) with or withour a linear trend (LT), the Bayesian evidences P(d|ℳk), and rms values.
We continued by adding a third Keplerian signal to the statistical model and performed samplings of the corresponding parameter space. The Markov chains quickly converged to a solution that contained the same periodic signal at 35.4 days that was also spotted by the recursive periodograms. The model with k = 3 Keplerians was found to have a posterior probability 2.0 × 105 times that of a model with k = 2 Keplerians (Table 3). The signal at 35.4 days corresponds to a planet candidate with a minimum mass of 11.5 M ⊕ . When sampling the parameter space of a four-Keplerian model, we identified a fourth strong signal in the data with a period of 3.60 days. This was, again, the same fourth period spotted by the recursive periodogram. Our solution of the model with k = 4 further increased the model probability by a factor of 2.8 × 1011 compared to a model with k = 3, so we could conclude that this 3.60 day periodicity was also very confidently present in the data (Table 3).
 |
Fig. 3 Distributions estimating the posterior densities of orbital periods (Px), radial velocity amplitudes (Kx) and eccentricities (ex), and three constrained Keplerian signals. The solid curve is a Gaussian density with the same mean (μ) and variance (σ2) as the parameter distribution. Additional statistics, mode, skewness (μ3) and kurtosis (μ4) of the distributions are also shown. |
The search for additional periodic signals failed to identify significant periodicities so we conclude that the model probabilities imply the existence of four Keplerian signals: the massive companion GJ 676Ab at 1.8 AU; a trend with some curvature suggesting the presence of another massive giant planet in a long-period orbit; and two previously unknown planet candidates with orbital periods of 3.60 and 35.4 days and minimum masses of 4.4 and 11.5 M ⊕ (Table 4; Fig. 2). These signals satisfied all detection criteria. That is, the radial velocity amplitudes were strictly positive and their periods, apart from the long-period signal, were well-constrained and had narrow distributions in the parameter space. In addition to the MAP parameter estimates, standard errors, and 99% BCSs in Table 4, we show the distributions of the periods, RV amplitudes, and eccentricities in Fig. 3. These distributions show that – apart from the eccentricities of the two new low-mass companions, which peaked close to zero – all densities were close to Gaussian in shape.
Orbital solution of the three innermost companions of GJ 676A and the excess RV jitter.
4.3. Robustness of the Bayesian solution
To assess the reliability of our solution to the GJ 676A RVs, and indeed that of the Bayesian methods in general in assessing the existence of Keplerian signals in RV data, we performed a test analysis of the first 50 epochs only. The purpose of this test was to investigate whether we could spot the same signals, and receive the same solution from a smaller number of observations. The 50 first epochs have a baseline of approximately 1199 days (roughly two thirds of the full baseline of 1794 days), and because of their lower number, we expected them to constrain the model parameters less, i.e. yielding broader posterior densities, and that the model probabilities are less strongly in favour of – possibly even against – the existence of the two new planet candidates reported in this work.
Again, we started with a model containing a single Keplerian signal and a linear trend. These were easy to spot from the partial RV set and we could identify the same massive planet candidate and trend reported by Forveille et al. (2011, 69 CCF measurements were used in that work). However, when we sampled the parameter space of a two-Keplerian model, we rapidly discovered another Keplerian signal at a 35.5 day period. The corresponding two-Keplerian solution together with the linear trend increased the posterior probability of the model by a factor of 1.0 × 104, which clearly exceeded the detection threshold of 150. Furthermore, we also identified a third periodicity at 3.60 days when increasing the complexity of the statistical model by adding another Keplerian signal to it. This model was 5.0 × 105 times more probable than the model with k = 2, so we could conclude that three planet candidates and a linear trend were already strongly suggested by these initial 50 RVs. Moreover, the two new low-amplitude periodic signals satisfy our detection criteria by having amplitudes strictly above zero (2.27 [1.00, 3.41] m s-1 and 2.83 [1.48, 4.04] m s-1 for GJ 676A e and d, respectively) and well-constrained orbital periods (3.6000 [3.5963, 3.6027] days and 35.48 [35.16, 35.90] days, respectively). This solution is consistent with the one received for the full data set in Table 4, which implies that the two new planets could already have been detected in the HARPS RVs when the 50th spectrum was obtained back in October 2009, possibly even earlier.
We performed the recursive periodogram analysis of the same 50 epochs. Again, the massive GJ 676Ab and the trend were also trivially detected. Then we attempted a recursive periodogram search for a third Keplerian. This search spotted the 35.5 day signal as the next most likely periodicity, but provided an analytic FAP of 15%, which did not satisfy our preliminary detection criteria (analytic FAP < 1%). In order to check if the 3.6 days candidate could be inferred by periodogram methods, we added the 35.5 days signal to the model and performed a recursive periodogram search for a fourth candidate. Although a peak at 3.6 days was present, it was not, by far, the most significant periodicity suggested as the fourth signal.
This result implies that Bayesian methods are clearly more sensitive in detecting low-amplitude signals compared to classic periodogram approaches (even compared to our newly developed recursive periodogram method). Even if a reasearcher prefers to obtain frequentist confirmation (e.g., empirical FAP) of a signal before announcing it, early Bayesian detections can be used to optimize observational strategies and sample the periods of interest. We are conducting simulations with synthetic dataset to identify failure modes of the proposed Bayesian methods (e.g., identify situations that could generate false positives) and refine the detection criteria accordingly.
5. Analysis of three activity indices
In this section we analyse the variability of some representative activity indices and discuss their possible relation to Doppler signals. HARPS-TERRA obtains the CaII H+K activity index (S-index in the Mount Wilson system, Baliunas et al. 1995) and collects the measurements provided by the HARPS-DRS for two of the cross-correlation function (CCF) parameters that are also sensitive to stellar activity: bisector span (or BIS), full-width at half-maximum of the CCF (or FWHM).
 |
Fig. 4 Periodograms of the bisector span (top) and the full-width-at-half-maximum of the cross-correlation function (bottom). No periodic signals with analytic FAP smaller than 5% were detected in either index. |
The S-index is directly measured by HARPS-TERRA on the blaze-corrected spectra using the definitions given by Lovis et al. (2011a) and is an indirect measurement of the chromospheric emission. Because the strength of the magnetic field affects the efficiency of convection, some spurious RV signals could correlate with variability in the S-index (Lovis et al. 2011a). Magnetically active regions can also introduce periodicities in the S-index as the star rotates (e.g. Bonfils et al. 2007). The BIS is a measure of the asymmetry of the average spectral line and should correlate with the RV if the observed offsets are caused by spots or plages rotating with the star (Queloz et al. 2001). The FWHM is a measure of the width of the mean spectral line and its variability is usually associated with changes in the convective patterns on the stellar surface that might also induce spurious RV offsets. Since the connection between activity and RV jitter on M dwarfs is still only poorly understood (Lovis et al. 2011a), we restrict our analyses to evaluate if any of the indices has periodicities similar to the detected RV candidates.
As shown in Fig. 4 (upper panel), no strong periodicities were detected on the BIS. However, diagnostics based on the line symmetries have low discriminating power for M dwarfs. A comparison active star with a similar spectral type is AD Leo (GJ 388), which is a fast rotator (P ~ 2.2 days) and is magnetically active (Morin et al. 2008). On AD Leo, BIS has been found to strongly correlate with RVs (Bonfils et al. 2012). The amplitude of the variability of BIS was found to be 10 times smaller (~2 m s-1Reiners et al. 2012) compared to the corresponding Doppler counterpart (~30 m s-1). Following the same approximate rule, and given that the rms of BIS on GJ 676A is 4.7 m s-1, only spurious Doppler signals substantially stronger than K ~ 5 m s-1 are expected to produce any measureable effect on the BIS. The two newly proposed candidates have amplitudes smaller than 3 m s-1 and, therefore the absence of periodicities in BIS does not provide a good diagnostic to assess the reality of these signals.
 |
Fig. 5 Periodograms (left) and phase folded plots (right) of the signals detected in the S-index. The mean S-index value S0 = 1.40 has been subtracted from the phase folded plots for visualization purposes. The periods of the newly proposed planet candidate signals are marked as black vertical bars. Their 95% confidence level ranges are smaller than the width of the lines. |
On M dwarfs, FWHM has been shown to be more effective in identifying activity induced Doppler signals. For example, FWHM measurements on GJ 674 (Bonfils et al. 2007) revealed that the second signal detected in the RVs (~35 days) was probably related to the presence of a persistant dark spot. Similarly, the Hα index, the S-index, and additional photometric follow-up revealed the same periodicity (which is likely related to the rotation period of the star). Another example is the FWHM periodicity reported by Anglada-Escudé et al. (2012) and Delfosse et al. (2012) on the M dwarf GJ 667C. Again, the FWHM and the S-index both showed a signal with almost identical period, strongly suggesting that distortions of the mean spectral line were caused by a magnetic feature corrotating with the star. This argument was used to cast doubts on the reality of a candidate Doppler signal at ~91 days (GJ 667Cd?). Applying the recursive periodogram method to the FWHM measurements of GJ 676A, we do detect a strong isolated periodicity at 80.75 days with an analytic FAP of 0.043% that could be related to the stellar rotation. The search for a second signal does not reveal any peak above the 10% analytic FAP threshold. None of the Doppler signals appear to be remotely related to this 80.75 day period.
We also performed a recursive periodogram analysis of the S-index, expecting to detect some counterpart to the FWHM variability. Surprinsingly, the S-index does show a signal, but with a period of ~930 days (FAP ~ 0.01%). Although the signal has a similar period as the GJ 676Ab candidate, this coincidence was not mentioned in the discovery paper by Forveille et al. (2011). Even if the periods are similar, two arguments favour the Keplerian interpretation of the candidate as a planet. First, the signal in the S-index is not in phase (or anticorrelated) with the Doppler one. Second, Gomes da Silva et al. (2012) have shown that RV offsets correlated with the variability of the S-index (or similar spectroscopic indices) are at the level of a few m s-1 while GJ 676Ab’s RV semi-amplitude is about 120 m s-1. Therefore, apparently the similarity in the periods is purely coincidental. Evidence for an activity cycle of ~1000 days is also supported by the analysis of the Na I-index performed by Gomes da Silva et al. (2012) using a subset of these observations. A search for a second signal in the S-index revealed a second periodicity at 40.6 days (analytic FAP ~ 0.028%). The signal is well reproduced by a sinusoid and could be related to a magnetic feature co-rotating with the star (40.6 days is approximately one-half of 80.7 days). While we detect a Doppler signal at 35.4 ± 0.07 days, this period is statistically very distinct to 40.65 days. The recursive periodogram of the S-index in the central panel of Fig. 5 shows a weaker peak at 34.7 days that would not qualify as a detection (analytic FAP ~ 6%) even if it were the dominant signal in the time-series. Moreover, this signal completely disappears when searching for a third periodicity using the recursive periodogram scheme (bottom panel in Fig. 5). As a double check, we forced a sinusoids solution to this 34.7 days period and computed the recursive periodogram for a third signal. In this case, a peak with a FAP of ~5% and P = 40.6 days still remained, providing additional indication that 40.6 days is indeed preferred by the S-index data. As shown in the bottom panel of Fig. 5, and after adding the 40.6 day sinusoid, no signal could be identified in the sarch for a third signal in the S-index.
In summary to the discussion of the activity, we detected one signal in the FWHM and two periodicities in the S-index (see Table 5). Compared to other M-dwarfs that show indications of activity-induced periodicities (e.g., GJ 433, GJ 674, GJ 667C), the periods found in the FWHM and the S-index do not match, which complicates their physical interpretation. While the long-period signal in the S-index is likely to be caused by a sun-like activity cycle, it is less clear if one or the other signal is truly related to stellar rotation (both signals could match typical rotation periods measured for M dwarfs with ages of a few Gyr, Irwin et al. 2011). In the absence of further diagnostics and in addition to other caveats applicable to any Doppler candidate, we find no reason to doubt on the Keplerian nature of the newly reported Doppler signals.
Summary of signals in activity indices.
6. Conclusions
We re-derived high-precision radial velocities of the public HARPS observations of GJ 676A using our newly developed HARPS-TERRA software, obtaining a significant improvement over the RVs obtained using the CCF approach. We developed a recursive periodogram method to enhance the sensitivity of least-squares solvers to low-amplitude signals when strong multiplanet correlations are present, and we provided a recipe to derive empirical FAPs. We compared the results obtained for the RV of GJ 676A to the candidates identified by a Bayesian analyses, obtaining compatible detection of the same four signals. We provided the favoured four planet solution together with the allowed parameter intervals as derived from the Bayesian MCMC samplings.
While it is clear that Bayesian methods are more general and provide a more complete description of the data, frequentists methods (e.g., empirical FAP computations) allow a simpler interpretation of the significance of a detection. The combination of criteria from both approaches provides great confidence in our results. We have shown that after the early Bayesian detection of four planets, 25 more measurements were sufficient to confirm the same candidates with periodogram based methods. Even if a researcher prefers frequentist confirmation of candidates, early Bayesian detection can be used to optimize follow-up programmes (Gregory 2005). This study shows that the confluence of recent data analysis developments (HARPS-TERRA, Bayesian toolbox, advanced periodograms) achieve a significant boost in sensitivity to very low mass companions, even in already existing datasets. Compared to the significant investment required in hardware development, developing improved data-analysis methods comes at a significantly lower cost, thus enabling a more efficient utilization of the observational resources.
GJ 676A shows indications of mild activity levels in the form of coherent variability in the width of the mean line profile (traced by the FWHM of the CCF) and two periodic signals present in its chromospheric emission. However, given that none of the signals coincides with the others, their physical interpretation is not clear. Systematic changes of a few m/s in the instrumental profile of HARPS have been reported by Lovis et al. (2011a), so it is possible that the detected variations of the FWHM have an instrumental origin.
Concerning the new two planet candidates, we find that they are both in the sub-Neptune mass regime. The shorter period candidate (GJ 676Ad) has a significant probability of transit (~5% according to Charbonneau et al. 2007), thus encouraging the photometric follow-up of the star. The long-period companion (massive planet or brown dwarf) is now clearly detected through significant curvature, and a period of ~4000 days or longer is tentatively suggested by the data. With GJ 876 (Rivera et al. 2010) and GJ 581 (Mayor et al. 2009), GJ 676A becomes the third M dwarf with four planet candidates detected. Except for the solar system itself, this planetary system has the broadest range of minimum masses and periods reported so far (from 5 M ⊕ to 5 Mjup, and from 3.6 days to 4000 or more days). Despite the abundance of candidates, the periods (and corresponding semi-major axis) are spaced far enough appart that we do not anticipate major dynamical stability problems. Compared to the more dynamically packed GJ 581 and GJ 876 systems, the orbits of the candidate planets leave ample room to detect more candidates in intermediate orbits whenever additional RV observations become available. Owing to the proximity of GJ 676A to our Sun (~16.4 pc), the long-period, massive candidates are attractive targets for direct imaging attempts (Lagrange et al. 2010). Given that the make-up of stars in binary systems should be similar, it would be very interesting to investigate whether GJ 676B (M3.5V) has been as prolific as GJ 676A in forming all kinds of planets.
Online material
Differential HARPS-TERRA RV measurements of GJ 676A measured in the solar system barycenter reference frame.
Acknowledgments
G.A.E. is supported by the German Federal Ministry of Education and Research under 05A11MG3. M. Tuomi is supported by RoPACS (Rocky Planets Around Cool Stars), a Marie Curie Initial Training Network funded by the European Commission’s Seventh Framework Programme. We are grateful for the advise, support and useful discussions obtained from Paul Butler (DTM), Ansgar Reiners (IAG), Mathias Zechmeister (AIG) and Hugh Jones (HU). We thank Sandy Keiser for setting up and managing the computing resources available at the Department of Terrestrial Magnetism-Carnegie Institution of Washington. This work is based on data obtained from the ESO Science Archive Facility under request number GANGLFGGCE178541. This research has made extensive use of the SIMBAD database, operated at CDS, Strasbourg, France; and the NASA’s Astrophysics Data System.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., López-Morales, M., & Chambers, J. E. 2010, ApJ, 709, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2012, A&A, in press, DOI: 10.1051/0004-6361/201014704 [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Burrows, A., & Laughlin, G. 2007, Protostars and Planets V, 701 [Google Scholar]
- Chib, S., & Jeliazkov, I. 2001, J. Am. Stat. Ass., 96, 270 [Google Scholar]
- Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2012 [arXiv:1202.2467] [Google Scholar]
- Forveille, T.,Bonfils, X., Lo Curto, G., et al. 2011, A&A, 526, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregory, P. C. 2005, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Haario, H., Saksman, E., & Tamminen, J. 2001, Bernouilli, 7, 223 [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Apps, K. 2009, ApJ, 699, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Ass., 90, 773 [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levenberg, K. 1944, Quart. Appl. Math., 2, 164 [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011a, A&A, submitted [arXiv:1107.5325] [Google Scholar]
- Lovis, C., Ségransan, D., Mayor, M., et al. 2011b, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Rupprecht, G., Avila, G., et al. 2003, in SPIE Conf. Ser., 4841, 1045 [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing, 2nd edn. (Cambridge: University Press) [Google Scholar]
- Queloz, D. 1995, in New Developments in Array Technology and Applications, eds. A. G. D. Philip, K. Janes, & A. R. Upgren, IAU Symp., 167, 221 [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Shulyak, D., Anglada-Escudé, G., et al. 2012, A&A, submitted [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M. 2011, A&A, 528, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M. 2012, A&A, 543, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., & Kotiranta, S. 2009, A&A, 496, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Pinfield, D., & Jones, H. R. A. 2011, A&A, 532, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilken, T., Lo Curto, G., & Probst, R. E. A. 2012, Nature, 485, 611 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wright, J. T., & Howard, A. W. 2009, ApJS, 182, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Analytic false-alarm probability of planet candidates e and d as a function of assumed stellar jitter.
Relative posterior probabilities of models with k = 1,...,4 Keplerian signals (ℳk) with or withour a linear trend (LT), the Bayesian evidences P(d|ℳk), and rms values.
Orbital solution of the three innermost companions of GJ 676A and the excess RV jitter.
Differential HARPS-TERRA RV measurements of GJ 676A measured in the solar system barycenter reference frame.
All Figures
 |
Fig. 1 Detection periodograms from most significant signal to less significant one (top to bottom). Black lines are least-squares periodograms computed on the residuals to the k-planet model. The red dots represent the refined orbital solution with k + 1-planets at each test period as obtained by the recursive periodogram. The resulting sampling of the red dots is not uniform in frequency because the tested k + 1 period is also allowed to adjust. |
| In the text | |
 |
Fig. 2 Phase-folded radial velocity curves of the reported new planet candidates. Even though curvature is clearly detected (top right panel), the orbit of the of longer period companion is still poorly constrained. |
| In the text | |
 |
Fig. 3 Distributions estimating the posterior densities of orbital periods (Px), radial velocity amplitudes (Kx) and eccentricities (ex), and three constrained Keplerian signals. The solid curve is a Gaussian density with the same mean (μ) and variance (σ2) as the parameter distribution. Additional statistics, mode, skewness (μ3) and kurtosis (μ4) of the distributions are also shown. |
| In the text | |
 |
Fig. 4 Periodograms of the bisector span (top) and the full-width-at-half-maximum of the cross-correlation function (bottom). No periodic signals with analytic FAP smaller than 5% were detected in either index. |
| In the text | |
 |
Fig. 5 Periodograms (left) and phase folded plots (right) of the signals detected in the S-index. The mean S-index value S0 = 1.40 has been subtracted from the phase folded plots for visualization purposes. The periods of the newly proposed planet candidate signals are marked as black vertical bars. Their 95% confidence level ranges are smaller than the width of the lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


