| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201220203 | |
| Published online | 12 November 2012 | |
Anisotropic diffusion of Galactic cosmic ray protons and their steady-state azimuthal distribution
Institut für Theoretische Physik IV, Ruhr Universität Bochum, 44780 Bochum, Germany
e-mail: fe@tp4.rub.de
Received: 10 August 2012
Accepted: 3 October 2012
Galactic transport models for cosmic rays involve the diffusive motion of these particles in the interstellar medium. Owing to the large-scale structured Galactic magnetic field, this diffusion is anisotropic with respect to the local field direction. We included this transport effect along with continuous loss processes in a quantitative model of Galactic propagation for cosmic ray protons that is based on stochastic differential equations. We calculated energy spectra at different positions along the Sun’s Galactic orbit and compared them to the isotropic diffusion case. The results show that a larger amplitude of variation and different spectral shapes are obtained in the introduced anisotropic diffusion scenario, which in turn emphasizes the need for accurate Galactic magnetic field models.
Key words: cosmic rays / astroparticle physics / diffusion / ISM: magnetic fields / methods: numerical
© ESO, 2012
1. Introduction
Modeling the cosmic ray (CR) transport in the galaxy is a fundamental topic in high-energy astrophysics. Such studies are of great importance in the analysis of CR origin, with the prime candidates being supernovae remnants or pulsar wind nebulae. The characteristics of the models depend on the properties of the interstellar medium (ISM) through which the particles travel and can thus give some insight into its fundamental constitution. For example, the Galactic magnetic field and its turbulent component are connected to the transport parameters in such models. A reference on general CR properties can be found, e.g., in the textbooks by Berezinskii et al. (1990), Gaisser (1990), Schlickeiser (2002), or Stanev (2004).
The basic propagation process of CRs in the ISM is the diffusive motion of the particles due to scattering at magnetic field fluctuations. From numerous studies in heliospheric physics, it is well known that the diffusive transport of energetic particles cannot be described by a scalar diffusion coefficient but requires a diffusion tensor that takes into account that parallel and perpendicular diffusion are different (e.g. Jokipii 1966; Potgieter 2011). In Galactic propagation studies, however, anisotropic diffusion of CRs has been investigated only for basic magnetic field configurations of partly localized applicability; see, e.g., Chuvilgin & Ptuskin (1993), Breitschwerdt et al. (2002), Snodin et al. (2006) and references therein. While the latter authors were interested in the consequences of anisotropic diffusion for energy equipartition, Hanasz & Lesch (2003) and Ryu et al. (2003) analyzed its importance for the Parker instability.
More recently, Hanasz et al. (2009) have found that anisotropic diffusion is an essential requirement for the CR-driven magnetic dynamo action in galaxies. Their assessment of the diffusion anisotropy is based on the full-orbit analysis performed by Giacalone & Jokipii (1999) who found the perpendicular diffusion to be significantly lower than the parallel one in a broad energy range and for both isotropic and composite turbulence. Moreover, a recent derivation of the perpendicular diffusion coefficient for Galactic propagation, using the enhanced nonlinear guiding center theory and a Goldreich-Sridhar turbulence model was performed by Shalchi et al. (2010) and resulted in ratios between the parallel and perpendicular diffusion coefficient, which were much lower than unity as well, namely κ ⊥ /κ∥ ≈ 10-4−10-1, depending on particle rigidity. An analysis for different turbulence spectra in the context of supernova remnant shock acceleration of CRs (Marcowith et al. 2006) or their transport in chaotic magnetic fields (Casse et al. 2002) has yielded similar values for this ratio.
Many popular models for Galactic CR transport, however, include only a single diffusion coefficient, such as the GALPROP code (Strong et al. 2010). Although Strong et al. (2007) principally acknowledge that anisotropic diffusion is important, they argue that owing to large-scale fluctuations in the magnetic field on scales on the order of 100 pc, the global diffusion will be spatially isotropic. Observations of the Galactic magnetic field indicate, though, that the field has a large-scale ordering with a regular field strength, which has about the same magnitude as the turbulent component (see, e.g., Ferrière 2001). A similar indication is given by observations of external spiral galaxies (Beck 2011; Fletcher et al. 2011), which show a global magnetic field structure aligned to the spiral arm pattern. Therefore, it must be concluded that anisotropic diffusion can have a strong effect on Galactic CR propagation.
Besides its fundamental astrophysical relevance, the spatial distribution of CR flux in the galaxy is also of interest in the context of long-term climatology. Shaviv (2002) proposed a CR-climate connection on the timescale of 108 years due to the transit of the solar system through the Galactic spiral arms during its orbit around the Galactic center. The argument assumes that the low-altitude cloud coverage increases due to an increased formation of cloud-condensation nuclei when the CR flux is high (Svensmark et al. 2007). Thus, an anti-correlation between temperature and CR flux is to be expected and is indeed reported by Shaviv & Veizer (2003). Most recently, Svensmark (2012) has found further evidence of a connection of nearby supernovae and their CR output and life on Earth. More details on the CR-climate connection can be found in Scherer et al. (2006). Although we do not state here that we adhere to this view in all aspects (see, e.g., the critical remarks in Overholt et al. 2009), we think that it gives a further interesting motivation to study the Galactic CR distribution, especially its longitudinal structure, in greater detail.
The aim of this investigation is to calculate Galactic CR spectra at different positions along the Sun’s orbit around the Galactic center and to analyze the influence of anisotropic diffusion on the longitudinal cosmic ray distribution. We first present the underlying propagation model and its relevant input, such as the diffusion tensor and its connection to the Galactic magnetic field, the three-dimensional source distribution of CR and its connection to the spiral-arm structure and supernova (SN) occurrence, and loss-processes in the ISM. We also introduce our numerical solution method to the CR transport equation based on stochastic differential equations. Finally, the calculated CR spectra and orbital flux variations are discussed and conclusion are drawn. Some earlier results on this topic can also be found in Effenberger et al. (2011).
2. The propagation model
The basic transport theory of CRs is described in many contemporary monographs, e.g. Schlickeiser (2002), Stanev (2004), and (Shalchi 2009). Recently, Strong et al. (2007) have surveyed the theory and experimental tests for the propagation of cosmic rays in the Galaxy. The considerations are commonly based on the following parabolic transport equation (e.g., Ptuskin et al. 2006): ![\begin{eqnarray} \displaystyle \frac{\partial N}{\partial t} = \nabla\cdot\left(\hat{\kappa}\cdot\nabla\, N - \vec{u} N \right) - \frac{\partial}{\partial p}\left[\dot{p} N - \frac{p}{3}(\nabla\cdot\vec{u}) N \right] + Q \label{tp1} \end{eqnarray}](/articles/aa/full_html/2012/11/aa20203-12/aa20203-12-eq3.png) (1)where N(r,p,t) = p2f(r,p,t) is the differential intensity of CRs and f their phase space density, which is assumed to be isotropic in momentum space. As usual, r,p, and t denote the location in space, momentum, and time, and we use a Galactic cylindrical coordinate system [r,ϕ,z]. The source term Q includes primary particle injection, which, in this study, is considered to be only by supernovae and their remnant shock features. The spatial diffusion, in general, should be described by a tensor, but in most applications to Galactic propagation so far, it is simplified to a scalar coefficient κs, i.e.
(1)where N(r,p,t) = p2f(r,p,t) is the differential intensity of CRs and f their phase space density, which is assumed to be isotropic in momentum space. As usual, r,p, and t denote the location in space, momentum, and time, and we use a Galactic cylindrical coordinate system [r,ϕ,z]. The source term Q includes primary particle injection, which, in this study, is considered to be only by supernovae and their remnant shock features. The spatial diffusion, in general, should be described by a tensor, but in most applications to Galactic propagation so far, it is simplified to a scalar coefficient κs, i.e. 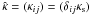 (see the discussion above). An ordered motion of the ISM can be taken into account via the convection velocity u (e.g., Fichtner et al. 1991; Ptuskin et al. 1997; Völk 2007), but is neglected for this study due to its decreasing importance for higher CR energies. Continuous momentum losses are described by the momentum change rate ṗ. Catastrophic loss processes, such as spallation, do not apply, since in this study only Galactic protons are considered.
(see the discussion above). An ordered motion of the ISM can be taken into account via the convection velocity u (e.g., Fichtner et al. 1991; Ptuskin et al. 1997; Völk 2007), but is neglected for this study due to its decreasing importance for higher CR energies. Continuous momentum losses are described by the momentum change rate ṗ. Catastrophic loss processes, such as spallation, do not apply, since in this study only Galactic protons are considered.
2.1. The anisotropic diffusion tensor
As discussed in the introduction, the diffusion of CRs in magnetic fields with a prominent ordered field component is generally anisotropic with respect to this field orientation, i.e. stronger in field-parallel direction and weaker in the perpendicular directions. This effect can be included in the propagation model by a diffusion tensor which is locally, that is, in a field-aligned coordinate system, diagonal: 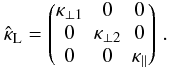 (2)Here, drift effects or aspects of non-axisymmetric turbulence (Weinhorst et al. 2008), which could lead to off-diagonal elements in the diffusion tensor, are neglected.
(2)Here, drift effects or aspects of non-axisymmetric turbulence (Weinhorst et al. 2008), which could lead to off-diagonal elements in the diffusion tensor, are neglected.
Since the CR transport is described in a global frame of reference (i.e. the Galactic frame with a cylindrical coordinate system in case of this study), the field-aligned tensor has to be transformed to this frame by the usual transformation 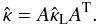 (3)This transformation is analogous to the Euler angle transformation known from classical mechanics. The matrix A = R3R2R1 describes three consecutive rotations Ri with A-1 = AT (since A ∈ SO3). These rotations are defined by the relative orientation of the local and the global coordinate system with respect to each other.
(3)This transformation is analogous to the Euler angle transformation known from classical mechanics. The matrix A = R3R2R1 describes three consecutive rotations Ri with A-1 = AT (since A ∈ SO3). These rotations are defined by the relative orientation of the local and the global coordinate system with respect to each other.
If the two perpendicular diffusion coefficients are not equal, this transformation is of particular importance in establishing the appropriate orientation in the calculation of the global diffusion tensor. Recently, Effenberger et al. (2012) established a generalized scheme based on the local field geometry to account for this. In the present study, however, both perpendicular diffusion coefficients are set equal to reduce the set of unknown parameters (connected to the unknown detailed turbulence properties in the ISM), i.e. κ⊥1 = κ⊥2 = κ⊥. Furthermore, since the Galactic magnetic field in consideration is to first order parallel to the Galactic disk (see the discussion in the following section), the field tangential et and the z-axis ez unit vectors provide, together with the completing third unit vector en = ez × et, a well-defined coordinate system. These unit vectors represent the columns of the transformation matrix A.
To complete the model of the diffusive part of CR propagation, the local tensor elements, i.e. κ∥ and κ⊥, have to be defined. For the parallel diffusion coefficient κ∥, we assume the same broken power-law dependence as has been taken for the scalar diffusion coefficient in Büsching & Potgieter (2008), namely: 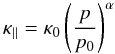 (4)with α = 0.6 for p > p0, α = −0.48 for p ≤ p0, κ0 = 0.027 kpc2/Myr, and p0 = 4 GeV/c.
(4)with α = 0.6 for p > p0, α = −0.48 for p ≤ p0, κ0 = 0.027 kpc2/Myr, and p0 = 4 GeV/c.
Originally, this particular break energy of 3 − 4 GeV was motivated to fit the plain diffusion model results like those in Moskalenko et al. (2002) to the observed boron to carbon ratios. A first refinement can be found in Ptuskin et al. (2006) and a more rigorous study has been performed by Shalchi & Büsching (2010). By including turbulence dissipation effects and replacing the quasilinear transport theory by a second-order diffusion theory, they confirm the possible existence of such a turnover in the parallel diffusion coefficient.
The perpendicular diffusion κ ⊥ is scaled to be a fraction of κ∥, i.e., 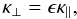 (5)where the diffusion-anisotropy ϵ is assumed to be in the range of 0.1 to 0.01 for Galactic protons with GeV energies (Shalchi et al. 2010). The actual variation in anisotropy with energy is an interesting aspect, but for the relatively narrow energy range up to 1 TeV considered in this study, the anisotropy can be regarded to first order as independent of energy, thus following Giacalone & Jokipii (1999). Since the latter author’s finding of energy independence is valid for both isotropic (see also the partially similar result by Casse et al. 2002) and composite turbulence, and given the, to some extent, different results found by Shalchi et al. (2010) assuming a Goldreich-Sridhar turbulence, conclusions about the detailed underlying turbulence properties should not be drawn on the basis of our study.
(5)where the diffusion-anisotropy ϵ is assumed to be in the range of 0.1 to 0.01 for Galactic protons with GeV energies (Shalchi et al. 2010). The actual variation in anisotropy with energy is an interesting aspect, but for the relatively narrow energy range up to 1 TeV considered in this study, the anisotropy can be regarded to first order as independent of energy, thus following Giacalone & Jokipii (1999). Since the latter author’s finding of energy independence is valid for both isotropic (see also the partially similar result by Casse et al. 2002) and composite turbulence, and given the, to some extent, different results found by Shalchi et al. (2010) assuming a Goldreich-Sridhar turbulence, conclusions about the detailed underlying turbulence properties should not be drawn on the basis of our study.
2.2. Galactic magnetic field models
As soon as anisotropic diffusion is considered, the knowledge of the large-scale magnetic field in the galaxy becomes important. Reviews of this subject have been written, e.g., by Beck et al. (1996), Ferrière (2001) and Heiles & Haverkorn (2012). Pulsar rotation measure data (Han et al. 2006) give evidence for a counter-clockwise field orientation (viewed from the north Galactic pole) in the spiral arms interior to the Sun’s orbit and weaker evidence for a counter-clockwise field in the Perseus arm, see however, the criticism by Wielebinski (2005). In interarm regions, including the solar neighborhood, the data suggest that the field is clockwise. Han (2006) proposed that the Galactic magnetic field in the disk has a bisymmetric structure with reversals on the boundaries of the spiral arms. Magnetic fields in the general class of spiral galaxies have been studied by, e.g., Wielebinski & Beck (2005) and Dettmar & Soida (2006) and can be compared with that of our own galaxy.
Fortunately, as long as drift effects are neglected, the actual sign-dependent orientation is not relevant for the diffusion along and perpendicular to the magnetic field, which enables us to employ a simplified model of the Galactic magnetic field that has no field reversals and is aligned to the spiral arm structure in the disk. Neglecting furthermore its weak halo-component, a simple model for the mean Galactic magnetic field in cylindrical coordinates is given by 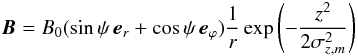 (6)which is divergence free by construction. Here, ψ is the counter-clockwise logarithmic spiral arm pitch-angle, which has an approximate value of ψ = 12°, according to the metastudy by Vallée (2005). The same spiral arm parametrization is employed for the source distribution function discussed in the following section. Note, that the halo-scale parameter σz,m is not relevant in this context, since only the magnetic field direction is used for constructing the diffusion tensor.
(6)which is divergence free by construction. Here, ψ is the counter-clockwise logarithmic spiral arm pitch-angle, which has an approximate value of ψ = 12°, according to the metastudy by Vallée (2005). The same spiral arm parametrization is employed for the source distribution function discussed in the following section. Note, that the halo-scale parameter σz,m is not relevant in this context, since only the magnetic field direction is used for constructing the diffusion tensor.
2.3. Source distribution
 |
Fig. 1 Orientation of the Galactic spiral arms in the present model. Norma, Scutum, Saggitarius, and Perseus arms are colored by green, blue, red, and purple, respectively. The black line shows the solar orbit, and the Galactic center region is marked in black. The four × -markings indicate the positions at 90°, 108°, 126°, and 144°, where the CR spectra have been calculated (see Sect. 3). |
For the injection of CRs we assume a source distribution that follows the Galactic spiral arm structure, where most of the supernovae (SN) supposedly occur. As a basis we take the same spiral arm model as mentioned above, i.e. the model established by Vallée (2002, 2005), which consists of four logarithmic and symmetrically positioned arms. Around these, we take a Gaussian shape (analogous to the approach in Shaviv 2003) to yield an analytic expression for the source term Q, by summing up over all four arms (n ∈ {1, 2, 3, 4}): 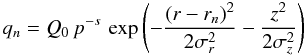 (7)with rn = r0exp(k(ϕ + ϕn)), where ϕn introduces the symmetric rotation of each arm by 90°, i.e. ϕn = (n − 1)π/2. k = cosψ with ψ = 12° is the constant pitch-angle cosine of the spiral arms. Figure 1 illustrates the orientation of the spiral arms relative to the Sun’s position and orbit. We take σr = σz = 0.2 kpc to have a reasonable interarm separation, while r0 = 2.52 kpc according to Vallée’s model. The model galaxy has the often assumed cylindrical shape with a radius of 15 kpc and a height of 4 kpc (Büsching et al. 2005), and the Sun’s orbit is at a radius of r⊙ = 7.9 kpc. The average spectral index s of the sources’ power law injection in momentum is set to s = 2.3, in agreement with recent estimates on CR source spectra (see e.g. Putze et al. 2011; Ave et al. 2009). Figure 2 gives a visualization of this source distribution. The overall source strength Q0 is a free parameter that can be fitted to a given reference like a local interstellar spectrum (LIS; see also the discussion in Sect. 3).
(7)with rn = r0exp(k(ϕ + ϕn)), where ϕn introduces the symmetric rotation of each arm by 90°, i.e. ϕn = (n − 1)π/2. k = cosψ with ψ = 12° is the constant pitch-angle cosine of the spiral arms. Figure 1 illustrates the orientation of the spiral arms relative to the Sun’s position and orbit. We take σr = σz = 0.2 kpc to have a reasonable interarm separation, while r0 = 2.52 kpc according to Vallée’s model. The model galaxy has the often assumed cylindrical shape with a radius of 15 kpc and a height of 4 kpc (Büsching et al. 2005), and the Sun’s orbit is at a radius of r⊙ = 7.9 kpc. The average spectral index s of the sources’ power law injection in momentum is set to s = 2.3, in agreement with recent estimates on CR source spectra (see e.g. Putze et al. 2011; Ave et al. 2009). Figure 2 gives a visualization of this source distribution. The overall source strength Q0 is a free parameter that can be fitted to a given reference like a local interstellar spectrum (LIS; see also the discussion in Sect. 3).
 |
Fig. 2 Volume rendering visualization of the input source distribution of CRs. The coloring indicates the source strength from red (low) to yellow (high) in arbitrary units. |
2.4. Loss processes
The two most dominant loss processes for CR protons during their propagation through the ISM are energy losses due to pion production for relativistic energies and ionization processes in the ISM plasma for lower energies (see Fig. 1 in Mannheim & Schlickeiser 1994).
According to Chapter 5 in Schlickeiser (2002), the pion losses can be approximated for Lorentz factors γ ≫ 1 as 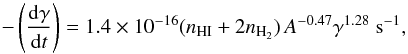 (8)where we assume a z-dependent ISM gas density with
(8)where we assume a z-dependent ISM gas density with 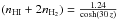 (in units of particles per cm3 and z in kpc, Büsching & Potgieter 2008). The mass number A of a proton is just unity. A similar formula for the ionization losses is given by
(in units of particles per cm3 and z in kpc, Büsching & Potgieter 2008). The mass number A of a proton is just unity. A similar formula for the ionization losses is given by 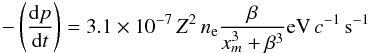 (9)where the electron density is the same as the above gas density and the charge state of protons Z is equal to 1. For the purpose of this study, the velocity factor β = v/c of the particles is always much greater than the thermal electron βe, which is related to xm by xm = (3/4π1/2)1/3βe = 1.10 βe. This means that the momentum loss rate scales approximately as p-2. The total momentum loss rate entering Eq. (1) is the sum of both loss processes.
(9)where the electron density is the same as the above gas density and the charge state of protons Z is equal to 1. For the purpose of this study, the velocity factor β = v/c of the particles is always much greater than the thermal electron βe, which is related to xm by xm = (3/4π1/2)1/3βe = 1.10 βe. This means that the momentum loss rate scales approximately as p-2. The total momentum loss rate entering Eq. (1) is the sum of both loss processes.
 |
Fig. 3 Sample paths of pseudo-particles in the Galactic magnetic spiral field, colored by three different colors for three particles, each starting at the same point in phase space (i.e. Earth’s position at 1 GeV) and projected onto the Galactic plane. The black lines show integrated magnetic field lines to illustrate the magnetic field orientation. The left panel shows sample paths for isotropic diffusion, with no visible effect of the magnetic field orientation. The right panel illustrates the preferential diffusion along the magnetic field for a simulation with anisotropy ϵ = 0.1. Note that the exit point of the red particle in the right panel is actually the radial boundary, while the other particles all exit through the halo’s z-boundary (not visible). |
2.5. The numerical solution method based on stochastic differential equations
To solve the transport equation for the problem setup introduced in this study, we employ a numerical solution scheme based on the It equivalence of a Fokker-Planck type equation and corresponding stochastic differential equations (SDEs) involving a random Wiener process. This method has become increasingly popular in CR transport studies because of its numerical simplicity and conformance with modern computer architecture, i.e. its straightforward parallelization and scalability. Mentioning only a few examples, a starting point for heliospheric studies of this kind can be found in the paper by Zhang (1999) where he applied the method to CR modulation. More recently, Pei et al. (2010) and Strauss et al. (2011) have applied SDEs in a more comprehensive heliospheric model. Farahat et al. (2008) employed SDEs for a CR propagation study in the Galaxy and, e.g., Marcowith & Kirk (1999), as well as Achterberg & Schure (2011) calculated the shock acceleration of energetic particles.
equivalence of a Fokker-Planck type equation and corresponding stochastic differential equations (SDEs) involving a random Wiener process. This method has become increasingly popular in CR transport studies because of its numerical simplicity and conformance with modern computer architecture, i.e. its straightforward parallelization and scalability. Mentioning only a few examples, a starting point for heliospheric studies of this kind can be found in the paper by Zhang (1999) where he applied the method to CR modulation. More recently, Pei et al. (2010) and Strauss et al. (2011) have applied SDEs in a more comprehensive heliospheric model. Farahat et al. (2008) employed SDEs for a CR propagation study in the Galaxy and, e.g., Marcowith & Kirk (1999), as well as Achterberg & Schure (2011) calculated the shock acceleration of energetic particles.
The basic idea in SDE schemes is to trace pseudo-particle trajectories from their origin forward in time or, alternatively, integrate backwards in time from the phase space point of interest. The particle trajectory is given by the integral of an SDE of the form 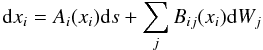 (10)where the relation
(10)where the relation 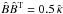 has to be fulfilled, that is, a root for the diffusion tensor
has to be fulfilled, that is, a root for the diffusion tensor 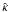 has to be determined. Here, dWj is a (multidimensional) Wiener process increment, which has a time-stationary, normal-distributed probability density with expectation value 0 and variance 1. The deterministic part is directly related to the convection velocity in the transport equation, i.e. Ai = −ui. Numerically, this SDE is integrated via a simple Euler-forward scheme and the Wiener-process is simulated with the Box-Muller method (e.g., Box & Muller 1958) by using
has to be determined. Here, dWj is a (multidimensional) Wiener process increment, which has a time-stationary, normal-distributed probability density with expectation value 0 and variance 1. The deterministic part is directly related to the convection velocity in the transport equation, i.e. Ai = −ui. Numerically, this SDE is integrated via a simple Euler-forward scheme and the Wiener-process is simulated with the Box-Muller method (e.g., Box & Muller 1958) by using 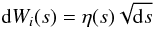 (11)where η(s) is equivalent to a Gaussian distribution
(11)where η(s) is equivalent to a Gaussian distribution 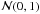 . The necessary random numbers are generated with the MTI19937 version of the so-called Mersenne Twister (Matsumoto & Nishimura 1998). The integration parameter s is related to physical time by
. The necessary random numbers are generated with the MTI19937 version of the so-called Mersenne Twister (Matsumoto & Nishimura 1998). The integration parameter s is related to physical time by 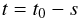 (12)where t0 is the final time for the backward method. The source contribution to the individual particle trajectory is added up by a path amplitude. Finally, for the backward method, all particle trajectories are weighted together to yield the resulting phase space density (i.e. the solution to the associated Fokker-Planck equation) at the starting phase space point. The boundary and initial conditions can be accounted for in the weighting, but for this study they are simply zero (corresponding to an escaping boundary condition for the CRs). We only apply the backward method in this study, since it is well-suited to the given problem. For more details on the numerical scheme and especially on determining the root of the diffusion tensor, we refer the reader to Kopp et al. (2012) and Strauss et al. (2011) where the basis of the code used in this study is discussed in greater detail.
(12)where t0 is the final time for the backward method. The source contribution to the individual particle trajectory is added up by a path amplitude. Finally, for the backward method, all particle trajectories are weighted together to yield the resulting phase space density (i.e. the solution to the associated Fokker-Planck equation) at the starting phase space point. The boundary and initial conditions can be accounted for in the weighting, but for this study they are simply zero (corresponding to an escaping boundary condition for the CRs). We only apply the backward method in this study, since it is well-suited to the given problem. For more details on the numerical scheme and especially on determining the root of the diffusion tensor, we refer the reader to Kopp et al. (2012) and Strauss et al. (2011) where the basis of the code used in this study is discussed in greater detail.
 |
Fig. 4 Calculated CR proton spectra (multiplied by E2) at four different positions along the Sun’s orbit (see Fig. 1 for the respective locations) in the Galactic plane (z = 0), where 90° corresponds approximately to the current solar system position and 126° is inside of the Saggitarius arm. The upper panel shows the spectra for isotropic diffusion, while the middle and lower panels include anisotropic diffusion with ϵ = 0.1 and ϵ = 0.01, respectively. The latter spectra have been rescaled by factors of 0.15 and 0.05 to account for the higher overall flux due to the stronger confinement in the disk in contrast to the isotropic case. The LIS from Webber & Higbie (2009) is plotted for comparison (black crosses). |
Exemples of pseudo-particle trajectories are shown in Fig. 3. There, the additional information contained in SDE calculations becomes obvious. The pseudo-particles’ paths follow the field lines during their stochastic motion as soon as anisotropic diffusion becomes relevant. Consequently, the modification to the diffusion process becomes directly visible in such trajectories. However, one has to keep in mind that these are not real particle trajectories or gyro-center motions, but only tracers of the phase space of the diffusion-convection problem.
3. The resulting spatial and spectral CR distribution
We calculated CR proton spectra within the introduced model at four different positions along the Sun’s Galactic orbit. The positions are indicated in Fig. 1. We took a very long integration time (t0 ≈ 10 000 Myr) to assure that we approached a steady state situation, which is confirmed by checking that all particles haveexited the computational domain. For each phase space point, 104 pseudo particle trajectories were computed. A comparison between the calculated spectra in the case of pure isotropic diffusion (upper panel) and two anisotropic cases, with weak (ϵ = 0.1, middle panel) and strong (ϵ = 0.01, lower panel) diffusion anisotropy, is shown in Fig. 4. For further comparison, the LIS given by Webber & Higbie (2009; WH09 hereafter) is included in the plots. We used the parametrization given in Herbst et al. (2010), where a comparison between a few proposed LIS can be found as well. In face of the still imprecisely known modulation effects on measured spectra inside the heliosphere (see, e.g., Florinski et al. 2011; Scherer et al. 2011), such an LIS parametrization can give only a rough orientation for what to expect for Galactic CR propagation studies. Our results have been rescaled to approximately fit the WH09 LIS in the isotropic diffusion case, by accounting for the free parameter Q0 in the source strength. The anisotropic spectra have been rescaled again, respectively. To yield the good agreement shown in both upper panels of Fig. 4 between the calculated spectra and the WH09 LIS, the break in the diffusion coefficient introduced above as well as both continuous loss processes, are required. Including the latter improves on earlier studies, such as Büsching & Potgieter (2008), where only a parametrized catastrophic loss term was considered.
The spectra for different positions along the Sun’s Galactic orbit show only very little variation in the isotropic diffusion case. Particularly, the variation is largely independent of energy over the entire energy range considered. In contrast to this, the variation is much stronger for the anisotropic scenario, depending on the imposed diffusion anisotropy. The differences are, in these cases, dependent on energy as well. For high energies, the spectra start to converge again towards the isotropic differences. This is due to the increasing dominance of escape losses for these high energies. For lower energies, the pion and ionization losses are much more important than in the isotropic case, because the confinement time of CRs is longer as a result of the reduced diffusion perpendicular to the disk.
Notably, the spectrum at Earth for the weak anisotropic case fits the reference LIS even better than the pure isotropic result, which shows that, depending on the overall parameter set, anisotropic diffusion scenarios can improve on the model results of conventional studies. In this context, one has to keep in mind, however, that the precise form of the low-energy LIS and its connection to the Galactic spectrum on a kpc scale is still unclear and depends on modulation effects in the heliosphere, as well as on similar effects in the local solar system environment (see, e.g., the discussion in Scherer et al. 2011). Furthermore, the assumed break in the diffusion coefficient may be different or even absent in a more complete propagation scenario, since up to now it has mainly been phenomenologically motivated, to yield the expected local spectra.
The spectra for the strong anisotropic case (ϵ = 0.01) show some significant deviations from the expected spectral shape owing to the largely increased relative importance of the loss processes, resulting, e.g., in a flatter high-energy spectrum. In the context of the model setup of this study, this means that such high diffusion anisotropy is probably unrealistic. Nevertheless, we included this case since it shows the resulting large orbital variation at lower energies (see also Fig. 5) where the spectral shape is still unclear. In addition, models with different structures in the Galactic halo, namely with different gas densities and halo heights, as well as a possible magnetic field component perpendicular to the disk, may alter the resultant spectra further, because of the changed influence of the loss processes. These aspects could be clarified further in a subsequent study that takes different CR species and more sophisticated magnetic field models into account.
In Fig. 5 the flux variation along the Sun’s orbit is plotted against longitude, to illustrate the variation with longitudinal position further. We consider two different energies, namely 1 GeV and 100 GeV and two Galactic distances of r = 5 kpc and r⊙ = 7.9 kpc, again for isotropic (left panel) and strong anisotropic (ϵ = 0.01, right panel) diffusion. Including a second radius at only 5 kpc is motivated by the recent claim that the Sun may have migrated outwards during its lifetime in the galaxy (Nieva & Przybilla 2012). It can be seen that the variation is much weaker in a closer Galactic orbit and has a different phase, as a result of the smaller interarm separation. For all cases, the overall shape of the variation is not a simple sinusoidal profile owing to the non-perpendicular transit of the Sun through the arms (see again Fig. 1). The amplitude of variation is much more pronounced for the anisotropic case; that is, it can be as large as a factor of 6, while in the isotropic case it is only a factor of about 2. An increased diffusion anisotropy ϵ will increase this difference even further.
4. Conclusions
In this study, the effects of anisotropic diffusion of Galactic CR protons have been analyzed. For the solution of the steady-state diffusion equation a numerical method based on stochastic differential equations was used, which also accounts for energy-loss processes. The computed spectra along the Sun’s Galactic orbit show larger variations for the anisotropic cases when compared to the scalar diffusion model. Furthermore, for the chosen parameters, a moderate diffusion anisotropy (ϵ = κ ⊥ /κ ∥ = 0.1) leads to a result that, in our setup, is more consistent with recent estimates of the local interstellar proton spectrum than the results for purely isotropic diffusion.
We therefore conclude that the diffusion tensor, as well as the CR source distribution, is an important feature in determining the solution of the transport equation in a three-dimensional model of Galactic CR propagation. This result fits well into the findings by Hanasz et al. (2009), who claimed that anisotropic diffusion is an essential requirement for the CR-driven Galactic dynamo effect. Additionally, these results imply that in the context of the recently proposed CR-climate connection (Shaviv & Veizer 2003) the expected CR flux variation may be even larger than previously estimated, although at present, this topic is still highly speculative.
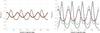 |
Fig. 5 Orbital variation of the CR proton flux along the Sun’s orbit, plotted against longitude (with Sun’s position at 90°). All curves are rescaled to an offset value of 1 for comparison. The black line and green crosses show the variation for an orbit at r = 7.9 kpc and z = 0 for 1 GeV and 100 GeV, respectively. The blue line and red boxes show the same energies for an orbit at r = 5 kpc. The left panel again shows the case of isotropic diffusion, while the right panel has ϵ = 0.01, and the variation is much more pronounced. |
We emphasize that the introduced model indicates further research opportunities by including additional effects such as a variable spectral source index and time-variable CR sources, depending on supernova type. The necessary time-dependent calculations are in principle possible with the current model setup, and the earlier work by Büsching & Potgieter (2008) shows some results on this already. Furthermore, the consideration of additional CR species and their relevant loss processes may yield further insight into constraining transport parameters. Finally, this study points at the necessity of acquiring more detailed models of the Galactic magnetic field, to assess its impact on the transport processes of CRs.
Acknowledgments
The work was carried out within the framework of the “Galactocauses” project (FI 706/9-1) funded by the Deutsche Forschungsgemeinschaft (DFG) and benefited from the DFG-Forschergruppe 1048 (project FI 706/8-1/2), the “Heliocauses” DFG-project (FI 706/6-3) and funding by the German Ministry for Education and Research (BMBF) through the “Verbundforschung Astroteilchenphysik” grant 05A11PC1. We thank A. Kopp, M. Pohl, and R. Schlickeiser for useful discussions with regard to the modeling approach in this study and an anonymous referee for helpful comments.
References
- Achterberg, A., & Schure, K. M. 2011, MNRAS, 411, 2628 [NASA ADS] [CrossRef] [Google Scholar]
- Ave, M., Boyle, P. J., Höppner, C., Marshall, J., & Müller, D. 2009, ApJ, 697, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2011, Space Sci. Rev., 135 [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of cosmic rays (Amsterdam: North-Holland) [Google Scholar]
- Box, G. E. P., & Muller, M. E. 1958, Ann. Math. Stat., 29, 610 [CrossRef] [Google Scholar]
- Breitschwerdt, D., Dogiel, V. A., & Völk, H. J. 2002, A&A, 385, 216 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Büsching, I., & Potgieter, M. S. 2008, Adv. Space Res., 42, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Büsching, I., Kopp, A., Pohl, M., et al. 2005, ApJ, 619, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, F., Lemoine, M., & Pelletier, G. 2002, Phys. Rev. D, 65, 023002 [Google Scholar]
- Chuvilgin, L. G., & Ptuskin, V. S. 1993, A&A, 279, 278 [NASA ADS] [Google Scholar]
- Dettmar, R.-J., & Soida, M. 2006, Astron. Nachr., 327, 495 [Google Scholar]
- Effenberger, F., Fichtner, H., Büsching, I., Kopp, A., & Scherer, K. 2011, Mem. Soc. Astron. Italiana, 82, 867 [NASA ADS] [Google Scholar]
- Effenberger, F., Fichtner, H., Scherer, K., et al. 2012, ApJ, 750, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Farahat, A., Zhang, M., Rassoul, H., & Connell, J. J. 2008, ApJ, 681, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Fichtner, H., Fahr, H. J., Neutsch, W., et al. 1991, Nuovo Cimento B Serie, 106, 909 [Google Scholar]
- Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Florinski, V., Ferreira, S. E. S., & Pogorelov, N. V. 2011, Space Sci. Rev., 111 [Google Scholar]
- Gaisser, T. K. 1990, Cosmic rays and particle physics [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Han, J. L. 2006, J. Phys. Conf. Ser., 47, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. L., Manchester, R. N., Lyne, A. G., Qiao, G. J., & van Straten, W. 2006, ApJ, 642, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., & Lesch, H. 2003, A&A, 412, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanasz, M., Otmianowska-Mazur, K., Kowal, G., & Lesch, H. 2009, A&A, 498, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Haverkorn, M. 2012, Space Sci. Rev., 166, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, K., Kopp, A., Heber, B., et al. 2010, J. Geophys. Res. (Space Phys.), 115, [Google Scholar]
- Jokipii, J. R. 1966, ApJ, 146, 480 [Google Scholar]
- Kopp, A., Büsching, I., Strauss, R. D., & Potgieter, M. S. 2012, Comput. Phys. Commun., 183, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K., & Schlickeiser, R. 1994, A&A, 286, 983 [NASA ADS] [Google Scholar]
- Marcowith, A., & Kirk, J. G. 1999, A&A, 347, 391 [NASA ADS] [Google Scholar]
- Marcowith, A., Lemoine, M., & Pelletier, G. 2006, A&A, 453, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsumoto, M., & Nishimura, T. 1998, ACM Trans. Model. Comput. Simul., 8, 3 [Google Scholar]
- Moskalenko, I. V., Strong, A. W., Ormes, J. F., & Potgieter, M. S. 2002, ApJ, 565, 280 [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Overholt, A. C., Melott, A. L., & Pohl, M. 2009, ApJ, 705, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, C., Bieber, J. W., Burger, R. A., & Clem, J. 2010, J. Geophys. Res. (Space Phys.), 115, 12107 [Google Scholar]
- Potgieter, M. S. 2011, Space Sci. Rev., 107 [Google Scholar]
- Ptuskin, V. S., Voelk, H. J., Zirakashvili, V. N., & Breitschwerdt, D. 1997, A&A, 321, 434 [NASA ADS] [Google Scholar]
- Ptuskin, V. S., Moskalenko, I. V., Jones, F. C., Strong, A. W., & Zirakashvili, V. N. 2006, ApJ, 642, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Putze, A., Maurin, D., & Donato, F. 2011, A&A, 526, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryu, D., Kim, J., Hong, S. S., & Jones, T. W. 2003, ApJ, 589, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Fichtner, H., Borrmann, T., et al. 2006, Space Sci. Rev., 127, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Fichtner, H., Strauss, R. D., et al. 2011, ApJ, 735, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [Google Scholar]
- Shalchi, A. 2009, Nonlinear Cosmic Ray Diffusion Theories Astrophysi. Space Sci. Lib., 362 (Berlin: Springer) [Google Scholar]
- Shalchi, A., & Büsching, I. 2010, ApJ, 725, 2110 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., Büsching, I., Lazarian, A., & Schlickeiser, R. 2010, ApJ, 725, 2117 [NASA ADS] [CrossRef] [Google Scholar]
- Shaviv, N. J. 2002, Phys. Rev. Lett., 89, 051102 [NASA ADS] [CrossRef] [Google Scholar]
- Shaviv, N. J. 2003, New A, 8, 39 [Google Scholar]
- Shaviv, N., & Veizer, J. 2003, GSA Today, 13, 4 [CrossRef] [Google Scholar]
- Snodin, A. P., Brandenburg, A., Mee, A. J., & Shukurov, A. 2006, MNRAS, 373, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Stanev, T. 2004, High Energy Cosmic Rays (Chichester: Springer) [Google Scholar]
- Strauss, R. D., Potgieter, M. S., Büsching, I., & Kopp, A. 2011, ApJ, 735, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., Porter, T. A., et al. 2010, Astrophysics Source Code Library, 10028 [Google Scholar]
- Svensmark, H. 2012, MNRAS, 423, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- Svensmark, H., Pedersen, J. O. P., Marsh, N. D., Enghoff, M. B., & Uggerhøj, U. I. 2007, Roy. Soc. London Proc. Ser. A, 463, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P. 2002, ApJ, 566, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P. 2005, AJ, 130, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J. 2007, Space Sci. Rev., 130, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Webber, W. R., & Higbie, P. R. 2009, J. Geophys. Res. (Space Phys.), 114, 2103 [Google Scholar]
- Weinhorst, B., Shalchi, A., & Fichtner, H. 2008, ApJ, 677, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Wielebinski, R. 2005, in The Magnetized Plasma in Galaxy Evolution, eds. K. T. Chyzy, K. Otmianowska-Mazur, M. Soida, & R.-J. Dettmar, 125 [Google Scholar]
- Wielebinski, R., & Beck, R., eds. 2005, Cosmic Magnetic Fields, Lect. Notes Phys. (Berlin: Springer Verlag), 664 [Google Scholar]
- Zhang, M. 1999, ApJ, 513, 409 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Orientation of the Galactic spiral arms in the present model. Norma, Scutum, Saggitarius, and Perseus arms are colored by green, blue, red, and purple, respectively. The black line shows the solar orbit, and the Galactic center region is marked in black. The four × -markings indicate the positions at 90°, 108°, 126°, and 144°, where the CR spectra have been calculated (see Sect. 3). |
| In the text | |
 |
Fig. 2 Volume rendering visualization of the input source distribution of CRs. The coloring indicates the source strength from red (low) to yellow (high) in arbitrary units. |
| In the text | |
 |
Fig. 3 Sample paths of pseudo-particles in the Galactic magnetic spiral field, colored by three different colors for three particles, each starting at the same point in phase space (i.e. Earth’s position at 1 GeV) and projected onto the Galactic plane. The black lines show integrated magnetic field lines to illustrate the magnetic field orientation. The left panel shows sample paths for isotropic diffusion, with no visible effect of the magnetic field orientation. The right panel illustrates the preferential diffusion along the magnetic field for a simulation with anisotropy ϵ = 0.1. Note that the exit point of the red particle in the right panel is actually the radial boundary, while the other particles all exit through the halo’s z-boundary (not visible). |
| In the text | |
 |
Fig. 4 Calculated CR proton spectra (multiplied by E2) at four different positions along the Sun’s orbit (see Fig. 1 for the respective locations) in the Galactic plane (z = 0), where 90° corresponds approximately to the current solar system position and 126° is inside of the Saggitarius arm. The upper panel shows the spectra for isotropic diffusion, while the middle and lower panels include anisotropic diffusion with ϵ = 0.1 and ϵ = 0.01, respectively. The latter spectra have been rescaled by factors of 0.15 and 0.05 to account for the higher overall flux due to the stronger confinement in the disk in contrast to the isotropic case. The LIS from Webber & Higbie (2009) is plotted for comparison (black crosses). |
| In the text | |
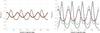 |
Fig. 5 Orbital variation of the CR proton flux along the Sun’s orbit, plotted against longitude (with Sun’s position at 90°). All curves are rescaled to an offset value of 1 for comparison. The black line and green crosses show the variation for an orbit at r = 7.9 kpc and z = 0 for 1 GeV and 100 GeV, respectively. The blue line and red boxes show the same energies for an orbit at r = 5 kpc. The left panel again shows the case of isotropic diffusion, while the right panel has ϵ = 0.01, and the variation is much more pronounced. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


