| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220068 | |
| Published online | 25 October 2012 | |
Microwave and radio emission of dusty star-forming galaxies: implication for the cosmic radio background
IAS, CNRS (UMR 8617), Université Paris-Sud 11, Bâtiment 121, 91400
Orsay, France
e-mail: nathalie.ysard@ias.u-psud.fr
Received:
20
July
2012
Accepted:
17
September
2012
We use the most up-to-date cosmological evolution models of dusty star-forming galaxies and radio sources to compute the extragalactic number counts and the cosmic background from 408 MHz to 12 THz (or 24 μm). The evolution model of star-forming galaxies reproduces the recent constraints obtained by Spitzer, Herschel, and ground-based submm and mm experiments: number counts, redshift distribution of galaxies, cosmic background intensity and anisotropies. The template spectral energy distributions used in this model are extrapolated to the radio domain adding three emission components: synchrotron, free-free, and spinning dust. To fix the synchrotron intensity, we use the well-known IR/radio flux ratio, q70, and a constant spectral index βS = −3, consistent with measurements made in local galaxies taking account the spinning dust emission. For a constant q70, our model added to the active galactic nucleus (AGN) contribution provides a good fit to the extragalactic number counts from 24 μm to 408 MHz, and to the cosmic background intensity in the far- and mid-IR. The spinning dust emission accounts for up to 20% of the cosmic microwave background produced by star-forming galaxies, but for only less than 10% of the total background when AGN are included. The star-forming galaxies account for 77.5% of the number counts at 1.4 GHz for a flux of 100 μJy. However, the model falls short of reproducing the cosmic radio background measured with the ARCADE2 balloon-borne experiment. Considering the case when q70 decreases strongly with redshift, this still does not explain the ARCADE2 measurements. It also yields to an overestimate of the low-flux number counts in the radio. As a result, we rule out a steep variation of q70 with the redshift at least for z ⩽ 3.5 . Then, adding a population of faint star-forming galaxies at high redshift (LIR ⩽ 1011 L⊙ and 4 ⩽ z ⩽ 6), which would be able to reproduce the ARCADE2 measurements, leads to predictions of the cosmic IR background much higher than what is currently observed, ruling out this as the explanation for the ARCADE2 results. Considering our findings and previous studies of the diffuse extragalactic radio emission, we conclude that if the radio emission measured by ARCADE2 is astrophysical in origin, it has to originate in the Galaxy or to originate in a new kind of radio sources (with no mid- to far-IR counterparts) or emission mechanism still to be discovered.
Key words: galaxies: evolution / cosmic background radiation / infrared: galaxies / radio continuum: galaxies
© ESO, 2012
1. Introduction
The extragalactic background light or cosmic background is dominated by the cosmic microwave background (CMB), a relic of the evolution of the early Universe. The remainder of the background is directly linked to the formation and evolution of all the galaxies in the Universe apart from our Galaxy. Even if less energetic, this background can teach us a lot about galaxy evolution throughout time and can be separated into five components: the X- and γ-ray backgrounds, the cosmic optical background, the cosmic infrared background (CIB), and the cosmic radio background (CRB). The CIB is produced by the emission of dust illuminated by the stars contained in infrared (IR) or dusty star-forming galaxies. The evolution of these galaxies is well constrained by direct measurements of the CIB, galaxy number counts from the mid- to the far-IR, and redshift distribution of galaxies. Star-forming galaxies are also expected to emit at radio frequencies because the stars they contain can ionise their gas content and thus produce free-free emission. Eventually, these stars will evolve into supernovae leading to synchrotron emission. Anomalous microwave emission (AME), assumed to be produced by spinning dust grains (Planck Collaboration 2011d,a), may also arise from dusty star-forming galaxies. The exact intensity and evolution of radio emission from star-forming galaxies is still a matter of debate.
Recent measurements of the CRB made by Fixsen et al. (2011) with the ARCADE2 experiment have renewed the interest in the contribution of star-forming galaxies at microwave wavelengths. Indeed, Fixsen et al. (2011) measured a background between 3 and 10 GHz that is at least 5σ above the CMB temperature estimated by COBE/FIRAS. Investigations made by Singal et al. (2010) showed that standard extragalactic radio sources cannot account for this radio excess and they concluded that it has to come from star-forming galaxies. However, up till now, no extragalactic source evolution model has been able to explain this excess (Massardi et al. 2010; Singal et al. 2010; Vernstrom et al. 2011; Ponente et al. 2011; Draper et al. 2011). Our aim is to provide a comprehensive evolution model of star-forming galaxies able to reproduce all the observations, cosmic background intensity and extragalactic number counts, from the mid-IR to the radio. To do so, we use the most up-to-date galaxy evolution models for both star-forming galaxies (Béthermin et al. 2011) and radio-loud active galactic nuclei (AGN; de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). Then, we test several hypothesis to try to explain the excess measured by the ARCADE2 team: extragalactic spinning dust emission? Variation of the well-known far-IR/radio flux ratio with redshift? Additional population of faint star-forming galaxies at high redshift?
The paper is organised as follows. Section 2 describes the evolution model of dusty star-forming galaxies we use, as well as the emission components added to explain radio emission (synchrotron, free-free, spinning dust). The models for the radio-loud AGN are described in Sect. 3. Our results are then presented in Sect. 4. Finally we give our conclusions in Sect. 5.
2. Evolution model for dusty star-forming galaxies
2.1. Luminosity function evolution and IR spectral energy distributions
We used the recent model of Béthermin et al. (2011) to compute the number counts of dusty star-forming galaxies at the radio wavelengths. Two ingredients come into play: the spectral energy distribution (SED) of galaxies and the luminosity function (LF) evolution.
The SEDs, from 4 μm to 1 mm, are from the template library of Lagache et al. (2004), which consists of two galaxy populations. First, a star-forming galaxy population with SEDs that vary with IR bolometric luminosities. Second, a normal-galaxy population with a fixed template SED that is colder than the star-forming galaxy templates. The normal and star-forming galaxies are dominant at low- and high-luminosity, respectively. The fraction of each galaxy population as a function of the bolometric luminosity is given by a smooth function ![\begin{equation} \label{eq:mixpop} \frac{\Phi_{\rm starburst}}{\Phi} = \frac{1+th \left[ {\rm log}_{10}(L_{\rm IR}/L_{\rm pop}) /\sigma_{\rm pop} \right ]}{2}, \end{equation}](/articles/aa/full_html/2012/11/aa20068-12/aa20068-12-eq9.png) (1)where th is the hyperbolic tangent function, Lpop the luminosity at which the number of normal and star-forming galaxies are equal, and σpop characterises the width of the transition between the two populations. At LIR = Lpop, the starbursts fraction is 50%.
(1)where th is the hyperbolic tangent function, Lpop the luminosity at which the number of normal and star-forming galaxies are equal, and σpop characterises the width of the transition between the two populations. At LIR = Lpop, the starbursts fraction is 50%.
Béthermin et al. (2011) assume that the luminosity function (LF) is a classical double exponential function: ![\begin{equation} \label{eq:lf} \Phi(L_{\rm IR}) = \Phi^\star \, \times \left( \frac{L_{\rm IR}}{L^\star} \right)^{1-\alpha} \, \times \exp \left[ -\frac{1}{2\sigma^2} {\rm log}_{10}^2 \left(1+\frac{L_{\rm IR}}{L^\star}\right) \right], \end{equation}](/articles/aa/full_html/2012/11/aa20068-12/aa20068-12-eq14.png) (2)where Φ(LIR) is the number of sources per logarithm of luminosity, and per comoving volume unit for an infrared bolometric luminosity LIR. Φ ⋆ is the normalisation constant characterising the density of sources, L ⋆ is the characteristic luminosity at the break, and 1 − α and 1 − α − 1/σ2/ln2(10) are the slopes of the asymptotic power-law behaviour at low- and high-luminosity respectively. To reproduce the observations in the infrared, Béthermin et al. (2011) allow the parameters of the LF to vary with redshift. In order to limit the number of free parameters and to avoid strong degeneracies, α and σ are fitted as constants with z. A continuous LF redshift-evolution in luminosity and density is assumed following broken power-laws: L⋆ ∝ (1 + z)rL and Φ⋆ ∝ (1 + z)rΦ, where rL and rφ are parameters driving the evolution in luminosity and density, respectively. It is impossible to reproduce the evolution of the LF with constant rL and rφ. Béthermin et al. (2011) consequently allow their value to change at two specific redshifts: three different values of rL and rφ are used at low redshift (0 < z < zbreak), intermediate redshift (zbreak < z < 2), and high redshift (z > 2). The position of the first redshift break is a free parameter and converges to the same final value (zbreak ~ 0.9) for initial values 0 < z < 2. The second break does not appear naturally in the fitting procedure and is fixed at z = 21.
(2)where Φ(LIR) is the number of sources per logarithm of luminosity, and per comoving volume unit for an infrared bolometric luminosity LIR. Φ ⋆ is the normalisation constant characterising the density of sources, L ⋆ is the characteristic luminosity at the break, and 1 − α and 1 − α − 1/σ2/ln2(10) are the slopes of the asymptotic power-law behaviour at low- and high-luminosity respectively. To reproduce the observations in the infrared, Béthermin et al. (2011) allow the parameters of the LF to vary with redshift. In order to limit the number of free parameters and to avoid strong degeneracies, α and σ are fitted as constants with z. A continuous LF redshift-evolution in luminosity and density is assumed following broken power-laws: L⋆ ∝ (1 + z)rL and Φ⋆ ∝ (1 + z)rΦ, where rL and rφ are parameters driving the evolution in luminosity and density, respectively. It is impossible to reproduce the evolution of the LF with constant rL and rφ. Béthermin et al. (2011) consequently allow their value to change at two specific redshifts: three different values of rL and rφ are used at low redshift (0 < z < zbreak), intermediate redshift (zbreak < z < 2), and high redshift (z > 2). The position of the first redshift break is a free parameter and converges to the same final value (zbreak ~ 0.9) for initial values 0 < z < 2. The second break does not appear naturally in the fitting procedure and is fixed at z = 21.
The model has 13 free parameters that were determined by fitting the model to published measurements of galaxy number counts and monochromatic LF measured at given redshifts:
-
Number counts: Spitzer counts at 24, 70 and160 μm, Herschel counts at 250, 350 and 500 μm, and AzTEC counts at 1.1 mm.
-
Monochromatic LFs: IRAS local LF at 60 μm, Spitzer LF at 24 μm at z = 0, at 15 μm at z = 0.6, at 12 μm at z = 1, and at 8 μm at z = 2.
-
FIRAS CIB spectrum between 200 μm and 2 mm.
The best-fit parameters, as well as their uncertainties and degeneracies, were obtained using a Monte Carlo Markov chain (MCMC) Metropolis-Hastings algorithm. The model is adjusted to reproduce deep counts and monochromatic LFs at key wavelengths. It also reproduces recent observations that constrain very well the models, such as the Jauzac et al. (2011) measured redshift distribution of the CIB.
We used the so-called mean model, which is obtained using the mean value of the parameters as given in Béthermin et al. (2011) with the lensing contribution that is available on the http://www.ias.u-psud.fr/irgalaxies/ web page.
The SED templates of Lagache et al. (2004) used in Béthermin et al. (2011) stop at λ = 1 mm. To predict the number counts and cosmic background at radio wavelengths of dusty star-forming galaxies, we need to extrapolate the SED templates into the radio domain. We consider three emission components: synchrotron (Sect. 2.2), free-free (Sect. 2.3), and spinning dust (Sect. 2.4).
2.2. Synchrotron
Synchrotron emission is produced by relativistic electrons interacting with a magnetic field. At first order, its emissivity can be expressed as a power-law: ϵS(ν) ∝ νβS. Using WMAP intensity and polarisation data, Miville-Deschênes et al. (2008) measured a spectral index βS = −3.0 ± 0.06 in our Galaxy between 408 MHz and 23 GHz, in agreement with previous measurements by Giardino et al. (2002) and Platania et al. (2003). In the nearby spiral galaxy M33, Tabatabaei et al. (2007) showed that, even if the synchrotron spectrum hardens from the outer parts of the galaxy to the star-forming regions, a constant emissivity spectral index, βS = −2.953 ± 0.285, is appropriate for global studies. Similar values were found by Peel et al. (2011) in three nearby star-forming galaxies (M82, NGC 253, and NGC 4945). Consequently, and for the sake of simplicity, we adopt a single power-law for the two galaxy templates of Lagache et al. (2003) with βS = −3.0.
The radio continuum and far-IR emissions are observed to be tightly correlated in external galaxies (Helou et al. 1985). This correlation is remarkable in the sense that it holds over five orders of magnitude of radio continuum luminosity (Yun et al. 2001), and both at the scale of an entire galaxy and at subgalactic scales (Tabatabaei et al. 2007; Hughes et al. 2006). The correlation is also observed in the Milky Way (Boulanger & Perault 1988) at large scale and down to a few parsecs scale (Zhang et al. 2010). Boulanger & Perault (1988) and Zhang et al. (2010) found that the far-IR/radio flux ratio, usually called q, has similar values in the Milky Way and in external galaxies. Because synchrotron is the dominant emission component at 1.4 GHz, we set its intensity using the far-IR/radio flux ratio, q70 = log (S70 μm/S1.4 GHz), of IR emission at 70 μm and radio emission at 1.4 GHz.
The possible evolution of q70 with redshift is still debated, some authors finding a constant relation (Ibar et al. 2008; Sargent et al. 2010), where others find a slow decrease with redshift (Seymour et al. 2009; Beswick et al. 2008; Ivison et al. 2010b). As a result, we will consider two cases in this paper. The first one assumes that the far-IR/radio flux ratio is constant over redshift and equal to q70 ~ 2.15 (Appleton et al. 2004; Frayer et al. 2006; Seymour et al. 2009). In the following, we will refer to it as case A. The resulting spectra for the normal spiral galaxy and starbust galaxy templates are displayed in Fig. 1. The second one assumes that the ratio evolves with redshift as q70(z) ~ 2.15−0.72log (1 + z). This relation comes from Seymour et al. (2009) and is the steepest that has been reported so far. We choose it to maximize the effect of varying q70 on extragalactic number counts. We will refer to it as case B. Case B will lead to a brighter synchrotron emission for high redshift and should consequently have a stronger impact on the prediction of the CRB than case A.
 |
Fig. 1 SED template for a galaxy with a bolometric luminosity of 1011 L⊙ (black line), contribution of IR dust emission (green line), free-free emission (blue line), synchrotron emission calculated for case A (cyan line), and spinning dust emission (red line). a) Normal spiral galaxy template. b) Star-forming galaxy template. |
2.3. Free-free
The free-free component is particularly difficult to estimate as it is never dominant at any wavelength. According to Peel et al. (2011) and Murphy et al. (2010), we model the free-free spectrum as a power-law with a spectral index βFF = −2.1. This value is similar to what is measured in our Galaxy (Miville-Deschênes et al. 2008; Dickinson et al. 2003). In previous studies, before anomalous microwave emission (or spinning dust) was observed in galaxies, the free-free intensity was often normalised to be equal to that of the synchrotron at about 30 GHz (Condon 1992; Ponente et al. 2011). This means that spinning dust emission was included in the free-free and/or synchrotron emission. However, the spectral shape of the spinning dust emission is a “bump” centred around 20–30 GHz while the free-free and synchrotron emissions span over a much broader range of frequencies. Thus, ignoring the spinning dust contribution can lead to a flatter spectral index for the free-free and/or synchrotron emissions that implies an overestimate of their intensity. Consequently, we use recent results taking into account spinning dust emission to normalise the free-free emission at 10 GHz. For the three nearby star-forming galaxies observed by Peel et al. (2011), the free-free emission is about half of that of the synchrotron at 10 GHz. Similar values are found in NGC 6946 by Murphy et al. (2010): the free-free intensity reaches about (52 ± 12)% of the synchroton intensity at 10 GHz throughout the galaxy. These values also match the observations of Tabatabaei et al. (2007) for M33. Consequently, we normalise the intensity of the free-free emission to be equal to 50% of the synchrotron at 10 GHz. The resulting spectra for the normal spiral galaxy and star-forming galaxy templates are displayed in Fig. 1 for case A.
2.4. Spinning dust emission
Anomalous microwave emission, peaking between 10 and 60 GHz, is observed everywhere in our Galaxy, from the Galactic plane (Planck Collaboration 2011a) to intermediate Galactic latitudes (Miville-Deschênes et al. 2008; Davies et al. 2006; Lagache 2003). AME is detected in various interstellar clouds from the most diffuse to dense molecular clouds (Planck Collaboration 2011d; Vidal et al. 2011; Casassus et al. 2008, 2006; Watson et al. 2005). Up to now, a few extragalactic detections have been reported in nearby star-forming galaxies (Peel et al. 2011; Murphy et al. 2010; Scaife et al. 2010) and in the Small Magellanic Cloud (Planck Collaboration 2011c; Bot et al. 2010). It is usually assumed that AME is due to the emission of rapidly rotating interstellar PAHs, the so-called spinning dust emission, as first suggested by Draine & Lazarian (1998). The rotation of the PAHs is driven by interactions with the interstellar gas particles and absorptions of UV/visible stellar photons. This means that any environment containing PAHs should emit in the microwave. The spectra of the dusty star-forming galaxies responsible for the CIB exhibit bands in the mid-IR (~3 to 20 μm) characteristic of the interstellar PAHs. Consequently, we add a spinning dust component to our galaxy templates to estimate its impact on the source counts and cosmic background intensity in the microwave and radio wavelengths.
The intensity and the peak frequency of the spinning dust spectrum depend on the strength of the interstellar radiation field heating the grains and on the local gas density and temperature (Draine & Lazarian 1998; Ysard et al. 2011). Thus, two parameters have to be set to determine the spinning dust component for star-forming galaxies: a mixture of environments and the radiation field intensity.
For the Milky Way, the component separation performed by Miville-Deschênes et al. (2008) using WMAP data allowed Ysard et al. (2010) to measure a ratio between the AME in the WMAP 23 GHz band and the PAH emission in the IRAS 12 μm band of L23 GHz/L12 μm = (5.36 × 10-3) ± (4 × 10-5) for the entire Galaxy. This ratio is valid for the radiation field illuminating our Galaxy. The intensity of the radiation field can be expressed in units of G0-factor, equal to 1 in the case of the interstellar standard radiation field (ISRF) illuminating the solar neighbourghood for which Boulanger et al. (1996) and Lagache et al. (1998) measured an average dust temperature of ~17.5 K. Using the FIRAS spectrum and the DIRBE 100 μm data averaged over the entire Galaxy, we determine the mean dust temperature of the Milky Way by fitting a modified blackbody with a constant spectral index β = 2 for 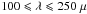 m. We find a dust temperature equal to TSED ~ 18 K leading to
m. We find a dust temperature equal to TSED ~ 18 K leading to 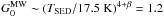 (Ysard et al. 2010). Then, we proceed to the same fitting procedure to get estimates of the intensities of the mean radiation fields required to explain the far-IR spectra of our galaxy templates. For normal spiral galaxies, we get G0 ~ 2 (TSED = 19.5 K), and for star-forming galaxies with bolometric luminosities of LIR = 1010, 1011, and 1012L⊙, we get G0 ~ 13, 22, and 45, respectively (TSED ~ 27, 29, and 33 K, respectively). Note that the exact β value and wavelength range used to compute the temperature are not critical as long as the same parameters are used for both the Galactic spectrum (the reference) and the extragalactic SED templates.
(Ysard et al. 2010). Then, we proceed to the same fitting procedure to get estimates of the intensities of the mean radiation fields required to explain the far-IR spectra of our galaxy templates. For normal spiral galaxies, we get G0 ~ 2 (TSED = 19.5 K), and for star-forming galaxies with bolometric luminosities of LIR = 1010, 1011, and 1012L⊙, we get G0 ~ 13, 22, and 45, respectively (TSED ~ 27, 29, and 33 K, respectively). Note that the exact β value and wavelength range used to compute the temperature are not critical as long as the same parameters are used for both the Galactic spectrum (the reference) and the extragalactic SED templates.
Then, the spectral shape of the spinning dust spectrum is determined with the spinning dust model described in Silsbee et al. (2011). We assume that the ISM of galaxies can be approximated with a mixture of environments (Dopita & Sutherland 2003; Cox 2005) composed by: 20% of warm ionised medium (WIM, with a proton density of nH = 0.1 cm-3), 20% of warm neutral medium (WNM, nH = 0.4 cm-3), 30% of cold neutral medium (CNM, nH = 30 cm-3), and 30% of molecular cloud (MC, nH = 300 cm-3), and illuminated by the ISRF scaled with the G0 values determined previously. Then, we integrate the galaxy template spectra in the IRAS 12 μm filter in order to normalise them to the L23 GHz/L12 μm ratio measured by Ysard et al. (2010) in the Milky Way. To take into account the lower 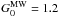 value measured in the Milky Way, we multiply the spinning dust spectrum by a factor equal to the ratio of the integrated intensity in the WMAP 23 GHz band of this spinning dust spectrum computed for a given G0 value and the same but computed for
value measured in the Milky Way, we multiply the spinning dust spectrum by a factor equal to the ratio of the integrated intensity in the WMAP 23 GHz band of this spinning dust spectrum computed for a given G0 value and the same but computed for 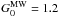 . This factor is equal to 1.00 in the case of normal spiral galaxies, and to 1.15, 1.28, and 1.45 for star-forming galaxies with bolometric luminosities of LIR = 1010, 1011, and 1012L⊙, respectively.
. This factor is equal to 1.00 in the case of normal spiral galaxies, and to 1.15, 1.28, and 1.45 for star-forming galaxies with bolometric luminosities of LIR = 1010, 1011, and 1012L⊙, respectively.
The resulting spectra are displayed in Fig. 1 for case A (constant q70). For normal spiral galaxies, the spinning dust emission at 23 GHz accounts for 31.7% of the total intensity. For star-forming galaxies with LIR = 1010, 1011, and 1012 L⊙, it accounts for 25.3%, 18.5%, and 12.8% of the total intensity, respectively. If q70 varies with the redshift (case B), the spinning dust component is then fully dominated by the synchrotron and free-free emissions.
3. Evolution model for the AGN-powered radio sources
The extragalactic radio number counts are dominated by radio-loud active galactic nuclei (AGN) for bright flux densities, S ≳ 1 mJy (Ibar et al. 2008; Condon 1992). These radio-loud AGN are also expected to account for about half of the surface brightness of the CRB (Massardi et al. 2010). To take into account the contribution of radio galaxies, we use two different models, depending on the frequency. For ν = 408 MHz, 610 MHz, 1.4 GHz, 2.7 GHz, 5 GHz, 15.7 GHz, 30 GHz, 44 GHz, and 70 GHz, we use the model of Massardi et al. (2010). For ν = 8.44 GHz, 20 GHz, 100 GHz, 143 GHz, and 214 GHz, we use the model C2Ex of Tucci et al. (2011).
These two models provide good fits to the extragalactic number counts in the radio but the model of Tucci et al. (2011) gives a better repartition of the counts between the flat- and steep-spectrum galaxies. The model of Massardi et al. (2010) assumes two flat-spectrum populations with different luminosity functions and one steep-spectrum population. For each population, they adopt a power-law spectrum Sν ∝ ν−α with α = 0.1 or α = 0.8. The model of Tucci et al. (2011) allows for a Gaussian distribution for the spectral indices. They also introduce an additional population with an inverted spectrum and define frequency breaks for the slopes of the flat-spectrum populations.
4. Results and discussion
4.1. Constant q70 and spinning dust emission (case A)
 |
Fig. 2 Differential extragalactic number counts (green triangles) for ν = 408 MHz a), 610 MHz b), 1.4 GHz c), 2.7 GHz d), 4.8−5 GHz e), 8.4 GHz f), 15 GHz g), 20 GHz h), 30 GHz i), 44 GHz j), 100 GHz k), 143−145−148 GHz l), 214−217 GHz m), 250 μm n), and 24 μm o). The counts are a compilation from several surveys (see Table 1 for references). The black solid and dashed lines are the predictions of our evolution model with and without spinning dust emission, respectively, in the case of a constant far-IR/radio flux ratio (see case A of Sect. 2.2) and using the LF-parameters of the mean model of Béthermin et al. (2011). The grey areas show the 1-σ error calculated from the MCMC fit of the LF by Béthermin et al. (2011). The dotted lines are the predictions of evolution models for radio-loud AGN as described in Sect. 3 (de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). The red lines show the sum of the contribution of radio-loud AGN and star-forming galaxies when spinning dust emission is included to the SED templates. |
The predictions for the differential extragalactic number counts in case A (constant q70, Sect. 2.2) are presented in Fig. 2. The contributions of both dusty star-forming galaxies and AGN are included (de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). For the dusty star-forming galaxies, Fig. 2 also presents the uncertainties on the counts calculated from the MCMC fit of the LF by Béthermin et al. (2011) in the case of the SEDs described in Sects. 2.3, 2.2, and 2.4.
In agreement with Massardi et al. (2010), we find that the low-flux bump of the counts in the radio (610 MHz and 1.4 GHz) can be accounted for by standard star-forming galaxies. Moreover, our model can explain all the galaxy number counts from the mid-IR (24 μm) to the radio (408 MHz). Our model shows that star-forming galaxies account for 84.5% of the extragalactic number counts at 1.4 GHz for a flux of 50 μJy and 77.5% for 100 μJy.
The CRB predicted by our model can be calculated by summing the galaxy number counts. The results are shown in Fig. 3 and the corresponding surface brightness from 408 MHz to 217 GHz are listed in Table 2. The contribution of star-forming galaxies to the CRB reaches 39.1% at 408 MHz, 37.2% at 610 MHz, and 32.2% at 1.4 GHz. These values are much higher than those found by Ponente et al. (2011), who used a model based on an empirical relation between the 1.4 GHz luminosity and the star formation rate density (SFRD). This discrepancy could be caused by the fact that these authors used a SFRD/radio conversion ratio that is the same for all redshifts. This ratio should rather be weighted by the luminosity of the galaxies that dominate the averaged SFRD at a given redshift. According to Lagache et al. (2004), the IR output energy is dominated by galaxies with bolometric luminosities around LIR ~ 8 × 1010L⊙ at z = 0, whereas it is dominated by galaxies with LIR ~ 3 × 1012L⊙ at z = 2. Furthermore, Ponente et al. (2011) do not consider spinning dust emission and assume slopes of β = −2.7 for the radio emission, respectively. For local galaxies, the measurements made taking into account the presence of spinning dust emission show that it is steeper with β ~−3.
As can be seen from Fig. 2, the contribution of spinning dust to the galaxy number counts is significant at 8.44, 15.7, 20, and 30 GHz. However, deeper surveys would be required to validate the model in this frequency range as the star-forming galaxies dominate the counts only for S ~ 10μJy, where no data are available. Then, spinning dust emission accounts for about 10 to 20% of the cosmic background produced by star-forming galaxies in the microwave (14.8% at 8.44 GHz, 21.6% at 15.7 GHz, 19.8% at 20 GHz, and 11.1% at 30 GHz). However, this represents only less than 10% of the total background when AGN are included (5.1% at 8.44 GHz, 8.5% at 15.7 GHz, 8.3% at 20 GHz, and 5% at 30 GHz).
Finally, Fig. 3 shows that even if our model is able to reproduce all the galaxy number counts and the cosmic background in the mid- and far-IR, it cannot explain the excess radio emission reported by ARCADE2 (Fixsen et al. 2011).
4.2. Evolution of q70 with redshift (case B)
 |
Fig. 3 Cosmic background spectrum predicted by our model for dusty star-forming and normal spiral galaxies without (dotted line) and with (dashed line) spinning dust emission. The solid line shows the spectrum when the contribution of radio-loud AGN is included (de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). The blue triangles show direct measurements of the CRB obtained by ARCADE2 (Fixsen et al. 2011) and older surveys reprocessed using the model developed by the ARCADE2 team to measure the CRB (408 MHz and 1.4 GHz). The green triangles show direct measurements of the CIB at 250, 350, and 500 μm using FIRAS data processed as in Lagache et al. (1999). The red triangle shows the CIB measured in the MIPS 24 μm band by Béthermin et al. (2010). |
Surface brightness of the cosmic background for case A (first column), contribution of AGN (second column), and contribution of the IR galaxies (third column).
 |
Fig. 4 Differential extragalactic number counts (green triangles) for ν = 610 MHz a) and 1.4 GHz b), in the case of a variable far-IR/radio flux ratio q70(z) = 2.15−0.72log (1 + z) (see case B in Sect. 2.2). |
The predictions of the differential extragalactic number counts for case B (q70 decreasing with redshift, see Sect. 2.2) are presented in Fig. 4 at 610 MHz and 1.4 GHz. As expected, allowing q70 to vary increases the radio emissivity of star-forming galaxies and leads to an increase in the CRB of about 70%, which is however still not enough to explain ARCADE2 data: ARCADE measurements are still greater than the model predictions by a factor of 5 at 408 MHz and of 11.4 at 1.4 GHz. Then, case B yields an overestimate of the galaxy counts in the radio range (Fig. 4). This suggests that the far-IR/radio flux ratio should rather be constant or at least decrease less rapidly with redshift as suggested by Ivison et al. (2010b). According to the compilation of data made by Ponente et al. (2011, see their Fig. 1), it seems reasonable to consider that the far-IR/radio ratio is constant at first order for z ≲ 3.5 (Bell 2003; Murphy 2009; Ivison et al. 2010a,b; Michałowski et al. 2010; Sargent et al. 2010; Bourne et al. 2011).
We test the case of star-forming galaxies having the properties of case A for 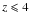 and an enhanced radio emission above. The value of
and an enhanced radio emission above. The value of 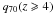 needs to be equal to ~0 for the model predictions to reach the ARCADE2 radio excess. However, this again yields to an overestimate of the galaxy counts in the radio range, even worse than for case B. As a result, even if the far-IR/radio flux ratio decreases only for high redshift, it cannot explain ARCADE2 excess without being in contradiction with extragalactic number counts.
needs to be equal to ~0 for the model predictions to reach the ARCADE2 radio excess. However, this again yields to an overestimate of the galaxy counts in the radio range, even worse than for case B. As a result, even if the far-IR/radio flux ratio decreases only for high redshift, it cannot explain ARCADE2 excess without being in contradiction with extragalactic number counts.
4.3. An additional population of faint galaxies at high redshift?
 |
Fig. 5 a)–c) Differential extragalactic number counts at 1.4 GHz, 250 μm, and 24 μm (linestyles and symbols are the same as in Fig. 2) predicted by our model when a population of faint galaxies is added at high redshift (see Sect. 4.3 for details). d) Corresponding cosmic background. Linestyles are the same as in Fig. 3. |
If we suppose that the radio excess observed by ARCADE2 originates in star-forming galaxies, then the only remaining way to increase the CRB is to consider an additional population of faint IR galaxies at high redshift. It is important to consider faint and not bright galaxies not to disrupt the galaxy number counts and also because we do not expect a large amount of bright galaxies to be undetected even at high redshift.
We use the galaxy templates of case A (Sect. 2.2) and start with the luminosity functions of Béthermin et al. (2011). We multiply them by a constant for 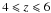 and for
and for 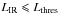 . The lowest Lthres allowing to reproduce the ARCADE2 radio excess is Lthres = 1011L⊙. For lowest threshold luminosities, it is not possible to fit simultaneously the background surface brightness at 408 MHz and 5 GHz. Higher threshold luminosities predict too many galaxy number counts at low flux (
. The lowest Lthres allowing to reproduce the ARCADE2 radio excess is Lthres = 1011L⊙. For lowest threshold luminosities, it is not possible to fit simultaneously the background surface brightness at 408 MHz and 5 GHz. Higher threshold luminosities predict too many galaxy number counts at low flux (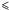 1 mJy) that we ruled out by current observational constraints. The model predictions for Lthres = 1011L⊙ are presented in Fig. 5. The increase in the luminosity function required to match the ARCADE2 excess overproduces the CIB by a factor of 4.6 at 24 μm, 8.5 at 250 μm, 11.6 at 350 μm, and 21.5 at 500 μm. We conclude that a population of faint galaxies at high redshift able to account for the radio excess reported by ARCADE2 is ruled out by direct measurements of the CIB.
1 mJy) that we ruled out by current observational constraints. The model predictions for Lthres = 1011L⊙ are presented in Fig. 5. The increase in the luminosity function required to match the ARCADE2 excess overproduces the CIB by a factor of 4.6 at 24 μm, 8.5 at 250 μm, 11.6 at 350 μm, and 21.5 at 500 μm. We conclude that a population of faint galaxies at high redshift able to account for the radio excess reported by ARCADE2 is ruled out by direct measurements of the CIB.
5. Conclusions
The aim of this paper was to check if star-forming galaxies could be responsible for the radio excess reported by Fixsen et al. (2011) in the CRB with ARCADE2 data. To do so, using up-to-date detailed star-forming and radio galaxy evolution models, we considered three scenarios: (i) contribution of spinning dust emission; (ii) variation with redshift of the far-IR/radio flux ratio; and (iii) additional population of faint IR galaxies at high redshift.
-
(i)
Our model, including the contribution of synchrotron, free-free, and spinning dust emissions, and considering a constantfar-IR/radio flux ratio, accounts for all the extragalactic numbercounts from the mid-IR to the radio (24 μm to 408 MHz). It also accounts for the cosmic background in the mid- and far-IR. However, it does not reproduce the ARCADE2 excess. We note that our model agrees with the findings of Zannoni et al. (2008), Gervasi et al. (2008b), and Tartari et al. (2008), who could explain the TRIS observations with no need for an excess in the radio range (600 MHz, 820 MHz, and 2.5 GHz). Our model also accounts for the CRB intensity as estimated by Wall et al. (1970) at 320 and 707 MHz. Finally, we confirm that radio-loud AGN dominate the counts for
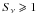 mJy (Ibar et al. 2008).
mJy (Ibar et al. 2008). -
(ii)
In order to increase the radio emission of the star-forming galaxies, we considered a possible decrease in the far-IR/radio flux ratio, q70, with redshift. The steepest relation available in the litterature does not yield an acceptable fit to the extragalactic number counts at 610 MHz and 1.4 GHz. We conclude that varying q70 with redshift cannot explain the ARCADE2 radio excess. These two results suggest that the far-IR/radio flux ratio should rather be constant, or at least decrease less rapidly with redshift than what was measured by Seymour et al. (2009).
-
(iii)
Finally, we tested the hypothesis of an additional population of faint star-forming galaxies at high redshift. We show that the amount of faint galaxies required to explain the ARCADE2 radio excess leads to a predicted CIB much higher than what is actually observed at 250, 350, and 500 μm.
Consequently, we exclude the star-forming galaxies as the origin of the ARCADE2 radio excess. Furthermore, Singal et al. (2010) investigated the contribution to the CRB of radio-quiet quasars, radio supernovae, emission from hot gas in galaxy clusters, and diffuse emission from regions far from galaxies. They found that they cannot account for more than about 10% of the excess. Considering our results, and the results of Singal et al. (2010), we conclude that if the radio excess reported by Fixsen et al. (2011) is astrophysical, it has to have a Galactic origin or to originate in a new kind of radio sources (with no mid- to far-IR counterparts) or emission mechanism still to be discovered.
Numerical values and details about the fitting procedure are given in Béthermin et al. (2011).
Acknowledgments
We thank our anonymous referee for useful comments. We also thank M. Béthermin for his help and making his model available. We thank H. Dole, M. Zannoni, M. Tucci, and N. Seymour for useful discussions and making their data and models available. We are also grateful to D. Dicken for his help concerning the English language! N.Y. acknowledges the support of a CNES post-doctoral research grant.
References
- AMI Consortium, Davies, M. L., Franzen, T. M. O., et al. 2011, MNRAS, 415, 2708 [Google Scholar]
- Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS, 154, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
- Beswick, R. J., Muxlow, T. W. B., Thrall, H., Richards, A. M. S., & Garrington, S. T. 2008, MNRAS, 385, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Dole, H., Beelen, A., & Aussel, H. 2010, A&A, 512, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Lagache, G., Le Borgne, D., & Penin, A. 2011, A&A, 529, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Le Floc’h, E.,Ilbert, O., et al. 2012, A&A, 542, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulanger, F., & Perault, M. 1988, ApJ, 330, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Reach, W. T., Abergel, A., et al. 1996, A&A, 315, L325 [NASA ADS] [Google Scholar]
- Bourne, N., Dunne, L., Ivison, R. J., et al. 2011, MNRAS, 410, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Cabrera, G. F., Förster, F., et al. 2006, ApJ, 639, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Dickinson, C., Cleary, K., et al. 2008, MNRAS, 391, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Davies, R. D., Dickinson, C., Banday, A. J., et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- de Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 2003, Astrophysics of the diffuse universe [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Draper, A. R., Northcott, S., & Ballantyne, D. R. 2011, ApJ, 741, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J., Kogut, A., Levin, S., et al. 2011, ApJ, 734, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Fadda, D., Yan, L., et al. 2006, AJ, 131, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Gervasi, M., Tartari, A., Zannoni, M., Boella, G., & Sironi, G. 2008a, ApJ, 682, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Gervasi, M., Zannoni, M., Tartari, A., Boella, G., & Sironi, G. 2008b, ApJ, 688, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Giardino, G., Banday, A. J., Górski, K. M., et al. 2002, A&A, 387, 82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Hughes, A., Wong, T., Ekers, R., et al. 2006, MNRAS, 370, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Ibar, E., Cirasuolo, M., Ivison, R., et al. 2008, MNRAS, 386, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Alexander, D. M., Biggs, A. D., et al. 2010a, MNRAS, 402, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Magnelli, B., Ibar, E., et al. 2010b, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jauzac, M., Dole, H., Le Floc’h, E., et al. 2011, A&A, 525, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagache, G. 2003, A&A, 405, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagache, G., Abergel, A., Boulanger, F., & Puget, J.-L. 1998, A&A, 333, 709 [NASA ADS] [Google Scholar]
- Lagache, G., Puget, J.-L., & Gispert, R. 1999, Ap&SS, 269, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Dole, H., Puget, J.-L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Marriage, T. A., Baptiste Juin, J., Lin, Y.-T., et al. 2011, ApJ, 731, 100 [Google Scholar]
- Massardi, M., Bonaldi, A., Negrello, M., et al. 2010, MNRAS, 404, 532 [NASA ADS] [Google Scholar]
- Michałowski, M., Hjorth, J., & Watson, D. 2010, A&A, 514, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Ysard, N., Lavabre, A., et al. 2008, A&A, 490, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J. 2009, ApJ, 706, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Condon, J. J., et al. 2010, ApJ, 709, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Peel, M. W., Dickinson, C., Davies, R. D., Clements, D. L., & Beswick, R. J. 2011, MNRAS, 416, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Platania, P., Burigana, C., Maino, D., et al. 2003, A&A, 410, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponente, P. P., Ascasibar, Y., & Diego, J. M. 2011, MNRAS, 418, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Schinnerer, E., Murphy, E., et al. 2010, ApJS, 186, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Scaife, A. M. M., Nikolic, B., Green, D. A., et al. 2010, MNRAS, 406, L45 [NASA ADS] [Google Scholar]
- Seymour, N., Huynh, M., Dwelly, T., et al. 2009, MNRAS, 398, 1573 [Google Scholar]
- Silsbee, K., Ali-Haïmoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]
- Singal, J., Stawarz, Ł., Lawrence, A., & Petrosian, V. 2010, MNRAS, 409, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Beck, R., Krügel, E., et al. 2007, A&A, 475, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tartari, A., Zannoni, M., Gervasi, M., Boella, G., & Sironi, G. 2008, ApJ, 688, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci, M., Toffolatti, L., de Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernstrom, T., Scott, D., & Wall, J. V. 2011, MNRAS, 415, 3641 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, M., Casassus, S., Dickinson, C., et al. 2011, MNRAS, 414, 2424 [NASA ADS] [CrossRef] [Google Scholar]
- Vieira, J. D., Crawford, T. M., Switzer, E. R., et al. 2010, ApJ, 719, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Wall, J. V., Chu, T. Y., & Yen, J. L. 1970, Aust. J. Phys., 23, 45 [NASA ADS] [Google Scholar]
- Watson, R. A., Rebolo, R., Rubiño-Martín, J. A., et al. 2005, ApJ, 624, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Miville-Deschênes, M. A., & Verstraete, L. 2010, A&A, 509, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Juvela, M., & Verstraete, L. 2011, A&A, 535, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Zannoni, M., Tartari, A., Gervasi, M., et al. 2008, ApJ, 688, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Hopkins, A., Barnes, P. J., et al. 2010, PASA, 27, 340 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Surface brightness of the cosmic background for case A (first column), contribution of AGN (second column), and contribution of the IR galaxies (third column).
All Figures
 |
Fig. 1 SED template for a galaxy with a bolometric luminosity of 1011 L⊙ (black line), contribution of IR dust emission (green line), free-free emission (blue line), synchrotron emission calculated for case A (cyan line), and spinning dust emission (red line). a) Normal spiral galaxy template. b) Star-forming galaxy template. |
| In the text | |
 |
Fig. 2 Differential extragalactic number counts (green triangles) for ν = 408 MHz a), 610 MHz b), 1.4 GHz c), 2.7 GHz d), 4.8−5 GHz e), 8.4 GHz f), 15 GHz g), 20 GHz h), 30 GHz i), 44 GHz j), 100 GHz k), 143−145−148 GHz l), 214−217 GHz m), 250 μm n), and 24 μm o). The counts are a compilation from several surveys (see Table 1 for references). The black solid and dashed lines are the predictions of our evolution model with and without spinning dust emission, respectively, in the case of a constant far-IR/radio flux ratio (see case A of Sect. 2.2) and using the LF-parameters of the mean model of Béthermin et al. (2011). The grey areas show the 1-σ error calculated from the MCMC fit of the LF by Béthermin et al. (2011). The dotted lines are the predictions of evolution models for radio-loud AGN as described in Sect. 3 (de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). The red lines show the sum of the contribution of radio-loud AGN and star-forming galaxies when spinning dust emission is included to the SED templates. |
| In the text | |
 |
Fig. 3 Cosmic background spectrum predicted by our model for dusty star-forming and normal spiral galaxies without (dotted line) and with (dashed line) spinning dust emission. The solid line shows the spectrum when the contribution of radio-loud AGN is included (de Zotti et al. 2005; Massardi et al. 2010; Tucci et al. 2011). The blue triangles show direct measurements of the CRB obtained by ARCADE2 (Fixsen et al. 2011) and older surveys reprocessed using the model developed by the ARCADE2 team to measure the CRB (408 MHz and 1.4 GHz). The green triangles show direct measurements of the CIB at 250, 350, and 500 μm using FIRAS data processed as in Lagache et al. (1999). The red triangle shows the CIB measured in the MIPS 24 μm band by Béthermin et al. (2010). |
| In the text | |
 |
Fig. 4 Differential extragalactic number counts (green triangles) for ν = 610 MHz a) and 1.4 GHz b), in the case of a variable far-IR/radio flux ratio q70(z) = 2.15−0.72log (1 + z) (see case B in Sect. 2.2). |
| In the text | |
 |
Fig. 5 a)–c) Differential extragalactic number counts at 1.4 GHz, 250 μm, and 24 μm (linestyles and symbols are the same as in Fig. 2) predicted by our model when a population of faint galaxies is added at high redshift (see Sect. 4.3 for details). d) Corresponding cosmic background. Linestyles are the same as in Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


