| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219737 | |
| Published online | 24 October 2012 | |
Hanle diagnostics of weak solar magnetic fields:
Inversion of scattering polarization in C2 and MgH molecular lines
1 Lagrange Laboratory, UMR 9273, Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Campus Valrose, 06108 Nice, France
e-mail: marianne.faurobert@unice.fr
2 Astronomical observatory Belgrade, Volgina 7, 11060 Belgrade, Serbia
e-mail: milic@aob.rs
Received: 1 June 2012
Accepted: 4 September 2012
Context. The quiet Sun magnetism has been intensively investigated in recent years by various observational techniques. But several issues, such as the question of the isotropy and of the energy density spectrum of the mixed polarity turbulent magnetic fields, are still under debate.
Aims. Here we present an inversion method that allows us to constrain the depth-dependence of the magnetic field strength. We use the center-to-limb variations of linear scattering polarization measured in molecular lines of C2 and MgH molecules with different sensitivities to the Hanle effect. We consider six C2-triplets and one MgH line in the spectral range between 515.7 nm and 516.1 nm observed with the THEMIS Telescope.
Methods. One of the delicate problems with Hanle diagnostics is to disentangle the effects of elastic depolarizing collisions from the depolarization due to the Hanle effect of the magnetic field. By making use of the different sensitivities of the molecular lines in our spectral range to microturbulent magnetic fields and, by using a non-LTE radiative transfer modeling of the line formation, we are able to determine both the depolarizing collision cross-section and the magnetic strength. We use a standard 1D quiet Sun atmospheric model and we invert the full set of center-to-limb polarization rates measured at line centers, with a depth-dependent magnetic field described by three free parameters. The depolarizing collision cross-section is also treated as a free parameter. A downhill simplex method is used to find the best-fitting values for the collisional and magnetic strength parameters.
Results. For the elastic depolarizing collisions cross-section for the C2 lines we obtain α(2) = 1.6 ± 0.4 × 10-9 cm3 s-1, which is within an order of magnitude of the value previously obtained for MgH lines from a differential Hanle effect analysis. The observational constraints provided by the MgH and C2 line polarization give access to the altitude range between z = 200 km and z = 400 km above the base of the photosphere. We find that the turbulent magnetic field strength decreases from 95 Gauss at the altitude z = 200 km to 5 Gauss at z = 400 km.
Conclusions. The turbulent magnetic field strength that we derive from the Hanle effect shows a strong vertical gradient in the upper photosphere. We point out that this behavior may explain why very different turbulent magnetic field strengths have been inferred from the interpretation of Hanle depolarization when using different lines formed at different altitudes. We notice that the presence of a strong depth gradient is not compatible with the assumption of isotropy of the turbulent field.
Key words: line: formation / techniques: spectroscopic / Sun: photosphere
© ESO, 2012
1. Introduction
The Hanle effect is an important tool for determining quiet Sun magnetic fields. Microturbulent (i.e. weak and unresolved) magnetic fields decrease the linear polarization that appears in spectral lines formed by scattering of photons, allowing us to estimate the magnetic field strength from the observations of the so-called “second solar spectrum”. Apart from microturbulent magnetic fields, lines may also be depolarized by elastic collisions. However, for most transitions, depolarizing elastic collision cross-sections are not known. In this paper we also address that issue.
Analysis of linear polarization in molecular lines has proved to be a useful diagnostic tool by applying the so-called differential Hanle effect method (Berdyugina & Fluri 2004; Bommier et al. 2006; Kleint et al. 2010, 2011). This procedure relies on comparing the polarization in lines of the same species, formed in the same physical conditions, but with different sensitivities to the magnetic field, i.e. with different Landé factors. Molecular lines of MgH and C2 should be a convenient choice for this procedure, because they are numerous in the range between 500 nm and 520 nm and show significant linear polarization close to the solar limb. Some of these lines have already been studied by Berdyugina et al. (2002) and Berdyugina & Fluri (2004), but without taking depolarizing collisions into account. However, when interpreting on-the-limb observations, those collisions are an important effect to consider. Ignoring depolarizing collisions would lead to a significant overestimation of the magnetic field strength as shown in Bommier et al. (2006). Furthermore, the C2 and MgH lines we are considering are not optically thin lines, so implementing the differential Hanle effect method requires solving polarized radiative transfer equations for each of them using a prescribed atmospheric model. We also take sphericity effects into account, which play an important role in interpreting observations performed very close to the solar limb, typically closer than 5 arcsec (see Milić & Faurobert 2012).
THEMIS observations, presented in Faurobert & Arnaud (2003) provide us with measurements of the linear polarization in the wavelength range between 515.6 nm and 516.2 nm, containing two lines of MgH and six triplets of C2, at nine positions between 40′′ and 1′′ inside the solar limb. We stress that these observations have been performed with the spectrograph slit oriented at 45° with respect to the solar South pole, intercepting the limb, so that all the limb distances were recorded at once and are known precisely. In this paper we take advantage of the different sensitivities of the lines to the Hanle effect to obtain constraints on both the depth variations of the turbulent magnetic fields and the depolarizing collision cross-section for the C2 lines. This is performed through an inversion procedure of the observations based on NLTE radiative transfer modeling of the molecular lines, in a quiet Sun 1D-spherical atmospheric model with a depth-dependent turbulent magnetic field lying in the horizon plane, with a random azimuth. The mean magnetic strength at z = 200 km, z = 300 km, and z = 400 km are three free parameters. We assume that magnetic field strength varies linearly with depth in between these three altitudes and that it is constant below z = 200 km and above z = 400 km. The depolarizing collision cross-section for the C2 lines is the fourth free parameter of our model. For the MgH line, we use the collisional cross-section previously derived by Bommier et al. (2006). A simplex minimization procedure is applied in order to determine the values of the parameters leading to the best fit between the observed and computed polarization rates at line centers for all the nine positions with respect to the solar limb.
We recall that depolarizing collision cross-sections are very difficult to derive from the quantum mechanical calculations of collisions. The differential Hanle effect is thus a valuable tool for estimating these quantities from the observed polarization rates in several lines of the same branch. Writing the depolarizing collision rate as D(2) = nHα(2), where nH denotes the hydrogen density, we find that α(2) = 1.6 ± 0.4 × 10-9 cm3 s-1 for the C2 lines of our wavelength range. This is in excellent agreement with the previous determination that we performed in Milić & Faurobert (2012), using observations presented in Gandorfer’s Atlas (Gandorfer 2000) of the second solar spectrum, where we found α(2) ≈ 1.7 × 10-9 cm3 s-1. We find that the microturbulent magnetic field strength shows a strong vertical gradient in the upper photosphere, where it decreases from ≈ 95 Gauss, at 200 km above the photosphere base, to ≈ 5 Gauss at the height of 400 km. We compare this behavior with the results of previous works relying on the Hanle effect in C2 and MgH lines, which resulted in different magnetic field strengths, ranging from a few Gauss to a few tens of Gauss (Berdyugina & Fluri 2004; Bommier et al. 2006; Asensio Ramos & Trujillo Bueno 2005). We show that this may be understood simply by considering that the various lines are formed at different depths in the photosphere where the magnetic strength takes very different values. We discuss this strong vertical gradient and show that such a decreasing magnetic field cannot be isotropic.
2. Method
In this paper we consider six C2 triplets belonging to the P branch of the d3Πg − a3Πu electronic transition, in the spectral range between 515.7 nm and 516.1 nm. In the same spectral region there are also two MgH lines belonging to the Q branch of A2Π − X2Σ + electronic transition. To self-consistently model the radiative transfer in the lines, we use the same approach as Milić & Faurobert (2012). We now briefly describe the method again.
2.1. Polarized radiative transfer
The polarized NLTE radiative transfer problem consists of solving the coupled equation of radiative transfer and equation of statistical equilibrium for a two-level atom. This problem can be efficiently solved by first using some fast method to solve the NLTE scalar unpolarized problem and then solving the coupled equations in turn until convergence (i.e. by doing Λ iteration for the polarization). For the first step we use “forth-and-back” implicit lambda iteration method by Atanacković-Vukmanović et al. (1997). A further simplification for this part is that solar sphericity is only important for rays that do not intersect the solar disk, so one can use a plane-parallel model. For the second step we use an along-the-ray approach to perform a formal solution of the radiative transfer equation. Detailed equations are given in Milić & Faurobert (2012). We recall that the source function for the linear polarization Stokes parameter Q, depends on two factors, namely, the collisional depolarization parameter Wc and the Hanle depolarization parameter WH in the following way: ![\begin{eqnarray} S^Q(\mu,\nu) & = & \frac{1}{2} W_2 W_{\rm c} W_{\rm H} (1-\epsilon) \nonumber\\ &&\times \!\int_{-1}^{1} \! \int_0^{\infty}\left[P_{21}I(\mu',\nu') + P_{22}Q(\mu',\nu')\right]\varphi_{\nu'}{\rm d}\nu' {\rm d}\mu'. \end{eqnarray}](/articles/aa/full_html/2012/11/aa19737-12/aa19737-12-eq26.png) (1)Here ϕν′ is the line absorbtion profile (taken to be same as the line emission profile, since complete frequency redistribution approximation is valid for these weak lines), and P21 and P22 are elements of the Raighley’s scattering matrix. The photon destruction probability is denoted by ϵ and is given by ϵ = Cul/(Aul + Cul) where Aul and Cul are the Einstein coefficient of spontaneous emission and upper level collisional lifetime, respectively. Collisional de-excitations are mainly due to collisions with neutral hydrogen atoms, so we use the expression Cul = α T0.3nH, where α is the inelastic collision cross-section, T the temperature, and nH the number density of neutral hydrogen. For more details on estimating cross-sections of inelastic collisions for these molecules see Milić & Faurobert (2012), where the explicit ϵ(h) dependency is also given. W2 is the intrinsic line polarization parameter, which depends on the rotational quantum numbers of upper and lower transition levels. The collisional depolarization parameter is given by
(1)Here ϕν′ is the line absorbtion profile (taken to be same as the line emission profile, since complete frequency redistribution approximation is valid for these weak lines), and P21 and P22 are elements of the Raighley’s scattering matrix. The photon destruction probability is denoted by ϵ and is given by ϵ = Cul/(Aul + Cul) where Aul and Cul are the Einstein coefficient of spontaneous emission and upper level collisional lifetime, respectively. Collisional de-excitations are mainly due to collisions with neutral hydrogen atoms, so we use the expression Cul = α T0.3nH, where α is the inelastic collision cross-section, T the temperature, and nH the number density of neutral hydrogen. For more details on estimating cross-sections of inelastic collisions for these molecules see Milić & Faurobert (2012), where the explicit ϵ(h) dependency is also given. W2 is the intrinsic line polarization parameter, which depends on the rotational quantum numbers of upper and lower transition levels. The collisional depolarization parameter is given by 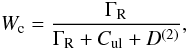 (2)where ΓR and Cul are respectively the inverse radiative and collisional lifetimes of the upper transition level and D(2) is rate of depolarizing collisions. Neglecting the temperature dependence, it can be written as D(2) = nHα(2) where nH is the number density of neutral hydrogen atoms and α(2) the cross-section for depolarizing collisions. For a turbulent magnetic field with an isotropic distribution, the Hanle depolarization parameter is given by
(2)where ΓR and Cul are respectively the inverse radiative and collisional lifetimes of the upper transition level and D(2) is rate of depolarizing collisions. Neglecting the temperature dependence, it can be written as D(2) = nHα(2) where nH is the number density of neutral hydrogen atoms and α(2) the cross-section for depolarizing collisions. For a turbulent magnetic field with an isotropic distribution, the Hanle depolarization parameter is given by ![\begin{equation} W_{\rm H}=1-\frac{2}{5}\left[\frac{\Gamma_{\rm H}^2}{1+\Gamma_{\rm H}^2} + \frac{4\Gamma_{\rm H}^2}{1+4\Gamma_{\rm H}^2}\right], \label{W_Hiso} \end{equation}](/articles/aa/full_html/2012/11/aa19737-12/aa19737-12-eq45.png) (3)where
(3)where 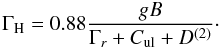 (4)Here g is the so-called Landé factor and B the strength of the microturbulent magnetic field. For mostly horizontal turbulent magnetic fields with random azimuths, the Hanle depolarization parameter is given by (see Stenflo 1995)
(4)Here g is the so-called Landé factor and B the strength of the microturbulent magnetic field. For mostly horizontal turbulent magnetic fields with random azimuths, the Hanle depolarization parameter is given by (see Stenflo 1995) ![\begin{equation} W_{\rm H}=1-\frac{3}{4}\left[\frac{4\Gamma_{\rm H}^2}{1+4\Gamma_{\rm H}^2}\right]\cdot \label{W_Hhor} \end{equation}](/articles/aa/full_html/2012/11/aa19737-12/aa19737-12-eq49.png) (5)In our numerical computations we have used Eq. (5). From the last four equations we see the interplay between magnetic field and depolarizing collisions in the line-formation process. It is important to stress that collisions affect all the lines in the same way, while some transitions have g ≈ 0, which makes them “immune” to the Hanle effect.
(5)In our numerical computations we have used Eq. (5). From the last four equations we see the interplay between magnetic field and depolarizing collisions in the line-formation process. It is important to stress that collisions affect all the lines in the same way, while some transitions have g ≈ 0, which makes them “immune” to the Hanle effect.
For the C2 P-triplets of interest, the blue part consists of two lines, one of which has negligible sensitivity to the magnetic field, and the other one has approximately the same Landé factor as the third one, in the red part of the triplet. Increasing the magnetic field would unevenly decrease the polarization in the blue and red parts of the triplet, while increasing the depolarizing cross-section would decrease the polarization in an even way, thus keeping the ratio between the polarization in the two parts approximately the same. This simple reasoning is exact for the optically thin approximation. Even though we here perform a detailed radiative transfer modeling, it is important to keep in mind the nature of these effects on the observed polarization.
2.2. Atmosphere and molecule models
To compare computed and observed line polarization we use the FALC 1D-semi-empirical model of the quiet Sun by Fontenla et al. (1993). All molecular constants for the C2 molecule are taken from Herzberg (1950) and Berdyugina et al. (2002), with up-to-date values where available. Molecular constants for the MgH molecule are from Bommier et al. (2006). Inelastic collision cross-sections (figuring in parameter Cul) are generally unknown. We use the values determined in Milić & Faurobert (2012) where we explain in detail how we could estimate them. After all, two unknown quantities remain: the magnetic field strength, which is generally depth-dependent, and the depolarizing collisions cross-section, α(2) for C2 transitions.
2.3. First results of forward modeling with a constant turbulent magnetic field
Figure 1 shows examples of observed and computed intensity and polarization profiles in a C2 triplet (where the red part is formed by two blended lines) and one MgH lines lying close together in the second solar spectrum. The computed profiles have been obtained assuming depth-independent magnetic fields of 12 Gauss, 23 Gauss, and 28 Gauss. Depolarizing collision cross-sections have been obtained self-consistently in the same way as when using a depth-dependent magnetic field model (see the minimization procedure described in the following section). The procedure gives values within the same interval as with depth-dependent magnetic strength models (i.e. α(2) = 1.4 − 1.9 × 10-9 s-1 cm-3). We observe that, whereas the amplitude of the blended C2 line polarization observed at μ = 0.1 is recovered by assuming that B = 12 Gauss, the two other lines are not well fitted; in particular, the polarization of the MgH line is definitely overestimated. At μ = 0.2, the blended C2 line polarization is well fitted with B = 28 Gauss, but here again, the MgH line polarization is overestimated. It is clear that the polarization rates observed in the three lines and at different limb distances cannot be explained by assuming a depth-independent magnetic field. This is actually the main motivation for this work. We see in the following that the three kinds of lines of our data set (blended C2 lines, unblended C2 lines, and MgH lines) are formed over different height intervals in the photosphere and that the center-to-limb variations of their polarization rates can indeed be fitted with a depth-dependent mixed polarity magnetic field with a strong depth gradient.
We now present the inversion method that we implemented.
2.4. Minimization procedure
In the fitting procedure one varies the model parameters in order to obtain the best agreement between observed and computed quantities, thus inferring the most probable value of the parameters. There are numerous ways to perform this nonlinear fitting. Here we use the downhill simplex method (see, e.g., Press et al. 2002). This method does not require computation of partial derivatives, which is particulary time-saving in this case where computation time of NLTE radiative transfer solution is significant, due to the large number of angles in spherical geometry. Its main flaw, which is slow convergence once the method is close to the exact solution, is partly compensated for by observational errors that are non-negligible, therefore allowing us to seek more approximate fits.
 |
Fig. 1 Comparison of observed and computed I/Ic and − Q/I profiles at μ = 0.1 (upper panel), and at μ = 0.2 (lower panel). Left to right: (P1 + P2) C2 lines (at 515.946 nm), (P3) C2 line (at 515.960 nm), and MgH line (at 515.975 nm). The intensity profiles have been multiplied by a scaling number to fit in the same figures as the polarization rates. Plus symbols: observed intensity; full lines: computed intensity profiles. Cross symbols: observed Q/I spectrum. Dotted lines: polarization profiles computed with a depth-independent magnetic strength B = 12 G. Dashed lines: depth-independent magnetic strength B = 28 G. Dot-dashed lines: depth-independent magnetic strength B = 23 G |
 |
Fig. 2 Contribution functions for − Qν/Ic for different observational positions on the disk at frequencies corresponding to line centers of C2 blended and unblended (latter scaled by factor of 0.5) and MgH lines, respectively. All contribution functions have been computed with depth-independent magnetic field equal to 30 Gauss. |
One standard approach is to invert the data for each molecule, at each limb distance, separately assuming a depth-independent magnetic strength. The inferred magnetic field strength is then ascribed to the depth where the contribution function shows a maximum, or to the depth where the optical depth at line center along the line-of-sight is unity. In Fig. 2 we show examples of contribution functions for Q/Ic computed with the FALC solar model and a constant magnetic field of 30 Gauss. The contribution function, expressed in terms of the height h as an independent variable is given by 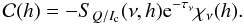 (6)Here χν is the frequency-dependent total opacity (line + continuum), τν is the monochromatic optical depth and SQ/Ic the source function for the quantity of interest, Q/Ic, where Ic denotes the continuum intensity. More details on computing contribution functions are given in, for example, Magain (1986) and Grossmann-Doerth et al. (1988).
(6)Here χν is the frequency-dependent total opacity (line + continuum), τν is the monochromatic optical depth and SQ/Ic the source function for the quantity of interest, Q/Ic, where Ic denotes the continuum intensity. More details on computing contribution functions are given in, for example, Magain (1986) and Grossmann-Doerth et al. (1988).
It can be seen from Fig. 2, that the contribution functions for Q/Ic have a significant width of approximately 200 km, which is within the order of magnitude as the height difference between the maxima of these functions for the MgH and C2 line polarizations. Contribution functions are useful quantities to estimate the depth range where the line polarization is formed, but they cannot be used to derive the depth variations of atmospheric parameters within this depth range from the observed emergent radiation.
We directly performed the inversion of the line-center polarization measured in the full set of lines at the nine positions on the solar disk, taking the depth dependence of the magnetic field strength into account. The contribution function analysis described above shows that our observational data can give information on the magnetic field strength in the depth range between z = 200 km and z = 400 km. We considered the magnetic strength at h = 200 km, 300 km, and 400 km as free parameters, we assumed that it varies linearly with h between these positions and that it remains constant below h = 200 km and above h = 400 km, i.e., in layers that are respectively below and above the line formation depths. An additional free parameter is the depolarizing collision cross-sections for the C2 molecule.
3. Results
3.1. Observations
We applied the method described above to the spectral region between 515.7 nm and 516.1 nm observed by Faurobert & Arnaud (2003) at THEMIS solar telescope. In this region, there are a total of six C2 triplets and two MgH lines. From theoretical considerations, we expect negligible differences between triplet lines belonging to close rotational quantum numbers, at least when compared to observational uncertainties. We therefore averaged the observed polarization between the triplets in order to get more reliable values. To obtain observational errors, we first find signal-to-noise ratio for the point closest to the disk center (around 104, for μ = 0.33 in this case, see Faurobert & Arnaud 2003). Errors at other limb distances scale with inverse square of the intensity, i.e. σ(μ) ∝ I(μ) − 1/2, which allows us to estimate other error bars. There is an additional difficulty in estimating the polarization values because the spectra are contaminated by fringes, which make estimating the “continuum” (which is actual continuum polarization + noise from the fringes + other noise) much harder. To deal with this problem we linearly interpolated the polarization in between the two sides of the line and subtracted that value from the total polarization. Since we are only interested in the maximum line polarization, this procedure should only introduce small errors into this quantity. Concerning the MgH lines, only one of them is clearly distinguished at all the positions (the one at 515.98 nm). We therefore used that line only in to estimate the magnetic field at the MgH line-forming height. This brings us to total of four parameters and 27 data points to constrain these parameters.
3.2. Inversion for the CLV observations with a depth-dependent magnetic field
For the depolarizing collision cross-section, the minimization procedure yields α(2)(C2) = 1.6 ± 0.4 × 10-9 cm3 s-1. This is very similar to the value we obtained previously by applying the differential Hanle effect method to observations in Gandorfer’s Atlas (see Milić & Faurobert 2012, where we obtained α(2)(C2) = 1.7 × 10-9 cm3s-1 ), we can thus safely assume that this value can be used in future modeling.
The best-fitting magnetic field is shown in Fig. 3. “Referent” magnetic field strengths at h = 200,300, and 400 km are 95 ± 30 Gauss, 22 ± 9 Gauss, and 5 ± 3 Gauss, respectively. We find a significant gradient in the magnetic field strength in the investigated depth range. It can be said that this gradient is much stronger than what was expected from previous works. In Fig. 3 we also show the magnetic field run that corresponds to the smallest possible gradient consistent with the observations.
 |
Fig. 3 Run of estimated magnetic field strength with height above the continuum formation level. Full line: best-fitting magnetic field. Dashed line: magnetic field with the smallest gradient that is still consistent with the data. |
 |
Fig. 4 Comparison of observed (cross symbols) and computed (full lines) − Q/I profiles at μ = 0.1 (upper panel), and at μ = 0.2 (lower panel), for our best fit depth-dependent magnetic field model. |
Figure 4 shows the polarization profiles at μ = 0.1 and μ = 0.2 and their fit with our “referent” magnetic model, for the same spectral domain as in Fig. 1. To get another idea of the quality of the fit, we show in Fig. 5 the center-to-limb variations of the line polarization computed with the depth-dependent magnetic field derived here, and we compare them to the observed rates for the C2 unblended and blended components of the triplets and for the MgH line. Figure 5 also shows best fits computed with depth-independent magnetic field fitting either: i) only C2 observations (B = 12 Gauss); ii) only MgH observations(B = 28 Gauss); iii) both observations simultaneously (B = 22 Gauss). It is evident, even to a naked eye, that the overall best fit is achieved by introducing a depth-dependent magnetic field. Computations of reduced χ2 shows that 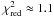 for the fit computed with depth-dependent magnetic field, which can be considered satisfactory. However, for a constant magnetic field, the best value is
for the fit computed with depth-dependent magnetic field, which can be considered satisfactory. However, for a constant magnetic field, the best value is 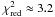 . This is usually considered as strong evidence that the model is not fitting the data. All computations with a depth independent magnetic field were performed with selfconsistent values of α(2), as discussed above.
. This is usually considered as strong evidence that the model is not fitting the data. All computations with a depth independent magnetic field were performed with selfconsistent values of α(2), as discussed above.
 |
Fig. 5 Center-to-limb variations of linear polarization rates, computed with various values of the microturbulent magnetic field. Top: line-center polarization in blended pair of C2 lines; middle: unblended C2 line; bottom: MgH line. |
We can now compare our results to those obtained by Derouich et al. (2006) where center-to-limb observations of the scattering polarization in the SrI 460.7 nm line were analyzed. A depth-dependent turbulent magnetic field was obtained, although a narrower range of depths was probed and the gradient of magnetic field strength with depth was smaller (but with larger uncertainties). However, both analyses result in magnetic fields that decrease when going from lower to upper atmospheric layers. We note that Derouich et al. (2006) consider depth-independent magnetic fields for interpreting each observed limb-distance and used cruder way of relating the limb position to the atmospheric depth (the depth where the line center optical depth is unity on the line of sight). As stressed above, a more realistic inversion is obtained when one deals directly with a depth-dependent magnetic field model. It is worthwhile to also compare our results with those obtained by Kleint et al. (2010, 2011), where scattering polarization was analyzed for both P and R bands of the C2 molecule. In these works magnetic fields in between 5 and 10 Gauss have been found, which is similar to the magnetic field in the upper layers of our model. It is also interesting to notice that Kleint et al. (2010) do not find any significant discrepancy in the C2 line ratios between different limb distances, which would imply a more or less constant magnetic field (and they do indeed fit their observed center-to-limb variations of scattering polarization with a depth-independent magnetic field). Those observations were done during the minimum of the solar activity cycle, while observations published in Faurobert & Arnaud (2003) were done in the peak of solar activity. Long-term measurements of limb polarization in C2 and MgH lines would be necessary to clarify this issue.
4. Additional remarks
4.1. Validity of the two-level atom model
Polarized radiative transfer computations in C2 lines taking multilevel effects into account have been performed by Asensio Ramos & Trujillo Bueno (2003). While it is evident that such computations increase the level of realism of the model, it is not explicitly shown how big the error induced by the two level atom model is. On the other hand, it is known that MgH lines may be modeled with a two-level atom assumption. Since both molecules considered here result in mutually-consistent magnetic field values, we find that the two-level atom model is a safe approximation for estimations of this kind. It is also authors’ opinion that although multilevel approach could change the values of the estimated magnetic field, the behavior of the magnetic field with depth would be the same, that is, it would show a significant depth gradient.
Another major assumption of this paper, the one-dimensionality of the solar atmosphere, will be tested in a future work. However, the application of inversion procedures that use 2 or even 3D solar atmosphere models is very limited as multidimensional computations last significantly longer and besides that, there are presently no multidimensional semi-empirical models of the solar atmosphere.
4.2. Isotropy of the turbulent magnetic field
Our inversion results show that the strength of the turbulent magnetic field has a strong vertical gradient in the solar upper photosphere. We argue here that this behavior is hardly compatible with the assumption of isotropy that is often used for such turbulent fields.
When using the Hanle effect we actually derive the quadratic quantity ⟨ B2 ⟩ where the brackets denote a large-scale spatial averaging due to the limited spatial resolution of our observations (see Eqs. (3) and (5)). Introducing the horizontal and vertical components of the magnetic field, 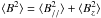 , where B// denotes the magnetic component parallel to the surface, we write the vertical gradient of the magnetic strength quadratic mean, as
, where B// denotes the magnetic component parallel to the surface, we write the vertical gradient of the magnetic strength quadratic mean, as 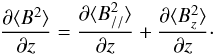 (7)Since the divergence of the magnetic field vanishes, we may write
(7)Since the divergence of the magnetic field vanishes, we may write 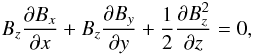 (8)where Bx, By and Bz are the components of the magnetic field vector. Then the vertical gradient of
(8)where Bx, By and Bz are the components of the magnetic field vector. Then the vertical gradient of 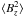 is given by
is given by 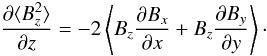 (9)If we assume that the vertical and horizontal components of the turbulent magnetic field do not show any large-scale correlations, the spatial average that appears on the right hand side of Eq. (9) vanishes. In that case the quadratic mean of the vertical magnetic component on our resolution element has to be depth-independent, and the vertical gradient that we measure is only the vertical gradient of the average horizontal component, so in that situation, the turbulent magnetic field measured on a large scale is not isotropic and becomes more and more vertical when z increases. This seems to contradict recent observations performed with different instruments, such as THEMIS or Hinode/SOT (see, e.g., Bommier 2011; Orozco Suárez & Bellot Rubio 2012), showing that the intranetwork magnetic field in the quiet Sun is very inclined most of the time on the solar surface.
(9)If we assume that the vertical and horizontal components of the turbulent magnetic field do not show any large-scale correlations, the spatial average that appears on the right hand side of Eq. (9) vanishes. In that case the quadratic mean of the vertical magnetic component on our resolution element has to be depth-independent, and the vertical gradient that we measure is only the vertical gradient of the average horizontal component, so in that situation, the turbulent magnetic field measured on a large scale is not isotropic and becomes more and more vertical when z increases. This seems to contradict recent observations performed with different instruments, such as THEMIS or Hinode/SOT (see, e.g., Bommier 2011; Orozco Suárez & Bellot Rubio 2012), showing that the intranetwork magnetic field in the quiet Sun is very inclined most of the time on the solar surface.
Another hypothesis is that the turbulent magnetic field is horizontal with an isotropic distribution in azimuths. This does not to lead to any inconsistency with the existence of a vertical gradient of ⟨ B2 ⟩ on a large scale, so it seems that a “simple” model, still consistent with the vertical gradient that we measure and with other quiet Sun observations is a model with a horizontal turbulent magnetic field. This is actually the model that we have been using in the inversion procedures presented in this paper.
Another, more complex but probably more realistic model, is a “turbulent” magnetic field, with some kind of large scale correlations leading to a nonvanishing value of the average 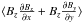 . This would be the case, for example, if the small-scale magnetic field lines formed magnetic loops or of magnetic “dips”, where the vertical component of the field is always oriented in the same direction as the horizontal gradient (loop) or always in the opposite direction (dips). It seems to us that such small-scale magnetic structures make sense in the solar context, because they also do appear in recent MHD numerical simulations of the solar photosphere (see, e.g., Schüssler & Vögler 2008).
. This would be the case, for example, if the small-scale magnetic field lines formed magnetic loops or of magnetic “dips”, where the vertical component of the field is always oriented in the same direction as the horizontal gradient (loop) or always in the opposite direction (dips). It seems to us that such small-scale magnetic structures make sense in the solar context, because they also do appear in recent MHD numerical simulations of the solar photosphere (see, e.g., Schüssler & Vögler 2008).
5. Conclusion
In this paper we have described an inversion procedure that enables us to deduce the run of the microturbulent magnetic field of the quiet Sun with depth. By using observations made at different limb distances and in different lines probing different heights in the photosphere, we are able to obtain best-fitting values of the magnetic field strength and depolarizing collision rates.
Our results show a significant variability in the quadratic mean of the magnetic field strength on a relatively short span of heights. We are interested in performing this procedure on a larger and more precise set of observations. The importance of reliable, high-precision data cannot be stressed enough for this kind of analysis. We also hope to probe a greater range of depths, with new observations and other spectral lines, in order to check the agreement with modern 3D-MHD simulations. Another line that is well-suited to this type of inversion is the SrI line at 460.7 nm, which could also be used to complement those estimations.
Acknowledgments
Ivan Milić is grateful to the Observatoire de la Côte d’Azur for supporting this work through a Poincaré Junior fellowship and to the CNRS for a grant from the Programme National Soleil-Terre. We also acknowledge the support of the Ministry of Education and Science of the Republic of Serbia through the project 176004, “Stellar physics” and the financial support of Institut français de Belgrad.
References
- Asensio Ramos, A., & Trujillo Bueno, J. 2003, in Solar Polarization, eds. J. Trujillo-Bueno, & J. Sanchez Almeida, ASP Conf. Ser., 307, 195 [Google Scholar]
- Asensio Ramos, A., & Trujillo Bueno, J. 2005, ApJ, 635, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Atanacković-Vukmanović, O., Crivellari, L., & Simonneau, E. 1997, ApJ, 487, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Stenflo, J. O., & Gandorfer, A. 2002, A&A, 388, 1062 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bommier, V. 2011, A&A, 530, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bommier, V., Landi Degl’Innocenti, E., Feautrier, N., & Molodij, G. 2006, A&A, 458, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Bommier, V., Malherbe, J. M., & Landi Degl’Innocenti, E. 2006, A&A, 457, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faurobert, M., & Arnaud, J. 2003, A&A, 412, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gandorfer, A. 2000, The Second Solar Spectrum: A high spectral resolution polarimetric survey of scattering polarization at the solar limb in graphical representation, ed. A. Gandorfer [Google Scholar]
- Grossmann-Doerth, U., Larsson, B., & Solanki, S. K. 1988, A&A, 204, 266 [NASA ADS] [Google Scholar]
- Herzberg, G. 1950, Molecular spectra and molecular structure, ed. G. Herzberg [Google Scholar]
- Kleint, L., Berdyugina, S. V., Shapiro, A. I., & Bianda, M. 2010, A&A, 524, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleint, L., Shapiro, A. I., Berdyugina, S. V., & Bianda, M. 2011, A&A, 536, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magain, P. 1986, A&A, 163, 135 [NASA ADS] [Google Scholar]
- Milić, I., & Faurobert, M. 2012, A&A, 539, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orozco Suárez, D., & Bellot Rubio, L. R. 2012, ApJ, 751, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++: the art of scientific computing, eds. W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery [Google Scholar]
- Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 1995, Solar magnetic fields. Polarized radiation diagnostics (Kluwer) [Google Scholar]
All Figures
 |
Fig. 1 Comparison of observed and computed I/Ic and − Q/I profiles at μ = 0.1 (upper panel), and at μ = 0.2 (lower panel). Left to right: (P1 + P2) C2 lines (at 515.946 nm), (P3) C2 line (at 515.960 nm), and MgH line (at 515.975 nm). The intensity profiles have been multiplied by a scaling number to fit in the same figures as the polarization rates. Plus symbols: observed intensity; full lines: computed intensity profiles. Cross symbols: observed Q/I spectrum. Dotted lines: polarization profiles computed with a depth-independent magnetic strength B = 12 G. Dashed lines: depth-independent magnetic strength B = 28 G. Dot-dashed lines: depth-independent magnetic strength B = 23 G |
| In the text | |
 |
Fig. 2 Contribution functions for − Qν/Ic for different observational positions on the disk at frequencies corresponding to line centers of C2 blended and unblended (latter scaled by factor of 0.5) and MgH lines, respectively. All contribution functions have been computed with depth-independent magnetic field equal to 30 Gauss. |
| In the text | |
 |
Fig. 3 Run of estimated magnetic field strength with height above the continuum formation level. Full line: best-fitting magnetic field. Dashed line: magnetic field with the smallest gradient that is still consistent with the data. |
| In the text | |
 |
Fig. 4 Comparison of observed (cross symbols) and computed (full lines) − Q/I profiles at μ = 0.1 (upper panel), and at μ = 0.2 (lower panel), for our best fit depth-dependent magnetic field model. |
| In the text | |
 |
Fig. 5 Center-to-limb variations of linear polarization rates, computed with various values of the microturbulent magnetic field. Top: line-center polarization in blended pair of C2 lines; middle: unblended C2 line; bottom: MgH line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


