| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219722 | |
| Published online | 01 November 2012 | |
The strongest gravitational lenses
I. The statistical impact of cluster mergers
1
Zentrum für Astronomie der Universität Heidelberg, Institut für
Theoretische Astrophysik,
Albert-Ueberle-Str. 2,
69120
Heidelberg,
Germany
e-mail:
matthias.redlich@stud.uni-heidelberg.de
2
Dipartimento di Astronomia, Università di Bologna,
via Ranzani 1, 40127
Bologna,
Italy
3
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
4
INFN, Sezione di Bologna, viale Berti Pichat 6/2,
40127
Bologna,
Italy
5
Department of Astronomy, University of Florida,
211 Bryant Space Science Center,
Gainesville, FL
32611,
USA
Received:
31
May
2012
Accepted:
3
September
2012
For more than a decade now, it has been controversial whether or not the high rate of giant gravitational arcs and the largest observed Einstein radii are consistent with the standard cosmological model. Recent studies indicate that mergers provide an efficient mechanism to substantially increase the strong-lensing efficiency of individual clusters. Based on purely semi-analytic methods, we investigated the statistical impact of cluster mergers on the distribution of the largest Einstein radii and the optical depth for giant gravitational arcs of selected cluster samples. Analysing representative all-sky realizations of clusters at redshifts z < 1 and assuming a constant source redshift of zs = 2.0, we find that mergers increase the number of Einstein radii above 10″ (20″) by ~35% (~55%). Exploiting the tight correlation between Einstein radii and lensing cross sections, we infer that the optical depth for giant gravitational arcs with a length-to-width ratio ≥ 7.5 of those clusters with Einstein radii above 10″ (20″) increases by ~45% (~85%). Our findings suggest that cluster mergers significantly influence in particular the statistical lensing properties of the strongest gravitational lenses. We conclude that semi-analytic studies must inevitably take these events into account before questioning the standard cosmological model on the basis of the largest observed Einstein radii and the statistics of giant gravitational arcs.
Key words: cosmology: theory / gravitational lensing: strong / galaxies: clusters: general / methods: statistical
© ESO, 2012
1. Introduction
Both the abundance of gravitational arcs and the distribution of Einstein radii in galaxy clusters are valuable cosmological probes (Bartelmann 2010). Therefore, the result of Bartelmann et al. (1998), who reported that we observe ten times as many giant gravitational arcs on the sky as theoretically expected, poses a serious challenge. Various aspects of strong gravitational lensing that could potentially mitigate the tension between theory and observations were studied in a long series of subsequent works (see e.g. Fedeli et al. 2008; or Bartelmann 2010, Sect. 5.2, for summaries), and references therein). In particular, Torri et al. (2004) analysed numerically simulated mergers of galaxy clusters. These authors found that mergers substantially change the shape of the critical curves and can boost a cluster’s efficiency to produce giant arcs by an order of magnitude. Fedeli et al. (2006) employed semi-analytic methods to estimate that cluster mergers approximately double the statistical strong-lensing efficiency of clusters at redshifts z > 0.5. Fedeli and coworkers argued that mergers might possibly explain the excess of gravitational arcs in observed galaxy clusters at moderate and high redshifts. However, Fedeli et al. (2006) made several simplifying assumptions that we revise here: First, galaxy clusters were described by elliptically distorted spherical lens models instead of adopting more realistic triaxial density profiles (Jing & Suto 2002; Oguri et al. 2003). This approximation reduces the required computing time substantially, since the calculation of deflection angles for triaxial density profiles involves numerical integrations (Schramm 1990b), while simple analytic expressions exist in the case of elliptically distorted density profiles (Schneider et al. 1992). Second, all mergers were simulated with a fixed direction of motion and relative orientation of the merging clusters, neglecting two important degrees of freedom (see Sect. 5.2).
Recent studies indicate that the distribution of Einstein radii might also be in conflict with theory. More precisely, the largest observed Einstein radii (e.g. Halkola et al. 2008; Umetsu & Broadhurst 2008; Zitrin et al. 2011) were claimed to exceed the maximum possible expectations of the standard cosmological model (Broadhurst & Barkana 2008; Meneghetti et al. 2011; Oguri & Blandford 2009). These conclusions were drawn by either comparing the largest observed Einstein radii to those found in numerical simulations or by semi-analytically estimating the probability of finding the strongest observed lens systems in a ΛCDM universe. While studies of Einstein radii in numerical simulations are probably most realistic, they always suffer from a limited sample size. The simulated boxes might simply be too small to contain a sufficient number of extraordinarily strong gravitational lenses, which forbids solid statistical conclusions. In a follow-up paper, we will show that this limitation is indeed decisive in the context of extreme value statistics (Waizmann et al. 2012). Semi-analytic methods – admittedly based on a set of simplifying assumptions – can overcome this limitation because they are computationally less demanding and hence can be used to analyse large samples of particularly strong gravitational lenses within a comparably short time. However, we note that so far all semi-analytic studies of cosmological distributions of Einstein radii have only considered samples of isolated galaxy clusters. One important goal of this paper is to extend these previous approaches and to present a new semi-analytic method for studying distributions of Einstein radii that incorporates the impact of cluster mergers.
New findings of Meneghetti et al. (2011) suggest that the excess of giant arcs and the too large Einstein radii are closely related. Analysing selected samples of strong gravitational lenses in the MareNostrum simulation (Gottlöber & Yepes 2007), Meneghetti and collaborators discovered a remarkably tight correlation between lensing cross sections and Einstein radii of cluster-sized dark matter haloes. This correlation plays an important role for the structure and line of reasoning of this work.
This paper is structured as follows. Section 2 summarizes an analytic model of triaxial gravitational lenses. In Sect. 3, we compare three different methods for computing lensing cross sections for giant gravitational arcs and show how the alternative algorithms need to be adjusted so that they yield equally reliable results. Having identified a reliable measure of lensing cross sections, we first investigate the correlation between Einstein radii and lensing cross sections in Sect. 4 and then study how the correlation evolves during cluster mergers in Sect. 5. Finally, in Sect. 6, we introduce a semi-analytic method for computing cosmological distributions of Einstein radii that properly includes cluster mergers. Our conclusions are presented in Sect. 7.
In this paper, we consider two different sets of cosmological parameters obtained from the Wilkinson Microwave Anisotropy Probe (WMAP). These are the best-fitting parameters from the WMAP one-year (WMAP1; Spergel et al. 2003), (Ωm0,ΩΛ0,Ωb0,h,σ8) = (0.7,0.3,0.045,0.7,0.9) and from the seven-year data (WMAP7; Larson et al. 2011), (Ωm0,ΩΛ0,Ωb0,h,σ8) = (0.727,0.273,0.0455,0.704,0.811).
2. Triaxial gravitational lenses
2.1. The density profile of triaxial dark matter haloes
Jing & Suto (2002, hereafter JS02) performed a combined analysis of triaxiality in twelve high-resolution dark matter halo simulations to study the detailed shape of single haloes as well as haloes embedded in large cosmological simulations, to gather statistical information about halo profiles. These authors found that the universal, spherical density profile discovered by Navarro et al. (1996, hereafter NFW) can be generalized to a triaxial model and showed that this generalization significantly improves the fit to simulated haloes. Moreover, by analysing large cluster populations in their cosmological simulations, JS02 derived probability density functions for the profile concentrations and axis ratios of triaxial dark matter haloes. The statistical description provided in JS02 allows constructing random catalogues of triaxial dark matter haloes that resemble realistic cosmological populations in numerical simulations.
Jing & Suto (2002) parametrized the
spatial density profile of a triaxial dark matter halo by means of Cartesian coordinates
x′ = (x′,y′,z′)
in the principal axis frame. Using this parametrisation, they proposed a generalization of
the NFW density profile 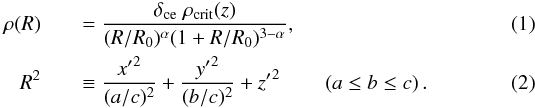 Here,
z denotes the halo’s redshift, R0 is the
scale radius (cf. Eq. (13)),
δce is the characteristic density (cf. Eq. (14)) and
ρcrit(z) denotes the critical density of
the universe. The exact numerical value of the inner slope α of the
density profile is still being discussed. While NFW originally proposed
α = 1.0, other authors argued that steeper profiles with values up to
α = 1.5 provide a better fit to observations and numerical simulations
(Jing & Suto 2000; Limousin et al. 2008; Moore et al.
1999; Navarro et al. 2004; Power et al. 2003). In contrast, recent combined
strong- and weak-lensing analyses of selected clusters indicate shallower mass profiles
with inner slopes α < 1 (see Newman et al. 2011, for instance). Following Oguri et al. (2003), we consider both
α = 1 and α = 1.5 to cover a broad range of the
predicted values and discuss some consequences of varying inner slopes on strong-lensing
statistics.
Here,
z denotes the halo’s redshift, R0 is the
scale radius (cf. Eq. (13)),
δce is the characteristic density (cf. Eq. (14)) and
ρcrit(z) denotes the critical density of
the universe. The exact numerical value of the inner slope α of the
density profile is still being discussed. While NFW originally proposed
α = 1.0, other authors argued that steeper profiles with values up to
α = 1.5 provide a better fit to observations and numerical simulations
(Jing & Suto 2000; Limousin et al. 2008; Moore et al.
1999; Navarro et al. 2004; Power et al. 2003). In contrast, recent combined
strong- and weak-lensing analyses of selected clusters indicate shallower mass profiles
with inner slopes α < 1 (see Newman et al. 2011, for instance). Following Oguri et al. (2003), we consider both
α = 1 and α = 1.5 to cover a broad range of the
predicted values and discuss some consequences of varying inner slopes on strong-lensing
statistics.
To draw a random triaxial dark matter halo of virial mass M at redshift
z, we first sample its axis ratios using the empirically derived
probability density functions from JS02, ![\begin{eqnarray} \label{eq:p_ac} &&p(a/c) = \frac{1}{\sqrt{2\pi}\sigma_{\rm s}} \exp\left[-\frac{(a_{\mathrm{sc}}-0.54)^2}{2\sigma_{\mathrm{s}}^2}\right]\frac{\mathrm{d}a_{\mathrm{sc}}}{\mathrm{d}(a/c)} , \\ &&a_{\mathrm{sc}} = \frac{a}{c} \left( \frac{M}{M_*} \right)^{0.07[\Omega_{\rm m}(z)]^{0.7}} , \\ &&p(a/b|a/c) \! =\! \begin{cases}\! \dfrac{3}{2(1\!-\!r_{\mathrm{min}})}\left[\!1\!-\!\left(\dfrac{2a/b\!-\!1-r_{\mathrm{min}}}{1\!-\!r_{\mathrm{min}}}\right)^2\!\right] & a/b \ge r_{\mathrm{min}}\\ \label{eq:r_min} 0 & \!a/b\! < \!r_{\mathrm{min}} \end{cases}\! , \quad\quad\\ &&\!r_{\mathrm{min}}\! =\! \operatorname{max}\left(a/c,0.5\right) . \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq26.png) Here,
M ∗ is the characteristic nonlinear mass scale where
σ(M ∗ ,z) = δc(z).
According to JS02, the best-fitting parameter for the width of the axis ratio distribution
p(a/c) is
σs = 0.113.
Here,
M ∗ is the characteristic nonlinear mass scale where
σ(M ∗ ,z) = δc(z).
According to JS02, the best-fitting parameter for the width of the axis ratio distribution
p(a/c) is
σs = 0.113.
The concentration ce is defined by
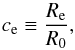 (7)where
Re is determined such that the mean density within the
ellipsoid of the major axis radius Re equals
Δe(z)Ω(z)ρcrit(z),
where
(7)where
Re is determined such that the mean density within the
ellipsoid of the major axis radius Re equals
Δe(z)Ω(z)ρcrit(z),
where 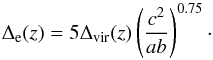 (8)Δvir(z)
is the overdensity of objects virialized at redshift z, which we
approximate according to Nakamura & Suto
(1997). JS02 found a log-normal distribution for the concentration,
(8)Δvir(z)
is the overdensity of objects virialized at redshift z, which we
approximate according to Nakamura & Suto
(1997). JS02 found a log-normal distribution for the concentration, ![\begin{equation} \label{eq:concentration_distribution} p\left(c_{\mathrm{e}}\right) = \frac{1}{\sqrt{2\pi}\sigma_{\mathrm{c}}}\exp\left\{-\frac{\left[\operatorname{ln}(c_{\mathrm{e}})-\operatorname{ln}(\bar{c}_{\mathrm{e}})\right]^2}{2\sigma_{\rm c}}\right\}\frac{1}{c_{\mathrm{e}}} , \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq37.png) (9)with a dispersion
of σc = 0.3. Following Oguri
et al. (2003), we include a correlation between the axis ratio
a/c and the mean concentration,
(9)with a dispersion
of σc = 0.3. Following Oguri
et al. (2003), we include a correlation between the axis ratio
a/c and the mean concentration,
![\begin{eqnarray} \label{eq:concentration} \bar{c}_{\mathrm{e}} &&= f_{\mathrm{c}} \, A_{\mathrm{e}} \sqrt{\frac{\Delta_{\mathrm{vir}}(z_{\rm c})}{\Delta_{\mathrm{vir}}(z)}} \left( \frac{1 + z_{\rm c}}{1 + z} \right) , \\ \label{eq:concentration_correction} f_{\mathrm{c}} &&= \mathrm{max} \left\{0.3, 1.35 \exp \left[ - \left(\frac{0.3}{a_{\mathrm{sc}}} \right)^2 \right] \right\} \cdot \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq40.png) In
Eq. (11), we adopted a correction
introduced by Oguri & Blandford (2009),
forcing fc ≥ 0.3 to avoid unrealistically low concentrations
for particularly low axis ratios asc. Additionally, as noted
earlier by e.g. Oguri & Keeton (2004),
triaxial haloes with particularly low axis ratios asc (and
hence also low concentrations ce) are highly elongated objects
whose lens potential is dominated by masses well outside the virial radius. While previous
studies (e.g. Baltz et al. 2009; Oguri & Blandford 2009) tried to avoid these
unrealistic scenarios by simply truncating the density profile (cf. Eq. (1)) outside the virial radius, we alternatively
force all sampled axis ratios asc to lie within the range of
two standard deviations. Since this manipulation may affect the statistics of the largest
predicted Einstein radii, we will investigate the consequences in our follow-up work
(Waizmann et al. 2012). The numerical value of
the free parameter Ae depends on the underlying cosmology.
Throughout, we set Ae = 1.1, which was proposed by JS02 for a
standard ΛCDM model. The above expressions only apply to an inner slope of
α = 1.0. In the case of α = 1.5, we used the simple
relation
In
Eq. (11), we adopted a correction
introduced by Oguri & Blandford (2009),
forcing fc ≥ 0.3 to avoid unrealistically low concentrations
for particularly low axis ratios asc. Additionally, as noted
earlier by e.g. Oguri & Keeton (2004),
triaxial haloes with particularly low axis ratios asc (and
hence also low concentrations ce) are highly elongated objects
whose lens potential is dominated by masses well outside the virial radius. While previous
studies (e.g. Baltz et al. 2009; Oguri & Blandford 2009) tried to avoid these
unrealistic scenarios by simply truncating the density profile (cf. Eq. (1)) outside the virial radius, we alternatively
force all sampled axis ratios asc to lie within the range of
two standard deviations. Since this manipulation may affect the statistics of the largest
predicted Einstein radii, we will investigate the consequences in our follow-up work
(Waizmann et al. 2012). The numerical value of
the free parameter Ae depends on the underlying cosmology.
Throughout, we set Ae = 1.1, which was proposed by JS02 for a
standard ΛCDM model. The above expressions only apply to an inner slope of
α = 1.0. In the case of α = 1.5, we used the simple
relation 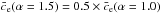 (Keeton & Madau 2001; JS02).
zc denotes the typical collapse redshift of a dark matter
halo of mass M and is computed using the complementary error function,
(Keeton & Madau 2001; JS02).
zc denotes the typical collapse redshift of a dark matter
halo of mass M and is computed using the complementary error function,
![\begin{equation} \label{eq:collapse_redshift} \operatorname{erfc} \left\{ \frac{\omega(z_{\rm c})-\omega(0)}{\sqrt{2 \left[ \sigma^2(fM) - \sigma^2(M) \right]}} \right\} = \frac{1}{2}\cdot \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq47.png) (12)Here,
σ2(M) is the top-hat smoothed variance of
the power-spectrum extrapolated to the redshift z = 0 and
ω(z) = δc(z)/D(z),
where D(z) is the linear growth factor. Following JS02,
we adopted f = 0.01. The typical collapse redshift can be derived within
the framework of extended Press-Schechter theory (Lacey
& Cole 1993). It corresponds to the typical time when the most massive
progenitor of a dark matter halo contained the mass fraction fM. However,
note that JS02 defined the typical collapse redshift such that it does not depend on the
halo’s actual redshift.
(12)Here,
σ2(M) is the top-hat smoothed variance of
the power-spectrum extrapolated to the redshift z = 0 and
ω(z) = δc(z)/D(z),
where D(z) is the linear growth factor. Following JS02,
we adopted f = 0.01. The typical collapse redshift can be derived within
the framework of extended Press-Schechter theory (Lacey
& Cole 1993). It corresponds to the typical time when the most massive
progenitor of a dark matter halo contained the mass fraction fM. However,
note that JS02 defined the typical collapse redshift such that it does not depend on the
halo’s actual redshift.
All other profile parameters can be inferred from the axis ratios and the concentration.
Using an empirical relation (found by JS02) between Re and the
spherical virial radius rvir,
Re/rvir ≈ 0.45,
the scale radius R0 is given by ![\begin{equation} \label{eq:scale_radius} R_0 = 0.45 \, \frac{r_{\mathrm{vir}}}{c_{\rm e}} = \frac{0.45}{c_{\rm e}} \left[ \frac{3M}{4\pi\Delta_{\mathrm{vir}}(z)\Omega_{\rm m}(z)\rho_{\mathrm{crit}}(z)} \right]^{1/3}\cdot \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq57.png) (13)Finally, the
characteristic density δce of the density profile (1)is defined in terms of the concentration,
(13)Finally, the
characteristic density δce of the density profile (1)is defined in terms of the concentration,
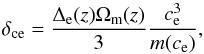 (14)where
(14)where
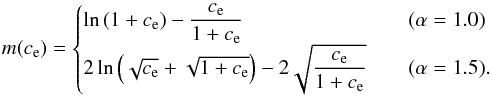 (15)
(15)
2.2. Basics of gravitational lensing
Since the theory of gravitational lensing is well known, we abstain from giving a thorough introduction but instead refer to Bartelmann (2010) for a recent review. We only summarize the quantities that are particularly important here.
Working in the thin-screen approximation, gravitational lensing essentially reduces to a
mapping between the lens plane and the source plane. The lens mapping is given by the lens
equation, 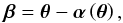 (16)which describes the
relation between the position β of a source, the position
θ of the lensed image and the reduced deflection angle
(16)which describes the
relation between the position β of a source, the position
θ of the lensed image and the reduced deflection angle
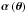 .
The magnification introduced by gravitational lensing is given by
.
The magnification introduced by gravitational lensing is given by 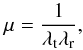 (17)where
λt and λr denote the tangential
and the radial eigenvalue of the lens mapping. Points on the lens plane where at least one
eigenvalue vanishes are called critical points. The set of critical
points forms closed curves called critical curves. Their images on the
source plane are called caustics. Equation (17)indicates that sources located close to caustics are strongly
magnified by the lens mapping. Their images – such as giant arcs – appear in the regions
close to the critical curves in the lens plane.
(17)where
λt and λr denote the tangential
and the radial eigenvalue of the lens mapping. Points on the lens plane where at least one
eigenvalue vanishes are called critical points. The set of critical
points forms closed curves called critical curves. Their images on the
source plane are called caustics. Equation (17)indicates that sources located close to caustics are strongly
magnified by the lens mapping. Their images – such as giant arcs – appear in the regions
close to the critical curves in the lens plane.
2.3. Gravitational lensing by triaxial dark matter haloes
Equation (1)defines the density profile of triaxial dark matter haloes in their principal axis frame. However, their lensing properties are determined by their projected surface mass density in the observer’s frame. Since observed haloes may have arbitrary orientations and the required line-of-sight projection requires us to express the spatial density profile in terms of coordinates with respect to the observer, we first introduce an appropriate coordinate transformation.
Adopting the notation of Eq. (1),
x′ = (x′,y′,z′)
denote the Cartesian coordinates in the principal axis frame of the halo, so that the
z′-axis lies along the major axis of the ellipsoid.
Moreover, we assume that the z-axis is aligned with the line-of-sight
direction of the observer. Then, we can locally construct another Cartesian frame for the
observer’s coordinate system, denoted by
x = (x,y,z). The origins of both
coordinate systems are placed at the centre of the halo. Oguri et al. (2003) exclusively investigated the lensing properties of
individual triaxial haloes and hence could fix the relative orientation of the projected
surface mass density profile in the x-y plane at will.
This freedom allowed them to use a simplified rotation matrix to parametrize the
coordinate transformation between both frames. In Sect. 5.2, we show that the relative orientation of the projected mass density
profiles of merging clusters plays an important role and accordingly we cannot adopt this
practical simplification. Instead we have to introduce a general coordinate transformation
between both frames. To this end, we introduce the three Euler angles
(ψ,θ,φ) and adopt the so-called
z-x′-z′′-convention
illustrated in Fig. 1. The halo’s coordinate system
is rotated about the z-axis by the angle ψ, then about
its new x′-axis by the angle θ, and finally
about the new z′′-axis by the angle φ. The
coordinate transformation is given by
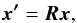 (18)where the rotation
matrix R is the product of the three rotation matrices about
the axes. Using this coordinate transformation, we can express the density profiles of
arbitrarily oriented triaxial dark matter haloes in terms of the observer’s coordinates.
From here on, the derivation of all lensing properties of triaxial dark matter haloes
follows Oguri et al. (2003), hence we refer the
reader to their work. However, since we had to introduce a more general coordinate
transformation, some algebraic coefficients are more complicated in our approach. We
provide the necessary expressions in Appendix A.
Moreover, we present a practical method to speed up the computation of deflection angles
by a factor of ~10 in Appendix B.
(18)where the rotation
matrix R is the product of the three rotation matrices about
the axes. Using this coordinate transformation, we can express the density profiles of
arbitrarily oriented triaxial dark matter haloes in terms of the observer’s coordinates.
From here on, the derivation of all lensing properties of triaxial dark matter haloes
follows Oguri et al. (2003), hence we refer the
reader to their work. However, since we had to introduce a more general coordinate
transformation, some algebraic coefficients are more complicated in our approach. We
provide the necessary expressions in Appendix A.
Moreover, we present a practical method to speed up the computation of deflection angles
by a factor of ~10 in Appendix B.
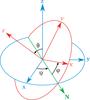 |
Fig. 1 Visualisation of the Euler angles in the z-x′-z′′ convention, which are used to parametrize the coordinate transformation between the observer’s frame and the principal axis frame of the triaxial dark matter halo (figure adapted from Wikipedia (Lionel Brits)). |
In the following sections, we analyse strong-lensing properties of randomly drawn
cosmological populations of triaxial dark matter haloes. Therefore we also need to sample
random halo orientations. For that purpose, special care must be taken, since we cannot
simply uniformly distribute the three angles (ψ,θ,φ) in the corresponding
angle bins. Instead, we have to apply the correct Haar measure (Haar 1933). Only ψ and
φ can be uniformly distributed in the range
[0,2π] . To sample θ, we first
draw a uniformly distributed random number r in the range
[0,1) and then compute
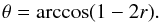 (19)
(19)
3. Computation of lensing cross sections
3.1. Definition of the lensing cross section
The strong-lensing efficiency of an arbitrary mass distribution is typically measured by the so-called lensing cross section σp, which is defined as the area of the region on the source plane where a source with given characteristics (morphology, orientation, surface brightness profile, etc.) has to lie in order to produce at least one image with properties p. This definition is quite general and needs to be additionally specified for the following applications. Throughout, we exclusively computed the lensing cross section σ7.5, which measures the efficiency of a gravitational lens to produce highly elongated images (i.e. giant arcs) with length-to-width ratios exceeding 7.5. For determining this area, each of the three following methods places random sources in the relevant regions of the source plane and analyses their lensed images. As was shown by e.g. Bartelmann et al. (1995) or Oguri (2002), the size and the morphology of the background sources influence the resulting lensing cross section for gravitational arcs significantly, therefore a precise definition of these characteristics must be given. Following the common convention of previous works (e.g. Bartelmann et al. 1995; Meneghetti et al. 2000, 2003; Puchwein et al. 2005), we model the background sources as elliptical galaxies with constant surface brightness. Their size is chosen such that it equals the size of a circular source with a radius of r = 0.5″. Their orientation (in the source plane) and minor-to-major axis ratios are randomly drawn from the ranges [0,π] and [0.5,1] , respectively.
 |
Fig. 2 Illustration of the image fitting algorithm and the length- and perimeter-correction of the ray-tracing method A (figure from Puchwein et al. 2005). |
3.2. Ray-tracing method A
The first method for computing lensing cross sections was introduced by Miralda-Escude (1993), adopted to nonanalytic lens models by Bartelmann & Weiss (1994) and further extended by subsequent works (Meneghetti et al. 2000, 2003; Puchwein et al. 2005). Elaborate descriptions of this method including all technical details are given there, hence we restrict ourselves to a brief summary of the aspects relevant for the following discussion.
First, the lens plane is covered with a Cartesian grid. At each grid point, the light deflection from gravitational lensing is computed to end up with a map of deflection angles. The resolution of this map must be sufficiently high so that the simulated images are resolved accurately and pixelisation effects are negligible (see below). Second, the source plane is covered with a Cartesian grid whose resolution is adaptively refined in regions close to the caustics. Next, the algorithm loops over each point of the refined grid and repeats the following set of operations. A random elliptical source is placed on the current grid point. Then, the images of this source are simulated using ray-tracing. A bundle of light rays starting at the observer is traced through the lens plane and mapped (by means of the lens equation) to the source plane. If a ray hits the source, the corresponding pixel on the lens plane is marked as an image point. After that procedure, the distinct resulting images are identified using a standard connected-component labelling algorithm and are separately analysed by a simple image-fitting algorithm, which is illustrated in Fig. 2. This algorithm sequentially determines three characteristic image points:
-
1.
Point (a), which represents the arc centre and is given by the point whose image on the source plane falls nearest to the source centre.
-
2.
Point (b) on the boundary, which is farthest away from the arc centre (a).
-
3.
Point (c) on the boundary, which is farthest away from (b).
After that, a circle is fitted through the points (a), (b), (c) and the length of the arc connecting these three points is preliminarily set as the image length L. Next, the perimeter is measured by walking along the ordered boundary points and summing up their mutual distances. Since the images are simulated using discrete grids, pixelisation effects have to be taken into account. Puchwein et al. (2005) correctly noted that cells on the lens plane are only classified as belonging to the image if their centres fall within the source. Thus, boundary points are on average half a grid constant farther inside the image. To compensate for this effect, four grid constants must be added to the measured perimeter and the measured length must be elongated by one grid constant. The area A of the image is found by simply counting the number of image pixels (blue points in Fig. 2) and summing up their corresponding cell sizes on the lens plane. Next, four different figures are fitted to the image:
-
1.
A rectangle with area A, length L, and setting the width to W = A/L.
-
2.
An ellipse with area A and assuming that the length of the major axis equals the measured image length L. The image width W is then defined as the length of the minor axis, W = A/(πL).
-
3.
A ring with outer radius rout = L/2 and choosing the inner radius rin such that the area of the ring equals the measured area A of the image. The image length is then redefined as L = π(rout + rin) and the width is set to the width of the ring, W = rout − rin.
-
4.
A circle with radius
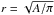 and hence defining r = L = W.
and hence defining r = L = W.
After this fitting routine, the algorithm determines the best approximation of the real image shape by singling out the figure whose circumference agrees best with the measured image perimeter. If the length-to-width ratio of the chosen figure is higher than 7.5, the corresponding cell size on the source plane is added to the lensing cross section σ7.5. If the length-to-width ratios of multiple images of the considered source exceed that threshold, the cell size is multiplied by the corresponding image number.
Performing the above procedure for all points of the adaptive grid on the source plane yields an accurate estimate of the lensing cross section σ7.5.
3.3. Ray-tracing method B
During a series of tests with method A, we observed that removing the length- and perimeter-correction introduced by Puchwein et al. (2005) on average decreases the computed lensing cross sections by roughly 25%, indicating that (unavoidable) errors in the length- and perimeter-measurements also have a significant impact on the results. Moreover, realistic shapes of gravitational arcs are rather irregular and only barely agree with the fitted, idealized geometric figures. To cross-check the results of method A, we developed a new ray-tracing method that employs an alternative algorithm to determine length-to-width ratios of lensed images. As in method A, randomly drawn elliptical sources are placed on an adaptively refined grid on the source plane. Again, the corresponding image configurations are found by tracing bundles of light rays through the lens plane. To identify the distinct lensed images, we employ the component-labelling algorithm proposed by Chang et al. (2004), since it returns a clockwise ordered list of boundary points by construction. This property is important for our alternative length-to-width measurement, which is illustrated in Fig. 3. As with method A, we first identify the characteristic image points (a), (b), and (c) and fit a circle through them. Next, we determine the length of the (green) arc and correct for pixelisation effects by adding one grid constant. After that, we use points (b) and (c) to split the boundary into two parts. The first part consists of pixels connecting (b) and (c) in clockwise direction (upper part of the boundary) and the second group of pixels connects both points in anti-clockwise direction (lower part of the boundary). This separation of boundary points allows us to measure the average width of the image. For this, we first subdivide the angle that is enclosed by the arc connecting (b) and (c) into small bins. Then, we consider each angular bin separately, scan both boundaries for pixels that lie in the current range and use them to determine the image width at the considered position. Figure 3 visualizes this procedure for two specific angular bins along the arc. Finally, we define the average of all measured widths as the width of the image. Again, we correct for pixelisation effects by adding one grid constant. In the same way as in method A, we determine the number of images whose length-to-width ratio is higher than 7.5 for each source. We multiply this number with the corresponding cell size on the source plane and add this area to the final lensing cross section σ7.5.
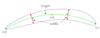 |
Fig. 3 Illustration of the new algorithm to measure length-to-width ratios of gravitational arcs. The image length is measured by fitting a circular arc (green arc) through the points (a), (b) and (c). Instead of fitting idealized, geometric figures to infer the width of the image, the average width is measured along the arc. |
When we had completed this new algorithm, we realized that Meneghetti et al. (2008) used the same approach to measure the length-to-width ratio of arcs in realistic observations. But instead of averaging the widths of the distinct angle bins, they computed the median in order to be less sensitive to observational noise, which produces extreme outliers. Because we did not experience these problems in our purely theoretical computations, the simple average is expected to yield similar results.
3.4. Semi-analytic method
These ray-tracing simulations have a significant drawback: they can become computationally quite expensive. As already mentioned, the ray-tracing part requires computing a map of deflection angles. The resolution of this map must be sufficiently high so that pixelisation effects1 do not significantly falsify the measured length-to-width ratios. Performing a series of convergence tests, we found that the images of unmagnified circular sources with radius r = 0.5″ should at least be represented by ~250 pixels on the lens plane, which amounts to a grid constant of ~0.056″. The deflection angle map needs to cover the entire region of the lens plane in which gravitational arcs can occur. Hence, for particularly strong gravitational lenses, the required side lengths can easily reach values of ~200″ or more, which in turn lead to Cartesian grids with roughly 3500 × 3500 pixels or more. For triaxial gravitational lenses, the calculation of deflection angles involves numerical integrations and hence the computation of the deflection angle map can become rather expensive. Moreover, we note that the component-labelling algorithms, which are the most expensive operation of the ray-tracing methods, require more and more time as the resolution of the deflection angle map is increased because images are represented by ever larger ensembles of pixels. Finally, the resolution of the adaptive grid in the source plane must also be sufficiently high for a precise estimate of the lensing cross section. Consequently, many random sources must be placed and their images need to be simulated.
If arc statistics is meant to be used as a cosmological probe, lensing cross sections of large cluster samples need to be computed. In addition, these computations need to be repeated for different sets of cosmological parameters. Given the above requirements, this task quickly becomes computationally extremely demanding. To overcome this problem, Fedeli et al. (2006) developed a fast and elegant method to calculate lensing cross sections semi-analytically. They found that their alternative method is faster than ray-tracing simulations by a factor of ~30 and yields equally reliable results. Since we aim to compare their method to the previously discussed ray-tracing simulations, a basic understanding of their new approach is required. Again, we only briefly outline the principal ideas and the most important formulae. We refer the reader to Fedeli et al. (2006) for a thorough introduction including all technical details.
We note in the beginning that the intrinsic ellipticity of sources has a significant
impact on the lensing cross section for giant gravitational arcs (cf. Bartelmann et al. 1995). Keeton (2001b) developed a simple and elegant formalism to treat this aspect
mathematically, which we adopt as described by Fedeli et
al. (2006). Without going into detail here, we assume that we possess an
appropriate method for computing the average of the eigenvalue ratio
⟨ ql ⟩
(ql = max[| λt/λr|,|λr/λt |])
over arbitrary images at arbitrary positions in the lens plane. Then, the area of the
stripe in the lens plane where gravitational arcs with a length-to-width ratio equal to or
higher than 7.5 occur is simply given by
![\begin{equation} B_l = \int H \left[ \langle {q}_{\mathrm{obs}} \rangle (\boldsymbol{\theta}) - 7.5 \right] \; \mathrm{d}^2\theta , \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq111.png) (20)where
H(x) is the Heaviside step function and the
integration is carried out over the lens plane. The notation
⟨ qobs ⟩ indicates that we use the average eigenvalue
ratio ⟨ ql ⟩ for computing the observed axis ratio. Using
the lens equation, Bl can be mapped to an area
Bs on the source plane, which is by definition the lensing
cross section σ7.5 we are searching for. Taking the
magnification caused by the lens mapping into account, the lensing cross section is thus
given by
(20)where
H(x) is the Heaviside step function and the
integration is carried out over the lens plane. The notation
⟨ qobs ⟩ indicates that we use the average eigenvalue
ratio ⟨ ql ⟩ for computing the observed axis ratio. Using
the lens equation, Bl can be mapped to an area
Bs on the source plane, which is by definition the lensing
cross section σ7.5 we are searching for. Taking the
magnification caused by the lens mapping into account, the lensing cross section is thus
given by ![\begin{equation} \label{eq:sa_lcs_int} \sigma_{7.5} = \int H \left[ \langle q_{\mathrm{obs}} \rangle(\boldsymbol{\theta}) - 7.5 \right] |\operatorname{det}A\left(\boldsymbol{\theta}\right)| \; \mathrm{d}^2\theta , \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq116.png) (21)where
(21)where
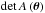 denotes the Jacobian determinant of the lens mapping. Effectively, this elegant
approximation reduces the lensing cross section computation to a simple area integral,
which can be evaluated numerically.
denotes the Jacobian determinant of the lens mapping. Effectively, this elegant
approximation reduces the lensing cross section computation to a simple area integral,
which can be evaluated numerically.
3.5. Comparison of the different methods
We are now in the position to carry out the comparison between the three different methods to check their reliability. To this end, we sampled 300 random triaxial haloes placed at redshift zl = 0.5 and computed their lensing cross sections σ7.5 using each of the three algorithms. The halo masses were logarithmically uniformly distributed within (5 × 1014 − 2 × 1015) M⊙ h-1, and we adopted α = 1.0 for the inner slope of their density profile. The source plane was placed at redshift zs = 2.0.
 |
Fig. 4 Lensing cross sections σ7.5 in the range of 0−400 arcsec2 according to method A (blue crosses), the semi-analytic method (turquoise crosses) and method A fitting ellipses only (yellow triangles) as a function of the lensing cross sections σ7.5 computed with method B for a sample of 300 massive dark matter haloes (see text). The red dashed line indicates the bisector of the σ7.5–σ7.5 plane. The violet dashed line represents the best linear fit of the semi-analytic lensing cross sections. |
Figure 4 shows the lensing cross sections σ7.5 computed with ray-tracing method A and the semi-analytic method as a function of the lensing cross sections σ7.5 computed with ray-tracing method B. For reasons to be clarified below, we also plot the results according to method A but fitting only ellipses to the simulated images.
Obviously, both ray-tracing methods agree excellently in the range σ7.5 ≲ 225 arcsec2, although they employ inherently different algorithms to measure length-to-width ratios of lensed images. For lensing cross sections σ7.5 ≳ 225 arcsec2, the results computed with method A tend to be slightly higher. However, we solely attribute these deviations to technical limitations. The implementation of method A was written in Fortran-77 and we experienced problems when allocating large amounts of memory. Accordingly, we had to limit the maximum possible grid dimension for the deflection angle maps to 2048 × 2048 pixels. For the largest shown lensing cross sections (σ7.5 ≳ 225 arcsec2), the considered field sizes might simply be too large for the highest possible resolution, leading to coarsely resolved images. Hence the errors due to pixelisation effects increase and account for the differences between both ray-tracing simulations. Given these explanations, we conclude that both ray-tracing methods yield equally reliable results.
In contrast to Fedeli et al. (2006), however, we
cannot reproduce the good agreement between the semi-analytic method and the ray-tracing
simulations. Instead, the semi-analytic lensing cross sections are systematically too
small. In order to quantify the deviations, we computed the best linear fit: 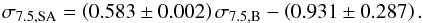 (22)Here,
σ7.5,SA and
σ7.5,B denote the lensing cross sections
computed with the semi-analytic method and method B, respectively. In Fig. 4, the above linear relation (22)is indicated by the violet dashed line.
Evidently the scatter around the linear relation is small, indicating a strong correlation
between both quantities. The small fluctuations with respect to the linear fit can be
explained by different realisations of the randomly drawn source populations: as shown by
Keeton (2001b), the observed length-to-width
ratios of lensed images depend on the sources’ intrinsic ellipticities and relative
orientations with respect to the eigenvectors of the magnification tensor. Since these
properties are randomly drawn when placing the sources on the adaptive grid, some cells
only contribute to the lensing cross section if the source placed on top of them has
favourable properties. Thus the lensing cross sections experience statistical
fluctuations.
(22)Here,
σ7.5,SA and
σ7.5,B denote the lensing cross sections
computed with the semi-analytic method and method B, respectively. In Fig. 4, the above linear relation (22)is indicated by the violet dashed line.
Evidently the scatter around the linear relation is small, indicating a strong correlation
between both quantities. The small fluctuations with respect to the linear fit can be
explained by different realisations of the randomly drawn source populations: as shown by
Keeton (2001b), the observed length-to-width
ratios of lensed images depend on the sources’ intrinsic ellipticities and relative
orientations with respect to the eigenvectors of the magnification tensor. Since these
properties are randomly drawn when placing the sources on the adaptive grid, some cells
only contribute to the lensing cross section if the source placed on top of them has
favourable properties. Thus the lensing cross sections experience statistical
fluctuations.
The above observations suggest that there must be a fundamental difference between the semi-analytic method and the ray-tracing simulations. As already mentioned, we additionally computed the lensing cross sections with a slightly modified version of method A. Instead of probing four different geometrical shapes, we fitted the simulated images with ellipses only. Obviously, this modified ray-tracing algorithm yields results that agree well with the semi-analytic method. This information turns out to be useful in the next section.
3.6. Reconciling the semi-analytic method with the ray-tracing simulations
The findings of the previous sections suggest a simple way for reconciling the semi-analytic method with the ray-tracing simulations. We recall that we found excellent agreement between both ray-tracing methods although their algorithms for determining the width of lensed images differ substantially. However, further analysis reveals that method A fits ~99% of the detected arcs with rectangles, which effectively equals method B’s measuring the average image widths without imposing additional geometrical constraints. Method A yields almost identical results to the semi-analytic method if only ellipses are fitted to the simulated images. These findings simply confirm that the semi-analytic method works as it should: by assuming that the averaged observable axis ratios ⟨ qobs ⟩ equal the length-to-width ratios of images, the method implicitly assumes that the lensed images roughly look like ellipses. Hence the good agreement with the modified version of method A is rather reassuring than indicating a failure of the semi-analytic approximations.
We thus find a simple solution reconciling the semi-analytic method with the ray-tracing
simulations. We therefore consider an arbitrary image with area A and
length L. Fitting a rectangle, we first obtain the width
W = A/L, and thus
the length-to-width ratio is given by 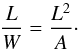 (23)Alternatively, we can
also fit an ellipse. Using the following relation between the area of an ellipse, its
length and its width,
(23)Alternatively, we can
also fit an ellipse. Using the following relation between the area of an ellipse, its
length and its width, 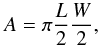 (24)we obtain the
length-to-width ratio
(24)we obtain the
length-to-width ratio 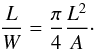 (25)Obviously, if we
fix the area A and the length L (as both ray-tracing
methods do), rectangles have higher length-to-width ratios than ellipses and the
difference is simply given by a factor of π/4. That is
precisely the reason why lensing cross sections decrease by ~40% if only ellipses are
fitted to the simulated images. The measured length-to-width ratios are lower and
therefore fewer images are recognized as giant arcs. On the other hand, this suggests an
easy solution for adapting the semi-analytic method to the ray-tracing simulations.
Recalling that the majority of arcs seems to be better approximated by rectangles, we can
simply multiply the calculated observed axis ratio qobs by
4/π to estimate the correct length-to-width ratio of
most images. This simple multiplication is the mathematical equivalent of fitting images
with rectangles instead of ellipses. To verify this idea, we sampled another random
population of triaxial haloes following the same recipe as in the previous section and
computed their lensing cross sections with the modified semi-analytic method and method B.
Figure 5 clearly indicates that the agreement between
both methods is now reasonably good and the deviations typically remain well below 15%.
(25)Obviously, if we
fix the area A and the length L (as both ray-tracing
methods do), rectangles have higher length-to-width ratios than ellipses and the
difference is simply given by a factor of π/4. That is
precisely the reason why lensing cross sections decrease by ~40% if only ellipses are
fitted to the simulated images. The measured length-to-width ratios are lower and
therefore fewer images are recognized as giant arcs. On the other hand, this suggests an
easy solution for adapting the semi-analytic method to the ray-tracing simulations.
Recalling that the majority of arcs seems to be better approximated by rectangles, we can
simply multiply the calculated observed axis ratio qobs by
4/π to estimate the correct length-to-width ratio of
most images. This simple multiplication is the mathematical equivalent of fitting images
with rectangles instead of ellipses. To verify this idea, we sampled another random
population of triaxial haloes following the same recipe as in the previous section and
computed their lensing cross sections with the modified semi-analytic method and method B.
Figure 5 clearly indicates that the agreement between
both methods is now reasonably good and the deviations typically remain well below 15%.
 |
Fig. 5 Lensing cross sections σ7.5 in the range of 0−400 arcsec2 computed with the modified semi-analytic method as a function of the lensing cross sections σ7.5 calculated with ray-tracing method B. The red dashed line indicates the bisector of the σ7.5–σ7.5 plane. The lensing cross sections were computed for a sample of 300 massive triaxial dark matter haloes (cf. Sect. 3.5). |
We therefore note that the significant and systematic deviations between the semi-analytic method and the ray-tracing simulations are simply caused by different definitions of length-to-width ratios of images. Gravitational arcs have irregular shapes and barely agree with idealized, geometrical figures, leaving no natural definition of a length-to-width ratio. Since Fig. 4 and Eqs. (23)−(25)clearly show that the actual definition has a significant impact on the final lensing cross section, it is particularly important to state precisely which convention is used to yield comparable results. Moreover, the semi-analytic method can be reconciled with the ray-tracing simulations by introducing a simple correction, so that it still provides a fast, reliable alternative for computationally demanding problems. Nevertheless, for the remainder of this paper, we always use ray-tracing method B to compute of lensing cross sections.
4. The correlation between Einstein radii and lensing cross sections
4.1. Two definitions of Einstein radii
Einstein radii measure the size of the tangential critical curve. While a natural choice exists for the Einstein radius in the case of axially symmetric lenses, it is not obvious how this concept can be transferred to arbitrary lenses with irregular tangential critical curves. For this reason various alternatives were proposed by several authors (Broadhurst & Barkana 2008; Meneghetti et al. 2011; Oguri & Blandford 2009; Zitrin et al. 2011). The following two definitions turned out to be most useful for our purposes.
The first definition is of statistical nature. Let
θt denote the set of
tangential critical points. The median Einstein radius
θE,med is defined as the median
distance of these points with respect to the lens’ centre
θc,
 (26)This definition
was introduced by Meneghetti et al. (2011), who
analysed strong-lensing properties of numerically simulated clusters with irregular shapes
that also showed substructure. The centres of those clusters were defined as the location
of the maximum of the smoothed projected density distribution. We note that the
median was chosen in order to be less sensitive to extreme outliers of
irregular critical curves.
(26)This definition
was introduced by Meneghetti et al. (2011), who
analysed strong-lensing properties of numerically simulated clusters with irregular shapes
that also showed substructure. The centres of those clusters were defined as the location
of the maximum of the smoothed projected density distribution. We note that the
median was chosen in order to be less sensitive to extreme outliers of
irregular critical curves.
The second definition is of geometrical nature. Let A denote the area
enclosed by the tangential critical curve. Then, the effective Einstein radius
θE,eff is defined by
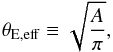 (27)such that a circle with
radius θE,eff has the area
A. Evidently, the median Einstein radius and the effective Einstein
radius both agree with the original definition for axially symmetric lenses.
(27)such that a circle with
radius θE,eff has the area
A. Evidently, the median Einstein radius and the effective Einstein
radius both agree with the original definition for axially symmetric lenses.
 |
Fig. 6 Strong correlation between the median Einstein radii θE,med and the strong-lensing cross sections σ7.5 of a sample of massive clusters with masses M > 5 × 1014 M⊙ h-1 and redshifts zl > 0.5 extracted from the MareNostrum Universe. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,med) (figure from Meneghetti et al. 2011). |
4.2. Correlation for numerical clusters
Meneghetti et al. (2011) extracted a sample of
massive clusters
(M > 5 × 1014 M⊙ h-1)
at redshifts zl > 0.5 from the
MareNostrum Universe (Gottlöber & Yepes
2007) and performed a statistical analysis of their strong-lensing properties.
Figure 6 shows parts of their results, indicating a
tight correlation between the lensing cross sections σ7.5 and
the median Einstein radii θE,med of their
cluster sample. Performing a linear fit to all data points in the
log (θE,med)−log (σ7.5)
plane, they obtained 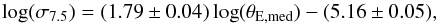 (28)with a Pearson
correlation coefficient of r = 0.94, confirming the tight correlation
between both quantities.
(28)with a Pearson
correlation coefficient of r = 0.94, confirming the tight correlation
between both quantities.
These findings are important for several reasons. First, as already noted by Meneghetti et al. (2011), they clearly indicate the strong connection between the problem of too large Einstein radii and the arc statistics problem. A particularly strong gravitational lens, whose Einstein radius is too large for the ΛCDM model, will most likely also have a lensing cross section that exceeds the maximum theoretical expectations. Hence, if we were to observe too large Einstein radii, we would also expect an excess of gravitational arcs. On the other hand, we note that the converse is not true and care must be taken, since both problems are not identical. Even if there were a way to explain the particularly large Einstein radii within the ΛCDM model, this would not necessarily solve the arc statistics problem. While the distribution of largest Einstein radii only tests the extreme cases, an arc statistic additionally measures the cumulative lensing efficiency of the entire halo population, so that it is also sensitive to the pure abundance of relatively unspectacular lenses, for instance. Thus, if the observed universe simply contained more strong gravitational lenses than theoretically predicted, we could hypothetically still observe an excess of gravitational arcs without having the problem of too large Einstein radii.
Secondly, the correlation discovered might enable us to compute arc statistics for certain halo samples following a new approach. Even by means of the fast semi-analytic method, the calculation of lensing cross sections for large halo samples is a computationally demanding problem, since complete maps of deflection angles have to be computed for each individual lens. In comparison, the calculation of Einstein radii can be fast because only few deflection angles near critical curves need to be computed (see Sect. 6.2). Hence, the idea is to sample cosmological distributions of dark matter haloes, compute their Einstein radii, and finally infer their lensing cross sections by means of the correlation. To this end, we need to investigate if we can reproduce the findings of Meneghetti et al. (2011) with analytic mass profiles for triaxial haloes.
4.3. Correlation for clusters with analytic mass profile
We mimicked the cluster sample from Meneghetti et al. (2011) by drawing random cosmological populations of massive (M > 5 × 1014 M⊙ h-1) triaxial dark matter haloes at redshifts zl > 0.5 (cf. Appendix C). To investigate the impact of variations of the cosmological parameters on the precise functional form of the correlation, we analysed cluster samples within both a WMAP1 and a WMAP7 cosmology. Furthermore, since the steepness of the inner core of dark matter density profiles is known to substantially change the strong-lensing properties of galaxy clusters (see Bartelmann 2010), we additionally considered the two extreme values of the inner slope, namely α = 1.0 and α = 1.5.
Results of the least-squares fits for the relation between Einstein radii and
lensing cross sections, assuming a correlation of the form
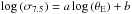 .
.
 |
Fig. 7 Comparison between effective and median Einstein radii for a cosmological population of triaxial dark matter haloes with masses M > 5 × 1014 M⊙ h-1 at redshifts zl > 0.5, assuming a WMAP7 cosmology and adopting density profiles with inner slope α = 1.0. Each cross represents a pair of Einstein radii. The red dashed line indicates the bisector of the log (θE,med)-log (θE,eff) plane. The effective Einstein radii are systematically smaller, as is to be expected for ellipsoidal surface mass densities. |
Before we analyse the discussed correlation for the different settings, we begin with a short comparison of the alternative definitions of Einstein radii. Figure 7 shows effective versus median Einstein radii for one specific population of dark matter haloes, namely assuming a WMAP7 cosmology and adopting triaxial density profiles with inner slope α = 1.0. We note that these plots qualitatively look the same for all other realisations (WMAP1 cosmology or steeper density profiles). Obviously, the agreement between the two definitions is moderate, and the absolute deviations increase with larger Einstein radii. Moreover, almost all points lie below the bisector, indicating that effective Einstein radii are systematically smaller than median Einstein radii. However, this was to be expected, since both definitions only agree for axially symmetric lenses and start to differ (θE,eff < θE,med) as soon as ellipticity is introduced. The deviation is especially pronounced when highly ellipsoidal surface mass density profiles are considered.
 |
Fig. 8 Strong correlation between median Einstein radii θE,med and lensing cross sections σ7.5 for a cosmological population of triaxial dark matter haloes (M > 5 × 1014 M⊙ h-1) at redshifts zl > 0.5, adopting a density profile with inner slope α = 1.0. The population was drawn assuming a WMAP7 cosmology. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,med). The correlation breaks down for small Einstein radii (θE,med ≲ 8″). |
In Fig. 8, we plot lensing cross sections σ7.5 as a function of median Einstein radii θE,med for the same cluster sample as before. We can evidently reproduce the findings of Meneghetti et al. (2011). The correlation is especially tight for large Einstein radii, and thus also for large lensing cross sections. The scatter progressively increases as the size of the Einstein radii decreases until the correlation finally breaks down for Einstein radii θE,med ≲ 8″. We recall that we considered elliptical sources with an equivalent radius of rs = 0.5″ to compute lensing cross sections. In the regime where the correlation breaks down, the size of these sources is roughly of the same order as the size of the caustics, so that the efficiency to produce highly elongated images rapidly drops. Hence, as soon as the considered Einstein radii become too small, the correlation cannot be used anymore to infer lensing cross sections. Of course this breakdown also occurs in the case of effective Einstein radii.
The correlation qualitatively looks the same for all other settings and using effective
Einstein radii θE,eff instead. Hence we
performed a least-squares fit for all data sets, assuming a linear relation of the form
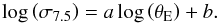 (29)Additionally, we
computed Pearson’s correlation coefficient r. The results of this
procedure are summarized in Table 1 and suggest the
following conclusions. First, we note that the coefficients of the linear fits are not
sensitive to the precise choice of the cosmological parameters. Furthermore, all Pearson
correlation coefficients are close to unity, indicating that not only median, but also
effective Einstein radii can be used to infer lensing cross sections in statistical
studies. As may have been expected, the best-fittting linear relations between median and
effective Einstein radii agree moderately.
(29)Additionally, we
computed Pearson’s correlation coefficient r. The results of this
procedure are summarized in Table 1 and suggest the
following conclusions. First, we note that the coefficients of the linear fits are not
sensitive to the precise choice of the cosmological parameters. Furthermore, all Pearson
correlation coefficients are close to unity, indicating that not only median, but also
effective Einstein radii can be used to infer lensing cross sections in statistical
studies. As may have been expected, the best-fittting linear relations between median and
effective Einstein radii agree moderately.
Next, steeper density profiles produce slightly larger Einstein radii, while the lensing cross sections increase substantially (Oguri 2004). This difference between steeper and flatter profiles manifests itself in systematically larger intercepts b of the linear fits for steeper density profiles with inner slope α = 1.5. Furthermore, it explains why the Pearson correlation coefficients indicate that the correlations are systematically stronger for α = 1.5. The distribution of Einstein radii is shifted towards higher values and, as already mentioned, the overall scatter of the correlation decreases as the Einstein radii increase. Additionally, fewer Einstein radii fall into the region where the correlation breaks down. Both effects can be verified in Fig. 9, which shows effective Einstein radii vs. lensing cross sections for the sample assuming a WMAP7 cosmology and adopting an inner slope α = 1.5. Besides having different intercepts, we note that the slopes of the best linear fits are systematically flatter for α = 1.5. We conclude that steeper density profiles lead to flatter correlations between Einstein radii and lensing cross sections. We confirmed this assumption with the following simple test. We generated another random sample of triaxial dark matter haloes and placed all lenses at one single redshift, namely zl = 0.5. In that case, the geometrical configuration of the lens system is such that arcs occur farther away from the halo centres where the logarithmic slope of the density profile is steeper. Consequently, we found a substantially flatter correlation for that specific sample.
 |
Fig. 9 Strong correlation between effective Einstein radii θE,eff and lensing cross sections σ7.5 for a cosmological population of triaxial dark matter haloes (M > 5 × 1014 M⊙ h-1) at redshifts zl > 0.5, adopting a density profile with inner slope α = 1.5. The population was drawn assuming a WMAP7 cosmology. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,eff). |
4.4. Comparison between numerical and analytical clusters
We now compare our results to the findings of Meneghetti et al. (2011) in detail. As indicated by Fig. 10, the lensing cross sections of triaxial haloes as a function of median Einstein radii are systematically larger than those of the numerical clusters throughout the entire range where the correlation between both quantities holds (θE,med ≳ 8″). This discrepancy even increases as the gravitational lenses become stronger. Since there is no obvious explanation for the above deviations, we briefly discuss the main differences between the two cluster samples. First, the MareNostrum simulation contains baryons, which are known to enhance the lensing cross sections of galaxy clusters (Mead et al. 2010; Puchwein et al. 2005; Rozo et al. 2008; Wambsganss et al. 2008). Second, we describe dark matter haloes as ellipsoids with constant axis ratios, although numerical simulations indicate that these ratios slightly decrease towards the halo centres (Jing & Suto 2002). Hence we slightly underestimate the ellipticity in the inner part of the density profile. Third, numerically simulated clusters naturally contain substructure and incorporate the effect of cluster mergers, whereas we only considered isolated dark matter haloes. All these previous aspects, i.e. asymmetry, substructure, and cluster mergers, are known to substantially increase the strong-lensing efficiency of galaxy clusters (Bartelmann et al. 1995; Fedeli et al. 2006; Meneghetti et al. 2007; Torri et al. 2004).
Given these differences, the lensing cross sections of numerical clusters should be significantly larger. We speculate that the inclusion of substructure and cluster mergers is the main difference between the cluster samples. If this is indeed the case, Fig. 10 suggests that these cluster properties become increasingly important for stronger gravitational lenses. Substructure leads to irregular critical curves with some extreme outliers. These, however, should be compensated for by the computation of median Einstein radii. Hence, we expect that substructure, on average, increases the median Einstein radii only slightly, whereas lensing cross sections are likely significantly enhanced. Evidently, the comparison of the correlations in Fig. 10 indicates exactly the opposite trend, implying that substructure alone cannot explain the deviations. On the other hand, the evolution of lensing cross sections as a function of median Einstein radii during cluster mergers is far from obvious. In Sect. 5.3, we show that these events might indeed explain the discrepancy between the results of Meneghetti et al. (2011) and our findings.
 |
Fig. 10 Best linear fits of the correlation between median Einstein radii θE,med and lensing cross sections σ7.5 for numerical and analytic clusters. The blue solid line indicates the best linear fit for numerical clusters (cf. Eq. (28)). The red dashed and the green dotted line indicate the best linear fits for cosmological populations of triaxial dark matter haloes (cf. Table 1) with inner profile slopes α = 1.0 and α = 1.5, respectively, assuming a WMAP1 cosmology. The lensing cross sections of triaxial dark matter haloes are systematically larger in the range θE,med ≳ 8″. |
 |
Fig. 11 Evolution of the tangential critical curves during a merger of two massive (Mmain = 1 × 1015M⊙ h-1,Msub = 2.5 × 1014M⊙ h-1) triaxial dark matter haloes. Starting with an initial separation of d = 0.57Mpch-1 in the top left panel, the distance between the two haloes is successively reduced until their centres finally overlap in the bottom right panel. |
5. The evolution of strong-lensing properties during cluster mergers
5.1. Evolution of tangential critical curves
We now discuss the evolution of a tangential critical curve during a cluster merger by means of the following simplified toy model (cf. Torri et al. 2004). We considered two massive triaxial haloes merging at the fixed redshift zl = 0.5. The source plane was placed at zs = 2.0. The main halo (Mmain = 1 × 1015 M⊙ h-1) was assumed to rest at the coordinate origin, while the second halo (Msub = 2.5 × 1014 M⊙ h-1) was placed at an initial distance d ~ 1Mpch-1 from the main halo. Since the precise properties (concentration, axis ratios, orientation) of both haloes do not matter for the following discussion, we simply state that their shape and orientation were chosen such that both lensing potentials are considerably elliptical. We simulated the merger by successively reducing the separation between both haloes in a series of discrete steps until their centres finally overlapped. At each step, we computed the resulting tangential critical curves.
Figure 11 illustrates the evolution of the tangential critical curves for a selection of intermediate steps of the simulated merger. As can be seen, we oriented the main halo such that the semi-major axis of its elliptical surface mass density profile was aligned with the direction of motion, whereas the elliptical projected mass profile of the second halo was rotated by 90 degrees. In the beginning (top left panel), the separation between the haloes is large so that both have their own isolated and almost unperturbed tangential critical curves. As soon as the haloes approach, the shear in the region between them grows and stretches both tangential critical curves along the direction of motion until they finally merge to build one large, highly elongated structure (d ≈ 0.32Mpch-1). Given the tight correlation between Einstein radii and lensing cross sections, we expect that these configurations are particularly efficient in producing thin arcs (see next section). As the smaller halo continues to approach the main halo, the highly elongated tangential critical curve typically starts to shrink along the direction of motion. Finally, however, the two mass profiles start to overlap significantly so that the convergence of the inner region grows substantially. As a consequence, the tangential critical curve again starts to expand almost isotropically.
This interpretation of the evolution of critical curves during cluster mergers was first given by Torri et al. (2004), and we refer the reader to their work for more details. It goes without saying that there are more sophisticated studies of cluster mergers that take virialization and other important physical processes properly into account. However, these models clearly go beyond the scope of our fast, semi-analytic approach to investigate the statistical strong-lensing properties of large cosmological populations of triaxial dark matter haloes.
5.2. Evolution of Einstein radii and lensing cross sections
Torri et al. (2004) numerically simulated cluster mergers and found that these events are capable of boosting the lensing cross sections for giant arcs by about one order of magnitude. In a subsequent work, Fedeli et al. (2006) showed that these events are not only important for the lensing cross sections of individual clusters, but also for the overall statistical strong-lensing efficiency of the cosmic cluster population. Motivated by these results, we performed a series of tests using the above toy model to study (1) whether we are able to reproduce the increase of the strong-lensing efficiency during mergers by modelling clusters with triaxial density profiles, (2) which parameters dominate the strength of this effect, and (3) whether the correlation between Einstein radii and lensing cross sections still holds during these events.
Our most important results can be summarized as follows. Naturally, a notable enhancement of the strong-lensing efficiency can only be observed during major mergers (i.e. Msub/Mmain ≫ 0.05). If the mass ratio Msub/Mmain is too low, the elongation of the tangential critical curve enclosing the main halo is negligible. Conversely, the effect is particularly strong for mergers of clusters with comparable mass. Furthermore, the relative orientation of the ellipsoids plays a dominant role. Figure 12 sketches four particular relative orientations of merging triaxial dark matter haloes. The blue ellipsoid in the middle represents the projected mass density of the main halo, while the red ellipsoids display the surface mass densities of the infalling subhaloes. As discussed above, the enhancement of the strong-lensing efficiency can be observed shortly before the two initially separated tangential critical curves merge to form one large, extremely elongated structure. This effect is especially pronounced when the direction of motion and the semi-major axis of the main halo’s surface mass density profile are aligned (mergers (B) and (D) in Fig. 12). The most extended tangential critical curves form in situation (B), where the semi-major axes of both projected mass profiles are aligned and additionally point along the direction of motion. Then, the elongation of the two separated tangential critical curves sets in relatively early and the diameter of the merged critical curve is particularly large. We emphasize that we can reproduce an increase of the lensing cross section by factors of ~2 for typical mass ratios Msub/Mmain ~ 0.25 if, and only if, this distinguished merger configuration is chosen and the surface mass density profiles of both haloes are appreciably elliptical (see below). In all other cases, the enhancement caused by mergers is notably smaller. Clearly, we cannot reproduce the order-of-magnitude increase found by Torri et al. (2004). Particularly in the least favourable configuration (C) there is almost no enhancement at all.
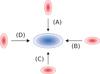 |
Fig. 12 Schematic sketch of four particular orientations of merging triaxial dark matter haloes. The blue ellipsoid in the middle represents the projected mass density profile of the main halo. The red ellipsoids visualize the surface mass density profiles of the infalling subhaloes, which have different relative orientations with respect to the main halo. The black arrows indicate the directions of motion of the infalling structures. |
To quantify these general remarks, we exemplarily consider two specific cluster mergers
in detail. In both cases, we simulated triaxial haloes of masses
Mmain = 1 × 1015M⊙ h-1
and
Msub = 2.5 × 1014M⊙ h-1,
with axis ratios a/c = 0.4 and
b/c = 0.6, mean concentration
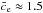 (cf. Eq. (10)), inner profile slope
α = 1.0 and projected along the
y′-direction.
(cf. Eq. (10)), inner profile slope
α = 1.0 and projected along the
y′-direction.
We first consider a merger choosing orientation (D). Figure 13 shows the evolution of different definitions of Einstein radii and the lensing cross section as a function of the distance between the haloes’ centres. In both diagrams, the dashed vertical line indicates the moment when the initially separated tangential critical curves merge. The blue solid and the red dashed lines in the left panel indicate the effective and median Einstein radii, respectively, computed for the tangential critical curve enclosing the main halo only. These definitions take into account that both haloes initially have their own independent critical structures and are thus distinguishable systems from the lensing point of view. In contrast, the green dotted line indicates the median Einstein radius of all tangential critical points relative to the centre of the main halo. Here, “all” means that for the larger distances, where both clusters have their own critical curves, also the critical points enclosing the merging subhalo are taken into account for computing the median Einstein radius. This definition closely resembles that used by Meneghetti et al. (2011), who measured the distances of all tangential critical points with respect to the highest mass peak. We note that the effective Einstein radius seems to capture the isotropic expansion of the tangential critical curve as the density profiles of the two haloes start to overlap significantly and the convergence of the central regions grows. However, it does not indicate a substantial boost of the strong-lensing efficiency when the critical curves merge. This effect is better captured by median Einstein radii, which on the other hand do not reflect the isotropic growth of the tangential critical curve for short distances. The right panel of Fig. 13 shows the evolution of the total lensing cross section σ7.5 of the two clusters. Obviously, the strong-lensing efficiency grows substantially shortly before the critical curves merge. For that specific orientation, we observe an increase of ~170% in comparison to the initial value. After that peak, the lensing cross section passes through a minimum – reflecting the fact that the elongation of the tangential critical curve decreases and the corresponding caustic becomes less cuspy – before it finally increases by ~200% as a consequence of the overlapping mass profiles.
 |
Fig. 13 Figure showing the evolution of different definitions of Einstein radii (see text) and the lensing cross section during a simulated cluster merger, assuming configuration (B) in Fig. 12. All quantities are plotted as a function of the distance between both halo centres. The dashed vertical line indicates the moment when the tangential critical curves merge. |
 |
Fig. 14 Evolution of different definitions of Einstein radii (see text) and the lensing cross section during a simulated cluster merger, assuming configuration (A) of Fig. 12. All quantities are plotted as a function of the distance between the two halo centres. The dashed vertical line indicates the moment when the tangential critical curves merge. |
 |
Fig. 15 Comparison of the correlation between Einstein radii and lensing cross sections for a sample of isolated triaxial dark matter haloes to the same correlation for a sample of merging triaxial dark matter haloes. The red solid line in the left (right) diagram indicates the best linear fit relation between median (effective) Einstein radii and lensing cross sections found for a sample of triaxial dark matter haloes at redshift zl = 0.5. The blue crosses represent selected pairs of Einstein radii and lensing cross sections during cluster mergers (see text for details). |
For comparison, Fig. 14 shows the same diagrams for orientation (A), which corresponds to a direction of motion perpendicular to the major axis of the main halo’s surface mass density profile. Evidently, the evolution of the strong-lensing properties differs substantially from the previous merger. The elongation of the critical curve surrounding the central halo sets in later and the resulting Einstein radii are smaller. Moreover, the separation between the two clusters needs to be smaller for the critical curves to merge. The first peak of the lensing cross section is significantly smaller and coincides with the increase caused by the growing mass concentration in the central regions.
5.3. Correlation between Einstein radii and lensing cross sections
Our main motivation for studying the evolution of Einstein radii and lensing cross sections is to investigate whether or not the correlation between the two quantities still holds during mergers. If the relation is still valid, we can later simply compute all Einstein radii (θE ≳ 8″) on the sky and infer their lensing cross sections by means of the correlation instead of actually computing them with one of the discussed methods (cf. Sect. 3). This approach would save much computing time. This final application may also justify why we plotted different definitions of Einstein radii in the left panels of Figs. 13 and 14, since the first two of them only consider the tangential critical curve enclosing the main halo and are hence clearly more appropriate for our purpose.
The following analysis focuses only on the regions where both critical curves have already merged (i.e. left of the dashed vertical lines in Figs. 13 and 14). First, we observe that none of the definitions of Einstein radii is able to preserve the tight correlation with lensing cross sections. In any case, there are regions where the Einstein radii decrease while the lensing cross sections increase, and vice versa. The correlation seems to break down completely if median Einstein radii are used. In comparison, effective Einstein radii trace the evolution of lensing cross sections better. However, by our definition of measuring only the area that is enclosed by the tangential critical curve surrounding the main halo, they do not capture the enhancement of the strong-lensing efficiency shortly before the tangential critical curves merge. We observe in passing that the definition of effective Einstein radii is more natural for cluster mergers, because it does not require an arbitrarily chosen fiducial point.
In Sect. 5.1, we assumed a constant lens redshift of zl = 0.5 for our simplified models of cluster mergers. For reference, we therefore again generated a sample of 300 random triaxial haloes (mass range 5 × 1014 − 2 × 1015M⊙ h-1, inner profile slope α = 1.0) placed at zl = 0.5 and computed the best linear fits for the correlation between the two different definitions of Einstein radii and lensing cross sections. Figure 15 plots these fits, where the left and the right diagrams correspond to median and effective Einstein radii, respectively. In addition, we simulated all four merger configurations of Fig. 12 using the same dark matter haloes as in the previous section and computed their Einstein radii and lensing cross sections at each discrete simulation step. The blue crosses in the left and right diagrams indicate the results of all those discrete steps that correspond to distances with merged tangential critical curves. Evidently, for median Einstein radii, the pairs (θE,med,σ7.5) systematically lie below the correlation found for isolated clusters. This can easily be understood from Figs. 13 and 14. Starting at d = 0.0, the median Einstein radii increase as a function of distance, whereas the lensing cross sections decrease, so there is indeed an anti-correlation. This observation provides a possible explanation for the discrepancy between the linear relation found by Meneghetti et al. (2011) and our results (cf. Sect. 4.4). We expect that a certain fraction of Meneghetti and coworkers’ numerically simulated clusters are actively merging so that their contribution flattens the results of the least-squares fit. If that line of reasoning is correct, we expect that the correlations found for numerical clusters predict smaller lensing cross sections as a function of Einstein radii. It would be an interesting task to verify this assumption by studying selected cluster samples in numerical simulations. The right-hand side diagram of Fig. 15 shows that the pairs of effective Einstein radii and lensing cross sections during cluster mergers agree significantly better with the corresponding linear fit found for isolated dark matter haloes. Hence we conclude that effective Einstein radii capture the evolution of strong-lensing properties during cluster mergers better and the correlation can still be used to approximate lensing cross sections in statistical lensing studies.
6. Impact of cluster mergers on the statistics of the largest Einstein radii
6.1. A semi-analytic approach to sample large cosmological halo populations that incorporates cluster mergers
While large cosmological N-body simulations are probably the most realistic framework for studying the impact of mergers on the statistical lensing properties of selected cluster samples, they are computationally costly. As an alternative, we now introduce a fast, semi-analytic method that allows us to study the statistical impact of mergers within a fraction of the computing time required for N-body simulations. We follow this approach because we aim to be able to repeat our calculations for large cosmic volumes, varying a multitude of boundary conditions (i.e. different properties of the triaxial density profile, cosmological parameters, mass functions, etc.), within a reasonably short time. This ability is important for our follow-up work, where we plan to employ methods of extreme value statistics to investigate the probability distribution of the largest Einstein radius expected within a ΛCDM cosmology (Waizmann et al. 2012). We require our new approach to be fully self-consistent within the framework of the extended Press-Schechter theory (Lacey & Cole 1993), which means that in particular the predicted merger rates and the Press-Schechter mass function (cf. Press & Schechter 1974) must be reproduced accurately. This way, our results should be comparable with those derived from numerical simulations and real observations.
Let us assume that we intend to analyse the strong-lensing properties of a representative all-sky realization of dark matter haloes in the mass and redshift range [Mmin,Mmax] and [zmin,zmax], respectively. To do this, we sequentially perform the following steps:
-
1.
Initial halo population: we use a common Monte Carlo approach (cf. Oguri & Blandford 2009, and Appendix C) to populate the considered cosmic volume with an initial sample of dark matter haloes at the present time (z = 0). We subdivide the mass range into logarithmically equidistant bins of typical size Δ(log (M)) = 0.02 and calculate the mean expected number
 of haloes in each bin using the Press-Schechter mass function
dn(M,z = 0)/dM,
of haloes in each bin using the Press-Schechter mass function
dn(M,z = 0)/dM,
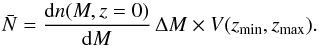 (30)Here,
V(zmin,zmax)
denotes the comoving volume of the spherical shell between the minimum and the
maximum redshift (with respect to an observer at the coordinate origin). We then
generate a random integer number N from the Poisson distribution
with mean
(30)Here,
V(zmin,zmax)
denotes the comoving volume of the spherical shell between the minimum and the
maximum redshift (with respect to an observer at the coordinate origin). We then
generate a random integer number N from the Poisson distribution
with mean 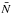 and sample N haloes with logarithmically uniformly distributed
masses in the corresponding bin. Since strongly lensing clusters are rare objects
that are generally separated by large distances, we can neglect any kind of large
scale structure correlation and simply uniformly distribute these N
sampled haloes in the considered cosmic volume. To this end, we assign each halo a
random position on the sky, generate a uniformly distributed random number
x in the range [0,1) and then compute the comoving distance
r with respect to the observer,
and sample N haloes with logarithmically uniformly distributed
masses in the corresponding bin. Since strongly lensing clusters are rare objects
that are generally separated by large distances, we can neglect any kind of large
scale structure correlation and simply uniformly distribute these N
sampled haloes in the considered cosmic volume. To this end, we assign each halo a
random position on the sky, generate a uniformly distributed random number
x in the range [0,1) and then compute the comoving distance
r with respect to the observer,
![\begin{equation} r = \left[ x r^3(z_{\mathrm{max}})+(1-x)r^3(z_{\mathrm{min}}) \right]^{1/3} , \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq222.png) (31)where
r(zmin) and
r(zmax) denote the comoving distance
to the minimum and maximum redshift, respectively. This formula takes the varying
volume (as a function of radius) of spherical shells into account. Given the
comoving radius r, we can easily infer each halo’s redshift
zobs with respect to the observer.
(31)where
r(zmin) and
r(zmax) denote the comoving distance
to the minimum and maximum redshift, respectively. This formula takes the varying
volume (as a function of radius) of spherical shells into account. Given the
comoving radius r, we can easily infer each halo’s redshift
zobs with respect to the observer. -
2.
Reverse time evolution: we evolve the initial halo population backwards in time. More precisely, we adopt the efficient Monte Carlo approach proposed by Zhang et al. (2008, see “method B”) to simulate a representative merger tree of each individual halo up to its previously determined observation redshift zobs. Since Zhang et al. (2008) provide a nicely written step-by-step description of “method B”, we refer the reader to their work for details. Generally, merger tree algorithms generate representative formation histories by evolving the initial halo mass backwards in time taking discrete time steps (typical step size Δz ≈ 0.02). At the first time step, the halo is split into smaller progenitors by means of the conditional mass function (Lacey & Cole 1993). At the next time step, these new progenitors are again split into yet smaller progenitors using the same recipe, and so forth. Applying that scheme to all arising progenitors, this finally yields the full, tree-like formation history (i.e. the merger tree) of the initial halo. Given our predefined mass range, however, we discard all progenitors with masses below Mmin. We note that we verified that our implementation accurately reproduces the Press-Schechter mass function as well as the theoretically predicted merger rates at any look-back time.
-
3.
Kinematics of merger trees: to follow the trajectories of all arising progenitors in the considered cosmic volume, we additionally need to describe the kinematics of the merger trees. For that purpose, we adopt the following simplistic approach, which was first introduced by Fedeli & Bartelmann (2007). Each time a merger between two haloes of masses M1 and M2 occurs, we estimate its duration using the dynamical time scale
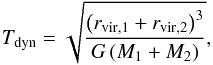 (32)where
rvir,1 and rvir,2 denote
the virial radii of both haloes. These dynamical time scales are typically of the
order of a several hundred Myr, which agrees well with merger durations measured in
numerical simulations (see Torri et al. 2004,
for instance). Assuming a uniform linear motion, we compute the relative velocity of
the two haloes,
(32)where
rvir,1 and rvir,2 denote
the virial radii of both haloes. These dynamical time scales are typically of the
order of a several hundred Myr, which agrees well with merger durations measured in
numerical simulations (see Torri et al. 2004,
for instance). Assuming a uniform linear motion, we compute the relative velocity of
the two haloes, 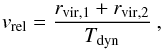 (33)and finally sample
a random direction of motion. We apply this scheme to all mergers. This way, we can
easily compute the spatial positions of all progenitors of the considered merger
tree at the observation redshift zobs. We emphasize that
our model of cluster mergers is clearly simplistic and neglects certain physical
details. For instance, we implicitly assumed central cluster collisions although the
centres of merging clusters can typically be separated by up to several hundred kpc
(see e.g. Sarazin 2002, for a semi-analytic
approximation). Finite impact parameters may certainly influence the detailed
evolution of the strong-lensing properties during individual cluster mergers, and it
would be interesting to study refinements of our simplified model in future works.
However, we do not expect that these simplifications have a significant impact on
the cumulative lensing efficiency of cosmological samples of merging clusters.
(33)and finally sample
a random direction of motion. We apply this scheme to all mergers. This way, we can
easily compute the spatial positions of all progenitors of the considered merger
tree at the observation redshift zobs. We emphasize that
our model of cluster mergers is clearly simplistic and neglects certain physical
details. For instance, we implicitly assumed central cluster collisions although the
centres of merging clusters can typically be separated by up to several hundred kpc
(see e.g. Sarazin 2002, for a semi-analytic
approximation). Finite impact parameters may certainly influence the detailed
evolution of the strong-lensing properties during individual cluster mergers, and it
would be interesting to study refinements of our simplified model in future works.
However, we do not expect that these simplifications have a significant impact on
the cumulative lensing efficiency of cosmological samples of merging clusters.
We conclude this section with a final remark on the specific choice of the mass function. Our algorithms are based on the Press-Schechter mass function (Press & Schechter 1974) throughout, although improved variants of the mass function with better accuracy have been proposed (see Jenkins et al. 2001; Sheth & Tormen 2002; Tinker et al. 2008; Warren et al. 2006, for instance). This choice is motivated by the fact that the Press-Schechter mass function is based on the theory of spherical collapse and only within this framework exact analytic expressions for the conditional mass function – which is the fundamental quantity for the computation of merger trees – can be derived. In contrast, most improved variants are empirical fits to numerical simulations and hence there is no theoretical framework to derive the corresponding expressions for the conditional mass function. Since we aim to compare the statistics of Einstein radii of samples of isolated haloes to those of halo samples that incorporate cluster mergers in a fully self-consistent way, we are restricted to the mass functions based on the spherical (or ellipsoidal) collapse. The moderate deviations of the Press-Schechter mass function are negligible for our principal conclusions in this work. In contrast, if we were to perform a detailed comparison between our theoretical predictions and observations, the precise choice of the mass function would play an important role. This is mainly because the strongest gravitational lenses stem from the exponentially suppressed high-mass tail of the mass function, which is particularly sensitive to the exact calibration. Because the Press-Schechter mass function is known to underestimate the abundance of haloes in the high-mass tail, our approach also slightly underestimates the number of extreme lensing events. We refer the interested reader to our follow-up work (Waizmann et al. 2012), where we provide a detailed discussion of the impact of different mass functions on the statistics of the single largest Einstein radius.
 |
Fig. 16 Sketch illustrating our new algorithm for generating realistic cosmological halo populations that incorporates clusters mergers. An initial halo population at redshift z = 0 is evolved backwards in time using extended Press-Schechter merger trees and is finally projected onto the observer’s past null cone. |
 |
Fig. 17 Comparison of the distributions of the largest Einstein radii including (blue patterned histogram) and excluding (red solid histogram) cluster mergers. The left (right) plot shows the histograms of all Einstein radii larger than 10″ (20″). |
6.2. Computation of Einstein radii
The previous step populates the observer’s past null cone with (merging) dark matter haloes. We now describe an efficient method for computing the distribution of Einstein radii of that halo population.
First, we sort the masses in descending order and begin with the computation of the Einstein radius of the most massive halo M1. To this end, we scan the region around that halo for neighbouring subhaloes Mi whose distance d is shorter than the sum of both virial radii, d ≤ (rvir,1 + rvir,i). If any surrounding subhaloes satisfy this condition, they are taken into account for the computation of deflection angles. All other haloes that are farther away do not influence the strong-lensing properties of the considered massive halo M1 and can safely be ignored. Next, we assign a random triaxial density profile and a random orientation with respect to the observer to each relevant halo. This enables us to determine the tangential critical curve that encloses the massive halo M1. To do this, we place halo M1 at the coordinate centre of a Cartesian grid whose side length is chosen to be sufficiently long to contain all relevant subhaloes. Instead of computing the deflection angle map of the complete field and determining the tangential critical curve afterwards, we simply need to detect the first tangential critical point left of the coordinate origin and employ a standard friend-of-friend algorithm to identify the entire tangential critical curve. This way, we only have to compute deflection angles in small stripes surrounding the critical curve, which renders the algorithm very fast. If we aimed to compute the lensing cross section of the considered configuration instead, we would not be able to use this efficient method but instead would have to calculate the complete deflection angle map. This important difference illustrates why the determination of Einstein radii is computationally far less expensive and why it is of great advantage to infer lensing cross sections from Einstein radii using the discussed correlation between both quantities. Finally, we detect all haloes which are enclosed by the computed tangential critical curve and mark them as haloes which do not have an independent Einstein radius. We repeat the above procedure for all remaining, unmarked haloes of the sorted mass list so that we end up with a complete catalogue of Einstein radii.
6.3. Comparison of the statistics of Einstein radii with and without cluster mergers and inferred optical depths
We can now quantify the statistical impact of cluster mergers on the strongest gravitational lenses (θE,eff ≥ 10″) in our universe. To this end, we generated a first sample of single dark matter haloes using the conventional Monte Carlo approach (see Appendix C) and a second sample using our newly developed technique to incorporate cluster mergers (see Sect. 6.1). Since the largest observed Einstein radii, which may challenge the standard cosmological model, were all found at redshifts well below unity (cf. Broadhurst & Barkana 2008; Zitrin et al. 2011), we focused our analysis on the redshift range z ∈ [0,1]. In anticipation of the following results, we note that the masses of all single haloes with effective Einstein radii above 10″ are larger than 1014 M⊙/h. Recalling that the mass ratio Msub/Mmain of two merging clusters at least needs to exceed 5% to notably boost the strong-lensing efficiency of the main halo, we could therefore safely ignore all haloes with masses below Mmin = 5 × 1012 M⊙/h. In particular, we pruned all branches (i.e. progenitors) of the merger trees whose masses dropped below that threshold. In this section, we modelled all haloes by means of triaxial density profiles with an inner slope α = 1, adopted a WMAP7 cosmology and assumed that the source plane is placed at redshift zs = 2.0.
Figure 17 and Table 2 clearly demonstrate that cluster mergers do have a significant impact on the distribution of the largest Einstein radii. While we find 4132 Einstein radii larger than 10″ in the single halo run, that number increases by 36% up to 5622 haloes if mergers are taken into account. The effect is even more significant if we only consider the number of systems with Einstein radii above 20″, in which case we find an increase of 74%. Another interesting aspect to be analysed is the frequency of cluster mergers. To do this, we classified observed systems as being actively merging if more than one halo is enclosed by the tangential critical curve. Clearly, this definition does not cover those cases where merging clusters are already close to each other, but still have their own, highly elongated critical curves. Nevertheless, our choice should be sufficiently accurate for a qualitative estimate. We find that 35% of the systems with Einstein radii larger than 10″ are actively merging. This number increases to 55% if we only consider those clusters with Einstein radii larger than 20″. Given these results and the above number counts of Einstein radii, we can conclude that (1) cluster mergers are an important mechanism to increase the statistical lensing efficiency of cosmological halo populations and that (2) these events become increasingly dominant for particularly strong gravitational lenses.
Comparison of the strong-lensing statistics of two representative samples of dark matter haloes (M > 5 × 1012 M⊙/h, z ∈ [0,1] ) including and excluding cluster mergers, adopting a WMAP7 cosmology and a constant source redshift zs = 2.0.
 |
Fig. 18 Tangential critical curves of the systems with the largest (left diagram), second largest (middle diagram), and third largest (right diagram) Einstein radius in our simulation including cluster mergers. The black cross in the centre indicates the position of the main halo. The red crosses mark the positions of all subhaloes that are enclosed in the tangential critical curve. |
Additional evidence in favour of these conclusions is provided by considering the very largest lenses in detail. In the simulation including mergers, eight out of the ten largest Einstein radii stem from actively merging systems. Moreover, the largest Einstein radius in the single halo run has the size θE,eff = 38.5″, while we find a notably larger maximum of θE,eff = 50.8″ in the run with mergers. Needless to say, these maxima are subject to statistical fluctuations. Since the considered halo populations were randomly drawn, it may well be that for other realizations the single halo maximum is larger than the one found with merging haloes. However, we can safely conclude that cluster mergers need to be taken into account in semi-analytic, statistical studies that aim to challenge the standard cosmological model on the basis of the largest observed Einstein radii. The left panel of Fig. 18 shows the critical curve of the largest observed Einstein radius, which belongs to an extraordinary system at redshift z = 0.43. Starting with an initial mass of M = 1.8 × 1015 M⊙/h at redshift z = 0, the halo was split into 20 progenitors with masses above the minimum mass threshold Mmin before it finally reached the observer’s past null cone. Six of these 20 progenitors are enclosed in the critical curve shown. The most massive halo in the centre has a mass of M = 1.1 × 1015 M⊙/h. The masses of the five surrounding subhaloes lie in the range 6.7 × 1012 − 1.5 × 1014 M⊙/h. To further demonstrate the importance of mergers, we removed these subhaloes and computed the Einstein radius of the main halo alone, finding that it drops by ~20″ to now only θE,eff = 30.9″. Moreover, we can use that system to verify our choice of the minimum mass threshold Mmin = 5.0 × 1012 M⊙/h. The smallest enclosed subhalo has a mass of M = 6.7 × 1012 M⊙/h, which is close to Mmin. If we ignore that halo for the computation of the tangential critical curve, the Einstein radius drops only slightly by ~1.4% to θE,eff = 50.1″, confirming that our mass cut-off only leads to negligible errors. There are mainly two reasons for introducing such a mass cut-off in general: (1) we can discard a considerable amount of small-mass branches of the merger trees and (2) we can limit the number of (irrelevant) subhaloes that need to be taken into account for the computation of the critical curves. Both aspects substantially improve the performance of our algorithm.
 |
Fig. 19 (Normalized) redshift distribution of the strong gravitational lenses with effective Einstein radii larger than 10″ including (blue solid histogram) and excluding (black patterned histogram) cluster mergers. In addition, the red stacks indicate the fraction of actively merging systems of all strong gravitational lenses represented by the blue solid histogram, i.e. including cluster mergers. Systems are classified as actively merging if more than one halo is enclosed by the tangential critical curve (see text). |
The framework of hierarchical structure formation suggests that relatively young clusters at intermediate and high redshifts (z ≳ 0.5) are dynamically more active than older systems at low redshifts. Therefore, it is to be expected that mergers mainly increase the number of strong lenses in the upper redshift range of our simulation volume. Although Fig. 19 confirms this expectation, the net shift of the overall population of strong-lensing clusters to higher redshifts due to mergers is only moderate. Instead, the redshift distribution of the strongest lenses is predominantly determined by the chosen lensing geometry with sources at redshift zs = 2.0.
Finally, we used the correlation between Einstein radii and lensing cross sections to
infer the impact of cluster mergers on the statistics of giant gravitational arcs from the
distributions of Einstein radii just computed. Since we concentrated on the strongest
gravitational lenses only, we are well inside the regime where the correlation between
both quantities is particularly tight and hence our following estimate should be
reasonably accurate. First, we randomly picked ~400 haloes of our catalogue with
Einstein radii above 10″ and computed their lensing cross sections
σ7.5. We then used these results to calibrate the best
linear fit relation for the correlation: 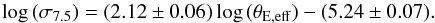 (34)The cumulative
lensing efficiency of cluster samples is usually characterized by their optical
depth τ for giant gravitational arcs, which is given by the
sum of the individual lensing cross sections
σ7.5,i divided by the size of the entire
source sphere,
(34)The cumulative
lensing efficiency of cluster samples is usually characterized by their optical
depth τ for giant gravitational arcs, which is given by the
sum of the individual lensing cross sections
σ7.5,i divided by the size of the entire
source sphere, 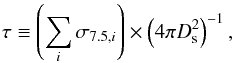 (35)where
Ds denotes the angular diameter distance to the source
plane. Assuming that the individual lensing cross sections do not overlap in the source
plane, the optical depth corresponds to the probability that an arbitrarily placed source
with the specified characteristics produces a gravitational arc with a length-to-width
ratio higher than 7.5. We find that cluster mergers increase the optical depth of all
haloes with Einstein radii above 10″ by roughly 45%. Furthermore, as was to be expected,
the impact on those systems with Einstein radii above 20″ is even stronger: we find that
mergers statistically increase the number of giant arcs produced by these particularly
strong lenses by roughly 85%.
(35)where
Ds denotes the angular diameter distance to the source
plane. Assuming that the individual lensing cross sections do not overlap in the source
plane, the optical depth corresponds to the probability that an arbitrarily placed source
with the specified characteristics produces a gravitational arc with a length-to-width
ratio higher than 7.5. We find that cluster mergers increase the optical depth of all
haloes with Einstein radii above 10″ by roughly 45%. Furthermore, as was to be expected,
the impact on those systems with Einstein radii above 20″ is even stronger: we find that
mergers statistically increase the number of giant arcs produced by these particularly
strong lenses by roughly 85%.
7. Conclusions
Our main results can be briefly summarized as follows. As a first preparatory step, we carried out a detailed comparison between three alternative methods to compute lensing cross sections. We showed that the fast, semi-analytic method originally proposed by Fedeli et al. (2006) systematically deviates from ray-tracing algorithms due to a differing definition of the length-to-width ratio of lensed images. However, this discrepancy can easily be resolved by a trivial correction, after which the semi-analytic method yields equally reliable results as the well-probed ray-tracing codes. Hence, our findings confirm that the semi-analytic method represents an extremely valuable tool for computationally demanding problems. Moreover, our analysis clearly indicates that the precise definition of the length-to-width ratio of lensed images has a significant impact on the final lensing cross section. Thus, special care must be taken to adopt consistent definitions, in particular when comparing theoretical predictions with real observations in the context of the arc statistics problem.
Secondly, we investigated the correlation between Einstein radii and lensing cross sections that was found recently by Meneghetti et al. (2011) for a selected sample of numerical clusters. Considering single haloes only, we showed that we can reproduce the tight correlation, using both median and effective Einstein radii to measure the size of tangential critical curves. However, modelling cluster mergers by means of simplified toy models, we demonstrated that the strict correlation between median Einstein radii and lensing cross sections breaks down during these events. In comparison, effective Einstein radii capture the evolution of the lensing cross sections notably better. Furthermore, we found that the relative orientation of two merging triaxial haloes plays a significant role for the evolution of the strong-lensing properties. While we were able to reproduce an enhancement of the strong-lensing efficiency by factors of a few choosing the most beneficial relative orientation, we showed that this effect completely vanishes when averaging other alignments.
The correlation between effective Einstein radii and lensing cross sections is tight enough to infer sufficiently accurate estimates of optical depths for giant arcs from cosmological distributions of Einstein radii. This approach is computationally far less demanding than explicitly calculating individual lensing cross sections, since the computation of Einstein radii can be implemented in a particularly efficient way. We therefore developed a new, semi-analytic algorithm for computing cosmological distributions of Einstein radii that incorporates the impact of cluster mergers. Using this new technique, we were able to compare the statistical strong-lensing properties of one sample of single (isolated) dark matter haloes and a second sample of dark matter haloes that includes cluster mergers. Assuming a constant source redshift of zs = 2.0, we found that cluster mergers increase the theoretically expected number of Einstein radii above 10″ (20″) by roughly 36% (74%), indicating that these events provide a highly efficient mechanism to enhance the lensing efficiency of particularly strong gravitational lenses. These results clearly show that semi-analytic studies need to take cluster mergers into account if they aim to question the standard cosmological model by comparing the largest observed Einstein radii to theoretical expectations. Furthermore, we estimated that the optical depth for giant gravitational arcs of those haloes with Einstein radii above 10″ (20″) increases by roughly 45% (85%), which highlights the importance of cluster mergers for the statistics of giant gravitational arcs. Still, we were unable to reproduce the doubling of the optical depth found by Fedeli et al. (2006). However, this discrepancy can be attributed to the following important differences between both studies:
-
Instead of adopting triaxial density profiles with varying properties (i.e. concentration and axis ratios), Fedeli et al. (2006) modelled clusters as spherically symmetric density profiles and elliptically distorted their lensing potentials by a constant amount. Moreover, these authors used an alternative concentration-mass relation. Consequently, their lens model produces surface mass densities with different properties, which are decisive for the strength of the boost of the strong-lensing efficiency during cluster mergers.
-
Analyses of cluster mergers in numerical simulations reveal that (1) the major axes of infalling substructures are intrinsically aligned with the major axis of the main halo due to its tidal field and (2) subhaloes preferentially approach the main halo along its major axis (Altay et al. 2006; Lee et al. 2005; Zhang et al. 2009). Motivated by these findings, Fedeli et al. (2006) throughout modelled mergers by perfectly aligning the major axes of both haloes and assuming that the subhalo always approaches the main halo exactly along its major axis. As shown in Sect. 5.2, these orientations are most favourable and produce the strongest possible enhancement of the strong-lensing efficiency during cluster mergers. On the other hand, this assumption clearly is an idealization that might lead to an overestimation of the net effect of mergers. Since there is no reliable theoretical framework that allows us to predict those alignments realistically, we chose the fairly conservative approach to sample the relative orientations of merging haloes randomly, without taking their axis correlations and preferred directions of motion into account. Hence, we expect that our results slightly underestimate the net effect of mergers.
-
While we only computed the optical depth of particularly strong lenses with Einstein radii above 10″, Fedeli et al. (2006) determined the optical depth of all clusters at redshifts z > 0.5. Hence, their computation additionally incorporates the following important effect. Cluster mergers tend not only to increase the lensing cross section of the strongest gravitational lenses, but are also capable of transforming clusters to strong gravitational lenses that would otherwise be subcritical. More precisely, it may well be that two relatively small clusters with vanishing individual lensing cross sections produce a nonvanishing, joint lensing cross section while merging. Consequently, mergers are an effective mechanism to substantially increase the optical depth of clusters in the lower mass range. Given the steepness of the mass function, these objects dominate the total optical depth and thus their contribution is likely significant for the doubling of the optical depth found by Fedeli et al. (2006).
In this work, we mainly focused on the development of new techniques for incorporating the impact of cluster mergers into semi-analytic, statistical strong-lensing studies. We did not conduct a detailed comparison between theory and observations, in particular with regard to the problem of too large Einstein radii. Such analyses will be performed in our follow-up work, where we plan to apply methods of extreme value statistics to investigate whether or not cluster mergers are required (and sufficient) to explain the largest observed Einstein radii within the framework of the standard cosmological model (Waizmann et al. 2012).
The perimeter measurement is particularly sensitive to pixelisation effects. When images have an unfortunate orientation with respect to the Cartesian grid on the lens plane, their boundary, which should normally be smooth, is fairly rugged owing to their discrete representation on the grid. Thus, by summing the mutual distances between the ordered list of boundary points, the measured perimeter overestimates the correct circumference.
Acknowledgments
We are grateful to Massimo Meneghetti and Ewald Puchwein for kindly providing us their ray-tracing implementations for computing lensing cross sections, and we also acknowledge many stimulating discussions. We would also like to thank Francesco Pace for helpful discussions and his tireless translations from ancient Fortran scripts. Finally, we would like to thank the anonymous referee for his/her constructive und clarifying comments. M.R.’s work was supported in part by contract research “Internationale Spitzenforschung II-1” of the Baden-Württemberg Stiftung. J.C.W. acknowledges financial contributions from contracts ASI-INAF I/023/05/0, ASI-INAF I/088/06/0, ASI I/016/07/0 COFIS, ASI Euclid-DUNE I/064/08/0, ASI-Uni Bologna-Astronomy Dept. Euclid-NIS I/039/10/0 and PRIN MIUR 2008 Dark energy and cosmology with large galaxy surveys. C.F. acknowledges support from the University of Florida through the Theoretical Astrophysics Fellowship. M.B. is supported in part by the Transregional Collaborative Research Centre TR 33 “The Dark Universe” of the German Science Foundation.
References
- Altay, G., Colberg, J. M., & Croft, R. A. C. 2006, MNRAS, 370, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Baltz, E. A., Marshall, P., & Oguri, M. 2009, J. Cosmology Astropart. Phys., 1, 15 [Google Scholar]
- Bartelmann, M. 2010, Class. Quan. Grav., 27, 233001 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T. J., & Barkana, R. 2008, MNRAS, 390, 1647 [NASA ADS] [Google Scholar]
- Bartelmann, M., & Weiss, A. 1994, A&A, 287, 1 [NASA ADS] [Google Scholar]
- Bartelmann, M., Steinmetz, M., & Weiss, A. 1995, A&A, 297, 1 [NASA ADS] [Google Scholar]
- Bartelmann, M., Huss, A., Colberg, J. M., Jenkins, A., & Pearce, F. R. 1998, A&A, 330, 1 [NASA ADS] [Google Scholar]
- Chang, F., Chen, C.-J., & Lu, C.-J. 2004, Comput. Vis. Image Underst., 93, 206 [Google Scholar]
- Fedeli, C., & Bartelmann, M. 2007, A&A, 461, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2006, A&A, 447, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C., Bartelmann, M., Meneghetti, M., & Moscardini, L. 2008, A&A, 486, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gottlöber, S., & Yepes, G. 2007, ApJ, 664, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Haar, A. 1933, The Annals of Mathematics, 34, 147 [CrossRef] [Google Scholar]
- Halkola, A., Hildebrandt, H., Schrabback, T., et al. 2008, A&A, 481, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2000, ApJ, 529, L69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2001a [arXiv:astro-ph/0102341] [Google Scholar]
- Keeton, C. R. 2001b, ApJ, 562, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R., & Madau, P. 2001, ApJ, 549, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., Kang, X., & Jing, Y. P. 2005, ApJ, 629, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Richard, J., Kneib, J.-P., et al. 2008, A&A, 489, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mead, J. M. G., King, L. J., Sijacki, D., et al. 2010, MNRAS, 406, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bolzonella, M., Bartelmann, M., Moscardini, L., & Tormen, G. 2000, MNRAS, 314, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bartelmann, M., & Moscardini, L. 2003, MNRAS, 340, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bartelmann, M., Jenkins, A., & Frenk, C. 2007, MNRAS, 381, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Melchior, P., Grazian, A., et al. 2008, A&A, 482, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Fedeli, C., Zitrin, A., et al. 2011, A&A, 530, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Miralda-Escude, J. 1993, ApJ, 403, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Quinn, T., Governato, F., Stadel, J., & Lake, G. 1999, MNRAS, 310, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T. T., & Suto, Y. 1997, Prog. Theor. Phys., 97, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., & Sand, D. J. 2011, ApJ, 728, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2002, ApJ, 573, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2004, Ph.D. Thesis, The University of Tokyo [Google Scholar]
- Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Keeton, C. R. 2004, ApJ, 610, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Lee, J., & Suto, Y. 2003, ApJ, 599, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Power, C., Navarro, J. F., Jenkins, A., et al. 2003, MNRAS, 338, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., Bartelmann, M., Dolag, K., & Meneghetti, M. 2005, A&A, 442, 405 [Google Scholar]
- Rozo, E., Nagai, D., Keeton, C., & Kravtsov, A. 2008, ApJ, 687, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 2002, in Merging Processes in Galaxy Clusters, eds. L. Feretti, I. M. Gioia, & G. Giovannini, Astrophys. Space Sci. Lib., 272, 1 [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Springer) [Google Scholar]
- Schramm, T. 1990a, in Gravitational Lensing, eds. Y. Mellier, B. Fort, & G. Soucail, Lect. Notes Phys. (Berlin: Springer Verlag), 360, 46 [Google Scholar]
- Schramm, T. 1990b, A&A, 231, 19 [NASA ADS] [Google Scholar]
- Sheth, R. K., & Tormen, G. 2002, MNRAS, 329, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Torri, E., Meneghetti, M., Bartelmann, M., et al. 2004, MNRAS, 349, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., & Broadhurst, T. 2008, ApJ, 684, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Waizmann, J.-C., Redlich, M., & Bartelmann, M. 2012, A&A, 547, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wambsganss, J., Ostriker, J. P., & Bode, P. 2008, ApJ, 676, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, M. S., Abazajian, K., Holz, D. E., & Teodoro, L. 2006, ApJ, 646, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Fakhouri, O., & Ma, C.-P. 2008, MNRAS, 389, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Yang, X., Faltenbacher, A., et al. 2009, ApJ, 706, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Broadhurst, T., Barkana, R., Rephaeli, Y., & Benítez, N. 2011, MNRAS, 410, 1939 [NASA ADS] [Google Scholar]
Appendix A: Gravitational lensing by triaxial dark matter haloes with generalized coordinate transformation
As mentioned in Sect. 2.3, we need to introduce a
more general rotation matrix than Oguri et al.
(2003) to describe the coordinate transformation between the principal axis frame
of triaxial haloes and the rest frame of the observer. Consequently, some algebraic
expressions in the derivation of the lensing properties of triaxial haloes are more
complicated. Adopting the same notation as Oguri et al.
(2003), the corresponding expressions are given by ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:f} f &&= \cos^2\theta + \sin^2\theta \left( \frac{c^2}{a^2} \sin^2\phi + \frac{c^2}{b^2} \cos^2\phi \right) , \\ g &&= \sin\theta \left\{\sin \psi \cos \theta \left[ \cos 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) + 2 - \frac{c^2}{a^2} - \frac{c^2}{b^2} \right] + \cos \psi \sin 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) \right\} \, x \notag\\ && \quad + \sin\theta \left\{ -\cos \psi \cos \theta \left[ \cos 2 \phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) +2 - \frac{c^2}{a^2} - \frac{c^2}{b^2} \right] + \sin\psi\sin 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) \right\} \, y , \\ h &&= \left[ \sin^2\psi \sin^2\theta + \frac{c^2}{a^2} \left( \cos \psi \cos \phi - \sin \psi \cos \theta \sin \phi \right)^2 + \frac{c^2}{b^2} \left( \cos \psi \sin \phi + \sin \psi \cos \theta \cos \phi \right)^2 \right] \, x^2 \notag\\ && \quad + \Bigg\{ - \sin 2 \psi \sin^2 \theta + 2 \frac{c^2}{a^2} \left[ \left( \cos \psi \cos \theta \sin \phi + \sin\psi \cos \phi \right) \left( \cos \psi \cos \phi - \sin \psi \cos \theta \sin \phi \right) \right] \notag \\ && \quad - 2 \frac{c^2}{b^2} \left[ \left( \sin\psi\cos\theta\cos\phi + \cos \psi \sin\phi \right) \left( \cos\psi\cos\theta\cos\phi - \sin\psi\sin\phi \right) \right] \Bigg\} \, xy \notag \\ && \quad + \Bigg[ \cos^2 \psi \sin^2 \theta + \frac{c^2}{a^2} \left( \cos \psi \cos \theta \sin \phi + \sin \psi \cos \phi \right)^2 + \frac{c^2}{b^2} \left( \cos\psi \cos\theta\cos\phi - \sin\psi\sin\phi \right)^2 \Bigg] \, y^2 . \\ A && \equiv \Bigg[ \sin^2\theta \left( \frac{c^2}{a^2}\sin^2\phi + \frac{c^2}{b^2}\cos^2\phi \right) + \cos^2\theta \Bigg] \times \Bigg[ \frac{c^2}{a^2} \left( \cos\psi\cos\phi - \sin\psi \cos\theta \sin\phi \right)^2 \notag \\ && \quad + \frac{c^2}{b^2} \left( \sin\psi \cos\theta \cos\phi + \cos\psi \sin\phi \right)^2 + \sin^2\psi \sin^2\theta \Bigg] \notag \\ && \quad - \frac{\sin^2\theta}{4} \Bigg\{ \sin\psi \cos\theta \left[ \cos 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) + 2 - \frac{c^2}{a^2} - \frac{c^2}{b^2} \right] + \cos\psi \sin 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) \Bigg\}^2 , \\ B && \equiv \quad \left[ \sin^2\theta \left(\frac{c^2}{a^2} \sin^2\phi + \frac{c^2}{b^2}\cos^2\phi \right) + \cos^2\theta \right]\times \Bigg[ 2 \frac{c^2}{a^2} \left( \cos\psi\cos\theta\sin\phi + \sin\psi\cos\phi\right) \left( \cos\psi\cos\phi - \sin\psi\cos\theta\sin\phi \right) \notag \\ && \quad -2 \frac{c^2}{b^2} \left( \sin\psi\cos\theta\cos\phi + \cos\psi\sin\phi \right) \left( \cos\psi\cos\theta\cos\phi - \sin\psi\sin\phi \right) - \sin^2\theta\sin 2\psi \Bigg] \notag \\ && \quad + \frac{\sin^2\theta}{2} \Bigg\{ \left[ \sin\psi \cos\theta \left( \cos 2\phi \left( \frac{c^2}{b^2} - \frac{c^2}{a^2} \right) + \frac{c^2}{a^2} + \frac{c^2}{b^2} - 2 \right) + \cos\psi \sin 2\phi \left( \frac{c^2}{b^2} - \frac{c^2}{a^2} \right) \right] \notag \\ && \quad \times \left[ \sin\psi \sin 2\phi \left( \frac{c^2}{a^2}-\frac{c^2}{b^2} \right) - \cos\psi \cos\theta \left( \cos 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) + 2 -\frac{c^2}{a^2} - \frac{c^2}{b^2} \right) \right] \Bigg\} , \\ C && \equiv \left[ \sin^2\theta \left( \frac{c^2}{a^2} \sin^2\phi + \frac{c^2}{b^2} \cos^2\phi \right) + \cos^2\theta \right] \times \Bigg[ \frac{c^2}{a^2} \left( \cos\psi \cos\theta \sin\phi + \sin\psi \cos\phi \right)^2 \notag \\ && \quad + \frac{c^2}{b^2} \left( \cos\psi \cos\theta \cos\phi - \sin\psi \sin\phi \right)^2 + \cos^2\psi \sin^2\theta \Bigg] \notag \\ && \quad - \frac{\sin^2\theta}{4} \left\{ \cos\psi \cos\theta \left[ \cos 2\phi \left( \frac{c^2}{a^2} - \frac{c^2}{b^2} \right) + 2 -\frac{c^2}{a^2} - \frac{c^2}{b^2} \right] + \sin\psi \sin 2\phi \left( \frac{c^2}{b^2} - \frac{c^2}{a^2} \right) \right\}^2 \cdot \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq290.png)
Appendix B: A method for accelerating the computation of deflection angles
Oguri et al. (2003) show that the surface mass
density profiles of triaxial haloes are ellipsoidal. Let q denote the
corresponding minor-to-major axis ratio (cf. Oguri et al.
2003, Eq. (35)). Then, the components of the deflection angle
α = (αx,αy)
can be expressed as one-dimensional integrals of the convergence
κ(ζ) (see also Keeton
2001a; Schramm 1990a):  where
the integrals Jn(x,y) are
defined as
where
the integrals Jn(x,y) are
defined as ![\appendix \setcounter{section}{2} \begin{eqnarray} J_n(x,y) &&= \int_0^1\frac{\kappa\left[\zeta(v)\right]}{\left[1-\left(1-q^2\right)v\right]^{n+1/2}} \; \mathrm{d}v , \\ \zeta^2(v) &&= v\left[y^2 + \frac{x^2}{1-\left(1-q^2\right)v}\right] \cdot \label{eq:zeta_of_v} \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq296.png) The
numerical evaluation of these integrals is computationally quite expensive. Since
limv → 0ζ(v) = 0 and
limζ → 0κ(ζ) = ∞ (cf.
Eqs. (40) and (41) from Oguri et al. 2003), the
integrand is singular at the lower integration boundary. Accordingly the numerical
integration routines converge only slowly. We found that this inconvenient behaviour can
be avoided by two subsequent substitutions. First, we invert Eq. (B.4)and solve for v:
The
numerical evaluation of these integrals is computationally quite expensive. Since
limv → 0ζ(v) = 0 and
limζ → 0κ(ζ) = ∞ (cf.
Eqs. (40) and (41) from Oguri et al. 2003), the
integrand is singular at the lower integration boundary. Accordingly the numerical
integration routines converge only slowly. We found that this inconvenient behaviour can
be avoided by two subsequent substitutions. First, we invert Eq. (B.4)and solve for v:
![\appendix \setcounter{section}{2} \begin{equation} v(\zeta) = \begin{cases} \dfrac{\zeta^2\left(1-q^2\right)+x^2+y^2\pm\sqrt{\left[\zeta^2\left(1-q^2\right)+x^2+y^2\right]^2-4\zeta^2y^2\left(1-q^2\right)}}{2y^2\left(1-q^2\right)} & \quad (y \neq 0) \\ \dfrac{\zeta^2}{x^2+\left(1-q^2\right)\zeta^2} & \quad (y = 0). \end{cases} \end{equation}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq300.png) (B.5)For
y ≠ 0,
limv → 0ζ(v) = 0 implies
that the negative branch must be the correct solution for ζ ≪ 1. Since
(B.5)For
y ≠ 0,
limv → 0ζ(v) = 0 implies
that the negative branch must be the correct solution for ζ ≪ 1. Since
![\hbox{$\left\{\left[\zeta^2(1-q^2)+x^2+y^2\right]^2-4\zeta^2y^2(1-q^2)\right\}^{1/2}$}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq303.png) never vanishes for y ≠ 0 and the solution must be continuous, the
negative branch is the unique solution for the complete interval. Given this relation, we
substitute v by ζ(v) and obtain
never vanishes for y ≠ 0 and the solution must be continuous, the
negative branch is the unique solution for the complete interval. Given this relation, we
substitute v by ζ(v) and obtain
![\appendix \setcounter{section}{2} \begin{eqnarray} J_n(x,y) &= \int_0^1\frac{\kappa\left[\zeta(v)\right]}{\left[1-\left(1-q^2\right)v\right]^{n+1/2}} \; \mathrm{d}v \\ &= \int_0^{\zeta(1)}\frac{\kappa(\zeta)}{\left[1-\left(1-q^2\right)v\left(\zeta\right)\right]^{n+1/2}} \; \frac{\mathrm{d}v}{\mathrm{d}\zeta} \; \mathrm{d}\zeta , \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq305.png) where
where
![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}v}{\mathrm{d}\zeta} &= \begin{cases} \dfrac{\zeta}{y^2}-\dfrac{\zeta\left[\left(1-q^2\right)\zeta^2+x^2+y^2\right]-2y^2}{y^2\left\{\left[\left(1-q^2\right)\zeta^2+x^2+y^2\right]^2-4\zeta^2y^2\left(1-q^2\right)\right\}^{1/2}} & \quad (y \neq 0) \\ & \\ \dfrac{2\zeta x^2}{{\left[x^2+\left(1-q^2\right)\zeta^2\right]}^2} & \quad (y = 0). \end{cases} \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq306.png) (B.8)The
obvious singularity at the lower integration boundary vanishes after this transformation,
but the integrand is not smooth at the origin yet. We overcome this problem by making the
additional substitution ζ = t2, so that
(B.8)The
obvious singularity at the lower integration boundary vanishes after this transformation,
but the integrand is not smooth at the origin yet. We overcome this problem by making the
additional substitution ζ = t2, so that
![\appendix \setcounter{section}{2} \begin{eqnarray} J_n(x,y) &= \int_0^{\sqrt{\zeta(1)}}\frac{\kappa(t)}{\left[1-\left(1-q^2\right)v(t)\right]^{n+1/2}} \; 2t \; \frac{\mathrm{d}v}{\mathrm{d}\zeta} \; \mathrm{d}t . \end{eqnarray}](/articles/aa/full_html/2012/11/aa19722-12/aa19722-12-eq308.png) (B.9)These
simple integral transformations speed up our computations by a factor of ~10.
(B.9)These
simple integral transformations speed up our computations by a factor of ~10.
Appendix C: Sampling cosmological populations of dark matter haloes
In several sections of this paper, we needed to sample realistic catalogues of dark
matter haloes, where “realistic” means that they should have similar mass spectra as halo
populations in numerical simulations and the observed universe. For that purpose, we
adopted the following common Monte Carlo approach (see Oguri & Blandford 2009, for instance), which is based on the
Press-Schechter mass function (Press & Schechter
1974). Let us assume we need to draw a random population of dark matter haloes
within the mass range
[Mmin,Mmax]
and the redshift interval
[zmin,zmax] .
Then, we first subdivide both ranges into smaller, equidistant bins, adopting typical bin
sizes of Δz = 0.02 and Δ(log (M)) = 0.02. Next, we
calculate the mean expected number 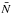 of haloes in each bin using the Press-Schechter mass function
dn(M,z)/dM,
of haloes in each bin using the Press-Schechter mass function
dn(M,z)/dM,
 (C.1)where
dV/dz denotes the differential
comoving volume. After that, we generate a random integer number N from
the Poisson distribution with mean
(C.1)where
dV/dz denotes the differential
comoving volume. After that, we generate a random integer number N from
the Poisson distribution with mean  .
Finally, we sample N haloes within the current bin and assign them
uniformly distributed masses and redshifts out of the corresponding ranges.
.
Finally, we sample N haloes within the current bin and assign them
uniformly distributed masses and redshifts out of the corresponding ranges.
This Monte Carlo method is simple and efficient. It reliably generates random halo catalogues whose deviations from the Press-Schechter mass function remain within the limits of Poisson noise.
All Tables
Results of the least-squares fits for the relation between Einstein radii and
lensing cross sections, assuming a correlation of the form
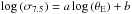 .
.
Comparison of the strong-lensing statistics of two representative samples of dark matter haloes (M > 5 × 1012 M⊙/h, z ∈ [0,1] ) including and excluding cluster mergers, adopting a WMAP7 cosmology and a constant source redshift zs = 2.0.
All Figures
 |
Fig. 1 Visualisation of the Euler angles in the z-x′-z′′ convention, which are used to parametrize the coordinate transformation between the observer’s frame and the principal axis frame of the triaxial dark matter halo (figure adapted from Wikipedia (Lionel Brits)). |
| In the text | |
 |
Fig. 2 Illustration of the image fitting algorithm and the length- and perimeter-correction of the ray-tracing method A (figure from Puchwein et al. 2005). |
| In the text | |
 |
Fig. 3 Illustration of the new algorithm to measure length-to-width ratios of gravitational arcs. The image length is measured by fitting a circular arc (green arc) through the points (a), (b) and (c). Instead of fitting idealized, geometric figures to infer the width of the image, the average width is measured along the arc. |
| In the text | |
 |
Fig. 4 Lensing cross sections σ7.5 in the range of 0−400 arcsec2 according to method A (blue crosses), the semi-analytic method (turquoise crosses) and method A fitting ellipses only (yellow triangles) as a function of the lensing cross sections σ7.5 computed with method B for a sample of 300 massive dark matter haloes (see text). The red dashed line indicates the bisector of the σ7.5–σ7.5 plane. The violet dashed line represents the best linear fit of the semi-analytic lensing cross sections. |
| In the text | |
 |
Fig. 5 Lensing cross sections σ7.5 in the range of 0−400 arcsec2 computed with the modified semi-analytic method as a function of the lensing cross sections σ7.5 calculated with ray-tracing method B. The red dashed line indicates the bisector of the σ7.5–σ7.5 plane. The lensing cross sections were computed for a sample of 300 massive triaxial dark matter haloes (cf. Sect. 3.5). |
| In the text | |
 |
Fig. 6 Strong correlation between the median Einstein radii θE,med and the strong-lensing cross sections σ7.5 of a sample of massive clusters with masses M > 5 × 1014 M⊙ h-1 and redshifts zl > 0.5 extracted from the MareNostrum Universe. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,med) (figure from Meneghetti et al. 2011). |
| In the text | |
 |
Fig. 7 Comparison between effective and median Einstein radii for a cosmological population of triaxial dark matter haloes with masses M > 5 × 1014 M⊙ h-1 at redshifts zl > 0.5, assuming a WMAP7 cosmology and adopting density profiles with inner slope α = 1.0. Each cross represents a pair of Einstein radii. The red dashed line indicates the bisector of the log (θE,med)-log (θE,eff) plane. The effective Einstein radii are systematically smaller, as is to be expected for ellipsoidal surface mass densities. |
| In the text | |
 |
Fig. 8 Strong correlation between median Einstein radii θE,med and lensing cross sections σ7.5 for a cosmological population of triaxial dark matter haloes (M > 5 × 1014 M⊙ h-1) at redshifts zl > 0.5, adopting a density profile with inner slope α = 1.0. The population was drawn assuming a WMAP7 cosmology. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,med). The correlation breaks down for small Einstein radii (θE,med ≲ 8″). |
| In the text | |
 |
Fig. 9 Strong correlation between effective Einstein radii θE,eff and lensing cross sections σ7.5 for a cosmological population of triaxial dark matter haloes (M > 5 × 1014 M⊙ h-1) at redshifts zl > 0.5, adopting a density profile with inner slope α = 1.5. The population was drawn assuming a WMAP7 cosmology. The red solid line indicates the best linear fit relation between log (σ7.5) and log (θE,eff). |
| In the text | |
 |
Fig. 10 Best linear fits of the correlation between median Einstein radii θE,med and lensing cross sections σ7.5 for numerical and analytic clusters. The blue solid line indicates the best linear fit for numerical clusters (cf. Eq. (28)). The red dashed and the green dotted line indicate the best linear fits for cosmological populations of triaxial dark matter haloes (cf. Table 1) with inner profile slopes α = 1.0 and α = 1.5, respectively, assuming a WMAP1 cosmology. The lensing cross sections of triaxial dark matter haloes are systematically larger in the range θE,med ≳ 8″. |
| In the text | |
 |
Fig. 11 Evolution of the tangential critical curves during a merger of two massive (Mmain = 1 × 1015M⊙ h-1,Msub = 2.5 × 1014M⊙ h-1) triaxial dark matter haloes. Starting with an initial separation of d = 0.57Mpch-1 in the top left panel, the distance between the two haloes is successively reduced until their centres finally overlap in the bottom right panel. |
| In the text | |
 |
Fig. 12 Schematic sketch of four particular orientations of merging triaxial dark matter haloes. The blue ellipsoid in the middle represents the projected mass density profile of the main halo. The red ellipsoids visualize the surface mass density profiles of the infalling subhaloes, which have different relative orientations with respect to the main halo. The black arrows indicate the directions of motion of the infalling structures. |
| In the text | |
 |
Fig. 13 Figure showing the evolution of different definitions of Einstein radii (see text) and the lensing cross section during a simulated cluster merger, assuming configuration (B) in Fig. 12. All quantities are plotted as a function of the distance between both halo centres. The dashed vertical line indicates the moment when the tangential critical curves merge. |
| In the text | |
 |
Fig. 14 Evolution of different definitions of Einstein radii (see text) and the lensing cross section during a simulated cluster merger, assuming configuration (A) of Fig. 12. All quantities are plotted as a function of the distance between the two halo centres. The dashed vertical line indicates the moment when the tangential critical curves merge. |
| In the text | |
 |
Fig. 15 Comparison of the correlation between Einstein radii and lensing cross sections for a sample of isolated triaxial dark matter haloes to the same correlation for a sample of merging triaxial dark matter haloes. The red solid line in the left (right) diagram indicates the best linear fit relation between median (effective) Einstein radii and lensing cross sections found for a sample of triaxial dark matter haloes at redshift zl = 0.5. The blue crosses represent selected pairs of Einstein radii and lensing cross sections during cluster mergers (see text for details). |
| In the text | |
 |
Fig. 16 Sketch illustrating our new algorithm for generating realistic cosmological halo populations that incorporates clusters mergers. An initial halo population at redshift z = 0 is evolved backwards in time using extended Press-Schechter merger trees and is finally projected onto the observer’s past null cone. |
| In the text | |
 |
Fig. 17 Comparison of the distributions of the largest Einstein radii including (blue patterned histogram) and excluding (red solid histogram) cluster mergers. The left (right) plot shows the histograms of all Einstein radii larger than 10″ (20″). |
| In the text | |
 |
Fig. 18 Tangential critical curves of the systems with the largest (left diagram), second largest (middle diagram), and third largest (right diagram) Einstein radius in our simulation including cluster mergers. The black cross in the centre indicates the position of the main halo. The red crosses mark the positions of all subhaloes that are enclosed in the tangential critical curve. |
| In the text | |
 |
Fig. 19 (Normalized) redshift distribution of the strong gravitational lenses with effective Einstein radii larger than 10″ including (blue solid histogram) and excluding (black patterned histogram) cluster mergers. In addition, the red stacks indicate the fraction of actively merging systems of all strong gravitational lenses represented by the blue solid histogram, i.e. including cluster mergers. Systems are classified as actively merging if more than one halo is enclosed by the tangential critical curve (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


