| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219396 | |
| Published online | 18 October 2012 | |
Analysis of the rotation period of asteroids (1865) Cerberus, (2100) Ra-Shalom, and (3103) Eger – search for the YORP effect⋆
1
Astronomical Institute, Faculty of Mathematics and Physics, Charles
University,
V Holešovičkách 2,
18000
Prague,
Czech Republic
e-mail: durech@sirrah.troja.mff.cuni.cz
2
Astronomical Observatory of Taras Shevshenko National University,
Astronomichna str.
3, Kiev,
Ukraine
3
Astronomical Observatory Institute, Faculty of Physics, Adam
Mickiewicz University, Słoneczna
36, 60-286
Poznań,
Poland
4 Ulugh Beg Astronomical Institute, Uzbek Academy of Sciences,
Astronomicheskaya 33, Tashkent 100052, Uzbekistan
5
Sonoita Research Observatory, 1442 E Roger Rd, Tuscon, AZ
85719,
USA
6
Physics and Astronomy Department, Appalachian State
University, Boone,
NC
28608,
USA
7
Crimean Astrophysical Observatory, Simeiz
Department, Simeiz
98680,
Ukraine
8
Kharadze Abastumani Astrophysical Observatory, Ilia State
University, G.Tsereteli str.
3, Tbilisi
0162,
Georgia
9
Department of Mathematics, Tampere University of
Technology, PO Box
553, 33101
Tampere,
Finland
10
Institute of Astronomy of Kharkiv National University,
Sumska str. 35,
Kharkiv
61022,
Ukraine
11
The Central (Pulkovo) Astronomical Observatory of the Russian
Academy of Sciences, Pulkovskoye
chaussee 65/1, St.-Petersburg
196140,
Russia
12
University of California at Berkeley, Department of
Astronomy, 601 Campbell
Hall, Berkeley,
CA
94720,
USA
13
Carl Sagan Center, SETI institute, 189 Bernardo Av.,
Mountain View
CA
94043,
USA
14
Keldysh Institute of Applied Mathematics,
RAS, Miusskaya sq.
4, 125047
Moscow,
Russia
15
Kingsgrove Observatory, 23 Monaro Ave., Kingsgrove, NSW, Australia
16
Department of Earth, Atmospheric, and Planetary Sciences,
Massachusetts Institute of Technology, Cambridge, MA
02139,
USA
17
Ondřejov Observatory, AV ČR, 251 65
Ondřejov, Czech
Republic
18
Konkoly Observatory of the Hungarian Academy of Sciences,
PO Box 67,
1525
Budapest,
Hungary
19
Goat Mountain Astronomical Research Station, 11355 Mount Johnson
Court, Rancho
Cucamonga, CA
91737,
USA
20
Department of Experimental Physics, University of
Szeged, Dóm tér 9,
6720
Szeged,
Hungary
21
Institut de Mécanique Céleste et de Calcul des Éphémérides,
Observatoire de Paris, UMR8028 CNRS, 77 Av. Denfert-Rochereau, 75014
Paris,
France
22
Palmer Divide Observatory, 17955 Bakers Farm Rd., Colorado Springs, CO
80908,
USA
23
ELTE Gao-Lendület Research Group, 9700
Szombathely,
Hungary
Received: 12 April 2012
Accepted: 5 September 2012
Context. The spin state of small asteroids can change on a long timescale by the Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect, the net torque that arises from anisotropically scattered sunlight and proper thermal radiation from an irregularly-shaped asteroid. The secular change in the rotation period caused by the YORP effect can be detected by analysis of asteroid photometric lightcurves.
Aims. We analyzed photometric lightcurves of near-Earth asteroids (1865) Cerberus, (2100) Ra-Shalom, and (3103) Eger with the aim to detect possible deviations from the constant rotation caused by the YORP effect.
Methods. We carried out new photometric observations of the three asteroids, combined the new lightcurves with archived data, and used the lightcurve inversion method to model the asteroid shape, pole direction, and rotation rate. The YORP effect was modeled as a linear change in the rotation rate in time dω/dt. Values of dω/dt derived from observations were compared with the values predicted by theory.
Results. We derived physical models for all three asteroids. We had to model Eger as a nonconvex body because the convex model failed to fit the lightcurves observed at high phase angles. We probably detected the acceleration of the rotation rate of Eger dω/dt = (1.4 ± 0.6) × 10-8 rad d-2 (3σ error), which corresponds to a decrease in the rotation period by 4.2 ms yr-1. The photometry of Cerberus and Ra-Shalom was consistent with a constant-period model, and no secular change in the spin rate was detected. We could only constrain maximum values of |dω/dt| < 8 × 10-9 rad d-2 for Cerberus, and |dω/dt| < 3 × 10-8 rad d-2 for Ra-Shalom.
Key words: minor planets, asteroids: individual: (1865) Cerberus / minor planets, asteroids: individual: (2100) Ra-Shalom / minor planets, asteroids: individual: (3103) Eger / methods: data analysis / techniques: photometric
Tables 1–3 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The anisotropic reflection of sunlight and thermal emission of an asteroid results in a net torque that modifies the asteroid’s spin state in the long term. This effect, called Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP), is important for the spin-state evolution of asteroids in the size range from ~1 m to ~40 km (Bottke et al. 2006). In particular, YORP can reorient the asteroid’s spin axis, slow down or spin up their rotation, and trigger a tumbling state. YORP has been found to be a key element in understanding the peculiar rotation pole distribution of large Koronis-family members (Vokrouhlický et al. 2003), the distribution of small members in moderately young asteroid families (Vokrouhlický et al. 2006), and the distribution of the rotation rate of small main-belt asteroids (Pravec et al. 2008; Polishook & Brosch 2009). Thanks to its ability to bring asteroid rotation toward the fission limit, it has been suggested that it is a universal formation mechanism for small binary asteroids (Scheeres 2007; Pravec & Harris 2007; Walsh et al. 2008) and asteroid pairs (Vokrouhlický & Nesvorný 2008; Pravec et al. 2010). Although the importance of YORP is now widely recognized, the YORP effect has been detected on only three asteroids so far: (1862) Apollo (Kaasalainen et al. 2007), (54509) YORP (Lowry et al. 2007; Taylor et al. 2007), and (1620) Geographos (Ďurech et al. 2008). Here we extend this list with a new YORP detection for asteroid (3103) Eger.
The primary importance of YORP detection for specific bodies consists in the possibility of validating the theoretical modeling of YORP itself. This is especially important after several studies have demonstrated possible difficulties in the theoretical prediction of the YORP effect magnitude, such as a non-uniform distribution of density (Scheeres & Gaskell 2008), a sensitive dependence on small-scale irregularities in the shape (Statler 2009; Breiter et al. 2009) and the degree of thermal beaming (Rozitis & Green 2012). As a result, some cases of nondetections might be as important as the positive detections (Scheeres & Gaskell 2008; Breiter et al. 2009). These are the cases where the simple YORP theory predicts a possible detection for a present data set, yet an accurate analysis of the observations does not reveal any sign of it.
Motivated by the discussion above, we present new photometric observations of near-Earth asteroids (1865) Cerberus, (2100) Ra-Shalom, and (3108) Eger. We derived a shape model and spin state for these asteroids and detected the acceleration of the rotation rate of Eger, which we believe is produced by the YORP effect1. For the two other asteroids we studied – (1865) Cerberus and (2100) Ra-Shalom – we set only upper limits on the change in the rotation rate. While in the Ra-Shalom case this observational bound is about the upper limit of the expected theoretical YORP value for a body of its size and heliocentric orbit, in the case of Cerberus, the constraint is much stronger. Reminiscent of the case of (25143) Itokawa, the expected Cerberus YORP value is a factor of ~3 higher than its observed limit.
2. Lightcurve inversion and search for the rotation-period change
We used the lightcurve inversion method of Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001) to derive asteroids’ shape, sidereal rotation period, and spin axis direction from the observed lightcurves. Following the method of Kaasalainen et al. (2003), we assumed that the rotation rate ω changes linearly with time as ω(t) = ω0 + υt. Both ω0 and υ ≡ dω/dt were free parameters of the optimization. We analyzed the difference (measured by the χ2 values of the goodness-of-fit) between a constant-period model (υ = 0) and a model with υ ≠ 0. If this difference is small, the data can be fitted with the constant-period model and no deviation from the uniform rotation is detected. If, on the other hand, the fit for υ ≠ 0 is significantly better than for υ = 0, the change in the rotation rate is detected.
We found a significant change in the rotation period only for asteroid Eger. For Cerberus and Ra-Shalom, the constant-period model fitted the available data well, and the free parameter υ did not improve the fit significantly. To estimate the maximum value of |dω/dt| that still agrees with observations, we increased or decreased υ and found the value of χ2, for which the discrepancy between the data and the model became significant.
2.1. (3103) Eger
Kaasalainen et al. (2002) have derived a preliminary shape model of Eger from 13 lightcurves observed between 1986 and 1997. These lightcurves were obtained by Wisniewski (1987), Wisniewski (1991), Velichko et al. (1992), de Sanctis et al. (1994), and Pravec et al. (1998). The data were archived in the Uppsala Asteroid Photometric Catalog (UAPC) (Lagerkvist et al. 2001). We observed Eger during its seven apparitions between 1997 and 2012. The aspect data for these new photometric observations are listed in Table 1. A detailed description of the reduction and measurement procedures at the Wise Observatory can be found in Polishook & Brosch (2008). CCD observations and data processing at Kharkiv, Simeiz, Maidanak, Lisnyky, and Kitab observatories were done in the standard way, and the details can be found in Krugly et al. (2002). It is particularly important that during three apparitions – 1997, 2007, and 2009 – our observations were not taken at the Earth close encounters of Eger, thus providing data at new viewing geometries. This is because Eger is presently close to the 3/5 exterior mean motion resonance with the Earth (Milani et al. 1989), and so the viewing geometry at close approaches repeats.
The photometric data set consists of 70 lightcurves covering more than twenty years. Some of them were observed at unusually high phase angles larger than 75deg. The usual approach of lightcurve inversion – using the convex shape model, together with the combination of Lommel-Seeliger and Lambert scattering laws – did not succeed in fitting these high-phase lightcurves. The large discrepancy between the data and the model was an indication of a significant nonconvexity of the shape of Eger (Ďurech & Kaasalainen 2003). When we used Hapke’s scattering model, the fit improved but was still not good. However, we obtained a good fit when modeling the shape of Eger as a general nonconvex body using the approach of Kaasalainen & Viikinkoski (2012).
We derived a unique solution for the sidereal rotation period P, the change in the rotation rate υ, the pole direction λ,β in ecliptic coordinates, and the shape. The best-fit parameters are as follows: λ = 226° ± 15°, β = −70° ± 4°, P = 5.710156 ± 0.000007 h (for JD 2446617.0), and υ = (1.4 ± 0.6) × 10-8 rad d-2. These parameters and their uncertainties were derived using the weights of individual lightcurves that corresponded to the inverse of the noise. When all lightcurves have the same weight regardless of their quality, the formal best-fit value of υ is 1.2 × 10-8 rad d-2. The fit to the lightcurves for υ = 0 is very good with only small phase shifts between the model and the data. However, using nonzero values for the υ parameter improves the fit significantly. The uncertainty intervals were estimated from the increase in χ2 when varying the model parameters. The reported errors correspond to 3σ for the χ2 distribution with ~4700 degrees of freedom2. Although the relative uncertainty of υ is large, the zero value is outside the formal uncertainty interval. For υ = 0, the fit is significantly worse (30% higher χ2) than for the best model. We also note that the angular difference of ~55° between our solution and the best-fit solution by Kaasalainen et al. (2002) is significant and arises from the limited number of lightcurves used to derive the previous model. The pole direction is very well constrained and is not sensitive to the value of υ, the scattering model, or the shape parametrization. The 3σ uncertainty region is shown in Fig. 1.
 |
Fig. 1 Statistical quality of Eger pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 226° and β = −70° is marked with a full circle. The solid line shows the contour with the χ2 value 6% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. |
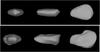 |
Fig. 2 Convex (top) and nonconvex (bottom) shape models of Eger shown from equatorial level (left, center) and pole-on (right). |
 |
Fig. 3 Examples of Eger’s photometric data (points) fitted with synthetic lightcurves based on the convex shape model. The solid curve corresponds to the best model with the rotation rate accelerated by υ = 1.2 × 10-8 rad d-2, while the dashed curve corresponds to the best constant-period model with υ = 0. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
As an additional check of consistency, we note that our pole solution closely matches a constraint that was suggested from the 1991 and 1996 radar observations (Benner et al. 1997). In particular, the viewing geometry at the end of July 1996 was nearly equatorial for our pole as suggested by this reference. In 1991 Aug. 10, the line of sight was indeed closer to the pole by ~15°.
The shape model of Eger is shown in Fig. 2. Although some of the lightcurves (those published by Pravec et al. 1998) were accurately calibrated to standard R or V magnitudes, they did not cover the viewing/illumination geometry sufficiently to use them for constraining the model. Therefore, we treated all the calibrated lightcurves as relative.
In general, nonconvex models are much less stable than convex ones with respect to the errors in the data, the level of regularization, the scattering model, etc. However, this is the first time the nonconvex shape fits the lightcurves that were observed at large phase angles significantly better than the convex one. The nonconvex model in Fig. 2 is only one of many similar models that we obtained using different regularization, scattering models, and resolution. Apparently, the model contains many details that may lead to misinterpretation. The main concavity is likely to be real because it repeats for models with different regularization. The other details differ from model to model and are instead artifacts of the modeling process.
The lightcurve fits for models with υ = 0 and υ ≠ 0 are shown in Fig. 3. The difference between the two models is clearly visible only for lightcurves from 1986, 1987, and 1996. Because both the number of lightcurves and the number of data points in the lightcurves increase towards more recent observations, there is almost no phase shift between the models for observations between 2006–2012. The sign of the phase shift is different for different epochs.
This is further demonstrated in Fig. 4, where the shift in phase between the observed and modeled lighcurves is plotted. Although the scatter in the phase shifts is of minutes, there is a clear quadratic trend for the constant period model (top panel), which is what we expect if the rotation rate changes linearly in time. The best-fit quadratic function corresponds to υ = 0.8 × 10-8 rad d-2. This is different from the value obtained by the lightcurve inversion, because with lightcurve inversion, the difference between the observed and modeled brightness is minimized, not the phase shift between the observed and modeled lightcurves. In the bottom panel, the phase differencies are plotted for the YORP model with υ = 1.2 × 10-8 rad d-2 (equal weights for all lightcurves). For this value of υ, there is no quadratic trend, and the points are randomly distributed along the zero value.
However, the period analysis depends critically on the observations from 1986/87 and is very sensitive to possible systematic errors. Although the data came from three different works (Wisniewski 1987, 1991; de Sanctis et al. 1994), which should largely eliminate any possible observational errors, there is an insufficient check against potential systematic model errors. Therefore, our detection of the acceleration of Eger’s rotation due to YORP appears plausible, but it will have to be nailed down with more observations in upcoming apparitions (2014, 2016, 2017, 2019, etc.) so that it becomes a robust detection. With more observations, the time line will be enlarged and the quadratic trend seen in Fig. 4 can be confirmed.
2.2. (1865) Cerberus
Cerberus lightcurves are characterized by unusually large amplitude, up to 2.3 mag, which is the largest lightcurve amplitude observed so far for any asteroid. The UAPC contains the photometry of Cerberus from 1980 (Harris & Young 1989), 1989 (Wisniewski et al. 1997), and 1998 (Sárneczky et al. 1999), while additional photometric observations were published by Szabó et al. (2001). Until now, any pole solution had not been determined. We observed Cerberus during three apparitions in 1999, 2008, and 2009. The circumstances of these observations are listed in Table 2.
 |
Fig. 4 Shift in phase between the observed and modeled lightcurves for the constant-period model (top) and the model with YORP (bottom), υ = 1.2 × 10-8 rad d-2. The points in the top panel are fitted with a quadratic function. |
We derived a physical model of Cerberus with the sidereal rotation period P = 6.80328 ± 0.00001 h and the pole direction λ = 298° ± 40°, β = −72° ± 10°. The pole direction is well constrained, and the 3σ uncertainty region is shown in Fig. 7. The convex shape model (Fig. 5) is very elongated with semiaxis ratios a/c ≃ 4.5 and b/c ≃ 1.5, suggesting that the real shape of Cerberus might be bilobed or even consist of a close synchronous binary. When using calibrated lightcurves, the model is even more elongated and flat with a/c ~ 7 and b/c ~ 2. The constant-period model fits well with all available lightcurves. Introducing the υ ≠ 0 parameter into the modeling did not improve the fit. We estimated the maximum allowed absolute value of the period change to be |υ| < 8 × 10-9 rad d-2. If the change in the rotation rate were higher, it would be detectable in the lightcurve set as a shift between observations and the model of about 10°.
2.3. (2100) Ra-Shalom
The UAPC contains lightcurves of Ra-Shalom from 1978 to 1997 obtained by Harris et al. (1992), Ostro et al. (1984), and Pravec et al. (1998). Kaasalainen et al. (2004) used this dataset, together with a few Ondřejov lightcurves from Ra-Shalom’s apparition in 2000, to construct a pole and shape model. Because their data set was limited, they flagged their model to be only a preliminary attempt. Indeed, it is significantly different from the new one we present here, because we used additional photometry from 2003 and 2009 listed in Table 3. The derived shape model is shown in Fig. 8 and the fit to selected lightcurves in Fig. 9. While our model is an improvement, it is still not perfect. In particular, the pole direction is still not well constrained, with the formally best solution at λ = 313° and β = −45°. The statistically admissible solutions cover an irregularly-shaped region on the sky as shown in Fig. 10. The contour corresponds to solutions with an 8% higher value of χ2 than the minimum. Because the number of degrees of freedom is ν ≃ 2300, the 8% increase corresponds to 3σ in the χ2 distribution (see the footnote on page ). The statistical weight of prograde-rotating spin solutions is negligible. All solutions in our formal 3σ region correspond to a retrograde sense of rotation for Ra-Shalom. That our zone of admissible pole solutions is a subset of a similar zone presented by Shepard et al. (2008) (see Fig. 7 in this reference), who carefully analyzed radar and other wavelength observations of Ra-Shalom, gives us an increased confidence in our solution. The sidereal rotation period is P = 19.8201 ± 0.0004 h. No deviation from uniform rotation has been detected so far. The maximum value of the change in the rotation rate was estimated to − 4 × 10-8 < υ < 2 × 10-8 rad d-2.
3. Discussion
Two of our pole solutions, namely those of Eger and Cerberus, correspond to a near-extreme obliquity value: we have ε ≃ 176° for Eger and ε ≃ 178° for Cerberus. Both values have about a 10° uncertainty in realistic terms. While the formal obliquity value of the best-fit solution for Ra-Shalom is ≃ 144°, Fig. 10 indicates that basically all retrograde values are possible, including the value near 180° (note location of the orbital south pole in this figure), so at least two, possibly even all three, of our asteroids belong to the most populated class of near-Earth objects, those with an extremely high value of obliquity (La Spina et al. 2004; Kryszczyńska et al. 2007).
The retrograde sense of rotation for all our targets is consistent with an independent estimate of the Yarkovsky acceleration in their orbits. Chesley et al. (2008) attempted to estimate Yarkovsky effect in orbits of all near-Earth asteroids by including a formal along-track acceleration in their orbital fit and by estimating the related parameter da/dt, namely a secular change in the orbital semimajor axis a (see also Nugent et al. 2012). Because the diurnal variant of the Yarkovsky effect is dominant in the dynamics of near-Earth asteroids, a positive/negative value for da/dt value implies a prograde/retrograde sense of rotation of the asteroid (see, for example, Bottke et al. 2006). In the case of all three asteroids discussed in this paper, Chesley et al. (2008) give a negative best-fit value for da/dt, thus requiring a retrograde sense of their rotation. This is especially important for Ra-Shalom, for which the previous solution by Kaasalainen et al. (2004) implies prograde rotation, while here we find a retrograde solution.
3.1. Theoretical YORP strengths
We now proceed with a theoretical estimation of the YORP strength for our targets. In a sense, this is merely a consistency check that the observed secular increase in the rotation rate υ (in the case of Eger) can be interpreted as a YORP effect detection. This is because a number of parameters, such as exact size, bulk density, and surface conductivity, are only weakly constrained, and even knowledge of the large-scale surface-shape features may still not be enough for precise YORP computations (Statler 2009; Breiter et al. 2009; Rozitis & Green 2012; Golubov & Krugly 2012).
 |
Fig. 5 Convex shape model of Cerberus shown from equatorial level (left, center) and pole-on (right). |
 |
Fig. 6 Examples of Cerberus’ lightcurves fitted with synthetic ones based on the convex shape model. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
 |
Fig. 7 Statistical quality of Cerberus pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 298° and β = − 72° is marked with a full circle. The solid line shows the contour with the χ2 value 10% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. |
(3103) Eger.
We used the model of Breiter & Vokrouhlický (2011) to estimate the YORP value of υ for our shape of Eger. We considered parameters of the Hapke scattering model of the E-type asteroids (Breiter & Vokrouhlický 2011) and varied the value of geometric albedo between 0.4 and 0.6. This is because the latest solutions presented by Trilling et al. (2010) and Harris et al. (2011) give a little larger size of D ≃ 1.78 km for a lower albedo value of p ≃ 0.39, while previous solutions had smaller sizes of D ≃ 1.5 km and larger albedo (Benner et al. 1997). We also varied the bulk density value between 2.5 and 3 g/cm3 and assumed surface thermal conductivity of 0.01 W/m/K. However, as was shown by Breiter et al. (2010), for 1D thermal models, the resulting YORP value of υ does not depend on the value of conductivity. We scaled the lightcurve-inversion shape model (Fig. 2) to have the same volume as a sphere of 1.78 km size. A straightforward use of our model gives values for υ between 4.1 × 10-8 rad d-2 and 8.3 × 10-8 rad d-2. However, we note that the lightcurve inversion technique does not a priori constrain the axes of the shape model to coincide with the principal axes of the inertia tensor. Obviously a large difference would signal a suspicious model. Assuming a homogeneous density distribution, we find there is about a 5° tilt between the z-axes of the two systems, which is too small an angle for the correction to be determined by photometry analysis. Assuming thus that the body rotates about its shortest axis of the inertia tensor, and preserving the body’s shape, we now obtain υ values between 4.4 × 10-8 rad d-2 and 7.5 × 10-8 rad d-2. Compared to the observed value υ = (1.4 ± 0.6) × 10-8 rad d-2, our estimates are a factor of three to six times higher, a situation similar to the case of (54509) YORP (Lowry et al. 2007; Taylor et al. 2007). In the latter case, the lightcurve and radar data were not able to sample signal from about 30% of the surface, which was one of the sources of the difference between the observed and computed υ values. In the case of Eger, we only have knowledge of the large-scale features of the asteroid shape – the lightcurve data do not give any information about the small-scale irregularities of the shape and the effects of thermal beaming. We believe this is the main source of the difference between the observed value for υ and the one computed from YORP theory. Indeed, Benner et al. (1997) provide a hint from the analysis of the radar ranging to Eger that these small-scale features might actually be very significant.
 |
Fig. 8 Convex shape model of Ra-Shalom shown from equatorial level (left, center) and pole-on (right). |
 |
Fig. 9 Examples of Ra-Shalom’s lightcurves fitted with synthetic ones based on the convex shape model. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
 |
Fig. 10 Statistical quality of Ra-Shalom pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 313° and β = − 45° is marked with a full circle. The solid line shows the contour with the χ2 value 8% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. The pole of the orbital plane corresponding to 180° obliquity, shown by the triangle, is located close to this zone. |
(1865) Cerberus.
The shape of Cerberus derived above suggests that even its large-scale structures were not accurately determined by our convex model. Obviously, we could have tried to resolve some nonconvexities in the model, too, but the currently available set of the photometric observations is not large enough to derive a unique model. We thus consider our convex model as the current, but certainly preliminary, state-of-the-art representation of its shape. We used the mean Hapke parameters of the S-type asteroids in this case (Breiter & Vokrouhlický 2011) and scaled the shape model to have the same volume as a sphere with the diameter of 1.6 km (Mainzer et al. 2011). We also varied the geometric albedo value between 0.1 and 0.2. The bulk density was 2.5 g/cm3. With these values, we obtained the YORP-predicted υ ≃ 2 × 10-8 rad d-2, which was two to three times larger than the conservative bound we obtained from the observations in Sect. 2.2. Obviously, this difference may be due to a number of unconstrained factors, the inaccurate shape model first of all. The key to further analysis of the Cerberus case consists in obtaining additional observations, which are needed not only for possible future detection of the YORP effect but also for improving the shape model itself. A good opportunity occurred in October 2016, when this asteroid could be observed at large phase angles, and from September to November 2017.
It is interesting to note that the photometric data are consistent with a highly nonconvex, bilobed model, but they might also be fitted with a very close binary system. Using the analysis performed by Bellerose & Scheeres (2008) or Scheeres (2009), we note there are possible stable equilibria of two ellipsoids (or an ellipsoid and a sphere) with reasonable density values between 1 and 3 g/cm3 that could match a synchronously rotating system with Cerberus’ observed period of ~6.81 h and small separations.
(2100) Ra-Shalom.
In the case of Ra-Shalom, we scaled our shape model to be equivalent to a sphere of ~2.3 km size (Shepard et al. 2008; Trilling et al. 2010; Harris et al. 2011) and took a geometric albedo of 0.1 (Ra-Shalom is an S-type asteroid). We used a bulk density of 2 g/cm3 and our best-fit formal solution for the pole. The formal obliquity value ε ≃ 144° tends to minimize the computed effect because YORP has been found to have a node υ ≃ 0 near ε ≃ 125° for generic shapes (Čapek & Vokrouhlický 2004; Vokrouhlický & Čapek 2002). With these parameter values, we obtained υ ≃ − 6 × 10-8 rad d-2, a little larger than its upper bound derived from the lightcurve observations (Sect. 2.3). For this value, we had a negative value of υ = dω/dt, implying that, for a given shape model, YORP should decelerate the rotation rate of the body. This conclusion would seem consistent with the rather long rotation period of ≃ 19.82 h of this asteroid. However, we should point out the large current uncertainty in the obliquity of the pole solution (Fig. 10). For instance, sampling the uncertainty region by pole positions along the meridian of the formally best solution (i.e., keeping longitude equal to 313°) and taking latitude values from −10° to −75°, we obtain υ values from 2 × 10-8 rad d-2 to −9 × 10-8 rad d-2. As expected, for obliquities below ~125°, we obtain a positive value for υ; however, for obliquities greater than ~125°, which includes the formally best-fit solution, the value for υ is negative. While positive υ values still cannot be excluded, the majority of pole solutions in the uncertainty interval shown in Fig. 10 correspond to negative υ values. As a result, if carefully observed during the next few years (notably in late summer 2013 and 2016), Ra-Shalom might become the first asteroid for which YORP will be found to decrease the rotation rate.
Online material
Aspect data for new observations of Eger.
Aspect data for new observations of Cerberus.
Aspect data for new observations of Ra-Shalom.
The whole lightcurve dataset, shape model parameters, and other details are available from the DAMIT website http://astro.troja.mff.cuni.cz/projects/asteroids3D (see also Ďurech et al. 2010).
Acknowledgments
We thank an anonymous referee for helpful comments that improved the final version. The work of J.Ď. and D.V. was supported by grants P209/10/0537, 205/08/0064, and P209/12/0229 of the Czech Science Foundation and by the Research Program MSM0021620860 of the Ministry of Education. The work of S.B. was supported by the Polish National Science Center – grant NN 203404139. The work of M.K. was supported by the Academy of Finland. The work of P.P. was supported by grant P209/12/0229 of the Czech Science Foundation. D.P. is grateful to the AXA research fund and to the continuous support from the Wise Observatory staff. F.M. was supported by the National Science Foundation under award number AAG-08077468. G.S. was supported by Hungarian OTKA Grants K-104607, MB08C 81013, a “Lendulet” Programme and a Bolyai Research Fellowship of the Hungarian Academy of Sciences.
References
- Bellerose, J., & Scheeres, D. J. 2008, Celest. Mech. Dyn. Astron., 100, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Benner, L. A. M., Ostro, S. J., Giorgini, J. D., et al. 1997, Icarus, 130, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, Jr., W. F.,Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [Google Scholar]
- Breiter, S., & Vokrouhlický, D. 2011, MNRAS, 410, 2807 [Google Scholar]
- Breiter, S., Bartczak, P., Czekaj, M., Oczujda, B., & Vokrouhlický, D. 2009, A&A, 507, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breiter, S., Bartczak, P., & Czekaj, M. 2010, MNRAS, 408, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Vokrouhlický, D., Ostro, S. J., et al. 2008, LPI Contributions, 1405, 8330 [NASA ADS] [Google Scholar]
- de Sanctis, M. C., Barucci, M. A., Angeli, C. A., et al. 1994, Planet. Space Sci., 42, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Vokrouhlický, D., Kaasalainen, M., et al. 2008, A&A, 488, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golubov, O., & Krugly, Y. N. 2012, ApJ, 752, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. W. 1989, Icarus, 81, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Dockweiler, T., et al. 1992, Icarus, 95, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Mommert, M., Hora, J. L., et al. 2011, AJ, 141, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Viikinkoski, M. 2012, A&A, 543, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Piironen, J. 2002, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Pravec, P., Krugly, Y. N., et al. 2004, Icarus, 167, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Ďurech, J., Warner, B. D., Krugly, Y. N., & Gaftonyuk, N. M. 2007, Nature, 446, 420 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kaasalainen, S., Piironen, J., Kaasalainen, M., et al. 2003, Icarus, 161, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Krugly, Y. N., Belskaya, I. N., Shevchenko, V. G., et al. 2002, Icarus, 158, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Kryszczyńska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef] [Google Scholar]
- LaSpina, A., Paolicchi, P., Kryszczyńska, A., & Pravec, P. 2004, Nature, 428, 400 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagerkvist, C.-I., Piironen, J., & Erikson, A. 2001, Asteroid photometric catalogue, fifth update (Uppsala Astronomical Observatory) [Google Scholar]
- Lowry, S. C., Fitzsimmons, A., Pravec, P., et al. 2007, Science, 316, 272 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mainzer, A., Grav, T., Bauer, J., et al. 2011, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Carpino, M., Hahn, G., & Nobili, A. M. 1989, Icarus, 78, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, C. R., Margot, J. L., Chesley, S. R., & Vokrouhlický, D. 2012, AJ, 144, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Ostro, S. J., Harris, A. W., Campbell, D. B., Shapiro, I. I., & Young, J. W. 1984, Icarus, 60, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., & Brosch, N. 2008, Icarus, 194, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., & Brosch, N. 2009, Icarus, 199, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., & Harris, A. W. 2007, Icarus, 190, 250 [CrossRef] [Google Scholar]
- Pravec, P., Wolf, M., & Šarounová, L. 1998, Icarus, 136, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Vokrouhlický, D., et al. 2008, Icarus, 197, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Vokrouhlický, D., Polishook, D., et al. 2010, Nature, 466, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Rozitis, B., & Green, S. F. 2012, MNRAS, 423, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sárneczky, K., Szabó, G., & Kiss, L. L. 1999, A&AS, 137, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheeres, D. J. 2007, Icarus, 189, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J. 2009, Celest. Mech. Dyn. Astron., 104, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., & Gaskell, R. W. 2008, Icarus, 198, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Shepard, M. K., Clark, B. E., Nolan, M. C., et al. 2008, Icarus, 193, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S. 2009, Icarus, 202, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G. M., Csák, B., Sárneczky, K., & Kiss, L. L. 2001, A&A, 375, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, P. A., Margot, J.-L., Vokrouhlický, D., et al. 2007, Science, 316, 274 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trilling, D. E., Mueller, M., Hora, J. L., et al. 2010, AJ, 140, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Velichko, F. P., Krugly, Y. N., & Chiorny, V. G. 1992, Astronomicheskij Tsirkulyar, 1553, 37 [NASA ADS] [Google Scholar]
- Vokrouhlický, D., & Čapek, D. 2002, Icarus, 159, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2008, AJ, 136, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vokrouhlický, D., Brož, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A. 2006, Icarus, 182, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Richardson, D. C., & Michel, P. 2008, Nature, 454, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Wisniewski, W. Z. 1987, Icarus, 70, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Wisniewski, W. Z. 1991, Icarus, 90, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Wisniewski, W. Z., Michalowski, T. M., Harris, A. W., & McMillan, R. S. 1997, Icarus, 126, 395 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Statistical quality of Eger pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 226° and β = −70° is marked with a full circle. The solid line shows the contour with the χ2 value 6% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. |
| In the text | |
 |
Fig. 2 Convex (top) and nonconvex (bottom) shape models of Eger shown from equatorial level (left, center) and pole-on (right). |
| In the text | |
 |
Fig. 3 Examples of Eger’s photometric data (points) fitted with synthetic lightcurves based on the convex shape model. The solid curve corresponds to the best model with the rotation rate accelerated by υ = 1.2 × 10-8 rad d-2, while the dashed curve corresponds to the best constant-period model with υ = 0. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
| In the text | |
 |
Fig. 4 Shift in phase between the observed and modeled lightcurves for the constant-period model (top) and the model with YORP (bottom), υ = 1.2 × 10-8 rad d-2. The points in the top panel are fitted with a quadratic function. |
| In the text | |
 |
Fig. 5 Convex shape model of Cerberus shown from equatorial level (left, center) and pole-on (right). |
| In the text | |
 |
Fig. 6 Examples of Cerberus’ lightcurves fitted with synthetic ones based on the convex shape model. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
| In the text | |
 |
Fig. 7 Statistical quality of Cerberus pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 298° and β = − 72° is marked with a full circle. The solid line shows the contour with the χ2 value 10% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. |
| In the text | |
 |
Fig. 8 Convex shape model of Ra-Shalom shown from equatorial level (left, center) and pole-on (right). |
| In the text | |
 |
Fig. 9 Examples of Ra-Shalom’s lightcurves fitted with synthetic ones based on the convex shape model. The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α. |
| In the text | |
 |
Fig. 10 Statistical quality of Ra-Shalom pole solutions given in sinusoidal projection of the sky in ecliptic coordinates. The grade of shading and the scale bar on the right indicate the χ2 of the fit divided by the number of data points. The formally best-fit case with λ = 313° and β = − 45° is marked with a full circle. The solid line shows the contour with the χ2 value 8% higher than the minimum value of the best-fit solution. It represents our region of admissible solutions. The pole of the orbital plane corresponding to 180° obliquity, shown by the triangle, is located close to this zone. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


