| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201118418 | |
| Published online | 19 October 2012 | |
Relativistic quantum mechanical calculations of electron-impact broadening for spectral lines in Be-like ions
1
Data Center for High Energy Density Physics, Institute of Applied Physics
and Computation Mathematics,
100088
Beijing,
PR China
e-mail: alexduan1967@hotmail.com, duan_bin@iapcm.ac.cn
2
Pakistan Atomic Energy Commission, PO Box 1114,
44000
Islamabad,
Pakistan
3
HEDPS, Center for Applied Physics and Technology, Peking
University, 100871
Beijing, PR
China
Received:
8
November
2011
Accepted:
6
August
2012
Aims. We present relativistic quantum mechanical calculations of electron-impact broadening of the singlet and triplet transition 2s3s ← 2s3p in four Be-like ions from N IV to Ne VII.
Methods. In our theoretical calculations, the K-matrix and related symmetry information determined by the colliding systems are generated by the DARC codes.
Results. A careful comparison between our calculations and experimental results shows good agreement. Our calculated widths of spectral lines also agree with earlier theoretical results. Our investigations provide new methods of calculating electron-impact broadening parameters for plasma diagnostics.
Key words: line: profiles / atomic processes / atomic data
© ESO, 2012
1. Introduction
Generally, radiation damping of an excited atom leads to broadening of spectral lines. In dense plasmas, radiation damping stems from the interactions of an emitting atom or ion with perturbing plasma constituents. Among these interactions, the electron colliding with ions can lead to excitations and broadening of ionic spectral lines. The electron-impact broadening is a major contributor to radiative acceleration in stellar interiors and is of particular importance as a diagnostic tool in high-temperature plasmas. Not only is it important to precision spectroscopy, but also reveals dependence on major plasma characteristics, such as density and temperature. In the case of plasma diagnostics, the careful analysis of line profiles is a powerful technique for studying atomic and molecular interactions. The knowledge of electron-impact broadening is paramount for probing matter under extreme physical conditions such as in stellar atmospheres. In stellar interiors, electron-impact broadening contributes significantly to radiative acceleration, because of high electron density, and is imperative for evolutionary models, atomic abundances, and radiative opacity calculations.
To study electron-impact broadening, several theoretical methods and techniques have been used in the literature (Griem 1974; Dimitrijević & Konjević1980). However, there have been very few quantum mechanical calculations of electron-impact broadening and shift in spectral lines. Recently, the full quantum mechanical calculations for electron impact broadening of the 2s3s−2s3p transitions for the four Be-like ions from N IV to Ne VII have been performed by Elabidi et al. (2008). These calculations are based on the nonrelativistic quantum mechanics and intermediate coupling. In the context of quantum mechanics, electron-impact broadening and shift of spectral lines is studied by two different methods, i.e., calculating the scattering cross sections and generating the K-matrix. In the present work, we adopt the latter approach, defined by calculating K-matrix, which is similar to the method adopted by Seaton (1987).
The main aim of this paper is to perform quantum mechanical calculations of electron-impact broadening of the transition 2s3s ← 2s3p in Be-like ions, i.e., N IV, O V, F VI, and Ne VII. We also report new electron-impact broadening parameters for transitions in Be-like ions. We employ the impact approximation theory to obtain line broadening and shift parameters at various plasma conditions. In our numerical computations, Dirac Atomic R-matrix Codes (DARC) and General Purpose Relativistic Atomic Structure Package (GRASP0-10.10; Norrington 2009) are used to solve (N + 1)-electron colliding systems so that the scattering matrices (reactance matrices) are obtained. The paper is organized as follows. Section 2 gives details of the methods used to calculate electron-impact broadening parameters. It also outlines the impact approximation and scattering matrix theory. Section 3 explains our strategy for constructing the atomic structure of each ion and selection of configurations. The comparison between experimental and theoretical data, accuracy of our results, final selected data of spectral line widths, the content and organization of the delivered tables are described in Sect. 4. Our conclusions are given in Sect. 5.
2. Theory and methods
2.1. Impact approximation theory
In dense plasmas, spectral line broadening arises from perturbations by the constituents
of the plasma (both ions and electrons). Ions have large masses than electron and always
move much slowly, so in evaluating line broadening parameters it is often a good
approximation to treat them as being stationary. The effect of stationary ions is equal to
an average ion microfield, introduced by Hooper (1966). This microfield perturbs the radiating ions by Stark effect and leads to
spectral line broadening, known as Stark broadening. Similarly, the high-speed electrons
also perturb the emitting ions through collisions, and cause the interruption of
spontaneous emission. This interruption will broaden the widths of emission lines, and is
known as electron-impact broadening. The radiative transition of spontaneous emission
between upper (Xb) and lower
state (Xa) of radiating ion is written as:
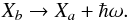 (1)The
impact approximation theory was first formulated by Baranger (1958a−c) and later reviewed by Griem (1974). The theory considers a single binary collision between the perturber and
the perturbed ion. During the time of electron collision with a radiating ion, the
interaction between perturbing ions is ignored, and at a time each electron interacts only
with one perturbed ion. Within impact approximation and the isolated line approximation,
the line profile is Lorentzian, i.e.,
(1)The
impact approximation theory was first formulated by Baranger (1958a−c) and later reviewed by Griem (1974). The theory considers a single binary collision between the perturber and
the perturbed ion. During the time of electron collision with a radiating ion, the
interaction between perturbing ions is ignored, and at a time each electron interacts only
with one perturbed ion. Within impact approximation and the isolated line approximation,
the line profile is Lorentzian, i.e.,
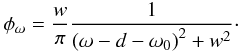 (2)Where
ω0 is the central line frequency, d is the
shift, and 2w is the spectral line full width at half maximum. The width
and shift of a spectral line are linearly proportional to electron
density Ne and depend on the scattering
matrix S for binary collisions. The final expression relating
the shift and width of a spectral line could be obtained by averaging over Maxwell
distribution of electron velocities. A simplified and compact expression has independently
also been derived by Elabidi et al. 2004 in
intermediate coupling scheme:
(2)Where
ω0 is the central line frequency, d is the
shift, and 2w is the spectral line full width at half maximum. The width
and shift of a spectral line are linearly proportional to electron
density Ne and depend on the scattering
matrix S for binary collisions. The final expression relating
the shift and width of a spectral line could be obtained by averaging over Maxwell
distribution of electron velocities. A simplified and compact expression has independently
also been derived by Elabidi et al. 2004 in
intermediate coupling scheme: 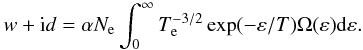 (3)Where
parameter α = 2.8674 × 10-23 eV cm3. The units
of electron density Ne is cm-3. Electron
temperature Te and colliding electron
energy ε are in Rydberg, and spectral line width w and shift d are
in eV. The electron collision strength Ω(ε) in jj coupling is defined by
Peach (1996) (if intermediate coupling is
considered, Ω(ε) can be found in the works of Elabidi et al. 2004; or Elabidi et al. 2008), i.e.,
(3)Where
parameter α = 2.8674 × 10-23 eV cm3. The units
of electron density Ne is cm-3. Electron
temperature Te and colliding electron
energy ε are in Rydberg, and spectral line width w and shift d are
in eV. The electron collision strength Ω(ε) in jj coupling is defined by
Peach (1996) (if intermediate coupling is
considered, Ω(ε) can be found in the works of Elabidi et al. 2004; or Elabidi et al. 2008), i.e., ![\begin{eqnarray} \Omega(\varepsilon) &= \sum\limits_{J^{T}_{i} J^{T}_{f} jj^{'} \ell \ell^{'}} (-1)^{J_{i}+J_{i^{'}}+2{J^{T}_{f}}+ j+j^{'}} {1 \over 2 } \left(2 J^{T}_{i}+1\right) \nonumber\\[1.5mm] &\quad\times \left(2 J^{T}_{f}+1\right)\displaystyle \left\{ \begin{array}{ccc} J^{T}_{f} & J^{T}_{i}& 1\\[1.5mm] J_{i} & J_{f}& j \end{array} \displaystyle \right\} \displaystyle \left\{ \begin{array}{ccc} J^{T}_{f} & J^{T}_{i}& 1\\[1.5mm] J_{i^{'}} & J_{f^{'}}& j^{'}\\ \end{array} \displaystyle \right\} \nonumber\\[1.5mm] &\quad\times \displaystyle {1 \over 2 } \displaystyle \left[ \delta _{\ell \ell{'}} \delta _{jj^{'}} \delta _{J_{i} J_{ i^{'}}} \delta_{J_{f} J_{f^{'}}} -\textbf{S}_{I}\left(J_{i^{'}} \ell {'} j^{'}J^{T}_{i},J_{i} \ell j J^{T}_{i}\right) \right.\nonumber\\[1.5mm] &\quad\times \left.\textbf{S}^{*}_{F}\left(J_{f^{'}} \ell {'} j^{'}J^{T}_{f},J_{f} \ell j J^{T}_{f}\right) \displaystyle \displaystyle \right]. \end{eqnarray}](/articles/aa/full_html/2012/11/aa18418-11/aa18418-11-eq24.png) (4)Where
two { ... } are the “6j” symbols. The upper and lower
states of the transition are represented by the total angular momentum states
|JiMi ⟩
and |JfMf ⟩
respectively, and
(4)Where
two { ... } are the “6j” symbols. The upper and lower
states of the transition are represented by the total angular momentum states
|JiMi ⟩
and |JfMf ⟩
respectively, and 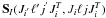 is a scattering matrix element
corresponding to an colliding electron scattered by the upper
state Xb
is a scattering matrix element
corresponding to an colliding electron scattered by the upper
state Xb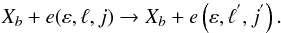 (5)Where
ℓ,ℓ′ and
j,j′ are the orbital and total
angular momentum of colliding electrons before and after the collision with the target
ion Xb respectively. During the colliding
process, the total energy
EI = Eb + ε = Ea + ε + ω,
total parity Π, total spin angular
momentum ST and total angular
momentum
(5)Where
ℓ,ℓ′ and
j,j′ are the orbital and total
angular momentum of colliding electrons before and after the collision with the target
ion Xb respectively. During the colliding
process, the total energy
EI = Eb + ε = Ea + ε + ω,
total parity Π, total spin angular
momentum ST and total angular
momentum 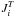 of
(N + 1)-electron colliding system are conserved. The
of
(N + 1)-electron colliding system are conserved. The
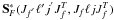 is the conjugate matrix of a
scattering matrix S corresponding to colliding process of the
lower
state Xa
is the conjugate matrix of a
scattering matrix S corresponding to colliding process of the
lower
state Xa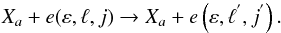 (6)In
Eq. (6), the total energy
EF = Ea + ε,
parity Π, total spin angular momentum ST and
total angular momentum
(6)In
Eq. (6), the total energy
EF = Ea + ε,
parity Π, total spin angular momentum ST and
total angular momentum 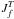 of
(N + 1)-electron colliding system are conserved. The above two
scattering processes, described in Eqs. (5) and (6) will share the same total spin angular
momentum ST and opposite parity Π when only
electric dipole transition is considered. This information is useful for the later
numerical calculations.
of
(N + 1)-electron colliding system are conserved. The above two
scattering processes, described in Eqs. (5) and (6) will share the same total spin angular
momentum ST and opposite parity Π when only
electric dipole transition is considered. This information is useful for the later
numerical calculations.
2.2. Scattering matrix
The calculation of scattering matrices SI
and SF is necessary to obtain electron
collision strength Ω(ε). These two matrices are closely related to
collision processes by Eqs. (5) and (6), which are (N + 1)-electron
colliding systems. Generally, a colliding system is constructed from
N-electron target states
Φi = |JiMi ⟩
(possibly including pseudo states) and single particle wavefunctions
φij = |jm ⟩ of the
continuum electron. A state of such colliding system is well defined by the wavefunction
in Berrington (1977) and Norrington (2009)
![\begin{eqnarray} \Psi_{k} = \sum\limits_{ij}c_{ijk}\Im \left[\Phi_{i},\phi_{ij}\right] + \sum\limits_{\rm m} d_{mk}\theta_{\rm m}. \end{eqnarray}](/articles/aa/full_html/2012/11/aa18418-11/aa18418-11-eq48.png) (7)Where
ℑ is an antisymmetric operator to account for the electron exchange, j is
the continuum basis function index for a particular κ value
(κ = −ℓ − 1, if
κ < 0, else
κ = ℓ), and θm is a
capture state in which all of the (N + 1)-electrons are bound.
(7)Where
ℑ is an antisymmetric operator to account for the electron exchange, j is
the continuum basis function index for a particular κ value
(κ = −ℓ − 1, if
κ < 0, else
κ = ℓ), and θm is a
capture state in which all of the (N + 1)-electrons are bound.
The (N + 1)-electron colliding system, defined by Eqs. (5) or (6), is
solved by using DARC to obtain a reactance K-matrix which is real
symmetric matrix. With K-matrix, scattering
matrix S is defined as:
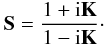 (8)From
Eq. (8), S is an unitary matrix, and its real part and imaginary
part are written out as
(8)From
Eq. (8), S is an unitary matrix, and its real part and imaginary
part are written out as ![% subequation 889 0 \begin{eqnarray} {\rm Re}\, \mathbf{S} &=& \displaystyle {1-\mathbf{K^2} \over \left(1+\mathbf{K}^{2}\right)}\!\cdot\\[1.5mm] {\rm Im}\, \mathbf{S} &=& \displaystyle {2\mathbf{K} \over \left(1+\mathbf{K}^{2}\right)}\cdot \end{eqnarray}](/articles/aa/full_html/2012/11/aa18418-11/aa18418-11-eq57.png) These
two expressions are directly used in our numerical calculations.
These
two expressions are directly used in our numerical calculations.
3. Numerical calculations in detail
To obtain electron collision strength Ω(ε), we solved the colliding system which consists of an N-electron target ion and a colliding electron. The states of an N-electron target in DARC calculations are prepared first by a fully relativistic atomic structure code called GRASP0-10.10 as explained in the next section.
3.1. Atomic structure
In our calculations, the atomic structure data of four Be-like ions from N IV to Ne VII are obtained by using the multi-configuration Dirac-Fock (MCDF) atomic structure program GRASP0-10.10 developed by Dyall et al. (1989) and Parpia et al. (1996) included in DARC. The original GRASP0-10.10 have been partly improved by us according to our previous works (Duan et al. 2008; Bari et al. 2011) so that all the following atomic structure data can be calculated by extended average-level (EAL) mode. To calculate the atomic structure of the four Be-like ions, i.e., N IV, O V, F VI and Ne VII, we have selected the following electronic configurations: 1s22s2, 1s22s2p, 1s22s3s, 1s22s3p, 1s22s3d, 1s22s4s, 1s22s4p, 1s22s5s, and 1s22s5p. With the selection of these configurations, it is easy to obtain the electronic orbitals, the energy levels and states of target ions. These atomic data are incorporated as input in solving (N + 1)-electron colliding system by DARC.
3.2. From K to S
With the atomic structure data of target ions, the (N + 1)-electron colliding systems of Eqs. (5) and (6) are solved by DARC, and their K matrices and quantum numbers of angular momentum are also obtained. Then K matrix is used to calculate the real and imaginary parts of scattering matrix S with Eqs. (9). The transformation from K to S is performed by a code developed by us.
4. Numerical results and discussion
In this paper, the electron-impact broadening widths of the transition arising from the
2s3s ← 2s3p configuration in Be-like ions N IV, O V, F VI and Ne VII are calculated. In
these calculations, we have used the GRASP0-10.10 package included in DARC to provide the
fine-structure wavefunctions, energy levels, wavelengths, and transition rates. We obtained
the electron impact collision strengths by DARC. For those configurations, each target ion
has 27 bound states. All of these target states are selected as target basis in our
calculations. To generate and construct the (N + 1)-electron colliding
systems defined in Eqs. (5) and (6), two parameters of the colliding electron are defined by
specific boundary limits i.e., the quantum number of orbital angular momentum is
ℓ ≤ 10 and the total number of continuum basis function for a
given κ is 14. The electron collision strength Ω(ε)
defined in Eq. (4) is a function of colliding electron energy ε and is
computed in an increasing energy sequence with an energy step of Δε = 0.02
Rydberg by the same procedure. To realize and confirm our numerical calculations, it is
necessary for us to study the convergence of collision strength Ω(ε) with
both the orbital angular momentum ℓ and the colliding electron
energy ε. In Fig. 1 the maximum
ℓ of the colliding electron in Eq. (4) is limited by 10 or 15,
and Ω(ε) are present as a function ε in transition
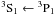 in N IV ion. It can be
seen that Ω(ε) converges with the orbital angular
momentum ℓ if ℓ is large enough, and that it also
decreases with the colliding electron energy ε. Thus the electron impact
broadening in Eq. (3) is numerically calculated by the trapezoidal integration technique.
The full width at half maximum (FWHM
W = 2w) for transitions 2s3s ← 2s3p for various
electron temperature Te and electron
density Ne are given in Tables 1−7. The full quantum mechanical
calculations of line widths w2 and its simplified
calculations w1 by Elabidi et al. (2008) are also listed in Tables 1−7 for comparison purposes.
These w2 and w1 were calculated in
an intermediate coupling framework by including the fine-structure effects and relativistic
corrections resulting from breakdown of the LS coupling approximation for the target ions. A
comparison between these calculations and experimental results has proven to be a good
agreement for the first time for highly charged ions. The line
widths wc calculated by Ralchenko et al. (2001) with convergent close-coupling methods are also
presented. These authors find (i) that calculated widths are generally smaller than both
those measured and most of theoretical line widths from semiclassical calculations; and (ii)
that the deviation between experiment and theory monotonically increases along the
isoelectronic sequence, reaching a factor of 2 for Ne VII.
in N IV ion. It can be
seen that Ω(ε) converges with the orbital angular
momentum ℓ if ℓ is large enough, and that it also
decreases with the colliding electron energy ε. Thus the electron impact
broadening in Eq. (3) is numerically calculated by the trapezoidal integration technique.
The full width at half maximum (FWHM
W = 2w) for transitions 2s3s ← 2s3p for various
electron temperature Te and electron
density Ne are given in Tables 1−7. The full quantum mechanical
calculations of line widths w2 and its simplified
calculations w1 by Elabidi et al. (2008) are also listed in Tables 1−7 for comparison purposes.
These w2 and w1 were calculated in
an intermediate coupling framework by including the fine-structure effects and relativistic
corrections resulting from breakdown of the LS coupling approximation for the target ions. A
comparison between these calculations and experimental results has proven to be a good
agreement for the first time for highly charged ions. The line
widths wc calculated by Ralchenko et al. (2001) with convergent close-coupling methods are also
presented. These authors find (i) that calculated widths are generally smaller than both
those measured and most of theoretical line widths from semiclassical calculations; and (ii)
that the deviation between experiment and theory monotonically increases along the
isoelectronic sequence, reaching a factor of 2 for Ne VII.
 |
Fig. 1 Real part of the collision strength as a function of the colliding electron energy for two values of the maximum angular momentum lmax. Squares: lmax = 10. Circles: lmax = 15. |
Electron-impact widths W (FWHM) for the N IV
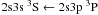 transitions at various
electron temperatures Te and electron
densities Ne.
transitions at various
electron temperatures Te and electron
densities Ne.
Electron-impact widths W (FWHM) for 2s3s 1S1 ← 2s3p 1P1 transitions of N IV, where the line widths are listed as a function of electron temperature Te under electron density Ne = 1018 cm-3.
Electron-impact widths W (FWHM) for the O V 2s3s 3S ← 2s3p 3P transitions.
Electron-impact widths W (FWHM) for the O V 2s3s 1S ← 2s3p 1P transitions.
We performed calculations for each ion for the temperature values for which the experimental data are available. Principally, all the corresponding experimental results cited in the present work have been published by two groups. The first group (Blagojević et al. 1999, 2000) used a low-pressure pulsed arc and the second group (Wrubel et al. 1996, 1998) used a gas-liner pinch. The accuracy of the experimental line widths is generally given by Konjević et al. (2002) except for the few cases where other references have been mentioned. For 2s3s 1S ← 2s3p 1P transitions in F VI ions, we compared our results with w1 of Elabidi et al. (2008) as there are no experimental results available yet.
To assess the quality of our calculations, we performed systematic comparisons with earlier
experimental and theoretical data. Our results in Tables 1−7 agree well with both the experimental
results and the previous theoretical calculations. Our results for the triplet transitions
of N IV, for both the singlet and triplet transitions of O V, and singlet transitions
of Ne VII are found to be in excellent agreement with the corresponding experimental
results. However, the line widths for triplet transitions of Ne VII revealed a significant
difference between our calculations and the corresponding measurements (see Table 6). Our calculated width of the transition line
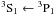 at vacuum
wavelength 1992.06 Å is about 0.308 Å, while the corresponding measurement is about 0.45 Å
and the difference amounts to 32%. We summarize our results by examining them in the
following section by presenting line widths
W = 2w (FWHM) of singlet and triplet
transitions 2s3s ← 2s3p in four Be-like ions from N IV to Ne VII:
at vacuum
wavelength 1992.06 Å is about 0.308 Å, while the corresponding measurement is about 0.45 Å
and the difference amounts to 32%. We summarize our results by examining them in the
following section by presenting line widths
W = 2w (FWHM) of singlet and triplet
transitions 2s3s ← 2s3p in four Be-like ions from N IV to Ne VII:
-
Line widths of N IV. In Tables 1and 2, we present our results forthe line widths of singlet and triplet transitions2s3s ← 2s3p of N IV ion for various electron temperatures and densities along with the experimental results (Blagojević et al. 1999, 2000; Wrubel et al. 1996, 1998). The previous theoretical calculations wc of Ralchenko et al. 2001), the full quantum mechanical calculations w2 and its simplified calculations w1 of Elabidi et al. (2008) are also listed in Tables 1 and 2.
Table 5Electron-impact widths W (FWHM) for the F VI 2s3s 1S ← 2s3p 1P transitions listed as a function of electron temperature Te under electron density Ne = 1018 cm-3.
The experimental measurements wm give singlet and triplet transitions 2s3s ← 2s3p line widths of N IV ions at different electron temperatures. The measurements by Milosavljević & Djenize (1998) were carried out for electron temperature Te = 5.4 × 104 K, while Blagojević et al. (1999) considered some lower temperatures, and Wrubel et al. (1998) measured at higher temperatures. From Table 1, our results are in good agreement with the experimental values. In detail, most of the other spectral line widths are in good agreement with wm within 5%. The difference for the majority of the spectral lines amounts to 10% and the most significant difference reaches to 18%. Additionally, there are a few cases where the difference between our results and existing experimental values is large. For example, in the transition
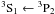 under plasma
condition Te = 9.63 × 104 K and
Ne = 8.1 × 1017 cm-3, the
difference in the line width reaches to 18%. Similarly, the transitions
under plasma
condition Te = 9.63 × 104 K and
Ne = 8.1 × 1017 cm-3, the
difference in the line width reaches to 18%. Similarly, the transitions
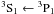 and
and
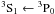 in Table 1 have two and four exceptional cases,
respectively, which our results show as large deviations from experimental values.
For singlet transitions listed in Table 2, it
can be seen that the discrepancies between W and two experimental
results wm cited by Bochum Group (Wrubel et al. 1996, 1998) are within 33%. Our results are less than
experimental wm in contrast
to w1. When compared
with wm, our results are better
than w2, but worse
than w1. Overall, our results W for
triplet transitions are always better than those of singlet transitions.
in Table 1 have two and four exceptional cases,
respectively, which our results show as large deviations from experimental values.
For singlet transitions listed in Table 2, it
can be seen that the discrepancies between W and two experimental
results wm cited by Bochum Group (Wrubel et al. 1996, 1998) are within 33%. Our results are less than
experimental wm in contrast
to w1. When compared
with wm, our results are better
than w2, but worse
than w1. Overall, our results W for
triplet transitions are always better than those of singlet transitions. -
Line widths of O V. In Tables 3 and 4, we compare our theoretical calculations of line widths for the singlet and triplet transitions 2s3s ← 2s3p of O V ion for various electron temperatures and densities. We also note that the measured widths are determined with an error of 23%: the error of the temperature determination is 18−27% and 15% for the density determination (Elabidi et al. 2008).
Table 6Electron-impact widths W (FWHM) for the Ne VII 2s3s 3S ← 2s3p 3P transitions under electron density of Ne = 3 × 1018 cm-3.
Table 7Electron-impact widths W (FWHM) for the Ne VII 2s3s 1S ← 2s3p 1P transitions under electron density of Ne = 3.5 × 1018 cm-3 and electron temperature Te = 2.205 × 105 K.
In triplet transitions in O V, our results are consistent with w1 and agree with each other, but w2 are closer to the experimental values when compared to our calculations. However, in singlet transitions, w1 is the best in two first lines of the table, and our results are the best in two last lines, while w2 is the worst. Most of our line width results are within an error of 15%, and the maximum error is about 25% in comparison to the experimental results.
-
Line widths of F VI. In Table 5, we list our results W as a function of electron temperature under an electron density Ne = 1018 cm-3. There are no experimental results available for F VI
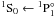 line widths.
Only the quantum mechanical calculations w1 of Elabidi
et al. (2008) are listed in Table 5 for comparison purposes. Our calculations show
large differences from w1 results. Regarding this
discrepancy between the quantum mechanical
calculation w1 and our theoretical calculations, the
reader may wonder about the cause of such a difference. At present, we cannot
understand this discrepancy. The reasons of this discrepancy need to be investigated
both experimentally and theoretically in future.
line widths.
Only the quantum mechanical calculations w1 of Elabidi
et al. (2008) are listed in Table 5 for comparison purposes. Our calculations show
large differences from w1 results. Regarding this
discrepancy between the quantum mechanical
calculation w1 and our theoretical calculations, the
reader may wonder about the cause of such a difference. At present, we cannot
understand this discrepancy. The reasons of this discrepancy need to be investigated
both experimentally and theoretically in future. -
Line widths of Ne VII. In Table 6, we report our results for the triplet transitions of Ne VII along with the experimental line widths measured by the Bochum group (Wrubel et al. 1996, 1998) at electron density Ne = 3 × 1018 cm-3 and electron temperature Te = 2.38 × 105 K. A comparison between our results and the measurements yields a maximum difference of 32%. Our results are in good agreement with the theoretical calculations w1. In Table 7, we present the line widths for singlet transition of Ne VII ion at electron density Ne = 3.5 × 1018 cm-3 and electron temperature Te = 2.205 × 105 K. A comparison between W and wm (Wrubel et al. 1998) shows that the difference is within 22%. It indicates that our results W for line widths of Ne VII are in good agreement with wm and are more accurate than w1 but less accurate than w2.
5. Conclusions
In the present work, a new set of electron-impact broadening of the singlet and triplet transition 2s3s ← 2s3p in four Be-like ions from N IV to Ne VII have been obtained by solving the (N + 1)-electron colliding systems of Be-like ions with DARC on the basis of relativistic quantum mechanical approach. Spectral line widths of triplet transitions of N IV ion are in best agreement with experimental values. A maximum discrepancy of 32% appears between W and wm for triplet transitions of Ne VII ion at electron density Ne = 3 × 1018 cm-3 and electron temperature Te = 2.38 × 105 K, which can be considered as tolerable agreement with respect to the accuracy of the experiment. Overall, one can conclude that our results for all defined temperatures agree with the experimental values within 10%, 20%, and 30% for N IV, O V, and Ne VII respectively. For singlet transitions in F VI ion (see Table 5), our results are quite different from w1, which needs clarification in future studies. Our calculations further support the argument of good agreement between quantum mechanical calculations and experiments for line widths of △ n = 0 transitions in highly charged ions in accordance with the conclusion of Elabidi et al. (2008). Our present calculations will be used for plasma diagnostics.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11275029) and the Foundation for Development of Science and Technology of Chinese Academy of Engineering Physics (Grant Nos. 2011A0102007 and 2009A0102006).
References
- Baranger, M. 1958a, Phys. Rev., 111, 481 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baranger, M. 1958b, Phys. Rev., 111, 494 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baranger, M. 1958c, Phys. Rev., 112, 855 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bari, M. A., Salahuddin, M., Duan, B., Nasim, M. H., & Hussain, S. A. 2011, J. Phys. B, 44, 225004 [NASA ADS] [CrossRef] [Google Scholar]
- Berrington, K. A., Burke, P. G., Dufton, P. L., & Kington, A. E. 1977, J. Phys. B, 8, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Blagojević, B., Popović, M. V., Konjević, N., & Dimitrijević, M. S. 1999, J. Quant. Spectr. Radiat. Trans., 61, 361 [Google Scholar]
- Blagojević, B., Popović, M. V., & Konjević, N. 2000, J. Quant. Spectr. Radiat. Trans., 67, 9 [Google Scholar]
- Dimitrijević, M. S., & Konjević, N. 1980, J. Quant. Spectr. Radiat. Trans., 24, 451 [Google Scholar]
- Duan, B., Bari, M. A., Zhong, J. Y., et al. 2008, A&A, 488, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Elabidi, H., Ben Nessib, N., & Sahal-Bréchot, S. 2004, J. Phys. B, 37, 63 [Google Scholar]
- Elabidi, H., Ben Nessib, N., Cornille, M., Dubau, J., & Sahal-Bréchot, S. 2008, J. Phys. B, 41, 025702 [NASA ADS] [CrossRef] [Google Scholar]
- Griem, H. R. 1974, Spectral Line Broadening by Plasma (NewYork, USA: Academic press) [Google Scholar]
- Hooper, C. F. Jr. 1966, Phys. Rev., 149, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Konjević, N., Lesage, A., Fuhr, J. R., & Wiese, W. L. 2002, J. Phys. Chem. Ref. Data, 31, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Milosavljević, V., & Djenize, S. 1998, A&AS, 128, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norrington, P. 2009, DARC manual, http://www.am.qub.ac.uk /users/p.norrington [Google Scholar]
- Ralchenko, Y., Griem, H. R., Bray, I., & Fursa, D. V. 1999, Phys. Rev. A, 59, 1890 [NASA ADS] [CrossRef] [Google Scholar]
- Ralchenko, Y., Griem, H. R., Bray, I., & Fursa, D. V. 2001, J. Quant. Spectr. Radiat. Trans., 71, 595 [Google Scholar]
- Seaton, M. J. 1987, J. Phys. B, 20, 6431 [Google Scholar]
- Parpia, F. A., Froese Fischer, C., & Grant, I. P. 1996, Comput. Phys. Commun., 94, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Peach, G. 1996, in Atomic, Molecular & Optical Physics Handbook, ed. G. W. F. Drake (New York: AIP Press), 669 [Google Scholar]
- Wrubel, Th., Glenzer, S., Bücher, S., Kunze, H. J., & Alexiou, S. 1996, A&A, 307, 1023 [NASA ADS] [Google Scholar]
- Wrubel, Th., Ahmad, I., Bücher, S., Kunze, H. J., & Glenzer, S. 1998, Phys. Rev. E, 57, 5972 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Electron-impact widths W (FWHM) for the N IV
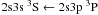 transitions at various
electron temperatures Te and electron
densities Ne.
transitions at various
electron temperatures Te and electron
densities Ne.
Electron-impact widths W (FWHM) for 2s3s 1S1 ← 2s3p 1P1 transitions of N IV, where the line widths are listed as a function of electron temperature Te under electron density Ne = 1018 cm-3.
Electron-impact widths W (FWHM) for the F VI 2s3s 1S ← 2s3p 1P transitions listed as a function of electron temperature Te under electron density Ne = 1018 cm-3.
Electron-impact widths W (FWHM) for the Ne VII 2s3s 3S ← 2s3p 3P transitions under electron density of Ne = 3 × 1018 cm-3.
Electron-impact widths W (FWHM) for the Ne VII 2s3s 1S ← 2s3p 1P transitions under electron density of Ne = 3.5 × 1018 cm-3 and electron temperature Te = 2.205 × 105 K.
All Figures
 |
Fig. 1 Real part of the collision strength as a function of the colliding electron energy for two values of the maximum angular momentum lmax. Squares: lmax = 10. Circles: lmax = 15. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


