| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219947 | |
| Published online | 28 September 2012 | |
An extended source of GeV gamma rays coincident with the supernova remnant HB 21
1
IFAE, Edifici C7b, Campus UAB, 08193
Bellaterra, Spain
e-mail: ignasi@ifae.cat
2
Max-Planck-Institut für Kernphysik, PO Box 103980, 69029
Heidelberg,
Germany
3
Now at Institut de Ciències de l’Espai (IEEC-CSIC),
08193
Bellaterra,
Spain
4
Institució Catalana de Recerca i Estudis Avançats
(ICREA), 08010
Barcelona,
Spain
Received:
4
July
2012
Accepted:
22
August
2012
We analyze 3.5 years of public Fermi/LAT data around the position of the supernova remnant HB 21, where four point-like sources from the 2nd Fermi/LAT catalog are located. We determine that the gamma-ray source is produced by a single extended source. We model the observed morphology as a uniform circle. The spectral energy distribution is best described by a curved power law, with a maximum at 413 ± 11 MeV. We divide the circle into three regions defined by previously identified shocked molecular clouds, and find that one of these regions has a softer spectrum. The >3 GeV gamma-ray emission of the soft spectrum region is bow-shaped and coincident with the supernova remnant shell seen at radio wavelengths. We suggest that the gamma-ray emission from HB 21 can be understood as a combination of emission from shocked/illuminated molecular clouds, one of them coincident with the supernova remnant shell itself.
Key words: acceleration of particles / ISM: supernova remnants / ISM: clouds / gamma rays: general / gamma rays: ISM / cosmic rays
© ESO, 2012
1. Introduction
Gamma-ray emission from SNRs is key for understanding the processes that lead to particle acceleration in the Galaxy and, in particular, to the production of cosmic rays. Since protons cannot be traced back to distant sources, proton acceleration in SNRs may be probed by observing their effects on dense molecular clouds located in the vicinity of the accelerating region (Gabici et al. 2009). In particular, the observation of gamma rays from neutral pion decay is considered to be the smoking gun of cosmic-ray production, since they trace the collisions of accelerated protons with nucleons from the ambient medium. Examples of such interaction are firmly established in cases like that of the SNR W44 (Uchiyama et al. 2012), where GeV gamma rays emanate from regions clearly offset from the SNR shell.
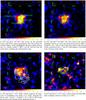 |
Fig. 1 S/N maps above 100 MeV, 500 MeV, 1 GeV, and 3 GeV. The color scale represents signal-to-noise ratio (defined as real counts minus model counts divided by square root of model counts) for the null hypothesis. Different multiwavelength information is included in each panel. |
HB 21 (G89.0+4.7) is a 19 000 year old1 (Leahy & Aschenbach 1996) mixed-morphology supernova remnant (SNR) at a distance of 0.8 kpc (Tatematsu et al. 1990). As seen in radio continuum images, the SNR displays an elliptical shell of 2° × 1.5° (Condon et al. 1994) (mean diameter of ~25 pc), slightly tilted in the northwest (NW)-southeast (SE) direction. Only weak, center-filling X-ray emission of thermal origin is associated with HB 21 (Lazendic & Slane 2006).
The interaction of HB 21 with the surrounding interstellar medium (ISM) has been intensively studied. Given the absence of OH masers around HB 21 (Frail et al. 1996), the evidence of interaction between the blast wave and the ISM is established by means of local dynamic effects that broaden emission lines. In the following paragraph we briefly describe the clouds that present such broad emission lines. We refer to Fig. 1 in Byun et al. (2006) for a detailed view of the interacting clouds, or Fig. 1 in this work for a schematic view.
Evidence of shocked molecular gas was found by Koo et al. (2001) in the northern and in the southern parts of the shell. The northern cloud (cloud N hereafter) consists of several small, bright clumps plus a diffuse component extending to the E. The southern cloud (cloud S) presents a complex filamentary structure, with a velocity spread of up to 40 km s-1 for some particular clumps, and it is coincident with a mass of shocked atomic gas detected by Koo & Heiles (1991). There is also a bow-shaped cloud at the NW rim of the radio shell (cloud NW) (Byun et al. 2006), and the central thermal X-ray bright area is occupied by small evaporating clouds. Moreover the so-called clouds A, B, and C (Tatematsu et al. 1990) are aligned N-S in the approximately straight E rim of the SNR. These clouds may be regarded as overdensities of the giant molecular cloud of the Cyg OB7 association (Huang & Thaddeus 1986), which provides the distance estimate for HB 21. Clouds A, B, and C are located where the eastward blast wave apparently collides with the so-called wall. The wall consists of a sharp edge of otherwise smoothly distributed atomic gas, which extends beyond the SNR boundary, both N and S, therefore suggesting that it is a pre-existing structure that affects the evolution of the SNR and not the other way around. Probably, the wall is the border of the cavity resulting from a former HII region around the HB 21 progenitor, which might be a former member of the Cyg OB7 association (Tatematsu et al. 1990). There is also the possibility that the coincidence of the A, B, C clouds and the wall with the SNR shell is a projection effect, where the clouds are indeed in the vicinity of the SNR, but they lie in front or behind it (Koo et al. 2001). Byun et al. (2006) suggested that the SNR could be as far as 1.7 kpc, in which case the whole Cyg OB7 complex would be in the foreground.
According to Nolan et al. (2012) three point-like sources (2FGL J2041.5+5003, 2FGL J2043.3+5105 and 2FGL J2046.0+4954) in the second Fermi/LAT source catalog (2FGL catalog hereafter) are coincident with the extended radio emission of HB 21. In this article we report a detailed analysis of the public Fermi/LAT data that will lead to a deeper understanding of the gamma-ray emission from this object.
2. Data analysis
We analyzed Fermi/LAT data with the LAT analysis software, the Science Tools version v9r27p12. We analyzed Pass-7 data corresponding to the period between August 4th 2008 (start of science operations) and February 2, 2012. Since HB 21 is almost off the galactic plane, it allows for a notably background-reduced analysis with respect to the sources found at lower galactic latitudes. To exploit this advantage, we defined a region of interest (ROI, i.e. the sky region whose LAT photon events are considered) as a circle of radius centered on the position , which is displaced by toward positive galactic latitudes with respect to the catalog position of HB 21 (Ferrand & Safi-Harb 2012). We selected class 2 events in the energy range between 100 MeV and 100 GeV. We applied a set of quality cuts, including the requirement for the spacecraft to be in normal operation mode (LAT_CONFIG==1), data to be flagged as good quality (DATA_QUAL==1), and a cut on the rocking angle of the spacecraft (ABS(ROCK_ANGLE) < 52). In addition, we applied a zenith angle cut of in order to prevent event contamination from the Earth limb. Data are binned in sky coordinates with the gtbin tool, using square bins of side. We refer later to the two-dimensional histograms resulting from gtbin as count maps.
To study the morphological and spectral properties of HB 21, we performed a three-dimensional (two spatial dimensions plus the energy) maximum likelihood analysis, using the standard gtlike tool. In this method, the likelihood is computed for different models defined by the position and morphology of the sources producing gamma rays in the ROI. For each source, a different spectral shape is assumed, and the spectral parameters are left free in the likelihood maximization. Our starting point consists of the standard galactic and extragalactic diffuse emission models provided in the Science Tools, plus the point-like sources in the 2FGL catalog lying up to away of the ROI center, excluding 2FGL J2041.5+5003, 2FGL J2043.3+5105, 2FGL J2046.0+4954 and 2FGL J2051.8+5054. We note that according to Nolan et al. (2012), the source 2FGL J2051.8+5054 is not associated to HB 21, but it lies very close to the NE edge of the SNR shell, in remarkable coincidence with the above-mentioned cloud A (see Fig. 1a). For this reason, in the following section we consider 2FGL J2051.8+5054 as part of the gamma-ray emission related to HB 21. We refer to this model as the null hypothesis, since it assumes that the gamma-ray emission from HB 21 is faint enough to not be distinguished from the background. Next, we compare the maximum likelihood obtained with the null hypothesis to those of several models that include various morphological descriptions of the GeV emission from HB 21. First, we include the four point-like sources mentioned above. In addition, we explore the possibility that the observed emission is from an extended, resolved source. For this, the four point-like sources associated to HB 21 are replaced by extended source templates. The scenarios considered are detailed in Sect. 3.1. For each model, the goodness of the likelihood fit is estimated by means of a test statistic (TS) defined as 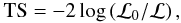 (1)where ℒ0 and ℒ are the likelihood of the null hypothesis and the tested models respectively. Since TS is a likelihood ratio of two nested models, it asymptotically follows a χ2 distribution with a number of degrees of freedom equal to the extra number of parameters of the test hypothesis with respect to the null one (Abdo et al. 2009a). Despite some caveats (Protassov et al. 2002), it is normally accepted TS = 25 as a detection threshold of a source with two spectral parameters (flux normalization and spectral index), which corresponds to a statistical significance of 4.6 sigma. In all cases, gtlike is run in a two-step procedure: first allowing a loose tolerance up to 10% in the fit parameters and using the MINUIT method and, second, using the output of MINUIT as the initial value for a refitting of the model parameters with a tighter requirement of 0.1% tolerance and using the NEWMINUIT method. The output of gtlike allows us to generate synthetic maps with the expected source shape and brightness, given the model best-fit parameters. These synthetic maps can be subtracted from the counts maps in order to visualize the disagreements between the real data and its parametrization, in the form of a residuals map. We then divide, pixel by pixel, the residuals map by the square root of the number of counts in the synthetic map, thus obtaining a measure of the significance of the disagreement in every pixel, which we will call the signal-to-noise ratio (S/N) map.
(1)where ℒ0 and ℒ are the likelihood of the null hypothesis and the tested models respectively. Since TS is a likelihood ratio of two nested models, it asymptotically follows a χ2 distribution with a number of degrees of freedom equal to the extra number of parameters of the test hypothesis with respect to the null one (Abdo et al. 2009a). Despite some caveats (Protassov et al. 2002), it is normally accepted TS = 25 as a detection threshold of a source with two spectral parameters (flux normalization and spectral index), which corresponds to a statistical significance of 4.6 sigma. In all cases, gtlike is run in a two-step procedure: first allowing a loose tolerance up to 10% in the fit parameters and using the MINUIT method and, second, using the output of MINUIT as the initial value for a refitting of the model parameters with a tighter requirement of 0.1% tolerance and using the NEWMINUIT method. The output of gtlike allows us to generate synthetic maps with the expected source shape and brightness, given the model best-fit parameters. These synthetic maps can be subtracted from the counts maps in order to visualize the disagreements between the real data and its parametrization, in the form of a residuals map. We then divide, pixel by pixel, the residuals map by the square root of the number of counts in the synthetic map, thus obtaining a measure of the significance of the disagreement in every pixel, which we will call the signal-to-noise ratio (S/N) map.
3. Results
3.1. Morphology
To visualize a possible gamma-ray source associated to HB 21, we produce the S/N map corresponding to the null hypothesis, in different energy ranges (Fig. 1). The point spread function3 (PSF) of Fermi/LAT is up to at 100 MeV energies, improves to at 1 GeV and achieves above 10 GeV (Rando 2009). Therefore, at the lowest energies (Fig. 1a) it is not possible to distinguish any structure beyond a more or less flat emission extended throughout the SNR shell. Above 500 MeV (Fig. 1b) and above 1 GeV (Fig. 1c) a shell-like structure becomes visible.
TS of the spatial models above different minimum energies.
 |
Fig. 2 Radial profile of the excess (real counts minus model counts generated with the null hypothesis model). Red curve represents the profile expected from a flat circular emission region of radius. Green curve represents the profile expected from a gamma-ray emission following the radio continuum emission at 4850 MHz. |
Above 3 GeV (Fig. 1d) we can identify several structures. The most remarkable feature is the NW arc, which coincides with the SNR shell and the position of cloud NW. There is also a bright spot close to cloud A. This component seems to become more prominent with increasing energy. The center of the SNR does not show especially bright emission, whereas the S part of the shell presents an enhancement roughly coinciding with cloud S. We show below that the emission above 3 GeV is still significant (Table 1).
To evaluate the morphological properties of the source, several scenarios were considered:
-
1.
the four point-like sources from 2FGL coincident with HB 21;
-
2.
the 4850 MHz map from (Condon et al. 1994), where the quasar 3c418.0 was removed from the radio map (see discussion below);
-
3.
a circle of flat emission centered on the catalog position of HB 21.
All the templates were rebinned to match the field of view and the pixel size of the Fermi/LAT maps. In Table 1 we show the TS values for each model in several energy regimes, as well as the number of additional parameters in each model. The point-like sources model introduces additional degrees of freedom for the flux normalization of each of the four sources, plus the spectral indices. 2FGL J2043.3+5105 and 2FGL J2046.0+4954 contain an additional parameter β which allows an energy-dependent spectral index −α−βlog (E/1000 GeV). The spectrum of the circle and the 4850 MHz templates are described by a power-law function at this stage.
Spectral analysis of the different circle segments above 100 MeV.
All of the models listed above provide a good description of the HB21 field compared to that of the null hypothesis. Thus, one or more sources are detected in the HB 21 region with high significance, even at energies above 3 GeV. However, we discard the description by means of point-like sources, since it provides the highest TS only at the lowest energies (Table 1), where the broad PSF of Fermi/LAT does not allow disentangling any substructure. The model with the point-like sources introduces ten degrees of freedom. Therefore we consider that the improvement in TS at low energies comes from the greater number of parameters and not from the point-like source model being a better description of the morphology. With only two degrees of freedom, the overall emission can be described well at all energies by a circle of radius centered on the catalog position of the SNR. The radius of the circle is chosen to provide the highest TS after varying it from 0.75 to in steps of (one pixel). Initially, we assume a simple power-law function as spectral model.
To further investigate the possibility of a shell-like morphology we produced the radial profiles of the excess (real counts minus model counts, for the null hypothesis) in each energy range, and we compared this profile with the one expected from models (2) and (3) (Fig. 2). In view of the profiles, it is not conclusive whether the gamma-ray emission can be related to a shell-like structure. However, given the hints obtained so far, we considered this possibility by testing several ring-shaped models with various inner and outer radii. The outer radius is varied within the same range as for the optimization of the flat circle, whereas we considered inner radii ranging from 0 (circle) to , also in steps of 0.125. The best combination at all energies is for the inner radius and for the outer radius. However, the difference in TS is about 0.1 for all energies, which is not significant. In addition, we consider that smearing by the PSF would prevent such a narrow hole (of only two pixels) from being distinguished if used, so we continued to use the flat circle for the subsequent analysis.
We addressed the possibility of having additional point-like sources besides the above-mentioned ones. First, the NW corner of the radio shell reveals a bright point-like radio source due to the presence of the quasar 3c418.0 at z = 1.6865 (Paturel et al. 2002). We considered the possibility that this quasar contributes to the gamma-ray emission. To do so, we looked for variability in the GeV signal by means of an aperture analysis within a radius of one degree around 3c418.0. After several temporal binnings we did not find any significant variability in the photon rate around the quasar. Therefore, we conclude that if this object has any contribution, we cannot disentangle it from that of the SNR with the current data set. Secondly, in the 1 GeV map (Fig. 1c) two spots appear SW of the SNR. Comparing with the CO large-scale distribution around the SNR we find that these spots are roughly coincident with local maxima of the gas distribution. Taking this possibility into account, we repeated the likelihood analysis adding two sources at the position of the gas overdensities. None of these sources were significant, whether in the analysis above 100 MeV energies or above 1 GeV.
 |
Fig. 3 Spectral energy distribution of the gamma-ray emission from HB 21 modeled as a flat circle of 1.125 radius. Red error bar is statistical uncertainty. An additional systematic uncertainty of 10% (E < 560 MeV) and of 5% (E > 560 MeV) is represented by the black error bar. The solid thin black curve is the log-parabola (Eq. (3)) used to model the overall spectrum. Curves with extreme values of α and β, within statistical uncertainty are also shown (solid thick black curves). Dotted, dashed, and dash-dotted curves are the best spectral descriptions for segments NW, S, and NE respectively (see Table 2). |
3.2. Spectral energy distribution
We divide the considered energy range (100 MeV to 100 GeV) into twelve bins and compute the spectral energy distribution of the whole source by extracting its flux in each bin (Fig. 3). Only those bins with TS > 10 (~3.2σ) are shown as spectral points. The last significant bin is the one from 3.2 GeV to 5.6 GeV. In addition we show 95% confidence level upper limits for the explored energy range, up to 100 GeV. The upper limits correspond to the flux providing a likelihood value such that 2Δlog ℒ = 4.
We notice that the spectrum deviates from a power-law function and suggests the presence of a peak at few hundred MeV. We test the possibility that the gamma ray emission is described by a smoothly broken power law of the form 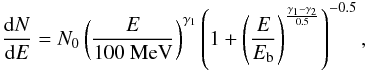 (2)or a curved power law (log-parabola)
(2)or a curved power law (log-parabola) 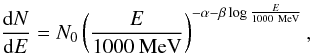 (3)or a power law with a cut-off
(3)or a power law with a cut-off 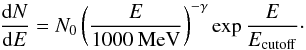 (4)We use the likelihood ratio −2log (ℒpl/ℒmodel) as a measure of the improvement of the likelihood fit with respect to the simple power law, when different spectral shapes are used. We use Eqs. (2) (two extra degrees of freedom), (3), and (4) (one extra degree of freedom), resulting in likelihood ratios of 143, 146, and 130, respectively. Provided that the log-parabola introduces an additional parameter (β) to the simple power law, we conclude that the chance probability of the log-parabola being a better description of the spectrum is 1.5 × 10-33. The TS of the flat circle (with log-parabolic spectral shape) with respect to the null hypothesis is 988, which roughly corresponds to a detection significance at the level of 31 standard deviations. The best fit parameters are N0 = (17.5 ± 0.2) × 10-12 cm-2 s-1 MeV-1, α = 2.596 ± 0.013, β = 0.338 ± 0.008, where uncertainties are only statistical. The total energy flux is (1.10 ± 0.03) × 10-4 MeV cm-2 s-1, with a maximum in the spectral energy distribution at 413 ± 11 MeV.
(4)We use the likelihood ratio −2log (ℒpl/ℒmodel) as a measure of the improvement of the likelihood fit with respect to the simple power law, when different spectral shapes are used. We use Eqs. (2) (two extra degrees of freedom), (3), and (4) (one extra degree of freedom), resulting in likelihood ratios of 143, 146, and 130, respectively. Provided that the log-parabola introduces an additional parameter (β) to the simple power law, we conclude that the chance probability of the log-parabola being a better description of the spectrum is 1.5 × 10-33. The TS of the flat circle (with log-parabolic spectral shape) with respect to the null hypothesis is 988, which roughly corresponds to a detection significance at the level of 31 standard deviations. The best fit parameters are N0 = (17.5 ± 0.2) × 10-12 cm-2 s-1 MeV-1, α = 2.596 ± 0.013, β = 0.338 ± 0.008, where uncertainties are only statistical. The total energy flux is (1.10 ± 0.03) × 10-4 MeV cm-2 s-1, with a maximum in the spectral energy distribution at 413 ± 11 MeV.
To explore possible spectral differences throughout HB 21, we divided the circle in three pieces covering each and let them acquire different values for the N0, α and β. In this way, segment NE covers clouds A and N; segment NW covers cloud NW and segment S covers cloud S. We used the likelihood ratio −2log (ℒsegment/ℒcircle), where ℒsegment refers to the segmented circle without the tested segment. With this likelihood ratio, two thirds of the circle may be regarded as part of the null hypothesis, thus providing a measure of the significance of the tested segment. All three segments contribute significantly to the overall emission. The likelihood ratio values of each of these segments are summarized in Table 2, along with the flux corresponding to each segment and their spectral parameters. The maximum energy flux is attained at 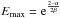 GeV. To evaluate the uncertainty in Emax, the uncertainties in α and β are taken into account, as well as their covariance. We find a hint that the segment NW has a softer spectrum, peaking at lower energies than the other two regions (see also Fig. 3).
GeV. To evaluate the uncertainty in Emax, the uncertainties in α and β are taken into account, as well as their covariance. We find a hint that the segment NW has a softer spectrum, peaking at lower energies than the other two regions (see also Fig. 3).
4. Discussion
The luminosity between 100 MeV and 5.6 GeV is L = (1.34 ± 0.03stat) × 1034(d/0.8 kpc)2 erg/s. Unless d = 1.7 kpc is confirmed, HB 21 belongs to the group of low-luminosity, GeV-emitting SNRs, such as Cygnus Loop (Katagiri et al. 2011) or S147 (Katsuta et al. 2012), which are clearly less luminous than the first GeV-emitting SNRs that were discovered. For instance, W51C (Abdo et al. 2009b), IC 443 (Abdo et al. 2010b), W49B (Abdo et al. 2010c), or Cas A (Abdo et al. 2010a) have luminosities L > 1035 erg/s. Also the break in energy is found at lower energy in HB 21 than in the case of the luminous SNRs.
Gamma-ray emission from supernova remnants can be produced by several non-exclusive mechanisms. Electrons and positrons in the supernova remnant shell interact by inverse Compton scattering with ambient photon fields (such as infrared starlight) to produce gamma rays. Another possibility is that electron-atom or electron-molecule interactions in a dense medium result in bremsstrahlung radiation. These mechanisms involve electrons accelerated up to the energies of the observed gamma rays. Complementarily, gamma rays can also be produced by neutral pion decay, where π0s result from the collision of accelerated protons (or heavier nuclei) with nucleons of the ambient gas. The absence of nonthermal X-ray emission favors a hadronic origin of the observed gamma-ray emission. Moreover, the rapid steepening of the spectrum above few GeV is the kind of signature expected from the re-acceleration of pre-existing cosmic rays (Blandford & Cowie 1982; Uchiyama et al. 2010), where high energy cosmic rays escape from the SNR confinement region (Zirakashvili & Aharonian 2010).
To check the viability of the leptonic and hadronic scenarios from the energetics point of view, we consider the energy from the supernova explosion that is converted into accelerated particles, W = L × τ. In this expression, L is the gamma-ray luminosity and τ the characteristic cooling time of the dominant accelerated particle type. When the gamma-ray luminosity is hadronic-dominated, τp ~ 5.3 × 107(n/1 cm-3)-1 years is the cooling time of the accelerated protons as a function of the ambient proton density n (Aharonian 2004). According to Koo et al. (2001), cloud S has density ~7000 cm-3, and central evaporating clouds have densities ~4 × 104 cm-3. Moreover, Tatematsu et al. (1990) quote a density of about 100 cm-3 for cloud A. We computed our own estimate of the average density of the region. To estimate the total mass we used the CO data from CfA 1.2 m Millimeter-Wave Telescope (Dame et al. 1987). We assumed a standard linear relationship between the velocity integrated CO intensity, ICO, and the molecular hydrogen column density, N(H2): 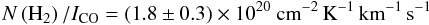 (5)as derived by Dame et al. (2001). This equation yields
(5)as derived by Dame et al. (2001). This equation yields 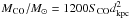 , where dkpc is the distance to the cloud in kpc, and SCO the CO emission integrated over velocity and the angular extent of the cloud in K km s-1 arcdegree2. We conclude that there are as many as 12 000 solar masses of molecular gas coinciding with the gamma-ray emission in the velocity range from −20 to 0 km s-14. Assuming that this gas is in a spherical volume of 25 pc diameter we obtain an average density of about 60 protons per cubic centimeter, and therefore Wp ~ 4 × 1047 erg. Instead, in case the gamma-ray luminosity is leptonic-dominated, the cooling time due to bremsstrahlung interactions depends on the ambient density as τbrems ~ 4 × 107(n/cm3)-1 (Aharonian 2004), which leads to a live time τbrems ~ 7 × 105 years and requires an energy budget similar to the hadronic interactions, We ~ 3 × 1047 erg. Alternatively, the cooling time of electrons due to synchrotron losses is τsync ~ 1.3 × 1010(B/1 μG)-2(Ee−/1 GeV)-1 years (Gaisser et al. 1998). Therefore, an Ee− = 3 GeV electron in a typical interstellar magnetic field of 3 μG would have a live time of τsync ~ 5 × 108 years. Only with a magnetic field as high as 80 μG, could the synchrotron losses become efficient enough to make them comparable to the losses due to bremsstrahlung interactions. Although detailed modeling is needed to confirm these considerations, our order-of-magnitude estimates favor the view that the high-density regions surrounding the SNR determine the dominant emission process. This is supported further by the coincidence of the gamma-ray bright regions with dense clumps of molecular gas (Fig. 1). In any case, energy budget considerations are not sufficient to distinguish between electron-dominated and proton-dominated scenarios under the assumption that the supernova explosion has a typical energy release of about 1051 erg.
, where dkpc is the distance to the cloud in kpc, and SCO the CO emission integrated over velocity and the angular extent of the cloud in K km s-1 arcdegree2. We conclude that there are as many as 12 000 solar masses of molecular gas coinciding with the gamma-ray emission in the velocity range from −20 to 0 km s-14. Assuming that this gas is in a spherical volume of 25 pc diameter we obtain an average density of about 60 protons per cubic centimeter, and therefore Wp ~ 4 × 1047 erg. Instead, in case the gamma-ray luminosity is leptonic-dominated, the cooling time due to bremsstrahlung interactions depends on the ambient density as τbrems ~ 4 × 107(n/cm3)-1 (Aharonian 2004), which leads to a live time τbrems ~ 7 × 105 years and requires an energy budget similar to the hadronic interactions, We ~ 3 × 1047 erg. Alternatively, the cooling time of electrons due to synchrotron losses is τsync ~ 1.3 × 1010(B/1 μG)-2(Ee−/1 GeV)-1 years (Gaisser et al. 1998). Therefore, an Ee− = 3 GeV electron in a typical interstellar magnetic field of 3 μG would have a live time of τsync ~ 5 × 108 years. Only with a magnetic field as high as 80 μG, could the synchrotron losses become efficient enough to make them comparable to the losses due to bremsstrahlung interactions. Although detailed modeling is needed to confirm these considerations, our order-of-magnitude estimates favor the view that the high-density regions surrounding the SNR determine the dominant emission process. This is supported further by the coincidence of the gamma-ray bright regions with dense clumps of molecular gas (Fig. 1). In any case, energy budget considerations are not sufficient to distinguish between electron-dominated and proton-dominated scenarios under the assumption that the supernova explosion has a typical energy release of about 1051 erg.
Northeast of the circle there is a spot that becomes bright with increasing energy (Fig. 1). We discuss the possibility that this comes from a hard gamma-ray emission component related to cloud A. This cloud most likely already existed at the time of the SNR explosion, it is not shocked, and its velocity is not significantly different from that of the wall (Tatematsu et al. 1990). According to Koo et al. (2001), this cloud does not present broad line emission, so there is no direct evidence of interaction with HB 215. Moreover, cloud A coincides with a concavity of the SNR shell. The coincidence of cloud A with this feature in the radio continuum emission suggests that the overtaking of this cloud leads to retardation of the shock front in comparison to the surrounding, although high-resolution CO maps from Koo et al. (2001) did not find such evidence. There is still the possibility that the shock is dissociative, and molecules have not been reformed (thus being omitted in the search of broad line emission regions), but the shock velocity of 20 km s-1 observed by Koo is in principle not enough for molecule dissociation (which typically requires 25−50 km s-1). Finally, the infrared emission of cloud A is caused by dust heated by the ambient radiation fields in their surface, whereas in clouds N and S it is due to lines from shock-excited molecules (Koo et al. 2001). In fact, Koo et al. (2001) mentions a diffuse component connecting clouds N and A. All in all, there is evidence that cloud A is different to other molecular clouds in the vicinity of HB 21. As mentioned in Sect. 1 there is also the suggestion that cloud A could be in the foreground of HB 21, related to the Cyg OB7 association (i.e. at 0.8 kpc), whereas HB 21 could be in the background, at 1.7 kpc or more. If we assume that the gamma-ray brightness of cloud A is due to runaway protons from HB 21, we can estimate the maximum distance between the two objects by the relation 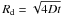 , where D ~ 1028 cm2 s-1 (Gabici et al. 2009, Eq. (11)) is the diffusion coefficient of cosmic rays protons of 10 GeV (which originate 1 GeV gamma rays). In this case the separation between cloud A and HB 21 would be roughly 50 pc. We note that D is completely unknown, and this distance is not to be taken as a measure of the separation between the cloud and the SNR, but only a suggestion that cloud A is indeed close to the SNR. We cannot conclude the same about the two other clouds (B and C) on the eastern rim detected by Tatematsu et al. (1990). These are dark in gamma rays and therefore they may be well in the foreground, as suggested by Byun et al. (2006).
, where D ~ 1028 cm2 s-1 (Gabici et al. 2009, Eq. (11)) is the diffusion coefficient of cosmic rays protons of 10 GeV (which originate 1 GeV gamma rays). In this case the separation between cloud A and HB 21 would be roughly 50 pc. We note that D is completely unknown, and this distance is not to be taken as a measure of the separation between the cloud and the SNR, but only a suggestion that cloud A is indeed close to the SNR. We cannot conclude the same about the two other clouds (B and C) on the eastern rim detected by Tatematsu et al. (1990). These are dark in gamma rays and therefore they may be well in the foreground, as suggested by Byun et al. (2006).
Finally, we consider it interesting that the part of the circle related to cloud NW presents a spectral break at lower energies than the rest of the SNR. From the E > 3 GeV map (Fig. 1d), we see that the majority of the emission in this region comes from a bow-shaped structure that resembles the SNR shell itself. We suggest that the gamma-ray emission from this region originates in the shell itself, or from a molecular cloud (probably cloud NW) that was overtaken at an earlier stage than those producing the emission in the remaining two thirds of the remnant.
5. Conclusions
The analysis of 3.5 years of public Fermi/LAT data leads to a clear detection of an extended source of gamma rays coincident with the SNR HB 21. Our own method for visualizing the morphology allows us to describe the source as a flat circle with uniform emission, although we resolve a clumpy structure at the highest energies. The spectral analysis reveals a peak of the gamma-ray emission at 413 ± 11 MeV. However, we conduct a dedicated spectral analysis for three regions, which show particularly bright emission above 500 MeV coincident with dense molecular hydrogen clumps. We find indications that the gamma-ray emission peaks at somewhat lower energies (0.26 ± 0.06 GeV) in the NW region of the shell (coincident with cloud NW and the shell itself), whereas in the NE (coincident with clouds N and A) and the S regions (coincident with cloud S) the peak is found around ~0.5 GeV.
Such spectral breaks are expected in middle-aged SNRs like HB 21 due to the escape of CRs from the confinement region. In HB 21 the break occurs at lower energies than in other similar objects. This could be related to the proximity of very dense molecular clouds to the supernova explosion progenitor, which could have slowed down the shock rapidly (Ohira et al. 2011). The spectrum from the region related to the bow-shaped emission in the NW peaks at lower energies than the spectrum from clouds N and S. This fact matches the understanding that the most energetic particles related to the SNR may have already escaped the NW region, due to a smaller confinement volume, or because cloud NW was shocked at an earlier stage than clouds N or S. Moreover, in the S/N map above 3 GeV, we see how a spot coincident with cloud A that becomes relatively brighter than the other clouds with increasing energy. We suggest that this is because cloud A is separated from the SNR, and it is now reproducing the spectrum of the SNR at an earlier stage due to particles that diffused away from the shock (Aharonian & Atoyan 1996).
Therefore, given that HB 21 appears as an extended object even for gamma-ray telescopes, it provides the opportunity to observe the production and diffusion of accelerated particles (most likely protons), from the SNR shell to distant molecular clouds acting as targets.
We quote here the commonly accepted age for this object, but we note that there are indications that HB 21 could have an age of the order of 5000 years (Lazendic & Slane 2006).
Data and software are publicly available at http://fermi.gsfc.nasa.gov/ssc
Byun et al. (2006) show that the majority of the emission is concentrated in the range −20 to 0 km s-1. Although there is some emission at higher velocities, at about 3 km s-1, telluric CO emission corrupts the spectra. To avoid this issue, and for simplicity, we took the velocity range −20 to 0 km s-1.
The lack of broad line emission is also the case for 3c391, where the interaction with molecular clouds is certain (Reach et al. 2002).
Acknowledgments
This work has been funded by projects DE2009-0064 and FPA2009-07474 from the Spanish Ministry of Research, Development and Innovation (former MICINN). We are thankful to professor Felix Aharonian for the very useful discussion and suggestions.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJS, 183, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 706, L1 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 710, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 722, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2004, Very high energy cosmic gamma radiation: a crucial window on the extreme Universe (World Scientific) [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Cowie, L. L. 1982, ApJ, 260, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, D.-Y., Koo, B.-C., Tatematsu, K., & Sunada, K. 2006, ApJ, 637, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Broderick, J. J., Seielstad, G. A., Douglas, K., & Gregory, P. C. 1994, AJ, 107, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrand, G., & Safi-Harb, S. 2012, Adv. Space Res., 49, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Goss, W. M., Reynoso, E. M., et al. 1996, AJ, 111, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S., Aharonian, F. A., & Casanova, S. 2009, MNRAS, 396, 1629 [NASA ADS] [CrossRef] [Google Scholar]
- Gaisser, T. K., Protheroe, R. J., & Stanev, T. 1998, ApJ, 492, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y.-L., & Thaddeus, P. 1986, ApJ, 309, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Katagiri, H., Tibaldo, L., Ballet, J., et al. 2011, ApJ, 741, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuta, J., Uchiyama, Y., Tanaka, T., et al. 2012, ApJ, 752, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, B.-C., & Heiles, C. 1991, ApJ, 382, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, B.-C., Rho, J., Reach, W. T., Jung, J., & Mangum, J. G. 2001, ApJ, 552, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Lazendic, J. S., & Slane, P. O. 2006, ApJ, 647, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., & Aschenbach, B. 1996, A&A, 315, 260 [NASA ADS] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2011, MNRAS, 410, 1577 [NASA ADS] [Google Scholar]
- Paturel, G., Dubois, P., Petit, C., & Woelfel, F. 2002, LEDA, , [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Rando, R. 2009 [arXiv:0907.0626] [Google Scholar]
- Reach, W. T., Rho, J., Jarrett, T. H., & Lagage, P.-O. 2002, ApJ, 564, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Tatematsu, K., Fukui, Y., Landecker, T. L., & Roger, R. S. 1990, A&A, 237, 189 [NASA ADS] [Google Scholar]
- Uchiyama, Y., Blandford, R. D., Funk, S., Tajima, H., & Tanaka, T. 2010, ApJ, 723, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Funk, S., Katagiri, H., et al. 2012, ApJ, 749, L35 [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 S/N maps above 100 MeV, 500 MeV, 1 GeV, and 3 GeV. The color scale represents signal-to-noise ratio (defined as real counts minus model counts divided by square root of model counts) for the null hypothesis. Different multiwavelength information is included in each panel. |
| In the text | |
 |
Fig. 2 Radial profile of the excess (real counts minus model counts generated with the null hypothesis model). Red curve represents the profile expected from a flat circular emission region of radius. Green curve represents the profile expected from a gamma-ray emission following the radio continuum emission at 4850 MHz. |
| In the text | |
 |
Fig. 3 Spectral energy distribution of the gamma-ray emission from HB 21 modeled as a flat circle of 1.125 radius. Red error bar is statistical uncertainty. An additional systematic uncertainty of 10% (E < 560 MeV) and of 5% (E > 560 MeV) is represented by the black error bar. The solid thin black curve is the log-parabola (Eq. (3)) used to model the overall spectrum. Curves with extreme values of α and β, within statistical uncertainty are also shown (solid thick black curves). Dotted, dashed, and dash-dotted curves are the best spectral descriptions for segments NW, S, and NE respectively (see Table 2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


