| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219824 | |
| Published online | 28 September 2012 | |
Dynamics of pebbles in the vicinity of a growing planetary embryo: hydro-dynamical simulations
1
Dep. Lagrange, UNSA, CNRS, OCA,
BP 4429,
06304
Nice Cedex 4,
France
e-mail: morby@oca.eu
2
Dept. of Space Sudies, SwRI, Boulder, CO, USA
Received: 15 June 2012
Accepted: 25 August 2012
Context. Understanding the growth of the cores of giant planets is a difficult problem. Recently, Lambrechts & Johansen (2012, A&A, 544, A32, LJ12) proposed a new model in which the cores grow by the accretion of pebble-size objects, as the latter drift towards the star due to gas drag.
Aims. We investigate the dynamics of pebble-size objects in the vicinity of planetary embryos of 1 and 5 Earth masses and the resulting accretion rates.
Methods. We use hydrodynamical simulations, in which the embryo influences the dynamics of the gas and the pebbles suffer gas drag according to the local gas density and velocities.
Results. The pebble dynamics in the vicinity of the planetary embryo is non-trivial, and it changes significantly with the pebble size. Nevertheless, the accretion rate of the embryo that we measure is within an order of magnitude of the rate estimated in LJ12 and tends to their value with increasing pebble-size.
Conclusions. The model by LJ12 has the potential to explain the rapid growth of giant planet cores. The actual accretion rates however, depend on the surface density of pebble size objects in the disk, which is unknown to date.
Key words: accretion, accretion disks / hydrodynamics / planets and satellites: formation
© ESO, 2012
1. Introduction
The formation of the massive cores of giant planets within the short timescale allowed by the survival of a proto-planetary disk of gas and solids (a few My; Haisch et al. 2001) is still an open problem. In the classical view, these cores form by collisional coagulation from a disk of km-sized planetesimals, through the well-known processes of runaway (Greenberg et al. 1978; Wetherill & Stewart 1989) and oligarchic growth (Ida & Makino 1993; Kokubo & Ida 1998). In principle these processes should continue until the largest objects achieve an isolation mass, which is a substantial fraction of the initial total mass of local solids. If the initial disk is sufficiently massive (about 10 times the so-called Minimal Mass Solar Nebula or MMSN; Weidenschilling 1977a,b; Hayashi 1981), it is expected that cores of ~10 Earth masses (ME) form beyond the so-called snowline (the orbital radius beyond which temperature is cold enough that water condenses into ice; Podolak & Zucker 2004), as required in the core-accretion model for giant planet formation (Thommes et al. 2003; Goldreich et al. 2004; Chambers 2006).
N-body simulations, though, show that reality is not so simple. When the cores achieve a mass of about 1 M⊕ they start to scatter the planetesimals away from their neighborhood, instead of accreting them (Ida & Makino 1993; Levison et al. 2010), which slows their accretion rate significantly. It has been proposed that gas drag (Wetherill & Stewart 1989) or mutual inelastic collisions (Goldreich et al. 2004) prevent the dispersal of the planetesimals by damping their orbital eccentricities, but in this case the cores open gaps in the planetesimal disk (Levison & Morbidelli 2007; Levison et al. 2010), like the satellites Pan and Daphis open gaps in Saturn’s rings. Thus the cores isolate themselves from the disk of solids. This effectively stops their growth. It has been argued that planet migration (Alibert et al. 2004) or the radial drift of sub-km planetesimals due to gas drag (Rafikov 2004) break the isolation of the cores from the disk of solids but, again, N-body simulations show that the relative drift of planetesimals and cores simply collects the former in resonances with the latter (Levison et al. 2010); this prevents the planetesimals from being accreted by the cores. In fact, only planetesimals smaller than a few tens of meters drift in the disk fast enough to avoid trapping in any resonance with a growing core (Weidenschilling & David 1985).
In a recent paper, Lambrechts & Johansen (2012, hereafter LJ12), have proposed a new model of core growth, which argues that, if the mass in the disk is predominantly carried by pebbles of a few decimeters in size, the largest planetesimals accrete pebbles very efficiently, rapidly growing to several Earth masses (see also Johansen & Lacerda 2010; Ormel & Klahr 2010; Murray-Clay et al. 2011). More specifically, this model builds on the recent planetesimal formation model (Youdin & Goodman 2005; Johansen et al. 2006, 2007, 2009) in which large planetesimals (with sizes from ~100 up to ~1000 km) form by the collapse of a self-gravitating clump of pebbles, concentrated to high densities by disk turbulence and the streaming instability. The mechanism by which, once formed, planetesimals can keep accreting background pebbles is described hereafter.
Pebbles are strongly coupled with the gas; thus they encounter the already-formed planetesimals with a velocity Δv that is equal to the difference between the Keplerian velocity and the orbital velocity of the gas (slightly sub-Keplerian due to the outward pressure gradient). LJ12 define the planetesimal Bondi radius as the distance at which the planetesimal exerts a deflection of one radian on a particle approaching with a velocity Δv: 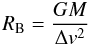 (1)where G is the gravitational constant and M is the planetesimal mass (obviously the deflection is larger if the particle passes closer than RB). LJ12 showed that all pebbles with a stopping time ts smaller than the Bondi time tB = RB/Δv that pass within a distance R = (ts/tB)1/2RB spiral down towards the planetesimal and are accreted by it. Thus, the growth rate of the planetesimal is:
(1)where G is the gravitational constant and M is the planetesimal mass (obviously the deflection is larger if the particle passes closer than RB). LJ12 showed that all pebbles with a stopping time ts smaller than the Bondi time tB = RB/Δv that pass within a distance R = (ts/tB)1/2RB spiral down towards the planetesimal and are accreted by it. Thus, the growth rate of the planetesimal is: 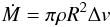 (2)where ρ is the volume density of the pebbles in the disk.
(2)where ρ is the volume density of the pebbles in the disk.
From (1), the Bondi radius grows with the planetesimal mass. LJ12 also showed that, when the Bondi radius exceeds the scale height of the pebble layer, the accretion rate becomes 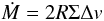 (3)where Σ is the surface density of the pebbles. Moreover, when the Bondi radius exceeds the Hill radius RH, the accretion rate becomes
(3)where Σ is the surface density of the pebbles. Moreover, when the Bondi radius exceeds the Hill radius RH, the accretion rate becomes 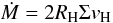 (4)where vH is the Hill velocity (i.e. the difference in Keplerian velocities between two circular orbits separated by RH).
(4)where vH is the Hill velocity (i.e. the difference in Keplerian velocities between two circular orbits separated by RH).
With these formulae, and assuming that Σ stays constant and is close to the nominal density of solids in the MMSN, LJ12 showed that the formation of 10 ME cores is possible within 1 My essentially anywhere in the disk (up to ~50 AU).
There are two main advantages in the LJ12 model. First, it can form 10 ME cores of giant planets within the lifetime of the disk, a result very difficult to achieve by other models. Second, because the accretion rate (2) is very sensitive on the planetesimal mass (Ṁ ∝ M2), in practice only the largest planetesimals formed in the turbulent model can effectively grow in mass by this process: the minimal mass for triggering significant Bondi accretion (see Eq. (2)) is about the mass of Ceres in the asteroid belt and about the mass of Pluto in the Kuiper belt. Thus this model explains the maximal sizes observed in the asteroid and Kuiper belt populations. In essence, in this model bodies smaller than Ceres (respectively Pluto for the Kuiper belt) remained small bodies (the asteroids and KBOs we see today), whereas those bigger than this threshold kept accreting pebbles and became massive objects (embryos) which then were removed by migrating away and (possibly) participating to the build-up of the giant planets. Both these aspects of the model are very appealing.
However the study conducted in LJ12, both in the analytic and in the numerical parts, assumes that the motion of the gas is not perturbed by the planetesimal. This assumption is good for a Ceres-mass planetesimal, accreting as in (2), but it is far from reality for planetary embryos (Earth mass or larger), accreting through their Hill sphere as in (4). In fact, these objects modify the gas streamlines significantly: a spiral density wave is formed in the disk and the gas near the orbit of the planet has horseshoe motion. An over-density of gas is also formed inside the planet’s Hill sphere. It is not clear a priori what are the effects of these structures on the pebble accretion rate. This is precisely what we investigate in this paper with more realistic hydro-dynamical simulations.
In Sect. 2, we describe our methods: the simulation tool that we have developed and the parameters that we adopt. In Sect. 3 we present our results, for two embryo masses and 4 pebble sizes. Our goal is three-fold: (i) describe and understand the dynamics of the pebbles for the different mass and size cases; (ii) evaluate the accretion rate by the embryo and compare it with the LJ12 estimate and (iii) evaluate the “filtering factor”, that is the fraction of the pebbles that do not drift by the orbit of the planet because they are accreted by the embryo. This factor is important. If it is large, of a sequence of embryos radially distributed in the disk, only the outermost one(s) can accrete; instead, if it is small then the full system of embryos can grow, in an oligarchic fashion. Our conclusions and discussion of a coherent scenario of giant planet formation conclude the paper in Sect. 4.
2. Methods
Our simulation software is based on the hydro-dynamical code FARGO, developed to study planet-disk interactions in Masset (2000) and publicly available at http://fargo.in2p3.fr/spip.php?auteur1. In that code, however, the N-body interaction among the bodies in the system is studied with a Runge-Kutta integrator of 5th order. Because the time-step of the integration is fixed, the Runge-Kutta algorithm is not adequate to treat accurately the close encounters between objects (e.g. the encounters between the pebbles and the planetary embryo). Also, there is no prescription in the original code to detect collisions.
Thus, we replaced the Runge-Kutta subroutine in FARGO with a code known as Symba. The latter is a variable-timestep symplectic code developed in Duncan et al. (1998) to simulate quasi-Keplerian N-body systems with mutual close encounters. Symba also identifies collisions and merges the bodies that collide. A technical difficulty in interfacing FARGO with Symba was that the former is written in C-language and the latter in Fortran. This required extensive modifications of several subroutines of the FARGO package.
In our simulations, the embryo is a massive object: it influences the evolution of the gas but, for simplicity, we cancel the influence of the gas disk on the embryo, so that the latter remains on a fixed, non-migrating orbit. This approximation is reasonable, as long as the migration of the embryo is slow compared to the radial drift of the pebbles due to gas drag.
In the FARGO code, the gas is discretized over a polar two-dimensional grid. However, in our modified code, the pebbles can evolve in a three-dimensional space. The gas drag on the pebbles is then computed as follows. We consider a spherical coordinate system r,θ,φ, where r,θ are the radial and azimuthal coordinates on the disk mid-plane. At each timestep we identify the disk grid cell where the spherical projection of the pebble falls on the midplane. This depends on the r,θ coordinates of the pebble. We consider the values of the gas surface density Σ and radial and tangential velocities vr,vθ that the gas has in that cell as well as in its 8 neighboring cells. We interpolate the set of 9 values for each field with a polynomial function of type (a + bx + cx2) + (a′ + b′x + c′x2)y + (a′′ + b′′x + c′′x2)y2 and we use it to evaluate Σ,vr and vθ of the gas at the r,θ location of the pebble. Moreover, we assume that the vertical velocity of the gas vz is zero. This sets the local relative velocity δv of the gas and the pebble. The local volume density of the gas at the pebble location is computed as 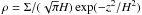 where z is the vertical coordinate of the pebble and H/r is the assumed aspect ratio of the disk, given as an input of the simulation. Finally, the drag suffered by the pebble is computed as
where z is the vertical coordinate of the pebble and H/r is the assumed aspect ratio of the disk, given as an input of the simulation. Finally, the drag suffered by the pebble is computed as 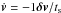 , where ts is the stopping time. The stopping time is also evaluated locally following Adachi et al. (1976), given the size and bulk density of the pebble (given as an input of the simulation) and the local volume density of the gas and Mach & Knudsen numbers.
, where ts is the stopping time. The stopping time is also evaluated locally following Adachi et al. (1976), given the size and bulk density of the pebble (given as an input of the simulation) and the local volume density of the gas and Mach & Knudsen numbers.
2.1. Simulation parameters
Our simulations follow the dynamics of one embryo and a set of pebbles. We consider planetary embryos of 1 or 5 ME. They are placed on a circular non-migrating orbit at 0.8 AU. The disk’s surface density is equal to 1800 g/cm2 at 1 AU, corresponding to the MMSN, with a radial profile proportional to 1/r. The aspect ratio is 5.6%. We follow an α-prescription for the disk’s viscosity (Shakura & Sunyaev 1973), with α = 6 × 10-3. The parameters above constitute just one set of (typical) disk parameters. Different disk parameters would affect mainly the pebble stopping time. Given that we will study the dynamics of pebbles over a wide range of sizes, our exploration of the stopping-time parameter space will be exhaustive even if working with just one disk model.
The disk is modeled over a grid extended from 0.75 to 1.12 AU, with a resolution of 160 concentric rings and 720 sectors. As the disk radial extension is narrow, we use non-reflecting boundary conditions, so that the spiral density wave launched by the embryo does not make the surface density of the disk rough with multiple reflections.
An image of the surface density of the disk is shown in Fig. 1, with a color scale. The black curves show streamlines of the gas in the reference frame corotating with the embryo. The position of the embryo is highlighted by a local maximum of the disk’s surface density. Notice that the spiral density wave (the slanted over-density structure departing from the planet) does not have any reflection at the border of the frame. Therefore, it is not necessary to simulate a wider radial portion of the disk.
 |
Fig. 1 Color map of the surface density of the gas in a disk in the presence of a 5 ME embryo at r = 0.8,θ = 3.22. The black curves show some gas streamlines and the blue, red, yellow and white curves depict the trajectories of 5 cm, 20 cm, 1 m and 10 m pebbles, respectively, in the frame corotating with the embryo. |
The gravitational interaction between the embryo and the gas is smoothed as 1/(Δ + ϵ)2 where Δ is the distance between the embryo and a gas fluid element and ϵ is a smoothing parameter. We adopt the quite standard choice ϵ = 0.6 RH.
We simulated pebbles of 5 cm, 20 cm, 1 m and 10 m in radius, with a bulk density of 1 g/cm3. With our disk model this corresponds to the following stopping times at 1 AU: 0.017, 0.22, 2.78, 74.07 cu respectively, where cu is the time code unit, which is 1/2π of an year. Even if some of these particles are rather boulder-sized, we still call them pebbles, for simplicity. The pebbles are assumed to orbit on the same plane as the disk and the embryo so that our simulations become effectively two-dimensional. A trajectory of one pebble of each size is shown in Fig. 1 and described in the next section. The timestep used in the integration is the minimum between 1/4 of the particle stopping time and 0.1 cu. The latter is the timestep dt imposed by the CFL condition (Courant et al. 1928) for the numerical solution of the hydrodynamical equations, given the resolution and the extension of our grid. Remember that the Symba algorithm effectively reduces the timestep for the integration of the particles approaching the embryo, through a clever subdivision of the embryo’s gravitational potential (Duncan et al. 1998).
To measure the accretion rate and the filtering factor (see last paragraph of Sect. 1) we proceed in two steps. We first integrate one pebble starting from the outer boundary of the disk at r = 1.12 AU at opposition with respect to the embryo. As the pebble migrates inward, we record the sequence of heliocentric distance values rk that the pebble has at subsequent oppositions. We denote by rN the smallest of the rk values with rK > 0.8 AU, i.e. the heliocentric distance at the last opposition before crossing the orbit of the embryo1. Then, we simulate a large number of pebbles (usually 100, but this number can change from case to case to achieve an appropriate resolution), initially at opposition and with heliocentric distances uniformly distributed in the range [rN,rN − 1] . Of this beam of pebbles, we measure the fraction F that are accreted by the planet. F is the “filtering factor” defined in the introduction, while 1 − F is the fraction of the beam that drift across the orbit of the embryo. The accretion rate is then: 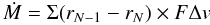 (5)where Δv is the difference in orbital velocity between the embryo and a pebble placed in the middle of the [rN,rN − 1] interval and Σ is the surface density of the disk of pebbles. Thus, our result is parametric in Σ and can be directly compared with the expression (4) from LJ12.
(5)where Δv is the difference in orbital velocity between the embryo and a pebble placed in the middle of the [rN,rN − 1] interval and Σ is the surface density of the disk of pebbles. Thus, our result is parametric in Σ and can be directly compared with the expression (4) from LJ12.
3. Results
Figure 1 shows the trajectory of one pebble for each of the 4 sizes that we consider in this study. The evolution is shown in a rotating reference frame, with the embryo fixed at r = 0.8 AU and θ = 3.22. Only the last synodic revolution is shown, i.e. that leading to the crossing of the orbit of the embryo. The trajectories of the 5 cm, 20 cm, 1 m and 10 m pebbles are depicted in blue, red, yellow and white, respectively. The mass of the embryo is 5 ME.
Several considerations should be made, by looking at these trajectories. First, notice that the stopping time (which increases with particle size) is not simply related to the migration speed. The particles with the fastest radial migrations are those with radii of 20 cm and 1 m (with migration rates roughly equal to each other). This is well known (Weidenschilling 1977b). The 5 cm particle migrates more slowly because it is more coupled with the gas (which does not have any net radial motion); the 10 m particle migrates more slowly than the 1 m particles because it is less sensitive to gas drag.
The U-turns drawn by the trajectories of the 20 cm and 1 m pebbles are not related to horseshoe dynamics. They are simply due to the fact that the angular velocity of a Keplerian orbit decreases as 1/r3/2 so that, in a reference system corotating with an object at a fixed distance r0 (like Fig. 1 corotating with the embryo at r0 = 0.8 AU) a particle moves from the right to the left if it has r > r0 and from the left to the right if it has r < r0. Thus, as the particle drifts from r > r0 to r < r0 it has to make a U-turn. In other terms, these bended trajectories are not due to the gravitational effect of the embryo but just to the rigid rotation of the reference frame. Only particles passing close to the embryo (shown below) are affected by the gravitational attraction of the latter.
Instead, the U-turn of the 5 cm pebble is due to horseshoe dynamics. This is apparent from the fact that the radial motion is fast only in the vicinity of the embryo. The particle shown in Fig. 1 traces approximately the maximal width of a particle horseshoe trajectory. Notice that the width of the horseshoe region for the particles is much narrower than that for the gas, highlighted by the U-turning streamlines.
Finally, the trajectory of the 10 m object shows radial oscillations as it approaches towards the embryo. This is due to its orbital eccentricity, acquired during previous passages at conjunction with the embryo, and not fully damped by the gas drag in half a synodic period (i.e. from conjunction to opposition). This is not the case from the other particles for two reasons: gas drag is stronger and erases the eccentricity faster (e.g. the 5 cm pebbles) and/or given their fast radial drift the pebbles passed too far from the embryo at the previous conjunction to acquire a large eccentricity (e.g. the 20 cm and 1 m particles).
We now focus on the dynamics in the very vicinity of the embryo, leading to pebble accretion and the embryo’s growth.
 |
Fig. 2 The trajectories of 5 cm pebbles approaching a 1 ME embryo in relative r,θ coordinates. |
Figure 2 shows the trajectories of several 5 cm pebbles as they pass close to the 1 ME embryo. Each line is a different particle. The x-axis reports the difference δθ between the θ values of the pebble and the embryo. Notice on the right hand side of the figure the particles doing the horseshoe U-turn (those which always have δθ > 0). Instead, the particles that are initially in circulation, i.e. that have r > 0.8 AU and δθ passing from positive to negative, eventually cross the embryo’s orbit far behind the embryo itself, when δθ < −0.6. Notice that the U-turn of the pebbles occurs at r ~ 0.798, i.e. slightly inside the embryo’s orbit (r = 0.8). This is because these pebbles are strongly coupled with the gas, which has a sub-Keplerian orbital velocity; thus the exact corotation radius is shifted towards the Sun. In total, 7 pebbles collide with the embryo, assumed to have the Earth’s radius, as one can see from the trajectories diving towards the point with coordinate (0,0.8). Six of these pebbles collide with the embryo in the approach phase, when δθ is evolving from positive to negative. However, one pebble hits the embryo “from the back”, i.e. after having crossed the embryo’s orbit and with δθ evolving from negative to positive.
Figure 3 is the same but for 20 cm pebbles. The figure is qualitatively similar to the previous one, but the trajectories are much more inclined due to the fact that these pebbles drift much faster towards the Sun (beware that the scales in Figs. 2 and 3 are different) and, consequently, the particles that cross the orbit of the embryo at negative δθ do so closer to the embryo (with δθ > −0.2 instead of <−0.6). The thick ellipse drawn around (0,0.8) marks a circle centered on the embryo with a radius equal to 1/3 of its Hill radius. The resolution of the output of the simulation is too coarse to resolve the trajectories inside this radius. However, the internal timestep of the Symba algorithm is good enough to resolve the physical collision of the pebbles with the embryo. There are 18 pebbles entering inside the circle, 4 of which enter “from the back”, i.e. after having crossed the embryo’s orbit. Of these 18 pebbles, 13 physically collide with the embryo. The remaining ones are slingshot away by the embryo during the close encounter and exit the domain covered by our grid.
Figure 4 is for one-meter particles. The major difference with respect to the previous figure is the strong kink that particles receive when passing from positive to negative δθ. This happens because these particles are less coupled to the gas and therefore they can be scattered to large eccentricity when they pass in conjunction with the embryo. Consequently, the 1-m particles pass much further away from the embryo than the 20 cm-particles when they cross the embryo’s orbit, and therefore they cannot collide with the embryo “from the back”.
Figure 5 is for 10 m-particles. For these particles we change the scale of the plot, showing the whole disk up to r = 0.86 AU. This is because gas drag is weak, and the particles conserve part of the eccentricity that they acquire during the previous conjunction with the embryo for a full synodic period. Consequently, their dynamical behavior when crossing the embryo’s orbit inherits the dynamical history recorded over several synodic revolutions. Because the radial drift during a synodic revolution is small, all particles have to pass eventually very close to the embryo, so that many of them (40%) are accreted. The particles that safely cross the embryo’s orbit do so with a horseshoe U-turn at δθ > 0. If the embryo is more massive the fraction of accreted particles increases and, for a 5 ME embryo, the accretion efficiency is 100% (see Fig. 6).
We now come to a synthesis of the results for what concerns the embryo’s mass accretion rate and filtering factor.
 |
Fig. 7 The accretion rate as a function of pebble size for embryos of 1 ME (filled dots) and 5 ME (open dots) respectively. The dotted and dashed lines indicate the accretion rates estimated in LJ12 for these two embryo masses. |
Figure 7 shows the mass accretion rate for the embryos of masses 1 ME (filled dots) and 5 ME (open dots) respectively, as a function of the pebbles size. The mass accretion rate is normalized by Σ (the surface density of the pebbles). The dotted and dashed horizontal lines show the accretion rate estimated by LJ12, for embryos of masses 1 ME and 5 ME respectively. As one can see, our numerically measured accretion rates are within an order of magnitude of the estimated rates, and tend asymptotically to the estimated values for growing pebble sizes. The drop of the accretion rate with particle size is due mainly because a larger fraction of the particles that enter the Hill sphere of the embryo are dragged away by the flow of the gas, instead of falling onto the central object. This phenomenon was expected in LJ12, who predicted that their accretion rate is valid for pebbles with stopping time of the order 0.1−1. Remember that 20 cm pebbles in our simulation have ts = 0.22. Thus, our results suggest that the nominal accretion rate of LJ12 applies instead from ts ~ 1; however, it remains valid up to stopping times larger than predicted, i.e. up to at least ~100 (the value of ts for the 10 m particles is 75).
The scaling relative to the embryo’s mass predicted by LJ12 (Ṁ ∝ Rhvh, i.e. Ṁ ∝ M2/3) is confirmed by our numerical simulations for all tested pebble sizes.
 |
Fig. 8 The filtering factor as a function of pebble size for embryos of 1 ME (filled dots) and 5 ME (open dots) respectively. |
Figure 8 shows the filtering factor as a function of pebble size, again for 5 ME (open dots) and 1 ME (filled dots) embryos. The filtering factor scales again as M2/3. The filtering factor decreases with increasing drift speed and therefore it is the smallest for the m-sized particles. Except for particles of multiple meters, the filtering factor is small (a few percent to 10%), which implies that a system of numerous embryos (with a number of objects roughly proportional to 1/F) can grow simultaneously in the disk. Notice that the embryos should grow in an oligarchic fashion, due to the M2/3 dependence of the accretion rate. Instead, if the disk is dominated by multi-meter particles, only a few embryos can grow, with eventually the outermost one capturing all the material.
In the LJ12 model, there is no upper limit in mass for an accreting embryo, as long as pebbles are available: an embryo keeps accreting at a rate proportional to M2/3Σ. In reality, however, if the total mass of the planet (the mass of the solid embryo plus the mass of the gas eventually accreted in its atmosphere) becomes large enough, the surface density of the gas distribution is modified. The neighborhood of the planet orbit becomes partially depleted of gas (a shallow gap is opened) and this changes the pressure gradient in the disk and the angular velocity of the gas. Eventually the gas becomes super-Keplerian at some location outside of the planet’s orbit and this stops the inward radial drift of pebbles and small planetesimals. The accretion of the planet by the LJ12 mechanism suddenly stops. Figure 9 shows the ratio between the azimuthal velocity of the gas and that of a Keplerian circular orbit as a function of radius, for planet masses of 30, 50 and 100 ME placed at r = 0.8. For these tests, we have increased the disk’s radial extension to the interval 0.5−1.3 AU. For the disk parameters that we chose (see Sect. 2.1), we find that the disk becomes locally super-Keplerian if the planet’s mass is ~50 ME. This mass would be reduced if the disk had a lower viscosity and/or scale height. Whatever the exact value of the limit mass of the planet, our result shows that the LJ12 mechanism is capable of feeding a solids to a giant planet until its mass is several tens of Earth masses.
 |
Fig. 9 The gas azimuthal velocity relative to the Keplerian value, as a function of orbital radius, for disks with embedded planets of 30, 50 and 100 Earth masses. The horizontal line marks the boundary between sub-Keplerian and super-Keplerian rotation. |
This result has two main implications. First, the runaway accretion of the atmosphere onto the embryo might start earlier than in the classic Pollack et al. (1996) model. In fact, in Pollack et al. the embryo’s accretion stalls when the mass of the embryo is about 10 ME, because the feeding zone for solids is strongly depleted. Then, the embryo’s accretion of both gas and solids continues very slowly, with the consequence that the critical mass for triggering runaway capture of gas (~30 ME) is reached only after several My. In the LJ12 scenario, the mass accretion of the embryo would not slow down, so that the runaway accretion of gas, in principle, might start at an earlier time. We notice however that a high accretion rate of solids has also a negative effect on gas accretion because it releases a lot of energy on the embryo which needs to be evacuated (Dodson-Robinson & Bodenheimer 2010); thus, the net effect of pebble-accretion on gas-accretion will need to be investigated in hydrodynamical simulations accounting for heat transfer. Second, the accretion of pebbles until the planet mass achieves ~50 ME can help explaining the large ratio between heavy elements and hydrogen and helium in the atmosphere of Jupiter, which is 3−4 times solar (Wong et al. 2004). Enriching the giant planets in heavy elements is not straightforward (Guillot & Gladman 2000) by other mechanisms; thus this is another appealing aspect of the LJ12 model.
4. Conclusions
In this paper we have tested the scenario of giant planet core formation proposed by LJ12 with hydrodynamical simulations that fully account for (i) the interaction between the growing core and the gas of the disk and (ii) the local drag exerted by the gas on pebbles and boulders.
We have found that the pebble dynamics in the vicinity of the planetary embryo is non-trivial, and that it changes significantly with the pebble size. Nevertheless, the accretion rate of the embryo that we measure is within an order of magnitude of the rate estimated in LJ12 and tends to their value with increasing pebble-size.
The accretion of pebbles can continue until the embryo’s mass is of the order of 50 Earth masses (in solids and gas). This may have important implications on the onset of runaway accretion of gas by the growing giant planets and can help explaining the enrichment in solids observed in Jupiter’s atmosphere.
The actual accretion rate of an embryo depends on the amount of mass Σ available in pebbles, which is not known a priori, given that pebbles are consumed by the formation of planetesimals and by the accretion of the embryos themselves. Nevertheless, the accretion rates that we find in Fig. 7 are potentially large. For instance, if a MMSN of solids (20 g/cm2 at 1 AU) were available in 20 cm pebbles, the mass doubling time for a 1 ME embryo would be only 5500 years! This illustrates the importance of the LJ12 model for the growth of giant planets cores.
Given that the LJ12 model is built in the same framework as the model that explains the rapid formation of planetesimals (Johansen et al. 2007), we believe that the community has now, for the first time, a coherent scenario to explain the the early phases of planet growth. However, we do not see any evident reason for which only a small number (4−6) of giant planet cores should grow in the disk, as suggested by the number of giant planets of our solar system, including rogue ice-giants potentially lost during the dynamical evolution that followed planet formation (Nesvorny 2011; Nesvorny & Morbidelli 2012). Thus, we think that, most likely, the LJ12 model explains the formation of massive planetary embryos of a few Earth masses, but an additional stage is needed to form the giant planet cores (10 Earth masses or more).
This is the scenario that we envision. The embryos formed by the LJ12 mechanism, once massive enough, start to migrate in the disk due to planet-disk interactions. Recent results on migration in radiatively cooling disks (Paardekooper & Mallema 2006; Baruteau & Masset 2008; Kley & Crida 2008; Paardekooper et al. 2010; Masset & Casoli 2010; Bitsch & Kley 2011) show that the embryos migrate from all directions toward an orbital radius where migration is canceled out by the compensation of competing torques. This convergent migration towards the same region can promote the mutual accretion of embryos, eventually reducing a system of a large number of embryos into a system of a smaller number of larger objects, i.e. a handful of giant planet cores (Horn et al. 2012). Admittedly, this scenario is still speculative and more work is needed to prove its validity. We stress, however, that a final phase of core formation characterized by mutual collisions of embryos would explain, in a natural way, the massive impacts that are needed to explain the current obliquities of Uranus and Neptune (Morbidelli et al. 2012).
Acknowledgments
Alessandro Morbidelli thanks Germanys Helmholtz Alliance for providing support through its Planetary Evolution and Life programme. David Nesvorny thanks the Observatoire de la Côte d’Azur for hospitality during his sabbatical in Nice. Both authors thank an anonymous reviewer for reading the manuscript in details.
References
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baruteau, C., & Masset, F. 2008, ApJ, 672, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Kley, W. 2011, A&A, 536, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. 2006, Icarus, 180, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Mathematische Annalen, 100, 32 [Google Scholar]
- Dodson-Robinson, S. E., & Bodenheimer, P. 2010, Icarus, 207, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., Lithwick, Y., & Sari, R. 2004, ApJ, 614, 49 [Google Scholar]
- Greenberg, R., Hartmann, W. K., Chapman, C. R., & Wacker, J. F. 1978, Icarus, 35, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Gladman, B. 2000, Disks, Planetesimals, and Planets, 219, 475 [Google Scholar]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Horn, B., Lyra, W., Mac Low, M.-M., & Sándor, Z. 2012, ApJ, 750, 34 [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Johansen, A., Klahr, H., & Henning, T. 2006, ApJ, 636, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Levison, H. F., & Morbidelli, A. 2007, Icarus, 189, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., & Casoli, J. 2010, ApJ, 723, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Batygin, K., Crida, A., & Gomes, R. 2012, Icarus, 219, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Murray-Clay, R., Kratter, K., & Youdin, A. 2011, AAS/Division for Extreme Solar Systems Abstracts, 2, 804 [Google Scholar]
- Nesvorný, D. 2011, ApJ, 742, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2012, AJ, in press [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., Crida, A., & Kley, W. 2010, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., & Zucker, S. 2004, MAPS, 39, 1859 [NASA ADS] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, ApJ, 128, 1348 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2003, Icarus, 161, 431 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977a, Ap&SS, 51, 153 [Google Scholar]
- Weidenschilling, S. J. 1977b, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Davis, D. R. 1985, Icarus, 62, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W., & Stewart, G. R. 1989, Icarus, 77, 330 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Color map of the surface density of the gas in a disk in the presence of a 5 ME embryo at r = 0.8,θ = 3.22. The black curves show some gas streamlines and the blue, red, yellow and white curves depict the trajectories of 5 cm, 20 cm, 1 m and 10 m pebbles, respectively, in the frame corotating with the embryo. |
| In the text | |
 |
Fig. 2 The trajectories of 5 cm pebbles approaching a 1 ME embryo in relative r,θ coordinates. |
| In the text | |
 |
Fig. 3 The same as Fig. 2 but for 20 cm pebbles. |
| In the text | |
 |
Fig. 4 The same as Fig. 2 but for 1 m particles. |
| In the text | |
 |
Fig. 5 The same as Fig. 2 but for 10 m particles. |
| In the text | |
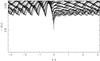 |
Fig. 6 The same as Fig. 5 but for a 5 ME embryo. |
| In the text | |
 |
Fig. 7 The accretion rate as a function of pebble size for embryos of 1 ME (filled dots) and 5 ME (open dots) respectively. The dotted and dashed lines indicate the accretion rates estimated in LJ12 for these two embryo masses. |
| In the text | |
 |
Fig. 8 The filtering factor as a function of pebble size for embryos of 1 ME (filled dots) and 5 ME (open dots) respectively. |
| In the text | |
 |
Fig. 9 The gas azimuthal velocity relative to the Keplerian value, as a function of orbital radius, for disks with embedded planets of 30, 50 and 100 Earth masses. The horizontal line marks the boundary between sub-Keplerian and super-Keplerian rotation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


