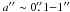| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 5 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201219774 | |
| Published online | 08 October 2012 | |
Dynamical masses of a selected sample of orbital binaries⋆
1
Observatorio Astronómico Ramón María Aller, Universidade de Santiago de
Compostela, Avenida das Ciencias
s/n, 15782
Santiago de Compostela,
Spain
2
Institute of Astronomy of the Russian Academy of
Sciences, 48 Pyatnitskaya
Street, 119017
Moscow,
Russia
e-mail: malkov@inasan.ru
3
Faculty of Physics, Moscow State University,
119992
Moscow,
Russia
Received: 8 June 2012
Accepted: 7 September 2012
Orbital binary stars are essential objects for determining dynamical and physical properties of stars through a combined analysis of photometric and astrometric data. We compiled a set of orbital binaries with known trigonometric parallaxes and orbits of high quality, using data from current versions of the Catalogue of Orbits and Ephemerides of Visual Double Stars and the Sixth Catalog of Orbits of Visual Binary Stars as well as including updated information from WDS and SIMBAD. We constructed distributions of orbital binaries among dynamical mass, period, semi-major axis, and eccentricity of systems, which characterize the set. Some problems related to the parameterization of orbital binaries are also discussed in the paper.
Key words: binaries: visual
Full Tables 1 and 2 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/546/A69
© ESO, 2012
1. Introduction
Orbital binary stars (visual binaries with orbit solutions) are essential objects for determining dynamical and physical properties of stars, especially masses, through a combined analysis of photometric and astrometric data. Along with double-lined eclipsing binaries (see details in Popper 1980; Torres et al. 2010), orbital binaries with known distances are the only types of detached binary systems that enable one to determine stellar masses and semi-major axes of orbits.
Orbital binaries are quite numerous: current (June 2012) versions of principal catalogues of orbital binaries contain data on 1700 (Observatorio Astronómico Ramón María Aller Catalogue of Orbits and Ephemerides of Visual Double Stars, hereafter OARMAC, Docobo et al. 2001, 2012a,b) to 2000 pairs (Sixth Catalog of Orbits of Visual Binary Stars, hereafter ORB6, Hartkopf et al. 2001). However, the former catalogue contains outdated photometry and lacks orbital parameter uncertainties. The latter one contains neither spectral classification nor parallax information and the period and semi-major axis are not provided for a few stars. Although they both represent the best collections of published data on orbital binaries, they are not exhaustive.
The main goal of this work is to estimate dynamical masses of orbital binaries, independently of those sometimes published with the orbits, and draw preliminary conclusions concerning the distribution of systems along principal parameters (mass, period, semi-major axis, eccentricity). To make this possible, one needs to construct a list of orbital binaries (hereafter orbit list) that contains orbital elements as well as magnitudes and spectral types of components, distances, and an indication of spectroscopic and eclipsing phenomena.
The orbit list compilation procedure is described in Sect. 2. A statistical analysis of a “refined” subset of the list is given in Sect. 3. Finally, in Sect. 4, we draw conclusions.
2. The orbit list compilation
To compile the orbit list, we combined data from both OARMAC and ORB6. At this stage, we maintained systems without parallax, but removed systems without a period/semi-major axis. The resulting list contains 3139 orbits for 2278 pairs: 1588 pairs have a single orbit, 548 pairs have two orbits, 120 pairs have three orbits, 19 pairs have four orbits, one pair has five orbits, and two pairs have seven orbits. Those 2278 pairs combine into 2016 binaries, 76 triples, 26 quadruples, 5 quintuples, and 2 septuples. Orbital solutions for 1319 orbits in OARMAC and ORB6 coincide, while the orbit list contains 832 and 988 original orbits from OARMAC and ORB6, respectively.
Recent photometry and spectral classification, when absent, was added from WDS. The following data were added from SIMBAD: magnitudes and spectral types (if absent from the original catalogues and WDS), the parallax with its corresponding uncertainty (taken from van Leeuwen 2007), and an indication of the spectroscopic and eclipsing nature of systems. In addition, we used coordinates from SIMBAD to estimate interstellar extinction, which is an important value for photometric mass calculation (see discussion in Sect. 3 below).
Orbit list, first twenty five lines.
The resulting orbit list contains the following data (numbers of columns in Table 1 are indicated):
-
Identifications: (1) WDS designation; (2) discoverer designation and components involved (if no components are listed, the orbit is of the AB pair); (3) Hipparcos number; (4) ADS number; (5) number of pairs in the system and current number of the pair, number of orbits for the pair and current number of the orbit.
-
Astrophysical quantities: (6, 7) Visual magnitudes (V) of components taken from WDS; (8) spectral type(s); (9, 10) trigonometric parallax with uncertainty, mas; (11) interstellar extinction, mag.
-
Orbital elements used (with uncertainties): (12, 13) Period (P), year; (14, 15) semi-major axis (a), arcsec; (16, 17) eccentricity (e);
-
Quality grades and notes: (18) Orbit quality grade in ORB6 (reliability of a given orbit, varies from 1 for definitive orbits to 5 for indeterminate orbits, grade 8 is given for interferometric binaries, astrometric orbits received grade 9); (19) orbit quality grade in OARMAC (system’s capacity to own a reliable orbit, denoted by letter A, B or C); (20) “note in ORB6” flag; (21) “comment in OARMAC” flag; (22) “note in OARMAC” flag; (23) “eclipsing binary” flag; (24) “spectroscopic binary” flag.
![\begin{equation} A_{\rm V} = \frac{a_0 \beta}{|\sin b|} \left[ 1 - {\rm e}^{-\frac{r|\sin b|}{\beta}} \right], \end{equation}](/articles/aa/full_html/2012/10/aa19774-12/aa19774-12-eq5.png) (1)where β is the scale height
and a0 is the extinction to an object located in the galactic
plane behind the absorbing layer. The values of 1.6 mag/kpc and 114 pc were accepted for
a0 and β, respectively, according to Sharov’s
(1963) study. Malkov & Kilpio (2002) have shown that this map, although rather old,
quite adequately represents interstellar extinction for relatively short (up to 1 kpc)
distances, where most of orbital binaries reside.
(1)where β is the scale height
and a0 is the extinction to an object located in the galactic
plane behind the absorbing layer. The values of 1.6 mag/kpc and 114 pc were accepted for
a0 and β, respectively, according to Sharov’s
(1963) study. Malkov & Kilpio (2002) have shown that this map, although rather old,
quite adequately represents interstellar extinction for relatively short (up to 1 kpc)
distances, where most of orbital binaries reside.
In 650 records of the orbit list there is no available photometry for the secondary component, in 65 records there is no available spectral type, and the parallax for 270 records is unknown, zero, or negative.
3. A refined list of orbital binaries
To carry out a statistical analysis of orbital binaries, one needs to “refine” the resulting orbit list. We removed triples and systems of higher multiplicity to avoid biases in dynamical mass distribution. We also removed systems with an unknown, zero, or negative parallax. Poor-quality orbits and astrometric orbits (ORB6 quality grades 4, 5 or 9 and OARMAC quality grade C) were also removed from the refined list. This refined list contains orbits of 652 systems.
Finally, the resulting orbit list often contains several orbits per pair, which is not convenient for statistical studies. Because the quality grades of these orbits are usually equal and both catalogues do not provide other criteria to distinguish the rms or m.a. of the residuals, etc., the only criterion to choose one pair from two or more is to calculate the mass of the system and compare it with that estimated from photometric and spectral data.
Period and semi-major axis, combined with parallax, yield the total mass of the system,
according to Kepler’s law:
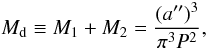 (2)where P is the orbital period
(in years), M1,2 are the masses (in solar mass),
a′′ and π are the semi-major axis and the parallax (both
in arcsec), respectively.
(2)where P is the orbital period
(in years), M1,2 are the masses (in solar mass),
a′′ and π are the semi-major axis and the parallax (both
in arcsec), respectively.
System list, first twenty five lines.
The masses of the components can also be estimated from observed photometry, trigonometric
parallax, and a mass-luminosity relation. The appropriate formula is
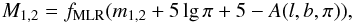 (3)where m1,2 are the
apparent magnitudes, A is the interstellar extinction value, and
fMLR is the mass-luminosity relation depending on the stellar
luminosity class (LC). It is worth noting that the conformity of components to the
mass-luminosity relation (in V band, in particular) is likely not exact,
especially at the lower part of the main sequence, because of the stellar evolution and
chemical abundance variations (Bonfils et al. 2005).
(3)where m1,2 are the
apparent magnitudes, A is the interstellar extinction value, and
fMLR is the mass-luminosity relation depending on the stellar
luminosity class (LC). It is worth noting that the conformity of components to the
mass-luminosity relation (in V band, in particular) is likely not exact,
especially at the lower part of the main sequence, because of the stellar evolution and
chemical abundance variations (Bonfils et al. 2005).
Another route requires spectral classification of both components and reliable
mass-spectrum relation, fMSR:
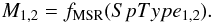 (4)Let us call the masses, determined with Eqs.
(2)–(4), dynamical (Md), photometric
(Mph), and spectral
(Msp), respectively. We computed the
photometric mass for every pair and dynamical mass for every orbit. In the case of multiple
orbits, we compared their values to choose the orbit that yields the most reliable mass.
(4)Let us call the masses, determined with Eqs.
(2)–(4), dynamical (Md), photometric
(Mph), and spectral
(Msp), respectively. We computed the
photometric mass for every pair and dynamical mass for every orbit. In the case of multiple
orbits, we compared their values to choose the orbit that yields the most reliable mass.
For photometric mass estimation, we used the MLR of Malkov (2007) for upper-MS, Henry & McCarthy (1993) for lower-MS, and Henry et al. (1993) for lowest masses. Subgiants and early-type (O-F6) giants were considered to be 1 mag brighter than dwarfs (Halbwachs 1986). Lastly, for the few remaining late-giant and supergiant stars, photometric masses were estimated with Tables II and VI of Straizys & Kuriliene (1982). Pairs with unknown LC were considered to be MS-systems. The LC of secondary component, when unknown, was considered to be the same as for the primary. If the secondary magnitude was unknown (35 of 652 systems), equal brightness of components was assumed, and, consequently, an upper limit for photometric mass was estimated. The photometric mass is absent in 17 cases, where the estimated absolute stellar magnitude is inappropriate for a given LC.
We also calculated the dynamical mass uncertainty. OARMAC does not contain uncertainties of P and a′′, and we estimated the following: σP to be 5%, 10%, 20% for A, B, C quality grades, respectively, and σa to be 3%, 6%, 12% for A, B, C quality grades, respectively.
As can be seen from Eq. (3), the absolute magnitude uncertainty depends mainly on the
parallax uncertainty, and for the vast majority of our systems it does not exceed
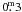 . However, the main factor that contributes
to the photometric mass uncertainty for a given absolute magnitude is the mass-luminosity
relation accuracy. For intermediate mass MS-stars, the MLR slope and its standard deviation
value (see, e.g., Malkov 2007) produce about 0.06 for
the log M uncertainty (i.e. mass uncertainty is about 15%). For stars of
other LCs, however, we estimate that uncertainty to be 2−3 times worse, mainly because of
higher MLR standard deviation values.
. However, the main factor that contributes
to the photometric mass uncertainty for a given absolute magnitude is the mass-luminosity
relation accuracy. For intermediate mass MS-stars, the MLR slope and its standard deviation
value (see, e.g., Malkov 2007) produce about 0.06 for
the log M uncertainty (i.e. mass uncertainty is about 15%). For stars of
other LCs, however, we estimate that uncertainty to be 2−3 times worse, mainly because of
higher MLR standard deviation values.
Spectral masses were estimated from Table VI of Straizys & Kuriliene (1981). If the secondary spectral type was unknown, the listed spectral mass is the primary mass (i.e., it represents a minimum mass of the system). Main sequence is assumed if the luminosity class was unknown, which seems to be a reasonable assumption for our relatively nearby orbital binaries. Spectral mass is not available for six entries, which include Am, Be, L stars, and stars with inexact classification, e.g. M:. We estimated the spectral mass uncertainty to be about 20% for MS-stars (we refer to Straizys & Kuriliene 1981, Fig. 1) and about 30% for stars of other luminosity classes (see, e.g., Piskunov 1977, and the corresponding discussion in Straizys & Kuriliene 1981).
 |
Fig. 1 Difference between the magnitudes of the components vs. the semi-major axis of the
orbit (upper panel) and the magnitudes of the primaries
(lower panel). The dashed lines mark the area that satisfies the
definition of selected systems, |
The final list (so-called system list, Table 2) contains 652 systems. This list is large enough for a reliable statistical analysis of this class of binary systems.
First of all, we note that some systems exhibit obviously incorrect dynamical masses and/or a large discrepancy between dynamical and photometric masses. In particular, the masses of two systems are smaller than 0.01 (hereafter, in solar mass) and the masses of another four systems exceed 100. The most obvious reason for that are poorly known parallaxes and/or orbital elements as well as the presence of a third still-undetected body (or subcomponents) that lead to dynamical mass overestimation (Tamazian et al. 2006). Examples include WDS 01083+5455 WCK 1Aa,Ab (Md = 0.01), where obviously incorrect orbital elements were taken into OARMAC, and WDS 00174+0853 A 1803AB (Md = 0.02), where the initial-Hipparcos trigonometric parallax π = 15.3 mas produced a quite reasonable mass (Pavlovic & Todorovic 2005). Among other reasons for a discrepancy between dynamical and photometric masses, we can mention incorrect spectral classification, interstellar extinction underestimation, and variability of components. These systems need further study. In particular, Tamazian et al. (2006) reported a generally good agreement between dynamical masses for 11 nonvariable, virtually single K and M dwarfs with the mass sums of individual components calculated through standard mass-luminosity calibrations. Docobo et al. (2008) showed that Hipparcos parallaxes of distant visual binaries can be refined by using relevant orbital and spectral data.
It is well known that observational selection limits the possibilities of observation of binary systems of different types and can seriously distort the results of the analysis. Here we analyse the main selection effects that determine the sample of orbital binaries.
The overwhelming majority of binaries in the system list have apparent magnitudes of the
primary components 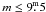 . Also, the majority of systems have
semi-major axes
. Also, the majority of systems have
semi-major axes 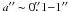 : closer systems are not resolved by
instruments with aperture D ~ 100 cm, which are generally used to
detect visual binaries, and wider systems usually do not exhibit significant orbital motion.
: closer systems are not resolved by
instruments with aperture D ~ 100 cm, which are generally used to
detect visual binaries, and wider systems usually do not exhibit significant orbital motion.
The distribution with respect to the magnitude difference of the components dm gives, in principle, the possibility of estimating the mass ratio of the components. However, the dm distribution is also strongly distorted by selection. First, among the closest binaries, only pairs with comparable luminosities are detectable. Second, among binaries with the primary magnitude close to the limiting magnitude, only pairs with small dm are detected, and pairs with the secondaries fainter than the limiting magnitude appear as single stars and do not contribute to statistics.
 |
Fig. 2 Dynamical mass (see Eq. (2)) distribution of all 652 listed systems (grey bars) and
the selected 207 systems with |
In Fig. 1, the stars we investigated have been plotted
on the plane of the semi-major axis of the orbit (upper panel) and the magnitudes of the
primaries (lower panel) vs. the difference between the magnitudes of the components. It can
be seen that the mean value of dm increases with increasing
a′′ and increases with increasing brightness. One can see that, for
systems with 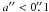 , or a′′ > 1′′, or
, or a′′ > 1′′, or
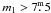 , or dm > 2m
the set is definitely incomplete. Note, however, that the restricted sample (systems with
, or dm > 2m
the set is definitely incomplete. Note, however, that the restricted sample (systems with
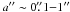 ,
, 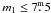 , dm ≤ 2m) surely
does not include all visual binaries with corresponding restrictions posed on their
magnitudes and angular separations. For example, a distant
(d ~ 2.5 kpc) wide (a ~ 500 AU) gravitationally
bound system can be observed like a visual binary, but its orbital motion is so slow that it
would not exhibit evident orbital motions and, hence, would not contribute to the sample as
orbital binary.
, dm ≤ 2m) surely
does not include all visual binaries with corresponding restrictions posed on their
magnitudes and angular separations. For example, a distant
(d ~ 2.5 kpc) wide (a ~ 500 AU) gravitationally
bound system can be observed like a visual binary, but its orbital motion is so slow that it
would not exhibit evident orbital motions and, hence, would not contribute to the sample as
orbital binary.
For 207 systems of the 652 listed systems, a′′, m1 and dm satisfy these criteria. The distributions of these selected 207 systems, together with those of all 652 systems, among dynamical mass, semi-major axis, and eccentricity are shown in Figs. 2–4, respectively.
 |
Fig. 3 Semi-major axis distribution of all 652 listed systems (grey bars) and the selected
207 systems with |
 |
Fig. 4 Eccentricity distribution of all 652 listed systems (grey bars) and the selected 207
systems with |
Our sample is, inevitably, restricted at large a (see Fig. 3) due to long orbital periods of wide binaries, hence the number of binaries significantly drops at a > 50 AU. The distribution has a broad, nearly flat peak at 10 < a < 50, and is steep again for close binaries with a < 10 AU due to their small projected angular separations.
It should be noted that the resulting distributions (Figs. 2−4) are heavily distorted by the selection effects inherent to the OARMAC and ORB6 catalogues, and cannot be mistaken for initial or present-day distributions of binary parameters. They can be simulated using initial distributions on masses and orbital elements and involving stellar evolution and observational selection effects. However, before these effects are quantified, simulations cannot be compared to the catalogue and conclusions on the initial distributions cannot be made.
4. Conclusions
We collected and investigated visual binaries with known orbital parameters to construct a list of orbital binaries from the OARMAC and ORB6 catalogues, with additional photometric and spectral information from WDS and SIMBAD. The resulting orbit list contains 3139 orbits of 2278 orbital binaries and
represents the most comprehensive list to date of orbital binaries with known distances, photometry, spectral classification, and indication of the spectroscopic and eclipsing nature of the binary.
Next, we compiled a refined subset of the orbit list. For 207 systems that satisfy the
criteria 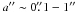 ,
, 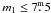 , and dm ≤ 2m, we
constructed distributions among dynamical mass, period, semi-major axis, and eccentricity.
These distributions can be used to construct the initial mass function and star formation
history of wide binaries. This is a subject for future study. Our list of orbital binaries,
containing orbital parameters from OARMAC and ORB6 as well as photometric and spectral
information from WDS and SIMBAD, will be updated regularly, as all of the sources mentioned
above are constantly updated.
, and dm ≤ 2m, we
constructed distributions among dynamical mass, period, semi-major axis, and eccentricity.
These distributions can be used to construct the initial mass function and star formation
history of wide binaries. This is a subject for future study. Our list of orbital binaries,
containing orbital parameters from OARMAC and ORB6 as well as photometric and spectral
information from WDS and SIMBAD, will be updated regularly, as all of the sources mentioned
above are constantly updated.
Acknowledgments
We thank the referee, whose comments greatly helped us to improve the paper. This work was supported by the Russian Foundation for Fundamental Research grants 10-02-00426, 12-02-31904 and 12-07-00528, the Federal Science and Innovations Agency under contract 02.740.11.0247, the Presidium RAS program “Leading Scientific Schools Support” 3602.2012.2, and the Federal task program “Research and operations on priority directions of development of the science and technology complex of Russia for 2007-2012” (contract 16.518.11.7074). This research has been also supported by the Spanish Ministry of Economy and Compatitiveness under the Project AYA2011-26429. This study was conducted while OM was an invited visiting professor at the Ramón María Aller Astronomical Observatory at the University of Santiago de Compostela, Spain. This research has made use of the SIMBAD database, operated at the Centre de Données astronomiques de Strasbourg, the Washington Double Star Catalog maintained at the US Naval Observatory, and NASA’s Astrophysics Data System Bibliographic Services.
References
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Docobo, J. A., Ling, J. F., Prieto, C., et al. 2001, Acta Astron. 51, 353 [Google Scholar]
- Docobo, J. A., Tamazian, V. S., Andrade, M., Melikian, N. D., & Karapetian, A. A. 2008, AJ, 136, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Docobo, J. A., Ling, J. F., & Campo, P. P. 2012a, Catalog of Orbits and Ephemerids of Visual Double Stars, Version On-Line (www.usc.es/astro/catalog.htm) [Google Scholar]
- Docobo, J. A., Ling, J. F., & Campo, P. P. 2012b, in Binaries Inside and Outside the Local Interstellar Bubble, eds. J. A. Docobo, V. S. Tamazian, & Yu. Yu. Balega, Santiago de Compostela, February 2011, AIP Conf. Proc., 1452, 30 [Google Scholar]
- Halbwachs, J.-L. 1986, A&A, 168, 161 [NASA ADS] [Google Scholar]
- Hartkopf, W. I., Mason, B. D., & Worley, C. E. 2001, Sixth Catalog of Orbits of Visual Binary Stars, http://www.ad.usno.navy.mil/wds/orb6/orb6.html [Google Scholar]
- Henry, T. J., & McCarthy, D. W. Jr. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Franz, O. G., Wasserman, L. H., et al. 1999, ApJ, 512, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, O. 2007, MNRAS, 382, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, O. Yu., & Kilpio, T. Yu. 2002, ApSS, 280, 115 [NASA ADS] [Google Scholar]
- Parenago, P. P. 1940, Astron. Zh., 17, 3 [Google Scholar]
- Pavlovic, R., & Todorovic, N. 2005, Serbian AJ, 171, 49 [Google Scholar]
- Piskunov, A. E. 1977, Scientific Information Astron. Council, Moscow, 37, 31 [Google Scholar]
- Popper, D. M. 1980, ARA&A, 18, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Sharov, A. S. 1963, Astron. Zh., 40, 900 [NASA ADS] [Google Scholar]
- Straizys, V., & Kuriliene, G. 1981, ApSS, 80, 363 [NASA ADS] [Google Scholar]
- Tamazian, V. S., Docobo, J. A., Melikian, N. D., & Karapetian, A. A. 2006, PASP, 118, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Difference between the magnitudes of the components vs. the semi-major axis of the
orbit (upper panel) and the magnitudes of the primaries
(lower panel). The dashed lines mark the area that satisfies the
definition of selected systems, |
| In the text | |
 |
Fig. 2 Dynamical mass (see Eq. (2)) distribution of all 652 listed systems (grey bars) and
the selected 207 systems with |
| In the text | |
 |
Fig. 3 Semi-major axis distribution of all 652 listed systems (grey bars) and the selected
207 systems with |
| In the text | |
 |
Fig. 4 Eccentricity distribution of all 652 listed systems (grey bars) and the selected 207
systems with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.