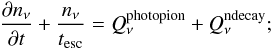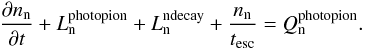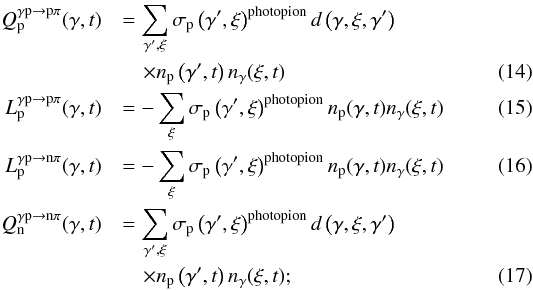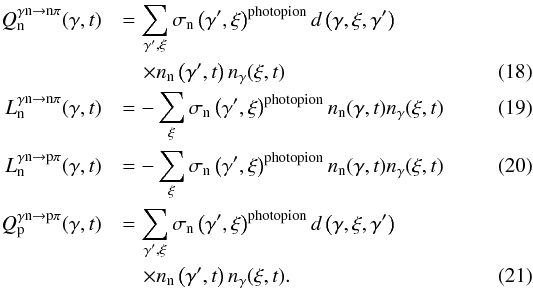| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219770 | |
| Published online | 18 October 2012 | |
The time-dependent one-zone hadronic model
First principles
1
Department of PhysicsUniversity of Athens,
Panepistimiopolis,
15783
Zografos,
Greece
e-mail: sdimis@phys.uoa.gr
2
Department of Physics (School of Chemistry and Physics),
University of Adelaide, North
Terrace, Adelaide,
SA
5005,
Australia
3 Institut für Theoretische Physik, und Institut für Astro- und
Teilchenphysik, Universität Innsbruck, Austria
Received: 6 June 2012
Accepted: 6 August 2012
We present a time-dependent approach to the one-zone hadronic model in the case where the photon spectrum is produced by ultrarelativistic protons interacting with soft photons that are produced from protons and low magnetic fields. Assuming that protons are injected at a certain rate in a homogeneous spherical volume containing a magnetic field, the evolution of the system can be described by five coupled kinetic equations, for protons, electrons, photons, neutrons, and neutrinos. Photopair and photopion interactions are modelled using the results of Monte-Carlo simulations and, in particular, from the SOPHIA code for the latter. The coupling of energy losses and injection introduces a self-consistency in our approach and allows the study of the comparative relevancy of processes at various conditions, the efficiency of the conversion of proton luminosity to radiation, the resulting neutrino spectra, and the effects of time variability on proton injection, among other topics. We present some characteristic examples of the temporal behaviour of the system and show that this can be very different from the one exhibited by leptonic models. Furthermore, we argue that, contrary to the wide-held belief, there are parameter regimes where the hadronic models can become quite efficient. However, to keep the free parameters at a minimum and facilitate an in-depth study of the system, we have only concentrated on the case where protons are injected; i.e., we did not consider the effects of a co-accelerated leptonic component.
Key words: radiation mechanisms: non-thermal / radiative transfer / galaxies: active
© ESO, 2012
1. Introduction
BL Lac objects and flat-spectrum radio quasars (commonly termed blazars) display a spectral energy distribution (SED) that extends from radio to γ-rays, in the shape of two broad humps – one in the radio to UV or X-ray frequency range and the other in the X-ray to γ-ray range. Both components are non-thermal and very likely originate in the blazar’s jet, which is closely aligned with the line of sight of the observer. While the lower-energy hump is widely acknowledged to result from synchrotron radiation from relativistic electrons in the emitting region, the origin of the higher-energy hump is subject to differing interpretations.
According to the leptonic models, the high-energy component emerges from inverse Compton scattering of electrons on soft target photons. Those photons may be the product of synchrotron radiation of the same electrons (Maraschi et al. 1992; Bloom & Marscher 1996; Inoue & Takahara 1996) or an indigenous population of external photons (Dermer et al. 1992; Sikora et al. 1994). Hadronic models, on the other hand, assume that protons, which are accelerated along with electrons, contribute much of the high-energy component via photopion interactions (Mannheim 1998; Mücke et al. 2003; Böttcher et al. 2009). The target photons may either be produced inside the jet via synchrotron emission from a co-accelerated population of electrons (Mannheim 1993), originate outside the jet (Protheroe 1997; Bednarek & Protheroe 1999; Atoyan & Dermer 2001), or be produced via synchrotron emission from the protons themselves (Aharonian 2000; Mücke & Protheroe 2001a). In addition proton-proton interactions were taken into account for the first time in the AGN case by Protheroe & Kazanas (1983) and were later applied to jets by Siewert et al. (2004) and Reynoso et al. (2011). For a recent review of the features of leptonic versus hadronic models see Boettcher (2012). Although similar models are used to study gamma ray bursts (Bottcher & Dermer 1998; Kazanas et al. 2002; Mastichiadis & Kazanas 2006; Asano & Inoue 2007; Asano et al. 2009; Mastichiadis & Kazanas 2009) and γ-ray emitting compact binary systems (Romero et al. 2003; Paredes et al. 2005; Romero et al. 2005), the former demand large magnetic fields, while the latter demand high proton densities, making inelastic pp-collisions more important than photohadronic interactions. However, it should be noted that both photo-pair and photo-meson production are included in recent models of compact binaries, and they are shown to be significant when proton and electron luminosities are near equipartition (Vila et al. 2012). The processes and range of variables used in this work are, instead, tailored to photon-dominated systems such as blazars, although they can indice similar effects in other systems, and thus are qualitatively relevant to them.
While leptonic models have often made use of time-dependent codes to solve the kinetic equations of electrons and photons (Mastichiadis & Kirk 1997; Krawczynski et al. 2002; Böttcher & Chiang 2002; Katarzyński et al. 2005), hadronic models have been very difficult to investigate in a similar manner, owing to the greater complexity of the particle interactions involved and the resulting time-consuming nature of simulations. First efforts (Mastichiadis & Kirk 1995) used simple δ-functions for the secondary production, while the effects of Bethe-Heitler pair production were calculated in a time-dependent manner in Mastichiadis et al. (2005) who used the Monte Carlo results of Protheroe & Johnson (1996) to model the process. In the present paper we extend this method to incorporate photopion interactions in detail. For this we have required the use of the SOPHIA Monte-Carlo event generator for hadronic interactions (Mücke et al. 2000), whose results have been adapted into a time-dependent code.
The paper is structured as follows. In Sect. 2 we present the time-dependent kinetic equations for all five particle types and show the coupling that emerges when all leptonic and hadronic processes are taken into account. In Sect. 3 we discuss the integration of the SOPHIA code’s results into our model and its verifications through energy-loss tests. In Sect. 4 we present various results from monoenergetic proton injection in a magnetic field, noticing the transition in importance from photopair to photopion when the injected proton energy is increased, and the transition from linear to non-linear proton cooling when the injected proton compactness is increased; also the effects of time variability in proton injection. We move on to power-law proton injection in Sect. 5, while in Sect. 6 we show some characteristic time-dependent cases. Finally, in Sect. 7 we conclude with a summary and make some remarks on the results of the previous sections.
2. The kinetic equation approach
2.1. Setup of the problem
Relativistic protons in compact sources undergo a series of processes that can be quite complicated to model. Thus protons interact with photons creating pions, neutrons, and neutrinos (all from photopion interactions), as well as electron-positron pairs (from photopair). Since the magnetic field in the cases examined in this paper is low (B ≤ 10 G) and the maximum proton Lorentz factor does not exceed γp = 108, the pions and their resulting muons decay almost instantaneously, as compared with any other relevant timescale of the problem, creating photons and more electrons, positrons, and neutrinos. For higher magnetic fields, those pions and muons would suffer significant energy losses through synchrotron radiation before decaying (see e.g. Mücke & Protheroe 2001b; Mücke et al. 2003, and Reynoso & Romero 2009) The electrons and positrons cool by producing photons, which can, in turn, interact with protons, in turn creating more secondaries. At the same time, neutrinos will escape, while neutrons, depending on the opacity, can either escape, interact, or decay inside the source. Since the target material in the studied environment has low density, proton-proton interactions and bremsstrahlung can be neglected. To treat this complicated system, we used the kinetic equation approach as described in Mastichiadis & Kirk (1995, henceforth MK95) and Mastichiadis et al. (2005, henceforth MPK05). However, in the present treatment we have extended the set of equations by including, in addition to the three for protons, electrons/positrons, and photons, two more equations, one for neutrons and one for neutrinos. The target photons and all other particle distributions are again taken to be isotropic.
As in MPK05 we can write the kinetic equations for a homogeneous region containing relativistic hadrons and leptons in the compact form 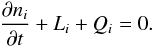 (1)Here, index i refers to protons (denoted by “p”), electrons/positrons (“e”), photons (“γ”), neutrons (“n”) and neutrinos (“ν”). The functions to be determined are the dimensionless differential number densities of the five species, which can be produced/injected in the source through the operators Qi and destroyed/escape through the operators Li. They are normalised from the ordinary differential number densities
(1)Here, index i refers to protons (denoted by “p”), electrons/positrons (“e”), photons (“γ”), neutrons (“n”) and neutrinos (“ν”). The functions to be determined are the dimensionless differential number densities of the five species, which can be produced/injected in the source through the operators Qi and destroyed/escape through the operators Li. They are normalised from the ordinary differential number densities 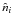 in the following way:
in the following way: 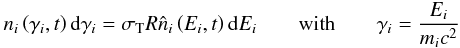 (2)where R is the radius of the source and σT the Thomson cross section. The photon and neutrino energy is normalised with respect to the electron rest mass. Time is also normalised, to the light-crossing time of the source
(2)where R is the radius of the source and σT the Thomson cross section. The photon and neutrino energy is normalised with respect to the electron rest mass. Time is also normalised, to the light-crossing time of the source 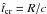 , so
, so 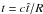 , where
, where 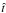 is the actual time.
is the actual time.
The processes that we have included are
-
1.
Proton-photon pair production,
-
2.
Proton-photon pion production,
-
3.
Proton synchrotron radiation,
-
4.
Electron synchrotron radiation,
-
5.
Synchrotron self absorption,
-
6.
Electron inverse Compton scattering,
-
7.
Photon-photon pair production,
-
8.
Electron-positron annihilation,
-
9.
Compton scattering of photons on cool pairs,
-
10.
Triplet pair production.
The modelling of the leptonic processes (4−9) has been discussed in MK95 and Mastichiadis & Kirk (1997). Photopair production (1) has been extensively discussed and modelled in MPK05. Modelling of proton synchrotron radiation (3) was done in a manner analogous to electron synchrotron. Triplet pair production (10) was modelled according to (Mastichiadis et al. 1986; Mastichiadis 1991). However, the basic improvement of the present paper is for photopion production (2). This process was modelled in MK95 with δ-function approximations and without taking neutrons and neutrinos into account in the injection and energy loss terms. Here we revisit the process by doing a modelling based on the results of SOPHIA (Mücke et al. 2000), which we discuss in the next section. A similar modelling of the above processes was recently undertaken by Vieyro & Romero (2012), but in a strongly magnetised and “dirtier” environment, with a stronger emphasis on proton-proton interactions and a weaker emphasis on the precise modelling of photopion interactions, which uses the approximations discussed in Romero et al. (2010).
By including the various relevant terms, the kinetic equations for each species become
The operators are labelled according to the processes that produce them, i.e. proton-photon pair production (BH), proton-photon pion production (photopion), electron synchrotron (syn), proton synchrotron (psyn), synchrotron self absorption (ssa), inverse Compton scattering (ics), photon-photon pair production (γγ), triplet pair production (tpp), neutron decay (ndecay) and electron-positron annihilation (ann), while (ext) refers to external injection. tp,esc and te,esc are the escape times for protons and electrons, respectively, while tesc is the escape time for neutrally charged particles. Compton scattering of photons on cool pairs is approximated by multiplying the photon escape term, tγ,esc, by the factor 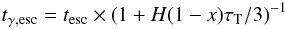 (8)where τT is the Thomson optical depth and H(1 − x) is the Heavyside function (Lightman & Zdziarski 1987), with x = hν/mec2 the dimensionless photon energy.
(8)where τT is the Thomson optical depth and H(1 − x) is the Heavyside function (Lightman & Zdziarski 1987), with x = hν/mec2 the dimensionless photon energy.
2.2. Photopion interactions: Loss and source terms
Photopion interactions produce a distribution of neutrons that is similar in energy to the outgoing protons, since the two basic channels  are about equally probable. Neutrons can escape the emission region essentially in a crossing time, but they are susceptible to two processes along the way. They can interact with ambient photons in much the same way as protons, leading to a mirror image of the previous channels
are about equally probable. Neutrons can escape the emission region essentially in a crossing time, but they are susceptible to two processes along the way. They can interact with ambient photons in much the same way as protons, leading to a mirror image of the previous channels  or they can decay into protons, with a mean lifetime of τ = 881.5 ± 1.5 s (Nakamura et al. 2010)
or they can decay into protons, with a mean lifetime of τ = 881.5 ± 1.5 s (Nakamura et al. 2010) 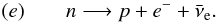 (13)In channels (a)−(d), the initial nucleons lose a portion of their energy that depends on the inelasticity of the interaction, kp, but that is not a uniform process. SOPHIA simulation results show a distribution of nucleons after each interaction, with their maximum energies close to that of the initial nucleon and their minimum energies forming a tail that can extend over several orders of magnitude. Although these distributions have recently been approximated analytically (see Kelner & Aharonian 2008), we made use of them in their original form, representing their effect with a coefficient d(γ,ξ,γ′), where γ is the resulting nucleon’s energy, ξ the target photon energy, and γ′ the initial nucleon’s energy. Each interaction can be seen as removing the initial nucleon from its energy bin and creating the distribution of new ones, so that translates into a catastrophic loss term coupled with an injection term. The cross section σN(γ′,ξ)photopion is related to the interaction time τN(γ′,ξ)photopion for a single nucleon in a monoenergetic photon field of density 1cm-3, so that σN(γ′,ξ)photopion = 1/(τN(γ′,ξ)photopionc), where N is the type of nucleon.
(13)In channels (a)−(d), the initial nucleons lose a portion of their energy that depends on the inelasticity of the interaction, kp, but that is not a uniform process. SOPHIA simulation results show a distribution of nucleons after each interaction, with their maximum energies close to that of the initial nucleon and their minimum energies forming a tail that can extend over several orders of magnitude. Although these distributions have recently been approximated analytically (see Kelner & Aharonian 2008), we made use of them in their original form, representing their effect with a coefficient d(γ,ξ,γ′), where γ is the resulting nucleon’s energy, ξ the target photon energy, and γ′ the initial nucleon’s energy. Each interaction can be seen as removing the initial nucleon from its energy bin and creating the distribution of new ones, so that translates into a catastrophic loss term coupled with an injection term. The cross section σN(γ′,ξ)photopion is related to the interaction time τN(γ′,ξ)photopion for a single nucleon in a monoenergetic photon field of density 1cm-3, so that σN(γ′,ξ)photopion = 1/(τN(γ′,ξ)photopionc), where N is the type of nucleon.
Therefore, the contributions to the loss and injection terms in the proton and neutron kinetic equations from the above processes are (respectively)
Neutron decay produces complementary loss and injection terms for the neutrons and protons, respectively:  However, since neutrons are produced predominantly with energies close to that of the protons undergoing photopion interactions, their Lorentz factors are high enough to ensure that neutron decay occurs mostly outside the source. We ignore the ensuing interactions of the products. Neutrinos are only produced in photopion interactions, and they freely escape the emission region, with an escape time equal to the crossing time of the source. In the code the neutrino flux is the sum of all flavours since we may assume that there will be complete mixing after propagation. Since neutrinos escape without interaction, their spectra is proportional to their injection spectrum. We neglect neutrinos from neutron decay.
However, since neutrons are produced predominantly with energies close to that of the protons undergoing photopion interactions, their Lorentz factors are high enough to ensure that neutron decay occurs mostly outside the source. We ignore the ensuing interactions of the products. Neutrinos are only produced in photopion interactions, and they freely escape the emission region, with an escape time equal to the crossing time of the source. In the code the neutrino flux is the sum of all flavours since we may assume that there will be complete mixing after propagation. Since neutrinos escape without interaction, their spectra is proportional to their injection spectrum. We neglect neutrinos from neutron decay.
3. Modelling photopion interactions
3.1. The SOPHIA code
At low interaction energies, photohadronic processes are dominated by the Δ(1232) resonance, so their cross section can be approximated by a δ-function. However, such an approximation neglects processes that become dominant for higher energies and are still important in lower ones. To remedy this, the SOPHIA Monte-Carlo event generator was developed (see Mücke et al. 2000), taking into account the following interaction processes: resonance production, direct pion production and diffractive and non-diffractive multipion production.
3.2. Modeling SOPHIA results
The photopion spectra are calculated indirectly from the results of this SOPHIA Monte Carlo code. Protons of three distinct energies (γp = 106.1,γp = 109.1,γp = 1012, where the subscript p refers to protons) are allowed to interact with isotropically distributed target photons of energies ranging from ξ = 10-9.1 to ξ = 100.1 in logarithmic steps of 0.1. This provides us with interaction rates and energy distributions of all secondary particles, including protons (since the original protons are treated as having sustained catastrophic losses, giving rise to a new distribution over a wide range of energies) for those three specific initial proton energies. Specifically, we obtain an energy loss term for protons, and injection terms for photons, electrons, protons, neutrons, and neutrinos. The last result from pions and muons, which are assumed to decay instantaneously.
The energy grids used in our program are equally spaced in the logarithm of γ, with a resolution of ten bins per decade for protons and electrons and five bins per decade for photons. Furthermore, the lowest grid point for both protons and electrons is γmin = 100.1, while for photons it is taken to be 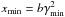 , since the softest photons are assumed to be produced by electron synchrotron radiation, b = B/Bc being the magnetic field in units of the critical field
, since the softest photons are assumed to be produced by electron synchrotron radiation, b = B/Bc being the magnetic field in units of the critical field 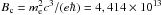 G.
G.
Each particle’s injection term is calculated as the energy distribution term from SOPHIA over the interaction time for the initial proton and photon energies, times the number densities of those initial protons and photons, all normalised to our dimensionless units, 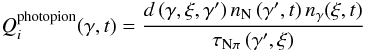 (24)where d(γ,ξ,γ′) is the energy distribution term, as described in Sect. 2.2, τNπ(γ′,ξ) is the interaction time, N the type of nucleon, i the particle type, and γ is substituted by x for photons and Eν/mec2 for neutrinos.
(24)where d(γ,ξ,γ′) is the energy distribution term, as described in Sect. 2.2, τNπ(γ′,ξ) is the interaction time, N the type of nucleon, i the particle type, and γ is substituted by x for photons and Eν/mec2 for neutrinos.
Since the produced spectra depend on the product γp·ξ, for any proton of energy γp interacting with a photon of energy ξ the effects will be identical to those of a proton of energy 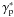 interacting with a photon of energy
interacting with a photon of energy 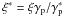 , the only difference being that the energies of the secondaries will be shifted by
, the only difference being that the energies of the secondaries will be shifted by 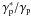 . Therefore, we can use the three distinct proton energies (γp = 106.1,γp = 109.1,γp = 1012) to calculate the spectra for protons of all intermediate or lower energies with this scaling approach. These three energies were chosen for technical reasons (in the present paper injected protons have γp ≪ 1012). It comes at an acceptably small loss of accuracy but at a gain in computing time and memory.
. Therefore, we can use the three distinct proton energies (γp = 106.1,γp = 109.1,γp = 1012) to calculate the spectra for protons of all intermediate or lower energies with this scaling approach. These three energies were chosen for technical reasons (in the present paper injected protons have γp ≪ 1012). It comes at an acceptably small loss of accuracy but at a gain in computing time and memory.
When the initial particle is a neutron instead of a proton, we can use the same data but with switched labels; neutrons instead of protons, and all particles switched with their antiparticles. Comparisons with SOPHIA results from neutron-photon interactions show this method to be sufficiently accurate, since the error in energy of the switched distributions is no higher than 3.5%.
3.3. Energy losses
To test the additions to the code, we performed both single-interaction checks and full runs for various cases of monoenergetic protons injected into black body radiation fields. In Fig. 1 we show the distributions resulting from interactions of monoenergetic protons of Lorentz factor γp = 106.1 with photons with ξ = 10-2.8. There, 95.6% of the proton’s energy is conserved in the secondaries, whose contribution by particle type corresponds almost perfectly to the ones in the SOPHIA data. If we run the same test with photons of ξ = 10-3.8 and ξ = 10-0.2, corresponding to the lowest and highest energy photons for which we can test the results directly, the energy conserved in the secondaries is 90% and 98%, respectively.
 |
Fig. 1 Test distributions from the interaction of monoenergetic protons (γp = 106.1) with photons (ξ = 10-2.8) as produced by the numerical code. Units in the y axis are arbitrary. These have been checked against the SOPHIA results and are in very good agreement. |
 |
Fig. 2 Average energy loss times of protons interacting with ambient black body radiation of temperature 3 × 105 K with R = 1015 cm introduced here purely for the purpose of checking energy losses. Long-dashed line corresponds to pair production, while full line corresponds to photopion interaction. Units in the y axis are dimensionless, normalised to the light crossing time. |
In Fig. 2 we show the energy losses of protons in a black body radiation field (introduced merely for this test and not used elsewhere) from both photopion interactions and pair production. The relative contribution of each process for each proton energy is as expected (Stanev et al. 2000).
4. Monoenergetic proton injection
4.1. Spectral signatures
Adopting the standard picture of the one zone radiation model, we can assume a spherical volume of radius R and a tangled magnetic field of strength B. We consider only the case where protons are injected in the system and set the external injection of electrons equal to zero. The simplest way of treating proton injection in Eq. (3) is to assume that protons are injected with a δ-function at some energy γ0. This will faciliate some tests of the radiative signatures of the different hadronic processes discussed in the previous paragraph. Thus we write 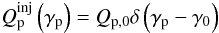 (25)where Qp,0 is the proton normalisation, considered as independent of time. In the present treatment we find it more convenient, instead of defining Qp,0, to equivalently define the proton compactness which is given by the relation (as in MK95)
(25)where Qp,0 is the proton normalisation, considered as independent of time. In the present treatment we find it more convenient, instead of defining Qp,0, to equivalently define the proton compactness which is given by the relation (as in MK95) 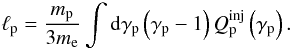 (26)With the δ-function assumption, we can write
(26)With the δ-function assumption, we can write 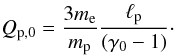 (27)As was shown in MPK05, the actual injected proton luminosity is related to ℓp by the relation
(27)As was shown in MPK05, the actual injected proton luminosity is related to ℓp by the relation 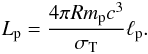 (28)It will also prove useful to define, in a similar manner, the compactnesses
(28)It will also prove useful to define, in a similar manner, the compactnesses 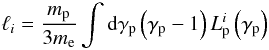 (29)where i refers to each process that creates a loss term for protons in Eq. (3).
(29)where i refers to each process that creates a loss term for protons in Eq. (3).
In addition to γ0, ℓp, and tp,esc, one needs to specify initial conditions for the five unknowns to fully determine the system. Without loss of generality, we can assume that at t = 0, np(γp,0) = ne(γe,0) = nγ(x,0) = nn(γn,0) = nν(Eν,0) = 0. Then we can integrate the system forward in time.
Therefore, qualitatively speaking, one expects that for t > 0, protons will start accumulating in the source. At the same time, according to Eq. (3) protons will lose energy by synchrotron and, possibly, by photopair and photopion production, while a fraction will physically escape at a rate 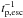 from the source region. In this case secondaries will be created making Eqs. (4) to (7) relevant for the evolution of the system.
from the source region. In this case secondaries will be created making Eqs. (4) to (7) relevant for the evolution of the system.
As a first example, we show the results obtained when R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, tp,esc = tcr, and γ0 = 2.5 × 106. The magnetic field strength is such as would be expected at a distance of roughly 0.1 pc from the base of the jet (Komissarov et al. 2007; O’Sullivan & Gabuzda 2009). The parameters were chosen in such a way that the radiated photons will cause minimal losses on the protons, therefore the proton steady-state distribution is very close to the one derived from Eq. (3) when all loss terms are ignored, i.e. 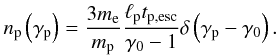 (30)This simple form of the proton distribution function faciliates the investigation of some important points regarding the injected electron and radiated photon spectrum. For this reason we do not consider the presence of an external photon distribution. In this and the next test cases, the proton synchrotron photons serve as targets.
(30)This simple form of the proton distribution function faciliates the investigation of some important points regarding the injected electron and radiated photon spectrum. For this reason we do not consider the presence of an external photon distribution. In this and the next test cases, the proton synchrotron photons serve as targets.
 |
Fig. 3 Production rate of secondary electrons for R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, tp,esc = tcr and γ0 = 2.5 × 106. Full line depicts the injection resulting from charged pion decay while long-dashed line is the photopair (Bethe-Heitler) injection. Short-dashed line depicts the pairs injected from γγ absorption, which is negligible for the particular set of the initial parameters chosen. |
At low compactnesses, as we are considering here, electrons are injected into the system as secondaries mainly through two channels (i) from photopair and (ii) from photopion. (At higher compactness photon-photon pair production becomes important but we can neglect this for the time being.) These two processes are in direct competition with each other and their relative importance depends on such parameters as γ0 and the soft photons which serve as targets. Figure 3 plots the injection functions of these two processes for the initial parameters given above. We note that the two distributions have different characteristics. The injection function of photopair electrons is broader and has a peak at energies γe ≃ γp. The injection function of photopion electrons, on the other hand, is flatter and peaks at much higher energies, of the order of γe = ηπeγp, with ηπe ≃ 150.
In the case we are considering here, the photon spectrum will show four distinctive features. Two of them are connected to the synchrotron radiation of the injected electron populations discussed above, while the two other features are connected to proton synchrotron and π0-decay. Putting all of them in ascending order with frequency we have
-
1.
Proton synchrotron radiation: since the proton distribution function is a δ-function at γ0, the radiated photon spectrum will have a peak at
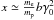 (where b = B/Bc,
(where b = B/Bc, 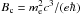 ).
). -
2.
Synchrotron radiation from photopair electrons: as stated above, the electron injection function resulting from photopair interactions is rather broad with a peak at γe ≃ γp. Synchrotron cooling of electrons and consequent radiation results in a photon spectrum with peak at
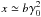 .
. -
3.
Synchrotron radiation from photopion electrons: in complete analogy to the photopair, the peak of this distribution will be at x ≃ b(ηπeγ0)2.
-
4.
γ-rays from π0-decay: a monoenergetic proton distribution produces a well defined peak at x ≃ ηπγγ0, with ηπγ ≃ 350.
It is interesting to note that the ratio of where the three first peaks occur is fixed, i.e. 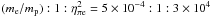 , which implies that the proton synchrotron peak will always be about eight orders of magnitude below the synchrotron peak of photopion electrons. Only the γ-ray peak from neutral pion decay is not connected to the other three – since it does not involve the magnetic field, but for all astrophysically relevant magnetic field values, it should always be the highest energy peak. These features can be seen in Fig. 4 where the multi-wavelength (MW) spectrum corresponding to the parameters adopted above is plotted. The inverse Compton scattering component of the electrons is negligible.
, which implies that the proton synchrotron peak will always be about eight orders of magnitude below the synchrotron peak of photopion electrons. Only the γ-ray peak from neutral pion decay is not connected to the other three – since it does not involve the magnetic field, but for all astrophysically relevant magnetic field values, it should always be the highest energy peak. These features can be seen in Fig. 4 where the multi-wavelength (MW) spectrum corresponding to the parameters adopted above is plotted. The inverse Compton scattering component of the electrons is negligible.
 |
Fig. 4 Steady state MW spectrum of photons resulting from monoenergetic proton injection with minimal cooling. Parameters are as in the previous figure. Full line is the synchrotron spectrum corresponding to the electrons injected from photopair (dotted line) and photopion (dot-dashed line) – see previous figure. Long dashed line is the proton synchrotron component while short dashed line are the γ-rays resulting from π0 decay. |
4.2. Increasing the injected proton energy: the transition in importance from photopair to photopion
While protons will always radiate through synchrotron radiation, it is a matter of the choice of the initial parameters whether they will undergo substantial photopair and photopion production. The rate of these processes reaches a maximum when the energy of the collision between the peak of the proton synchrotron radiation and the relativistic proton is above their respective thresholds. If we denote the proton synchrotron typical energy by 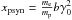 , then if
, then if 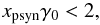 (31)then obviously the proton-photon collisions cannot produce copious photopairs because most of the collisions occur below threshold for this process. If
(31)then obviously the proton-photon collisions cannot produce copious photopairs because most of the collisions occur below threshold for this process. If 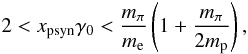 (32)then the collisions between xpsyn and γ0 are above the threshold for photopair but not for photopion; note however the synchrotron radiation from the produced photopairs can produce photopions, therefore we expect such a component even in this case, albeit at a low level. Finally, for
(32)then the collisions between xpsyn and γ0 are above the threshold for photopair but not for photopion; note however the synchrotron radiation from the produced photopairs can produce photopions, therefore we expect such a component even in this case, albeit at a low level. Finally, for 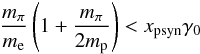 (33)we expect that protons can produce both pairs and pions directly in collisions with proton synchrotron photons.
(33)we expect that protons can produce both pairs and pions directly in collisions with proton synchrotron photons.
The above relations help us define two characteristic proton energies that are functions of the magnetic field only; i.e., 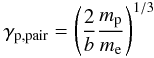 (34)and
(34)and 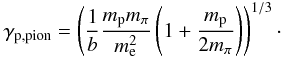 (35)Depending on the proton injected energy γ0 with respect to γp,pair and γp,pion, the protons can produce either photopairs or both photopairs and photopions. We emphasise, however, that the above characteristic proton energies are only indicative. Since we are using the full emissivities, rather than delta-function approximations for the energies of secondary particles and photons, it is possible to have photopairs even if Eq. (31) does not strictly hold, as relativistic protons can always pair produce with photons at the tail of the synchrotron distribution.
(35)Depending on the proton injected energy γ0 with respect to γp,pair and γp,pion, the protons can produce either photopairs or both photopairs and photopions. We emphasise, however, that the above characteristic proton energies are only indicative. Since we are using the full emissivities, rather than delta-function approximations for the energies of secondary particles and photons, it is possible to have photopairs even if Eq. (31) does not strictly hold, as relativistic protons can always pair produce with photons at the tail of the synchrotron distribution.
 |
Fig. 5 Steady state MW spectrum of photons resulting from a monoenergetic proton injection with γ0 = 3 × 105 (dotted line), 3 × 106 (full line), and 3 × 107 (dashed line). The other parameters are R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, and tp,esc = tcr. |
Figure 5 shows the MW photon spectrum in the case of monoenergetic proton injection with γ0 = 3 × 105, 3 × 106, and 3 × 107, while all the other parameters have been kept constant to the values given in the previous paragraph. The run for γ0 = 3 × 105 marginally satisfies the photopair condition and not the photopion one. Thus the photon spectrum consists of the proton synchrotron peak and the photopair synchrotron emission. The run for γ0 = 3 × 106 satisfies both conditions, and the photon spectrum shows all four features, as discussed in the previous section. Finally, the run for γ0 = 3 × 107 has a much stronger photopion than photopair component, and as a result the synchrotron signature of the latter lies below that of the former, resulting in only one peak for the synchrotron spectrum, i.e. the photopion one.
To systematise the above results, we have plotted the injected compactness of each individual proton process (as defined in Eq. (26), but for 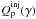 corresponding to each particular process, rather than to total proton injection) in Fig. 6 as a function of γ0, while all other parameters have been kept constant. For the injected photopion compactness we considered the sum of γ-rays and electrons resulting from neutral and charged pion decay, respectively, since both contribute to the photon spectrum. We note that, while the proton synchrotron term varies linearly with the injected energy, the photopair and photopion terms show much more complex behaviour. Both increase initially reaching a maximum, and subsequently decrease. As discussed above, photopair is more important for lower injected proton energies, but as the injection energy increases, photopion becomes dominant – for the assumed magnetic field, γp,pair = 5 × 105, while γp,pion = 5 × 106. We also note that proton synchrotron is more important as a loss/injection process than the other two for all energies, but this depends on the value of the injected proton compactness. As we show in the next section this trend changes as the proton compactness increases.
corresponding to each particular process, rather than to total proton injection) in Fig. 6 as a function of γ0, while all other parameters have been kept constant. For the injected photopion compactness we considered the sum of γ-rays and electrons resulting from neutral and charged pion decay, respectively, since both contribute to the photon spectrum. We note that, while the proton synchrotron term varies linearly with the injected energy, the photopair and photopion terms show much more complex behaviour. Both increase initially reaching a maximum, and subsequently decrease. As discussed above, photopair is more important for lower injected proton energies, but as the injection energy increases, photopion becomes dominant – for the assumed magnetic field, γp,pair = 5 × 105, while γp,pion = 5 × 106. We also note that proton synchrotron is more important as a loss/injection process than the other two for all energies, but this depends on the value of the injected proton compactness. As we show in the next section this trend changes as the proton compactness increases.
 |
Fig. 6 The compactnesses of proton processes for a δ-function proton injection as a function of the energy γ0. Full line is for proton synchrotron, dashed line for photopair, and dotted line for photopion. For this process the sum of photon and electron injection resulting from neutral and charged pion decay is plotted. The other parameters are R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, and tp,esc = tcr. |
4.3. Increasing the injected proton compactness: from linear to non-linear proton cooling
We turn next to investigating the effects that the injected proton compactness has on the photon spectra. In the case of proton-only injection like the one we are considering here, there are, up to a degree, profound analogies to the synchrotron – SSC relationship of a leptonic system. There the electrons radiate synchrotron photons, and consequently upscatter them through inverse Compton scattering interactions. As long as the magnetic energy density dominates the synchrotron photon density, the system can be considered in the linear regime. This situation changes when the synchrotron photon density dominates and the system becomes non-linear leading to the well-known Compton catastrophe.
 |
Fig. 7 Steady state MW photon spectra for δ-function proton injection at energy γ0 = 2.5 × 106 and different injection compactnesses ℓp = 0.4, 1.3, 4, 13, and 40 (bottom to top). The other parameters are R = 3 × 1016 cm, B = 1 G, tp,esc = tcr. |
One can consider something analogous for the system we are considering at present – see also Sect. 2 in Petropoulou & Mastichiadis (2012b). In hadronic systems and for the example we have examined above one can argue that the system is also in the linear regime, because protons radiate by synchrotron and the thus-radiated photons are used as targets for photopair and photopion production. As can be seen from Fig. 6, the synchrotron luminosity dominates, which means that the cooling, however small, is regulated by this process. Figure 6 can also be viewed in terms of the energy-loss time scales for each process. Although the compactnesses depend on the proton density, the system’s very low efficiency (as discussed in the next section) means that, for a given proton injection, that density will be practically constant. Then, for each proton injection 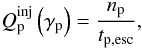 (36)the loss terms will be
(36)the loss terms will be 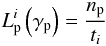 (37)where i can be “syn”, “BH” or photopion (“pγ”). Substituting in Eqs. (26) and (29), we find
(37)where i can be “syn”, “BH” or photopion (“pγ”). Substituting in Eqs. (26) and (29), we find 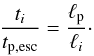 (38)Therefore the question that becomes relevant is what happens to the system if the proton injection luminosity is increased further while the magnetic field value is kept constant. This would essentially mean that the photon density of the system increases over the magnetic one, and as a result the photopair and photopion losses/injection increase more than the proton synchrotron ones. This occurs because, while the synchrotron luminosity depends on the proton density, the photopair and photopion luminosities depend on both the proton and photon density. Since the photon density depends on the proton density, we conclude that the above processes depend quadratically on the proton density provided that both use the proton synchrotron photons as targets, which holds whenever γ0 > γp,pion (cf. Eq. (35)).
(38)Therefore the question that becomes relevant is what happens to the system if the proton injection luminosity is increased further while the magnetic field value is kept constant. This would essentially mean that the photon density of the system increases over the magnetic one, and as a result the photopair and photopion losses/injection increase more than the proton synchrotron ones. This occurs because, while the synchrotron luminosity depends on the proton density, the photopair and photopion luminosities depend on both the proton and photon density. Since the photon density depends on the proton density, we conclude that the above processes depend quadratically on the proton density provided that both use the proton synchrotron photons as targets, which holds whenever γ0 > γp,pion (cf. Eq. (35)).
The above can be seen in Fig. 7, which depicts the steady state MW spectrum in the case where the injection proton compactness takes the values ℓp = 0.4, 1.3, 4, 13, and 40 (bottom to top). One notices that, as the injection compactness increases, the synchrotron component increases linearly while the photopair and photopion increase quadratically. However, for ℓp ≃ 40, the system undergoes a transition, and the photon luminosity goes up by a factor of 104. These types of transitions are a sign that the system becomes supercritical and are caused by various feedback mechanisms – like the pair production – synchrotron loop (Kirk & Mastichiadis 1992) and the automatic photon quenching one (Stawarz & Kirk 2007; Petropoulou & Mastichiadis 2011) – which cause a very fast, non-linear proton cooling with simultaneous exponential increase in the secondaries. The system then can either reach a steady state, as in the example shown above, or show limit cycles (Stern & Svensson 1991; Mastichiadis et al. 2005; Petropoulou & Mastichiadis 2012b). A systematic search of their effects are beyond the scope of the present work, but we will investigate their properties fully in a forthcoming paper; see, however, Dimitrakoudis et al. (2012) for some preliminary results. For the present, it suffices to say that once the behaviour shown in Fig. 7 is typical, i.e. for fixed initial parameters, there is always a value of ℓp above which the system becomes supercritical. We define this value as ℓp,cr(R,B,γmax) and we refer to it in Sect. 6. A final remark concerning the above figure is that the ratio between the photopair and photopion injection rates, which has remained constant as long as the system was in the subcritical regime, starts changing as the system becones supercritical. This is because the spectrum of the target photons changes causing the respective rates to change accordingly.
Figure 8 shows the injected luminosity from each proton process. We note that synchrotron remains linear throughout, while photopair and photopion are initially quadratic before they become highly non-linear once the proton density enters the supercritical regime.
 |
Fig. 8 The compactnesses of proton processes for a δ-function proton injection as a function of the proton compactness ℓp. Full line is for proton synchrotron, dashed line for photopair, dotted line for photopion – for this last process the sum of photon and electron injection resulting from neutral and charged pion decay is plotted. The other parameters are as in the previous figure. |
An interesting result of the above analysis is the following. In cases where γp,pair < γ0 < γp,pion, then, according to the discussion in the previous subsection, protons can directly produce photopairs on proton synchrotron photons but not photopions. The latter, however, can be still created on the synchrotron radiation of the produced photopairs. Thus, any variation in the injection rate will cause the proton synchrotron photons to vary linearly, the radiation from photopairs quadratically (as already explained above), and the radiation fron photopions cubically, since their rate depends on protons and photopairs. We return to this point in Sect. 6.
 |
Fig. 9 Spectra of photons (small dashed line), neutrons (long dashed line) and neutrinos (full line) escaping from the source for initial parameters: s = 2, ℓp = 30, tp,esc = tcr, γp,min = 10, γp,max = 106, R = 3 × 1016 cm, and B = 1 G. For comparison we have drawn the proton injected spectrum with a dotted line. |
5. Power-law proton injection
We next examine the case where the injected protons form a power law, i.e. the injection function is 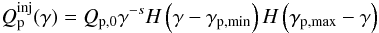 (39)where γp,min and γp,max are the lower and upper cut-offs of the proton distribution, respectively, Qp,0 is the proton normalisation (considered, for the time being, as independent of time), and H(x) is the Heaviside function. From Eq. (39) one can define a proton compactness in complete analogy to the monoenergetic case – cf. Eq. (26).
(39)where γp,min and γp,max are the lower and upper cut-offs of the proton distribution, respectively, Qp,0 is the proton normalisation (considered, for the time being, as independent of time), and H(x) is the Heaviside function. From Eq. (39) one can define a proton compactness in complete analogy to the monoenergetic case – cf. Eq. (26).
Figure 9 depicts the spectra of photons, neutrons, and neutrinos of all flavours emerging from a source with parameters γp,min = 10, γp,max = 106, R = 3 × 1016 cm, B = 1 G, s = 2, ℓp = 30, and tp,esc = tcr. For comparison reasons we have also plotted the injected proton spectrum. The neutrino spectrum peaks at high energies and has a distribution that resembles that of γ-rays resulting from π0-decay. The neutrons, on the other hand, are more sharply peaked with a maximum in their distribution that is very close to γp,max. Another interesting point is that of efficiency, i.e. of the fraction of the luminosity that goes into radiation, neutrons, and neutrinos with respect to the total power injected into protons, which is quite low, at least for the parameters of the present example. Thus photons take about 10-7 of the available luminosity in protons, while a comparable amount goes to neutrons and neutrinos. We mention that for these low compactnesses, neutrons escape the source practically unattenuated and deposit their energy in the surrounding region once they are transformed back to protons (Kirk & Mastichiadis 1989; Giovanoni & Kazanas 1990). Their resulting radiation will peak at UHE energies from π0 decay and at VHE energies from synchrotron cooling of produced protons (Mastichiadis & Protheroe 1990).
In Fig. 10, which is analogous to Fig. 5 for the monoenergetic injection case, we treat γp,max as a free parameter, taking values from 105.5 to 108 in increments of 0.5 in logarithm. For γp,max = 105.5 the photopair threshold is just satisfied in collisions between proton synchrotron photons and protons. Even so, there is a low-lumimosity photopion component created from collisions between synchrotron photons from photopair electrons and protons. Generally, in close analogy to the monoenergetic case, we find that as γp,max increases, photopion dominates the photopair; however, at very high energies of proton injection the spectrum starts saturating as photon-photon absorption becomes dominant.
 |
Fig. 10 Steady-state spectra of photons resulting from a power-law proton injection s = 2, ℓp = 0.3, tp,esc = tcr, γp,min = 10, and γp,max = 105.5−108 with increments of 0.5 in logarithm (bottom to top). The other parameters are R = 3 × 1016 cm and B = 1 G. |
 |
Fig. 11 MW steady-state spectra of photons resulting from a power-law proton injection with γp,min = 10, γp,max = 106, s = 2, tp,esc = tcr, and ℓp taking the values of 0.3 to 100 with logarithmic increments of 0.5 (bottom to top). The other parameters are R = 3 × 1016 cm and B = 1 G. |
In Fig. 11 we plot the steady state spectra as a function of the initial proton luminosity. It is analogous to Fig. 7 and one notices again the two basic features discussed for that figure, i.e. the quadratic nature of the photopair and photopion processes as opposed to the linear behaviour of the proton synchrotron radiation and the non-linear transition of the system to high luminosities once the protons have reached a certain critical density.
Figure 12 treats the proton injection slope s as a free parameter. Since in each case the injected proton luminosity is the same, injection of harder power laws mean that more of the luminosity is concentrated in higher energies, resulting in flatter spectra for the proton synchrotron component and also in an increase in the luminosity going to the photopair and photopion components. The latter can be seen more clearly in Fig. 13, where the resulting luminosities are plotted against s. Because we adopted a high value of the upper proton cutoff (γp,max = 108), photopion dominates photopair production for flat injection spectra, while the two processes become comparable for steeper spectra.
 |
Fig. 12 MW steady-state spectra of photons resulting from variable power-law proton injection with γp,min = 10, γp,max = 108, ℓp = 0.1, tp,esc = tcr, R = 3 × 1016 cm, B = 1 G, and s taking the values of 1.5 to 2.5 with increments of 0.25 (top to bottom). |
 |
Fig. 13 Steady-state luminosity of photons produced by proton synchrotron (full line), electron synchrotron from pair production (long dashed lines), and electron synchrotron from photopion interactions (short dashed line), plotted against s. All other initial parameters are as in the previous figure. |
The neutrinos emitted from those same proton power laws at steady state are plotted in Fig. 14. Close to their upper cutoff they resemble power laws, which are harder than the proton ones by a factor of about (s − 0.5)/2.5.
6. Time variability
The numerical scheme introduced through Eqs. (3) to (7) can simulate time variability by treating one or more of the free parameters as time-dependent. Here we adopt the standard procedure followed in such cases; i.e., we use initially constant injection parameters until the system reaches a steady state and then we introduce a perturbation in one of the parameters and record the produced photon spectrum at each instant.
 |
Fig. 14 MW steady-state spectra of (electron and muon) neutrinos resulting from variable power-law proton injection as in Fig. 12. |
As an indicative example, we chose first as initial parameters those that led to the steady state obtained in Fig. 4 – see also Fig. 7, bottom curve. We chose the particular example because, for this case, each hadronic component leaves a clear signature on the MW spectrum, and thus it will be straightforward to examine the time response of each component. We also introduce a time variation to the proton injection parameter 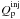 in the form of a Lorentzian profile
in the form of a Lorentzian profile  (40)The above quantity reaches a maximum for t = t0, i.e. fL(t0;t0,w,n) = n, assuming n > 1. The quantity w is the full width at half maximum since fL(t0 ± w;t0,w,n) = (n + 1)/2. For the present application the parameters used were n = 3.16, t0 = 100tcr, and w = 10tcr.
(40)The above quantity reaches a maximum for t = t0, i.e. fL(t0;t0,w,n) = n, assuming n > 1. The quantity w is the full width at half maximum since fL(t0 ± w;t0,w,n) = (n + 1)/2. For the present application the parameters used were n = 3.16, t0 = 100tcr, and w = 10tcr.
Figure 15 shows the resulting energy-centred (i.e. with the horizontal axis centred on the time when the proton energy injection becomes maximum) photon lightcurves obtained for energies (expressed in logarithm) x1 = −3.84, x2 = −1.24, and x3 = 3.15. According to the discussion made following Fig. 4, for the initial conditions used, proton synchrotron contributes mainly to x1, while synchrotron from photopairs and electrons from photopions to x2, and electron synchrotron to x3. It becomes apparent that the lightcurve at energy x1, to which proton synchrotron is contributing, follows the variation in the proton injection very closely. The other energies have a clear quadratic dependence on proton variation, in accordance to the discussion given in Sect. 4.1.
Figure 16 repeats the calculations, but now we take a proton energy injection value that satisfies the relation γp,pair < γ0 < γp,pion. The bottom full line curve that corresponds to proton synchrotron varies linearly, while the middle and top ones, which are at the photopair and photopion electron characteristic synchrotron energies, respectively, vary quadratically and (almost) cubically. The reason behind this has already been explained in Sect. 4.1.
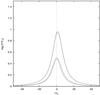 |
Fig. 15 Energy centered lightcurves for photon energies x1 = 10-3.85 (dashed line), x2 = 10-1.25 (dot-dashed line), and x3 = 103.15 (short dashed line) resulting from a Lorentzian variation of the proton injection parameter |
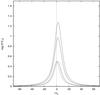 |
Fig. 16 A flare produced in the case with γp,pair < γp,max < γp,pion. Full lines are at the characteristic energies for proton (bottom), photopair (middle) and photopion (top) synchrotron emission. |
The above results are relevant when the system is in the subcritical regime. The situation changes drastically when the system is entering supercriticality. For example, Fig. 17 shows the energy-centred lightcurves obtained from such a case. Comparing the produced lightcurves with those of the two previous figures, we find some interesting differences. (i) Even though the proton compactness has been increased by a factor of 3, the photon luminosity increases by a factor of ~100 in all bands, demonstrating the high non-linearity of the system. (ii) The lightcurves peak about 10tcr after the peak of the perturbation, while in the previous examples the time lags were shorter. (iii) The relation between the three components discussed above is destroyed by the onset of the intense electromagnetic cascade caused by the supercriticality.
To further show the complex behaviour of the system when it becomes supercritical, we plot in Fig. 18 a flare caused by the sum of two identical Lorentzians which are with peaks shifted by 30tcr. The ensuing flare is asymmetrical with the second one producing much higher luminosity than the first one.
 |
Fig. 17 A flare produced when the system is supercritical. The parameters for the Lorentzian are as in Fig. 15. The full lines are contributions from the various processes with the same order as in Fig. 16. |
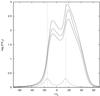 |
Fig. 18 A flare produced when the system is supercritical by the sum of two Lorentzians of the same amplitude. Here n = 2 while the two peaks occur at t1 = 85tcr and t2 = 115tcr respectively. For comparison with the previous Figure, we have chosen t0 = 100tcr. |
Therefore, it becomes evident from the above that a hadronic system exhibits far more complex behaviour than a leptonic one. The exact relationship between its main radiating components (proton synchrotron, photopair, and photopion) depends on both the injected proton energy and the proton luminosity and needs further investigation. Nevertheless, we present below, for the sake of completeness, a summary of our previous results:
-
1.
Subcritical regime: for proton injection ℓp < ℓp,cr(R,B,γmax) the system behaves linearly; i.e., variations in proton injection cause linear variations in the proton synchrotron component. The photopair component, however, always varies quadratically, while the photopion one varies either cubically (for γp,max ≤ γp,pion) or quadratically (γp,max > γp,pion). In either case, the efficiency of the system is rather low.
-
2.
Supercritical regime: for ℓp > ℓp,cr(R,B,γmax) the system undergoes an abrupt phase transition. At the onset of it, even small perturbations in the proton injection can cause high amplitude variations in the secondaries. As in all dynamical systems, its exact behaviour depends sensitively and in a non-linear way on the initial conditions and the parameters of the perturbation. On the other hand, the relation between the various components lose the mostly quadratic dependence found in the subcritical regime owing to the electromagnetic cascading, which contributes to all bands. Finally, the efficiency of the system can be quite high.
7. Discussion/Summary
Hadronic models have been used extensively for fitting the γ-ray emission of blazars. According to their basic premises, γ-rays can be produced either directly via proton synchrotron radiation or via the radiation of the secondaries resulting from photopion collisions. In the present paper which, in many respects, is an extension of earlier work by MK95 and MPK05, we have approached the model by writing and solving five coupled partial differential equations, one for protons and the rest for the four stable species which result from proton-photon interactions, namely electrons, photons, neutrons and neutrinos, thus our approach is self-consistent in the sense that it conserves energy. However, the major improvement of the present work over MK95 and MPK05 was its modelling the spectra of secondaries from photopion interactions (Sect. 3). For this we have made systematic use of the SOPHIA results (Mücke et al. 2000) which were suitably parametrised in a way so the derived distribution functions of secondaries can serve as source functions for their corresponding equations. We then modelled the proton losses caused by these interactions so as to maintain a detailed balance between the energy lost by protons and that gained by the secondaries. This approach enables us to address topics such as the stability of the system, the efficiency of proton luminosity conversion into radiation and the relation between the underlying proton distribution with the emitted photon and neutrino spectra.
Assuming a hadronic model with a monoenergetic proton injection and without any primary electron injection (Sect. 4), we have showed that for low proton energies the only important process, apart from proton synchrotron radiation, is photopair (Bethe-Heitler) production photopion operates, albeit at relatively low rates. The resulting photon spectrum shows two features, both of synchrotron origin, one from protons and one from the produced Bethe-Heitler pairs. For even higher proton injection energies, photopion becomes relevant and the photon spectrum shows two more features, one due to the synchrotron radiation from electrons and positrons produced through charged pion decay and one due to γ-rays from π0-decay (see Figs. 4 and 5). The relative importance of photopair and photopion depends critically on the injected proton energy: for low proton energies photopair dominates, while the situation is reversed for high energies (Fig. 6).
The above simple picture holds when the proton injected luminosity (or compactness) is low and proton cooling minimal, which means that the proton distribution function does not deviate significantly from that at injection. In this case the proton synchrotron luminosity is dominant while the other two processes contribute a smaller fraction to the total radiated luminosity. However, as the proton compactness increases, the photopair and photopion losses increase quadratically. – note, however, that depending on the value of the proton energy, the two components can vary quadratically and cubically respectively, while the proton synchrotron increases only linearly. This means that the relative contribution of the two photo-processes becomes progressively more significant. Furthermore, the contribution of photon-photon cascading becomes important in redistributing the photon luminosity, thus complicating the spectral shape. Finally, above some critical proton luminosity, the system becomes supercritical and, as a result, electrons and radiation rise in an auto-regulatory way causing non-linear proton energy losses (see Figs. 7 and 8).
This is a very charactersitic property of the hadronic systems, which can lead it to high efficiencies. A detailed study of the system in the supercritical regime is left for a forthcoming publication. Preliminary calculations show that there are at least two loops operating that can very efficiently extract energy from the protons and give it to leptons and photons, namely the proton-synchrotron loop at low proton energies (KM92) and the automatic photon quenching (Stawarz & Kirk 2007; Petropoulou & Mastichiadis 2011) at higher ones. The latter loop was studied analytically by Petropoulou & Mastichiadis (2012b). Furthermore, it was shown that for typical blazar parameters this loop can lead to adoption of high Doppler factors for the outflow δ; lower values of δ imply higher proton luminosities leading the system to supercriticality and to an overproduction of X-rays (Petropoulou & Mastichiadis 2012a).
The above results generally hold in the case where the monoenergetic proton distribution is replaced by the more astrophysically relevant power law (Sect. 5). In this case, the maximum energy of proton injection becomes an important parameter. In addition, results are also sensitive to the choice of the proton spectral slope. Interestingly enough, the calculated neutrino flux is flatter than the producing proton power law. This might be relevant to neutrino experiments, like Ice Cube.
In the present paper we have focussed on the case where the soft photons required as targets for photopair and photopion interactions are provided from the synchrotron radiation of protons themselves. While this might not be a realistic case for some applications – for example, in the case where there is a co-accelerated leptonic component, the radiated synchrotron photons will be in direct competition with the proton synchrotron ones for the hadronic interactions – this approach allowed us to investigate the time variability in an analogous way to the more familiar synchrotron-SSC coupling of leptonic models. We found (Sect. 6) that, while the proton synchrotron part always remains linear to the proton injection, the synchrotron radiation from photopairs, which peaks at higher energies, varies quadratically with it. Thus the hadronic models can reproduce the quadratic behaviour of the SSC leptonic models and do so for the exact same reasons. Perhaps more interesting is that, under certain circumstances, the photopion component that peaks at even higher energies (see Sect. 4) shows a cubic behaviour with respect to the proton injection and therefore to the proton synchrotron component. This is a unique feature of the hadronic models; if also considers the flaring behaviour exhibited when these systems enter the supercritical regime, then it is clear that their temporal behaviour can be quite rich.
In conclusion, we would like to emphasise two key issues in our approach which, in our opinion, improve the concept of hadronic modelling. (i) The energy conserving scheme that is introduced through the kinetic equation approach can successfully treat the inherent non-linearity of the system. Therefore, once the initial conditions are chosen, the solution of the system can lead either to a subcritical linear solution or to a supercritical nonlinear one that, occasionally, might be oscillatory. There is no way that the behaviour of the system can be determined a-priori. Therefore, time-independent approaches (e.g., adopting a ready distribution function for the protons) might entirely miss this point and lead to erroneous results. (ii) The careful modelling of photopair and photopion is crucial. We have found that the omission of photopair production can also lead to erroneous results – even in cases where the choice of initial parameters do not seem to favour it – when the system settles in a state where the internally produced soft photons from photopair production are non-negligible. Therefore, models that do not include it suffer a severe drawback.
Overall, the code presented here can be a useful tool in examining the one-zone hadronic models of active galactic nuclei and gamma ray bursts – the latter only in the case where the magnetic field is assumed to be low enough not to cause substantial synchrotron losses to pions and muons before they decay. It can simultaneously calculate the photon and the neutrino fluxes from sources with the only assumption that relativistic protons are injected there. It takes both photopair and photopion production into account with high accuracy, which are very difficult to model. Finally the energy-conserving scheme of our approach ensures that we can consider the hadronic models as dynamical systems and study their tempora behaviour.
Acknowledgments
We would like to thank Maria Petropoulou for insightful discussions, and an anonymous referee whose comments helped improve the manuscript. A.R. acknowledges support by Marie Curie IRG grant 248037 within the FP7 Programme.
References
- Aharonian, F. A. 2000, New A, 5, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, K., & Inoue, S. 2007, ApJ, 671, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, K., Inoue, S., & Mészáros, P. 2009, ApJ, 699, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Atoyan, A., & Dermer, C. D. 2001, Phys. Rev. Lett., 87, 221102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bednarek, W., & Protheroe, R. J. 1999, MNRAS, 310, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Boettcher, M. 2012 [arXiv:1205.0539] [Google Scholar]
- Böttcher, M., & Chiang, J. 2002, ApJ, 581, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bottcher, M., & Dermer, C. D. 1998, ApJ, 499, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Reimer, A., & Marscher, A. P. 2009, ApJ, 703, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Schlickeiser, R., & Mastichiadis, A. 1992, A&A, 256, L27 [NASA ADS] [Google Scholar]
- Dimitrakoudis, S., Petropoulou, M., & Mastichiadis, A. 2012, Int. J. Mod. Phys. Conf. Ser., 8, 19 [CrossRef] [Google Scholar]
- Giovanoni, P. M., & Kazanas, D. 1990, Nature, 345, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, S., & Takahara, F. 1996, ApJ, 463, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kazanas, D., Georganopoulos, M., & Mastichiadis, A. 2002, ApJ, 578, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., & Mastichiadis, A. 1989, A&A, 213, 75 [NASA ADS] [Google Scholar]
- Kirk, J. G., & Mastichiadis, A. 1992, Nature, 360, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Lightman, A. P., & Zdziarski, A. A. 1987, ApJ, 319, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K. 1993, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Mannheim, K. 1998, Science, 279, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Mastichiadis, A. 1991, MNRAS, 253, 235 [NASA ADS] [Google Scholar]
- Mastichiadis, A., & Kazanas, D. 2006, ApJ, 645, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Mastichiadis, A., & Kazanas, D. 2009, ApJ, 694, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Mastichiadis, A., & Kirk, J. G. 1995, A&A, 295, 613 [NASA ADS] [Google Scholar]
- Mastichiadis, A., & Kirk, J. G. 1997, A&A, 320, 19 [NASA ADS] [Google Scholar]
- Mastichiadis, A., & Protheroe, R. J. 1990, MNRAS, 246, 279 [NASA ADS] [Google Scholar]
- Mastichiadis, A., Marscher, A. P., & Brecher, K. 1986, ApJ, 300, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Mastichiadis, A., Protheroe, R. J., & Kirk, J. G. 2005, A&A, 433, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mücke, A., & Protheroe, R. J. 2001a, Astropart. Phys., 15, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., & Protheroe, R. J. 2001b, in Int. Cosmic Ray Conf., 3, 1153 [Google Scholar]
- Mücke, A., Engel, R., Rachen, J. P., Protheroe, R. J., & Stanev, T. 2000, Comput. Phys. Comm., 124, 290 [Google Scholar]
- Mücke, A., Protheroe, R. J., Engel, R., Rachen, J. P., & Stanev, T. 2003, Astropart. Phys., 18, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, K., et al. (Particle Data Group 2010), J. Phys. G, 37, 075021; and 2011 partial update for the 2012 edition [Google Scholar]
- O’Sullivan, S. P., & Gabuzda, D. C. 2009, MNRAS, 400, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M., Bosch-Ramon, V., & Romero, G. E. 2005, in Astrophysical Sources of High Energy Particles and Radiation, eds. T. Bulik, B. Rudak, & G. Madejski, AIP Conf. Ser., 801, 224 [Google Scholar]
- Petropoulou, M., & Mastichiadis, A. 2011, A&A, 532, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petropoulou, M., & Mastichiadis, A. 2012a, MNRAS, 426, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, M., & Mastichiadis, A. 2012b, MNRAS, 421, 2325 [Google Scholar]
- Protheroe, R. J. 1997, in Accretion Phenomena and Related Outflows, eds. D. T. Wickramasinghe, G. V. Bicknell, & L. Ferrario, IAU Colloq. 163, ASP Conf. Ser., 121, 585 [Google Scholar]
- Protheroe, R. J., & Johnson, P. A. 1996, Astropart. Phys., 4, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Protheroe, R. J., & Kazanas, D. 1983, ApJ, 265, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, M. M., & Romero, G. E. 2009, A&A, 493, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynoso, M. M., Medina, M. C., & Romero, G. E. 2011, A&A, 531, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E., Torres, D. F., Kaufman Bernadó, M. M., & Mirabel, I. F. 2003, A&A, 410, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E., Christiansen, H. R., & Orellana, M. 2005, ApJ, 632, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Vieyro, F. L., & Vila, G. S. 2010, A&A, 519, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siewert, M., Pohl, M., & Schlickeiser, R. 2004, A&A, 425, 405 [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Stanev, T., Engel, R., Mücke, A., Protheroe, R. J., & Rachen, J. P. 2000, Phys. Rev. D, 62, 093005 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, Ł., & Kirk, J. G. 2007, ApJ, 661, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, B., & Svensson, R. 1991, in Relativistic Hadrons in Cosmic Compact Objects, Lecture Notes in Physics (Berlin: Springer Verlag), eds. A. A. Zdziarski, & M. Sikora, 391, 41 [Google Scholar]
- Vieyro, F. L., & Romero, G. E. 2012, A&A, 542, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vila, G. S., Romero, G. E., & Casco, N. A. 2012, A&A, 538, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Test distributions from the interaction of monoenergetic protons (γp = 106.1) with photons (ξ = 10-2.8) as produced by the numerical code. Units in the y axis are arbitrary. These have been checked against the SOPHIA results and are in very good agreement. |
| In the text | |
 |
Fig. 2 Average energy loss times of protons interacting with ambient black body radiation of temperature 3 × 105 K with R = 1015 cm introduced here purely for the purpose of checking energy losses. Long-dashed line corresponds to pair production, while full line corresponds to photopion interaction. Units in the y axis are dimensionless, normalised to the light crossing time. |
| In the text | |
 |
Fig. 3 Production rate of secondary electrons for R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, tp,esc = tcr and γ0 = 2.5 × 106. Full line depicts the injection resulting from charged pion decay while long-dashed line is the photopair (Bethe-Heitler) injection. Short-dashed line depicts the pairs injected from γγ absorption, which is negligible for the particular set of the initial parameters chosen. |
| In the text | |
 |
Fig. 4 Steady state MW spectrum of photons resulting from monoenergetic proton injection with minimal cooling. Parameters are as in the previous figure. Full line is the synchrotron spectrum corresponding to the electrons injected from photopair (dotted line) and photopion (dot-dashed line) – see previous figure. Long dashed line is the proton synchrotron component while short dashed line are the γ-rays resulting from π0 decay. |
| In the text | |
 |
Fig. 5 Steady state MW spectrum of photons resulting from a monoenergetic proton injection with γ0 = 3 × 105 (dotted line), 3 × 106 (full line), and 3 × 107 (dashed line). The other parameters are R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, and tp,esc = tcr. |
| In the text | |
 |
Fig. 6 The compactnesses of proton processes for a δ-function proton injection as a function of the energy γ0. Full line is for proton synchrotron, dashed line for photopair, and dotted line for photopion. For this process the sum of photon and electron injection resulting from neutral and charged pion decay is plotted. The other parameters are R = 3 × 1016 cm, B = 1 G, ℓp = 0.4, and tp,esc = tcr. |
| In the text | |
 |
Fig. 7 Steady state MW photon spectra for δ-function proton injection at energy γ0 = 2.5 × 106 and different injection compactnesses ℓp = 0.4, 1.3, 4, 13, and 40 (bottom to top). The other parameters are R = 3 × 1016 cm, B = 1 G, tp,esc = tcr. |
| In the text | |
 |
Fig. 8 The compactnesses of proton processes for a δ-function proton injection as a function of the proton compactness ℓp. Full line is for proton synchrotron, dashed line for photopair, dotted line for photopion – for this last process the sum of photon and electron injection resulting from neutral and charged pion decay is plotted. The other parameters are as in the previous figure. |
| In the text | |
 |
Fig. 9 Spectra of photons (small dashed line), neutrons (long dashed line) and neutrinos (full line) escaping from the source for initial parameters: s = 2, ℓp = 30, tp,esc = tcr, γp,min = 10, γp,max = 106, R = 3 × 1016 cm, and B = 1 G. For comparison we have drawn the proton injected spectrum with a dotted line. |
| In the text | |
 |
Fig. 10 Steady-state spectra of photons resulting from a power-law proton injection s = 2, ℓp = 0.3, tp,esc = tcr, γp,min = 10, and γp,max = 105.5−108 with increments of 0.5 in logarithm (bottom to top). The other parameters are R = 3 × 1016 cm and B = 1 G. |
| In the text | |
 |
Fig. 11 MW steady-state spectra of photons resulting from a power-law proton injection with γp,min = 10, γp,max = 106, s = 2, tp,esc = tcr, and ℓp taking the values of 0.3 to 100 with logarithmic increments of 0.5 (bottom to top). The other parameters are R = 3 × 1016 cm and B = 1 G. |
| In the text | |
 |
Fig. 12 MW steady-state spectra of photons resulting from variable power-law proton injection with γp,min = 10, γp,max = 108, ℓp = 0.1, tp,esc = tcr, R = 3 × 1016 cm, B = 1 G, and s taking the values of 1.5 to 2.5 with increments of 0.25 (top to bottom). |
| In the text | |
 |
Fig. 13 Steady-state luminosity of photons produced by proton synchrotron (full line), electron synchrotron from pair production (long dashed lines), and electron synchrotron from photopion interactions (short dashed line), plotted against s. All other initial parameters are as in the previous figure. |
| In the text | |
 |
Fig. 14 MW steady-state spectra of (electron and muon) neutrinos resulting from variable power-law proton injection as in Fig. 12. |
| In the text | |
 |
Fig. 15 Energy centered lightcurves for photon energies x1 = 10-3.85 (dashed line), x2 = 10-1.25 (dot-dashed line), and x3 = 103.15 (short dashed line) resulting from a Lorentzian variation of the proton injection parameter |
| In the text | |
 |
Fig. 16 A flare produced in the case with γp,pair < γp,max < γp,pion. Full lines are at the characteristic energies for proton (bottom), photopair (middle) and photopion (top) synchrotron emission. |
| In the text | |
 |
Fig. 17 A flare produced when the system is supercritical. The parameters for the Lorentzian are as in Fig. 15. The full lines are contributions from the various processes with the same order as in Fig. 16. |
| In the text | |
 |
Fig. 18 A flare produced when the system is supercritical by the sum of two Lorentzians of the same amplitude. Here n = 2 while the two peaks occur at t1 = 85tcr and t2 = 115tcr respectively. For comparison with the previous Figure, we have chosen t0 = 100tcr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} {{\partial n_{\rm p}} \over {\partial t}} + L^{\rm BH}_{\rm p} + L^{\rm photopion}_{\rm p}+ L^{\rm psyn}_{\rm p} + {n_{\rm p} \over t_{\rm p, esc}} &&=\notag\\[1.5mm] &&Q_{\rm p}^{\rm inj} + Q^{\rm photopion}_{\rm p} + Q^{\rm ndecay}_{\rm p}; \label{kineqpro} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19770-12/aa19770-12-eq20.png)
![\begin{eqnarray} {{\partial n_{\rm e}} \over {\partial t}} + L^{\rm syn}_{\rm e} + L^{\rm ics}_{\rm e} + L^{\rm ann}_{\rm e} + L^{\rm tpp}_{\rm e} + {n_{\rm e} \over t_{\rm e, esc}}&& = \nonumber\\[1.5mm] &&Q^{\rm ext}_{\rm e} + Q^{\rm BH}_{\rm e} + Q^{\rm \gamma \gamma}_{\rm e} + Q^{\rm photopion}_{\rm e} + Q^{\rm tpp}_{\rm e} + Q^{\rm ndecay}_{\rm e}; \label{kineqele} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19770-12/aa19770-12-eq21.png)
![\begin{eqnarray} {{\partial n_{\rm \gamma}} \over {\partial t}} + {n_{\rm \gamma} \over {t_{\rm \gamma, esc}}} + L^{\rm \gamma \gamma}_{\rm \gamma} + L^{\rm ssa}_{\rm \gamma} &&= \nonumber\\[1.5mm] &&Q^{\rm syn}_{\rm \gamma} + Q^{\rm psyn}_{\rm \gamma} + Q^{\rm ics}_{\rm \gamma} + Q^{\rm ann}_{\rm \gamma} + Q^{\rm photopion}_{\rm \gamma}; \label{kineqphot} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19770-12/aa19770-12-eq22.png)