| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219583 | |
| Published online | 15 October 2012 | |
GRB 091029: at the limit of the fireball scenario⋆
1
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße 1,
85748
Garching,
Germany
e-mail: filgas@mpe.mpg.de
2
Institute of Experimental and Applied Physics, Czech Technical
University in Prague, Horská
3a/22, 12800
Prague, Czech
Republic
3
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
4
Dark Cosmology Centre, Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
5
Mullard Space Science Laboratory, University College
London, Holmbury St.
Mary, Dorking
Surrey, RH5
6NT, UK
6
Università degli studi di Milano-Bicocca,
Piazza della Scienza 3,
20126
Milano,
Italy
7
Universe Cluster, Technische Universität München,
Boltzmannstraße 2, 85748
Garching,
Germany
8
Space Science and Applications, MS D466, Los Alamos National
Laboratory, Los
Alamos, NM
87545,
USA
9
Thüringer Landessternwarte Tautenburg, Sternwarte 5,
07778
Tautenburg,
Germany
10
Vintage Lane Observatory, Blenheim, New
Zealand
11
Auckland Observatory, PO Box 12-180, Auckland, New
Zealand
12
Institute for Advanced Study, Einstein Drive, Princeton, NJ
08540,
USA
13
AUT University, Auckland, New Zealand
14
Department of Physics, University of Auckland,
Auckland, New
Zealand
Received: 11 May 2012
Accepted: 13 September 2012
Aims. Using high-quality, broad-band afterglow data for GRB 091029, we test the validity of the forward-shock model for gamma-ray burst afterglows.
Methods. We used multi-wavelength (NIR to X-ray) follow-up observations obtained with the GROND, BOOTES-3/YA and Stardome optical ground-based telescopes, and the UVOT and the XRT onboard the Swift satellite. The resulting data of excellent accuracy allow us to construct a multi-wavelength light curve with relative photometric errors as low as 1%, as well as the well-sampled spectral energy distribution covering 5 decades in energy.
Results. The optical/NIR and the X-ray light curves of the afterglow of GRB 091029 are almost totally decoupled. The X-ray light curve shows a shallow rise with a peak at ~7 ks and a decay slope of α ~ 1.2 afterwards, while the optical/NIR light curve shows a much steeper early rise with a peak around 400 s, followed by a shallow decay with temporal index of α ~ 0.6, a bump and a steepening of the decay afterwards. The optical/NIR spectral index decreases gradually by over 0.3 before this bump, and then slowly increases again, while the X-ray spectral index remains constant throughout the observations.
Conclusions. To explain the decoupled light curves in the X-ray and optical/NIR domains, a two-component outflow is proposed. Several models are tested, including continuous energy injection, components with different electron energy indices and components in two different stages of spectral evolution. Only the last model can explain both the decoupled light curves with asynchronous peaks and the peculiar SED evolution. However, this model has so many unknown free parameters that we are unable to reliably confirm or disprove its validity, making the afterglow of GRB 091029 difficult to explain in the framework of the simplest fireball model. This conclusion provides evidence that a scenario beyond the simplistic assumptions is needed to be able to model the growing number of well-sampled afterglow light curves.
Key words: gamma rays: ISM / gamma-ray burst: individual: GRB 091029 / ISM: jets and outflows / X-rays: individuals: GRB 091029
Tables 5–9 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Since the first Gamma-Ray Burst (GRB) was discovered in the late 1960’s (Klebesadel et al. 1973), the GRB field has evolved rapidly, mainly thanks to three generations of dedicated satellites. The Compton Gamma-Ray Observatory was launched in 1991 and with its instrument BATSE showed that GRBs are isotropically distributed in the sky, suggesting they might have a cosmological origin (Meegan et al. 1992). This claim was confirmed in 1997 by Beppo-SAX, an Italian-Dutch satellite that detected and precisely localized GRBs at X-ray wavelengths (Costa et al. 1997) and enabled ground-based telescopes to perform follow-up observations (van Paradijs et al. 1997), including redshift measurements that confirmed the cosmological distances of these events (Metzger et al. 1997; Kulkarni et al. 1998). Finally, the Swift satellite (Gehrels et al. 2004), launched in 2004, allows for a study of the afterglow emission starting very early after the GRB is detected by the Burst Alert Telescope (BAT, Barthelmy et al. 2005), thanks to the rapid slewing capability of the spacecraft and a precise localization of the afterglow by onboard telescopes sensitive at X-ray (XRT, Burrows et al. 2005) and ultraviolet/optical (UVOT, Roming et al. 2005) wavelengths. Such precise and early localization allows ground-based follow-up telescopes to start observing the afterglow emission within tens of seconds of the burst onset.
The leading model for the afterglow emission is the fireball model (Meszaros & Rees 1997; Piran 1999; Mészáros 2002; Zhang & Mészáros 2004), where the afterglow arises from the synchrotron emission of shock-accelerated electrons in a fireball interacting with the circum-burst medium. While most of the afterglow light curves prior to Swift were consistent with this model (Halpern et al. 1999; Stanek et al. 1999), the more recent and detailed light curves of afterglows showed features that needed various additions and modifications to the simplest fireball model. The early steep decays of the optical light curves (Akerlof et al. 1999; Fox et al. 2003b,a; Rykoff et al. 2004) are interpreted as reverse shocks (Sari & Piran 1999a,b; Mészáros & Rees 1999; Kobayashi 2000). Some of the rebrightenings and bumps (Panaitescu et al. 1998; Granot et al. 2003; Guetta et al. 2007) are attributed to refreshed shocks (Rees & Meszaros 1998; Panaitescu et al. 1998), the others to density variations (Ramirez-Ruiz et al. 2001; Dai & Lu 2002; Dai & Wu 2003; Panaitescu & Kumar 2004) or two-component jets (Berger et al. 2003; Huang et al. 2004; Peng et al. 2005; Granot et al. 2006; Racusin et al. 2008; Filgas et al. 2011b). However, with the latest generation of GRB instruments capable of high sampling in both time and energy domains, the modifications made to the standard model still fall short to explaining the observed afterglows consistently (e.g., Nardini et al. 2011; Filgas et al. 2011a).
The Gamma-Ray burst Optical Near-infrared Detector (GROND, Greiner et al. 2008, 2007) has provided high-quality, very well-sampled, simultaneous data in seven bands since 2007, when it was mounted at the 2.2 m MPI/ESO telescope at La Silla observatory in Chile. The high-precision data obtained by GROND allow for a detailed study of afterglow light curves (Greiner et al. 2009b; Nardini et al. 2011), jets of GRBs (Krühler et al. 2009), the dust in their host galaxies (Krühler et al. 2008; Küpcü Yoldaş et al. 2010; Greiner et al. 2011; Krühler et al. 2011a; Schady et al. 2012), their redshifts (Greiner et al. 2009a; Krühler et al. 2011b), their associations with SNe (Olivares et al. 2012), and provide tools to test the standard fireball scenario and its modifications.
Here we provide details of the Swift/XRT, Swift/UVOT, GROND, BOOTES-3 and Stardome observations of the afterglow of GRB 091029 and discuss the light curves and spectral energy distributions (SEDs) in the context of the fireball shock model thanks to the very good energy and time-domain coverage of our high-quality data. Throughout the paper, we adopt the convention that the flux density of the GRB afterglow can be described as Fν(t) ∝ t−αν−β, where α is the temporal and β the spectral index. Unless stated otherwise in the text, all reported errors are at 1σ confidence level.
2. Observations
2.1. Swift
The Swift/BAT was triggered by the long GRB 091029 at T0 = 03:53:22 UT and started immediately slewing to the burst (Grupe et al. 2009). The mask-weighted light curve shows three overlapping peaks, starting at T0 − 10 s and ending at T0 + 70 s, with peaks at T0 + 2, +20, and +26 s. The measured T90 (15–350 keV) is 39.2 ± 5 s (Barthelmy et al. 2009). The BAT prompt emission spectrum from T0 − 1.8 to T0 + 60.2 s is best fitted using a power-law with an exponential cutoff. This fit gives a photon index of 1.46 ± 0.27 and an Epeak = 61.4 ± 17.5 keV. For this model the total fluence in the 15–150 keV energy range is 2.4 ± 0.1 × 10-6 erg/cm2 (Barthelmy et al. 2009). Using standard concordance cosmology (H0 = 71.0 km s-1 Mpc-1, ΩM = 0.27, ΩΛ = 0.73, Komatsu et al. 2009), and a redshift of z = 2.752 (Chornock et al. 2009), the bolometric (1 keV–10 MeV) energy release of GRB 091029 is Eiso = 8.3 × 1052 erg, with a rest-frame Epeak of ~230 keV.
The Swift/XRT started observations of the field of GRB 091029 79.3 s after the trigger (Grupe et al. 2009). XRT data were obtained from the public Swift archive and reduced in the standard manner using the xrtpipeline task from the HEAsoft package, with response matrices from the most recent CALDB release. The XRT light curve was obtained from the XRT light curve repository (Evans et al. 2007, 2009).
The Swift/UVOT began settled observations of the field of GRB 091029 91 s after the trigger (Marshall & Grupe 2009). The afterglow was detected in the White, U, B and V filters. For this analysis, we have reduced both image and event mode data. Before the count rates were extracted from the event lists, the astrometry was refined following the methodology in Oates et al. (2009). The photometry was then extracted from the event lists and image files using the FTOOLs uvotevtlc and uvotmaghist, respectively, using a source aperture centered on the optical position and a background region located in a source-free region. We used a 3′′ source aperture to avoid contamination from two neighbouring stars and applied aperture corrections to the photometry in order to be compatible with the UVOT calibration (Breeveld et al. 2011). The analysis pipeline used software HEADAS 6.10 and UVOT calibration 20111031. In order to be compatible with the GROND photometry, UVOT magnitudes are provided as AB magnitudes and listed in Table 5.
Secondary standards in the GRB 091029 field in the GROND filter bands used for the calibration.
2.2. GROND
GROND responded to the Swift GRB alert and initiated automated observations at 03:57 UT, 4.5 min after the trigger (Filgas et al. 2009), and imaged the field of GRB 091029 at seven later epochs until T0 + 56 days. A variable point source was detected in all bands by the automated GROND pipeline (Yoldaş et al. 2008). The position of the transient was calculated to be RA (J2000) = 04:00:42.62 and Dec (J2000) = −55:57:20.0 compared to USNO-B reference field stars (Monet et al. 2003) with an astrometric uncertainty of 0.′′3.
The optical and NIR image reduction and photometry were performed using standard IRAF tasks (Tody 1993) similar to the procedure described in detail in Krühler et al. (2008). A general model for the point-spread function (PSF) of each image was constructed using bright field stars and fitted to the afterglow. In addition, aperture photometry was carried out, and the results were consistent with the reported PSF photometry. All data were corrected for a Galactic foreground reddening of EB − V = 0.016 mag in the direction of the burst (Schlegel et al. 1998), corresponding to an extinction of AV = 0.05 using RV = 3.1. Optical photometric calibration was performed relative to the magnitudes of four secondary standards in the GRB field, shown in Fig. 1 and Table 1. During photometric conditions, an SDSS field (Smith et al. 2002) at RA (J2000) = 03:50:03.25, Dec (J2000) = −00:00:37.9 was observed within a few minutes of observations of the GRB field. The obtained zeropoints were corrected for atmospheric extinction and used to calibrate stars in the GRB field. The apparent magnitudes of the afterglow were measured with respect to the secondary standards reported in Table 1. The absolute calibration of the JHKs bands was obtained with respect to magnitudes of the Two Micron All Sky Survey (2MASS) stars within the GRB field obtained from the 2MASS catalog (Skrutskie et al. 2006) and converted to AB magnitudes. All GROND data are listed in Tables 6 and 7.
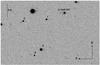 |
Fig. 1 GROND g′-band image of the field of GRB 091029 obtained 463 s after T0. The optical afterglow is shown inside the Swift XRT error circle with double diameter for better clarity. The secondary standard stars are numbered from 1 to 4 and their magnitudes reported in Table 1. |
2.3. Stardome and BOOTES-3/YA
The afterglow was observed with the Stardome 0.4 m telescope, located in Auckland (North Island, New Zealand), using a SBIG ST-L-6303E CCD. Images were obtained through a OG530 (Schott) filter1 that transmits wavelengths above 5300 Å. The observations consisted of 300 s exposures that were combined in sets of 6 to improve the signal-to-noise ratio (S/N). Further observations were obtained with the Yock-Allen (YA) robotic telescope at the BOOTES-3 astronomical station (Castro-Tirado 2011), a fast-slewing 0.6 m Ritchey-Chrétien telescope equipped with an iXon-889 EMCCD camera located in Blenheim (South Island, New Zealand). The observations consisted of a series of 60 s unfiltered exposures, which were combined in groups to improve the S/N. Image reduction was done using standard techniques in IRAF. Aperture photometry was performed, using PHOT with apertures equivalent to the seeing. For Stardome images, a PSF-matching photometry was preferred. All data were then cross-calibrated using GROND photometry to obtain consistent results and are listed in Tables 8 and 9.
3. Results
3.1. Afterglow light curve
The X-ray light curve of the afterglow of GRB 091029 (Fig. 2) shows a very steep decay (α = 3.69 ± 0.10) until ~200 s, consistent with being the tail of the GRB emission (Fenimore et al. 1996), connecting the prompt phase of the GRB and its afterglow. A steep X-ray flare follows after the decay , which declines rapidly with α = 3.91 ± 0.39. Given that the temporal decay indices before the flare and after its peak are consistent within 1σ, the possible scenario for this rapid rebrightening might involve a refreshed shock (Rees & Meszaros 1998; Panaitescu et al. 1998; Sari & Mészáros 2000; Kumar & Piran 2000; Zhang & Mészáros 2002), although the flare might be too rapid for this scenario (Huang et al. 2006). As we are predominantly interested in the afterglow phase of the GRB evolution, we exclude this flare from all our fits. The X-ray light curve after ~700 s (Fig. 3) is best fitted with a broken power-law with a smooth break (Beuermann et al. 1999). The best-fit (red. χ2 = 0.89) values of this model are αX1 = −0.12 ± 0.10, tbreak = 7.4 ± 1.8 ks and αX2 = 1.20 ± 0.04. The smoothness s iterated to a value of 1, which was set as a lower bound in the fit to better constrain the values of the temporal decay indices before and after the break.
 |
Fig. 2 Light curve of the X-ray (top panel) and ultraviolet, optical and near-infrared (bottom panel) afterglow of GRB 091029. Shown data are corrected for Galactic foreground extinction and are in AB magnitudes. Upper limits are not shown for better clarity. Gray regions show the time intervals where XRT data were obtained for the broad-band SEDs (Fig. 6). |
 |
Fig. 3 The smoothly broken power-law fit to the X-ray light curve of the GRB 091029 afterglow. The fitting was applied to datapoints after 700 s in order to exclude the early steep transition phase and flaring. |
The optical/NIR light curve of the GRB 091029 afterglow shows a steep initial rise from the start of the observations until the peak at around 400 s. The temporal slope of the rise, obtained from a fit of UVOT datapoints, is α = −2.90 ± 0.67, consistent with the jet expanding in an ISM environment (Panaitescu & Vestrand 2008). The early peak in the optical/NIR light curve is probably not the counterpart of the X-ray flare due to the time shift of both peaks. The decay following the initial peak has a slope of α = 0.58 ± 0.01 until around 5 ks, when it starts to flatten. This decay index is obtained from a simultaneous fit to the GROND datapoints between 0.6–5 ks in all bands.
However, fitting this shallow decay phase in each optical/NIR band separately shows a steepening of the temporal index with increasing wavelength of the GROND filters (see Table 2), suggesting that the afterglow gets bluer. To fit the whole complex optical/NIR light curve from the beginning to the end of the observations, a two-component model is proposed. The first component, which dominates the observed optical light curve up until the bump at T0 + 5 ks, is composed of three smoothly connected power-laws. The second component was needed to model the later hump and steep decay, and uses two smoothly connected power-laws. The obtained parameters of this fit (red. χ2 = 0.92) are listed in Table 3 and are discussed later.
Light-curve fit parameters for the afterglow of GRB 091029 in the time interval of 0.6–5 ks.
Light-curve fit parameters for the whole set of r′-band data obtained by GROND, Stardome and BOOTES-3/YA.
3.2. Afterglow SEDs
Given that the differences in decay slopes for each GROND filter point to a color evolution, we need to study the SEDs of the afterglow. Thanks to the simultaneous multi-band observing capabilities of GROND, it is possible to measure the spectral slope β of the optical/NIR data as a function of time. Figure 5 shows that the optical/NIR spectral index decreases from 0.57 ± 0.04 to 0.26 ± 0.03 between 0.4 and 9 ks, and then slowly increases again to a value of 0.49 ± 0.12 at around 100 ks. In addition, broad-band optical/NIR to X-ray SEDs were constructed at four different time intervals within this period, which are indicated in the light curve (Fig. 2). Spectra were grouped using the grppha task and fitted with the GROND data in XSPEC v12 using χ2 statistics. The combined optical/X-ray SEDs were fitted with power-law and broken power-law models and two absorbing columns: one Galactic foreground with a hydrogen column of NH = 1.14 × 1020 cm-2 (Kalberla et al. 2005) and another one that is local to the GRB host galaxy at z = 2.75. Only the latter was allowed to vary in the fits. To investigate the dust reddening in the GRB environment, the zdust model was used, which contains Large and Small Magellanic Clouds (LMC, SMC) and Milky Way (MW) extinction laws from Pei (1992). Fits of optical/NIR data alone as well as the broad-band fits resulted in a host dust extinction that was consistent with zero, therefore in all the models we assumed no host dust extinction for simplicity. With photometric data alone it was not possible to constrain the presence of Lyman-alpha absorption (Lamb & Reichart 2000) in the g′ band from neutral hydrogen within the host galaxy. The g′-band data were therefore removed from the SED fits.
Given that the broad-band SEDs proved to be inconsistent with a simple power-law model (red. χ2 = 16.5), we used models that include a break between the X-ray and optical/NIR data. We fitted all four epochs of broad-band SEDs simultaneously with a sharp broken power-law model, where the host-intrinsic absorbing column density and the X-ray spectral index are tied between each SED but left free to vary (Fig. 6), due to the fact that the X-ray hardness ratio does not change during the afterglow. The low-energy spectral indices and energy of the break were left untied between SEDs and free to vary. The best fit (red. χ2 = 0.94) gives values of the host-equivalent neutral hydrogen density NH,X = (3.0 ± 1.3) × 1021 cm-2 and a high-energy spectral index 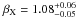 . The best-fit values of the low-energy spectral indices and break energies are listed in Table 4. This fit shows that the break evolves in time to shorter wavelengths between SEDs I and II, and then it evolves the opposite way towards longer wavelengths between SEDs II and IV. It also shows that below and above the cooling break Δβ ≠ 0.5 (with quite high and variable significance), which is a value demanded by theory (Sari et al. 1998). This is another indication that we are not seeing a simple single radiating electron population.
. The best-fit values of the low-energy spectral indices and break energies are listed in Table 4. This fit shows that the break evolves in time to shorter wavelengths between SEDs I and II, and then it evolves the opposite way towards longer wavelengths between SEDs II and IV. It also shows that below and above the cooling break Δβ ≠ 0.5 (with quite high and variable significance), which is a value demanded by theory (Sari et al. 1998). This is another indication that we are not seeing a simple single radiating electron population.
Best-fit parameters resulting from the broken power-law fit to the broad-band SEDs.
3.3. Closure relations
Using values obtained from the different fits we can test the closure relations (Granot & Sari 2002; Dai & Cheng 2001; Zhang & Mészáros 2004; Racusin et al. 2009; Panaitescu & Kumar 2000) between temporal and spectral indices. Assuming the break in the broad-band SEDs to be the cooling break νc, we see that the X-ray data are above this frequency and the optical/NIR data below it during the afterglow observations. The fit-derived X-ray spectral index 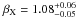 results in a power-law index of the electron energy distribution p = 2.17 ± 0.11. This spectral index and the late X-ray temporal slope of αX2 = 1.20 ± 0.04 are within 1σ consistent with the equation (Racusin et al. 2009) for p > 2 and a constant decay in the ν > νc regime, where the jet is interacting with either a homogeneous interstellar medium (ISM) or a wind and is in the slow or fast cooling phase.
results in a power-law index of the electron energy distribution p = 2.17 ± 0.11. This spectral index and the late X-ray temporal slope of αX2 = 1.20 ± 0.04 are within 1σ consistent with the equation (Racusin et al. 2009) for p > 2 and a constant decay in the ν > νc regime, where the jet is interacting with either a homogeneous interstellar medium (ISM) or a wind and is in the slow or fast cooling phase.
The late (t > 20 ks) optical/NIR single-component model decay index of α = 1.14 ± 0.02 and the late spectral index of β = 0.49 ± 0.12 are within 1σ consistent with the equation for a normal decay in the νm < ν < νc regime, where the jet is interacting with a wind medium and is in the slow cooling phase. However, the steep initial onset of the optical/NIR afterglow seems to exclude this scenario, as it is well consistent with the expected temporal index of α ~ −3 for the jet interacting with the ISM and νc > νopt, whereas the fastest possible rise for a wind medium is α ~ −0.5 (Panaitescu & Vestrand 2008). Moreover, during the early shallow decay in the optical/NIR bands, the spectral index is evolving with time and thus cannot be tested with the simple closure relations. In the case of the two-component scenario (Fig. 4), the resulting spectral index β is the superposition of the spectral indices of the narrow and the wide jet and evolves with time as the ratio between these two jets changes. Without knowing the spectral indices of each component, the closure relations for such a scenario cannot be tested.
 |
Fig. 4 The two-component fit to the r′-band data obtained by GROND, Stardome and BOOTES-3/YA. The parameters of the fit for both components (dotted lines) are listed in Table 3. The solid line represents the superposition of the two components and the best fit to the data. |
4. Discussion
The almost total decoupling of the optical/NIR and the X-ray light curves of the afterglow of GRB 091029 suggests a double outflow origin (Huang et al. 2004; Peng et al. 2005; Sheth et al. 2003; Jin et al. 2007; Wu et al. 2005; Resmi et al. 2005; Racusin et al. 2008; Filgas et al. 2011b). This is supported by our finding that the X-ray spectral hardness does not evolve synchronously with the optical spectral hardening at 0.3–10 ks. We discuss three possible scenarios, all based on a two-component jet, to explain the peculiar behavior of the light curve and the spectrum of this afterglow.
4.1. Continuous energy injection
In this scenario, the X-ray light curve after 700 s is produced by the wider, X-ray-dominating outflow, which has a deceleration time of a few ks. The pre-deceleration phase of the wide jet would cause the early shallow rise of the X-ray afterglow with the peak around 7.4 ks, after which the wide jet would turn into normal deceleration producing the αX2 ~ 1.2 decay. The same principle would apply to the early optical light curve, where the early rise and peak at ~400 s would be a result of a pre-deceleration phase of the narrower, optically dominating outflow. From the peak time of this narrower outflow, we can estimate the initial Lorentz factor in case of the ISM to be Γn ~ 300 using Molinari et al. (2007) or Γn ~ 120 using Ghirlanda et al. (2012), in both cases substituting the measured quantities and normalizing to the typical values n = 1 cm-3 and η = 0.2 (Bloom et al. 2003). The shallow decay of the optical/NIR light curve until 10 ks is then a result of some form of a continuous energy injection by the central engine (Rees & Meszaros 1998; Dai & Lu 1998; Panaitescu et al. 1998; Sari & Mészáros 2000; Zhang & Mészáros 2001; Zhang et al. 2006; Rossi et al. 2011). When this energy injection in the narrow jet ends at ~20 ks, the temporal slope steepens to α ~ 1.1, characteristic for a normal decay. However, this scenario cannot explain the time evolution of the optical/NIR spectral index during the injection time interval. The hardening of the optical spectrum would require that the electron index p changes in the outflow with time and after the injection ends, it changes back close to its original value (Fig. 5), making this scenario somewhat contrived.
 |
Fig. 5 The optical/NIR spectral slope as a function of time. |
Another issue with this scenario is the fact that in the standard interpretations, the narrow jet dominates the X-ray afterglow as it is more energetic, and the wider jet dominates the optical domain, especially at later times. The X-ray light curve is therefore expected to peak before the optical one. In such a standard interpretation, the reverse order of peaks in the light curves of the afterglow of GRB 091029 could be the result of an off-axis geometry of the jet as seen by the observer. If the observer was inside the cone of the wide, optically dominating jet, but outside of the beaming cone of the narrow, X-ray dominating jet, the optical light curve could start with a steep rise and early peak due to the pre-deceleration phase of the wide jet, and the X-ray light curve could follow with a later peak as the relativistically beamed emission cone of the narrow jet widens and gradually enters the sightline of the observer. However, given that neither the early shallow decay of the optical/NIR light curve nor the color evolution in the same domain are correlated with the temporal evolution of the narrow jet, this off-axis scenario has the same problems with the unfeasible temporal evolution of the electron energy distribution as the previous one.
4.2. Two outflows with different p parameters
The second scenario uses a different two-component model, without energy injection, where the optical/NIR light curve is a superposition of two components as described in Sect. 3.1 and shown in Fig. 4. The first component would represent a narrow, ultra-relativistic jet, with deceleration time of ~400 s, a normal decay phase afterwards, and a jet break at ~2.8 ks, followed by a steep post-jet-break decay. The second component represents a wider and mildly relativistic jet with the deceleration time of ~14 ks and a normal decay. While the residuals in Fig. 4 might hint at a possible jet break of the wider component around 100 ks, the data are within 3σ of the straight power-law and there is no visible break in the X-ray data at that time. Therefore we cannot make a reliable statement about the presence of such a jet break. The narrow jet would be dominant in the early part of the light curve and the wide one would be responsible for the late hump and dominate the optical/NIR light curve afterwards. The shallow decay between 0.4–5 ks would be a result of the superposition of fluxes from both outflows. Since the emission from the narrow component in the normal decay phase is decreasing and the the emission from the wide component in the pre-deceleration phase is increasing with time, the ratio of the fluxes of the two outflows in this time interval would vary. This model can explain the flattening of the spectral index during this period, assuming that each outflow with different Lorentz factors has a different electron energy distribution index p. As the ratio between the narrow jet with a higher p value (p ~ 2.1, estimated from the highest value of the optical/NIR spectral slope) and the wide jet with a lower p value (p ~ 1.5, estimated from the lowest value of the optical/NIR spectral slope) changes, the spectral index of the co-added flux is gradually evolving as well. The spectral index from the start of the GROND data is governed by the narrow outflow with the soft spectrum but gradually decreases as the flux from the wide component with the harder spectrum gets dominant (Fig. 4). However, this model does not explain the turnover of the spectral evolution at ~10 ks, where only the wide component with a constant p is dominant. The model also does not fit the shape of the X-ray light curve, which should be dominated the whole time by the narrow jet due to the X-ray spectral index βX being constant and consistent with p ~ 2.1 of the narrow jet.
 |
Fig. 6 Broad-band optical/NIR to X-ray SEDs fitted with a broken power-law. Mid-times of each SED are listed in Table 4 and regions where the X-ray data were taken for each SED are shown in Fig. 2. |
4.3. Two outflows in different stages of the spectral evolution
The third scenario uses a slightly modified two-component jet setup described in Sect. 4.2 (Fig. 4), in which now both outflows have the same value of p ~ 2.1 and are at different stages of the synchrotron spectral evolution (Sari et al. 1998). Both the X-ray and optical/NIR light curves can be modeled as superpositions of the two components. The flattening of the SEDs II and III in the optical/NIR region (Fig. 6) would then be a result of the wide jet having both the cooling break νc and the injection frequency νm between the X-ray and optical/NIR wavelengths (Nicuesa Guelbenzu et al. 2012), while the narrow jet has only the cooling frequency νc between X-ray and optical/NIR bands. In that case, the spectral slope in the optical/NIR bands of the narrow jet would be βX − 0.5 = 0.58 ± 0.06 and that of the wide jet would be −1/3 (Sari et al. 1998). As the ratio between these two outflows changes, it would explain the spectral hardening in the optical/NIR bands, while being consistent with the X-ray spectral slope staying constant thanks to equal p values in both outflows. The turnover in the spectral evolution at ~10 ks can be explained by the passage of the frequency νm through the GROND filters, after which the optical/NIR spectral index would be consistent with the spectral phase of the narrow jet. Given that the softening of the optical/NIR spectrum after ~10 ks is slow and gradual, the spectral break at the frequency νm must be very smooth (Granot & Sari 2002; Filgas et al. 2011a).
This model can also explain different break times in the X-ray and optical/NIR light curves, assuming that the deceleration time of the wide jet is defined by the X-ray light-curve peak but the movement of the break νm is counter-balancing the expected decay steepening in the optical/NIR bands until it passes through them and causes the late break in the light curve at T0 = 10 ks. Of course, it is questionable whether the movement of the break νm could counter-balance the turnover visible in the X-ray light curve so perfectly that it would in fact completely negate it in the optical/NIR domain and produce such a straight power-law as we see in the optical/NIR light curve between 0.4–5 ks. This scenario is difficult to confirm or disprove, though, by fitting the light curve and SEDs alone because this model has a large number of free parameters. Therefore it is very difficult to fit the broad-band SEDs with a model consisting of a double power-law and a triple power-law component and constrain all the spectral slopes and synchrotron break frequencies reliably. The fitting of light curves is confronted with similar difficulties. The optical/NIR light curve might need an even more complex model than the one presented in Fig. 4 in order to describe the effects of the moving frequency νm. However, as our data are the result of the superposition of two components, fitting of the data does not provide us with reliable constraints on the parameters of each component.
5. Conclusions
The growing number of well-sampled data sets from the latest generation of instruments like the Swift satellite and the GROND imager show that the radiative mechanism responsible for the optical to X-ray GRB afterglow emission is not as simple and well understood as previously believed. The simplest fireball model has an increasingly difficult time to explain the complex light curves of some GRB afterglows. In many cases, the optical and X-ray emission are seemingly decoupled, thus providing an indication that they are produced by different mechanisms. The afterglow of GRB 091029 is an extreme case, where the optical/NIR and the X-ray light curves are almost totally decoupled, as if they belonged to two different GRBs. Moreover, the GROND SEDs show a strong color evolution with the optical/NIR spectral index decreasing from 0.57 to 0.26 between 0.4 and 9 ks, and then increasing again to a value of ~0.49 at around 100 ks, while the X-ray spectral index remains constant throughout the observations. This observational evidence leads us to the conclusion that the emission in both energy bands needs to be produced by two different outflows.
We discuss several possible scenarios to explain this peculiar afterglow. The first one includes a continuous energy injection to explain the shallow initial decay of the optical/NIR light curve. However, this model is not able to explain the spectral evolution during the injection period, given that the theory assumes the electron energy distribution index p of the outflow is constant. To solve this, the second scenario uses two components with different p values. As the ratio between these two outflows changes, the resulting spectral index changes as well. This model is, however, not able to explain either the turnover in the optical/NIR spectral-slope evolution, nor the different times of the breaks in the X-ray and optical/NIR light curves. The third scenario offers a solution by putting the two outflows with similar p values into two different stages of the spectral evolution. The narrow jet, dominating the optical/NIR wavelengths before the hump, has a cooling break between the optical and the X-ray bands, while the wide jet, responsible for the late optical/NIR light curve, has both νc and νm frequencies between the optical and the X-ray bands. During the hump, the injection frequency νm passes through the GROND filters and the light curve becomes similar to the X-ray one.
Even though the last model can in principle explain the irregularities in the afterglow of GRB 091029, its complexity does not allow us to test it reliably, despite the large high-quality dataset presented in this work. Ironically, the data quality of the presented afterglow light curve is so good it rules out any simple model for the temporal-spectral evolution, but is not good enough to really constrain the more complex, constructed models. Rather than using the forward-shock scenario, alternative models might be needed to explain the multi-wavelength data of the afterglow of GRB 091029. For example a reverse-forward shock emission, where the optical afterglow is dominated by a long-lived reverse shock (Uhm & Beloborodov 2007; Genet et al. 2007) and the X-ray afterglow is from the forward shock. This model can decouple the two light curves almost completely, requires mass injection into the blast-wave and has many free parameters. Another alternative can be the cannonball model (Dado & Dar 2010), where the observed afterglow emission is described as the sum of thermal bremsstrahlung and synchrotron emission produced by one or more cannonballs decelerating in the circumburst medium. The last we mention is the late prompt model (Ghisellini et al. 2007, 2009; Kumar et al. 2008a,b; Nardini et al. 2010), which was proposed to explain the different temporal and spectral evolution in the optical and X-ray bands of certain long GRBs which show a late-time chromatic flattening. The authors interpret the complex broadband evolution as due to the sum of two separate processes: the standard forward shock and the emission produced by a late-time activity of the central engine (i.e., the so called late prompt emission).
Online material
UVOT photometric data.
GROND g′r′i′z′ photometric data.
GROND JHKs photometric data.
BOOTES-3/YA photometric data.
Stardome photometric data.
Acknowledgments
We thank the anonymous referee for constructive comments that helped to improve the paper. T.K. and D.A.K. acknowledge support by the DFG cluster of excellence Origin and Structure of the Universe. T.K. acknowledges support by the European Commission under the Marie Curie Intra-European Fellowship Programme. The Dark Cosmology Centre is funded by the Danish National Research Foundation. FOE acknowledges funding of his Ph.D. through the Deutscher Akademischer Austausch-Dienst (DAAD). S.K., A.R., D.A.K. and A.N.G. acknowledge support by DFG grant Kl 766/16-1. A.R. acknowledges support from the Jenaer Graduiertenakademie. M.N. and PS acknowledge support by DFG grant SA 2001/2-1. A.N.G., D.A.K. and A.R. are grateful for travel funding support through MPE. S.R.O. acknowledges support from the UK Space Agency. Work by SD was performed under contract with the California Institute of Technology (Caltech) funded by NASA through the Sagan Fellowship Program. We acknowledge support from the Spanish Ministry through project AYA 2009-14000-C03-01 (including FEDER Funds). GROND: Part of the funding for GROND (both hardware as well as personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger (DFG grant HA 1850/28-1). Swift: this work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester.
References
- Akerlof, C., Balsano, R., Barthelmy, S., et al. 1999, Nature, 398, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Baumgartner, W. H., Cummings, J. R., et al. 2009, GRB Coordinates Network, 10103, 1 [NASA ADS] [Google Scholar]
- Berger, E., Kulkarni, S. R., Pooley, G., et al. 2003, Nature, 426, 154 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beuermann, K., Hessman, F. V., Reinsch, K., et al. 1999, A&A, 352, L26 [NASA ADS] [Google Scholar]
- Bloom, J. S., Frail, D. A., & Kulkarni, S. R. 2003, ApJ, 594, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in AIP Conf. Ser. 1358, eds. J. E. McEnery, J. L. Racusin, & N. Gehrels, 373 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Tirado, A. J. 2011, Acta Polytechnica, 51, 020000 [Google Scholar]
- Chornock, R., Perley, D. A., & Cobb, B. E. 2009, GRB Coordinates Network, 10100, 1 [NASA ADS] [Google Scholar]
- Costa, E., Frontera, F., Heise, J., et al. 1997, Nature, 387, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Dado, S., & Dar, A. 2010, ApJ, 712, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Cheng, K. S. 2001, ApJ, 558, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1998, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 2002, ApJ, 565, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Wu, X. F. 2003, ApJ, 591, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Fenimore, E. E., Madras, C. D., & Nayakshin, S. 1996, ApJ, 473, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Filgas, R., Updike, A., & Greiner, J. 2009, GRB Coordinates Network, 10098, 1 [Google Scholar]
- Filgas, R., Greiner, J., Schady, P., et al. 2011a, A&A, 535, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filgas, R., Krühler, T., Greiner, J., et al. 2011b, A&A, 526, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, D. W., Price, P. A., Soderberg, A. M., et al. 2003a, ApJ, 586, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, D. W., Yost, S., Kulkarni, S. R., et al. 2003b, Nature, 422, 284 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Genet, F., Daigne, F., & Mochkovitch, R. 2007, MNRAS, 381, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., et al. 2012, MNRAS, 420, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Nava, L., & Firmani, C. 2007, ApJ, 658, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Nardini, M., Ghirlanda, G., & Celotti, A. 2009, MNRAS, 393, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Nakar, E., & Piran, T. 2003, Nature, 426, 138 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Granot, J., Königl, A., & Piran, T. 2006, MNRAS, 370, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2007, The Messenger, 130, 12 [NASA ADS] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Fynbo, J. P. U., et al. 2009a, ApJ, 693, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., McBreen, S., et al. 2009b, ApJ, 693, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupe, D., Cummings, J. R., Marshall, F. E., et al. 2009, GRB Coordinates Network, 10097, 1 [NASA ADS] [Google Scholar]
- Guetta, D., Fiore, F., D’Elia, V., et al. 2007, A&A, 461, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halpern, J. P., Kemp, J., Piran, T., & Bershady, M. A. 1999, ApJ, 517, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y. F., Wu, X. F., Dai, Z. G., Ma, H. T., & Lu, T. 2004, ApJ, 605, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y. F., Cheng, K. S., & Gao, T. T. 2006, ApJ, 637, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z. P., Yan, T., Fan, Y. Z., & Wei, D. M. 2007, ApJ, 656, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klebesadel, R. W., Strong, I. B., & Olson, R. A. 1973, ApJ, 182, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S. 2000, ApJ, 545, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Küpcü Yoldaş, A., Greiner, J., et al. 2008, ApJ, 685, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Greiner, J., Afonso, P., et al. 2009, A&A, 508, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., Greiner, J., Schady, P., et al. 2011a, A&A, 534, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., Schady, P., Greiner, J., et al. 2011b, A&A, 526, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulkarni, S. R., Djorgovski, S. G., Ramaprakash, A. N., et al. 1998, Nature, 393, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Piran, T. 2000, ApJ, 532, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Narayan, R., & Johnson, J. L. 2008a, MNRAS, 388, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Narayan, R., & Johnson, J. L. 2008b, Science, 321, 376 [NASA ADS] [CrossRef] [Google Scholar]
- KüpcüYoldaş, A., Greiner, J., Klose, S., Krühler, T., & Savaglio, S. 2010, A&A, 515, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, D. Q., & Reichart, D. E. 2000, ApJ, 536, 1 [Google Scholar]
- Marshall, F. E., & Grupe, D. 2009, GRB Coordinates Network, 10108, 1 [NASA ADS] [Google Scholar]
- Meegan, C. A., Fishman, G. J., Wilson, R. B., et al. 1992, Nature, 355, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2002, ARA&A, 40, 137 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Meszaros, P., & Rees, M. J. 1997, ApJ, 476, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1999, MNRAS, 306, L39 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Metzger, M. R., Djorgovski, S. G., Kulkarni, S. R., et al. 1997, Nature, 387, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, E., Vergani, S. D., Malesani, D., et al. 2007, A&A, 469, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, M., Ghisellini, G., Ghirlanda, G., & Celotti, A. 2010, MNRAS, 403, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, M., Greiner, J., Krühler, T., et al. 2011, A&A, 531, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- NicuesaGuelbenzu, A., Klose, S., Krühler, T., et al. 2012, A&A, 538, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oates, S. R., Page, M. J., Schady, P., et al. 2009, MNRAS, 395, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, E. F., Greiner, J., Schady, P., et al. 2012, A&A, 539, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2000, ApJ, 543, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2004, MNRAS, 353, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Vestrand, W. T. 2008, MNRAS, 387, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., Meszaros, P., & Rees, M. J. 1998, ApJ, 503, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, F., Königl, A., & Granot, J. 2005, ApJ, 626, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 1999, Phys. Rep., 314, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Racusin, J. L., Karpov, S. V., Sokolowski, M., et al. 2008, Nature, 455, 183 [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez-Ruiz, E., Dray, L. M., Madau, P., & Tout, C. A. 2001, MNRAS, 327, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Meszaros, P. 1998, ApJ, 496, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Resmi, L., Ishwara-Chandra, C. H., Castro-Tirado, A. J., et al. 2005, A&A, 440, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, A., Schulze, S., Klose, S., et al. 2011, A&A, 529, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rykoff, E. S., Smith, D. A., Price, P. A., et al. 2004, ApJ, 601, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Mészáros, P. 2000, ApJ, 535, L33 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sari, R., & Piran, T. 1999a, ApJ, 517, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1999b, ApJ, 520, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., Dwelly, T., Page, M. J., et al. 2012, A&A, 537, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, K., Frail, D. A., White, S., et al. 2003, ApJ, 595, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [Google Scholar]
- Stanek, K. Z., Garnavich, P. M., Kaluzny, J., Pych, W., & Thompson, I. 1999, ApJ, 522, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
- Uhm, Z. L., & Beloborodov, A. M. 2007, ApJ, 665, L93 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., Groot, P. J., Galama, T., et al. 1997, Nature, 386, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X. F., Dai, Z. G., Huang, Y. F., & Lu, T. 2005, MNRAS, 357, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Yoldaş, A. K., Krühler, T., Greiner, J., et al. 2008, in AIP Conf. Ser. 1000, eds. M. Galassi, D. Palmer, & E. Fenimore, 227 [Google Scholar]
- Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2002, ApJ, 566, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Secondary standards in the GRB 091029 field in the GROND filter bands used for the calibration.
Light-curve fit parameters for the afterglow of GRB 091029 in the time interval of 0.6–5 ks.
Light-curve fit parameters for the whole set of r′-band data obtained by GROND, Stardome and BOOTES-3/YA.
Best-fit parameters resulting from the broken power-law fit to the broad-band SEDs.
All Figures
 |
Fig. 1 GROND g′-band image of the field of GRB 091029 obtained 463 s after T0. The optical afterglow is shown inside the Swift XRT error circle with double diameter for better clarity. The secondary standard stars are numbered from 1 to 4 and their magnitudes reported in Table 1. |
| In the text | |
 |
Fig. 2 Light curve of the X-ray (top panel) and ultraviolet, optical and near-infrared (bottom panel) afterglow of GRB 091029. Shown data are corrected for Galactic foreground extinction and are in AB magnitudes. Upper limits are not shown for better clarity. Gray regions show the time intervals where XRT data were obtained for the broad-band SEDs (Fig. 6). |
| In the text | |
 |
Fig. 3 The smoothly broken power-law fit to the X-ray light curve of the GRB 091029 afterglow. The fitting was applied to datapoints after 700 s in order to exclude the early steep transition phase and flaring. |
| In the text | |
 |
Fig. 4 The two-component fit to the r′-band data obtained by GROND, Stardome and BOOTES-3/YA. The parameters of the fit for both components (dotted lines) are listed in Table 3. The solid line represents the superposition of the two components and the best fit to the data. |
| In the text | |
 |
Fig. 5 The optical/NIR spectral slope as a function of time. |
| In the text | |
 |
Fig. 6 Broad-band optical/NIR to X-ray SEDs fitted with a broken power-law. Mid-times of each SED are listed in Table 4 and regions where the X-ray data were taken for each SED are shown in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


