| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219063 | |
| Published online | 09 October 2012 | |
Stellar parameters and seismological analysis of the star 18 Scorpii
1
Department of AstronomyBeijing Normal University,
100875
Beijing,
PR China
e-mail: litanda@hotmail.com
2
Key Laboratory of Solar Activity, National Astronomical
Observatories, Chinese Academy of Sciences, 100012
Beijing, PR
China
Received:
17
February
2012
Accepted:
14
September
2012
Aims. We constructed models of the structure and evolution of the stars including diffusion and extra-mixing caused by rotation to estimate stellar parameters of the solar twin 18 Scorpii.
Methods. Based on the classical observed features, we considered three additional constraints, i.e., lithium abundance log N(Li), rotational period Proteq, and average large frequency separation ⟨△ν⟩, by combing stellar models with observations to determine stellar parameters and the possible evolutionary status of 18 Scorpii.
Results. More accurate results of mass and age were found by our model than in previous studies. We estimate that the mass and age of 18 Scorpii are 1.030 ± 0.010 M⊙ and 3.66-0.50+0.44 Gyr, respectively. Moreover, the model gave better constraints of atmospheric features due to the accurate age estimation.
Conclusions. The consideration of lithium, rotational period, and the average large frequency separation may help us in obtaining more accurate parameters of the star. Our results indicate that 18 Scorpii is a solar twin slightly more massive and younger than the Sun.
Key words: stars: individual: 18 Scorpii / stars: evolution / stars: rotation / stars: oscillations / stars: solar-type
© ESO, 2012
1. Introduction
Solar twins, defined by Cayrel de Strobel et al. (1981), are stars that are practically identical to the Sun. They allow us to carry out a precise differential analysis with regard to the Sun (Ramírez et al. 2009; Meléndez et al. 2009). To perform this analysis, the physical characteristics of the solar twins need to be precisely known. The star 18 Scorpii (HD 146233; HIP 79672; V = 5.5), suggested to be a solar twin by Porto de Mello & Da Silva (1997), has been studied several times. The atmospheric features of 18 Scorpii are similar to those of the Sun (Takeda et al. 2007; Ramírez et al. 2009; Meléndez & Ramírez 2007; Takeda & Tajitsu 2009; Meléndez et al. 2006; Valenti & Fischer 2005). Its rotation rate of 22.7 ± 0.5 d, which was provided by Petit et al. (2008), is also similar to the solar one. Recently, Bazot et al. (2011) found its radius and average large frequency separation, which are 1.010 ± 0.009 R⊙ and 134.4 ± 0.3 μHz, respectively.
The classical method for obtaining the stellar parameters is to compare theoretical evolutionary models with observed features in the Hertzsprung-Russell (H-R) diagrams. However, this in general makes it difficult to derive self-consistent, complete sets of stellar atmospheric parameters. Stellar structure and evolution models have several free, unconstrained parameters, which added to the uncertainties in the classical observations, lead to insufficient estimates of the masses, ages, and metallicities of stars (Bi et al. 2008).
Currently, asteroseismology has become an ideal tool to test theories of stellar structure and evolution. It is also a powerful technique for constraining stellar parameters. Its observational data, such as the stellar p-mode oscillation spectrum (for solar-like stars), which provides a very good measure of the age and size of the stars, are independent of metallicity in their uncertainty range. Additionally, the surface lithium abundance observed in solar-like stars was considered to be an extraordinarily sensitive diagnostic of stellar structure and evolution, because it is easily burned at the relatively low temperature of ~2.5 × 106 K in the stellar interior. Accurate lithium abundance measurement and non-standard models are able to provide more precise information about stellar parameters than determined by classical methods alone. do Nascimento et al. (2009) first used the lithium abundance to constrain mass and age of solar twins with rotating models. Subsequently, Castro et al. (2011) and Li et al. (2012) used the same method to study solar analogs and twins in M67 and solar analogs and twins in the field.
In this work, we constructed evolutionary models including microscopic diffusion and
rotationally driven mixing. Based on four classical observed constraints
(Teff, L, [Fe/H] and R), two
additional observed limits, lithium abundance log N(Li) and an average
large frequency ⟨△ν⟩ , were considered for constraining more accurate
stellar parameters. Because a rotating model is used in our analysis, the theoretical models
should also fit the observed rotational period 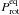 . However, this
parameter cannot be used to constrain the mass and age of the star due to the uncertainty of
its evolutionary history.
. However, this
parameter cannot be used to constrain the mass and age of the star due to the uncertainty of
its evolutionary history.
In Sect. 2, the observational characteristics of 18 Scorpii are summarized. Details of the evolutionary models and the computational method are given in Sect. 3. In Sect. 4 we described our modeling results. Finally, the discussion and conclusion are given in Sect. 5.
2. Observation of 18 Scorpii
The observed data we used for our theoretical analysis are summarized in Table 1. We collected three atmospheric features,
Teff, L, and [Fe/H] from Meléndez et al. (2006), Ramírez et al. (2009) and Meléndez &
Ramírez (2007). The lithium abundance log N(Li) was adopted
from the observations of Meléndez et al. (2006),
Takeda et al. (2007), and Meléndez & Ramírez (2007). Mean values of these four features
were calculated for the theoretical study. The radius and the average large separation were
provided by Bazot et al. (2011), who observed the star
over 12 nights from 10 to 21 May 2009 using the HARPS spectrograph on the 3.6-m telescope at
the La Silla Observatory, Chile. The equatorial rotational
period 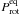 we used was
determined by Petit et al. (2008) from
high-resolution spectropolarimetric observations with the NARVAL spectropolarimeter at the
Telescope Bernard Lyot (Observatoire du Pic du Midi, France).
we used was
determined by Petit et al. (2008) from
high-resolution spectropolarimetric observations with the NARVAL spectropolarimeter at the
Telescope Bernard Lyot (Observatoire du Pic du Midi, France).
Collected data for 18 Scorpii.
3. Stellar models
Our stellar models were constructed by using the Yale rotational stellar evolution code (YREC), which includes diffusion, angular momentum loss, and rotationally driven mixing. Details of the physics can be found in Guenther et al. (1992), Chaboyer et al. (1995), and Li et al. (2003). We used the physical quantities of the OPAL equation-of-state tables EOS2005 (Rogers & Nayfonov 2002), the opacities GS98 (Grevesse & Sauval 1998) supplemented by the low-temperature opacities (Ferguson et al. 2005), and the atmosphere following the Eddington T − τ relation. Gravitational settling of helium and heavy elements is considered in stellar models, using the diffusion coefficients of Thoul et al. (1994).
Since rotation is considered in the construction of stellar models, the characteristics of
a model depend on six parameters: mass M, age t,
mixing-length parameter
α ≡ l/Hp for
convection, where l is the mixing length and Hp is the
pressure height scale; the two parameters (Yini,
Zini) describe the initial chemical composition of the star
and the rotation period 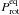 .
.
The initial model for each computation was selected to lie on the Hayashi line because pre-MS lithium-burning was considered. All models were evolved to the end of the hydrogen exhaustion in the core. In our calculations, we used the Yini of the Sun, which was 0.275 (Grevesse & Sauval 1998), as the initial He abundance of all models. Another six parameters were variable. The mass range of our grid computation was set to be 0.95−1.10 M⊙ with a step of 0.005 M⊙. The mass fraction of heavy elements Zini was derived by observed [Fe/H] and Z⊙. We used the solar abundance values of Grevesse & Sauval (1998), i.e. Z⊙ = 0.0170 and (Z/X)⊙ = 0.0230. According to the metallicity of 18 Scorpii, the range of Zini was from 0.010 to 0.025 with a step of 0.001. The mixing-length parameter α was set from 1.60 to 1.90 with an increment of 0.05. The rotational velocity at zero-age main sequence (VZAMS) was used to represent the rotational condition of our model. The range of VZAMS was from 20 km s-1 to 60 km s-1 with a step of 5 km s-1. The input parameters for the grid calculation are shown in Table 2.
3.1. Angular momentum loss
We adopted the braking law of Kawaler (1988) as
the angular momentum loss equation,
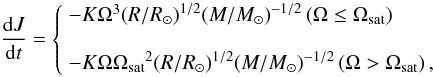 (1)where
the constant K is correlated with the magnetic field strength and is
usually taken to be a constant in all stars. Ωsat is the angular velocity at
which saturation occurs, which is adjustable in the model. Following Bouvier et al. (1997), we set
K = 2.0 × 1047 g cm2 s and
Ωsat = 14 Ω⊙.
(1)where
the constant K is correlated with the magnetic field strength and is
usually taken to be a constant in all stars. Ωsat is the angular velocity at
which saturation occurs, which is adjustable in the model. Following Bouvier et al. (1997), we set
K = 2.0 × 1047 g cm2 s and
Ωsat = 14 Ω⊙.
3.2. Extra mixing in the radiative region
Microscopic diffusion and rotation-induced mixing were considered in the radiative
region. The transport of angular momentum and element mixing can be described with two
diffusion equations as follows (Chaboyer et al.
1995): ![\begin{eqnarray} \rho{r^2}\frac{I}{M}\frac{{{\rm d}\Omega }}{{{\rm d}t}} &&= \frac{{\rm d}}{{{\rm d}r}}\left(\rho {r^2}\frac{I}{M}{D_{\rm rot}}\frac{{{\rm d}\Omega }}{{{\rm d}t}}\right), \\[1.5mm] \rho {r^2}\frac{{{\rm d}{X_i}}}{{{\rm d}t}} &&= \frac{{\rm d}}{{{\rm d}r}}\left[\rho{r^2}{D_{{\rm m},1}}{X_i} + \rho {r^2}\left({D_{{\rm m},2}} +{f_{\rm c}}{D_{\rm rot}}\right)\frac{{{\rm d}{X_i}}}{{{\rm d}t}}\right], \end{eqnarray}](/articles/aa/full_html/2012/10/aa19063-12/aa19063-12-eq58.png) where
Ω is angular velocity, Xi is the mass
fraction of chemical species i,
and I/M is the moment of inertia
per unit mass. Dm,1
and Dm,2 are derived from microscopic
diffusion coefficients. Drot is the diffusion coefficient
caused by rotation-induced mixing. Details of these three parameters can be found in Chaboyer et al. (1995). The adjustable
parameter fc is used to modify the effects of element mixing
caused by rotation. It is determined by requiring that the lithium depletion in the solar
model matches the observed depletion (Chaboyer et al.
1995).
where
Ω is angular velocity, Xi is the mass
fraction of chemical species i,
and I/M is the moment of inertia
per unit mass. Dm,1
and Dm,2 are derived from microscopic
diffusion coefficients. Drot is the diffusion coefficient
caused by rotation-induced mixing. Details of these three parameters can be found in Chaboyer et al. (1995). The adjustable
parameter fc is used to modify the effects of element mixing
caused by rotation. It is determined by requiring that the lithium depletion in the solar
model matches the observed depletion (Chaboyer et al.
1995).
Input parameters for the grid calculation.
In the solar calibration, we adjusted the mixing-length parameter α and the initial helium abundance Yini to reproduce the observed solar luminosity and radius at the solar age of 4.57 Gyr. The best solar model evolved with a VZAMS of 52.7 km s-1. When the model reached the solar age, the rotational rate and the lithium abundance were 2.8980 × 10-6 rad/s and 1.095 dex, respectively, which matched Ω⊙ = 2.9 × 10-6 rad/s provided by Bouvier et al. (1997) and log N(Li)⊙ = 1.10 ± 0.10 dex given in Grevesse & Sauval (1998), and we obtained fc = 2.95.
4. Results
Our study is based on the four classical features (Teff,
L, [Fe/H] and R) and three additional observed
quantities (log N(Li), 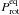 ,
⟨△ν⟩ ). The four classical
characters Teff, L, [Fe/H],
and R were considered to limit the parameters of 18 Scorpii. Then,
two additional observed features (log N(Li),
,
⟨△ν⟩ ). The four classical
characters Teff, L, [Fe/H],
and R were considered to limit the parameters of 18 Scorpii. Then,
two additional observed features (log N(Li),
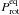 ) were added in turn
as additional constraints. Finally, seismic analyses were carried out to match the observed
⟨△ν⟩ .
) were added in turn
as additional constraints. Finally, seismic analyses were carried out to match the observed
⟨△ν⟩ .
 |
Fig. 1 Evolutionary tracks of 18 Scorpii in the H-R diagram constrained by a)
the four classical features; b) the classical features +
log N(Li); c) the classical features +
log N(Li) + |
4.1. Stellar parameters determined by nonasteroseismic features
At first, taking into account the four classical features, we obtained nearly 600 tracks,
which were considered as candidates for 18 Scorpii. The evolutionary tracks cover the
ranges of α from 1.60 to 1.90 and VZAMS
from 20 to 60 km s-1. These tracks in the H-R diagram are plotted in gray and
are shown in Fig. 1a. The first comparison
for 18 Scorpii gave us an estimate of its mass and age of
1.045 ± 0.035 M⊙
and 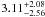 Gyr,
respectively, which is close to that of Meléndez &
Ramírez (2007).
Gyr,
respectively, which is close to that of Meléndez &
Ramírez (2007).
The second step was using lithium as a tracer to constrain the mass and age of the star.
Lithium is a key element because it is easily destroyed in stellar interiors. Its
abundance indicates the amount of internal mixing in the stars and its destruction is
strongly mass- and age- dependent (do Nascimento et al.
2009; Li et al. 2012). Among the tracks
obtained in the first step, we picked out those fitting the observed lithium
abundance log N(Li). We found 101 tracks ranging from 1.70 to 1.90
for α and from 20 km s-1 to 60 km s-1
for VZAMS. In this way, another estimate of mass and age was
obtained, which is 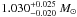 and
and 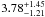 Gyr,
respectively. Moreover, since lithium abundance additionally constraints the range of
input parameters, the position of the star in the H-R diagram is restricted to a smaller
range than the above, which can be seen in Fig. 1b.
Gyr,
respectively. Moreover, since lithium abundance additionally constraints the range of
input parameters, the position of the star in the H-R diagram is restricted to a smaller
range than the above, which can be seen in Fig. 1b.
Yet another analysis, considering the observed 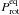 , among the
tracks obtained by two above two steps, 18 tracks were found to match the observation,
which are plotted in Fig. 1c. The ranges of input
parameters α and VZAMS were also
significantly constrained to 1.70−1.85 and 50−55 km s-1. The uncertainty
of VZAMS is reduced in this step. Some of the tracks with
improper rotating rate were removed at this step. We plot the rest in Fig. 1c.
, among the
tracks obtained by two above two steps, 18 tracks were found to match the observation,
which are plotted in Fig. 1c. The ranges of input
parameters α and VZAMS were also
significantly constrained to 1.70−1.85 and 50−55 km s-1. The uncertainty
of VZAMS is reduced in this step. Some of the tracks with
improper rotating rate were removed at this step. We plot the rest in Fig. 1c.
4.2. Pulsation analysis
As the final step, we used the stellar pulsation code of Guenther (1994) to preform the seismological analysis for the models by matching all nonasteroseismic features that we obtained in the third step.
The asteroseismic quantity we consider is the mean large separation ⟨△ν⟩ , which is defined as the difference between oscillation modes with the same angular degree and consecutive radial order n: △ν(n) ≡ νn,l − νn − 1,l. The mean value of the theoretical large separation is calculated from modes with a radial order n ranging from 10 to 25 for l = 0 and 1 modes, and for an order n ranging from 9 to 24 for l = 2 modes, which corresponds to the range 1500−3700 μHz considered in Bazot et al. (2011) when computing the Fourier transform of the spectrum.
Details of all selected models and our results are listed in Table 3. M, Z, α, and VZAMS are shown in Cols. 2−5 to describe the initial parameters of the models. Non-asteroseismic properties of the structure models are listed in Cols. 6−12. Column 13 contains the theoretical results of the mean large separation. To constrain the stellar parameters, we considered a 3σ error bar in the mean large separation. In this case, 13 models were found to match the observation. These are shown in Table 3.
Properties of the best-fitting models.
Stellar parameters of 18 Scorpii determined by different methods.
Comparison with previous studies.
After the four steps of our analysis, 13 models were obtained that fit all seven observed
features. We used the mean values of their mass, age, effective temperature, luminosity,
radius, and surface Z/X as the
estimates of stellar parameters. The ranges of the properties of the models provided the
corresponding uncertainties. The seismological analysis provided an even better estimate
of the mass and age, which is 1.030 ± 0.005 M⊙
and 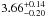 Gyr,
respectively. Additionally, Teff and L
of 18 Scorpii are estimated to be
Gyr,
respectively. Additionally, Teff and L
of 18 Scorpii are estimated to be 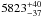 K
and 1.067 ± 0.032 L⊙, respectively. In Fig. 1d, the blue shadow in the error box indicates our
estimate based on the six nonasteroseismic properties, the red shadow represents the
estimate after the pulsation analysis, which suggests that 18 Scorpii is slightly hotter
and brighter than the Sun. The
metallicity (Z/X)s is
constrained within
K
and 1.067 ± 0.032 L⊙, respectively. In Fig. 1d, the blue shadow in the error box indicates our
estimate based on the six nonasteroseismic properties, the red shadow represents the
estimate after the pulsation analysis, which suggests that 18 Scorpii is slightly hotter
and brighter than the Sun. The
metallicity (Z/X)s is
constrained within 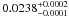 ,
corresponding to the [Fe/H] of
,
corresponding to the [Fe/H] of 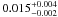 .
The result indicates that the star has a higher [Fe/H] than the Sun.
.
The result indicates that the star has a higher [Fe/H] than the Sun.
4.3. Uncertainty produced by model
The uncertainty of our estimation consists of two parts. One is associated with the
observation, which was discussed above. The other is produced by the model and mainly
depends on the increment δ of input parameters of our grid calculation
described in Table 2. The uncertainty of mass is
almost determined by δ of the input mass
(± 0.005 M⊙). The error of the age is more complex. It
is firstly associated with the time step set in evolutionary models, which is quite small
however, (~0.01 Gyr) and can be ignored. The increments of the other input parameters,
i.e., δ of M, Z, α,
and VZAMS, also influence the uncertainty of the age. We
compared the difference between ages of models with adjacent input parameters and similar
evolutionary state (for instance, comparing the age of a
M = 1.025 M⊙,
Zini = 0.0190, α = 1.70 and
VZAMS = 50 km s-1 model with that of a
M = 1.030 M⊙,
Zini = 0.0200, α = 1.75 and
VZAMS = 55 km s-1 model when they evolve to
similar Teff and L), and can estimate the
error of age produced by the model to be ~± 0.30 Gyr. In Table 4, we present the two parts of the error separately. Here we obtained
the final estimate for 18 Scorpii, which is
1.030 ± 0.010 M⊙
and 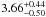 Gyr.
Gyr.
4.4. Comparison with previous results
The star 18 Scorpii has previously been studied by several researchers, their methods and
estimates are summarized in Table 5. Takeda et al. (2007) and Meléndez & Ramírez (2007) observed this star and provided its
mass and age calculated by classical methods. Moreover, do Nascimento et al. (2009) performed a theoretical analysis for 18 Scorpii and
obtained its mass and age constrained by lithium abundance. In their work, two different
estimates were given (shown in Table 5) based on
different observed data. The results inferred a
△M ~ 0.006 M⊙ and a
△t ~ 1.0 Gyr. Moreover, Bazot et al.
(2011) observed the star for seismology and interferometry, obtaining its average
large frequency separation and linear radii. From the homology relation
△ν ∝ M1/2 R−3/2
(Gough 1994), they suggested the mass
of 18 Scorpii to be 1.02 ± 0.03 M⊙. Very recently, Bazot et al. (2012) obtained another result of an
average large frequency separation (133.8 ± 0.2 μHz) of the star, which
indicates a mass of 1.01 ± 0.03 M⊙. Our estimates of mass
and age for the star are 1.030 ± 0.010 M⊙
and 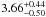 Gyr,
respectively. The mass determination was close to the results of Takeda et al. (2007), Meléndez
& Ramírez (2007), and Bazot et al.
(2011) but with higher precision. However, it is more massive than the two
results of do Nascimento et al. (2009). Compared
with the result of Bazot et al. (2012), our estimate
is also more massive because of the difference of average large frequency separation. Our
age determination generally agrees within the errors with all previous works. A comparison
of mass and age is given in Fig. 2.
Gyr,
respectively. The mass determination was close to the results of Takeda et al. (2007), Meléndez
& Ramírez (2007), and Bazot et al.
(2011) but with higher precision. However, it is more massive than the two
results of do Nascimento et al. (2009). Compared
with the result of Bazot et al. (2012), our estimate
is also more massive because of the difference of average large frequency separation. Our
age determination generally agrees within the errors with all previous works. A comparison
of mass and age is given in Fig. 2.
 |
Fig. 2 Comparison between mass and age determined in this work (the red error bar) and estimates of previous studies. The black and blue error bars represent the results of Takeda et al. (2007) and Meléndez & Ramírez (2007), respectively. The orange and the green one correspond to the two estimates provided by do Nascimento et al. (2009). |
5. Discussion and conclusion
We presented a new application of the do Nascimento et al. (2009) method to improve our knowledge of the physical state of the solar twin star 18 Scorpii (HD 146233, HIP 79672). Based on classical observed features, we used additional observed quantities including lithium abundance and average large frequency separation for better estimates of its stellar parameters.
For solar-type stars, lithium depletes as a function of mass, metallicity, age, and rotational velocity; asteroseismic quantities strongly correlate with the parameters of structure models. Therefore, theoretical analyses of these two additional features can significantly constrain the ranges of the input parameters and ensure a better self-consistent stellar model.
First, estimates of mass and age were calculated with the classical method alone. As we in
turn added lithium abundance and the average large frequency separation to our analysis,
more accurate determinations were obtained. Finally, an error produced by the model was
discussed. After the analysis above, we found the final estimates for mass and age
of 18 Scorpii, which are 1.030 ± 0.010 M⊙
and 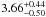 Gyr,
respectively. Moreover, due to the accurate age estimate, we constrained atmospheric
features to smaller ranges than the observation. The results locate the star more precisely
in the H-R diagram. It allowed us to clarify whether the star has the same observed
properties as the Sun.
Gyr,
respectively. Moreover, due to the accurate age estimate, we constrained atmospheric
features to smaller ranges than the observation. The results locate the star more precisely
in the H-R diagram. It allowed us to clarify whether the star has the same observed
properties as the Sun.
The rotational history of a star, especially its initial velocity, is difficult to estimate with classical methods. In this work, we found that the possible VZAMS of 18 Scorpii is about 55 km s-1.
The result is close to the solar one (52.7 km s-1), which was obtained in our
solar calibration (see Sect. 3). It means that the star may have experienced a similar
rotational evolution as the Sun. The estimate of the initial rotational condition was first
determined by the observed 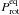 and the model
of angular momentum evolution. In addition, the interrelation of rotation, lithium
depletion, and asteroseismic property also play a role in this question. The change of
initial velocity causes a different degree of rotation-mixing in the radiative region,
resulting in different processes of lithium depletion (Li
et al. 2012). Moreover, rotational mixing also affects the asteroseismic properties
of solar-type stars, which has been discussed by Eggenberger
et al. (2010). Higher values of the large frequency separation were found for
rotating models than for non-rotating ones at the same evolutionary stage in Eggenberger et al. (2010), because rotational mixing
increased the effective temperature and to a smaller radius and hence to an increase of the
stellar mean density.
and the model
of angular momentum evolution. In addition, the interrelation of rotation, lithium
depletion, and asteroseismic property also play a role in this question. The change of
initial velocity causes a different degree of rotation-mixing in the radiative region,
resulting in different processes of lithium depletion (Li
et al. 2012). Moreover, rotational mixing also affects the asteroseismic properties
of solar-type stars, which has been discussed by Eggenberger
et al. (2010). Higher values of the large frequency separation were found for
rotating models than for non-rotating ones at the same evolutionary stage in Eggenberger et al. (2010), because rotational mixing
increased the effective temperature and to a smaller radius and hence to an increase of the
stellar mean density.
18 Scorpii was thought to be a solar twin because of the similar atmospheric parameters to the Sun. In this work, we estimated better stellar parameters for the star by combining the knowledge of lithium depletion, rotating evolution, pulsation analysis and classical method. Our estimates of its atmospheric features, mass, and age suggest that the star is a solar twin slightly more massive and younger than the Sun.
Acknowledgments
This work is supported by grants 10933002 and 11273007 from the National Natural Science Foundation of China, and the Fundamental Research Funds for the Central Universities.
References
- Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, L4 [Google Scholar]
- Bazot, M., Campante, T. L., Chaplin, W. J., et al. 2012, A&A, 544, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bi, S. L., Basu, S., & Li, L. H. 2008, ApJ, 673, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
- Cayrel de Strobel, G., Knowles, N., Hernandez, G., et al. 1981, A&A, 94, 1 [NASA ADS] [Google Scholar]
- Chaboyer, B., Demarque, P., Guenther, D. B., et al. 1995, ApJ, 446, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, M., do Nascimento, J. D., Jr.,Biazzo, K., et al. 2011, A&A, 526, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- do Nascimento, J. D., Jr.,Castro, M., Meléndez, J., et al. 2009, A&A, 501, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2010, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O. 1990, in Astrophysics: Recent Progress and Future Possibilities, eds. B. Gustafsson, & P. E. Nissen, 13 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, D. B. 1994, ApJ, 422, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, D. B., Demarque, P., Kim, Y. C., & Pinsonneault, M. H. 1992, ApJ, 387, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L. H., Basu, S., Sofia, S., et al. 2003, ApJ, 591, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. D., Bi, S. L., Chen, Y. Q., et al. 2012, ApJ, 746, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., & Ramírez, I. 2007, ApJ, 669, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006, ApJ, 641, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., et al. 2009, ApJ, 704, 66 [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Porto de Mello, G. F., & da Silva, L. 1997, ApJ, 482, 89 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., & Tajitsu, A. 2009, PASJ, 61, 471 [NASA ADS] [Google Scholar]
- Takeda, Y., Kawanomoto, S., Honda, S., et al. 2007, A&A, 468, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolutionary tracks of 18 Scorpii in the H-R diagram constrained by a)
the four classical features; b) the classical features +
log N(Li); c) the classical features +
log N(Li) + |
| In the text | |
 |
Fig. 2 Comparison between mass and age determined in this work (the red error bar) and estimates of previous studies. The black and blue error bars represent the results of Takeda et al. (2007) and Meléndez & Ramírez (2007), respectively. The orange and the green one correspond to the two estimates provided by do Nascimento et al. (2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


