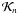| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219930 | |
| Published online | 20 September 2012 | |
What can be learned from the seismology of a coronal loop using only a handful of frequencies?
1 School of Mathematics and Statistics, The University of Sheffield, S3 7RH, UK
e-mail: R.Jain@sheffield.ac.uk
2 JILA and Department of Astrophysical and Planetary Sciences, University of Colorado at Boulder, CO 80309-0440, USA
e-mail: hindman@lcd.colorado.edu
Received: 1 July 2012
Accepted: 1 August 2012
Context. Transverse oscillating loops in the solar corona have been observed and the frequencies for a couple of low-order modes measured. These frequencies have been used as a diagnostic tool to investigate the internal properties of such oscillating loops. In particular, the density and magnetic field profiles along the loop are estimated by comparing the measured frequencies with those of a reference model. In this paper, we argue that only the kink speed may be assessed directly and there is no diagnostic capability for density or magnetic field independent of the wave speed. Further, with just a handful of measured frequencies available, only broad spatial averages of the kink speed may be obtained. We demonstrate using a frequency inversion procedure that with only two frequencies as inputs, at best one can assess the mean and the contrast of the kink speed along the loop. One requires access to the frequencies of many mode orders to perform inversions that offer kink speed determinations with high spatial resolution.
Aims. We suggest a rigorous mathematical formalism that describes the information content of the measured mode frequencies and we present a method to infer the kink speed within a coronal loop by inverting those frequencies.
Methods. We consider a single magnetic coronal loop and by using perturbation theory, relate its eigenfrequencies to the loop’s physical properties.
Results. We derive the sensitivity kernels that describe how each eigenfrequency contain the information about the kink speed and density along the loop.
Conclusions. We conclude that the eigenfrequencies contain information primarily about the kink speed, and do not strongly depend on the density. Therefore, all loop models with the same kink speed profile (but different density and magnetic field profiles) are seismically indistinguishable. To acheive the spatial resolution neccessary to uncover the non-uniform nature of the coronal loop, it is necessary to do inversion of many measured frequencies. Making inferences about the density stratification and magnetic field varying along the loop requires supplemental observations that are non-seismic in nature.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: fundamental parameters / Sun: oscillations / waves
© ESO, 2012
1. Introduction
Transverse oscillations in coronal loops have been observed (e.g., Aschwanden et al. 1999) and interpreted as fast kink modes of magnetic tubes (Nakariakov et al. 1999). Subsequently, Schrijver et al. (2002, see also Schrijver & Brown 2000; Aschwanden et al. 2002) reported 17 events observed with the Transition Region and Coronal Explorer (TRACE) during 1998 − 2001. Since then similar observations have been used as diagnostic tools to understand the structure of coronal loops. In particular, the observations reported by Verwichte et al. (2004) and van Doorsselaere et al. (2007) have been investigated in great detail. Each of these studies successfully measured two oscillation frequencies for different coronal loops and attributed these oscillations to trapped, resonant, kink mode oscillations, in particular the fundamental mode and its first overtone (i.e., ν1 and ν2). Verwichte et al. (2004) found the frequencies around ν1 ≈ 2.23 mHz and ν2 ≈ 4.05 mHz, whereas van Doorsselaere et al. (2007) find ν1 ≈ 2.29 mHz and ν2 ≈ 4.1 mHz.
Many theoretical studies have focussed on estimating the coronal density scale height by comparing the observed ratio of the frequency of the first overtone ν2 and the fundamental mode ν1 to theoretical estimates obtained from reference models (e.g., Andries et al. 2005; Goossens et al. 2006; Dymova & Ruderman 2006; Díaz et al. 2007; McEwan et al. 2008; Orza et al. 2012, and references therein). Subsequent studies of longitudinally stratified magnetic tubes, with or without circular cross-sections, have revealed disparate coronal density scale heights. For example, assuming a straight, axisymmetric magnetic tube with a length of 400 Mm and using the measured ratio ν2/ν1 ≈ 1.8 reported in Verwichte et al. (2004), van Doorsselaere et al. (2007) estimate the coronal density scale height to be 109 Mm. On the other hand, Ruderman et al. (2008) showed that if the magnetic tube has a cross-sectional radius that varies by a factor of 1.5 from footpoint to apex, then the estimated scale height for the same frequency ratio could be as low as 50 Mm. Verth & Erdélyi (2008) also quantified the effects of magnetic field variation in nullifying the effects of longitudinal density stratification in their model.
In all of these studies, the form of the magnetic field and density as a function of loop position is assumed and the eigenfrequencies are calculated from the kink tube wave equation. These eigenfrequencies are then compared with the measured ones. In this paper, we suggest that any estimate of the density scale height from just the seismic analysis of mode frequencies is nonunique. The eigenfrequencies contain information primarily about the kink speed, and are negligibly dependent on the direct effects of density. Therefore, all loop models with the same kink speed profile (but different density and magnetic field profiles) are seismically indistinguishable. Further, with access to only a handful of frequencies, only large-scale spatial averages of the kink speed may be deduced. Achieving the spatial resolution neccessary to uncover the non-uniform nature of the coronal loop may require the inversion of many measured frequencies. Making inferences about the density stratification and magnetic field varying along the loop requires supplemental observations that are non-seismic in nature.
 |
Fig. 1 Loop geometry. |
2. Information content of the eigenfrequecies
Consider an erect, semi-circular loop confined to a plane that intersects the photosphere at a right angle (see Fig. 1). If we assume that the magnetic loop is embedded in a field-free atmosphere and ignore tension forces arising from the varying curvature of the loop’s axis, the homogeneous equation governing the propagation of kink tube waves is (see Spruit 1981) 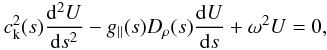 (1)where s is the axial coordinate along the curved axis of the tube, U is the transverse velocity of the tube, g ∥ is the component of the gravitational acceleration parallel to the loop’s axis, and ω is the wave frequency. For a semi-circular loop, the parallel component of gravity is given by the product of the full gravity g and a simple sinusoid,
(1)where s is the axial coordinate along the curved axis of the tube, U is the transverse velocity of the tube, g ∥ is the component of the gravitational acceleration parallel to the loop’s axis, and ω is the wave frequency. For a semi-circular loop, the parallel component of gravity is given by the product of the full gravity g and a simple sinusoid, 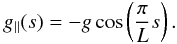 (2)We consider the domain from s ∈ [0,L] , with each endpoint anchored in the photosphere. The quantities ck(s) and Dρ(s) are, respectively, the kink wave speed and the non-dimensional overdensity of the tube,
(2)We consider the domain from s ∈ [0,L] , with each endpoint anchored in the photosphere. The quantities ck(s) and Dρ(s) are, respectively, the kink wave speed and the non-dimensional overdensity of the tube, ![\begin{equation} c_{\rm k}^2(s) \equiv \frac{B^2(s)}{4\pi\left[\rho(s)+\rho_{\rm ext}(s)\right]}, \; D_\rho(s) \equiv \frac{\rho(s) - \rho_{\rm ext}(s)}{\rho(s) + \rho_{\rm ext}(s)}, \end{equation}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq21.png) (3)where B is the axial magnetic field strength and ρ and ρext are the mass densities inside and outside the tube, respectively. Strictly speaking, the varying curvature of tube’s axis provides tension forces that should be taken into account, but we ignore such forces to illustrate our points without undue mathematical complication.
(3)where B is the axial magnetic field strength and ρ and ρext are the mass densities inside and outside the tube, respectively. Strictly speaking, the varying curvature of tube’s axis provides tension forces that should be taken into account, but we ignore such forces to illustrate our points without undue mathematical complication.
Equation (1) can be cast as a Sturm-Liouville equation through the use of an integrating factor f(s), 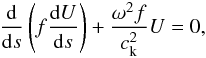 (4)with
(4)with 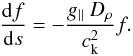 (5)Using the standard orthogonality relationship that preserves the physical units of the eigenfunctions, Un(s),
(5)Using the standard orthogonality relationship that preserves the physical units of the eigenfunctions, Un(s), 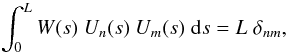 (6)with the weight function
(6)with the weight function 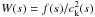 , the eigenfrequency for the nth mode,
, the eigenfrequency for the nth mode, 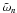 , can be expressed using the Rayleigh quotient,
, can be expressed using the Rayleigh quotient, 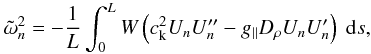 (7)with primes denoting differentiation with respect to s and where we have assumed Hermitian boundary conditions for Un.
(7)with primes denoting differentiation with respect to s and where we have assumed Hermitian boundary conditions for Un.
The previous expression clearly demonstrates that a mode eigenfrequency provides an integral measure of the tube’s physical properties. This relationship can be seen more explicitly if we introduce sensitivity kernels, which are spatial averaging functions that represent the “sensitivity” of the frequency to the quantities being averaged. We define sensitivity kernels for the nth mode for the square kink speed, 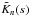 , and for the fractional overdensity,
, and for the fractional overdensity, 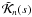 , as follows:
, as follows: ![\begin{eqnarray} \tilde{K}_n(s) &\equiv& -L^{-1} W(s) \ U_{n}(s) \ U_{n}^{\prime\prime}(s), \\[1.5mm] \tilde{\cal K}_n(s) &\equiv& L^{-1} W(s) \ g_\parallel(s) \ U_{n}(s) \ U_{n}^{\prime}(s). \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq37.png) Using these definitions, the Rayleigh quotient can be written explicitly as a weighted average, with the kernels being the weighting functions,
Using these definitions, the Rayleigh quotient can be written explicitly as a weighted average, with the kernels being the weighting functions, ![\begin{eqnarray} \tilde{\omega}_{n}^{2} = \int_0^L \left[c_{\rm k}^{2}(s)\tilde{K}_{n}(s) + D_{\rho}(s) \tilde{\cal K}_{n}(s)\right] \ {\rm d}s. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq38.png) (10)A difficulty arises from this formulation; the sensitivity kernels are unknown until the eigenfunctions can be obtained. Of course the eigenfunctions are different for different profiles of the kink speed and overdensity. Since our goal is to find a way of using the eigenfrequencies to estimate those exact properties of the flux tube, this equation at first appears impractical; however, we will now show that reliable determinations of kernels can be accomplished via perturbation theory.
(10)A difficulty arises from this formulation; the sensitivity kernels are unknown until the eigenfunctions can be obtained. Of course the eigenfunctions are different for different profiles of the kink speed and overdensity. Since our goal is to find a way of using the eigenfrequencies to estimate those exact properties of the flux tube, this equation at first appears impractical; however, we will now show that reliable determinations of kernels can be accomplished via perturbation theory.
Let us assume that we have a solar loop whose properties are quite similar to those of a known reference model. We express the wavefunction, overdensity, kink speed and mode frequencies of the observed coronal loop as small perturbations about the reference model, as follows: ![\begin{eqnarray} U_{n} &=& V_{n} + \Delta V_{n}, \hspace{1.5cm} \left| \frac{\Delta V_{n}}{V_{n}} \right| \ll 1, \\[1.5mm] D_{\rho} &=& D+\Delta D, \hspace{1.7cm} \left| \frac{\Delta D}{{D}} \right| \ll 1 , \\[1.5mm] c_{\rm k}^{2} &=& c^{2}+\Delta c^{2}, \hspace{1.65cm} \left| \frac{\Delta c^{2}}{c^{2}} \right| \ll 1 , \\[1.5mm] \tilde{\omega}_{n}^{2} &=& \omega_{n}^{2}+\Delta \omega_{n}^{2}, \hspace{1.5cm} \left| \frac{\Delta \omega_{n}^{2}}{\omega_{n}^{2}} \right| \ll 1. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq39.png) In these expression, Vn, D, c and ωn are the eigenfunctions, overdensity, kink speed and eigenfrequencies, respectively, of the reference model. By linearizing Eq. (7) in the perturbations, one can easily show that
In these expression, Vn, D, c and ωn are the eigenfunctions, overdensity, kink speed and eigenfrequencies, respectively, of the reference model. By linearizing Eq. (7) in the perturbations, one can easily show that 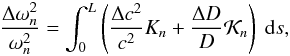 (15)where the sensitivity kernels, Kn(s) and
(15)where the sensitivity kernels, Kn(s) and 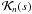 , are now for the fractional perturbations in the kink speed and overdensity, i.e., Δc2/c2 and ΔD/D,
, are now for the fractional perturbations in the kink speed and overdensity, i.e., Δc2/c2 and ΔD/D, ![\begin{eqnarray} \label{ckernel} {K}_{n}(s) &=& - L^{-1} W(s) \frac{c^2(s)}{\omega_{n}^{2}} V_{n}(s) \ V_{n}^{\prime\prime}(s), \\[1.5mm] {{\cal{K}}}_{n}(s) &=& L^{-1} W(s)\ \frac{g_\parallel(s) D(s)}{\omega_{n}^{2}} V_{n}(s) \ V_{n}^{\prime}(s). \label{Dkernel} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq49.png) This formulation grants the advantage that the kernels are now derived from completely known quantities, as the eigenfunctions, eigenfrequencies and tube profiles comprising these kernels are those corresponding to the chosen reference model.
This formulation grants the advantage that the kernels are now derived from completely known quantities, as the eigenfunctions, eigenfrequencies and tube profiles comprising these kernels are those corresponding to the chosen reference model.
Note, despite all of the qualifications and assumptions that were made, Eq. (1) is extremely general. Any configuration of magnetic field lines that results in a second-order differential wave equation will have a similar form with a suitable redefinition of the equation’s coefficients. Therefore, the arguments that we have made in this section have general validity, although the physical interpretation of the coefficients may change. In particular, the formalism we have developed is independent of whether curvature of the loop has been taken into account or whether the loop resides in a magnetized external atmosphere. We have adopted a simple loop model purely to enable clear presentation and illustration of our conceptual points.
3. Nature of the kernel functions
The sensitivity kernels embody everything that can be learned seismologically from measurements of mode frequencies. Already we can see from Eqs. (15) − (17) that potentially only two properties can be assessed independently, the kink speed and the overdensity. Of course, any quantity that can be derived from these two variables is also potentially accessible. We start by noting that the effects of buoyancy are rather weak for a typical coronal loop. We can estimate the importance that the overdensity plays in establishing the eigenfrequencies by taking the ratio of the two kernels. If we assume that 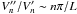 , we find that the magnitude of this ratio is characterized by ϵ, a non-dimensional measure of the buoyancy force to the tension force,
, we find that the magnitude of this ratio is characterized by ϵ, a non-dimensional measure of the buoyancy force to the tension force, ![\begin{eqnarray} &&\left| \frac{{\cal K}_n}{K_n} \right| \sim \frac{\epsilon}{n}, \\[1.5mm] &&\epsilon \equiv \frac{g D R}{c^2}, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq52.png) \arraycolsep1.75ptwhere R = L/π is the radius of the loop. If we use typical loop properties – i.e., L = 200 Mm, c = 1 Mm s-1 (Tomczyk et al. 2007), D = −1, and g = 2.7 × 10-4 Mm s-2, we find that this ratio is quite small for modes of any order i.e. ϵ ~ −1.7 × 10-2. Note, that a magnetic loop embedded in a field-free atmosphere is often underdense with negative D. For such a case (as considered here), just as the overdensity is negative, so is ϵ.
\arraycolsep1.75ptwhere R = L/π is the radius of the loop. If we use typical loop properties – i.e., L = 200 Mm, c = 1 Mm s-1 (Tomczyk et al. 2007), D = −1, and g = 2.7 × 10-4 Mm s-2, we find that this ratio is quite small for modes of any order i.e. ϵ ~ −1.7 × 10-2. Note, that a magnetic loop embedded in a field-free atmosphere is often underdense with negative D. For such a case (as considered here), just as the overdensity is negative, so is ϵ.
 |
Fig. 2 a) Eigenfunctions Vn for a reference model that consists of a loop with constant plasma parameter β and kink speed c. b) Sensitivity kernels Kn for the fractional kink speed perturbation made nondimensional by multiplying by the length scale L. c) Sensitivity kernels |
For illustrative purposes, we choose a particularly simple reference model, one in which the loop and atmosphere have a common temperature that is invariant as a function of height. For such a reference model, within the loop the kink speed c, the plasma parameter β, the overdensity D and our dimensionless parameter ϵ are all constants. Therefore, the eigenfunctions satisfy the equation 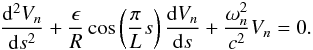 (20)While this equation does not have a simple direct analytic solution, it is quite amenable to a perturbation expansion because the coefficient of the first derivative term is small. When we apply the boundary condition of vanishing motion at the photosphere, Vn(s) = 0 at s = 0 and s = L, the eigenfunctions and eigenfrequencies to first order in ϵ are given by
(20)While this equation does not have a simple direct analytic solution, it is quite amenable to a perturbation expansion because the coefficient of the first derivative term is small. When we apply the boundary condition of vanishing motion at the photosphere, Vn(s) = 0 at s = 0 and s = L, the eigenfunctions and eigenfrequencies to first order in ϵ are given by 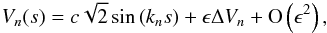 (21)with
(21)with ![\begin{eqnarray} \Delta V_{n}(s) &=& c\frac{n}{\sqrt{2}}\left[\frac{\cos\left(k_{n+1}s\right)}{2n+1} - \frac{\cos\left(k_{n-1} s\right)}{2n-1} \right. \\[1.5mm] && - \left. \frac{1}{n^{2} - 1/4}\left(\frac{s}{L} - \frac{1}{2} \right)\cos(k_n s)\right], \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq73.png) and
and ![\begin{eqnarray} \omega_n^2 = k_n^2 c^2 \left[ 1 - \epsilon \frac{\pi^{-1}}{n^2-1/4} + {\rm O}\left(\epsilon^2\right) \right], \label{eigenfreq} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq74.png) (24)with the wavenumbers kn
(24)with the wavenumbers kn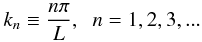 (25)To derive the kernels from these expressions, we need the integrating factor f(s), which can be obtained through direct integration of Eq. (5),
(25)To derive the kernels from these expressions, we need the integrating factor f(s), which can be obtained through direct integration of Eq. (5), ![\begin{equation} \label{fsol} f(s) = \exp\left[\epsilon \sin(\pi s/L)\right]. \end{equation}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq77.png) (26)The kernels are now obtained by direct substitution of Eqs. (21), (24), and (26) into Eqs. (16) and (17). To first order in the expansion parameter ϵ the kernels are
(26)The kernels are now obtained by direct substitution of Eqs. (21), (24), and (26) into Eqs. (16) and (17). To first order in the expansion parameter ϵ the kernels are ![\begin{eqnarray} \label{ckernsol} K_n(s) &=& 2L^{-1}\sin^2\left(k_n s\right) + \epsilon \frac{L^{-1}}{n} \Bigg[\cos \left(\frac{\pi}{L} s\right) \sin (2 k_{n} s) \nonumber\\[1.5mm] && + \frac{4}{c^{2}} \sin\left(k_{n} s\right) \Delta V_{n}(s)\Bigg] + O \left(\epsilon^{2}\right), \\[1.5mm] {\cal K}_n(s) &=& -\epsilon \frac{L^{-1} }{n} \ \cos\left(\frac{\pi}{L} s\right) \ \sin\left(2 k_n s\right) + {\rm O}\left(\epsilon^2\right). \label{Dkernsol} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq78.png) Figure 2 illustrates the eigenfunctions, Vn, and the associated sensitivity kernels, Kn and
Figure 2 illustrates the eigenfunctions, Vn, and the associated sensitivity kernels, Kn and 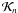 , for this simple reference model. The black, red, and blue colours denote n = 1,2, and 3 modes respectively. The various line styles (solid, dotted, and dashed) correspond to three different values of the parameter ϵ (0.0, −0.01, and −0.1). The kernels for the wave speed are (as expected) uniformly positive, whereas the overdensity kernels take on both positive and negative values. Both types of kernels are symmetric about the apex of the loop (s/L = 0.5); however, we note that the overdensity kernels always vanish at the apex. These properties can be deduced rather easily from Eqs. (27) and (28), where the zero-order terms in the kernels are positive definite and symmetric, while the first-order terms in both kernels can take on either sign. The negative lobes only appear because of buoyancy effects, which are rather weak. The perturbations arising from buoyancy are tiny for the eigenfunctions Vn and merely small for the wave speed kernels Kn. The overdensity kernels are, of course, proportional to ϵ – see Eq. (28) – and, therefore, the kernel itself is to leading order a perturbation and miniscule.
, for this simple reference model. The black, red, and blue colours denote n = 1,2, and 3 modes respectively. The various line styles (solid, dotted, and dashed) correspond to three different values of the parameter ϵ (0.0, −0.01, and −0.1). The kernels for the wave speed are (as expected) uniformly positive, whereas the overdensity kernels take on both positive and negative values. Both types of kernels are symmetric about the apex of the loop (s/L = 0.5); however, we note that the overdensity kernels always vanish at the apex. These properties can be deduced rather easily from Eqs. (27) and (28), where the zero-order terms in the kernels are positive definite and symmetric, while the first-order terms in both kernels can take on either sign. The negative lobes only appear because of buoyancy effects, which are rather weak. The perturbations arising from buoyancy are tiny for the eigenfunctions Vn and merely small for the wave speed kernels Kn. The overdensity kernels are, of course, proportional to ϵ – see Eq. (28) – and, therefore, the kernel itself is to leading order a perturbation and miniscule.
4. Discussion
We have used perturbation analysis twice to derive sensitivity kernels that describe how each eigenfrequency is a weighted average of the kink speed and overdensity along the loop. The first perturbation analysis involved linearising the loop properties (ck and Dρ) around a pre-defined reference model. This allowed us to write the sensitivity kernels using only the eigenfunctions for the known reference state. The second perturbation analysis was performed to solve for those eigenfunctions. The small parameter for this analysis was ϵ, the signed ratio of the buoyancy forces to the magnetic tension forces. This allowed the kernels to be expressed as an expansion in this small parameter.
4.1. The eigenfrequencies are insensitive to the density
The magnitude of the sensitivity kernels illustrated in Fig. 2, clearly indicate that for a typical coronal loop the eigenfrequencies of resonant kink waves are insensitive to the stratification within the loop. This is simply the result of the fact that buoyancy is usually a weak effect compared to magnetic tension (|ϵ| ≪ 1). From Eq. (24) we can see that buoyancy (and hence density) effects change the eigenfrequencies only at second order in the small parameter ϵ. A formidable implication of this insensitivity is that any two loops with the same kink speed profile but differing overdensity are seismically identical. The mode frequencies are, therefore, a poor direct diagnostic of the stratification within a coronal loop. We point out further, that the kernel for overdensity is multi-signed. This means that increasing the density in the loop at one position along the loop will increase the frequency, but an increase in density at a different position might have the opposite effect. Thus, a uniform density perturbation tends to produce an even smaller modulation of the eigenfrequencies than one might expect because much cancellation occurs when an integration is performed over the sensitivity kernels.
Despite the fact that the frequencies themselves lack direct diagnostic information about the density, the eigenfrequencies are an excellent measure of the kink speed. Since the kink speed is a function of both magnetic field strength and density (or temperature and plasma parameter), there is hope for estimating density as long as additional information from another observational source can exploited. For example, estimates of the temperature T of the loop (e.g., from spectral line-strength ratios), coupled with seismic estimates of the kink speed, would provide a measurement of the plasma-parameter. For our constant β model the relationship between the two is simply, 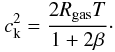 (29)Given the plasma parameter, we could estimate the overdensity using Dρ = −1/(1 + 2β). Therefore, while seismology in isolation is not sufficient to measure density, when used as part of a suite of different types of observations, much could be learned.
(29)Given the plasma parameter, we could estimate the overdensity using Dρ = −1/(1 + 2β). Therefore, while seismology in isolation is not sufficient to measure density, when used as part of a suite of different types of observations, much could be learned.
4.2. Only broad spatial averages can currently be assessed
Presently, we also face the fundamental obstacle that, for any given loop, the frequencies of only two modes have been successfully measured – n = 1 and 2 for some loops (e.g. Verwichte et al. 2004; van Doorsselaere et al. 2007; Verth et al. 2008) and n = 2 and 4 (or 5) for another (de Moortel & Brady 2007). Since these modes are low order, their eigenfunctions are long wavelength and the associated sensitivity kernels are large scale. This means that the frequencies contain information only about broad spatial averages of the wave speed. For a loop for which we only know the frequencies of the fundamental mode and the first overtone, even a cursory examination of the kernels reveals that we can only learn about the kink speed in a broad region near the apex of the loop (from the fundamental) and from a symmetric average over the legs of the loop (from the overtone). To gain high spatial resolution, one needs many modes of high order. Finally, we note that for the boundary conditions we have imposed, all of the eigenfunctions vanish at the endpoints; therefore, none of the eigenfrequencies (even higher-order ones that have yet to be observed) contain information about the footpoints of the loop.
To quantify this idea, let us consider a simple inversion. We start with a reference model with constant kink speed for an oscillating coronal loop. We will assume that buoyancy effects are negligible and only consider the first term of the integrand in Eq. (15). We can construct an average of the kink speed ⟨ Δc2/c2 ⟩ by taking a linear combination (sum over mode order n) of the handful of measured frequencies, ![\begin{eqnarray} \label{avekern} &&\left\langle \frac{\Delta c^{2}}{c^{2}}\right\rangle = \sum_{n} A_{n} \frac{\Delta \omega_{n}^{2}}{\omega_{n}^{2}} = \int_0^L \frac{{\Delta c^{2}}}{c^{2}}\hat{K}(s) \; {\rm d}s, \\[1.5mm] &&\hat{K}(s) \equiv \sum_{n} A_{n} K_{n}(s). \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq96.png) \arraycolsep1.75ptThe goal of the inversion is to choose the coefficients An such that the resulting weighting function
\arraycolsep1.75ptThe goal of the inversion is to choose the coefficients An such that the resulting weighting function 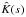 – called the averaging kernel – is sensible and has desirable properties. The exact desirable properties to seek is mutable. For example, a regularized least square (RLS) inversion (e.g., Pijpers & Thompson 1992) chooses the coefficients such that a model of the kink speed profile best matches the measurements in a least-squares sense, while at the same time enforcing some degree of smoothness through a regularization parameter. An optimally localized averages (OLA) inversion (see e.g. Christensen-Daalsgaard et al. 1995) instead tries to create averaging kernels that are as narrow as possible while avoiding negative sidelobes. Both of these methods are usually predicated on the existence of more than two oscillation frequencies. Therefore, we resort to a custom built, but slightly cruder, inversion. With only two frequencies, we will design two averaging kernels. One,
– called the averaging kernel – is sensible and has desirable properties. The exact desirable properties to seek is mutable. For example, a regularized least square (RLS) inversion (e.g., Pijpers & Thompson 1992) chooses the coefficients such that a model of the kink speed profile best matches the measurements in a least-squares sense, while at the same time enforcing some degree of smoothness through a regularization parameter. An optimally localized averages (OLA) inversion (see e.g. Christensen-Daalsgaard et al. 1995) instead tries to create averaging kernels that are as narrow as possible while avoiding negative sidelobes. Both of these methods are usually predicated on the existence of more than two oscillation frequencies. Therefore, we resort to a custom built, but slightly cruder, inversion. With only two frequencies, we will design two averaging kernels. One, 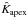 , will correspond to a choice of A1 and A2 such that the kernel is localized at the apex and the width of the peak is minimized. The other,
, will correspond to a choice of A1 and A2 such that the kernel is localized at the apex and the width of the peak is minimized. The other, 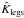 , will minimize the sensitivity at the apex. Both kernels are normalized to have unit integral. With only two coefficients to select, this minimization procedure is trivial with the result
, will minimize the sensitivity at the apex. Both kernels are normalized to have unit integral. With only two coefficients to select, this minimization procedure is trivial with the result ![\begin{eqnarray} &&\hat{K}_{\rm{apex}}(s) = \frac{2L^{-1}}{3}\left[4\sin^{2} \left(\frac{\pi}{L} s\right) - \sin^{2} \left(\frac{2\pi}{L} s\right)\right], \nonumber \\[1.5mm] &&\hat{K}_{\rm{legs}} = 2L^{-1}\sin^{2} \left(\frac{2\pi}{L} s\right). \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq103.png) (32)\arraycolsep1.75ptThrough the use of these two averaging kernels and Eq. (30) one obtains two estimates for the kink speed perturbation, yielding
(32)\arraycolsep1.75ptThrough the use of these two averaging kernels and Eq. (30) one obtains two estimates for the kink speed perturbation, yielding 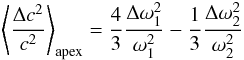 (33)and
(33)and 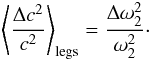 (34)We choose a reference model that has a kink speed such that the fundamental mode has exactly the measured frequency
(34)We choose a reference model that has a kink speed such that the fundamental mode has exactly the measured frequency 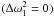 . By fixing the kink speed in this manner, we have ensured that the mean kink speed along the loop of the reference model is identical to that of the observed loop. Further, recall that the measured ratio ω2/ω1 < 2 (see e.g. Verwichte et al. 2004; van Doorsselaere et al. 2007). Therefore, the first overtone is downshifted in frequency compared to our reference model
. By fixing the kink speed in this manner, we have ensured that the mean kink speed along the loop of the reference model is identical to that of the observed loop. Further, recall that the measured ratio ω2/ω1 < 2 (see e.g. Verwichte et al. 2004; van Doorsselaere et al. 2007). Therefore, the first overtone is downshifted in frequency compared to our reference model 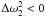 . Equations (33) and (34) tell us that the kink speed near the apex is less than that of the reference model, while that in the legs is more. Further, the magnitude of the difference at the apex is one third that in the legs of the loop.
. Equations (33) and (34) tell us that the kink speed near the apex is less than that of the reference model, while that in the legs is more. Further, the magnitude of the difference at the apex is one third that in the legs of the loop. 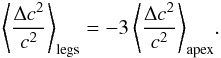 (35)No other detailed information can be revealed for such a loop with access to only two frequencies.
(35)No other detailed information can be revealed for such a loop with access to only two frequencies.
4.3. What if many frequencies could be measured?
If we had access to many observed frequencies, an inversion with high-spatial resolution would be possible. For example, we might use an RLS inversion, for which the first step is to express the perturbed wave speed and overdensity using a parameterization, 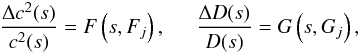 (36)with j = 1,2,...J, where J is usually much less than the number of measured frequencies. The functions F and G might be polynomial expansions (in the coordinate s) where the parameters Fj and Gj are the coefficients of each term in the expansion. Or, and perhaps more usefully, the parameters Fj and Gj might be the values of the perturbations at a pre-defined grid of positions sj – i.e., F(sj) = Fj and G(sj) = Gj, and the perturbations for values of s between the grid points are obtained by an interpolation scheme (such as splines). The goal of the RLS inversion is then to find the set of parameters Fj and Gj that best fit the data.
(36)with j = 1,2,...J, where J is usually much less than the number of measured frequencies. The functions F and G might be polynomial expansions (in the coordinate s) where the parameters Fj and Gj are the coefficients of each term in the expansion. Or, and perhaps more usefully, the parameters Fj and Gj might be the values of the perturbations at a pre-defined grid of positions sj – i.e., F(sj) = Fj and G(sj) = Gj, and the perturbations for values of s between the grid points are obtained by an interpolation scheme (such as splines). The goal of the RLS inversion is then to find the set of parameters Fj and Gj that best fit the data.
This is of course accomplished in a least squares manner. Assuming σn is an estimate of the fractional error in the square of the observed frequency ωn, one can invert the integrals in (15) by minimising the goodness of fit χ2 with respect to the parameters Fj and Gj, ![\begin{eqnarray} \label{chi} \chi^{2} &=& \sum_{n}\frac{1}{\sigma_n^2} \left\{\frac{\delta\omega_n^2}{\omega_n^2} - \int\left[F\left(s,F_j\right){K}_{n}(s) + G\left(s,G_j\right) {\cal K}_{n}(s) \right]{\rm d}s \right\}^{2} \nonumber \\[1.5mm] && + {\cal R}\left(F_j,G_j\right) \end{eqnarray}](/articles/aa/full_html/2012/09/aa19930-12/aa19930-12-eq123.png) (37)where ℛ is the regularization integral which is included to penalize solutions that lack smoothness. One common choice of regularization is based on first derviatives of the perturbation functions F and G,
(37)where ℛ is the regularization integral which is included to penalize solutions that lack smoothness. One common choice of regularization is based on first derviatives of the perturbation functions F and G, 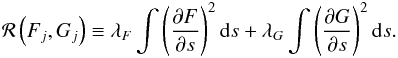 (38)The trade-off parameters λF and λG can be freely chosen. Large values enforce very smooth solutions but increase the formal error in the inversion, whereas small values minimise the propagation of error, but at the cost of decreased smoothness.
(38)The trade-off parameters λF and λG can be freely chosen. Large values enforce very smooth solutions but increase the formal error in the inversion, whereas small values minimise the propagation of error, but at the cost of decreased smoothness.
5. Conclusion
Transverse kink oscillations have been detected with TRACE in the solar corona. Various techniques such as polynomial fits to the time series, wavelet transforms, sinusoidal function fitting and Fast fourier transforms are used to measure the periods of oscillation. In some cases, the ratio of the periods of the fundamental to the first overtone have been found to be less than the canonical value of 2, leading to suggestions that the oscillatory waves are dispersive (e.g. Andries et al. 2009). Theoretical explanations are currently being sought to understand this departure from the value of 2 and the vigorous field of Coronal Seismology has arisen to detect new overtones, reduce error bars and compare the eigenmodes of reference coronal tube models to the observations, all with the aim of deducing the plasma properties of the loop. Initially, there was an extensive use of the theory developed by Edwin & Roberts (1983) for the identification of the modes. In recent times, there have been further developments in theoretical modelling of coronal loops with inclusion of various geometrical effects such as curvature, non-planar loops, finite tube widths, non-static coronal background, transverse variation in loop parameters, various heating functions etc. Since the coronal tubes are thin and the periods are detected at short time-scales, many of these effects are not considered very crucial for the low-order measured modes. Thus far, more emphasis has been put on estimating the density scale height and magnetic field strength by comparing theoretical eigenfrequencies with the measured ones. This is done by considering a reference model with prescribed magnetic field and density profiles and solving the kink-wave equation for its eigenfunctions and eigenfrequencies.
In this paper, we considered a typical coronal loop and found that the direct sensitivity of its eigenfrequencies to density is rather weak. The smallness of the overdensity kernel suggests that mode frequencies are almost completely determined by the wave speed. A corollary of this statement is that two thin coronal loops with identical kink speed but very different overdensities are seismically indistinguishable. Therefore, coronal seismology is a poor tool for discriminating between coronal loops with the same kink speed but different flaring rates, magnetic field strengths and densities. While seismology by itself is incapable of uniquely measuring density stratification, when used in conjunction with independent observations of loop properties, such as temperature or field strength, seismology could be used to constrain density.
From the measurement of only two frequencies ν1 and ν2 one cannot deduce more than two broad spatial averages of the kink speed along the loop. For example, assuming a loop length of 200 Mm and using the observations of Verwichte et al. (2004) – ν1 = 2.23 mHz and ν2 = 4.05 mHz, we can estimate that the wave speed averaged over a broad region near the apex of the loop is 0.63 Mm s-1 and averaged over the legs the wave speed is 0.90 Mm s-1. For different loop lengths these wave speeds would scale linearly.
Finally, it is worth mentioning that a magnetic loop in a field-free atmosphere is an overly-simplistic assumption. It is more probable that the observed oscillating loops are actually preferentially illuminated field lines that are an integral part of a larger coronal magnetic structure. Accounting for such a scenario adds complexity to the differential equations governing the propagation of kink waves. However, we believe it will not change the
main content of the current study. Also, note that the observed loop kink oscillations are generally transverse to the vertical plane of the loop, as opposed to oscillations in the plane as assumed in this study. For an isolated magnetic tube, in the absence of tension forces arising from the curvature of the loop (which we have ignored here), these two polarizations of motion are degenerate with the same eigenfrequencies. However, as we have already stated, real coronal loops are probably part of a larger magnetic structure, and those oscillations that are transverse to the plane of the loop are likely to interact strongly with other field lines in the structure, thereby lifting the degeneracy. Therefore, for a variety of reasons we expect the two polarizations to obey different differential equations, thereby possessing different sensitivity kernels.
Acknowledgments
This work is supported by MSRC (University of Sheffield) and STFC. B.W.H. acknowledges NASA grants NNX08AJ08G, NNX08AQ28G, and NNX09AB04G.
References
- Andries, J., Goosens, M., Hollweg, J. V., Arregui, I., & Van Doorsselaere, T. 2005, A&A, 430, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andries, J., Van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, G. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Daalsgaard, J., Larsen, R. M., Schou, J., & Thompson, M. J. 1995, in GONG1994: Helio and Asteroseismology, eds. R. K. Ulrich, E. J. Rhodes Jr., & W. Dappen, ASP Conf. Ser., 76 [Google Scholar]
- de Moortel, I., & Brady, C. S. 2007, ApJ, 664, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, A. J., Donelly, G. R., & Roberts, B. 2007, A&A, 476, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2006, A&A, 459, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Orza, B., Ballai, I., Jain, R., & Murawski, K. 2012, A&A, 537, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pijpers, F., & Thompson, M. J. 1992, A&A, 262, L33 [NASA ADS] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdéyi, R. 2008, ApJ, 686, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Brown, D. S. 2000, ApJ, 537, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Aschwanden, M. J., & Title, A. M. 2002, Sol. Phys., 206, 69 [NASA ADS] [CrossRef] [Google Scholar]
- van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., & Erdelyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., Erdelyi, R., & Jess, D. B. 2008, ApJ, 687, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 233, 77 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Loop geometry. |
| In the text | |
 |
Fig. 2 a) Eigenfunctions Vn for a reference model that consists of a loop with constant plasma parameter β and kink speed c. b) Sensitivity kernels Kn for the fractional kink speed perturbation made nondimensional by multiplying by the length scale L. c) Sensitivity kernels |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.