| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219873 | |
| Published online | 19 September 2012 | |
A two-component model for the high-energy variability of blazars
Application to PKS 2155-304
1 Instituto de Investigaciones Físicas de Mar del Plata (CONICET – UNMdP), Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Mar del Plata, Dean Funes 3350, (7600) Mar del Plata, Argentina
e-mail: mreynoso@mdp.edu.ar
2 Instituto Argentino de Radioastronomía, CCT La Plata-CONICET, 1894, Villa Elisa C.C. No. 5, Argentina
3 Irfu, Service de Physique des Particules, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
Received: 22 June 2012
Accepted: 11 August 2012
Aims. We study the production of very-high-energy emission in blazars as a superposition of a steady component from a baryonic jet and a time-dependent contribution from an inner e−e+ beam launched by the black hole.
Methods. Both primary relativistic electrons and protons are injected in the jet, and the particle distributions along it are found by solving a one-dimensional transport equation that accounts for convection and cooling. The short-timescale variability of the emission is explained by local pair injections in turbulent regions of the inner beam.
Results. For illustration, we apply the model to the case of PKS 2155-304, reproducing a quiescent state of emission with inverse Compton and synchrotron radiation from primary electrons, as well as proton-proton interactions in the jet. The latter also yield an accompanying neutrino flux that could be observed with a new generation km-scale detector in the northern hemisphere such as KM3NeT.
Key words: radiation mechanisms: non-thermal / BL Lacertae objects: individual: PKS 2155-304 / neutrinos
© ESO, 2012
1. Introduction
Blazars are the active galactic nuclei (AGNs) in which the jet points mainly in the direction of the line of sight. They exhibit the most extreme high-energy phenomena of all AGNs. Their spectral energy distributions (SEDs) are characterized by nonthermal continuum spectra with a broad low-frequency component from X-rays to γ-rays. Blazars show rapid variability across the entire electromagnetic spectrum. Variability at high energies on timescales of a few minutes has been observed for some of them, such as PKS 2155-304 (e.g. Aharonian et al. 2006).
In this work we present a two-component jet model with both relativistic leptons and hadrons to explain the high-energy emission from these objects. The basic scenario consists of a steady baryonic jet launched by the accretion disk, and an e+e− beam launched by the black hole ergosphere. The quiescent component of the signal is assumed to be produced by the jet, while the variable component is due to shocked regions in the inner e+e− beam. Inhomogeneities and turbulence can be generated by Kelvin-Hemholtz instabilities. In Sect. 2 we describe the basics of the model. Its application to PKS 2155-304 is presented in Sects. 3 and 4 for the quiescent and variable emission, respectively. In Sect. 5 we focus on the neutrino output expected for the same blazar, analyzing the detectability with a next generation neutrino telescope such as KM3NeT. We finish in Sect. 6 with a discussion.
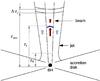 |
Fig. 1 Basic elements of the model. See the text for details. |
2. Description of the model
We assume that matter is captured by the central black hole through a dissipationless accretion disk (Kelner & Bogolobov 2010) and that a fraction of this accreted material is expelled by the accretion disk in two oppositely directed jets. An inner beam of relativistic electrons and positrons is launched by the spinning black hole. This two-component setup is similar to the ones implemented in several previous models (e.g. Sol et al. 1989; Romero 1995; Ghisellini et al. 2005; Boutelier et al. 2008). A sketch of the basic elements of the scenario is depicted in Fig. 1.
The introduction of a model with two components is motivated by observations as a means to reconciling available data with the unified AGN paradigm (e.g. Urry & Padovani 1995), as noted by Chiaberge et al. (2000). One-component jet models require high bulk Lorentz factors (10 − 20) when applied to blazars and lower values when applied to FR radiogalaxies. Including of a second component serves to solve this discrepancy, for example, through the combination of a fast spine and a slower (but still relativistic) layer, so that the emission at small viewing angles is dominated by the fast component, whereas the slow component dominates for larger angles.
Some additional observational facts also favor the two-component interpretation. For instance, the presence of a fast spine surrounded by a slower outflow can be inferred from the observed limb-brightened radio morphology of the radiogalaxies jets (Giroletti et al. 2004). On the other hand, whereas VLBI observations of powerful TeV BL Lacs suggest that the pc-scale jets move slowly (Piner & Edwards 2004; Giroletti et al. 2004), rapid variability of the TeV emission implies that, in the region where this emission is produced, the jet should be extremely relativistic (e.g., Dondi & Ghisellini 1995; Ghisellini et al. 2002; Konopelko et al. 2003).
On the theoretical side, the presence of both a spinning black hole and an accretion disk would unavoidably yield the launching of outflows through the BZ process (Blandford & Znajek 1977) and the BP process (Blandford & Payne 1982). The coexistence of both mechanisms has been investigated by Meier (2003), among others. Whereas the BZ process yields the launching of a Poynting flux that gives rise to a leptonic beam, the BP process can generate a baryon-rich jet launched centrifugally from the inner accretion disk (e.g. Komissarov et al. 2007; Sadowski & Sikora 2010).
The stability and structure of this type of jets have been discussed, for instance, in Hardee (2007), Narayan et al. (2009), and Perucho (2012). For general discussion of fluid instabilies see, e.g., Shore (2008).
For the jet, we adopt the model developed by Reynoso et al. (2011). Equipartition between jet kinetic energy and magnetic energy takes place at z0 = 50Rg from the black hole, the jet half-opening angle is ξj, the jet Lorentz factor is Γj at z0, and the viewing angle is ij. The bulk kinetic power of the jet at z0 is a fraction qj of the Eddington power, 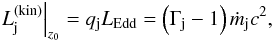 (1)and the cold particle density in the jet is
(1)and the cold particle density in the jet is 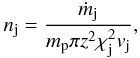 (2)with χj = tanξj. The magnetic field varies along the jet according to
(2)with χj = tanξj. The magnetic field varies along the jet according to 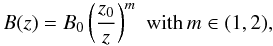 and the Γj increases slowly as magnetic energy density decreases along the jet.
and the Γj increases slowly as magnetic energy density decreases along the jet.
The e + e − -beam, with a half-opening angle ξb < ξj, is confined by the jet by requiring that the pressure is less than in the jet: Pb = ηbPj, where ηb < 1. The initial Lorentz factor of the beam is 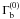 at distance
at distance 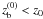 from the black hole, where equipartition with the beam magnetic energy holds. This condition is used to fix
from the black hole, where equipartition with the beam magnetic energy holds. This condition is used to fix 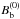 . For
. For 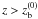 in the beam, we assume
in the beam, we assume 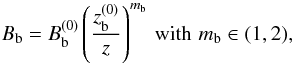 (3)so that the Lorentz factor of the beam also increases gradually along it. This behavior of the magnetic field also enables Kelvin-Hemlholtz instabilities to develop, as we discuss below in Sect. 4, where we deal with the production of variable emission in the beam. As mentioned, this contribution is added to the one from the quiescent jet, which is discussed in next.
(3)so that the Lorentz factor of the beam also increases gradually along it. This behavior of the magnetic field also enables Kelvin-Hemlholtz instabilities to develop, as we discuss below in Sect. 4, where we deal with the production of variable emission in the beam. As mentioned, this contribution is added to the one from the quiescent jet, which is discussed in next.
3. The quiescence emission from the jet
The quiescent state of the emission can be reproduced using a lepto-hadronic model for the jet. Acceleration of relativistic electrons and protons takes place at zacc > z0, where the power injected in these primary particles is Le and Lp = aLe, with a > 0. The total power in the injected, Lrel = Le(1 + a), is a fraction of the bulk kinetic power of the jet, 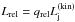 (see Reynoso et al. 2011). The distribution of particles in the steady jet, N(E,z) in units GeV-1 cm-3, is governed by an inhomogeneous transport equation with cooling and convection:
(see Reynoso et al. 2011). The distribution of particles in the steady jet, N(E,z) in units GeV-1 cm-3, is governed by an inhomogeneous transport equation with cooling and convection: 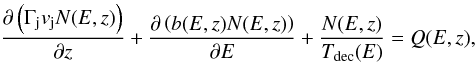 (4)where z is the distance to the black hole in the AGN frame, and
(4)where z is the distance to the black hole in the AGN frame, and 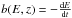 .
.
This equation is solved in the jet co-moving frame, and the injection or source term is taken as ![\begin{equation} Q(E,z) = K_i\left(\frac{z_{\rm acc}}{z}\right)^2{E}^{-s}\exp{\left[-\left(\frac{E}{{E}^{\left({\rm max}\right)}_{i}}\right)\right]}, \end{equation}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq34.png) (5)where the cut-off energy
(5)where the cut-off energy 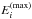 is determined by equating the acceleration rate to the cooling one. The particle injection is normalized in the AGN frame, that where the central black hole is at rest, as
is determined by equating the acceleration rate to the cooling one. The particle injection is normalized in the AGN frame, that where the central black hole is at rest, as 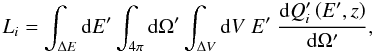 (6)where
(6)where ![\begin{equation} \frac{{\rm d} Q'_i\left(E',z\right)}{{\rm d}\Omega'} = \left[\frac{E'^2 - m_i^2c^4}{{E}^2- m_i^2c^4}\right]^{1/2} \frac{Q_i(E,z)}{4\pi}, \label{Qjet2obs} \end{equation}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq37.png) (7)and
(7)and 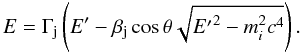 (8)The acceleration rate is given by
(8)The acceleration rate is given by 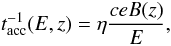 (9)with an efficiency η, and the loss rate corresponds to synchrotron emission, inverse Compton interactions, pp and pγ interactions, and adiabatic cooling (see Reynoso et al. 2011). In Fig. 2, we show the acceleration and cooling rates for electrons and protons at the position zacc in the jet. The list of assumed and derived parameters for the jet is shown in Table 1. The values for the black hole mass and redshift are taken as Mbh = 109 M⊙, and zrs = 0.116, respectively, following Aharonian et al. (2007), and the column density of HI is taken as NH = 1.3 × 1020 cm-2 after Lockman & Savage (1995). The rest of the parameters in Table 1 corresponds to the above described jet model, which is discussed in detail in Reynoso et al. (2011). These parameters are fixed to obtain a SED that fits the quiescence emission represented by the same set of observational data used in Aharonian et al. (2009).
(9)with an efficiency η, and the loss rate corresponds to synchrotron emission, inverse Compton interactions, pp and pγ interactions, and adiabatic cooling (see Reynoso et al. 2011). In Fig. 2, we show the acceleration and cooling rates for electrons and protons at the position zacc in the jet. The list of assumed and derived parameters for the jet is shown in Table 1. The values for the black hole mass and redshift are taken as Mbh = 109 M⊙, and zrs = 0.116, respectively, following Aharonian et al. (2007), and the column density of HI is taken as NH = 1.3 × 1020 cm-2 after Lockman & Savage (1995). The rest of the parameters in Table 1 corresponds to the above described jet model, which is discussed in detail in Reynoso et al. (2011). These parameters are fixed to obtain a SED that fits the quiescence emission represented by the same set of observational data used in Aharonian et al. (2009).
The SED is dominated by synchrotron and inverse Compton (IC) emission of the electrons, and pp orginated very-high-energy (VHE) gamma-rays, as shown in Fig. 3. In our calculations, the VHE energy emission has been corrected by the effect of extragalactic background light (EBL) absorption following Domínguez et al. (2011).
 |
Fig. 2 Acceleration and cooling rates for primary electrons and protons in the jet at zacc. |
 |
Fig. 3 SED corresponding to the quiescent state of PKS 2155-304. The contributions shown are electron synchrotron (black solid line), IC (dashed line), pp (dashed-dotted line), proton synchrotron (gray solid line), and pγ (gray dashed line). |
Model parameters for the quiecence emission from the jet of PKS 2155-304.
4. Variable emission from the beam
The variable emission is assumed here to have its origin in shocked regions in the internal e + e − beam that can arise, e.g., due to Kelving-Helmholtz (KH) instabilities. These instabilities will be able to develop in the beam if the magnetic field is below a critical value (e.g. Romero 1995): 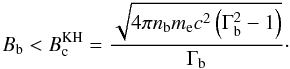 (10)In Fig. 4 we show the beam magnetic field and the critical value
(10)In Fig. 4 we show the beam magnetic field and the critical value 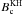 , considering that
, considering that 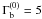 at
at 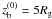 . It can be seen from this plot that for z ≳ 1016 cm KH instabilities start to develop and create inhomogeneities if the pinching modes dominate (see Romero 1995). The rarefactions produced in the beam by the instabilities act as obstacles for the fast plasma, and strong shocks are expected to appear at z ~ 1016 cm. These shocks reaccelerate the pairs (Araudo et al. 2010) producing a local injection of relativistic particles.
. It can be seen from this plot that for z ≳ 1016 cm KH instabilities start to develop and create inhomogeneities if the pinching modes dominate (see Romero 1995). The rarefactions produced in the beam by the instabilities act as obstacles for the fast plasma, and strong shocks are expected to appear at z ~ 1016 cm. These shocks reaccelerate the pairs (Araudo et al. 2010) producing a local injection of relativistic particles.
 |
Fig. 4 Magnetic field in the beam (red line) and critical magnetic field below which KH instabilities can develop. |
A shock front originating in the beam at a position zi with a Lorentz factor Γs will form a post-shocked region of a certain size 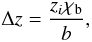 (11)with χb = tanξb, and particles are injected during a time
(11)with χb = tanξb, and particles are injected during a time 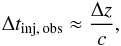 (12)as seen in the observer frame.
(12)as seen in the observer frame.
The distribution of the injected pairs is computed in the post-shock frame, where the population is assumed to be isotropic. The corresponding source term is a power law with an exponential cutoff at the maximum Lorentz factor γmax: 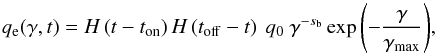 (13)is where H is the Heavyside step function, ton the time when the injection is switched on, and the time when it is switched off is
(13)is where H is the Heavyside step function, ton the time when the injection is switched on, and the time when it is switched off is 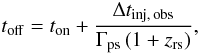 (14)both corresponding to the post-shock frame. We note that, for example, the onset time is transformed to the observer frame as
(14)both corresponding to the post-shock frame. We note that, for example, the onset time is transformed to the observer frame as 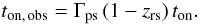 (15)The constant q0 is found through normalization taking into account the particle density in the post-shock frame:
(15)The constant q0 is found through normalization taking into account the particle density in the post-shock frame: 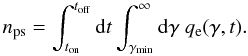 (16)This can be related to the beam density nb by the compresion factor ζ as
(16)This can be related to the beam density nb by the compresion factor ζ as 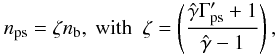 (17)where
(17)where 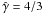 is the polytropic index,
is the polytropic index, 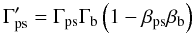 is the Lorentz factor of the shock in the undisturbed beam frame, and the Lorentz factor of the post-shock (ps) region is
is the Lorentz factor of the shock in the undisturbed beam frame, and the Lorentz factor of the post-shock (ps) region is 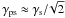 . The density of the beam, in turn, is fixed as a fraction λ of the jet density of Eq. (2):
. The density of the beam, in turn, is fixed as a fraction λ of the jet density of Eq. (2): 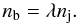 (18)The maximum Lorentz factor of the locally accelerated pairs γmax is obtained from the balance between the acceleration rate and the cooling rate, where the latter is due to synchrotron and synchrotron self-Compton (SSC) interactions.
(18)The maximum Lorentz factor of the locally accelerated pairs γmax is obtained from the balance between the acceleration rate and the cooling rate, where the latter is due to synchrotron and synchrotron self-Compton (SSC) interactions.
 |
Fig. 5 Light curves of gamma-rays above 200 GeV produced by e + e − injection in the beam at zi = 2.3 × 1016 cm with Γs = { 14,16,18,20 } in the left panel, and with Γs = 20 and b = { 50,70,100 } in the right panel. |
We solve the following kinetic equation to obtain the distribution of pairs as a function of time ne(γ,t): 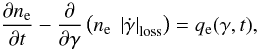 (19)where the loss term is given by
(19)where the loss term is given by 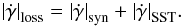 (20)An iterative process is implemented to work out ne(γ,t) from this equation. As a zero-order approximation, we adopt the solution corresponding to no SSC interactions, just synchrotron losses. Then, the solution is succesively improved by computing the SSC cooling term using the previus solutions found for ne(γ,t). This cooling rate is computed in the Thompson regime to save computing time, since this simplification was tested not to affect the final result. The self-synchrotron Thomson (SST) cooling rate is then (e.g. Schlickeiser & Lerche 2007):
(20)An iterative process is implemented to work out ne(γ,t) from this equation. As a zero-order approximation, we adopt the solution corresponding to no SSC interactions, just synchrotron losses. Then, the solution is succesively improved by computing the SSC cooling term using the previus solutions found for ne(γ,t). This cooling rate is computed in the Thompson regime to save computing time, since this simplification was tested not to affect the final result. The self-synchrotron Thomson (SST) cooling rate is then (e.g. Schlickeiser & Lerche 2007): 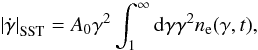 (21)where
(21)where 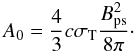 The synchrotron cooling rate is
The synchrotron cooling rate is 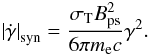 (22)The acceleration rate is worked out using Eq. (9) along with the magnetic field corresponding to the post-shock frame,
(22)The acceleration rate is worked out using Eq. (9) along with the magnetic field corresponding to the post-shock frame, 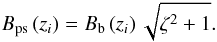 (23)For any injection point zi in the beam, we solve the kinetic equation, and work out the resulting synchrotron and SSC emission. In the local AGN frame, the emissivity is given by
(23)For any injection point zi in the beam, we solve the kinetic equation, and work out the resulting synchrotron and SSC emission. In the local AGN frame, the emissivity is given by 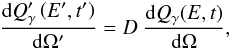 (24)where the Doppler factor is
(24)where the Doppler factor is 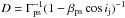 , E is the photon energy in the ps frame, and E′ = D E is the photon energy in the local AGN frame. In the case of synchrotron radiation, the emissivity in the ps-frame is
, E is the photon energy in the ps frame, and E′ = D E is the photon energy in the local AGN frame. In the case of synchrotron radiation, the emissivity in the ps-frame is 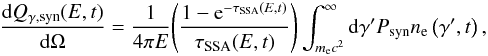 (25)where τSSA is the optical depth corresponding to synchrotron-self absorption, and the synchrotron power per unit energy emitted by the electrons is given by (Blumenthal & Gould 1970):
(25)where τSSA is the optical depth corresponding to synchrotron-self absorption, and the synchrotron power per unit energy emitted by the electrons is given by (Blumenthal & Gould 1970): 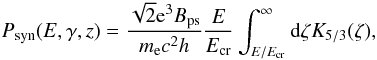 (26)where K5/3 is the modified Bessel function of order 5/3 and
(26)where K5/3 is the modified Bessel function of order 5/3 and 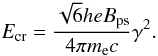 The soft photon density in the ps frame is
The soft photon density in the ps frame is 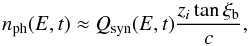 (27)and the IC emissivity in the this frame is
(27)and the IC emissivity in the this frame is 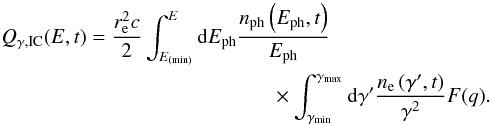 (28)Here re is the classical electron radius, and we integrate in the target photon energy Eph and in the electron Lorentz factors γ′ between
(28)Here re is the classical electron radius, and we integrate in the target photon energy Eph and in the electron Lorentz factors γ′ between 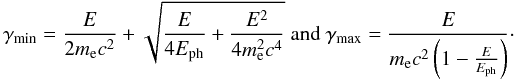 The function F(q) is given by
The function F(q) is given by 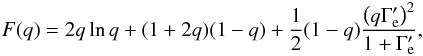 (29)with Γe = 4Ephγ′/(mec2) and
(29)with Γe = 4Ephγ′/(mec2) and 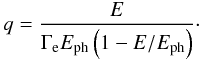 The differential photon flux is first obtained in the AGN local frame as
The differential photon flux is first obtained in the AGN local frame as ![\begin{equation} \frac{{\rm d}\Phi'_{\gamma}\left(E',t'\right)}{{\rm d}E'}= \left(\pi z_i^2\tan^2\xi_{\rm b} \Delta z\right) \frac{{\rm d} Q'_\gamma\left(E',t'\right)}{{\rm d}\Omega'} \frac{{\rm d}\Omega'}{{\rm d}A'} \exp{\left[-\tau_{\gamma\gamma}\right]}, \end{equation}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq138.png) (30)where
(30)where 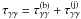 is the γγ optical depth due to the jet and the beam photons. The latter is estimated as
is the γγ optical depth due to the jet and the beam photons. The latter is estimated as 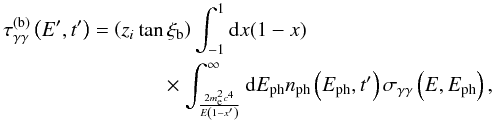 (31)and
(31)and 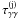 is obtained from a similar expression.
is obtained from a similar expression.
If dC is the comoving distance, then 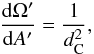 and taking into account that the observed energy and time are transformed as
and taking into account that the observed energy and time are transformed as 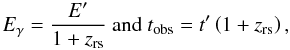 the differential photon flux arriving on Earth from a source at redshift zrs is
the differential photon flux arriving on Earth from a source at redshift zrs is ![\begin{eqnarray} \frac{{\rm d}\Phi_{\gamma} \left(E_\gamma,t_{\rm obs}\right)}{{\rm d}E_{\gamma}} = \frac{\left(1+z_{\rm rs}\right)^2}{d_{\rm L}^2} \frac{{\rm d} \Phi'_\gamma \left(E_\gamma \left(1 + z_{\rm rs}\right), \frac{t_{\rm obs}}{1+z_{\rm rs}}\right)}{{\rm d}E'} \nonumber\\ \times \exp{-\left[\tau_{\rm EBL} \left(E_\gamma,z_{\rm rs}\right)\right]}, \label{dgammaflux} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq146.png) (32)where dL is the luminosity distance and τEBL is the optical depth due to γγ absorption on the extragalactic background light. In these terms, the usual amount νFν in units erg cm-2 s-1 is expressed as
(32)where dL is the luminosity distance and τEBL is the optical depth due to γγ absorption on the extragalactic background light. In these terms, the usual amount νFν in units erg cm-2 s-1 is expressed as  . A light curve can be obtained simply by integrating Eq. (32) on the desired energy range for different times. In Fig. 5 we show the light curves that can be obtained if the injection point in the beam is zi = 2.3 × 1016 cm for different shock Lorentz factors Γs and sizes of the injection zone Δz = Rb/b. The values adopted for beam parameters are shown in Table 2. More complex light curves can be obtained, for instance, by succesive shock injections at the same position with Γs, b, and ton chosen randomly in the ranges:
. A light curve can be obtained simply by integrating Eq. (32) on the desired energy range for different times. In Fig. 5 we show the light curves that can be obtained if the injection point in the beam is zi = 2.3 × 1016 cm for different shock Lorentz factors Γs and sizes of the injection zone Δz = Rb/b. The values adopted for beam parameters are shown in Table 2. More complex light curves can be obtained, for instance, by succesive shock injections at the same position with Γs, b, and ton chosen randomly in the ranges: ![\begin{eqnarray} \Gamma_{\rm s} & \in & \{ 17,18,19 \} \\ b &\in& \{50,60,70,80,90\} \\ t_{\rm on} &\in& [1...15]~{\min}. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq155.png) Some example light curves obtained in this way are plotted in Fig. 6 with the parameters shown in Table 3.
Some example light curves obtained in this way are plotted in Fig. 6 with the parameters shown in Table 3.
Beam parameters.
 |
Fig. 6 Light curves of gamma-rays above 200 GeV produced by e + e − injection in the beam at zi = 2.3 × 1016 cm with the randomly chosen values for Γs, b, and ton of Table 3. |
In particular, in view of the flaring activity detected in 2006 (Aharonian et al. 2007), we see that a simillar lightcurve can be obtained for the flux of gamma-rays above 200 GeV by adding up six different injections at a fixed position in the beam, zi = 4 × 1016 cm, each being switched on at apropriate times ton, as seen in Fig. 7. The values of the different parameters are shown in Table 4. The multiple shock scenario resembles the one proposed to explain the rapid variability in gamma-ray bursts (GRBs), e.g., Kobayashi et al. (1997). The whole SED evolution shown in Fig. 8 shows that multiwavelength observations, including studies of rapid variability in radio, X-ray, and γ-ray bands, can be used to test the proposed model.
 |
Fig. 7 Lightcurve of gamma-rays above 200 GeV (blue line), generated as the superposition of six injections in the beam (lc1, lc2, lc3, lc4, lc5, lc6, in gray-dashed lines), as compared to data of the 2006 flare of PKS 2155-304. |
In Fig. 8, we show for illustration two instantaneus contributions to the SED due to the shocked beam at t1 ≃ 40 min and t2 ≃ 50 min. The acceleration and cooling rates corresponding to t1 are shown in Fig. 9, where it can be seen that the Lorentz factors of the electrons are ~ 106 in the post-shock frame. The inverse Compton interactions with target photons created in the jet was verified to be unimportant for the adopted value of zi.
 |
Fig. 8 Instantaneus SEDs originating in the beam at t1 ≃ 40 min, and t2 ≃ 50 min corresponding to the plot of Fig. 7. The quiescent SED is also shown (gray dashed lines). |
 |
Fig. 9 Acceleration and cooling rates in the post-shock frame corresponding to t1 ≃ 40 min in the lightcurve of Fig. 7. |
5. Neutrino emission
The acceleration of protons in the jet and their interactions with synchrotron photons and cold jet protons lead to the production of VHE gamma-rays after π0 decays, as seen in the SED of Fig. 3. These pγ and pp interactions also give rise to charged pions that decay to muons and neutrinos. The stationary distributions of pions and muons in the jet, Nπ(E,z) and Nμ(E,z), are found using the transport equation Eq. (4). The corresponding neutrino emissivity from direct pion decay can be computed in the jet comoving frame following Lipari et al. (2007): 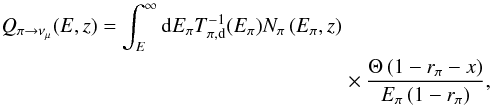 (36)with x = E/Eπ and Tπ,d = 2.6 × 10-8 s. The contribution from muon decays (
(36)with x = E/Eπ and Tπ,d = 2.6 × 10-8 s. The contribution from muon decays (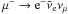 ,
,
Model parameters for the variable emission from the beam of PKS 2155-304.
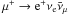 ) can be calculated as
) can be calculated as ![\begin{eqnarray} Q_{\mu\rightarrow\nu_\mu}(E,z) = \sum_{i=1}^4\int_{E}^{\infty}\frac{{\rm d}E_\mu}{E_\mu} T^{-1}_{\mu,\rm d}\left(E_\mu\right)N_{\mu_i}\left(E_\mu,z\right) \nonumber\\ \times \left[\frac{5}{3} - 3x^2 + \frac{4}{3}x^3\right]. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19873-12/aa19873-12-eq230.png) (37)In this expression, x = E/Eμ,
(37)In this expression, x = E/Eμ, 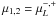 , Tμ,d = 2.2 × 10-6 s, and
, Tμ,d = 2.2 × 10-6 s, and 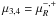 .
.
In the local AGN frame, the differential neutrino emissivity, in units (GeV-1 cm-3 sr-1 s-1) is given by 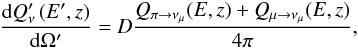 (38)where z is the distance from the black hole to the position in the jet in the AGN frame and
(38)where z is the distance from the black hole to the position in the jet in the AGN frame and 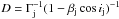 . The differential neutrino flux is then
. The differential neutrino flux is then 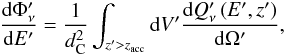 (39)and in the observer frame, since the redshifted neutrino energy is Eν = E′/(1 + zrs),
(39)and in the observer frame, since the redshifted neutrino energy is Eν = E′/(1 + zrs), 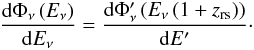 (40)On Earth, neutrino telescopes are used to observe this flux in the presence of the atmospheric neutrino background,
(40)On Earth, neutrino telescopes are used to observe this flux in the presence of the atmospheric neutrino background, 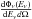 , which introduces more events depending on the size of the angular search bin of the detector,
, which introduces more events depending on the size of the angular search bin of the detector, 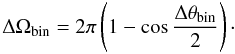 This depends on the resolution of the detector Δθbin, which is expected to be below 1° for KM3NeT. In the case of PKS 2155-304, we compare in Fig. 10 the predicted neutrino flux with the atmospheric background for Δθbin = { 0.5°,1° } .
This depends on the resolution of the detector Δθbin, which is expected to be below 1° for KM3NeT. In the case of PKS 2155-304, we compare in Fig. 10 the predicted neutrino flux with the atmospheric background for Δθbin = { 0.5°,1° } .
 |
Fig. 10 Predicted muon neutrino differential flux weighted by the squared neutrino energy as compared to the flux of atmospheric neutrinos for Δθbin = { 0.5°,1° } . |
The signal to be searched for in neutrino telescopes such as ANTARES or KM3NeT, can be calculated as 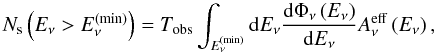 (41)where
(41)where 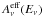 is the neutrino effective area of the detector and Tobs is the observation time. These signal events are to be detected among the background events caused by the flux of atmospheric neutrinos, which are given by
is the neutrino effective area of the detector and Tobs is the observation time. These signal events are to be detected among the background events caused by the flux of atmospheric neutrinos, which are given by 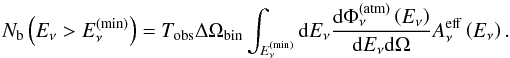 (42)Considering the neutrino effective area expected for this detector, we compute the predicted number of signal events of
(42)Considering the neutrino effective area expected for this detector, we compute the predicted number of signal events of 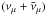 from PKS 2155-304 as a function of the observation time, and compare it with the background events corresponiding to Δθbin = 1° and 0.5°. The result is shown in Fig. 11 and corresponds to neutrinos above
from PKS 2155-304 as a function of the observation time, and compare it with the background events corresponiding to Δθbin = 1° and 0.5°. The result is shown in Fig. 11 and corresponds to neutrinos above 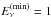 TeV, yielding many events in a few years.
TeV, yielding many events in a few years.
We can proceed to compute the cumulative probability that at least one of the total events corresponds to the signal, and not to the background, as a function of the observation time. This can be done by assuming that the ocurrence of the signal event and backgroungd events Ns and Nb follow Poisson distributions. As a result, the probability that out of a total of events Ntot = Ns + Nb we have at most Nb < Ntot can be expressed as 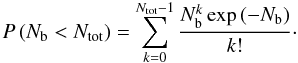 (43)We show this cumulative probability in Fig. 12 for both Δθbin = { 0.5°,1° } , where it can be seen that if PKS 2155-304 actually emits neutrinos at the level suggested here, a neutrino telescope like the planned KM3NeT would be able to ascribe at least one event to this blazar with a probability very close to one after an observation period of four years. We point out here that a resolution of 0.5° is actually conservative (e.g. Kappes et al. 2007; Bersani 2012).
(43)We show this cumulative probability in Fig. 12 for both Δθbin = { 0.5°,1° } , where it can be seen that if PKS 2155-304 actually emits neutrinos at the level suggested here, a neutrino telescope like the planned KM3NeT would be able to ascribe at least one event to this blazar with a probability very close to one after an observation period of four years. We point out here that a resolution of 0.5° is actually conservative (e.g. Kappes et al. 2007; Bersani 2012).
 |
Fig. 11 Muon neutrino events from PKS 2155-304 and atmospheric background for Δθbin = { 0.5°,1° } as a function of the observation time. |
 |
Fig. 12 Cumulative probability that at least one event corresponds to the neutrino signal from PKS 2155-304 as a function of the observation time. |
6. Discussion
We have implemented a two-component model to study the emission of the blazar PKS 2155-304. The quiescent state of electromagnetic emission was associated with the contribution produced in a heavy barionic jet, in which both electrons and protons can be accelerated. Specifically, this low state of emission is dominated by synchrotron and inverse Compton interactions of the primary electrons, and also by pp interactions in the jet. The time-dependent contribution is produced by multiple shocks in an internal electron-positron beam, surrounded by the jet. We showed that if shocks are injected in this beam, as would be expected as a consequence of Kelvin-Hemlholtz instabilities, then a variable emission can be generated via SSC interactions, giving rise to gamma-ray light curves similar to those observed by HESS.
Other important output predicted by the present model is in the form of VHE neutrinos produced by pp interactions. If this accompanying flux remains constantly produced over a period of four years, the detection of at least one event from PKS 2155-304 should be guaranteed in a detector like KM3NeT with a probability very close to one. This would be a very important piece of evidence for hadronic acceleration in the source. Conversly, if the neutrinos are not detected at this level, this would be evidence of a leptonic-dominated source.
Acknowledgments
The authors would like to thank Pierre Brun for fruitful discussions on EBL absorption. This work had the support from CONICET (PIP 112-200801-00587, and PIP 112-200901-00078).
References
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 664, L71 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, ApJ, 696, L150 [NASA ADS] [CrossRef] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2010, A&A, 522, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bersani, A. for the KM3NeT Consortium 2012, AIP Conf. Proc., 1441, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, R. L. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., & Kelner, S. R. 2010, IJMPD, 19, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Boutelier, T., Henri, G., & Petrucci, P.-O. 2008, MNRAS, 390, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Celotti, A., Capetti, A., & Ghisellini, G. 2000, A&A, 358, 104 [NASA ADS] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Dondi, L., & Ghisellini, G. 1995, MNRAS, 273, 583 [NASA ADS] [Google Scholar]
- Giroletti, M., Giovannini, G., Feretti, L., et al. 2004, ApJ, 600 127 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Celotti, A., & Costamante, L. 2002, A&A, 386, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005 A&A, 432fp, 401 [CrossRef] [EDP Sciences] [Google Scholar]
- Hardee, P. E. 2007, ApJ, 664, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kappes, A., Hinton, J., Stegmann, C., & Aharonian, F. A. 2007, ApJ, 656, 870, Erratum 2007, 661, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Konopelko, K., Mastichiadis, A., Kirk, J., De Jager, O. C., & Stecker, F. W. 2003, ApJ, 597, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Lipari, P., Lusignoli, M., & Meloni, D. 2007, Phys. Rev. D, 75, 123005 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J., & Savage, B. D. 1995, ApJS, 97, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. L. 2003, New Astron. Rev., 47, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Li, J., & Tchekhovskoy, A. 2009, ApJ, 697, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M. 2012, IJMP: Conf. Ser., 8, 241 [Google Scholar]
- Piner, B. G., & Edwards, P. G. 2004, ApJ, 600, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, M. M., Medina, M. C., & Romero, G. E. 2011, A&A, 531, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E. 1995, ApSS, 234, 49 [Google Scholar]
- Sadowski, A., & Sikora, M. 2010, A&A, 517, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlickeiser, R., & Lerche, I. 2007, A&A, 476, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shore, S. N. 2007, Astrophysical Hydrodynamics: An Introduction (Willey-VHC) [Google Scholar]
- Sol, H., Pelletier, G., & Asséo, E. 1989, MNRAS, 237, 441 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Basic elements of the model. See the text for details. |
| In the text | |
 |
Fig. 2 Acceleration and cooling rates for primary electrons and protons in the jet at zacc. |
| In the text | |
 |
Fig. 3 SED corresponding to the quiescent state of PKS 2155-304. The contributions shown are electron synchrotron (black solid line), IC (dashed line), pp (dashed-dotted line), proton synchrotron (gray solid line), and pγ (gray dashed line). |
| In the text | |
 |
Fig. 4 Magnetic field in the beam (red line) and critical magnetic field below which KH instabilities can develop. |
| In the text | |
 |
Fig. 5 Light curves of gamma-rays above 200 GeV produced by e + e − injection in the beam at zi = 2.3 × 1016 cm with Γs = { 14,16,18,20 } in the left panel, and with Γs = 20 and b = { 50,70,100 } in the right panel. |
| In the text | |
 |
Fig. 6 Light curves of gamma-rays above 200 GeV produced by e + e − injection in the beam at zi = 2.3 × 1016 cm with the randomly chosen values for Γs, b, and ton of Table 3. |
| In the text | |
 |
Fig. 7 Lightcurve of gamma-rays above 200 GeV (blue line), generated as the superposition of six injections in the beam (lc1, lc2, lc3, lc4, lc5, lc6, in gray-dashed lines), as compared to data of the 2006 flare of PKS 2155-304. |
| In the text | |
 |
Fig. 8 Instantaneus SEDs originating in the beam at t1 ≃ 40 min, and t2 ≃ 50 min corresponding to the plot of Fig. 7. The quiescent SED is also shown (gray dashed lines). |
| In the text | |
 |
Fig. 9 Acceleration and cooling rates in the post-shock frame corresponding to t1 ≃ 40 min in the lightcurve of Fig. 7. |
| In the text | |
 |
Fig. 10 Predicted muon neutrino differential flux weighted by the squared neutrino energy as compared to the flux of atmospheric neutrinos for Δθbin = { 0.5°,1° } . |
| In the text | |
 |
Fig. 11 Muon neutrino events from PKS 2155-304 and atmospheric background for Δθbin = { 0.5°,1° } as a function of the observation time. |
| In the text | |
 |
Fig. 12 Cumulative probability that at least one event corresponds to the neutrino signal from PKS 2155-304 as a function of the observation time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


