| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201219821 | |
| Published online | 17 September 2012 | |
Testing the concept of integral approach to derivatives within the smoothed particle hydrodynamics technique in astrophysical scenarios
1
Departement PhysikUniversität Basel,
Klingelbergstrasse 82,
4056
Basel,
Switzerland
e-mail: ruben.cabezon@unibas.ch
2
Dept. de Física i Enginyeria Nuclear, Universitat Politècnica de
Catalunya. Compte d’Urgell 187, 08036
Barcelona,
Spain
3
Institut d’Estudis Espacials de Catalunya,
Gran Capità 2-4,
08034
Barcelona,
Spain
Received:
15
June
2012
Accepted:
20
July
2012
Context. The smoothed particle hydrodynamics (SPH) technique is a well-known numerical method that has been applied to simulating the evolution of a wide variety of systems. Modern astrophysical applications of the method rely on the Lagrangian formulation of fluid Euler equations, which is fully conservative. A different scheme, based on a matrix approach to the SPH equations is currently being used in computational fluid dynamics. An original matrix formulation of SPH based on an integral approach to the derivatives, called IAD0, has been recently proposed and is fully conservative and well-suited to simulating astrophysical processes.
Aims. The behavior of the IAD0 scheme is analyzed in connection with several astrophysical scenarios, and compared to the same simulations carried out with the standard SPH technique.
Methods. The proposed hydrodynamic scheme is validated using a variety of numerical tests that cover important topics in astrophysics, such as the evolution of supernova remnants, the stability of self-gravitating bodies, and the coalescence of compact objects.
Results. The analysis of the hydrodynamical simulations of the above-mentioned astrophysical scenarios suggests that the SPH scheme built with the integral approach to the derivatives improves the results of the standard SPH technique. In particular, there is a better development of hydrodynamic instabilities, a good description of self-gravitating structures in equilibrium and a reasonable description of the process of coalescence of two white dwarfs. We also observed good conservations of energy and both linear and angular momenta that were generally better than those of standard SPH. In addition the new scheme is less susceptible to pairing instability.
Conclusions. We present a formalism based on a tensor approach to Euler SPH equations that we checked using a variety of three-dimensional tests of astrophysical interest. This new scheme is more accurate because of the re-normalization imposed on the interpolations, which is fully conservative and less prone to undergoing the pairing instability. The analysis of these test cases suggests that the method may improve the simulation of many astrophysical problems with only a moderate computational overload.
Key words: hydrodynamics / instabilities / methods: numerical
© ESO, 2012
1. Introduction
Multidimensional numerical hydrodynamics is one of the most powerful tools of modern astrophysics to comprehend the cosmos machinery. Among them, the smoothed particle hydrodynamics (SPH) is one of the most widely used techniques because of its ability to describe the evolution of fluids with complicated geometries and a diversity of length scales. Since it was formulated, more than thirty years ago, by Gingold & Monaghan (1977) and Lucy (1977), it has largely evolved incorporating, little by little, a plethora of methods that makes it competitive compared to grid-based methods of Eulerian type. Details of the modern mathematical formulation, as well as of the main features of the state-of-art of the SPH technique, can be found in the reviews by Monaghan (2005), Rosswog (2009), Springel (2010), and Price (2012).
García-Senz et al. (2012a, henceforth Paper I) recently suggested that the use of matrix methods, Dilts (1999), in astrophysics could improve the simulations with the SPH technique with an affordable computational cost. In this work, we focus on specific three-dimensional (3D) astrophysical applications of the scheme formulated in Paper I. In particular, we choose examples from different fields of astronomy to check the method and highlight its potential advantages over the standard SPH scheme. The suitability of IAD0 for describing hydrodynamic instabilities found in Paper I is confirmed by simulating the evolution of a supernova remnant (SNR). As the SNR evolves embedded in an uniform background of particles with negligible gravity, there are no numerical troubles affecting the outer limits of the system. The existence of boundaries becomes relevant to the second test, which is devoted to describing the equilibrium features of polytropes with different indexes and masses. For this problem, the interplay between pressure forces and gravity becomes crucial to ensure that the obtained structures are compatible with the analytical models. We show that the tensor method leads to polytropes where the central density and radius are slightly closer to the theoretical predictions than those obtained with the standard SPH technique. We also explore the ability of IAD0 to describe a very dynamical situation by simulating the coalescence of two white dwarfs. In this case, a catastrophic merging of the stars ensues after a few orbital periods. For this test, the tensor method gives results of, at least, comparable quality to those obtained using the standard SPH scheme, but displaying a more homogeneous mixing of the material of both stars. There are also some differences in the angular velocity distribution of the remnant. For a similar elapsed time, the matrix calculation does not lead to the complete rigid rotation of the core, which is, however, achieved in the simulation using the standard scheme.
The text is organized as follows. In Sect. 2, we review the mathematical formalism linked to IAD0 and discuss its most relevant features. In Sect. 3, we describe the three astrophysical tests aimed at validating the code and comparing its performance to that of standard SPH. Section 4 is devoted to incorporating thermal conductive transport in the tensor scheme, and to check the resulting algorithm. The benchmarking of the code is done in Sect. 5. Finally, the main conclusions of our work, as well as some comments about the shortcomings of the developed scheme and future lines of improvement, are outlined in the last section, which is devoted to our conclusions.
2. Main features of the IAD0 scheme
In Paper I, it was shown that a conservative SPH scheme can be deduced from an integral
approach to the derivatives. As starting point, we define the integral, ![\begin{equation} I(\vec{r})= \int_{V} \left[f(\vec{r}')-f(\vec{r})\right] (\vec{r}'-\vec{r}) W(\vert \vec{r}'-\vec{r}\vert, h) {\rm d}r'{^3} , \label{int} \end{equation}](/articles/aa/full_html/2012/09/aa19821-12/aa19821-12-eq3.png) (1)
(1)
where
W(| r′ − r|,h)
is a spherically symmetric interpolating function and h is called the
smoothing length. The integral I(r) can be
used to find the gradient of a function f(r)
in a way similar to that used to evaluate the Laplace operator based on another integral
expression in standard SPH, see Brookshaw (1985) and
Monaghan (2005). The IAD0 interpretation
of SPH is the consequence of approaching Eq. (1) with summations along with two reasonable simplifications 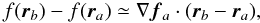 (2)where
a and b refer to neighboring particles with masses
ma and
mb, respectively, and
(2)where
a and b refer to neighboring particles with masses
ma and
mb, respectively, and 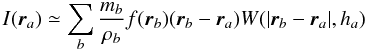 (3)is the
corresponding discrete expression for Eq. (1). Note that, because the kernel is spherically symmetric, the factor
f(ra) does not
appear in the expression above.
(3)is the
corresponding discrete expression for Eq. (1). Note that, because the kernel is spherically symmetric, the factor
f(ra) does not
appear in the expression above.
The direct application of Eqs. (1)–(3) to calculating the gradient of density, leads
to a matrix equation ![\begin{equation} \left[ \begin{array}{c} \partial \rho/\partial x_1\\ \partial \rho/\partial x_2\\ \partial \rho/\partial x_3\\ \end{array} \right]_a = \left[ \begin{array}{ccc} \tau_{11} & \tau_{12} & \tau_{13} \\ \tau_{21}&\tau_{22}&\tau_{23} \\ \tau_{31}&\tau_{32}&\tau_{33} \end{array} \right]^{-1} \left[ \begin{array}{c} I_1\\ I_2\\ I_3\\ \end{array} \right]\,, \label{matrix} \end{equation}](/articles/aa/full_html/2012/09/aa19821-12/aa19821-12-eq15.png) (4)where
(4)where 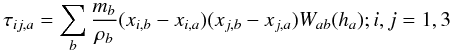 (5)and
(5)and
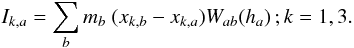 (6)It was shown in Paper I
that Eq. (4) leads to a formulation of the
SPH Euler equations that is compatible with the variational principle. These equations are
given by
(6)It was shown in Paper I
that Eq. (4) leads to a formulation of the
SPH Euler equations that is compatible with the variational principle. These equations are
given by 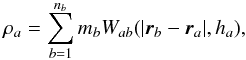 (7)
(7)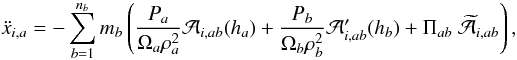 (8)
(8)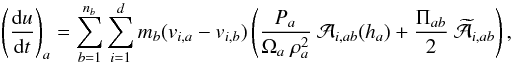 (9)where
(9)where
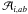 and
and 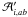 are
are
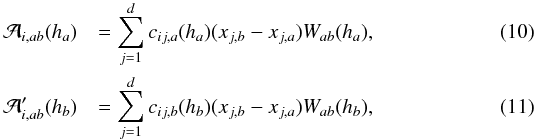 being
cij the coefficients of the inverse matrix
defined in Eq. (4) and d the
dimension of the space. The magnitude
Ωa = (1 − ∂ρ/∂h ∑ ama ∂Wab/∂h)
accounts for the gradient of the smoothing length. As usual, Πab
gives the viscous pressure due to the artificial viscosity (AV)
being
cij the coefficients of the inverse matrix
defined in Eq. (4) and d the
dimension of the space. The magnitude
Ωa = (1 − ∂ρ/∂h ∑ ama ∂Wab/∂h)
accounts for the gradient of the smoothing length. As usual, Πab
gives the viscous pressure due to the artificial viscosity (AV) 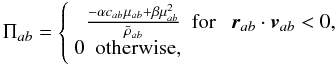 (12)and
the remaining symbols have their usual meaning. The coefficient
μab is
(12)and
the remaining symbols have their usual meaning. The coefficient
μab is
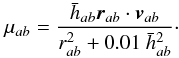 (13)To compute the viscous
acceleration, the arithmetic mean of
(13)To compute the viscous
acceleration, the arithmetic mean of 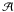 is taken to be
is taken to be ![\begin{equation} \widetilde{\mathcal A}_{i,ab}=\frac{1}{2}\left[{\mathcal A}_{i,ab}(h_a)+{\mathcal A'}_{i,ab}(h_b)\right] . \label{atilde} \end{equation}](/articles/aa/full_html/2012/09/aa19821-12/aa19821-12-eq32.png) (14)Therefore Eqs. (7)–(9) summarize the basis of the IAD0 formalism.
(14)Therefore Eqs. (7)–(9) summarize the basis of the IAD0 formalism.
It is worth noting the strong similitudes between the above equations and those of standard
SPH. The main difference is that vector expressions have been changed to tensor
relationships that encode the renormalization of the many summations that appear in the
SPH technique. Any expression of standard SPH can indeed be made compatible with
IAD0 by taking the kernel derivative as 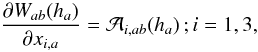 (15)where the
coefficients
(15)where the
coefficients 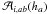 are defined by Eq. (10). If the matrix
coefficients in Eq. (4) are calculated
analytically, the matrix
are defined by Eq. (10). If the matrix
coefficients in Eq. (4) are calculated
analytically, the matrix 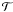 becomes diagonal. In this case, it can be shown that for Gaussian kernels the standard and
IAD descriptions are totally equivalent. Hereafter, the scheme obtained from the diagonal
form of
becomes diagonal. In this case, it can be shown that for Gaussian kernels the standard and
IAD descriptions are totally equivalent. Hereafter, the scheme obtained from the diagonal
form of 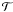 is referred to as vector-IAD0.
is referred to as vector-IAD0.
2.1. Harmonic kernels
All the simulations presented in this work were carried out using the so-called harmonic
kernels devised by Cabezón et al. (2008), to perform
the SPH interpolations. Being relatively unknown kernels with very interesting features,
their use warrants some explanation. They are defined as 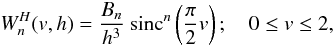 (16)where
(16)where
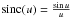 ,
n is the index of the kernel, and
Bn is the normalization constant. By
defining sinc(0) = 1, the function sinc is extended to an analytical function with compact
support on the real axis. Because of its connection with spectral analysis, the function
sinc(u) is of special relevance to signal analysis, from where it
borrows its name. The profile of the kernel for several values of the leading index
n is shown in Fig. 1, where it can
be seen that the profile of
,
n is the index of the kernel, and
Bn is the normalization constant. By
defining sinc(0) = 1, the function sinc is extended to an analytical function with compact
support on the real axis. Because of its connection with spectral analysis, the function
sinc(u) is of special relevance to signal analysis, from where it
borrows its name. The profile of the kernel for several values of the leading index
n is shown in Fig. 1, where it can
be seen that the profile of 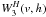 closely matches that of the
cubic spline. The behavior of
closely matches that of the
cubic spline. The behavior of 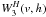 is therefore very similar to
that of the cubic spline, with the advantage that its second derivative is continuous and
can be differentiated many times. Switching the index to n = 2 gives the
is therefore very similar to
that of the cubic spline, with the advantage that its second derivative is continuous and
can be differentiated many times. Switching the index to n = 2 gives the
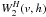 kernel, with a profile close
to that of the truncated Gaussian kernel, as shown in Fig. 1. The implementation of the
kernel, with a profile close
to that of the truncated Gaussian kernel, as shown in Fig. 1. The implementation of the 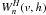 family of kernels adds more
flexibility to SPH, as one can, for example, take a different index n to
handle the artificial viscosity terms in either the momentum and energy equations or the
heat conduction equation, without changing the number of neighbors of the particle. They
are also useful for avoiding the pairing instability (see Sect. 2.2) because whenever two particles approach each other too closely, the
index of the kernel can be increased to block the development of the instability.
family of kernels adds more
flexibility to SPH, as one can, for example, take a different index n to
handle the artificial viscosity terms in either the momentum and energy equations or the
heat conduction equation, without changing the number of neighbors of the particle. They
are also useful for avoiding the pairing instability (see Sect. 2.2) because whenever two particles approach each other too closely, the
index of the kernel can be increased to block the development of the instability.
 |
Fig. 1 Profile of several kernels in one dimension. The Gaussian kernel is truncated at r = 2h. The Wn(H) belongs to the harmonic family of kernels described by Eq. (16) for n = 2, 3, and 6, respectively. |
The normalization constants Bn for a large
number of values of n were calculated in Cabezón et al. (2008), where a fitting analytical formula for
Bn was also provided. To increase the
computational speed, it is recommended that the value of
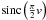 and its derivative be stored in a table as a function of
v, (0 ≤ v ≤ 2), and that a linear Taylor expansion be
used to calculate the value of sinc. This allows a fast computation of Eq. (16) and its derivative once the index
n has been chosen.
and its derivative be stored in a table as a function of
v, (0 ≤ v ≤ 2), and that a linear Taylor expansion be
used to calculate the value of sinc. This allows a fast computation of Eq. (16) and its derivative once the index
n has been chosen.
2.2. Pairing instability
The simulations oriented to benchmark the different SPH schemes reported here as well as
in Paper I, suggest that there is an additional advantage of the matrix method. In
general, calculations carried out using IAD0 are less affected by the pairing
instability. For a given interpolating kernel with spherical symmetry, there is a fiducial
distance to the center r0 at which the first derivative of the
kernel reaches its maximum absolute value. Within this critical radius, a pair of
neighboring particles feels an increasingly weaker repulsive force, which can lead to the
artificial clumping of the particles (but see Dehnen
& Hossam 2012 for a different explanation of the origin of this
instability). The exact location of r0 depends on the number
of neighbors and the peculiarities of the kernel. For either the cubic-spline kernel or
the harmonic kernel with index n = 3, its location is
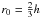 , while
for more centrally condensed kernels it is at yet smaller radii.
, while
for more centrally condensed kernels it is at yet smaller radii.
 |
Fig. 2 Profile of the gradient of the kernel calculated analytically in the standard SPH way (referred as analytical in the figures) as well as numerically, through Eq. (15) for two particle settings: bcc and pseudo-random, kernel indexes n = 3, 5, and different number of neighbors. |
The robustness of matrix methods to cope with pairing instability can be understood by confronting the analytical estimation of the gradient of the kernel within the standard framework, to the numerical value obtained using Eq. (15). The numerical derivative of Wab for the particle a located at the center of a 2D lattice was evaluated using two different particle settings and harmonic kernel indexes. Figure 2 shows the value of ∇aWab at different distances from the kernel origin. The left column stands for a bcc-type particle setting in a two-dimensional square lattice, while the column on the right represents a quasi-uniform distribution of particles, obtained by randomly perturbing the bcc distribution with a maximum perturbation amplitude of 0.3Δ, where Δ is the lattice spacing. The harmonic kernel index was set to n = 3 (thus, reproducing the cubic-spline kernel) and to n = 5 to see the effect of making the profile sharper. It can be seen that increasing n (keeping h constant) always raises the maximum of the kernel derivative, as expected for a more centrally condensed kernel, shifting the abscissa where the maximum is achieved closer to zero. For n = 3 and n = 5, the maximum is taken at r/h = 2/3 and r/h = 0.504, respectively. The effect of changing the numerical scheme also has an impact on the kernel derivative. According to Fig. 2, the maximum of the gradient of the kernel always appears closer to the origin than in the standard scheme, regardless of the number of neighbors. Moreover, the absolute value of the maximum is larger for IAD0. Together, this means that the tensor scheme is less affected by pairing instability than the standard SPH scheme.
2.3. Free surface conditions
Handling boundaries is often a difficult point of the SPH technique. In static gaseous configurations, such as stars or planets, the radius of the object is the result of the careful balance between gravity and pressure forces. The gradient in the pressure is, however, not as accurately estimated by SPH near the surface as in the star’s interior. Therefore, the radius of the configuration is a magnitude not as well-defined as others once the mechanical equilibrium is achieved.
 |
Fig. 3 Profile of coefficients τii/h2 and τij/h2,(j ≠ i) in a polytrope of index n = 5/2 fitted with 20 000 particles (model F1 of Table 2). The distance to the center is normalized to the radius of the polytrope, Rs. The analytical value of τii/h2 is also given (horizontal dashed line corresponding to β = 1). Basically, all the star interior has a value β ≥ 0.95, while beyond a radius Rs − 2hs (where hs is the smoothing length close to the surface) the value of β rapidly declines (see Sect. 2.3 for the definition of β). |
Unfortunately, the direct application of IAD0 to free surface boundaries does
not solve the problem. The reason is that the magnitudes
τij given by Eq. (5), which serve to normalize the derivatives,
are very sensitive to the presence of boundaries. Close to the edge of the system, the
gradient of pressure is overestimated and the equilibrium of the body is reached at a
larger radius than in the standard (STD) scheme. The impact of the free boundaries on the
τij coefficients is well-illustrated in
Fig. 3, which depicts the profile of these
magnitudes along the polytropic structure discussed in Sect. 3.2. The numerical estimation of
τij can be compared to their analytical
value calculated using 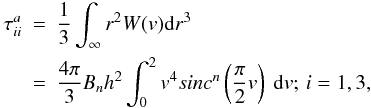 (17)
(17)
which for n = 3 gives 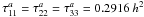 . We see that,
with the exception of the surface layers, the analytical and the numerical values agree
with an accuracy better than a 5%. These coefficients are, however, very sensitive to
boundaries and rapidly decay when the first particles belonging to the surface enter the
summations. This led some authors (e.g. Oger et al.
2007) to propose a practical algorithm for choosing the adequate value of
τii as
. We see that,
with the exception of the surface layers, the analytical and the numerical values agree
with an accuracy better than a 5%. These coefficients are, however, very sensitive to
boundaries and rapidly decay when the first particles belonging to the surface enter the
summations. This led some authors (e.g. Oger et al.
2007) to propose a practical algorithm for choosing the adequate value of
τii as 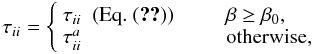 (18)where
(18)where
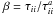 and
β0 ≃ 0.95. In Sect. 3.2, we discuss the impact of the different approaches to
τii in describing the structure of
polytropes with different indexes. We chose several values
for β0 ranging from β0 = 0
(fully tensor IAD0) to β0 = ∞
(vector-IAD0). The values
β0 = 0.90 and β0 = 0.97 suggested
by Oger et al. (2007) were also checked. Our main
conclusion is that the β0 = 0 fully tensor IAD0
scheme provides the best description of the structure of these polytropes, although the
numerical noise is larger than for the STD scheme. Interestingly, the vector-like approach
with β0 = ∞ give results as good as the STD scheme with the
same computational cost. Nevertheless, an additional advantage of the full tensor scheme
is that it improves the description of the growth of hydrodynamic instabilities, as
suggested in the tests described in Sect. 3 and
Paper I. On another note, we have not seen any particular advantage of using a hybrid
scheme with β0 ≃ 0.95 to handle self-gravitating bodies, which
has the negative side of increasing the numerical noise. Furthermore, a value of
β < 1 is not necessarily linked to a free
boundary because it may appear, for example, in the presence of mildly or strong shock
waves. For these reasons, we conclude that the renormalized IAD0 scheme
summarized by Eqs. (5) to (11) should be preferentially used to carry out
simulations of astrophysical systems.
and
β0 ≃ 0.95. In Sect. 3.2, we discuss the impact of the different approaches to
τii in describing the structure of
polytropes with different indexes. We chose several values
for β0 ranging from β0 = 0
(fully tensor IAD0) to β0 = ∞
(vector-IAD0). The values
β0 = 0.90 and β0 = 0.97 suggested
by Oger et al. (2007) were also checked. Our main
conclusion is that the β0 = 0 fully tensor IAD0
scheme provides the best description of the structure of these polytropes, although the
numerical noise is larger than for the STD scheme. Interestingly, the vector-like approach
with β0 = ∞ give results as good as the STD scheme with the
same computational cost. Nevertheless, an additional advantage of the full tensor scheme
is that it improves the description of the growth of hydrodynamic instabilities, as
suggested in the tests described in Sect. 3 and
Paper I. On another note, we have not seen any particular advantage of using a hybrid
scheme with β0 ≃ 0.95 to handle self-gravitating bodies, which
has the negative side of increasing the numerical noise. Furthermore, a value of
β < 1 is not necessarily linked to a free
boundary because it may appear, for example, in the presence of mildly or strong shock
waves. For these reasons, we conclude that the renormalized IAD0 scheme
summarized by Eqs. (5) to (11) should be preferentially used to carry out
simulations of astrophysical systems.
3. Astrophysical tests
A basic check of the new scheme was described in Paper I. For the most part, the technique was tested in two dimensions with particles located in ordered lattices and, sometimes, using particles with different masses. For these specific tests, the IAD0 scheme showed a good behavior because it was able to handle the Rayleigh-Taylor and Kelvin-Helmholtz instabilities better than standard SPH. Simulation of supersonic events (Sedov blast wave and wall-heating shock) were of similar quality, if not slightly better, than those computed using STD smoothed particle hydrodynamics. The total energy was always more well-conserved when the tensor method was used.
The only 3D calculation in Paper I was that used to simulate the evolution towards stability of a Sun-like polytrope. In that simulation, gravity was calculated using a multipolar expansion of the force (Hernquist & Katz 1989). The main conclusion of the test was that, although good equilibrium configurations were achieved in both methods, in the tensor method more energy is stored as numerical noise for the same elapsed time.
To check the code in realistic astrophysical scenarios, we chose three simulations related to different hydrodynamic processes. These include the growth of the RT instability in supernova remnants, the stability of polytropes of different masses and polytropic indexes, and the study of the coalescence process of a pair of compact stars. The calculations were carried out by choosing n = 3 in the harmonic kernels given in Eq. (16). Unless explicitly stated, the number of neighbors was kept constant to nb = 100 in all simulations. Precise details of the initial particle setting and physics included are presented in each subsection of the corresponding test.
3.1. Hydrodynamics of a supernova remnant
The evolution of supernova remnants has to be studied in more than one dimension to capture the fine details of their structure. Several things may contribute to cause the evolution to deviate from the spherical symmetry: the lack of symmetry of the exploding object that gives rise to the SNR, the inhomogeneities in the ambient medium (AM), or the interaction of the remnant with cosmic rays (Wang 2011). One of the physical phenomenae that was among the first to be studied as a source of spatial irregularities in SNRs was the Rayleigh-Taylor (RT) instability. In SNR, the RT instability may often develop in the region between the forward and reverse shocks, induced by the deceleration of the supernova shell. Pioneering 3D simulations of the impact of the RT instability on the evolution of the remnant were conducted by Chevalier et al. (1992), by taking a small slice of the full domain to enhance the resolution. More recently, 3D simulations encompassing the whole SNR were developed by Vigh et al. (2011). To reproduce the growth and structure of the instability, a large amount of computational cells are needed. Two-dimensional simulations carried out by Dwarkadas (2000) suggest that a minimum of 300 × 300 mesh zones (in 2D) have to be used to describe the growth of the RT fingers. Therefore, the ability to simulate the growth of the RT instability in SNR is a good test for 3D hydrocodes.
All multi-dimensional simulations performed so far have been carried out using grid-based codes, generally of Eulerian type. In spite of its wide use in astrophysics, SPH has scarcely been applied to the study of SNR. One exception was the study of García-Senz et al. (2012b), who used an axisymmetric SPH code to study the imprint of the secondary star on the geometry of the remnant resulting from a Type Ia supernova explosion. It is worth noting that SPH is able to describe the growth of the RT instabilities in 3D, using a smaller number of particles than those suggested in Dwarkadas (2000) (N ≃ 1.5 × 106 particles instead of 2−3 × 107 grid cells) because there is no waste of computational resources in the lowest density regions of the simulated domain.
To perform the SNR simulation, we built an exponential profile for the ejecta following the prescriptions given in Dwarkadas (2000). The profile was mapped to a 3D set of equal-mass particles and allowed to interact with an homogeneous ambient medium. A perfect-gas equation of state (EOS), where γ = 5/3 was assumed.
The density of the ejecta was 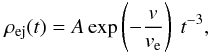 (19)
(19)
where the constants A and ve are
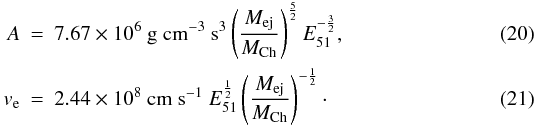 We
took Mej = MCh and
E51 = 1 in the expressions above. The time
t in Eq. (19) was set
to t0 = 2 × 109 s, and the velocity profile
at t0 was assumed to be homologous, with
v(r) = r/t0.
With these choices, the initial size of the ejecta was ≃ 1 pc and the density at the
outer edge matched that of the AM medium (assumed here to be homogeneous and have a value
ρAM = 2 × 10-24 g cm-3). The 1D
density profile of the ejecta was mapped onto a 3D sample of particles spread across a
sphere of radius 1 pc, according to the radial density profile given by Eq. (19), and where the angular location of the
particles was chosen at random. This random setting led to a blurred density profile,
which was finally driven to the spherical symmetry by means of a tangential relaxation of
the model using SPH. To do this, we allowed the particles to move under the action of
pressure forces, although their movement was constrained to ensure that the distance to
the center remained constant. The homogeneous AM was simply reproduced by sampling the
particles in a cubic-centered, bcc grid with a size of 10 pc. Using
Nej = 257 776 particles and
NAM = 1 206 576 particles, the mass ratio of particles
belonging to the AM to those in the ejecta is
mej/mAM ≃ 2.3.
To check that such a mass contrast has a negligible impact on the results, we recalculated
model B1 of Table 1 using a number of
particles for the ambient medium
We
took Mej = MCh and
E51 = 1 in the expressions above. The time
t in Eq. (19) was set
to t0 = 2 × 109 s, and the velocity profile
at t0 was assumed to be homologous, with
v(r) = r/t0.
With these choices, the initial size of the ejecta was ≃ 1 pc and the density at the
outer edge matched that of the AM medium (assumed here to be homogeneous and have a value
ρAM = 2 × 10-24 g cm-3). The 1D
density profile of the ejecta was mapped onto a 3D sample of particles spread across a
sphere of radius 1 pc, according to the radial density profile given by Eq. (19), and where the angular location of the
particles was chosen at random. This random setting led to a blurred density profile,
which was finally driven to the spherical symmetry by means of a tangential relaxation of
the model using SPH. To do this, we allowed the particles to move under the action of
pressure forces, although their movement was constrained to ensure that the distance to
the center remained constant. The homogeneous AM was simply reproduced by sampling the
particles in a cubic-centered, bcc grid with a size of 10 pc. Using
Nej = 257 776 particles and
NAM = 1 206 576 particles, the mass ratio of particles
belonging to the AM to those in the ejecta is
mej/mAM ≃ 2.3.
To check that such a mass contrast has a negligible impact on the results, we recalculated
model B1 of Table 1 using a number of
particles for the ambient medium 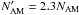 . There were no
significant changes in the evolution of the model.
. There were no
significant changes in the evolution of the model.
The evolution of the SNR was simulated for different initial conditions using both the STD and the IAD0 codes, with the goal of analyzing their performance.
A single mode perturbation in the initial radial-velocity field was seeded at
t = 0 yr according to the expression 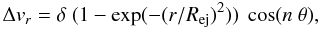 (22)
(22)
where Rej = 1 pc, θ is the azimuthal angle, θ = cos-1(z/r), and the parameter δ is close to the maximum perturbation velocity we wish to impose. The wavenumber was set to n = 12 in all models.
The inspection of the results summarized in Table 1 reveals that energy is always better conserved, by a factor ≃ 2, when the tensor method is used. Linear and angular momentum conservations are at least as good as in the standard formulation, independently of either the absence (models A1 and A2) or the presence (models B1 and B2) of the velocity perturbation. Figure 4 presents a color map of density in the YZ plane at t = 698 yr for models B1 and B2 of Table 1, calculated by assuming δ = 500 km s-1 in Eq. (22). The combined effect of the radial velocity perturbation and the anisotropies of the bcc lattice leads to the growth of the RT instability. At t = 698 yr, the development of the instability is already appreciably larger in the tensor calculation than in the STD scheme. The differences between both calculations become more pronounced at t = 951 yr, when the forward shock reaches the limits of the system. These results agree with the main conclusions of Paper I, in terms of the development of the RT instability in 2D stratified fluids inside a homogeneous gravitational field.
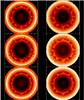 |
Fig. 4 Density color map depicting the growth of the RT instability in a SNR for models B1 (upper panels), B2 (middle panels), and B3 (lower panels) of Table 1 at times t = 698 yr (left columns) and t = 951 yr (right columns). The size of the box in all panels is 10 pc in each direction. |
Model B3 in Table 1 and the lower panels of Fig. 4 refer to vector-IAD0. As we can see, the evolution of the RT instability is similar to that of the STD scheme but total energy is better conserved and the density map seems to be slightly cleaner. Therefore, we conclude that the renormalization of the derivatives, which characterizes the fully tensor IAD0 method, makes it more suitable for describing the evolution of hydrodynamic instabilities. The importance of renormalization is highlighted in Fig. 5, which depicts the profile of the elements τii and τij calculated with Eq. (5). As we can see, there is a large deviation of τii from its analytical estimation through Eq. (17). Similarly, the off-diagonal matrix elements are not equal to zero. The re-normalization of the derivative then helps the growth of the instability, confirming the main conclusions given in Paper I.
Comparison between several magnitudes at t = 698 yr of evolution of the SNR computed using IAD0 and STD schemes.
 |
Fig. 5 Profile of the coefficients τii/h2 and τij/h2,(j ≠ i) for model B1 of Table 1. The analytical value of τii/h2 is also given (horizontal dashed line). |
As a final test, we built an developed model for the supernova ejecta using the stretched-grid method (Herant 1992; García-Senz et al. 1998). These models are labeled C1 and C2 in Table 1. This kind of initial models displays almost perfect spherically symmetric density profiles, but the price to pay is a large deformation of the particle lattice. Although no perturbation was seeded, the larger anisotropies of the grid soon lead to the growth of the RT instability in the region between the forward and reverse shocks. The results of the simulations are shown in Fig. 6. The upper panels depict the density profile after t = 698 yr of evolution, whereas the bottom ones show the radial velocity profile at the same elapsed time. We see that outside the region where the RT instability develops the profiles calculated using IAD0 show less dispersion than those computed with the STD scheme. In the RT unstable layer located between the forward and reverse shocks, the dispersion is larger, as expected. In addition, there is a factor of two enhancement in the energy conservation when the tensor method is used (last two rows in Table 1).
Main features of polytropes with polytropic indexes n = 3/2 and n = 5/2, respectively.
 |
Fig. 6 Density and velocity profiles of the SNR at elapsed time t = 698 yr for the stretched-grid models of the supernova ejecta (models C1 and C2 in Table 1). Outside the RT-unstable region, the spherical symmetry is better preserved when the tensor method is used. |
3.2. Polytropes of index n = 3/2 and n = 5/2 in equilibrium
Gaseous self-gravitating structures can usually be roughly approached using a polytrope with the appropriate index. Because of their simplicity and known theoretical properties, polytropes are often used to benchmark multidimensional hydrocodes (Steinmetz & Müller 1993; Price & Monaghan 2007). We explored the abilities of the tensor scheme in reproducing the equilibrium structure of polytropes of index n = 3/2 and n = 5/2, and confronted the results with the predictions of standard SPH models. A mass of M = 0.6 M⊙ and a radius of R = 8 × 108 cm were assigned to the n = 3/2 polytrope, so that it could represent a stable white dwarf with central density ρc = 3.3 × 106 g cm-3. For the n = 5/2 polytrope, we assigned it a mass of M = 1.35 M⊙ and a radius of 2 × 108 cm, which are both representative of a massive white dwarf with central density ρc = 1.9 × 109 g cm-3. Note that in this last case the mass is close to the Chandrasekhar-mass limit for a polytrope with n = 3. This second structure is then much more unstable than the 0.6 M⊙ star. The initial models were built by randomly spreading 2 × 104 particles in 3D, according to the mass density profile of the polytrope. In a second step, the models were relaxed in the non-radial direction to enhance their spherical symmetry. Afterwards, the particles were allowed to evolve freely in the 3D domain. The EOS was that of a perfect gas P = ρ(γ − 1)u, with γ = 5/3, 7/5 for n = 3/2, 5/2 polytropes, respectively. The main features of both polytropes are summarized in Table 2.
 |
Fig. 7 Evolution of central density and surface radius (normalized to the theoretical values) for polytropes with indexes n = 3/2 (upper panels, corresponding to models E1 and E2 in Table 2) and n = 5/2 (lower panels, corresponding to models F1 and F2 in Table 2). Continuum and dashed lines are for the tensor-IAD0 and standard schemes, respectively. |
Figure 7 represents the evolution of the central density and stellar radius for models E and F of Table 2. To smooth fluctuations, the central density and the radius were averaged over the closest particles to the center and the surface, respectively. The central density of the less massive structure converges to the analytical value after ten oscillatory cycles. The radius of the polytrope follows a similar evolution, although the value obtained with STD is ≃ 90% of the theoretical estimation owing to the small number of particles used in the simulation. We see that despite the lower convergence rate of the tensor calculation the final value of ρc and R are closer to the correct value than for the STD calculation. The relative error in the central density is ϵr(ρc) < 2% for the IAD0 calculation and a little higher, ϵr(ρc) ≃ 5% for STD. For the more massive polytrope, the differences between the SPH schemes become more accentuated, as shown in the bottom panels of Fig. 7. The fluctuation in the central density is much larger than in the previous case and the convergence towards the analytical value is less rapid. Nevertheless, the tensor calculation provides a more accurate estimation of the central density of the equilibrium configuration. According to Fig. 7, the relative errors in the central density at the last calculated models are ϵr(ρc) ≃ 33% and ϵr(ρc) ≃ 42% for the tensor and standard methods, respectively. It is worth noting that a lower particle clumping was observed when the matrix scheme was used, which may be the origin of the small differences in the value of the central density calculated with both methods.
Figure 8 shows the evolution of both polytropes calculated with vector-IAD0. The central density is much more closely reproduced than for the STD scheme but the radius of the configurations differs considerably from the actual value. Therefore, we conclude that the best combination of central density and surface radius is achieved by the full tensor IAD0 scheme.
 |
Fig. 8 Evolution of central density and surface radius (normalized to the theoretical values) for polytropes with indexes n = 3/2 (upper panels, corresponding to models E2 and E3 in Table 2) and n = 5/2 (lower panels, corresponding to models F2 and F3). Continuous and dashed lines are for vector-IAD0 and standard schemes, respectively. |
The leftmost panels of Fig. 9 depict the evolution of the ratio of the kinetic to internal energies, Ek/Eint, of both polytropes. The evolution of the kinetic energy is that of a damped system when standard SPH is used, while the IAD0 calculation is less dissipative. Therefore, the amount of kinetic energy stored in the configuration after several evolution cycles remains larger for the matrix calculation. All this points to the renormalization of the derivatives as the main agent behind the increase in numerical noise. To clarify this point, we ran two simulations, models E3 and F3 in Table 2, using the vector approach to IAD0. The evolution of the kinetic energy is shown in the rightmost panels of Fig. 9. As we can see, the damping of the systems is even faster that in the STD scheme and the final kinetic energy is lower.
 |
Fig. 9 Evolution of the ratio of kinetic to internal energies. Left column is for polytropes with indexes n = 3/2 (upper panel) and n = 5/2 (lower panel) calculated using tensor-IAD0 (continuum line) and STD (dashed line). Same for pictures on the right column, where, however, vector-IAD0 was used. |
The level of energy conservation at the last calculated model is correlated with the amount of kinetic energy. According to the last column of Table 2, energy is most accurately conserved for the vector approach to IAD0. For the n = 3/2 polytrope, there is a better conservation for STD than for tensor IAD0 but for the most unstable n = 5/2 polytrope the level of conservation is similar.
3.3. Merging of two white dwarfs
Because of its mesh-free features, a substantial amount of applications of SPH have been
devoted to the study of the coalescence of stellar objects. In this section we simulated
the merging of two twin polytropes of index n = 3/2
and mass 0.6 M⊙ with both the IAD0 and STD
schemes. In each calculation, the structure was that of the last calculated model
corresponding to models E1 and E2 in Table 2. The EOS used was that of a perfect gas with
γ = 5/3. Both stars were put in a circular
rigid-rotation orbit in the plane XY with radius 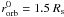 , where
Rs = 8000 km is the theoretical surface radius of the
polytrope, from the center of mass of the system. To enforce the coalescence, a braking
force proportional to the velocity
Fbra = − k(t)·v
was imposed during one revolution period P, according to the prescription
, where
Rs = 8000 km is the theoretical surface radius of the
polytrope, from the center of mass of the system. To enforce the coalescence, a braking
force proportional to the velocity
Fbra = − k(t)·v
was imposed during one revolution period P, according to the prescription
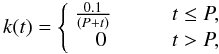 (23)where
t is the elapsed time and P = 29.3 s.
(23)where
t is the elapsed time and P = 29.3 s.
This scenario roughly accounts for the merging of twin white dwarfs described by an EOS dominated by the electrons in the partially degenerated regime.
The results of the simulations are summarized in Figs. 10 to 14. Figures 10 and 11 represent a density color map of both stars in the orbital plane as obtained with IAD0 and STD schemes, respectively. On the whole, the behavior is rather similar, although the coalescence evolves more slowly for the matrix method. We have to keep in mind, however, that the details of the evolution depend on the precise initial conditions (Dan et al. 2011). The initial equilibrium models for both calculations are similar, but not identical, because of the differences introduced during the relaxation process. The model E1 of Table 2, approached with the tensor method, has a larger radius and less clumping than model E2 calculated using the STD scheme. The details of the coalescence are also influenced by the errors in the estimation of gravity introduced by the tree-walk approach. These errors induce small differences that grow during the most dynamic phase of the merging. Thus, it is not straightforward to discern which part of the differences comes from the particular SPH scheme used in the simulation. On the other hand, both methods give the correct radius for Roche-Lobe (RL) overflow once the center of mass separation, d12, becomes similar to d12 = 17 100 km. Once the RL is crossed, the mass transfer becomes catastrophic and the merging of both stars takes place in a small fraction of one period.
 |
Fig. 10 Density color map of the coalescence process of two twin polytropes of index n = 3/2 at times t = 0.31P, t = 2.8P, t = 4.3P, and t = 7.7P, (P = 29.3 s) calculated using IAD0. |
 |
Fig. 11 Density color map of the coalescence process of two twin polytropes of index n = 3/2 at times t = 0.23P, t = 2.15P, t = 3.3P, and t = 7.4P (P = 29.3 s) calculated using the standard SPH scheme. |
Figure 12 shows the evolution of the Lz component of the angular momentum, orthogonal to the orbital plane. For t < P, there is a constant loss of angular momentum due to the imposed external braking force. At times t > P, but before the dynamical phase of the merging (t/P ≃ 4), the tensor scheme displays a rather good conservation of Lz, with small ripples induced by the multipolar approach to gravity. Conservation of Lz in this phase is not so good for the standard formulation. On another note, during the most violent phase of the coalescence and further bouncing of the core, the evolution of Lz follows a slightly different trend in both schemes. The tensor method leads to a monotonic increase in Lz until a maximum is reached followed by a steady decline. In the STD calculation, the behavior is the opposite. Nevertheless, the evolution of the angular momentum after the merging is complicated by the formation of an extended halo of particles, which is clearly seen in the last snapshot in Figs. 10 and 11. Although only a tiny amount of mass belongs to the halo, such mass produces a large torque on the core and any error in the estimation of gravity translates into a larger error in the angular momentum.
 |
Fig. 12 Left: evolution of the distance between the center of mass of both polytropes. Right: evolution of the orbital angular momentum, Lz, normalized to its initial value. An artificial braking force was acting before t/P = 1. |
An important challenge for the hydrocodes is to adequately represent the mix of the advected material during the coalescence process. In our system, the initial conditions are fully symmetric. Therefore, one would expect that a few minutes after the merging the core is homogeneously composed of the material of both stars. Figure 13 depicts the approximate distribution of the gas belonging to each star one minute after the catastrophic stage of the coalescence process. As we can see, the material of both white dwarfs is much more thoroughly mixed in the IAD0 calculation than the standard one. The merged core is made of successive thin, onion-like layers. In the calculation with the standard scheme, the onion-like structure is less pronounced, especially in the inner 10 km. We stress that the recipe to handle the artificial viscosity is exactly the same in both calculations. The only difference is the treatment of the gradient of the kernel, which seems ultimately to be the responsible for the larger amount of mixing obtained in the IAD0 calculation.
 |
Fig. 13 Mixing of material of both stars in the core as calculated by IAD0 at t = 227 s (upper picture) and with STD at t = 216 s (bottom picture). Blue and red colors refer to the gas belonging to each component of the original binary system. Mixed regions display a superposition of both colors. |
Figure 14 shows the angular velocity profile of the particles in the orbital plane as a function of their mass coordinate. As we can see, the standard calculation leads to an almost perfect rigid rotation for Mr < 0.8 M⊙, followed by a Keplerian velocity distribution beyond that point. This behavior agrees with the results obtained by Raskin et al. (2012) for a similar scenario. At distances Mr > 1 M⊙, the velocity profile obtained with IAD0 is also Keplerian, but below that mass, rigid rotation is never attained in the matrix calculation. In the standard calculation, the high amount of viscosity, which prevents the mixing of the core, now couples the different layers of the fluid so that the system rapidly approaches rigid rotation. Nevertheless, the time delay for core synchronization in nature is a function of the real physical viscosity. In the hydrodynamic models, the synchronization time is probably artificially shortened by the much larger numerical viscosity introduced by the codes. The impact of artificial viscosity in the final structure of the merged object was extensively discussed in Dan et al. (2011).
 |
Fig. 14 Angular velocity profiles at t ≃ 220 s as function of mass coordinate, calculated using IAD0 (red) and STD (blue), respectively. The Keplerian values for both calculations are given for reference. |
4. Adding thermal conduction to IAD0
It is not difficult to incorporate physics into the proposed matrix formulation of SPH by
simply using Eq. (15) to calculate the
gradient of the kernel whenever necessary. As an example, we work out an expression that can
be used to calculate the conductive heat transport and apply it to simulate the evolution of
a thermal wave. To do this, it is enough to consider the SPH thermal conduction equation
(Springel 2010) 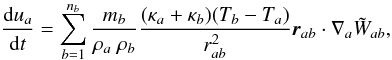 (24)
(24)
where κ is the thermal conductivity. If we estimate the gradient of the
kernel using Eq. (15), it leads to,
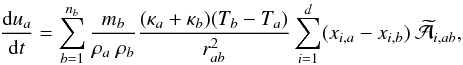 (25)where
d is the dimension of the space and the tilde symbol means the arithmetic
average of the magnitude, Eq. (14).
(25)where
d is the dimension of the space and the tilde symbol means the arithmetic
average of the magnitude, Eq. (14).
We applied Eq. (25) to the classical test
of simulating the propagation of a thermal wave in an homogeneous medium with
ρ = 1 g cm-3 and compared the results with those obtained
using Eq. (24). During the calculation, we
keep the particles at rest so that the energy equation, Eq. (9), reduces to the heat transport equation given by the expressions
above. An initial point-like discontinuity in energy was seeded at the center of the box. To
avoid numerical problems, the discontinuity was smoothed using a sharp Gaussian with
characteristic width of a few times the smoothing length parameter. To achieve this we made
use of the analytical expression for a spherically symmetric thermal-wave front in Landau & Lifshitz (1959)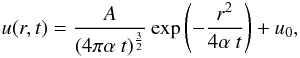 (26)
(26)
where α = κ/(cv ρ) is the thermal diffusivity and cv the specific heat capacity. The parameters in Eq. (26) were set to A = 105 erg cm3 g-1, u0 = 103 erg g-1, cv = 9.1 × 106 erg g-1 K-1, and κ = 3.9 × 109 erg s-1 cm-1 K-1.
To set the initial model, we put 47,707 identical particles at the nodes of a 3D regular lattice. The initial energy profile was that given by Eq. (26) for t = 0.04 s. The evolution of the thermal wave for different numbers of neighbors is depicted in Fig. 15. As we can see, the tensor scheme is in closer agreement with the analytical solution when the number of neighbors is small, nb ≃ 25. Nevertheless, above nb ≃ 50 neighbors both schemes lead to similar results. To investigate the influence of the initial setting of particles we carried out a second calculation, this time using a pseudo-ordered lattice. The new particle distribution was obtained after randomly perturbing the 3D ordered lattice with a maximum perturbation amplitude 0.3Δ, where Δ is the lattice spacing. In this new calculation the mass of the particles was conveniently arranged to keep the density constant, at ρ = 1 g cm-3, throughout the system. The maximum mass contrast between neighboring particles was lower than a factor of two. The results of this second calculation are summarized in Fig. 16. As we can see, the calculation with IAD0 always reproduces more closely the evolution of the heat wave, especially for a small number of neighbors but also even when a moderate, nb ≃ 50, amount of neighbors is chosen.
Average wall-clock time for the different benchmark tests and sections of the code relevant to the IAD0 calculation.
 |
Fig. 15 Evolution of a thermal wave propagating through an ordered lattice of particles at different times. The profile of internal energy is shown for both SPH schemes and two different numbers of neighbors. |
 |
Fig. 16 Evolution of a thermal wave propagating through a pseudo-ordered distribution of particles at different times. The profile of internal energy is shown for both SPH schemes and two different numbers of neighbors. |
5. Computational issues
In this section we conducted a benchmark test to assess the impact of the calculation of the IAD0 terms and the momentum and energy equations using Eqs. (8)–(11). To do this we generated a 3D distribution of particles using a quasi-random Sobol distribution. Using the stretching technique, we then displaced the particles to follow a spherical density profile for the central core of a pre-collapse 15 M⊙ star (see Heger et al. 2005). The hydrocode is OMP-parallelized, and includes a Barnes-Hut octal-tree solver to calculating the gravitational force up to the quadrupolar term, and the Lattimer-Swesty EOS (Lattimer & Swesty 1991). As we are only interested in the impact of the IAD0 calculation on the overall wall-clock time, we set the velocity of the particles to zero at each time-step (frozen structure).
Table 3 summarizes the outcome of the calculations.
We varied the number of particles and the number of threads to gain insight into both the
overhead and the scaling of the IAD0 calculation. Table 3 shows, from left to right, the number of particles, the number of
threads, the tolerance parameter θ, the wall-clock time per iteration for
the standard calculation ( ), the
wall-clock time spent by the code in the calculation of the standard momentum and energy
equations (
), the
wall-clock time spent by the code in the calculation of the standard momentum and energy
equations (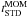 ), the wall-clock
time per iteration for the IAD0 calculation
(
), the wall-clock
time per iteration for the IAD0 calculation
(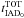 ), the wall-clock
time spent by the code in the calculation of the IAD0 coefficients
(
), the wall-clock
time spent by the code in the calculation of the IAD0 coefficients
(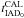 ), and the
wall-clock time spent by the code in the calculation of the IAD0 momentum and
energy equations (
), and the
wall-clock time spent by the code in the calculation of the IAD0 momentum and
energy equations (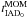 ). The last
column shows the IAD0 overhead as a percentage, with respect to the standard
simulation, and is calculated as
). The last
column shows the IAD0 overhead as a percentage, with respect to the standard
simulation, and is calculated as 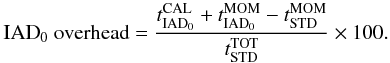 (27)All these times were
averaged over 1000−2000 iterations for each calculation, which was always performed on the
same 12-core AMD machine.
(27)All these times were
averaged over 1000−2000 iterations for each calculation, which was always performed on the
same 12-core AMD machine.
The parameter θ was used to control the criterion for choosing between opening a node in the tree (and using the particle-to-particle interaction to calculate gravity) and not opening the node (and using its global contribution via the multipolar expansion). The smaller the value of θ, the slower the tree-walk, because more nodes are opened and the calculation gets closer to N2 scaling. Typical values of θ, those actually used in calculations, are between 0.5 and 0.7. Here, we selected two values (0.3 and 0.6) to assess the relevance of the IAD0-related calculations to the gravity evaluation, which is typically the most important bottleneck of the code.
From these results, it can be seen that the inclusion of the IAD0 scheme in single-threaded (serial) calculations contributes with an overhead of approximately 18%, independently of the number of particles used, which means that, as expected, it has a linear dependence on them. This can be seen in Fig. 17 (left), where it is clear that the inclusion of IAD0 in the calculation, does not vary the slope of the curve. In the case of the standard calculation, the relationship between the wall-clock time and the number of particles is log (t) ≃ log (N)1.0907, while for the IAD0 calculation it is log (t) ≃ log (N)1.0919. Even more, Fig. 17 (right) shows that the overhead ratio of the IAD0-related calculations to their standard analogous tends to saturate at a factor slightly lower than 2. Noting that the momentum and energy calculations in the standard version of SPH takes around 20% of the time, this result is consistent with the IAD0 overhead.
 |
Fig. 17 Benchmarking of the impact of IAD0 on the computational time. Left: total wall-clock time per time-step in front of the number of particles. Right: overload ratio of the IAD0 related calculations (matrix coefficients + momentum and energy equations) to the standard momentum and energy calculation. |
These are desirable properties as they mean that this section of the code will have at least the same behavior in terms of parallelization as the rest of the code, and that the overhead is limited independently of the number of particles. This can also be seen when we compare the single-threaded results with the multi-threaded ones. The wall-clock time for the IAD0 sections in the 12-thread calculation is 9−10 times shorter than the time for the same sections in the serial work, which points to a good strong scaling and a considerable reduction in the IAD0 overhead to 9% of the overall wall-clock time.
The overhead reduction due to parallelization of course depends on how well the code is parallelized and the amount of it that remains serial. Nevertheless, the results that refer specifically to the IAD0 sections show relevant information on the low impact that IAD0 may have on the overall calculation when these sections are parallelized.
Finally, it can also be seen from the last two rows of Table 3 that the relevance of the IAD0 sections is reduced to ≃ 14% when gravity becomes more dominant. This can be taken as a lower limit of the IAD0 overhead in single-threaded calculations, as the parameter θ = 0.3 is rather extreme and is rarely used below that value.
6. Conclusions
We have checked the behavior of a novel SPH scheme where gradients are calculated using an integral approach. The main features of the technique, called IAD0, were described in detail in Paper I and summarized in Sect. 2 of this paper. The main virtue of the approach relies in that the re-normalization of the derivatives appears naturally, without any degradation of the conservative properties that characterize the SPH technique. Another relevant feature is that the basic mathematical formalism of IAD0 looks very similar to that of a standard SPH technique, making its implementation quite straightforward. As commented in Paper I, matrix methods based on a similar, although not identical, formulation have been used in computational fluid dynamics for the past decade (see for instance Dilts 1999), but have never been previously applied to astrophysics.
Three test cases of considerable astrophysical interest were selected to validate IAD0, as well as to detect its virtues and weaknesses. The performance of the method in describing the growth of the RT instability in a supernova remnant was analyzed in Sect. 3.1, with the conclusion that IAD0 provides a healthier development of the RT fingers. The method’s success in handling hydrodynamical instabilities relies on the re-normalization imposed on the derivatives, thus confirming the results obtained in Paper I using toy models.
The second test was addressed especially to the applications of the method to describing stellar objects (approached as polytropes with different indexes and known analytical properties). One important question here relies in the treatment of the outer boundary of the object, which is often a controversial point in matrix methods (Oger et al. 2007). We have entirely explored this issue using several recipes to handle the surface of the polytropes. These include the use of tensor and vector formulations of IAD0, as well as hybrid schemes that use the full matrix expressions in the interior but changes to vector-IAD0 near the surface, according to Eq. (18). The best results were obtained when the full tensor IAD0 scheme was used, especially for the most unstable polytrope with index n = 5/2. Nevertheless, the amount of numerical noise stored as residual kinetic energy at equilibrium was larger for tensor-IAD0 than for STD.
The ability of the tensor method to handle the coalescence and further merging of
stellar-like objects was checked in Sect. 3.3. Even
though for this particular test the simulations did not show any clear advantage of the
matrix method, it gave a good depiction of the coalescence process. Despite both schemes
being conservative by construction, complete preservation of angular momentum is impeded by
the use of the hierarchical cluster method in calculating gravity. Nevertheless, there are
indications that the angular momentum-component orthogonal to the orbital plane behaves
better in IAD0 than in the standard scheme (Fig. 12). The prompt product after the coalescence is a core surrounded by an extended
diluted halo of particles moving at Keplerian velocity. The calculations show that the
tensor method leads to a more homogeneous mixing of the material of both stars in the core
region. As the numerical recipe for implementing AV in both calculations is exactly the
same, we conclude that the different behavior is caused by the differences in the algorithm
used to compute the kernel derivative. Therefore, it seems that IAD0 is able to
provide a more effective hydrodynamical mixing than the standard scheme, but still avoid the
penetration of fluids in strong shocks, as suggested in Paper I. These differences also
affect the distribution of angular velocity in the core of the remnant, which in the STD
calculation soon reaches rigid rotation but in the matrix one does not, for a similar
elapsed time. A potential weakness of the tensor method in handling these kinds of
configurations comes from the computation and further inversion of matrix
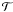 calculated with Eq. (5). In the case of the
isolation of a particle, as it could be for those belonging to the most diluted region of
the domain, matrix
calculated with Eq. (5). In the case of the
isolation of a particle, as it could be for those belonging to the most diluted region of
the domain, matrix 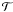 becomes singular leading to the complete breakdown of the simulation. In this sense, the
matrix scheme is less robust than the standard one. Nevertheless, current SPH schemes
usually include an algorithm to ensure that the number of neighbors of a given particle
remain constant during the simulation. This algorithm is necessary to reliably compute the
magnitude Ω in Eqs. (8) and (9) and, when working properly, to avoid the
singularity problems linked to matrix
becomes singular leading to the complete breakdown of the simulation. In this sense, the
matrix scheme is less robust than the standard one. Nevertheless, current SPH schemes
usually include an algorithm to ensure that the number of neighbors of a given particle
remain constant during the simulation. This algorithm is necessary to reliably compute the
magnitude Ω in Eqs. (8) and (9) and, when working properly, to avoid the
singularity problems linked to matrix 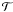 .
.
Other interesting features of the matrix method are its ability to avoid the pairing instability and the better handling of thermal conduction. The first one leads to less particle clustering, thus improving the quality of the interpolations; while in the second case, the results of Sect. 4 suggest that diffusion-like equations can be handled by IAD0 in a better way than in the standard framework.
We also conducted a benchmark test to evaluate the impact of the inclusion of the IAD0 formalism on the wall-clock time for a nominal calculation. According to Table 3 and Fig. 17, the computational overload introduced in a serial calculation by the re-normalization of the derivatives is low (≃ 20%), being practically independent of the total number of particles. The scaling of the code with the number of particles remains virtually untouched, and the IAD0-related sections of the code show a good behavior in front of parallelization.
Therefore, the analysis of the astrophysical tests discussed in this paper support the main conclusions of Paper I, where the basic implementation of the integral approach to the derivatives was discussed and checked. All this suggests that the use of the re-normalized, fully conservative IAD0 approach to the SPH equations may improve, in general, the quality of the simulations in astrophysics with a little computational overload penalty.
The smaller amount of viscous dissipation shown by IAD0, compared to STD for the same AV formalism, suggests that it could be of interest not only when handling hydrodynamic instabilities but also when simulating turbulence. Turbulence is at the heart of many astrophysical problems, being of especial relevance to understanding star formation (Federrath et al. 2010). In this respect, a full comparison of 3D astrophysical turbulence calculated with a variety of algorithms, both SPH and grid codes, was provided by Kitsionas et al. (2009); Price & Federrath (2010); and Kritsuk et al. (2011), with the result that both families of codes give similar results for an equivalent number of resolution elements in each direction in space. Nevertheless, these experiments also show that, owing to the higher dissipation, the scaling range of SPH codes is slightly shorter than that of grid-based codes, as demonstrated by Kitsionas et al. (2009). Therefore, it may be of great interest to check the ability of the proposed IAD0 scheme to handle astrophysical turbulence in the near future.
Acknowledgments
The authors acknowledge useful conversations with Stephan Rosswog. This work has been funded by the Spanish MEC grants AYA2010-15685, AYA2011-23102, and the Swiss Platform for High-Performance and High-Productivity Computing (HP2C) within the supernova project. It was also supported by ESF EUROCORES Program Eurogenesis through the MICINN grant EUI2009-04167 and by DURSI of the Generalitat de Catalunya. The rendered SPH plots were made using the freely available SPLASH code (Price 2007).
References
- Brookshaw, L. 1985, Proc. Astron. Soc. Aust., 6, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Cabezón, R. M., García-Senz, D., & Relaño, A. 2008, J. Comput. Phys., 227, 8523 [NASA ADS] [CrossRef] [Google Scholar]
- Dan, M., Rosswog, R., Guillonchon, J., & Ramirez-Ruiz, E. 2011, ApJ, 737, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Hossam, A. 2012, MNRAS, 425, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Dilts, G. A. 1999, Int. J. Numer. Methods, 44, 1115 [CrossRef] [Google Scholar]
- Dwarkadas, V. 2000, ApJ, 541, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P. C., & Klessen, R. S. 2010, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- García-Senz, D., Bravo, E., & Serichol, N. 1998, ApJS, 115, 119 [NASA ADS] [CrossRef] [Google Scholar]
- García-Senz, D., Cabezón, R. M., & Escartín, J. A. 2012a, A&A, 538, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Senz, D., Badenes, C., & Serichol, N. 2012b, ApJ, 745, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Blondin, J. M., & Emmering, R. T. 1992, ApJ, 392, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M. 1992, Mem. Soc. Astron. It., 65, 4 [Google Scholar]
- Hernquist, L., & Katz, N. 1989, ApJS, 70, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Kitsionas, S., Federrath, C., Klessen, R. S., et al. 2009, A&A, 508, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kritsuk, A. G., Nordlund, A., Collins, D., et al. 2011, ApJ, 737, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L., & Lifshitz, F. M. 1959, Course in Theoretical Physics, Fluid Mechanics (Oxford: Pergammon), 6 [Google Scholar]
- Lattimer, J. M., & Swesty, F. D. 1991, Nucl. Phys. A, 535, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J. 1992, ARA&A, 365, 199 [Google Scholar]
- Monaghan, J. J. 2005, Rep. Prog. Phys., 68, 1703 [Google Scholar]
- Morris, J., & Monaghan, J. J. 1997, J. Comput. Phys., 136, 41 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Oger, G., Doring, M., Alessandrini, B., & Ferrant, P. 2007, J. Comput. Phys., 225, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. 2007, PASA, 24, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. 2008, J. Comput. Phys., 227, 10040 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Price, D. 2012, J. Comput. Phys., 231, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D., & Federrath, C. 2010, MNRAS, 406, 1659 [NASA ADS] [Google Scholar]
- Price, D., & Monaghan, J. J. 2007, MNRAS, 1347, 1358 [Google Scholar]
- Raskin, C., Scannapieco, E., Fryer, C., Rockefeller, G., & Timmes, F. X. 2012, ApJ, 746, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S. 2009, New Astron. Rev., 53, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, ARA&A, 48, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., & Müller, E. 1993, ARA&A, 268, 391 [NASA ADS] [Google Scholar]
- Vigh, C. D., Velázquez, P. F., Gómez, D. O., et al. 2011, ApJ, 727, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C. 2011, MNRAS, 415, 83 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between several magnitudes at t = 698 yr of evolution of the SNR computed using IAD0 and STD schemes.
Main features of polytropes with polytropic indexes n = 3/2 and n = 5/2, respectively.
Average wall-clock time for the different benchmark tests and sections of the code relevant to the IAD0 calculation.
All Figures
 |
Fig. 1 Profile of several kernels in one dimension. The Gaussian kernel is truncated at r = 2h. The Wn(H) belongs to the harmonic family of kernels described by Eq. (16) for n = 2, 3, and 6, respectively. |
| In the text | |
 |
Fig. 2 Profile of the gradient of the kernel calculated analytically in the standard SPH way (referred as analytical in the figures) as well as numerically, through Eq. (15) for two particle settings: bcc and pseudo-random, kernel indexes n = 3, 5, and different number of neighbors. |
| In the text | |
 |
Fig. 3 Profile of coefficients τii/h2 and τij/h2,(j ≠ i) in a polytrope of index n = 5/2 fitted with 20 000 particles (model F1 of Table 2). The distance to the center is normalized to the radius of the polytrope, Rs. The analytical value of τii/h2 is also given (horizontal dashed line corresponding to β = 1). Basically, all the star interior has a value β ≥ 0.95, while beyond a radius Rs − 2hs (where hs is the smoothing length close to the surface) the value of β rapidly declines (see Sect. 2.3 for the definition of β). |
| In the text | |
 |
Fig. 4 Density color map depicting the growth of the RT instability in a SNR for models B1 (upper panels), B2 (middle panels), and B3 (lower panels) of Table 1 at times t = 698 yr (left columns) and t = 951 yr (right columns). The size of the box in all panels is 10 pc in each direction. |
| In the text | |
 |
Fig. 5 Profile of the coefficients τii/h2 and τij/h2,(j ≠ i) for model B1 of Table 1. The analytical value of τii/h2 is also given (horizontal dashed line). |
| In the text | |
 |
Fig. 6 Density and velocity profiles of the SNR at elapsed time t = 698 yr for the stretched-grid models of the supernova ejecta (models C1 and C2 in Table 1). Outside the RT-unstable region, the spherical symmetry is better preserved when the tensor method is used. |
| In the text | |
 |
Fig. 7 Evolution of central density and surface radius (normalized to the theoretical values) for polytropes with indexes n = 3/2 (upper panels, corresponding to models E1 and E2 in Table 2) and n = 5/2 (lower panels, corresponding to models F1 and F2 in Table 2). Continuum and dashed lines are for the tensor-IAD0 and standard schemes, respectively. |
| In the text | |
 |
Fig. 8 Evolution of central density and surface radius (normalized to the theoretical values) for polytropes with indexes n = 3/2 (upper panels, corresponding to models E2 and E3 in Table 2) and n = 5/2 (lower panels, corresponding to models F2 and F3). Continuous and dashed lines are for vector-IAD0 and standard schemes, respectively. |
| In the text | |
 |
Fig. 9 Evolution of the ratio of kinetic to internal energies. Left column is for polytropes with indexes n = 3/2 (upper panel) and n = 5/2 (lower panel) calculated using tensor-IAD0 (continuum line) and STD (dashed line). Same for pictures on the right column, where, however, vector-IAD0 was used. |
| In the text | |
 |
Fig. 10 Density color map of the coalescence process of two twin polytropes of index n = 3/2 at times t = 0.31P, t = 2.8P, t = 4.3P, and t = 7.7P, (P = 29.3 s) calculated using IAD0. |
| In the text | |
 |
Fig. 11 Density color map of the coalescence process of two twin polytropes of index n = 3/2 at times t = 0.23P, t = 2.15P, t = 3.3P, and t = 7.4P (P = 29.3 s) calculated using the standard SPH scheme. |
| In the text | |
 |
Fig. 12 Left: evolution of the distance between the center of mass of both polytropes. Right: evolution of the orbital angular momentum, Lz, normalized to its initial value. An artificial braking force was acting before t/P = 1. |
| In the text | |
 |
Fig. 13 Mixing of material of both stars in the core as calculated by IAD0 at t = 227 s (upper picture) and with STD at t = 216 s (bottom picture). Blue and red colors refer to the gas belonging to each component of the original binary system. Mixed regions display a superposition of both colors. |
| In the text | |
 |
Fig. 14 Angular velocity profiles at t ≃ 220 s as function of mass coordinate, calculated using IAD0 (red) and STD (blue), respectively. The Keplerian values for both calculations are given for reference. |
| In the text | |
 |
Fig. 15 Evolution of a thermal wave propagating through an ordered lattice of particles at different times. The profile of internal energy is shown for both SPH schemes and two different numbers of neighbors. |
| In the text | |
 |
Fig. 16 Evolution of a thermal wave propagating through a pseudo-ordered distribution of particles at different times. The profile of internal energy is shown for both SPH schemes and two different numbers of neighbors. |
| In the text | |
 |
Fig. 17 Benchmarking of the impact of IAD0 on the computational time. Left: total wall-clock time per time-step in front of the number of particles. Right: overload ratio of the IAD0 related calculations (matrix coefficients + momentum and energy equations) to the standard momentum and energy calculation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


