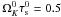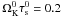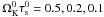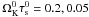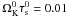| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219794 | |
| Published online | 20 September 2012 | |
Dust-trapping Rossby vortices in protoplanetary disks
1 Physikalisches Institüt & Center for Space and Habitability, Universität Bern, 3012 Bern, Switzerland
e-mail: meheut@space.unibe.ch
2 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
3 AstroParticule et Cosmologie (APC), Universite Paris Diderot, 10 rue A. Domon et L. Duquet, 75205 Paris Cedex 13, France
Received: 11 June 2012
Accepted: 10 August 2012
Context. One of the most challenging steps in planet formation theory is the one leading to the formation of planetesimals of kilometre size. A promising scenario involves the existence of vortices able to concentrate a large amount of dust and grains in their centres. Up to now this scenario has mostly been studied in 2D razor thin disks. A 3D study including, simultaneously, the formation and resulting dust concentration of the vortices with vertical settling, is still missing.
Aims. The Rossby wave instability self-consistently forms 3D vortices, which have the unique quality of presenting a large-scale vertical velocity in their centre. Here we aim to study how this newly discovered effect can alter the dynamic evolution of the dust.
Methods. We performed global 3D simulations of the RWI in a radially and vertically stratified disk using the code MPI-AMRVAC. After the growth phase of the instability, the gas and solid phases are modelled by a bi-fluid approach, where the dust is considered as a fluid without pressure. Both the drag force of the gas on the dust and the back reaction of the dust on the gas are included. Multiple grain sizes from 1 mm to 5 cm are used with a constant density distribution.
Results. We obtain in a short timescale a high concentration of the largest grains in the vortices. Indeed, in 3 rotations the dust-to-gas density ratio grows from 10-2 to unity leading to a concentration of mass up to that of Mars in one vortex. The presence of the radial drift is also at the origin of a dust pile-up at the radius of the vortices. Lastly, the vertical velocity of the gas in the vortex causes the sedimentation process to be reversed, the mm size dust is lifted and higher concentrations are obtained in the upper layer than in the midplane.
Conclusions. The Rossby wave instability is a promising mechanism for planetesimal formation, and the results presented here can be of particular interest in the context of future observations of protoplanetary disks.
Key words: planets and satellites: formation / protoplanetary disks / hydrodynamics / instabilities / accretion, accretion disks
© ESO, 2012
1. Introduction
In current formation theory, planets are supposed to be built from colliding planetesimals of kilometre or larger sizes, but the formation of these planetesimals is still an issue (Chiang & Youdin 2010). Owing to their intermediate sizes, they cannot stick through chemical bonds and van der Vaals forces, as opposed to microscopic dust (Dominik 2009; Blum & Wurm 2008). Moreover, their gravitational fields are too small to retain collision fragments (Benz 2000). Besides this, the gas is partially supported by the radial pressure gradient and is therefore sub-Keplerian. The solids in Keplerian rotation feel a head-on wind, which slows them down. This drag force induces a radial drift toward the central star on timescales as short as several hundred years for metre-sized solids (Weidenschilling 1977). This timescale appears to be even shorter when compared to the planet formation timescale of a few million years.
Multiple scenarios have been proposed to overcome this difficulty. The streaming instability (Youdin & Goodman 2005; Johansen et al. 2007) is an hydrodynamical instability that grows partially thanks to the strong coupling between gas and dust. But its domain of interest only includes regions with an increased dust-to-gas density ratio, compared with the standard value of ρd/ρg ~ 10-2. Another possibility that does not exclude the previous one is the presence of vortices in the protoplanetary disk. In this scenario the metre size barrier is outstripped by the vortices that can concentrate solids in their centre and accelerate the growth process. Barge & Sommeria (1995) used an analytical approach to show that anticyclonic vortices effectively concentrate solids in their centre, and this idea was further studied by Tanga et al. (1996). As this concentration effect by the vortices shares the same physics as the radial transport of solids toward the disk centre, the highest concentration is expected for the fastest drifting solids. Whereas these studies ignore the vertical structure of the disk, a 3D approach was proposed by Shen et al. (2006) and Heng & Kenyon (2010). Numerical simulations of these dusty vortices have also been performed in 2D (Bracco et al. 1999; Godon & Livio 1999, 2000) and 3D (Johansen et al. 2004) in order to investigate their ability to concentrate solids.
These works, however, leave the formation mechanism for the vortices and their long term evolution unspecified. Klahr & Bodenheimer (2003) and Klahr (2004) propose a non linear hydrodynamical instability growing in an entropy gradient (Petersen et al. 2007a,b), called the baroclinic instability, to form such structures. Lesur & Papaloizou (2010) show that these vortices are stable structures in 3D, whereas the MHD approach of Lyra & Klahr (2011) prove that this instability can form vortices only in the dead zone; however, the vortices migrate radially due to the radial pressure gradient (Paardekooper et al. 2010), and their long-term stability is not clear. Another proposed formation mechanism for the vortices is the Rossby wave instability (RWI). This is a linear instability that grows in the region of a pressure extremum, which avoids vortex migration (Meheut et al. 2012a). This instability was first studied in 2D both analytically (Lovelace et al. 1999) and numerically (Li et al. 2001; Varnière & Tagger 2006). The concentration of solids in Rossby vortices has been explored in numerical simulations (Inaba & Barge 2006; Lyra et al. 2009b). Recently, Regály et al. (2011) have proposed the RWI as an explanation for the non-axisymmetric submillimetre images of some transition disks. Moreover, an equivalent of the RWI can also exist in a magnetised disk (Tagger & Varnière 2006; Yu & Li 2009), extending its domain of application. One intriguing characteristic of these vortices is that the vertical displacements of gas in the vortices centres over the whole vertical scale height of the disk. This was first obtained in numerical simulations (Meheut et al. 2010) and then confirmed analytically (Meheut et al. 2012b; Lin 2012). These structures are of particular interest for the study of the dust concentration. Indeed, not only can they accelerate the concentration in the midplane at the centre of the vortices due to the downward flow, they also replenish the upper region of the disk with small particles thanks to the upward flow.
The goal of this paper is to investigate the behaviour of solid particles in 3D vortices formed by the RWI. To this end, we performed full 3D simulations of a disk subject to the RWI. When the vortices are formed, we followed the joint evolution of the gas and the dust, for multiple dust species, through bi-fluid simulations. Our paper is organised as follows. We first present the formation of the vortices, detailing the characteristics of the RWI, and explaining the numerical methods and the results of this gas-only simulation. Section 3 deals with the model we have used for the dust, which is considered as a pressure-less fluid, as well as the limits it sets. The resulting simulations are presented, and show the concentration of the dust in the midplane and its vertical stratification. We discuss these results in Sect. 5.
2. Formation of Rossby vortices
The aim of this study is to numerically follow the density of solids in Rossby vortices. Here we use the term “Rossby vortices” for vortices formed nonlinearly by the RWI. The first step of this study is therefore to obtain such structures through 3D numerical simulation of the RWI.
2.1. The Rossby wave instability
The RWI can be seen as an equivalent of the Kelvin-Helmholtz instability (see e.g. Drazin & Reid 2004) in the context of a differentially rotating disk. It is an inertial instability characterised by the formation of Rossby vorticity waves in the region of an inflexion point in the flow characteristics and spiral density waves propagating outward. The criterium for this instability is an extremum in the quantity ℒ related to the vorticity of the equilibrium flow. In a non-magnetised and isentropic thin disk, this quantity can be written as (Li et al. 2000) 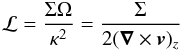 (1)where Σ is the surface density, v the velocity of the gas, Ω the rotation frequency, and κ2 = 4Ω2 + 2rΩΩ′ the squared epicyclic frequency (so that κ2/2Ω is the vorticity). Here the prime notes a radial derivative. A Rossby wave propagates in each gradient of ℒ, and the growth of the instability is related to the exchange of energy between these two waves. From this point of view, the instability can be considered as a global instability, and does not depend on the boundary conditions.
(1)where Σ is the surface density, v the velocity of the gas, Ω the rotation frequency, and κ2 = 4Ω2 + 2rΩΩ′ the squared epicyclic frequency (so that κ2/2Ω is the vorticity). Here the prime notes a radial derivative. A Rossby wave propagates in each gradient of ℒ, and the growth of the instability is related to the exchange of energy between these two waves. From this point of view, the instability can be considered as a global instability, and does not depend on the boundary conditions.
Such an extremum can be achieved by the presence of a density bump in the disk as expected at the boundaries of the dead zone. This is the region where the gas is ionised neither by stellar radiation nor by cosmic rays, and turbulence driven by magneto-rotational instability is ineffective (Gammie 1996). The different viscosity rates on each side of the dead zone is responsible for the formation of a pressure bump (Varnière & Tagger 2006; Lyra et al. 2008; Kretke et al. 2009). Very recently, Lyra & Mac Low (2012) have performed the first MHD simulation of the inner edge of the dead zone in unstratified 3D to show the formation of this bump and the growth of the RWI in this region. The region of the ice line is also expected to form an extremum in the density and entropy profile (Kretke & Lin 2007) and could be a region of vortex formation, as well as the edge of planet gaps (Koller et al. 2003; de Val-Borro et al. 2007; Lyra et al. 2009a; Yu et al. 2010; Lin & Papaloizou 2011).
2.2. Numerical methods
To simulate the growth of the RWI in the gas disk, we used the numerical methods presented in Meheut et al. (2012a), which we briefly summarise here. The governing equations are solved in cylindrical coordinates (r,φ,z), centred on the star, and read as 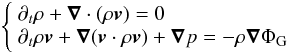 (2)where ρ is the density of gas, v its velocity, p the gas pressure, and ΦG the gravitational potential of the star. There is no energy equation, and the evolution of the gas is considered to be isentropic:
(2)where ρ is the density of gas, v its velocity, p the gas pressure, and ΦG the gravitational potential of the star. There is no energy equation, and the evolution of the gas is considered to be isentropic: 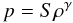 (3)with the adiabatic index γ = 5/3, S being a constant. The sound speed is given by
(3)with the adiabatic index γ = 5/3, S being a constant. The sound speed is given by 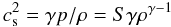 (4)and the temperature by
(4)and the temperature by 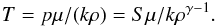 (5)with μ the mean molecular weight of the gas and k the Boltzmann constant. The evolution of the fluid is calculated with MPI-AMRVAC (Message Passing Interface-Adaptive Mesh Refinement Versatile Advection Code) presented in Keppens et al. (2012). We used the Lax-Friedrich scheme (see Tóth 1996) with a Koren limiter (Koren 1993). A global simulation of the disk is needed to fully capture the RWI, but as the instability is symmetric about the midplane of the disk we only need to compute the upper half of it (Meheut et al. 2010, 2012b). For those reasons, the disk is simulated on a cylindrical grid with r ϵ [1,6 AU] , ϕ ϵ [0,2π] , and z ϵ [0,0.5 AU] . Three AMR levels are used, which gives an increase of a factor of 8, allowing a resolution corresponding to (256,128,128) to be reached in the region of physical interest.
(5)with μ the mean molecular weight of the gas and k the Boltzmann constant. The evolution of the fluid is calculated with MPI-AMRVAC (Message Passing Interface-Adaptive Mesh Refinement Versatile Advection Code) presented in Keppens et al. (2012). We used the Lax-Friedrich scheme (see Tóth 1996) with a Koren limiter (Koren 1993). A global simulation of the disk is needed to fully capture the RWI, but as the instability is symmetric about the midplane of the disk we only need to compute the upper half of it (Meheut et al. 2010, 2012b). For those reasons, the disk is simulated on a cylindrical grid with r ϵ [1,6 AU] , ϕ ϵ [0,2π] , and z ϵ [0,0.5 AU] . Three AMR levels are used, which gives an increase of a factor of 8, allowing a resolution corresponding to (256,128,128) to be reached in the region of physical interest.
The initial condition is a protoplanetary disk with a pressure bump allowing the RWI to grow. The initial midplane density is 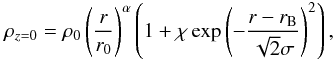 (6)with ρ0 = 10-10 g cm-3 the density at r0 = 1 AU, and α = −1.5 the power-law index of the underlying density. This value for the density slope gives a surface density varying approximately as Σ ~ r-0.5 in the absence of the bump. The shape of the Gaussian bump is defined by its amplitude χ = 1, width σ = 0.1 AU, and radial position rB = 3 AU. The vertical and radial equilibria are achieved thanks to the density and azimuthal velocity profiles:
(6)with ρ0 = 10-10 g cm-3 the density at r0 = 1 AU, and α = −1.5 the power-law index of the underlying density. This value for the density slope gives a surface density varying approximately as Σ ~ r-0.5 in the absence of the bump. The shape of the Gaussian bump is defined by its amplitude χ = 1, width σ = 0.1 AU, and radial position rB = 3 AU. The vertical and radial equilibria are achieved thanks to the density and azimuthal velocity profiles: ![\begin{eqnarray} \rho&=&\rho_{z=0}\Bigg[1-GM_*\frac{\gamma-1}{\gamma S\rho_{z=0}^{\gamma-1}}\left(\frac{1}{r}-\frac{1}{\sqrt{r^2+z^2}}\right)\Bigg]^{1/(\gamma-1)}\\[2mm] v_\varphi&=&\sqrt{\frac{GM_*}{r}+rS\gamma \rho_{z=0}^{\gamma-2}\partial_r\rho_{z=0}} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19794-12/aa19794-12-eq40.png) with S = 10-3. This gives a temperature of approximatively 2.5 × 102 K at a radius of 1 AU. On top of this equilibrium state, we added small random perturbations on the radial velocity with a relative amplitude to the inner azimuthal velocity of 10-4. If not specified, the length is given in AU, the time
with S = 10-3. This gives a temperature of approximatively 2.5 × 102 K at a radius of 1 AU. On top of this equilibrium state, we added small random perturbations on the radial velocity with a relative amplitude to the inner azimuthal velocity of 10-4. If not specified, the length is given in AU, the time 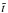 in the code time unit corresponding to 1/(2π) yr, and the densities are normalised to ρ0.
in the code time unit corresponding to 1/(2π) yr, and the densities are normalised to ρ0.
2.3. Growth of the instability
These conditions are favourable for the RWI, and the simulation shows its growth with the formation of Rossby vortices. After the exponential growth phase that lasts for a few rotations, the instability reaches saturation as expected. At this point the amplitude of the perturbations cease to grow exponentially and maintain a nearly constant value. Figure 1 shows the amplitude of the density perturbations on a logarithmic scale as a function of time. At the time 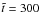 , the instability has fully reached the saturation, and there is no significant change in the structure of the disk on a timescale of a few rotations. This corresponds to approximately 50 yr and 14 rotations at the radius of the bump. This evolution and the longer term stability of Rossby vortices have been studied in the absence of dust by Meheut et al. (2012a), showing that the vortices survive over at least a few hundred years.
, the instability has fully reached the saturation, and there is no significant change in the structure of the disk on a timescale of a few rotations. This corresponds to approximately 50 yr and 14 rotations at the radius of the bump. This evolution and the longer term stability of Rossby vortices have been studied in the absence of dust by Meheut et al. (2012a), showing that the vortices survive over at least a few hundred years.
 |
Fig. 1 Amplitude of the total density perturbation and the main modes on a logarithmic scale as a function of time. The solid line is a fit of the linear growth giving a growth rate of 0.17ΩK(rB). |
In the same figure, the growth of a few modes is also plotted. A mode is an element of the Fourier transform of the density: 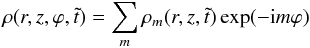 (9)where the azimuthal mode number m is a positive integer. The most unstable azimuthal mode during the exponential growth is the one with m = 5. This azimuthal mode number corresponds to the number of anticyclonic vortices, which are rotating counter to the Keplerian rotation and are high-pressure regions. These five high-pressure regions will be easily identified in Fig. 5. In Fig. 1, the linear fit of the amplitude growth of the density perturbation on a logarithmic scale is also plotted. This fit gives a growth rate of 0.17Ω(rB) that is consistent with a linear calculation (see also the discussion in Lin 2012 on the shape of the initial bump). The growth of the instability has already been widely studied, so we do not aim to discuss it further here. At
(9)where the azimuthal mode number m is a positive integer. The most unstable azimuthal mode during the exponential growth is the one with m = 5. This azimuthal mode number corresponds to the number of anticyclonic vortices, which are rotating counter to the Keplerian rotation and are high-pressure regions. These five high-pressure regions will be easily identified in Fig. 5. In Fig. 1, the linear fit of the amplitude growth of the density perturbation on a logarithmic scale is also plotted. This fit gives a growth rate of 0.17Ω(rB) that is consistent with a linear calculation (see also the discussion in Lin 2012 on the shape of the initial bump). The growth of the instability has already been widely studied, so we do not aim to discuss it further here. At 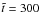 , we add a dust population in the disk to follow its concentration in the five anticyclonic vortices as explained in the next section. This defines the time t = 0, when we have
, we add a dust population in the disk to follow its concentration in the five anticyclonic vortices as explained in the next section. This defines the time t = 0, when we have 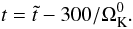 (10)
(10)
3. Dust and gas joint evolution
When the vortices are self-consistently formed in the gas-only disk, we start to model the joint evolution of gas and dust.
3.1. Bi-fluid model
In the cylindrical coordinates the bi-fluid equations are 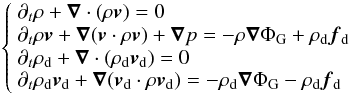 (11)where ρ and ρd are the density of gas and dust, v and vd their velocities, p the gas pressure, and ΦG the gravitational potential of the central star. The drag force fd between the gas and the dust is expressed in terms of the stopping time τs
(11)where ρ and ρd are the density of gas and dust, v and vd their velocities, p the gas pressure, and ΦG the gravitational potential of the central star. The drag force fd between the gas and the dust is expressed in terms of the stopping time τs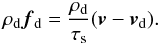 (12)The stopping time corresponds to the timescale of the coupling between gas and dust. A high stopping time corresponds to solids somewhat coupled to the gas, whereas the particles with τs ≪ 1 will strictly follow the gas displacements. The expression of the stopping time depends on the mean free path λ of the particle and eventually the Reynolds number of the flow. We assume here spherical grains with radius sp. The small particles with
(12)The stopping time corresponds to the timescale of the coupling between gas and dust. A high stopping time corresponds to solids somewhat coupled to the gas, whereas the particles with τs ≪ 1 will strictly follow the gas displacements. The expression of the stopping time depends on the mean free path λ of the particle and eventually the Reynolds number of the flow. We assume here spherical grains with radius sp. The small particles with 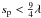 are in the Epstein regime with (Takeuchi & Lin 2002)
are in the Epstein regime with (Takeuchi & Lin 2002) 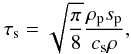 (13)where the
(13)where the 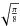 factor comes from the expression of the mean thermal velocity in 3D (Takeuchi & Artymowicz 2001), and the drag force is written as
factor comes from the expression of the mean thermal velocity in 3D (Takeuchi & Artymowicz 2001), and the drag force is written as 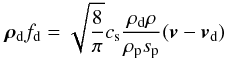 (14)with ρp the density of the individual solid particles. The internal density of a solid particle ρp is not to be confused with the density of the dust fluid ρd.
(14)with ρp the density of the individual solid particles. The internal density of a solid particle ρp is not to be confused with the density of the dust fluid ρd.
In the following, the particle species will be defined by the non-dimensional stopping time parameter 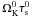 expressed in the midplane at the inner edge of the simulation. With an inner edge at 1 AU and a typical mass ratio of ρ0/ρp = 10-10 corresponding to an individual dust particle density of ρp = 1 g cm-3 we have
expressed in the midplane at the inner edge of the simulation. With an inner edge at 1 AU and a typical mass ratio of ρ0/ρp = 10-10 corresponding to an individual dust particle density of ρp = 1 g cm-3 we have 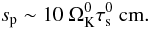 (15)We consider that each dust population corresponds to a dust size, but different stopping times could also correspond to the same size but different densities.
(15)We consider that each dust population corresponds to a dust size, but different stopping times could also correspond to the same size but different densities.
The back reaction of the dust on the gas is included in the simulation. From Eq. (12), one can define the gas stopping time τs,g as in 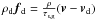 so
so 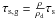 . This timescale for the back reaction decreases with increasing dust density. When the dust-to-gas ratio ρd/ρ is low, the dynamics are dominated by the gas. This is not the case any longer when the dust density is close to the gas density, and the back reaction of the dust on the gas cannot be neglected. Initially the back reaction is negligible but will become more and more important when the dust is concentrated in the vortices and approaches the gas density.
. This timescale for the back reaction decreases with increasing dust density. When the dust-to-gas ratio ρd/ρ is low, the dynamics are dominated by the gas. This is not the case any longer when the dust density is close to the gas density, and the back reaction of the dust on the gas cannot be neglected. Initially the back reaction is negligible but will become more and more important when the dust is concentrated in the vortices and approaches the gas density.
Extensive tests of the multi-fluid module of AMRVAC will be soon published, and first tests have already been presented in van Marle et al. (2011).
Characteristics of the eight dust populations.
3.2. Parameters
We performed eight simulations with the different populations of dust presented in Table 1. The range of dust sizes corresponds to the intermediate regime where the dust and the gas are partially coupled. The dust is added to the gas disk with a density of 1% of the initial gas density. The dust density is initially axisymmetric with a purely Keplerian velocity.
The simulation was run over 16 yr corresponding to three Keplerian rotations at the position of the vortices. The rotation period at the bump radius 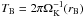 is used as a time unit.
is used as a time unit.
3.3. Validity of the model
Hersant (2009) has shown that the bi-fluid approximation where the dust is modelled as a pressureless fluid is only valid for an adimensional stopping time ΩKτs < 0.5 owing to the low velocity dispersion. This is the maximum value chosen at the inner edge of the disk, so the pressureless approximation is valid.
The model of the dust as a continuous fluid is valid if there are enough solid particles in each grid cell and enough collisions to define a mean state. These conditions are fulfilled as the Stokes number ΩKτs < 1.
The Epstein regime corresponds to particle sizes 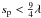 , where λ is the mean free path of the gas molecule. This condition is directly related to the Knudsen number Kn = λ/sp. Since the main constituent of the gas is molecular hydrogen, the mean free path is written as
, where λ is the mean free path of the gas molecule. This condition is directly related to the Knudsen number Kn = λ/sp. Since the main constituent of the gas is molecular hydrogen, the mean free path is written as 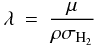 (16)where μ = 3.9 × 10-24g is the mean molecular weight of a 5:1 H2-He mixture, and σH2 = 2 × 10-15 cm2 is the cross section of molecular hydrogen. This gives a maximum grain size of 45 cm at 1 AU. The mean free path increases with distance to the central star as the gas density decreases. Because we consider here the region of the disk around 3 AU, the Epstein regime is valid for the grains we consider, with the maximum size around 5 cm. We also note that the Reynolds number is
(16)where μ = 3.9 × 10-24g is the mean molecular weight of a 5:1 H2-He mixture, and σH2 = 2 × 10-15 cm2 is the cross section of molecular hydrogen. This gives a maximum grain size of 45 cm at 1 AU. The mean free path increases with distance to the central star as the gas density decreases. Because we consider here the region of the disk around 3 AU, the Epstein regime is valid for the grains we consider, with the maximum size around 5 cm. We also note that the Reynolds number is 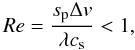 (17)which is consistent with the Epstein regime.
(17)which is consistent with the Epstein regime.
 |
Fig. 2 Radial velocity difference between dust and gas obtained in the simulation (dotted line), with the approach of Weidenschilling (1977) (dashed line). The upper and lower plots are obtained for |
 |
Fig. 3 Evolution of the midplane density of gas and 2 cm dust ( |
4. Results
4.1. Test of the dust radial drift
To test the numerical method in the context of protoplanetary disks, the results of the simulations were compared with the approach of Weidenschilling (1977). In the stationary limit, the difference between the radial velocity of the dust and the gas is given by 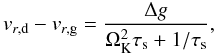 (18)with
(18)with 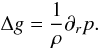 (19)The resulting radial velocities at the end of the simulations are plotted in Fig. 2 for populations 1 and 8 and compared to Eq. (18). Here, all the quantities have been azimuthally averaged to soften the dynamical effects of the spiral density waves and vortices. There is good agreement between the two approaches for all dust sizes, with a relative difference of about 3%.
(19)The resulting radial velocities at the end of the simulations are plotted in Fig. 2 for populations 1 and 8 and compared to Eq. (18). Here, all the quantities have been azimuthally averaged to soften the dynamical effects of the spiral density waves and vortices. There is good agreement between the two approaches for all dust sizes, with a relative difference of about 3%.
 |
Fig. 4 Maximum dust density relative to maximum gas density in the midplane and in a logarithmic scale as a function of time for different solid sizes. |
4.2. Time evolution
 |
Fig. 5 Midplane density of gas and dust for |
The time evolution of the gas and dust density over three Keplerian rotations are plotted in Fig. 3 for grains of intermediate size (2 cm). As the gas evolves, the vortices rotate during the simulation with the frequency given by the characteristics of the RWI. The dust follows this azimuthal displacement, while its concentration is modified by the presence of the vortices. Whereas the initial dust density is axisymetric, the vortices first seems to expel the dust from their centre: at t = 1.5TB the density of dust is then higher in the surroundings of the anticyclonic vortices than in their centres. This is a transitory phase since the primary effect of the vortices is to induce rotation around their centre. The length of the transitory phase is related to the stopping time (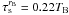 here) with a longer transitory phase for shorter stopping time when the dust is better coupled to the gas (in the limit of small solids: ΩKτs ≤ 1). The dust is then concentrated directly inside the high-pressure anticyclonic vortices. See also Fig. 6 showing the dust velocity streamlines, which is discussed in the next section. The decrease in the gas density in the vortices when the dust density reaches high values is discussed in Sect. 4.4.
here) with a longer transitory phase for shorter stopping time when the dust is better coupled to the gas (in the limit of small solids: ΩKτs ≤ 1). The dust is then concentrated directly inside the high-pressure anticyclonic vortices. See also Fig. 6 showing the dust velocity streamlines, which is discussed in the next section. The decrease in the gas density in the vortices when the dust density reaches high values is discussed in Sect. 4.4.
In Fig. 3 the colour bar used for the dust density changes from one plot to another. The reason is the constant increase in dust density. This is confirmed in Fig. 4, where the maximum value of the midplane dust density is plotted as a function of time. We recall that during the transitory phase, this maximum is not always reached at the centre of the vortices as can be seen in Fig. 3. In the first phase, the vortices collect the solids that are in their surroundings leading to a very fast increase in dust density. Then, for the populations that have reached the quasi-permanent state at the end of the simulation, namely those with 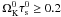 , the dust density continues to increase due to vertical settling and radial drift. This is also visible in Fig. 7, which is presented in the next section.
, the dust density continues to increase due to vertical settling and radial drift. This is also visible in Fig. 7, which is presented in the next section.
4.3. 3D dust concentration
The anticyclonic Rossby vortices effectively concentrate the solid particles with an efficiency depending on the dust size. Figure 5 shows the midplane densities of gas and dust at the end of selected simulations. The colour scale is the same for the gas density obtained in the different simulations but each dust population is plotted with a different colour scale because the values differ largely from one grain size to another. The 1 mm dust grains do not show a higher concentration inside the vortices even if some structures do appear. There is then a minimum size for the dust to be concentrated inside vortices on a rotation timescale. Due to the higher gas density in the anticyclonic vortices, the dust-to-gas ratio is even lower in these regions. In the midplane, the highest value of ρd/ρ is 0.015, corresponding to a small increase of 50% (Fig. 4). Indeed the smaller grains are coupled strongly to the gas and follow the gas streamlines plotted in Fig. 6. For larger particles, two different behaviours are observed at the end of the simulation. The 1 cm and smaller grains are in the transitory phase, as were the 5 cm grains at t = 2.1TB (Fig. 3). During this transitory phase, the dust density is lower in the centre of the vortices than in the surroundings. For the larger solids, such as the 2 cm population, the “stationary” phase is reached with the highest density in the centre of the anticyclonic vortices and a dust-to-gas ratio ρd/ρ ~ 0.4. For populations up to 3 cm the drag force of the dust on the gas is negligible and no important difference can be seen on the gas. The largest grains (5 cm) are highly concentrated in the five anticyclonic vortices reaching a dust-to-gas ratio ρd/ρ of the order of unity in the midplane (see also Fig. 10).
This fast concentration of dust is confirmed by the dust streamlines. The shape of the velocity streamlines are shown in Fig. 6 for both the gas and the 5 cm dust. The streamlines are calculated from the velocity field with a second-order Runge-Kutta integrator. No significative change is observed on the shape of the vortex streamlines of the gas when the dust is present. For both dust and gas the anticyclonic vortices have converging streamlines (corresponding to an upward flow), whereas the cyclonic vortices have diverging streamlines (corresponding to a downward flow). The streamlines corresponds either to a limit cycle around the vortex or to a direct displacement toward the centre in anticyclonic regions, the opposite is observed in cyclonic regions that expel the dust. It is interesting to note that the width of the dust vortex-like structures is larger than those of the gas. And the dust that reaches the border of these structures directly falls to the centre. The dust concentrated in the vortices was initially in a zone that is larger than the width of the vortices. The “feeding zone” has an approximate size of about ten times the width of the initial Gaussian density bump, which corresponds to about 1 AU in our case. Figure 7 shows the resulting midplane density profile averaged on the azimuthal direction, for the 5 cm grain population. This profile is characterised by a very high bump at the radius of the vortices but also a depletion in the surroundings. This depletion is not exactly symmetric toward the centre of the vortices, with a larger mass reduction in the inner region (r < rB). This is due to the global radial drift of the dust that refills the outward region, whereas the vortices forbid inward migration of dust. There is then a dust pile-up at the radius of the vortices.
 |
Fig. 6 Perturbed velocity streamlines of gas (left) and 5 cm grains (right) in a rotating frame. |
 |
Fig. 7 Mean midplane density (10-10g cm-3) of the |
 |
Fig. 8 Vertical density profiles in the vortices (r/r0 = 3) after 3 rotations for three different population of dust: |
One particularly interesting result of these simulations deals with the vertical stratification of the dust. This is shown in Fig. 8, where the dust density in the (ϕ,z) plane at the radius of the vortices is shown for different dust sizes. At the end of the simulation, the largest particles have settled and are concentrated in a very thin region (as can be seen on the upper plots). The presence of the vortices means that the larger grains ( ≥ 2 cm) do not form a continuous disk but a few piles with very high density corresponding to the positions of the five anticyclonic vortices.
The smaller grains (<2 cm) show a totally different vertical structure with a higher disk height, which is directly related to the dust size, but the same asymmetry is obtained with a thicker disk in the anticyclonic vortices. Unlike what could be expected for settling grains, the density of small particles is higher in the upper region than in the midplane (see for instance the 5 mm grains). This counter-intuitive result is related to the vertical displacement of the gas inside the vortices as plotted in Fig. 9 and detailed in Meheut et al. (2012a). This 3D structure of the vortices’ velocity streamlines is responsible for the positive vertical velocity of the small grains that are then lifted toward the upper region. The vertical profile of dust density in the centre of an anticyclonic vortex is presented in Fig. 10. Even with the log-log scale, the increase in density in the upper region is visible for the smaller grains (e.g.  ). Because the gas density decreases with height, the highest dust-to-gas ratio is then obtained in the upper region of the dust disk.
). Because the gas density decreases with height, the highest dust-to-gas ratio is then obtained in the upper region of the dust disk.
For each dust population, the gas density in the same vertical plane is also plotted. It should be noted that the vertical structure of the gas is the same for all grain sizes. Even the 5 cm grains with a high dust-to-gas ratio do not modify significantly the vertical extent of the gas. As obtained in our previous simulations, the height of the gas is not axisymmetric, with a thicker disk in the anticyclonic vortices.
4.4. Back reaction of the dust on the gas
The simulations include the back reaction of the dust on the gas. For most of the dust populations, this back-reaction is negligible thanks to a low dust-to-gas ratio. But for the 5 cm grains, the dust-to-gas ratio is of the order of unity in the anticyclonic vortices, and the back reaction modifies the evolution of the gas: the dust drags the gas. In the absence of the drag force, the dust rotates in Keplerian rotation, whereas the gas is sub-Keplerian in a negative pressure gradient. When the dust starts to affect the gas, it accelerates the rotation of the gas and the vortices amplitude decreases. While Johansen et al. (2004) observed a stretching of the vortex by differential rotation, our simulations with self-forming vortices show a split in two different vortices as shown in Fig. 11. This evolution appears only for the 5 cm grains, and no such behaviour is observed with smaller grains. This is correlated with the high dust-to-gas ratio reached with this dust population. The origin of this splitting of the vortices may be related to the evolution of the RWI under external forcing rather than to the heavy core instability (Chang & Oishi 2010), as the RWI is characterised by the presence of two Rossby waves, one on each side of the density maximum. Gas and dust mutually coupled are expected to trigger the streaming instability (Youdin & Goodman 2005). This instability starts to be relevant when the dust begins to drag the gas, and the simulations are performed up to this threshold.
In the absence of dust, the vortices rotate with nearly the azimuthal velocity of the gas at the density bump (r = 3 AU) which is Keplerian, so the vortices do approximatively three rotations over the simulation. See Meheut et al. (2012b) for the calculation of the vortices’s velocity when there is no back reaction of the dust on the gas. As the dust accelerates the rotation of the gas, the vortex frequency is no longer that of the wave amplified by the RWI. When not sustained by the instability, the vortices begin to decay. Of course, this applies to those vortices formed without dust and to those whose frequency is determined by the “classical” RWI. For this reason, a dusty RWI should be investigated, but this is beyond the scope of this paper.
5. Summary and outlooks
We have studied the concentration of dust particles in 3D vortices. To our knowledge this is the first time the dust-trapping mechanism has been explored in stable 3D Rossby vortices. We have first done a simulation of the self-consistent formation the vortices by the Rossby wave instability before including the dust particles. An important difference with the previous studies using analytical vortices (e.g. Kida 1981) is the presence of a vertical velocity in the inner part of the vortices. We have presented the dust-trapping properties of the 3D Rossby vortices. This mechanism is very efficient when the dust is only partially coupled to the gas (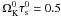 ), and a high dust density is reached in the midplane. The estimation of the dust mass concentrated in the vortices gives a value of approximately the mass of Mars in a sphere of radius 0.1 AU with a higher density reached in the centre.
), and a high dust density is reached in the midplane. The estimation of the dust mass concentrated in the vortices gives a value of approximately the mass of Mars in a sphere of radius 0.1 AU with a higher density reached in the centre.
 |
Fig. 9 Gas streamline in a vertical plane situated in an anticyclonic vortex. It shows the vertical displacements inside the vortices. The full 3D streamlines are shown in Meheut et al. (2012a). |
 |
Fig. 10 Vertical profile of dust and gas densities in an anticyclonic vortex on logarithmic scales. |
Those particles more coupled to the gas show a larger density in the upper region of the disk. For these intermediate size grains (mm to cm sizes), there is a competition between sedimentation toward the midplane and lifting toward the surface by the vertical velocity of the vortices. This high dust density in the upper region is of particular interest in the context of the forthcoming observation of protoplanetary disks but this needs to be confirmed by the use of a radiative transfer code with a full 3D approach. The results may differ from those obtained with a razor thin disk approach (Wolf & Klahr 2002; Regály et al. 2011).
 |
Fig. 11 Inverse of gas vortensity at t/TB = 3 for the simulation without any dust populations, and the two cases |
This mechanism is accordingly more convincing since its efficiency is the highest for the fastest drifting solids, namely when the stopping time is of the order of unity. Future work should study the growth of the instability in the presence of dust to understand how the dust modifies the instability. Moreover a simulation with multiple dust sizes in a multi-fluid simulation is necessary to understand how the small dust is concentrated if the vortices start to be accelerated by the larger particles. Furthermore, we have considered a Gaussian pressure bump without considering its formation process, which would give the proper shape of the bump, and then the characteristics, including amplitude, of the RWI. A global study, including accretion processes in the disk, is still needed to give the amplitude of the bump, the consequent number of vortices and then the amount of dust concentrated in such vortices. An important step in this direction was taken by Lyra & Mac Low (2012).
Finally, in this paper we associated a stopping time with a dust size and fixed density, but the opposite approach can also be used to study the behaviour of dust grains of the same size but different compositions.
Acknowledgments
This work was partially supported by the Swiss National Science Foundation. We thank M. Houck for his useful comments that helped to improve the manuscript.
References
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Benz, W. 2000, Space Sci. Rev., 92, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bracco, A., Chavanis, P. H., Provenzale, A., & Spiegel, E. A. 1999, Phys. Fluids, 11, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., & Oishi, J. S. 2010, ApJ, 721, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E., & Youdin, A. N. 2010, Ann. Rev. Earth Planet. Sci., 38, 493 [Google Scholar]
- de Val-Borro, M., Artymowicz, P., D’Angelo, G., & Peplinski, A. 2007, A&A, 471, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, C. 2009, in Cosmic Dust – Near and Far, eds. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 494 [Google Scholar]
- Drazin, P. G., & Reid, W. H. 2004, Hydrodynamic Stability (Cambridge University Press) [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., & Livio, M. 1999, ApJ, 523, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., & Livio, M. 2000, ApJ, 537, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Kenyon, S. J. 2010, MNRAS, 408, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Hersant, F. 2009, A&A, 502, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inaba, S., & Barge, P. 2006, ApJ, 649, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Oishi, J. S., Low, M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A., et al. 2012, J. Computat. Phys., 231, 718 [Google Scholar]
- Kida, S. 1981, J. Phys. Soc. Japan, 50, 3517 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. 2004, ApJ, 606, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Koller, J., Li, H., & Lin, D. N. C. 2003, ApJ, 596, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Koren, B. 1993, A robust upwind discretization method for advection, diffusion and source terms, Notes on numerical fluid mechanics, eds. C. B. Vreugdenhil, & B. Koren, 45, 117 [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., Lin, D. N. C., Garaud, P., & Turner, N. J. 2009, ApJ, 690, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Colgate, S. A., Wendroff, B., & Liska, R. 2001, ApJ, 551, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2012, ApJ, 754, 21 [Google Scholar]
- Lin, M.-K., & Papaloizou, J. C. B. 2011, MNRAS, 415, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Klahr, H. 2011, A&A, 527, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., & Mac Low, M.-M. 2012, ApJ, 756, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 491, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009a, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Zsom, A., Klahr, H., & Piskunov, N. 2009b, A&A, 497, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Keppens, R., Casse, F., & Benz, W. 2012a, A&A, 542, A9 [Google Scholar]
- Meheut, H., Yu, C., & Lai, D. 2012b, MNRAS, 2748 [Google Scholar]
- Paardekooper, S., Lesur, G., & Papaloizou, J. C. B. 2010, ApJ [Google Scholar]
- Petersen, M. R., Julien, K., & Stewart, G. R. 2007a, ApJ, 658, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Stewart, G. R., & Julien, K. 2007b, ApJ, 658, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2011, MNRAS, 1709 [Google Scholar]
- Shen, Y., Stone, J. M., & Gardiner, T. A. 2006, ApJ, 653, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M., & Varnière, P. 2006, ApJ, 652, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Artymowicz, P. 2001, ApJ, 557, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2002, ApJ, 581, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Babiano, A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, G. 1996, Astrophys. Lett. Comm., 34, 245 [Google Scholar]
- van Marle, A. J., Meliani, Z., Keppens, R., & Decin, L. 2011, ApJ, 734, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., & Klahr, H. 2002, ApJ, 578, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, C., & Li, H. 2009, ApJ, 702, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, C., Li, H., Li, S., Lubow, S. H., & Lin, D. N. C. 2010, ApJ, 712, 198 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Amplitude of the total density perturbation and the main modes on a logarithmic scale as a function of time. The solid line is a fit of the linear growth giving a growth rate of 0.17ΩK(rB). |
| In the text | |
 |
Fig. 2 Radial velocity difference between dust and gas obtained in the simulation (dotted line), with the approach of Weidenschilling (1977) (dashed line). The upper and lower plots are obtained for |
| In the text | |
 |
Fig. 3 Evolution of the midplane density of gas and 2 cm dust ( |
| In the text | |
 |
Fig. 4 Maximum dust density relative to maximum gas density in the midplane and in a logarithmic scale as a function of time for different solid sizes. |
| In the text | |
 |
Fig. 5 Midplane density of gas and dust for |
| In the text | |
 |
Fig. 6 Perturbed velocity streamlines of gas (left) and 5 cm grains (right) in a rotating frame. |
| In the text | |
 |
Fig. 7 Mean midplane density (10-10g cm-3) of the |
| In the text | |
 |
Fig. 8 Vertical density profiles in the vortices (r/r0 = 3) after 3 rotations for three different population of dust: |
| In the text | |
 |
Fig. 9 Gas streamline in a vertical plane situated in an anticyclonic vortex. It shows the vertical displacements inside the vortices. The full 3D streamlines are shown in Meheut et al. (2012a). |
| In the text | |
 |
Fig. 10 Vertical profile of dust and gas densities in an anticyclonic vortex on logarithmic scales. |
| In the text | |
 |
Fig. 11 Inverse of gas vortensity at t/TB = 3 for the simulation without any dust populations, and the two cases |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.