| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219651 | |
| Published online | 29 August 2012 | |
Fundamental properties of the Population II fiducial stars HD 122563 and Gmb 1830 from CHARA interferometric observations
1 Laboratoire Lagrange, UMR 7293, CNRS, Observatoire de la Côte d’Azur, Université de Nice Sophia-Antipolis, Nice, France
e-mail: orlaghc@gmail.com
2 Center for High Angular Resolution Astronomy, Georgia State University, PO Box 3965, Atlanta, Georgia 30302-3965, USA
3 Hubble Fellow
4 LESIA-Observatoire de Paris, CNRS UMR 8109, UPMC, Univerité Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
5 Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP. 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
6 European Southern Observatory, Alonso de Córdova 3107, Casilla 19001, Santiago 19, Chile
7 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
8 Centre for Star and Planet Formation, Natural History Museum of Denmark, University of Copenhagen, Øster Voldgade 5-7, 1350 Copenhagen, Denmark
9 Astronomical Observatory/Niels Bohr Institute, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
10 Lowell Observatory, 1400 West Mars Hill Road, Flagstaff, Arizona, 86001, USA
Received: 22 May 2012
Accepted: 19 July 2012
We have determined the angular diameters of two metal-poor stars, HD 122563 and Gmb 1830, using CHARA and Palomar Testbed Interferometer observations. For the giant star HD 122563, we derive an angular diameter θ3D = 0.940 ± 0.011 milliarcseconds (mas) using limb-darkening from 3D convection simulations and for the dwarf star Gmb 1830 (HD 103095) we obtain a 1D limb-darkened angular diameter θ1D = 0.679 ± 0.007 mas. Coupling the angular diameters with photometry yields effective temperatures with precisions better than 55 K (Teff = 4598 ± 41 K and 4818 ± 54 K – for the giant and the dwarf star, respectively). Including their distances results in very well-determined luminosities and radii (L = 230 ± 7 L⊙, R = 24.1 ± 1.1 R⊙ and L = 0.213 ± 0.002 L⊙, R = 0.665 ± 0.014 R⊙, respectively). We used the CESAM2k stellar structure and evolution code in order to produce models that fit the observational data. We found values of the mixing-length parameter α (which describes 1D convection) that depend on the mass of the star. The masses were determined from the models with precisions of <3% and with the well-measured radii excellent constraints on the surface gravity are obtained (log g = 1.60 ± 0.04, 4.59 ± 0.02 dex, respectively). The very small errors on both log g and Teff provide stringent constraints for spectroscopic analyses given the sensitivity of abundances to both of these values. The precise determination of Teff for the two stars brings into question the photometric scales for metal-poor stars.
Key words: stars: fundamental parameters / stars: individual: HD 122563 / stars: low-mass / stars: Population II / Galaxy: halo / stars: individual: HD 103095
© ESO, 2012
1. Introduction
Metal-poor stars are some of the oldest stars in the Galaxy and thus reflect the chemical composition of Galactic matter at the early stages of Galactic evolution. The determination of accurate observed fundamental properties, and in particular their location in the Hertzsprung-Russell (HR) diagram, is a key requirement if we aim to constrain the unobservable properties such as mass, age, and initial helium content by using stellar models. Among the most controversial observed parameter is the effective temperature (Teff) which can vary by more than 200 K for metal-poor stars from one method to another (see the PASTEL catalogue, Soubiran et al. 2010). In particular, local thermodynamic equilibrium (LTE) is usually assumed and non-LTE (NLTE) effects must be included in spectroscopic analyses especially for metal-poor stars where these effects are enhanced (Thévenin & Idiart 1999; Andrievsky et al. 2010; Merle et al. 2011) and this leads to even more discrepancy between literature values. One solution is to measure the angular diameter and convert this to Teff to provide a direct determination.
The large majority of metal-poor stars belong to the halo or the old disk of the Galaxy which means that their apparent magnitude and or angular diameters are extremely small and difficult to measure. However, some instruments, in particular those on the CHARA array (ten Brummelaar et al. 2005) are very capable of working at short wavelengths on long baselines to obtain the required angular resolution. Among the most exciting possible targets with CHARA working in the K band are HD 122563 (=HR 5270, HIP 68594, mV = 6.19 mag) and Gmb 1830 (=HD 103095, LHS 44, HIP 57939, mV = 6.45 mag) whose mean metallicities [Z/X] s1 are ~ –2.3 dex and –1.3 dex, respectively (see discussion in Sect. 4.1), where Z and X denote the metallicity and hydrogen (absolute) mass fraction in the star and the subscript refers to the observed surface value.
HD 122563, a standard example of a very metal-poor field giant (Wallerstein et al. 1963; Wolffram 1972), has been extensively studied and presents similarities with metal-poor giants found in globular clusters. Gmb 1830 is a metal-poor halo dwarf star recognized as exhibiting depleted Li (Deliyannis et al. 1994; King 1997) when compared to the mean value of halo dwarf stars (Spite & Spite 1993; Ryan 2005). It is also the nearest halo dwarf and has an excellent parallax measurement. Combining interferometric measurements of these stars with other already measured old moderately metal-poor stars, such as μ Cas ( [Z/X] s = −0.5 dex, Boyajian et al. 2008), offers an excellent opportunity to constrain the Teff scale of metal-poor stars over a wide range of metallicities with possible implications for Teff calibrations of globular cluster stars. In Table 1 we summarize some of the most recent determinations of the atmospheric properties of both targets. Note that HD 122563 and Gmb 1830 have also been defined as benchmark stars for the Gaia mission under the SAM2 working group.
Not only are temperature scales for metal-poor stars controversial, but stellar structure and evolution models often predict higher Teff than those observed for these stars (see e.g. Fig. 2 of Lebreton 2000). The difficulty encountered when trying to match evolutionary tracks to the observational data not only severely inhibits the determination of any fundamental properties but any chance of improving or testing the physics in the models is also limited.
Considering the difficulties mentioned above, in this paper we aim to determine accurate fundamental properties of HD 122563 and Gmb 1830 based on interferometric observations (Sect. 2). In Sect. 3 we present our analysis of the observations to determine the angular diameters of both stars. We then determine the observed values of Teff, luminosity L, and radius R, and subsequently use stellar models to constrain the unobservable properties of mass M, initial metal and helium content Zi,Yi, mixing-length parameter α and age (Sect. 4). We also predict their global asteroseismic properties in order to determine if such observations could further constrain the models.
Most recent photometric and spectroscopic determinations of atmospheric parameters for the target stars.
2. Observations
The observations were collected at the CHARA Array (ten Brummelaar et al. 2005), located at Mount Wilson Observatory (California), together with two beam combining instruments: CHARA Classic and FLUOR. CHARA Classic (ten Brummelaar et al. 2005) is a two-telescope, pupil-plane, open-air beam combiner working in both the H and K′ bands, and our observations correspond to the K′ band (the central wavelength is λ = 2.141 μm, from Bowsher et al. 2010). The raw data were reduced using the pipeline described in ten Brummelaar et al. (2005). FLUOR (Coudé du Foresto et al. 1998; Mérand et al. 2006) is a two-telescope beam combiner, but uses single-mode optical fibers for recombination. Single-mode fibers efficiently reduce the perturbations induced by the turbulent atmosphere on the stellar light wavefront, as the injected light corresponds only to the mode guided by the fiber (Ruilier 1999; Coudé du Foresto 1998). Most of the atmospherically corrupted part of the wavefront is lost into the cladding, and the beam combination therefore occurs between two almost coherent beams. This results in an improved stability of the measured fringe contrast. The FLUOR data reduction pipeline (Mérand et al. 2006; see also Kervella et al. 2004b) is based on the Fourier algorithm and was developed by Coudé du Foresto et al. (1997).
We observed HD 122563 and Gmb 1830 in late 2007 and 2008 with FLUOR and Classic. The corresponding visibility measurements V and uncertainties σ(V) are listed in Table 2 along with the projected baseline B and the baseline position angle PA measured clockwise from North. To monitor the interferometric transfer function, we interspersed the observations of our two science targets with calibrator stars. The calibrators for the FLUOR observations were selected from the catalog by Mérand et al. (2005), and these are listed in Table 3, and those for the CHARA Classic observations used the calibrators presented in Table 4.
CHARA observations of HD 122563 and Gmb 1830.
FLUOR calibrator stars.
CHARA classic calibrator stars.
PTI observations of HD 122563.
We also retrieved archival observations of HD 122563 in the K band obtained with the Palomar Testbed Interferometer (PTI) (Colavita et al. 1999) between 1999 and 2002, and these are listed in Table 5. The data processing algorithm that was employed to reduce the PTI observations has been described in detail by Colavita (1999). Due to the shorter baselines, the PTI observations resolve HD 122563 marginally, and therefore do not strongly constrain its angular diameter. However, thanks to the relatively large number of observations, they provide an independent method for testing any bias in the CHARA observations.
3. From visibilities to limb-darkened angular diameters
We employed a non-linear, least-squares fitting routine in IDL (MPFIT, Markwardt 2009) to fit uniform disk and limb-darkened visibility functions for a single star to the calibrated data points (see Hanbury Brown et al. 1974; Boyajian et al. 2012). We obtained a uniform disk diameter for HD 122563 and Gmb 1830 of θUD = 0.924 ± 0.011 mas and θUD = 0.664 ± 0.015 mas, respectively. We used the linear limb-darkening coefficients from Claret (2000) assuming [Fe/H] = −2.5, Teff = 4500 K, and log g = 1.0 for HD 122563 and [Fe/H] = −1.5, Teff = 5000 K, and log g = 4.5 for Gmb 1830. The assumptions on these parameters on the adopted coefficients have minimal influence on the final limb-darkened diameter, adding uncertainties of only a few tenths of a percent, well within the errors of our diameter measurements. We obtained θLD = 0.948 ± 0.012 and θLD = 0.679 ± 0.015 for HD 122563 and Gmb 1830, respectively.
We obtained a reduced χ2 value of 0.28 for HD 122563 and 0.18 for Gmb 1830 from the fits. These values, much less than 1, are indicative of our individual measurement errors being over estimated. We show the data and the visibility function fits for HD 122563 and Gmb 1830 in Figs. 1 and 2. The results from the fits to the data yield 1D limb-darkened angular diameters of HD 122563 and Gmb 1830 with a precision of ~2% (see Table 6), respectively.
Angular diameters.
 |
Fig. 1 Calibrated observations for PTI (black crosses), CHARA Classic (blue circles) and CHARA FLUOR (red squares) data plotted with the 1D limb-darkened visibility function fit for HD 122563. See Sect. 3 for details. |
 |
Fig. 2 Calibrated observations for CHARA Classic (blue circles) and CHARA FLUOR (red squares) data plotted with the limb-darkened visibility function fit for Gmb 1830. See Sect. 3 for details. |
3.1. 3D limb-darkened angular diameter for HD 122563
Convection plays a very important role in the determination of stellar limb-darkening. It has been shown that a 3D hydrodynamical treatment of the surface layers can lead to a significant change of temperature gradients compared to 1D hydrostatic modeling, which consequently affects the center-to-limb intensity variation (e.g. Allende Prieto et al. 2002; Bigot et al. 2006, 2011; Pereira et al. 2009; Chiavassa et al. 2010; Hayek et al. 2012). The 3D/1D limb-darkening correction for a giant star can be very significant (see Fig. 6 of Chiavassa et al. 2010) and is generally much stronger than for a dwarf star. We therefore used a radiative-hydrodynamical (RHD) surface convection simulation of a red giant for HD 122563 to determine the 3D limb-darkened angular diameter. The parameters of the model are ⟨ Teff ⟩ = 4627 ± 14 K (temporal average and standard deviation of the effective temperature), [Fe/H] = −3.0, and log g = 1.6 (Collet et al. 2009; Chiavassa et al. 2010). The computational domain of the RHD simulation represents only a small portion of the stellar surface (~1/30 of the circumference), however, it is sufficiently large to contain enough granules (~10−15) at each time step of the simulation. Hydrodynamical equations are solved on a staggered mesh with a conservative scheme. Details of the computation can be found in Collet et al. (2009).
We computed emergent intensity for a representative series of simulated snapshots and for wavelengths corresponding to the FLUOR filter (2.14 ± 0.26 μm, equivalent to that for CHARA) using the 3D pure-LTE3 radiative transfer code Optim3D (Chiavassa et al. 2009). It considers the Doppler shifts due to convective motions. Radiative transfer is solved monochromatically using pre-tabulated extinction coefficients for the same chemical compositions as the RHD simulations. It also uses the same extensive atomic and molecular opacity data as the latest generation of MARCS models (Gustafsson et al. 2008).
 |
Fig. 3 Best matching 3D-RHD synthetic visibility curves and PTI (black crosses), Classic (blue circles), and FLUOR (red squares) data for HD 122563. |
For each time-step, we solve the radiative transfer equation for different inclinations with respect to the vertical whose cosines are μ ≡ [1.000, 0.989, 0.978, 0.946, 0.913, 0.861, 0.809, 0.739, 0.669, 0.584, 0.500, 0.404, 0.309, 0.206, 0.104]. From these limb-darkened intensities, we derived the monochromatic visibility curves using the Hankel Transform. The visibilities are then averaged with the transmission function of the instrument in the considered filter wavelength domain. The procedure used in this work is the same as that of Bigot et al. (2011). The synthetic visibilities are used to fit the interferometric K band observations given in Tables 2 and 5.
Figure 3 displays the best fit of the visibility curve to the data that results in an angular diameter of θ3D = 0.940 ± 0.011 mas (Table 6) with a χ2 = 0.35. Its value lies between that of the uniformed disk and 1D limb-darkened diameters. This is a consequence of the fact that in realistic 3D hydrodynamical treatment of the stellar surface, the emergent intensity is less limb-darkened than the 1D hydrostatic case. We note that the choice of the exact fundamental parameters of the 3D simulation does not influence the limb-darkened intensity and the derived angular diameter by much.
The 3D/1D correction is important for determining the zero point of the effective temperature scale: Chiavassa et al. (2010) (Table 3) showed that, in the case of metal-poor stars like the one analyzed in this work, θ3D/θ1D ~ 2% in the K band (3.5% in the visible). This can result in corrections to the effective temperature of ~40 K in the K band. In this case the resulting correction to the effective temperature is ~15 K (see Sect. 4.1).
We note that González Hernández & Bonifacio (2009) predict 1D limb-darkened angular diameters for both of these stars using the infra-red flux method (IRFM)4. For HD 122563 they predict θ1D = 0.84 ± 0.04 mas and for Gmb 1830 θ1D = 0.61 ± 0.02 mas; both values are lower than our derived values. For HD 122563 this could be due to the fact that they use 2MASS photometry that is saturated for this star (saturation limit Ks ~4.0, Cutri et al. 2003).
Observed parameters of HD 122563 and Gmb 1830.
4. Constraints on stellar evolutionary models
4.1. Observed parameters
The list of observed parameters are summarized in the top part of Table 7. The magnitudes in the V band are taken from Johnson et al. (1966), those in the K bands are from Ducati (2002) for HD 122563 and Cutri et al. (2003) for Gmb 1830, and the Hipparcos parallax from van Leeuwen (2007). For HD 122563, we estimate an interstellar extinction of AV = 0.01 mag based on its galactic coordinates and distance. The bolometric flux Fbol is obtained by combining mV, AV, and the bolometric correction BCV, where BCV is obtained by interpolating the tables for giant stars from Alonso et al. (1999b). We started with an initial Teff of 4530 K (and [Fe/H] = −2.5) to calculate BCV from the tables, and then used this value to determine an initial Fbol. Using the initial Fbol and the derived θLD we determined Teff (see below). This new Teff was then used to rederive BCV, Fbol and Teff, and we iterated until we converged on the final Teff of 4582 K using BCV = −0.472 for θ1D and 4598 K using BCV = −0.466 for θ3D. We note that adopting these Teff and interpolating the tables from Houdashelt et al. (2000) yields BCV within our error bars (BCV ~ −0.46). For Gmb 1830, we used Fbol and AV from Boyajian et al. (2012), and then indirectly calculated BCV. We do not subsequently use BCV in this work but we report the value for reference. Both the 1D and 3D limb-darkened angular diameters θLD are given for HD 122563 and the 1D diameter is given for Gmb 1830 (see Table 6). The surface brightness relations from Kervella et al. (2004a,c) were used to provide an estimate of the 1D limb-darkened angular diameter θpred. The predicted values are lower than the derived values, although for HD 122563 the agreement is quite good (θpred = 0.928 mas, θ1D = 0.948 mas). These relations have been calibrated with a large sample of stars. However, the obvious lack of reliable measurements of metal-poor stars may lead to slight biases in the angular diameters predicted using these methods.
Combining the above mentioned measurements we determined the observed or model-independent fundamental properties of both stars; absolute magnitude MV, Teff, L, and R, where Teff is derived using the equation 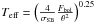 , σSB is the Stephan-Boltzmann constant and θ is the limb-darkened angular diameter.
, σSB is the Stephan-Boltzmann constant and θ is the limb-darkened angular diameter.
The most recently published NLTE iron abundance analysis of HD 122563 yielded [Fe/H] = −2.56 + − 0.07 dex using log g = 1.60 and Teff = 4600 K (Mashonkina et al. 2011). Mashonkina et al. (2008) derived NLTE abundances for two α elements: [Mg/H] = −2.2 and [Ca/H] = −2.3 to − 2.4 dex. In the PASTEL catalogue there are 15 spectroscopic determinations of [Fe/H] since 1990 (mostly LTE) with a mean value of − 2.7 dex, or 5 determinations since 2000 with a mean of − 2.6. The mean metallicity, which is a mixture of Fe peak and α elements then becomes [Z/X] s = −2.3 ± 0.1 dex. Spectroscopic log g values typically vary between 1.1 and 1.5 dex (see Table 1).
For Gmb 1830, Gehren et al. (2006) derived [Fe/H] = −1.35 ± 0.10 dex from Fe II lines, which are not supposed to be affected by NLTE, and an NLTE [Mg/Fe] abundance of +0.3. Using the latter for all α elements, this implies a [Z/X] s = −1.3 ± 0.1 dex. The spectroscopic log g of this star has been estimated to be ~4.70 (Thévenin & Idiart 1999) from NLTE studies but using a temperature hotter by about 200 K. The Teff reported in this work would result in a downward revision of this number.
 |
Fig. 4 HR diagram showing the observational error boxes for HD 122563 (left) and Gmb 1830 (right). Both figures show stellar models that pass through the error boxes which allow us to determine the stellar model properties and their uncertainties. Each panel shows the adopted central models (with arrows) obtained by considering the HR and metallicity constraints. Other models are also indicated to highlight the parameter uncertainties and correlations. Refer to Sects. 4.3.1 and 4.3.2 for details. |
Stellar properties and 1σ uncertainties derived from modeling HD 122563 (no atomic diffusion) and Gmb 1830 (with atomic diffusion).
4.2. CESAM2k models
In order to interpret the observations of HD 122563 and Gmb 1830 we used the CESAM2k stellar evolution and structure code (Morel 1997; Morel & Lebreton 2008). We tested the models using three different equations of state (EOS): the classical EFF EOS (Eggleton et al. 1973) with/without Couloumb corrections (CEFF/EFF), and the OPAL EOS (Rogers et al. 1996), and we found small differences in the derived parameters for Gmb 1830 only. For all of the models we used the OPAL opacities (Rogers & Iglesias 1992) supplemented with Alexander & Ferguson (1994) molecular opacities. The p-p chain, CNO, and triple-α nuclear reactions were calculated using the NACRE rates (Angulo 1999). We adopted the solar abundances of Grevesse & Noels (1993) (Z⊙ = 0.017, X⊙ = 0.694) and used the MARCS model atmospheres (Gustafsson et al. 2003). Microscopic diffusion was taken into account for Gmb 1830 and follows the treatment described by Burgers (1969), and we introduced extra mixing by employing a parameter, Reν = 1, as prescribed by Morel & Thévenin (2002) in order to slow down the depletion of helium and heavy elements. For HD 122563 no observable difference is found between diffusion and non-diffusion models for giants, except a small effect on the age of the star, i.e., for the same parameters the model with diffusion fits the observational data with an age ~ 0.3 Gyr older than the non-diffusion model. Convection in the outer envelope is treated by using the mixing-length theory described by Eggleton (1972), where l = αHp is the mixing-length that tends to 0 as the radiative/convective borders are reached, Hp is the pressure scale height, and α is an adjustable parameter. To match the solar luminosity, Teff, and oscillation frequencies (while including diffusion) we find a value of α = 2.04. We note that we did not include convective overshooting in our models because the primary effect that this extra parameter has on the determination of the stellar model is the age. This means that it is possible to find two equivalent stellar models with the same stellar parameters that differ only by age and the value of the overshoot parameter. Since we have no observable constraint to distinguish between these two parameters we chose not to include it.
Each stellar model is defined by a set of input model parameters – mass M, initial helium content Yi, initial metal to hydrogen ratio Zi/Xi, age t, and the mixing-length parameter α – and these result in model observables, such as a model Teff and a model L. By varying the parameters M, Yi, Zi/Xi, t, and α we aimed to find models that fitted the luminosity, Teff, and metallicity constraints as outlined in Table 7. We stopped the evolution of the models when an age of 14 Gyr was reached. For HD 122563 we chose to use the constraints from the more realistic 3D models, although we note that the difference between the 1D and 3D constraints leads to only very slight changes in the parameters of the stellar models (see Sect. 4.3.1 below).
4.3. Stellar parameters
Figure 4 shows two HR diagrams with the observational error boxes of both stars (left/right = HD 122563/Gmb 1830) as well as some models that lie somewhat away from the central position of the box, illustrative of the uncertainties that we find in the stellar parameters (see below). Table 8 lists the stellar parameters for both stars using the classical EFF, and for Gmb 1830 we also give the stellar properties for the CEFF and OPAL EOS models.
Given the few independent observational constraints and the large number of adjustable parameters in the models, a classical error analysis is not possible for both stars. In order to estimate the uncorrelated uncertainties we changed each of the reference parameters of the models individually until we reached the edges of the error box in the HR diagram, or the limits of each parameter, e.g. we did not test Yi < 0.20. These are the uncertainties that are given in the top part of Table 8. For the uncertainty in the age we give the 1σ uncertainty which corresponds to the central models approaching the upper and lower limit in luminosity (first number) and we also give the range of possible ages while considering the uncertainties in the four model parameters (second uncertainty). We also list the model observables and their uncertainties in the lower part of the table. We note that the uncertainties in the model observables cover the full range of values while considering the individual changes in each of the four model parameters.
4.3.1. HD 122563
For HD 122563 using the EFF EOS description we found a best model with M = 0.855 M⊙, Yi = 0.245, α = 1.31, and t = 12.6 Gyr. We fixed Zi/Xi = 0.0001 in order to have the correct observed [Z/X] s. This model is illustrated in Fig. 4 (left panel) by the thick line and is clearly labeled. We also show some models which illustrate the reported uncertainties: the black continuous line shows a model when α is changed by 0.08, the red continuous line shows the central model when Yi is decreased by 1σ, and finally the red dashed-dotted line shows the effect of increasing the mass by 1σ. We note that if we increase the mass to more than 0.88 M⊙ then the age of the model becomes too small (<10 Gyr) if we are to consider the giant a halo star. We also found correlations among the parameters M, Yi, and α, and adjusting two of the three at a time by a small amount reproduces the position of the central model, e.g. if we fix M then ΔY = + 0.01 < = > Δα = −0.01. However, these correlations are adequately accounted for in the uncertainties.
The dotted error box shows the constraints if we consider the 1D limb-darkened angular diameter. The stellar parameters of the model that passes through the center of the box need small adjustments when compared to the 3D diameter constraints. In particular, decreasing either M or Yi alone by less than 1σ or decreasing α by ~0.03 (or a combination of the three) would reproduce the central position of the error box with a slightly higher age. If the temperature constraint were even lower, then the only viable option would be reducing the mixing-length parameter α, because reducing M or Yi by much more would result in a model that fails to reach the minimum luminosity before 14 Gyr.
Inspecting the stellar parameters in Table 8 we highlight the excellent precision obtained in the mass of this single star. Generally such precisions can only be obtained if the star is in a binary system, where the solutions are then model-independent. Combining this value with the well-determined radius yields a very precisely determined log g (=1.60 ± 0.04 dex). This value is larger than most values used for spectroscopic analyses which typically ranges from 1.1 − 1.5 dex (see Table 1). More recent work using 3D hydro-dynamical simulations for stellar atmospheres quote values of 1.1 − 1.6 dex (see e.g. Barbuy et al. 2003; Collet et al. 2009; Ramírez et al. 2010).
4.3.2. Gmb 1830
In Table 8 right three columns we summarize the stellar parameters for Gmb 1830 using the EFF, CEFF, and OPAL EOS. In Fig. 4 we show the central model for the EFF EOS (arrow with “EFF”) with illustrative uncertainties. The model parameters are M = 0.635 ± 0.025 M⊙, Yi = 0.235 ± 0.025, [Zi/Xi] = 0.0016 ± 0.0004, α = 0.68 ± 0.10, and 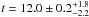 . We also show a CEFF and OPAL EOS evolution track using the central parameters obtained with the EFF model. A qualitative difference between the three EOS is notable, however, considering the uncertainties in the stellar parameters, these differences are not significant.
. We also show a CEFF and OPAL EOS evolution track using the central parameters obtained with the EFF model. A qualitative difference between the three EOS is notable, however, considering the uncertainties in the stellar parameters, these differences are not significant.
The uncertainties reported in Table 8 do not consider all of the correlations among the parameters. For example, reducing the mass by 1σ implies a necessary increase in Yi by 1σ in order to remain inside the error box and vice versa. In Fig. 4 we show effects of the uncertainties on the central model; the dotted black line shows the effect of decreasing α by 0.10, the dashed black line shows the effect of decreasing Zi/Xi by 1σ (denoted by ΔZ in figure), and the red continuous line right of the central model is when the mass is decreased by 1σ and Yi increased by 1σ. We note that by decreasing/increasing the mass or Yi alone leads to a very young stellar model (not consistent with a halo star), a model that is too hot, or at the age of 14 Gyr the luminosity does not reach the minimum required 0.210 L⊙.
4.4. Asteroseismic constraints
In Table 8 we predict two global asteroseismic quantities ⟨ Δν ⟩ and νmax based on scaling relations (Brown & Gilliland 1994; Kjeldsen & Bedding 1995) corresponding to the reference models. Both quantities are proportional to the mass and radius of the star, with the latter also having a small Teff-dependence; 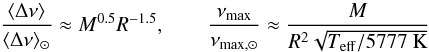 (1)where ⟨ Δν ⟩ ⊙ = 134.9 μHz and νmax, ⊙ = 3,050 μHz (Kjeldsen & Bedding 1995), and R and M are in solar units. Although the relations are approximate, they have been found to work quite well, e.g. Bedding & Kjeldsen (2003); Stello et al. (2008). ⟨ Δν ⟩ is the characteristic spacing between consecutive radial overtones of the same mode degree seen in the power (frequency) spectrum of a star with sun-like oscillations (e.g. see Fig. 6 from Butler et al. 2004), and it is proportional to the square root of the mean density of the star. Because it is a repetitive pattern (similar to a periodicity), it is relatively easy to determine from even low signal/noise data (see e.g. Huber et al. 2009; Mosser & Appourchaux 2009; Roxburgh 2009; Mathur et al. 2010; Verner et al. 2011 who discuss different methods to determine this value). The value of νmax is the frequency corresponding to the maximum amplitude of the bell-shaped amplitude/power spectrum, and it is also a quantity that can be more easily observed than, for example, individual oscillation modes.
(1)where ⟨ Δν ⟩ ⊙ = 134.9 μHz and νmax, ⊙ = 3,050 μHz (Kjeldsen & Bedding 1995), and R and M are in solar units. Although the relations are approximate, they have been found to work quite well, e.g. Bedding & Kjeldsen (2003); Stello et al. (2008). ⟨ Δν ⟩ is the characteristic spacing between consecutive radial overtones of the same mode degree seen in the power (frequency) spectrum of a star with sun-like oscillations (e.g. see Fig. 6 from Butler et al. 2004), and it is proportional to the square root of the mean density of the star. Because it is a repetitive pattern (similar to a periodicity), it is relatively easy to determine from even low signal/noise data (see e.g. Huber et al. 2009; Mosser & Appourchaux 2009; Roxburgh 2009; Mathur et al. 2010; Verner et al. 2011 who discuss different methods to determine this value). The value of νmax is the frequency corresponding to the maximum amplitude of the bell-shaped amplitude/power spectrum, and it is also a quantity that can be more easily observed than, for example, individual oscillation modes.
Because the radii and effective temperatures of these stars are well determined, the predicted seismic quantities depend only on the mass of the star. If we substitute directly the derived mass ranges into the equations then we can predict the range of possible values for these quantities corresponding to the central model, i.e. not taking into account the changes in α, Yi or Zi/Xi. For Gmb 1830 we find that for masses = [0.62, 0.64, 0.66] M⊙ we calculate νmax = [4773, 4927, 5081] μHz and ⟨ Δν ⟩ = [196, 199, 203] μHz, which correspond to typical periods of approximately 4 minutes. If we can detect these values, even with poor precision we will still be able to select the optimal mass range and discard certain solutions. We note that both M and Yi are very highly correlated, and so fixing M will present interesting constraints on Yi. Performing such observations from ground-based instrumentation should yield successful results (e.g. a 2+ m telescope equipped with a highly efficient and stable spectrograph). For HD 122563 we find for M = [0.84, 0.86, 0.88] M⊙, νmax = [5.03, 5.15, 5.26] μHz and ⟨ Δν ⟩ = [1.05, 1.06, 1.07] μHz. The dominant periods are approximately 2.5 days, and observations from ground-based instrumentation would be difficult. In order to use asteroseismic data to help constrain the models for HD 122563, we would require seismic data from space-borne instruments, such as with the CoRoT or Kepler missions, to provide the necessary precision and determine the individual oscillation modes.
5. Conclusions
We have determined the Teff, L, and R of HD 122563 and Gmb 1830 by using K band interferometric measurements (Table 7) and 3D/1D limb-darkening for the giant/dwarf. We find angular diameters of θ3D = 0.940 ± 0.011 mas and θ1D = 0.679 ± 0.015 mas for HD 122563 and Gmb 1830, respectively, and these convert into Teff = 4598 ± 41 K for HD 122563 and Teff = 4818 ± 54 K for Gmb 1830. These new precision temperatures increase the well-known difficulty of fitting the error boxes of these two metal-poor stars with evolutionary tracks. Using the CESAM2k stellar structure and evolution code we found that we could match models to the data by using values of the mixing length (the parameter α) very different from that of the Sun. We found values of α = 0.68 and 1.31 for the 0.63 M⊙ dwarf star and the 0.86 M⊙ giant, respectively. The order of these values seems consistent with recent model analyses (Yıldız et al. 2006; Kervella et al. 2008). We found that different equations of state lead to qualitatively but not quantitively different model parameters for the dwarf star but not for the giant. The initial helium content comes out similar to the big-bang value, the deduced masses are low and their ages are high, consistent with expected values for metal-poor halo stars (see Table 8). The masses are determined with a few percent precision and coupling these with the radii yields well-constrained values of log g. For the giant star we found log g = 1.60 ± 0.04 somewhat higher than the typical values (1.1 − 1.5) adopted by spectroscopic analyses according to the PASTEL catalogue (Soubiran et al. 2010) and for the dwarf star we obtain log g = 4.59 ± 0.02 dex. Barbuy et al. (2003) determined the O abundance of HD 122563 assuming two different (both justified) values of log g, and they concluded that their resulting [O/Fe] = +0.7 abundance seemed most consistent when they adopt the Hipparcos5 log g = 1.5 and not the value determined from ionization equilibrium of Fe, log g = 1.1, a result due possibly to NLTE effects. This work supports their O determination. With both log g and Teff now very precisely known, these provide very important inputs for any spectroscopic analyses, especially for the determination of neutron-capture element abundances which can constrain models of nucleosynthesis.
Finally, we have also predicted the asteroseismic signatures ⟨ Δν ⟩ and νmax for the two stars and we showed that determinations of these quantities for the dwarf star are possible using ground-based observations. For the giant, however, we would require very long time series in order to resolve the frequency content of the oscillations, and this would only be possible with space-borne instruments. The asteroseismic data would provide very important constraints because it would allow us to determine the mass with better precision (using the radius from this work), and thus the initial helium abundance.
[Z/X] = log Z/Xstar − log Z/X⊙ and Z/X⊙ = 0.0245, see Sect. 4.2.
The IRFM allows one to calculate Teff by comparing the ratio of infra-red to bolometric flux observed from Earth to the true intrinsic value obtained from theoretical models (see e.g. Casagrande 2008).
Acknowledgments
The CHARA Array is funded by the National Science Foundation through NSF grant AST-0908253 and by Georgia State University through the College of Arts and Sciences. The PTI archival observations of HD 122563 were collected through the efforts of the PTI Collaboration (http://pti.jpl.nasa.gov/ptimembers.html). The PTI was operated until 2008 by the NASA Exoplanet Science Institute/Michelson Science Center, and was constructed with funds from the Jet Propulsion Laboratory, Caltech as provided by the National Aeronautics and Space Administration. This work has made use of services produced by the NASA Exoplanet Science Institute at the California Institute of Technology. This research received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS and University Denis Diderot Paris 7. This research made use of the SIMBAD and VIZIER databases at CDS, Strasbourg (France), and NASA’s Astrophysics Data System Bibliographic Services. The authors acknowledge the role of the SAM collaboration in stimulating this research through regular workshops. We acknowledge financial support from the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. T.S.B. acknowledges support provided by NASA through Hubble Fellowship grant #HST- HF-51252.01 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555. U.H. acknowledges support from the Swedish National Space Board. A.C. is supported in part by an Action de recherche concertée (ARC) grant from the Direction générale de l’Enseignement non obligatoire et de la Recherche scientifique – Direction de la Recherche scietntifique – Communauté française de Belgique. A.C. is also supported by the F.R.S.-FNRS FRFC grant 2.4513.11. O.L.C. is a Henri Poincaré Fellow at the Observatoire de la Côte d’Azur. The Henri Poincaré Fellowship is funded by the Conseil Général des Alpes-Maritimes and the Observatoire de la Côte d’Azur.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999a, A&AS, 139, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999b, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2010, A&A, 509, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C. 1999, in AIP Conf. Ser., 495, 365 [Google Scholar]
- Barbuy, B., Meléndez, J., Spite, M., et al. 2003, ApJ, 588, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., & Kjeldsen, H. 2003, PASA, 20, 203 [Google Scholar]
- Bigot, L., Kervella, P., Thévenin, F., & Ségransan, D. 2006, A&A, 446, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigot, L., Mourard, D., Berio, P., et al. 2011, A&A, 534, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackwell, D. E., & Lynas-Gray, A. E. 1998, A&AS, 129, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowsher, E. C., McAlister, H. A., & Ten Brummelaar, T. A. 2010, in SPIE Conf. Ser., 7734 [Google Scholar]
- Boyajian, T. S., McAlister, H. A., Baines, E. K., et al. 2008, ApJ, 683, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., & Gilliland, R. L. 1994, ARA&A, 32, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Burgers, J. M. 1969, Flow Equations for Composite Gases [Google Scholar]
- Butler, R. P., Bedding, T. R., Kjeldsen, H., et al. 2004, ApJ, 600, L75 [Google Scholar]
- Casagrande, L. 2008, Phys. Scr. T, 133, 014020 [NASA ADS] [CrossRef] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Collet, R., Casagrande, L., & Asplund, M. 2010, A&A, 524, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Colavita, M. M. 1999, PASP, 111, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Colavita, M. M., Wallace, J. K., Hines, B. E., et al. 1999, ApJ, 510, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2009, Mem. Soc. Astron. It., 80, 719 [NASA ADS] [Google Scholar]
- Coudé du Foresto, V. 1998, in Fiber Optics in Astronomy III, eds. S. Arribas, E. Mediavilla, & F. Watson, ASP Conf. Ser., 152, 309 [Google Scholar]
- Coudé du Foresto, V., Ridgway, S., & Mariotti, J.-M. 1997, A&AS, 121, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coudé du Foresto, V., Perrin, G., Ruilier, C., et al. 1998, in SPIE Conf. Ser. 3350, ed. R. D. Reasenberg, 856 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Deliyannis, C. P., Ryan, S. G., Beers, T. C., & Thorburn, J. A. 1994, ApJ, 425, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog, II/237 [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] [Google Scholar]
- Gehren, T., Shi, J. R., Zhang, H. W., Zhao, G., & Korn, A. J. 2006, A&A, 451, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 331 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanbury Brown, R., Davis, J., & Allen, L. R. 1974, MNRAS, 167, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Hayek, W., Sing, D., Pont, F., & Asplund, M. 2012, A&A, 539, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houdashelt, M. L., Bell, R. A., & Sweigart, A. V. 2000, AJ, 119, 1448 [Google Scholar]
- Huber, D., Stello, D., Bedding, T. R., et al. 2009, Comm. Asteroseismol., 160, 74 [Google Scholar]
- Johnson, H. L., Mitchell, R. I., Iriarte, B., & Wisniewski, W. Z. 1966, Communications of the Lunar and Planetary Laboratory, 4, 99 [Google Scholar]
- Kervella, P., Bersier, D., Mourard, D., et al. 2004a, A&A, 428, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Ségransan, D., & Coudé du Foresto, V. 2004b, A&A, 425, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004c, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Pichon, B., et al. 2008, A&A, 488, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, J. R. 1997, PASP, 109, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Lebreton, Y. 2000, ARA&A, 38, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2006, AJ, 131, 3069 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006, in SPIE Conf. Ser., 6268 [Google Scholar]
- Merle, T., Thévenin, F., Pichon, B., & Bigot, L. 2011, MNRAS, 418, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T. V., & Kovtyukh, V. V. 2001, A&A, 370, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morel, P., & Thévenin, F. 2002, A&A, 390, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Collet, R., Lambert, D. L., Allen de Prieto, C., & Asplund, M. 2010, ApJ, 725, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W. 2009, A&A, 506, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruilier, C. 1999, Ph.D. Thesis, Université Paris 7 [Google Scholar]
- Ryan, S. G. 2005, in From Lithium to Uranium: Elemental Tracers of Early Cosmic Evolution, eds. V. Hill, P. François, & F. Primas, IAU Symp., 228, 23 [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, F., & Spite, M. 1993, A&A, 279, L9 [NASA ADS] [Google Scholar]
- Stello, D., Bruntt, H., Preston, H., & Buzasi, D. 2008, ApJ, 674, L53 [NASA ADS] [CrossRef] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Thévenin, F., & Idiart, T. P. 1999, ApJ, 521, 753 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, G. A., Elsworth, Y., Chaplin, W. J., et al. 2011, MNRAS, 415, 3539 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., Greenstein, J. L., Parker, R., Helfer, H. L., & Aller, L. H. 1963, ApJ, 137, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Wolffram, W. 1972, A&A, 17, 17 [NASA ADS] [Google Scholar]
- Yıldız, M., Yakut, K., Bakış, H., & Noels, A. 2006, MNRAS, 368, 1941 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Most recent photometric and spectroscopic determinations of atmospheric parameters for the target stars.
Stellar properties and 1σ uncertainties derived from modeling HD 122563 (no atomic diffusion) and Gmb 1830 (with atomic diffusion).
All Figures
 |
Fig. 1 Calibrated observations for PTI (black crosses), CHARA Classic (blue circles) and CHARA FLUOR (red squares) data plotted with the 1D limb-darkened visibility function fit for HD 122563. See Sect. 3 for details. |
| In the text | |
 |
Fig. 2 Calibrated observations for CHARA Classic (blue circles) and CHARA FLUOR (red squares) data plotted with the limb-darkened visibility function fit for Gmb 1830. See Sect. 3 for details. |
| In the text | |
 |
Fig. 3 Best matching 3D-RHD synthetic visibility curves and PTI (black crosses), Classic (blue circles), and FLUOR (red squares) data for HD 122563. |
| In the text | |
 |
Fig. 4 HR diagram showing the observational error boxes for HD 122563 (left) and Gmb 1830 (right). Both figures show stellar models that pass through the error boxes which allow us to determine the stellar model properties and their uncertainties. Each panel shows the adopted central models (with arrows) obtained by considering the HR and metallicity constraints. Other models are also indicated to highlight the parameter uncertainties and correlations. Refer to Sects. 4.3.1 and 4.3.2 for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


