| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219650 | |
| Published online | 18 September 2012 | |
Transverse kink oscillations of expanding coronal loops
Solar Physics and Space Plasma Research Centre
(SP 2RC), Department of Applied MathematicsThe
University of Sheffield,
Sheffield
S3 7RH,
UK
e-mail: i.ballai@sheffield.ac.uk; b.orzai@sheffield.ac.uk
Received:
22
May
2012
Accepted:
24
July
2012
Aims. We investigate the nature of transverse kink oscillations of loops expanding through the solar corona and examine how can oscillations be used to diagnose plasma parameters and the magnetic field. In particular, we aim to analyse how the temporal dependence of the loop length (here modelling the expansion) will affect the P1/P2 period ratio of transverse loop oscillations.
Methods. Due to the uncertainty of the loop’s shape through its expansion, we discuss separately the case of the loop that maintains its initial semi-circular shape and the case of the loop that evolves into an elliptical-shape loop from a semi-circular shape. The equations that describe the oscillations in an expanding flux tube are complicated due to the spatial and temporal dependence of coefficients. Using the WKB approximation, we find approximative values for periods and their evolution as well as the period ratio. For small values of time (near the start of the expansion), we can employ a regular perturbation method to find approximative relations for eigenfunctions and eigenfrequencies.
Results. Using simple analytical and numerical methods, we show that the period of oscillations are affected by the rising of the coronal loop. The change in the period due to the increase in the loop’s length is more pronounced for loops that expand into a more structured (or cooler) corona. The deviation of periods will have significant implications in determining the degree of stratification in the solar corona. The effect of expansion on the periods of oscillations is considerable only when the loop is expanding but not after it has reached its final stage.
Conclusions. The present study improves our understanding of the complexity of dynamical processes in the solar corona, in particular the changes of periods of kink oscillations due to temporal changes in the characteristics of the coronal loop. Our results clearly show that the problem of expansion of coronal loops can introduce significant changes in the period of oscillations, with consequences on the seismological diagnostics of the plasma and magnetic field.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: oscillations
© ESO, 2012
1. Introduction
Dynamical processes and transients observed in solar and space plasmas have received considerable attention due to their ability to help scientists to diagnose remotely the parameters of the medium (temperature, scale-height, density, transport coefficients, etc.) in which these events occur, the magnitude and structure of the magnetic field, and the stability of the plasma. Seismological techniques and methods, imported from Earth’s seismology and helioseismology, assume the combination of high-resolution observations (amplitude, wavelength, propagation speed, damping time/length) with theoretical models (dispersion and evolutionary equation) to derive quantities that cannot be measured directly or indirectly. In particular, coronal seismology has emerged as one of the most dynamically developing methods of solar physics (see, e.g. Roberts et al. 1984; Nakariakov et al. 1999; Ruderman & Roberts 2002; Andries et al. 2005, 2009; Ballai et al. 2005; Banerjee et al. 2007; Verth et al. 2007; Ballai 2007; Ruderman et al. 2008; Morton & Erdélyi 2009; Ruderman & Erdélyi 2009; Wang et al. 2012, etc.).
One important candidate in coronal seismology are transverse kink oscillations, i.e. oscillations that exhibit periodic movement about the loop’s symmetry axis. Recent Coronal Multi-Channel Polarimeter (CoMP) observations (Tomczyk et al. 2007) showed that the predominant motion of coronal loops is the transverse kink oscillation, which is also the easiest to generate. The triggering of these oscillations can be through a lateral forcing process at arbitrary height of the loop by a blast wave (or EIT wave) that emanates as a result of a sudden energy release by a flare and/or CME (see, e.g. Ballai 2007; Ballai et al. 2008). Kink oscillations can also be triggered by the transverse motion of footpoints due to the granular buffeting of flux tubes in the photosphere. This scenario is true not only for coronal structures, but also for all magnetic entities in the solar atmosphere that can serve as waveguides. Global EIT waves can additionally interact with prominence fibrils to generate kink waves and oscillations in prominences, as observed by, e.g. Ramsey & Smith (1966) and more recently by Eto et al. (2002), Jing et al. (2003), Okamoto et al. (2004), Isobe & Tripathi (2007), and Pintér et al. (2008) (for a comprehensive review see, e.g. Arregui et al. 2012).
The dispersion relations for many simple (and some quite complicated) plasma waves under the assumptions of ideal magnetohydrodynamics (MHD) are well known; they were derived long before accurate EUV observations were available (see, e.g. Edwin & Roberts 1983; Roberts et al. 1984) using simplified models within the framework of ideal and linear MHD. Although the realistic interpretation of many observations is made difficult by the insufficient spatial and temporal resolution of present-day satellites, considerable information about the state of the plasma and the structure and magnitude of the coronal magnetic field can still be obtained.
The mathematical description of waves and oscillations in solar structures is, in general, given by equations whose coefficients vary in space and time. It has been recognised by, e.g. Andries et al. (2005) that the longitudinal stratification (i.e. along the longitudinal symmetry axis of the tube that coincides with the direction of the magnetic field) is modifying the periods of oscillations of coronal loops. Accordingly, in the case of kink waves, these authors showed that the ratio P1/P2 (where P1 refers to the period of the fundamental transverse oscillation, while P2 describes the period of the first overtone of the same oscillation) can differ, sometimes considerably, from the canonical value of 2, that would be recovered if the loops were homogeneous. These authors also showed that the deviation of P1/P2 from 2 is proportional to the degree of stratification. This problem was also discussed in other studies, such as Dymova & Ruderman (2006), Diaz et al. (2007), McEwan et al. (2008), Ballai et al. (2011), Orza et al. (2012), etc. In a recent analysis, Ballai et al. (2011) discusses the ambiguity of the period ratio seismology, since other effects could result in the observation of multiple periods and each interpretation yields in different value for the magnetic field and/or degree of stratification.
Studies by, e.g. Verth et al. (2007) later showed that not only density stratification can modify the P1/P2 period ratio as the variation of the loop’s cross section area also has an effect on the period ratio. While density stratification tends to decrease the period ratio, a modification of the cross section (i.e. when the magnetic field is flaring up as we approach the apex) tends to increase the P1/P2 value.
The investigation of properties of oscillations of coronal loops when equilibrium parameters of the plasma depend on time is a relatively new area of dynamical studies in the solar atmosphere, in particular for coronal seismology. Morton & Erdélyi (2009) and Morton et al. (2010) studied the effect of cooling (i.e. temporal dependence of temperature) on the dynamics of kink oscillations and travelling waves. They found that the cooling of the plasma results in period decrease and amplification of oscillations and is thus a mean to dissipate the energy stored in waves propagating in an unbounded plasma. The same idea was used later by Morton et al. (2011) to study the properties of torsional Alfvén waves in coronal loops. The problem was recently reconsidered by Ruderman (2011a), who showed that the cooling also generates an amplification of kink oscillations. This amplification appears to be a competing effect with the damping due resonant absorption, as shown by Ruderman (2011b).
The problem of loop emergence and expansion through the solar atmosphere is one of the most challenging topics of solar physics because it involves analysing of the evolution of the magnetic field in different regions of the solar interior and atmosphere, where conditions can change from region to region. According to the standard theory, the magnetic field produced by the dynamo action in the tachocline is transported through the solar convective zone towards the solar surface by magnetic buoyancy coupled with convective motion (Parker 1955, 1988). Once at the surface, the emerged flux tube creates sunspots and bipolar active regions (Zwaan 1987). In the solar atmosphere, the rise of the flux tube continues due to an excess of the magnetic pressure inside the loop (e.g. Archontis et al. 2004). For the purpose of our investigation, we will assume that this excess is balanced at the transition region (TR) and that from this height the expansion is no longer a driven problem instead, the loop moves through the corona in the virtue of its inertia. During the emergence and expansion phase, the flux tube can interact with existing magnetic structure in the solar atmosphere, which might be responsible for the appearance of small-scale (e.g. compact flares, plasmoids, X-point brightenings) and large-scale events (flares and CMEs), as suggested by Archontis (2004). Loop emergence often is associated with strong upflows, as observed by, e.g. Harra et al. (2010, 2012).
It is straightforward to imagine what happens with oscillations in a loop when the length of the loop is increasing. As the length becomes larger, the frequency of oscillations becomes smaller, i.e. the periods of oscillations are expected to grow. In an inhomogeneous waveguide, however, particular periods will be differently affected by the combined effect of inhomogeneity and loop length increase. Therefore, we expect that the period ratio of oscillations will change not only with the degree of inhomogeneity but also with time.
The aim of this paper is to investigate the effect of loop expansion through the solar corona on the period ratio P1/P2 and the consequences of the inclusion of the length of the loop as a dynamical parameter on estimations of the degree of density stratification. The paper is structured in the following way: in Sect. 2, we introduce the mathematical formalism and obtain analytical results for an expanding loop that initially starts from a semi-circular shape, which is preserved throughout the expansion. In Sect. 3, we generalise our findings by assuming that the expansion of the loop in the solar corona does not occur with the same speed in the horizontal and vertical direction. In this case, the initial semi-circular loop transforms into a loop with elliptic shape. Our results are summarised in the last section.
2. The mathematical formulation of the problem
In our analysis, we will capture the dynamical behaviour of the loop once it has reached the transition region (TR). At this height, the loop can interact with a blast wave propagating in the low solar corona. This instigator could be easily identified with an EIT wave that propagates in the low corona over very large distances. EIT waves are known to be one of the major sources for kink oscillations of coronal loops (see, e.g. Ballai 2007). We assume that the height at which the loop starts its journey through the corona is at 3 Mm above the solar surface. A typical loop length is of the order of 300 Mm. For practical reasons, we consider that the height of the loop in its final position would be about 97, Mm resulting in a loop length of about 305 Mm.
The raising speed of loops is generally taken to be 10−15 km s-1 (Chou & Zirin 1988; Archontis 2008). Consequently, the time needed for the loop to travel the distance from the TR to its steady position can easily be estimated to be between 3.4 and 5.2 h. This time is at least two orders of magnitude larger than a typical period of kink oscillations, so there is enough time for the development of oscillations. Higher rising speeds are also possible. Recently, Schmidt & Ofman (2011) reported expansions of a post-flare loop with speeds of hundreds km s-1. Standing waves are formed if the speed of change in the length of the loop is smaller than the period of oscillations. This condition is easily satisfied for fast kink oscillations. We assume that the loop expands into the “empty” corona, i.e. it will not encounter any interaction with existing magnetic elements.
In the first instance, we assume that the semi-circular shape of the loop at the TR is
preserved throughout the expansion. Assuming an initial height of 3 Mm above the surface,
the distance between the footpoints of the loop is 6 Mm. When reaching the final height of
190 Mm, the footpoints travel over a distance of 197 Mm. In addition, we assume that the
expansion occurs at constant temperature (isothermal process) and that the expansion the
loop maintains its cross section constant throughout the expansion. Due to the increase in
the volume of the loop, a pressure difference is generated. This means that the plasma flows
along magnetic field lines, resulting in a density that depends not only on the height,
z, but also on time. As it raises through the solar corona, the tangent
to the loop is also changing monotonically. Therefore, the momentum equation in an
equilibrium state becomes 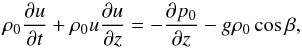 (1)where the angle
β is a function depending on time and space, u is the
equilibrium flow of the plasma, ρ0 and
p0 are the equilibrium density and pressure, and
g is the gravitational acceleration. In coronal loops, the flows are of
the order of a few tens of km s-1. As a result, in Eq. (1) we can neglect the terms on the left-hand side
because
(1)where the angle
β is a function depending on time and space, u is the
equilibrium flow of the plasma, ρ0 and
p0 are the equilibrium density and pressure, and
g is the gravitational acceleration. In coronal loops, the flows are of
the order of a few tens of km s-1. As a result, in Eq. (1) we can neglect the terms on the left-hand side
because
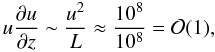 that is, two order of
magnitude smaller than the terms on the right-hand side. We can write pressure as
that is, two order of
magnitude smaller than the terms on the right-hand side. We can write pressure as
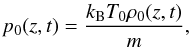 where
kB is the Boltzman constant, T0 is
the constant temperature and m is the mean atomic mass per particle.
Introducing this expression into the RHS of Eq. (1), we obtain that
where
kB is the Boltzman constant, T0 is
the constant temperature and m is the mean atomic mass per particle.
Introducing this expression into the RHS of Eq. (1), we obtain that 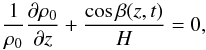 (2)where H is
the constant density scale-height. Focussing on the density distribution inside the loop, we
can integrate the above equation to obtain
(2)where H is
the constant density scale-height. Focussing on the density distribution inside the loop, we
can integrate the above equation to obtain ![\begin{equation} \rho_{\rm i}=\rho_{\rm f}\exp\left[-\int_0^z\frac{ \cos \beta(z',t)}{H}{\rm d}z'\right]. \label{eq:1.3} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq21.png) (3)Assuming that the loop is
semi-circular, we obtain that
β(z,t) = πz/L(t),
so that the density inside the coronal loop becomes
(3)Assuming that the loop is
semi-circular, we obtain that
β(z,t) = πz/L(t),
so that the density inside the coronal loop becomes ![\begin{equation} \rho_{\rm i}=\rho_{\rm f}\exp\left[-\frac{L(t)}{\pi H}\sin\frac{\pi z}{L(t)}\right], \label{eq:1.4} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq23.png) (4)where
ρf is the density of the plasma at the footpoint of the loop.
For simplicity we will assume that the external density can simply be written as
ρe = Dρi, where
throughout our calculations, we consider D = 0.5. Figure 1 depicts schematically the change of the equilibrium
density, both in space and time. Here, length was normalised to the length of the loop at
the start of the emergence (considered
L0 = 3π Mm), and time (here denoted
by τ) was normalised to the
quantity L0/vr,
where vr is the vertical rising speed of the
loop considered vr = 15 km s-1.
According to our expectations, the density of the loop decreases with time. We assume that
the flux tube is thin, even at the beginning of its expansion.
(4)where
ρf is the density of the plasma at the footpoint of the loop.
For simplicity we will assume that the external density can simply be written as
ρe = Dρi, where
throughout our calculations, we consider D = 0.5. Figure 1 depicts schematically the change of the equilibrium
density, both in space and time. Here, length was normalised to the length of the loop at
the start of the emergence (considered
L0 = 3π Mm), and time (here denoted
by τ) was normalised to the
quantity L0/vr,
where vr is the vertical rising speed of the
loop considered vr = 15 km s-1.
According to our expectations, the density of the loop decreases with time. We assume that
the flux tube is thin, even at the beginning of its expansion.
 |
Fig. 1 Schematic representation of the evolution of the equilibrium density measured on the vertical axis in the units of density at the footpoint. Here, lengths are given in units of the loop length at the start of the expansion in the corona (L0), and time is given in units of L0/vr, where vr is the constant rising speed in the vertical direction (here taken to be 15 km s-1). |
In the thin flux tube approximation, the dynamics of transverse kink oscillations is given
by (see, e.g. Ruderman 2010, 2011a) 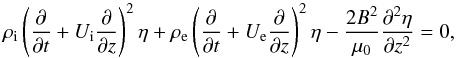 (5)where
Ui and Ue are the internal and
external flows, B is the magnetic field strength (here assumed to have
identical value inside and outside the loop), μ0 is the magnetic
permeability of the free space, and η is a complex valued displacement of
the loop, with
η = ηR + iηI.
In Cartesian coordinates, the loop’s displacement in the x and
y directions, ξx and
ξy, is given by
(5)where
Ui and Ue are the internal and
external flows, B is the magnetic field strength (here assumed to have
identical value inside and outside the loop), μ0 is the magnetic
permeability of the free space, and η is a complex valued displacement of
the loop, with
η = ηR + iηI.
In Cartesian coordinates, the loop’s displacement in the x and
y directions, ξx and
ξy, is given by
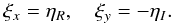 We assume a
quasi-stationary equilibrium, so that the characteristic time variation of equilibrium
quantities (tch) is much longer than the period of kink
oscillations (P), and introduce the small parameter ϵ, so
that P = ϵtch. Using the
definition of the period of oscillations, we can write
We assume a
quasi-stationary equilibrium, so that the characteristic time variation of equilibrium
quantities (tch) is much longer than the period of kink
oscillations (P), and introduce the small parameter ϵ, so
that P = ϵtch. Using the
definition of the period of oscillations, we can write 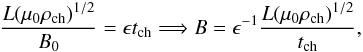 (6)meaning that we can
introduce a scaled magnetic field, so that
(6)meaning that we can
introduce a scaled magnetic field, so that  . As a result, the
equation describing the dynamics of the kink oscillations can be written as
. As a result, the
equation describing the dynamics of the kink oscillations can be written as 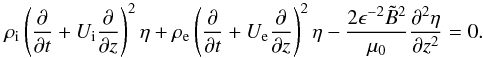 (7)The above equation
must be solved subject to standard boundary conditions, i.e.
(7)The above equation
must be solved subject to standard boundary conditions, i.e.
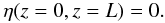 Following the solution
method proposed by Ruderman (2011a), we will solve
Eq. (7) using the
Wentzel-Kramers-Brillouin (WKB) method (see, e.g. Bender & Ország 1987) and assume that the solution of the equation will
be of the form
Following the solution
method proposed by Ruderman (2011a), we will solve
Eq. (7) using the
Wentzel-Kramers-Brillouin (WKB) method (see, e.g. Bender & Ország 1987) and assume that the solution of the equation will
be of the form ![\begin{equation} \eta=\sum_{k=0}^{\infty}\epsilon^kS_k(z,t)\exp\left[\frac{\rm i}{\epsilon}\Phi(t)\right]. \label{eq:1.8} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq53.png) (8)In the first order of
approximation (often called geometric optics), Eq. (7) reduces to
(8)In the first order of
approximation (often called geometric optics), Eq. (7) reduces to 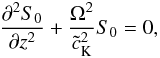 (9)where
(9)where
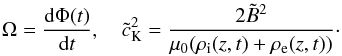 Equation (9) must be solved subject to the boundary
condition S0 = 0 when z = 0 and
z = L. Together with the line-tying condition,
Eq. (9) forms an eigenvalue problem, in
which Ω is the eigenvalue and Ω2 is a real function.
Equation (9) must be solved subject to the boundary
condition S0 = 0 when z = 0 and
z = L. Together with the line-tying condition,
Eq. (9) forms an eigenvalue problem, in
which Ω is the eigenvalue and Ω2 is a real function.
In the next order of approximation (also called the approximation of physical optics),
Eq. (7) reduces to ![\begin{equation} \frac{\partial^2 S_1}{\partial z^2}+\frac{\Omega^2}{{\tilde c_{\rm K}}^2}S_1=\frac{2{\rm i}\Omega}{{\tilde c_{\rm K}}^2}\left[\frac{\partial S_0}{\partial t}+\frac{S_0}{2\Omega}\frac{{\rm d}\Omega}{{\rm d}t}+\frac{\rho_{\rm i}U_{\rm i}+\rho_{\rm e}U_{\rm e}}{\rho_{\rm i}+\rho_{\rm e}}\frac{\partial S_0}{\partial z}\right], \label{eq:1.10} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq61.png) (10)which has to be solved
subject to the boundary condition
S1(z = 0,z = L) = 0.
The boundary-value problem determining S1 has a solution only
when the RHS of Eq. (10) satisfies the
compatibility condition, i.e. the orthogonality to S0. After the
RHS of Eq. (10) is multiplied by
S0 and integrated with respect to z in the
interval (0,L), the compatibility condition reduces to (similar to Ruderman
2011a)
(10)which has to be solved
subject to the boundary condition
S1(z = 0,z = L) = 0.
The boundary-value problem determining S1 has a solution only
when the RHS of Eq. (10) satisfies the
compatibility condition, i.e. the orthogonality to S0. After the
RHS of Eq. (10) is multiplied by
S0 and integrated with respect to z in the
interval (0,L), the compatibility condition reduces to (similar to Ruderman
2011a) 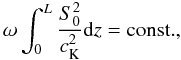 (11)where
(11)where
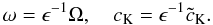 As a consequence,
the dynamics of kink oscillations in coronal loops is fully described by the system of
Eqs. (9) and (11). In deriving Eq. (11), we took into account the mass conservation
equation, relating the plasma flow and its density
As a consequence,
the dynamics of kink oscillations in coronal loops is fully described by the system of
Eqs. (9) and (11). In deriving Eq. (11), we took into account the mass conservation
equation, relating the plasma flow and its density 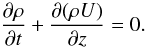 Let us now discuss a
special case when the density depends on time only. This case would correspond to an initial
expansion of the loop, when the height of the loop is less than the scale-height (assuming
expansion into an isothermal 1 MK corona, this height would correspond to 47 Mm). In this
case, we may expect that the amplitude of oscillations increases as the loop expands.
Indeed, it is easy to show that the amplitude of oscillations behaves as
Let us now discuss a
special case when the density depends on time only. This case would correspond to an initial
expansion of the loop, when the height of the loop is less than the scale-height (assuming
expansion into an isothermal 1 MK corona, this height would correspond to 47 Mm). In this
case, we may expect that the amplitude of oscillations increases as the loop expands.
Indeed, it is easy to show that the amplitude of oscillations behaves as 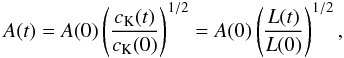 (12)where
A(0), cK(0) and L0
are the amplitude of oscillations, the kink speed and the length of the loop at
t = 0.
(12)where
A(0), cK(0) and L0
are the amplitude of oscillations, the kink speed and the length of the loop at
t = 0.
 |
Fig. 2 Variation of the periods of the fundamental mode and its first harmonic with the dimensionless time variable τ for three different values of stratification: H = 70.5 Mm (dotted line), H = 47 Mm (solid line), and H = 23.5 Mm (dashed line). |
A particular case worth discussing separately is when the expansion of the loop occurs
linearly with time and we write that 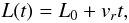 (13)where
L0 is the length of the loop at the initial time, i.e. at the
TR level (L0 = 3π Mm), and
vr is the rising speed, here assumed
constant. Accordingly, the kink speed becomes
(13)where
L0 is the length of the loop at the initial time, i.e. at the
TR level (L0 = 3π Mm), and
vr is the rising speed, here assumed
constant. Accordingly, the kink speed becomes ![\begin{equation} c_{\rm K}^2=c_{\rm Kf}^2\exp\left[\frac{L_0+v_rt}{\pi H}\sin\frac{\pi z}{L_0+v_rt}\right], \label{eq:1.16} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq77.png) (14)where
(14)where
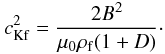 Returning to the
general case, the equations describing the dynamics of kink oscillations are
Returning to the
general case, the equations describing the dynamics of kink oscillations are 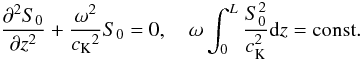 (15)Let us
introduce a new set of dimensionless quantities
(15)Let us
introduce a new set of dimensionless quantities 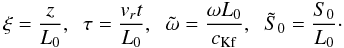 (16)In the new
variables, the equations to be solved transform into
(16)In the new
variables, the equations to be solved transform into ![\begin{equation} \frac{\partial^2\tilde{S}_0}{\partial \xi^2}+\exp\left[\frac{-L_0(1+\tau)}{\pi H}\sin\frac{\pi \xi}{1+\tau}\right] {\tilde \omega}^2{\tilde S}_0=0, \label{eq:1.19} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq81.png) (17)and
(17)and ![\begin{equation} {\tilde \omega}\int_0^{1+\tau}{\tilde S}_0^2 \exp\left[\frac{-L_0(1+\tau)}{\pi H}\sin\frac{\pi \xi}{1+\tau}\right] {\rm d}\xi={\rm const.}, \label{eq:1.20} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq82.png) (18)which should be solved
subject to the boundary conditions
S0(ξ = 0;ξ = 1 + τ) = 0.
The solution of the system (17)−(18) can be found numerically using, e.g. the
shooting method. In Fig. 2, we display first the
variation of periods of oscillations of the fundamental mode and its first harmonic for
three different values of H in terms of the dimensionless time variable,
τ.
(18)which should be solved
subject to the boundary conditions
S0(ξ = 0;ξ = 1 + τ) = 0.
The solution of the system (17)−(18) can be found numerically using, e.g. the
shooting method. In Fig. 2, we display first the
variation of periods of oscillations of the fundamental mode and its first harmonic for
three different values of H in terms of the dimensionless time variable,
τ.
 |
Fig. 3 Variation of the P1/P2 period ratio with respect to the dimensionless parameter τ, for a loop expanding in the solar corona with persisting semi-circular shape. The meaning of each line-style is identical to Fig. 2. |
The bands for each period are clearly labelled in the figure. The three distinct value of periods were obtained for three values of scale-height, keeping the initial length of the loop at 3π Mm. The dotted line corresponds to a scale-height of 70.5 Mm, which, assuming a plasma in hydrostatic equilibrium, would correspond to a plasma temperature of 1.5 MK. The solid line is plotted for a loop expanding into a corona where the constant scale-height is 47 Mm, corresponding to a 1 MK hot plasma. Finally, the dashed line stands for an expansion of the loop into a plasma, where the density scale-height is 23.5 Mm, corresponding to a plasma temperature of 0.5 MK. The two bands for the periods clearly show that the two oscillations are differently affected by the expansion, i.e. change in the length of the loop. This is also obvious in Fig. 3, where we plotted the ratio of the periods of the fundamental and first harmonic as a function of the time variable τ. The plot clearly shows that the oscillations of a loop expanding into a “hot” plasma (i.e. large scale-height) are the least affected, but in all three cases, the period ratio decreases with time. We should note here that the periods shown in Fig 2 do not start at the value of 2 because at the start of their expansion through the solar corona, they are already stratified and the least stratified is the case that corresponds to H = 1.5 MK. We ought to note that in observations, the identification of periods in coronal loops is a dynamical process, i.e. in EUV the intensity is measured in one location (or mega-pixel to reduce errors) for a long time-period. The duration of observation varies, and this duration is mostly driven either by the availability of the instrument or by the limited lifetime of oscillations before they are damped by, e.g. resonant absorption. Observations show, however, that not all loop oscillations damp (probably these oscillations are maintained by a constant lateral buffeting). Typically, for damped oscillations, the detection time is a few periods with a range of 6.7−90 min (Aschwanden 2004). In terms of the dimensionless quantity τ, this range would correspond to τ = 0.64−8.6. Although the lower limit is too small to count in the effect of expansion, a duration of τ = 8.6 would add an important effect in studying the transverse kink oscillations. Figure 3 shows that for one given value of internal structuring, the value of the period ratio can also change because of the expansion of the loop. Although the periods shown in Fig. 2 display a monotonic increase with the parameter τ, in reality these values will saturate, with saturation occurring faster for those modes that propagate in a highly structured plasma (e.g. for the case of H = 23.5 Mm, the saturation value of periods is about 400 s and saturation starts at about τ = 20). In addition, the period ratio for all cases discussed here tends to same value (near 1) for large values of τ. Significantly, the effect of expansion on the periods of oscillations and the period ratio is relevant only in the expansion phase of the loop.
Analytical solutions of Eq. (17) can be obtained for the limiting case of a loop at the beginning of its expansion through the solar corona, i.e. small values of τ (see Appendix). The results confirm the tendency of periods to increase with time and of the period ratio to decrease with time.
3. Noncircular emergence
In reality, the expansion of a loop in the empty corona so that the semi-circular shape is preserved is unlikely since the foot points have to move in a much denser plasma than the apex of the loop. Consequently, in this section we will assume that the expansion rate in the vertical direction is larger than the expansion of footpoints in the horizontal direction. The expansion still starts at the TR level, where the shape of the loop is semi-circular and we assume that the process remains isothermal. As a result of different expansion rates, the loop evolves so that the shape becomes more elliptical. The properties of transverse loop oscillations in an elliptical coronal loop was studied recently by Morton & Erdélyi (2009) who assumed that the semi-elliptical shape is reached in the emerging stage, before reaching a semi-circular shape. Although their topic is related to the research of the present study, the problem of expansion is a dynamical process that should be treated accordingly. They found that the difference in P1/P2 period ratio between the circular and elliptical shape is up to 6%.
Since the dynamics is going to be different over the two directions, it is more convenient
to introduce a polar coordinate system in which  (19)with
ȧ(t) < ḃ(t),
the overdot denotes the derivative with respect to time, and the length of the loop is
covered by the parameter θ that varies now between 0
and π. It is more convenient to use the coordinates along the
loop s, meaning that the dynamics of transverse kink oscillations can be
described by
(19)with
ȧ(t) < ḃ(t),
the overdot denotes the derivative with respect to time, and the length of the loop is
covered by the parameter θ that varies now between 0
and π. It is more convenient to use the coordinates along the
loop s, meaning that the dynamics of transverse kink oscillations can be
described by 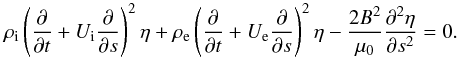 (20)A key parameter in our
discussion is the arc-length, which is defined as
(20)A key parameter in our
discussion is the arc-length, which is defined as 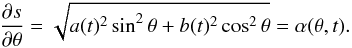 (21)In order to solve
Eq. (20), we would need to express the
density as function of s and t. However, it turns out that
it is much easier to deal with the variable θ instead. Therefore, we
express the derivatives in the governing equation as
(21)In order to solve
Eq. (20), we would need to express the
density as function of s and t. However, it turns out that
it is much easier to deal with the variable θ instead. Therefore, we
express the derivatives in the governing equation as 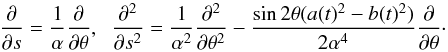 (22)Assuming again a
quasi-stationary equilibrium, described in the previous section, and introducing the small
parameter, ϵ, the governing equation for transverse kink oscillations can
be written as
(22)Assuming again a
quasi-stationary equilibrium, described in the previous section, and introducing the small
parameter, ϵ, the governing equation for transverse kink oscillations can
be written as ![\begin{eqnarray} \frac{\partial^2\eta}{\partial t^2}&+\frac{2}{\alpha}\left(\frac{\rho_{\rm i}U_{\rm i}+\rho_{\rm e}U_{\rm e}}{\rho_{\rm i}+\rho_{\rm e}}\right)\frac{\partial^2\eta}{\partial \theta \partial t}+\frac{1}{\alpha^2}\left[\frac{\rho_{\rm i}U_{\rm i}^2+\rho_{\rm e}U_{\rm e}^2}{\rho_{\rm i}+\rho_{\rm e}}\right.\notag \\ &&\left.-\frac{2\epsilon^{-2}B_0^2}{\mu_0(\rho_{\rm i}+\rho_{\rm e})}\right]\frac{\partial^2\eta}{\partial \theta^2}-\left[2\frac{\rho_{\rm i}U_{\rm i}+\rho_{\rm e}U_{\rm e}}{\rho_{\rm i}+\rho_{\rm e}}\frac{a\dot{a}\sin^2\theta+b\dot{b}\cos^2\theta}{\alpha^3}\right.\notag \\ &&\left.+\frac{\rho_{\rm i}U_{\rm i}^2+\rho_{\rm e}U_{\rm e}^2}{\rho_{\rm i}+\rho_{\rm e}}\frac{\sin2\theta(a(t)^2-b(t)^2)}{2\alpha^4}\right.\notag \\ \label{eq:2.5} &&\left. -2\frac{\epsilon^{-2}B_0^2}{\mu_0(\rho_{\rm i}+\rho_{\rm e})}\frac{\sin2\theta(a(t)^2-b(t)^2)}{2\alpha^4}\right]\frac{\partial \eta}{\partial \theta}=0, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq97.png) (23)which
has to be solved subject to the boundary conditions
η(θ = 0,θ = π) = 0.
(23)which
has to be solved subject to the boundary conditions
η(θ = 0,θ = π) = 0.
Again, we will solve this equation using the WKB approximation presented earlier and
suppose a solution identical to Eq. (8). In
the first order of approximation we obtain the equation 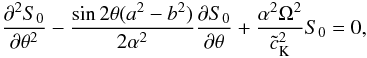 (24)together with the usual
boundary conditions at the two ends of the loop. In the next order of approximation, we
obtain
(24)together with the usual
boundary conditions at the two ends of the loop. In the next order of approximation, we
obtain ![\begin{eqnarray} \label{eq:2.7} \frac{\partial^2 S_1}{\partial \theta^2}&&-\frac{\sin2\theta(a^2-b^2)}{2\alpha^2}\frac{\partial S_1}{\partial \theta}+\frac{\alpha^2\Omega^2}{{\tilde c}_{\rm K}^2}S_1= \notag \\ \qquad&&\frac{2{\rm i}\alpha\Omega}{{\tilde c}_{\rm K}^2}\left[\frac{\partial S_0}{\partial t}+\frac{\alpha S_0}{2\Omega}\frac{\partial \Omega}{\partial t}+\frac{\rho_{\rm i}U_{\rm i}+\rho_{\rm e}U_{\rm e}}{\rho_{\rm i}+\rho_{\rm e}}\frac{\partial S_0}{\partial \theta}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq100.png) (25)This
equation has to be solved subject to the boundary condition
S1(θ = 0,θ = π) = 0.
Again, the equation for S1 will have a solution if the
right-hand side of the above equation satisfies the compatibility condition, i.e. the
orthogonality to S0. Following the same solving procedure as
presented earlier, it is easy to show that the condition reduces to
(25)This
equation has to be solved subject to the boundary condition
S1(θ = 0,θ = π) = 0.
Again, the equation for S1 will have a solution if the
right-hand side of the above equation satisfies the compatibility condition, i.e. the
orthogonality to S0. Following the same solving procedure as
presented earlier, it is easy to show that the condition reduces to 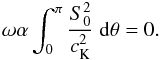 (26)Therefore, the system
of Eqs. (24) and (26) will determine completely the dynamics of
the expanding coronal loop.
(26)Therefore, the system
of Eqs. (24) and (26) will determine completely the dynamics of
the expanding coronal loop.
Let us assume that at t = 0, the loop is semi-circular and its length is
L0. In order to reproduce the different movement over the two
directions, we introduce two different expansion speeds in the horizontal
(vh) and vertical (vv) direction,
so that vh < vv. Again, we
suppose that the motion occurs linearly in time and write the dynamics over the two axes as
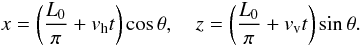 (27)Let us introduce a new set
of dimensionless quantities
(27)Let us introduce a new set
of dimensionless quantities 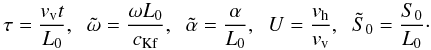 (28)In the new
variables, the governing equations become
(28)In the new
variables, the governing equations become ![\begin{eqnarray} \label{eq:2.11} \frac{\partial^2{\tilde S}_0}{\partial \theta^2}&&+{{\tilde \alpha}^2{\tilde \omega}^2}\exp\left[-\frac{L_0(1+\tau\pi)}{\pi H}\sin\theta\right]{\tilde S}_0 \notag \\ &&+\frac{\sin\theta\cos\theta[\tau^2\pi^2(1-U^2)+2\tau\pi(1-U)]}{1+\tau^2\pi^2(\sin^2\theta+U^2\cos^2\theta)+2\tau\pi(\sin^2\theta+U\cos^2\theta)} \notag \\ &&\times\frac{\partial{\tilde S}_0}{\partial \theta}=0, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq108.png) (29)and
(29)and
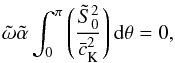 (30)where
(30)where
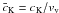 .
Figure 4 displays the evolution of the period of
oscillations for the fundamental mode and its first harmonic for three different values of
L0/H, similar values as used in the
previous section. Comparing the findings in Figs. 2 and 4, the effect of the expansion into
an elliptical shape compared to the constant semi-circular shape is evident. As time
progresses, the period of oscillations tends to a higher value for elliptical shape;
however, this conclusion is more true for the fundamental mode. The period of the
fundamental mode, corresponding to an expansion in a solar corona where scale height is
only 23.5 Mm (corresponding to a temperature of 0.5 MK in a loop in hydrostatic
equilibrium), saturates rather quickly.
.
Figure 4 displays the evolution of the period of
oscillations for the fundamental mode and its first harmonic for three different values of
L0/H, similar values as used in the
previous section. Comparing the findings in Figs. 2 and 4, the effect of the expansion into
an elliptical shape compared to the constant semi-circular shape is evident. As time
progresses, the period of oscillations tends to a higher value for elliptical shape;
however, this conclusion is more true for the fundamental mode. The period of the
fundamental mode, corresponding to an expansion in a solar corona where scale height is
only 23.5 Mm (corresponding to a temperature of 0.5 MK in a loop in hydrostatic
equilibrium), saturates rather quickly.
 |
Fig. 4 The same as in Fig. 2, but here we assume that the expansion of the loop occurs such that the loop evolves into a loop with a semi-elliptical shape. The meaning of different line-styles is identical to Fig. 2. |
 |
Fig. 5 The same as in Fig. 3, but here we assume that the expansion of the loop occurs such that the loop evolves into a loop with a semi-elliptical shape. The meaning of different line-styles is identical to Fig. 2. |
A more significant change is evident when comparing the P1/P2 period ratio of the expansion into an elliptical shape (shown in Fig. 5) to the variation of the period ratio for a semi-circular shape. For the same time interval, the decrease of the period ratio is much more significant, and, similar to the previous case, the period ratio is more affected for the case of strong stratification, i.e. small H.
4. Conclusions
The solar corona is a very dynamical environment, where changes in the dynamical state of the plasma and field occur on all sort of time scales. In the present study, we combined for the first time two kinds of dynamical events: the time-evolution of a coronal loop through its expansion into the “empty” corona and the transverse kink oscillations of coronal loops. The emergence and expansion of a coronal loop is a very complex phenomenon, but here we reduced our model to a simplified process, where the expansion is solely described by the change in the length of the loop with an associated temporal equilibrium density variation.
The governing equation for kink oscillations was solved in the WKB approximation, when the boundary conditions are time-dependent. As expected, due to the change in the length of the loop, the amplitude and periods of oscillations increase with time, while the period ratio of the fundamental mode and its first overtone decreases. This last physical parameter is of paramount importance for the remote determination of density structuring of coronal loops with the help of seismological approaches. In the first instance, we regarded the loop to have an initial semi-circular shape that is maintained through the expansion phase. Later, this restriction was lifted based on the natural assumption that the expansion into the vertical direction (i.e. into the direction of density decrease) occurs much more easily than into the horizontal direction. In this limit, the loop evolves into a semi-ellipse, with the major axis in the vertical direction. Comparing the results of the two approaches, it is clear that the behaviour of the period ratio is sensitive to the geometrical shape of the loop, a more significant drop in the P1/P2 ratio being achieved in the second case. Although our numerical results were obtained for three different structuring degrees (measured by the ratio of the initial loop length to the density scale-height), it is also evident that both the temporal change in the loop length and the stratification will have the same effect upon the period ratio, resulting in a mutual amplification of the effect.
Our model predicts that the amplitude of oscillations increases with time, however, due to the particular choice of density, damping processes were neglected. Once the density is allowed to vary also in the radial direction, according to the theory of resonant absorption (e.g. Goossens et al. 1992; Rudeman & Roberts 2002), loops will damp very quickly with the resonant position displaying a steady motion due to the change of the length of the loop. The amplitude of oscillations can also be damped because the cooling of the plasma (e.g. Morton et al. 2010), an effect that was also neglected here. In an expanding loop, the growth of the amplitude due to emergence and the decay of amplitude owing to resonant damping or cooling will be competing processes. The competition between these two effects will be discussed in a forthcoming paper.
Acknowledgments
I.B. acknowledges the financial support by NFS Hungary (OTKA, K83133). The authors are grateful to Prof M.S. Ruderman and Dr. V. Archontis for their help and comments.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Archontis, V. 2008, J. Geophys. Res., 113, A03S04 [Google Scholar]
- Archontis, V., Moreno-Insertis, F., Galsgaard, K., et al. 2004, A&A, 426, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Aschwanden, M. J. 2004, Physics of the Solar Corona (Berlin: Springer-Verlag) [Google Scholar]
- Ballai, I. 2007, Sol. Phys., 246, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Ballai, I., Erdélyi, R., & Pintér, B. 2005, ApJ, 633, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Ballai, I., Forgács-Dajka, E., & Marcu, A. 2007a, Astron. Nachr., 328, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Ballai, I., Jess, D., & Douglas, M. 2007b, A&A, 534, A13 [Google Scholar]
- Ballai, I., Douglas, M., & Marcu, A. 2008, A&A, 488, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, D., Erdélyi, R., Oliver, R., & O’Shea, E. 2007, Sol. Phys., 246, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, M., & Ország, S. A. 1987, Advanced Mathematical Methods for Scientists and Engineers (Singapore: McGraw-Hill) [Google Scholar]
- Chou, D.-Y., & Zirin, H. 1988, ApJ, 333, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz, A. J., Donelly, G. R., & Roberts, B. 2007, A&A, 476, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2006, A&A, 457, 1069 [Google Scholar]
- Eto, S., Isobe, H., Narukage, N., et al. 2002, PASJ, 54, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Hollweg, J. V., & Sakurai, T. 1992, Sol. Phys., 138, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., Magara, T., Hara, H., et al. 2010, Sol. Phys., 263, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., Archontis, V., Pedran, E., et al. 2012, Sol. Phys., 278, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, H., & Tripathi, D. 2007, A&A, 449, L17 [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., et al. 2003, ApJ, 584, L103 [NASA ADS] [CrossRef] [Google Scholar]
- McEwan, M. P., Donnelly, G. R., Díaz, A. J., & Roberts, B. 2006, A&A, 460, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meirovitch, L. 1970, Methods of Analytical Dynamics (Michigan, USA: McGraw-Hill) [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2009, A&A, 502, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Hood, A. W., & Erdélyi, R. 2010, A&A, 512, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Ruderman, M. S., & Erdélyi, R. 2011, A&A, 534, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Okamoto, T. J., Nakai, H., & Keiyama, A. 2004, ApJ, 608, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Orza, B., Ballai, I., Jain, R., & Murawski, K. 2012, A&A, 537, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 326, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Pintér, B., Jain, R., Tripathi, D., & Isobe, H. 2008, ApJ, 680, 1560 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsey, H. E., & Smith, S. F. 1966, AJ, 71, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2010, Sol. Phys., 267, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2011a, Sol. Phys., 271, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2011b, A&A, 534, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space Sci. Rev., 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdélyi, R. 2008, ApJ, 686, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, J. M., & Ofman, L. 2011, ApJ, 739, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., Van Doorsselaere, T., Erdélyi, R., & Goossens, M. 2007, A&A, 475, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwaan, C. 1987, ARA&A, 25, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Ofman, L., Davila, J., et al. 2012, ApJ, 751, 27 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Solutions to the wave equation in the case of the loop at the beginning of its expansion
An interesting insight into the character of the solution of the governing equation can be obtained analytically in the limiting case of
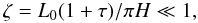 i.e. we restrict
ourselves to the first part of the emergence into the solar corona. In this case the
argument of the exponential function in Eq. (17) can be expanded (keeping only the first two terms) and the equation to be
solved reduces to
i.e. we restrict
ourselves to the first part of the emergence into the solar corona. In this case the
argument of the exponential function in Eq. (17) can be expanded (keeping only the first two terms) and the equation to be
solved reduces to 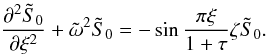 (A.1)Since we are looking
for periodic solutions and expect that both the amplitude and frequency will depend on
time, we will employ the Poincaré-Lindstedt method (Meirovitch 1970) to find corrections to the eigenfunctions and eigenfrequencies
(it can be easily shown that this method is similar to the re-normalization technique used
by Ballai et al. 2007, in the case of dispersive
shocks). We are looking for solutions in the form of series and write
(A.1)Since we are looking
for periodic solutions and expect that both the amplitude and frequency will depend on
time, we will employ the Poincaré-Lindstedt method (Meirovitch 1970) to find corrections to the eigenfunctions and eigenfrequencies
(it can be easily shown that this method is similar to the re-normalization technique used
by Ballai et al. 2007, in the case of dispersive
shocks). We are looking for solutions in the form of series and write 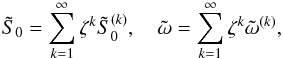 (A.2)where the functions
Si are periodic functions. We first concentrate on the
fundamental mode. After inserting the expansions (A.2) into the governing Eq. (A.1), we collect terms proportional to subsequent powers of ζ. In
the first order of approximation, collecting terms
(A.2)where the functions
Si are periodic functions. We first concentrate on the
fundamental mode. After inserting the expansions (A.2) into the governing Eq. (A.1), we collect terms proportional to subsequent powers of ζ. In
the first order of approximation, collecting terms 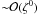 ,
results in
,
results in 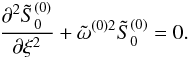 (A.3)Solving this
equation, subject to the aforementioned boundary conditions, yields in the case of the
fundamental mode
(A.3)Solving this
equation, subject to the aforementioned boundary conditions, yields in the case of the
fundamental mode 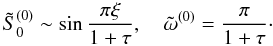 (A.4)In the next order
of approximation (i.e. terms ~O(ζ)) we obtain
(A.4)In the next order
of approximation (i.e. terms ~O(ζ)) we obtain
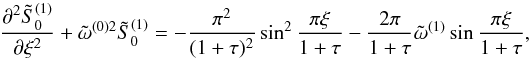 (A.5)which has to be
solved subject to the boundary conditions
(A.5)which has to be
solved subject to the boundary conditions 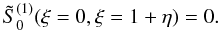 (A.6)The last term in
Eq. (A.5) will cause secular growth of
the solution, rendering the solution S1 nonperiodic. To
suppress this possibility, we choose
(A.6)The last term in
Eq. (A.5) will cause secular growth of
the solution, rendering the solution S1 nonperiodic. To
suppress this possibility, we choose 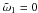 . As a result, the solution of
Eq. (A.5) together with the boundary
conditions is simply written as
. As a result, the solution of
Eq. (A.5) together with the boundary
conditions is simply written as 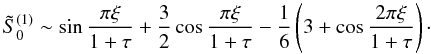 (A.7)In the next order of
approximation, we collect terms
(A.7)In the next order of
approximation, we collect terms 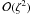 and obtain
and obtain 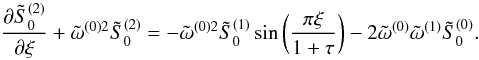 (A.8)Using the expression of
(A.8)Using the expression of
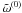 ,
,
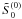 and
and 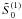 determined earlier, the RHS of the above equation can be written as
determined earlier, the RHS of the above equation can be written as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:1.26.3} {\it RHS}&&=\left[\frac{\pi^2}{3(1+\tau)^2}-\frac{2\pi{\tilde \omega}^{(2)}}{1+\tau}\right]\sin\frac{\pi\xi}{1+\tau}+A\sin^2\frac{\pi\xi}{1+\tau} \notag \\ &&\quad+B\sin\frac{2\pi\xi}{1+\tau}+C\sin\frac{3\pi\xi}{1+\tau}, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq131.png) (A.9)where
the coefficients of higher harmonics (A, B, and
C) are not needed for our discussion. In order to prevent nonperiodic
behaviour, we need to impose the condition that the coefficient of the first term is zero,
leading to
(A.9)where
the coefficients of higher harmonics (A, B, and
C) are not needed for our discussion. In order to prevent nonperiodic
behaviour, we need to impose the condition that the coefficient of the first term is zero,
leading to 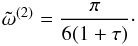 (A.10)As a result, the
eigenfunction and eigenfrequency of fundamental mode oscillations can be written as
meaning that the change in the frequency due to expansion is a second-order effect. It is
easy to show that the period of the fundamental mode in this approximation can be written
as
(A.10)As a result, the
eigenfunction and eigenfrequency of fundamental mode oscillations can be written as
meaning that the change in the frequency due to expansion is a second-order effect. It is
easy to show that the period of the fundamental mode in this approximation can be written
as 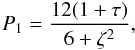 (A.11)proving the increase of
the period P1 with τ seen in Fig. 2.
(A.11)proving the increase of
the period P1 with τ seen in Fig. 2.
Repeating the same method for the first harmonic, where the eigenfunction and eigenfrequency in the zeroth-order approximation are
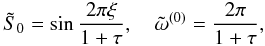 we obtain that
we obtain that
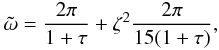 (A.12)meaning that the period
of the first harmonic in this approximation behaves like
(A.12)meaning that the period
of the first harmonic in this approximation behaves like 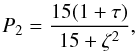 (A.13)showing an increasing
tendency with respect to τ. Now, using Eqs. (A.11) and (A.13), we can calculate the period ratio of the fundamental mode and
its first harmonic as
(A.13)showing an increasing
tendency with respect to τ. Now, using Eqs. (A.11) and (A.13), we can calculate the period ratio of the fundamental mode and
its first harmonic as ![\appendix \setcounter{section}{1} \begin{equation} \frac{P_1}{P_2}\approx 2\left(1-\frac{\zeta^2}{60}\right)=2\left[1-\frac{L_0^2(1+\tau)^2}{60\pi^2H^2}\right], \label{eq:1.26.9} \end{equation}](/articles/aa/full_html/2012/09/aa19650-12/aa19650-12-eq140.png) (A.14)so that the change in the
period ratio is very small but decreases with ζ.
(A.14)so that the change in the
period ratio is very small but decreases with ζ.
All Figures
 |
Fig. 1 Schematic representation of the evolution of the equilibrium density measured on the vertical axis in the units of density at the footpoint. Here, lengths are given in units of the loop length at the start of the expansion in the corona (L0), and time is given in units of L0/vr, where vr is the constant rising speed in the vertical direction (here taken to be 15 km s-1). |
| In the text | |
 |
Fig. 2 Variation of the periods of the fundamental mode and its first harmonic with the dimensionless time variable τ for three different values of stratification: H = 70.5 Mm (dotted line), H = 47 Mm (solid line), and H = 23.5 Mm (dashed line). |
| In the text | |
 |
Fig. 3 Variation of the P1/P2 period ratio with respect to the dimensionless parameter τ, for a loop expanding in the solar corona with persisting semi-circular shape. The meaning of each line-style is identical to Fig. 2. |
| In the text | |
 |
Fig. 4 The same as in Fig. 2, but here we assume that the expansion of the loop occurs such that the loop evolves into a loop with a semi-elliptical shape. The meaning of different line-styles is identical to Fig. 2. |
| In the text | |
 |
Fig. 5 The same as in Fig. 3, but here we assume that the expansion of the loop occurs such that the loop evolves into a loop with a semi-elliptical shape. The meaning of different line-styles is identical to Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


