| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 14 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219029 | |
| Published online | 12 September 2012 | |
The very low mass multiple system LHS 1070. A testbed for model atmospheres for the lower end of the main sequence⋆,⋆⋆
1
Université de Franche Comté, Institut UTINAM CNRS 6213, Observatoire des
Sciences de l’Univers THETA de Franche-Comté-Bourgogne, Observatoire de
Besançon,
BP 1615
25010,
Besançon Cedex,
France
e-mail: celine@obs-besancon.fr
2
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
3
CRAL, UMR 5574, CNRS, Université de Lyon, École Normale Supérieure de Lyon,
46 Allée d’Italie, 69364
Lyon Cedex 07,
France
4
Universitäts-Sternwarte München, Ludwig-Maximilians-Universität,
Scheinerstr. 1,
81679
München,
Germany
5
Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg,
Germany
6
Lund Observatory, Lund University, Department of Astronomy and
Theoretical Physics, Box
43, 221 00
Lund,
Sweden
7
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748
Garching,
Germany
Received: 13 February 2012
Accepted: 1 August 2012
Context. LHS 1070 is a nearby multiple system of low mass stars. It is an important source of information for probing the low mass end of the main sequence, down to the hydrogen-burning limit. The primary of the system is a mid-M dwarf and two components are late-M to early L dwarfs, at the star-brown dwarf transition. Hence LHS 1070 is a valuable object to understand the onset of dust formation in cool stellar atmospheres.
Aims. This work aims at determining the fundamental stellar parameters of LHS 1070 and to test recent model atmospheres: BT-Dusty, BT-Settl, DRIFT, and MARCS models.
Methods. Unlike in previous studies, we have performed a χ2-minimization comparing well calibrated optical and infrared (IR) spectra with recent cool star synthetic spectra leading to the determination of the physical stellar parameters Teff, radius, and log g for each of the three components of LHS 1070.
Results. With exception of the MARCS models which do not include dust formation, the models are able to reproduce the observations and describe the main features of the visible to IR spectra. This is consistent with the fact that dust formation prevails in the B and C component atmospheres. The parameters obtained with the DRIFT models confirm the values determined in earlier studies. But important differences between models are observed, where the MARCS model is too bright in the H and K bands, and the BT-Settl and BT-Dusty models systematically yield up to 100 K higher Teff in the case of the B and C components. This confirms a trend for models without, or with less efficient cloud formation, to predict higher Teff than models richer in dust (DRIFT). Even models including cloud physics however still produce slightly too bright J band flux, showing as too blue J − K colors. The onset of dust formation remains therefore a particularly challenging regime to understand.
Key words: Stars: atmospheres / Stars: fundamental parameters / Stars: low-mass / brown dwarfs / binaries: general
Based on observations made with the ESO Very Large Telescope at the Paranal Observatory under programme 072.C-0022 and under NACO commissioning, and with the UKIRT telescope on Mauna Kea under service proposal number 1465 and MAX guaranteed time. Also based on observations with the Hubble Space Telescope NICMOS instrument under proposal No. 7415, and with the infrared space observatory ISO, ISOPHOT instrument, under target observation number TDTNUM 37300619 and the ISOCAM instrument.
Reduced spectra used for the model comparison are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A85
© ESO, 2012
1. Introduction
The lower end of the Hertzsprung-Russel diagram has much importance as the vast majority of stars in the Galaxy are low mass stars. In the Galaxy, 70% of the stars are M dwarfs. They contribute over 40% of the total stellar mass content (Gould et al. 1996; Mera et al. 1996; Henry 1998). These M dwarfs have a mass that ranges from 0.6 M⊙ to the hydrogen burning limit of about 0.075 to 0.085 M⊙ depending on the metallicity (Chabrier & Baraffe 2000). These stars are found in any population, from young metal rich M-dwarfs in open clusters (Reid 1993; Leggett et al. 1994) to the several billion years old metal poor dwarfs in the galactic halo (Green & Morgan 1994) and in the globular clusters (Cool et al. 1996; Renzini et al. 1996). Such low mass stars are an important probe for our Galaxy as they carry fundamental information regarding the stellar physics, galactic structure and formation, and its dynamics. In addition, the existence of brown dwarfs or planets being discovered and confirmed around M-dwarfs (Butler et al. 2004; Bonfils et al. 2012, and references therein) plays an important role in understanding the formation of brown dwarfs and planets.
Despite their large number in the Galaxy, little is known about low mass stars because of the difficulty (i) to get a homogeneous sample with respect to the age and metallicity due to their intrinsic faintness, and (ii) to disentangle the parameter space (Teff, log g, and metallicity). Indeed a number of studies have shown that a change in temperature or gravity can compensate for a change in metallicity to some degree. An additional difficulty is the complexity of their atmospheres: convection in optically thin regimes, molecules, and dust cloud formation for the later types. Water vapor and CO bands dominate the Rayleigh-Jeans branch of the spectral energy distribution at IR wavelengths (>1.3 μm), while TiO, VO, and metal hydrides govern the corresponding visual (>4000 Å) to near-IR (<1.3 μm) spectral energy distribution. Convection reaches out to the optically thin (as far as to an optical depth τ ~ 10-3) portion of the atmospheres, flattening the temperature gradient of the atmosphere (Allard et al. 1997). Ludwig et al. (2002, 2006) have determined the mixing length based on a comparison of the mixing length theory used in 1D static model atmospheres and radiation hydrodynamic simulations. In M dwarfs later than M6 the outermost temperatures fall below the condensation temperatures of silicate grains, which leads to the formation of dust clouds (see e.g. Tsuji et al. 1996a,b; Allard et al. 1997; Ruiz et al. 1997; Allard & Hauschildt 1998; Allard et al. 1998). These processes complicate the understanding of these cool atmospheres.
One approach to study the physics at the low end of the main sequence is to compare observed spectra with synthetic spectra from various authors and modelling techniques. The determination of the physical parameters (effective temperature, gravity, metallicity, radius) is obtained by spectral synthesis, i.e. χ2 minimization.
LHS 1070 is a low mass multiple system of cool dwarfs discovered by Leinert et al. (1994), with visual magnitude 15. It is located at a distance of 7.72 ± 0.15 pc from the Sun (Costa et al. 2005) and is considered as a member of the disk population with a probable age of around 1 Gyr (Reiners et al. 2007b). The spectral types for the A, B, and C components were found to be M5.5–M6, M8.5, and M9–M9.5, respectively (Leinert et al. 2000). A fourth component was suspected very close to the primary by Henry et al. (1999) from Hubble Space Telescope (HST) Fine Guidance observations, but this detection is no longer considered to be real (Henry, priv. comm.). The latest orbit determination has been performed by Köhler et al. (2012), with semi major axes of 0.458′′ for the close pair BC and 1.112′′ for the wide orbit of BC around component A. For example, on December 12, 2003, component B was separated from A by 1.77′′ at position 13°, and component C from B by 0.41′′ at 178°.
Leinert et al. (1998, 2000) have derived effective temperatures of 2950 K, 2400 K and 2300 K for the components based on spectral analysis, and found that B and C showed clear signatures of dust in their spectra. They presented photometric mass estimates ranging from 0.109 to 0.079 M⊙ for the three stars based on theoretical isochrones, thus reaching right down to the minimum hydrogen burning mass. This mass range makes LHS 1070 a valuable system for understanding the formation of dust in cool atmospheres and the processes that occur at the star/brown dwarf transition. LHS 1070 is therefore a testbed to validate and define further developments of both atmospheric and interior models at the lower end of the main sequence. We assume the same age and composition for the three components of this system for simplicity.
In this paper, we present the spectral synthesis of the components A, B, and C. We determine their physical parameters by comparing the well-calibrated HST spectra in the optical (from FOS) and in near and mid-IR (from HST/NICMOS and ISOPHOT-S) with synthetic spectra computed from recent stellar atmosphere models: BT-Dusty and BT-Settl (Allard & Homeier 2012), MARCS (Gustafsson et al. 2008), and DRIFT (Witte et al. 2009). Observations and data reduction are described in Sect. 2. Section 3 presents the atmosphere models used in the analysis. In Sect. 4 we give the determination of the stellar parameters and show the comparison between observed and modeled spectra. Discussion and conclusion follow in Sect. 5.
Photometric data.
2. Observations and data reduction
Regarding the optical photometry and spectroscopy, the reader is referred to Leinert et al. (2000). The new input concerns the IR data.
2.1. Photometry
The J, H, K, and L′ photometry presented in Table 1 for LHS 1070 ABC refers to Leggett et al. (1998). We obtained M-band photometry with the UIST instrument on UKIRT on November 9, 2002, as well as N-band photometry with the MAX camera (Robberto & Herbst 1998) on the same telescope on August 27, 1996. The brightnesses of the individual components were then derived from the brightness ratios obtained with NACO (Rousset et al. 2003; Lenzen et al. 2003) for J, H, K on December 12, 2003, for L′ and M on December 6, 2001. The MAX observations in N-band yielded separate brightnesses only for component A and the sum B+C of the other two components.
The M band data were obtained in the Mauna Kea Observatory near-IR System (λcentral = 4.7 μm, 50%-width = 0.23 μm) in service mode. Aperture photometry was applied to the pipeline-reduced data. The N band photometry used a standard filter (λcentral = 10.47 μm, 5%-width = 4.65 μm). After the standard processing steps (bad pixel correction, combination of individual chop cycles after shift-and-add) we performed aperture photometry. The absolute calibration at 10.4 μm relied on the HR 6464 spectrophotometric standard model, produced by Hammersley using the procedure described in Hammersley et al. (1998), and made available on the ISO web page for ISO standards. HR 6464 has the same spectral type M0III as the standard HR 400 actually observed, and the flux ratio of the two was determined from their fluxes in the IRAS 12 μm band. Strictly speaking, the result is a narrow-band (0.25 μm) brightness at 10.4 μm under the assumption of an M0III type spectrum. The spectral slopes in this wavelength region are smooth and all are representing Rayleigh-Jeans tail emission. Uncertainties resulting from the difference in spectral type between M0III and our object therefore are not important. To be conservative, errors of ± 5 mJy, ± 4 mJy, and ± 3 mJy are taken for the fluxes of the combined system, of component A, and the sum of components B and C, respectively.
Our NACO observations were used in determining the relative brightnesses of the three components of LHS 1070, because of the superior spatial resolution of this instrument. After standard reduction (flat fielding, bad pixel correction), aperture photometry was applied. The NACO bandpasses closely match the MKO near-IR system for the J, H, K, L′ bands. The main difference is in the M band (4.8 μm for NACO versus 4.7 μm at Mauna Kea, 20% width of 0.64 μm for NACO versus 50% width of 0.23 μm at Mauna Kea). In this wavelength range, the slopes of the component spectra are very similar. Therefore the NACO-measured brightness ratios were applied to extract the component brightnesses from the MKO near-IR based total brightnesses.
LHS 1070 was observed with ISOCAM (Cesarsky et al. 1996) on the ISO satellite in the LW2 (6.7 μm) and LW3 (14.3 μm) filters on November 28, 1996 (PI H. Zinnecker). Near-IR narrow and medium-band photometry from 0.90 μm to 2.15 μm was obtained with the NIC1 and NIC2 cameras of the HST NICMOS instrument on Jan. 2, 1998. For the analysis we used pipeline reduced images. On each frame the system was clearly resolved, and it was possible to obtain separate photometric measurements for the three stars. Before performing aperture photometry for a given star, we removed the images of the other two objects by subtracting a scaled PSF template, constructed from component A and shifted to the known coordinates of the stars. An aperture correction, taken from the NICMOS Data Handbook, was applied, and photometric calibration was performed via multiplying by a conversion factor between the counts and Fν as stated in the Handbook. The results are given in Table 1.
2.2. Spectroscopic observations
Near-IR spectra of the individual components of LHS 1070 were taken with grisms G096, G141 and G206 and the NIC3 camera of the HST NICMOS instrument on January 2, 1998 for the J, H, and K bands. In a first step we removed from the four spectra we had for each grism the short wavelength and long wavelength ends. For grism G096 this left the range of 0.80–1.085 μm or 0.8–1.15 μm, depending on the local noise level. Similarly, G141 covered the range of 1.10–1.60 μm or 1.10–1.85 μm. G206 ranged from 1.65 μm to 2.45 μm. For each wavelength pixel, all spectra covering that wavelength were averaged using a weighted average, where the weights came from the formal uncertainties of the spectra (typically from 2% to 5%). The reduction was based on the NICMOSlook IDL-based data reduction package. For the extraction of the spectra, the “no weighting” option was used. The result for the A component was slightly scaled (by a few percent) to fit the NICMOS photometry. The extraction procedure also gave the combined spectrum of components B and C (separated only 0.4′′ on the detector), which was decomposed into the spectra of the individual components on basis of the brightness ratio as a function of wavelength as determined from the narrow- and medium band photometry. The spectral resolution of the NICMOS spectra is R = λ/Δλ = 200.
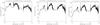 |
Fig. 1 Comparison between NICMOS and NACO spectra of the three components. |
Higher resolution spectra with R = 400, 1500, and 1400 in the J, H, and K bands, respectively, were taken with the VLT NACO instrument (Rousset et al. 2003; Lenzen et al. 2003) on telescope UT4 of the VLT for the individual components of LHS 1070. The camera/grism/filter settings were S27/Grism4/J, S54/Grism3/H, and S27/Grism3/K, respectively. The slit width was 86 milli-arcsec in all three bands. After subtracting the sky from the raw data, a flat normalized along the dispersion direction was applied. The spectra were then traced and extracted. Finally, the individual exposures were averaged. This procedure was also applied to the telluric standards. All telluric standards are of spectral type G2V, which allows a proper modelling of their intrinsic spectrum with that of the Sun. The Solar spectrum was constructed using the data and scripts provided by Maiolino et al. (1996). Wavelength calibration was obtained by arc lamp exposures. The additional effort to guarantee the absolute flux calibration was not taken, so only the relative shape of the spectrum was determined in each band. For each component, we used one scaling factor for each band to bring the spectra to the absolute level as resulting from the NICMOS observations. The errors, taken as the formal uncertainties of the averaging process, typically range from 5–10%. The number of pixels per resolution element in the J, H, and K band is about 3, 1.5, and 3. Because of the missing independent absolute calibration, the NACO spectra are used primarily for the study of spectral features. However, comparison with the NICMOS spectra, like in Fig. 1, gives confidence also in their spectral shape.
Spectra for the system from 2.5 μm to 11.7 μm were obtained with the ISOPHOT-S spectrometer on board of the ISO satellite on November 23, 1996 (PI: T. Tsuji) with an exposure time of 4096 s. ISOPHOT-S was the spectroscopic sub-instrument of ISOPHOT (Lemke et al. 1996). It had an entrance aperture of 24″ × 24″, covering simultaneously the 2.5 to 4.9 and 5.9 to 11.7 μm ranges. The spectral resolution of both channels ranged between 65 and 130. We processed the ISOPHOT-S observations using the Phot Interactive Analysis (PIA) V10.0 (Gabriel et al. 1997) following the standard data reduction scheme. The measurements were further reduced following our self-developed processing scheme (Kóspál et al., submitted), correcting for the slight off-center positioning of the source.
2.3. Spectroscopic features
Figure 2 shows the optical spectra of all the three components, with expected atomic and molecular features in the optical range between 5000 to 8500 Å. The most important ones are molecular bands of TiO, CaH, and VO, and atomic lines like CaI, NaI, and KI. The TiO bands get weaker toward lower temperature, from component A to C, due to condensation into dust species. The hydride CaH at 6380 Å and 6880 Å decreases in strength with decreasing temperature. The KI doublet at 7665 and 7699 Å is very strong and is useful for gravity determination. The NaI doublet at 8183 Å and 8195 Å is strong in all the components, whereas CaI at 6103 Å is weak at all temperatures.
Figure 3 shows the near-IR spectra obtained with NICMOS on HST for the three components as well as the thermal IR spectrum of the unresolved system A+B+C taken with ISOPHOT on ISO. Photometric results are superimposed on these spectra.
Figure 4 shows the NACO spectra obtained at the VLT of the three individual components in the J (upper panel), H (middle panel), and K (lower panel) band for components A, B, and C (from left to right). The main expected features are also indicated. The Paschen Beta and CaI lines can be seen in the J-band spectra with “equivalent widths” of 2−2.5 Å and 1.5−2 Å, respectively. The H-band spectra contain many relatively weak absorption features, which defy definite identifications, with possible exception of Mg (1.711 μm), OH (1.689 μm), and Al (1.675 μm). H2O bands define the shape of the J and H band peaks. Water absorption is most obvious in the J-band at 1.33 μm and strengthens through the later types: the flux ratio between the peak and the minimum of the absorption band increases from 1.09 ± 0.01 for component A to 1.30 ± 0.01 and 1.39 ± 0.01 for the cooler components. The K-band spectra of the three components show strong CO bands and more or less pronounced atomic features. The NaI lines weaken from the hotter component A to the cooler components B and C as dust forms.
 |
Fig. 2 Optical spectra of the components of LHS 1070 obtained with the Faint Object Spectrograph (FOS) on HST. The atomic and molecular features visible in all three components are shown in the upper panel. |
 |
Fig. 3 Near-IR spectra (solid line) and photometry (solid circles) obtained with NICMOS on HST for components A (upper left), B (upper right), and C (lower left). The ISOPHOT thermal IR spectra of the unresolved system is shown on the lower right panel, again with photometric measurements overplotted. |
3. Model atmospheres
The atmospheres of low-mass stars are mostly composed of molecular hydrogen and CO, and their spectra characterized by strong TiO bands in the optical, water vapor bands in the IR, chromospheric activity, flares, magnetic spots, and planet like properties (Allard et al. 1997). The discovery of the formation of dust clouds in M and L dwarfs makes it even more challenging to understand their spectral properties. An effective temperature of 2600 K and below is sufficiently low to give rise to enough silicate dust formation in the photospheric layers to affect the spectral properties of late type M dwarfs. These grains produce a “veiling” in the optical by dust scattering and an important greenhouse effect (redistribution of flux to the IR) which strongly influence the IR spectral properties. Tsuji et al. (1999); Allard et al. (2001) treated the dust formation in the low-mass stars in pure Chemical Equilibrium (hereafter CE). CE yields the formation of condensates from zirconium dioxide and silicates (Mg2SiO4) to refractory ceramics (CaTiO3, Al2O3), salts (CsCl, RbCl, NaCl), and ices (H2O, NH3, NH4SH4) depending on the temperature of the atmosphere from M through T and Y spectral types (Allard et al. 2001; Lodders & Fegley 2006). Helling et al. (2008a,b); Allard & Homeier (2012) explored the properties of the formation of the dust clouds in low-mass stars by determining the radial distribution and average size of the grains.
 |
Fig. 4 VLT (NACO) spectra of all the components in J, H and K bands with atomic and molecular lines indicated. |
We compared the flux-calibrated spectroscopic data of LHS 1070 with synthetic spectra computed from three recent atmosphere models for cool stars. These models are described below. In order to match the observed spectra, the synthetic spectra have been scaled by the dilution factor (R/d)2 where d is the distance of the system from Costa et al. (2005) and the stellar radius R is a free parameter ranging from 0.096 R⊙ to 0.142 R⊙ at a step of 0.002. The radius resulting from the fits can then be compared to predictions from stellar evolutionary models.
3.1. BT-Dusty and BT-Settl
Recently, the preliminary results of the BT-Cond/Dusty and BT-Settl models based on the Asplund et al. (2009) solar abundances have been published in a review by Allard & Homeier (2012), and those grids distributed via the PHOENIX web simulator (http://phoenix.ens-lyon.fr/Grids/BT-Settl/AGSS2009/). For this paper, we have developed a revision to these BT-Dusty and BT-Settl models based on the Caffau et al. (2011) solar abundances using slightly revised atomic and molecular opacities as well as cloud physics. Their detailed publication is in preparation. We summarize below the differences between the current version of the models and the published versions of Allard et al. (2001); Allard & Homeier (2012).
The BT appellation stands for the Barber and Tennyson so-called BT2 water vapor line list (Barber et al. 2006). The models are provided in several versions addressing different limiting treatment of the cloud physics. The Dusty and Cond appellation, as defined by Allard et al. (2001), refer to a CE treatment of dust formation where dust opacities (assuming spherical grains with interstellar grain size distribution) are ignored in the Cond models. The BT-Dusty and BT-Cond models reproduce the color properties of the 2001 AMES Dusty and Cond models in the brown dwarf regime, with minor differences relating to revised opacities for H2O, TiO (Plez 1998), VO and most of the hydrides, detailed damping profiles for the alkali lines (Allard et al. 2007), the damping constants of molecular lines (Homeier 2005), new line lists for CH4 (STDS, Homeier 2005), CO2 (CDSD, Tashkun et al. 2004), and CIA (Borysow et al. 2001; Abel et al. 2011) to mention the most important changes). We reserve the NextGen appellation, as chosen for the Hauschildt et al. (1999) models, for corresponding pure gas phase models.
The BT-Settl models described by Allard & Homeier (2012), on the other hand, include gravitational settling which is ignored in Dusty models, and which involves a cloud model. The growth of the grains is governed by the supersaturation ratio of the gas and is triggered by the actual collision rates between grains and gas molecules and, therefore, depends on the grain surface. A breakthrough was therefore achieved, compared to earlier versions (Allard et al. 2003, 2007; Reiners et al. 2007a; Helling et al. 2008c), by calculating locally the supersaturation instead of assuming the fixed conservative value proposed by Rossow (1978). The cloud model used in the BT-Settl models is based on Rossow (1978) and accounts for nucleation, condensation, supersaturation, gravitational settling or sedimentation, and advective mixing. The latter includes convective mixing based on the mixing length theory in the convection zone, an exponential overshoot according to Ludwig et al. (2006), and the gravity waves according to Freytag et al. (2010). The latter dominate the mixing in the uppermost atmosphere layers, i.e. the regions where clouds first begin to form in late M dwarfs. The grains are still considered spherical but the grain sizes (a unique or mean value per atmospheric layer) and grain number densities are determined by the comparison of the different timescales, and thus vary with depth to reach grain sizes of a few times the interstellar values at the cloud base. The BT-Settl models do not enforce grains to be in equilibrium with the gas phase as is the case of the Dusty and Cond models. However, the gas phase opacities reflects the depletion of elements from the gas phase caused by grain growth. The numerical solving on-the-fly of the gas phase CE in the BT-Settl models (unlike what is often done by other authors) costs computing time but allows to account for the cooling history of the atmospheric layers.
For the current BT-Settl model version, we have additionally explored the effects of nucleation in our cloud model by assuming a constant nucleation rate of 1 cm-3. This acts as a limiting factor to the creation, sedimentation and depletion of grains and thus leads to the persistence of grains higher up in the atmospheric structure than assuming unlimited grain production. We are using in general atomic damping constants according to Unsöld (1968) with a correction factor to the van der Waals widths of 2.5 (Valenti & Piskunov 1996), van der Waals broadening of molecular lines with generic widths according to Homeier et al. (2003). More accurate broadening data for neutral hydrogen collisions by Barklem et al. (2000) have been included for several important atomic transitions such as the Alkali, the Ca i and Ca ii resonance lines.
Grains are assumed here to be spherical and non-porous, and their Rayleigh to Mie scattering and absorptive properties are considered for 55 types of material including the species mentioned above and presented in Allard et al. (2001) and Ferguson et al. (2005), plus MnSiO3 and Na2O5Si2. The grain opacities are computed in each layer for pure spherical grains using the radius determined by the cloud model (assuming it represents an average radius of the grains in each layer) and the material density as measured in the laboratory. The opacity contributions of the various grain species present in each layer are finally summed.
The model atmospheres and synthetic spectra are computed with the PHOENIX radiative transfer code (Allard 1990; Allard & Hauschildt 1995; Allard et al. 2001) using hydrostatic equilibrium, convection based on the mixing length theory and a mixing length which varies from 2.2 to 1.6 from brown dwarfs to the Sun according to results of radiation hydrodynamical simulations (Ludwig et al. 1999, 2002, 2006), spherically symmetric radiative transfer using radii provided by published evolution models, micro-turbulence velocities from radiation hydrodynamical simulations (Freytag et al. 2010), and the latest solar abundances by Caffau et al. (2011).
The synthetic spectra are provided over the entire spectral range of interest at a spectral resolution of 0.05 Å in the optical and 0.1 Å in the IR. For this paper, we explored these model grids with parameters described as follows:
-
Teff from 2000 K to 3100 K with 100 K step, as expected for mid-M to L dwarfs;
-
log g = 4.5,5.0, and 5.5 dex;
-
[M/H] = −1.5, −1.0, −0.5,0.0, + 0.3, and + 0.5 dex.
3.2. MARCS
The MARCS code (Gustafsson et al. 2008) assumes hydrostatic equilibrium, Local Thermodynamic Equilibrium (LTE), chemical equilibrium, homogeneous plane-parallel stratification, and the conservation of the total flux (radiative plus convective; the convective flux being computed using the local mixing length recipe). The radiation field used in the model generation is calculated by assuming absorption from atoms and molecules by opacity sampling at approximately 100 000 wavelength points over the wavelength range 1300 Å –20 μm.
The code used for calculating the synthetic spectra is BSYN v. 7.12 which is based on routines from the MARCS code. The atomic line list used in our calculations is compiled from the VALD I database (Kupka & Ryabchikova 1999) updated according to Gustafsson et al. (2008). The molecular line lists include CO, SiO, TiO, ZrO, VO, OH, H2O, CN, C2, NH, CH, AlH, SiH, CaH (see references in Gustafsson et al. 2008), MgH (Skory et al. 2003), FeH (Dulick et al. 2003), and CrH (Burrows et al. 2002). Up-to-date dissociation energies and partition functions are used. The basic chemical composition adopted is that of the Sun as listed by Grevesse et al. (2007). The synthetic spectra were calculated in plane parallel symmetry. A constant micro-turbulence velocity of 2 km s-1 is assumed. The most important differences to the BT models are the different opacities sources, the solar abundances, and the fact that MARCS is a pure gas phase model with no dust formation.
Synthetic spectra are calculated for the wavelength region of 0.50−2.53 μm, with a resolution of R = 600 000. We used a grid of MARCS model atmosphere which spans the parameters as follows:
-
Teff from 2500 K to 3100 K with 100 K step (lower temperatures are not available);
-
log g = 4.5,5.0, and 5.5 dex;
-
[M/H] from −0.5 to 0.25 dex with 0.25 dex step.
3.3. DRIFT
The DRIFT-PHOENIX model atmosphere code has been developed by Dehn et al. (2007); Helling et al. (2008b); Witte et al. (2009). Both the DRIFT code by Helling et al. (2008a) and the BT-Settl code return a consistent dust cloud structure with corresponding opacities and the altitude-dependent depletion and redistribution of gas phase abundances, which feed back on both the thermodynamical structures and the radiation field. An iteration of these methods allows the determination of stationary atmosphere and dust cloud properties and yields the respective synthetic spectra. But solely in the case of the DRIFT code, the dust formation takes place via the formation of seed particles and their subsequent growth or evaporation, solving from top to bottom of the atmosphere. The BT-Settl models in contrast solve the timescale equations to calculate the depletion of refractory elements from bottom to top.
Derived parameters for the LHS 1070 system.
As in the BT-Settl model, the DRIFT model assumes dirty grains mixed according to the composition of each atmospheric layer. While the BT-Settl model assumes dirty grains in the timescales equations to calculate the growth and settling of the grains, it only sums the opacity contributions of each species in each layer as for an ensemble of pure grains. The DRIFT model instead uses composite optical constants calculated in effective mean theory from the composition of the grains (Bosch et al. 2000). The resulting absorption and scattering properties of the grains are therefore different than those of the BT-Settl models, possibly producing more opaque clouds. However, since the opacities are dominated by atomic and molecular opacities over most of the spectral distribution in this spectral type range, the impact of those differences are difficult to identify. The largest differences between the BT-Dusty, BT-Settl and DRIFT models are the differences in the local number density, the size of dust grains, as well as their mean composition, which are the direct results of the cloud model approach.
The DRIFT model also considers only seven of the most important solids (TiO2, Al2O3, Fe, SiO2, MgO, MgSiO3, Mg2SiO4) made of six different elements, found to form below an effective temperature of 2800 K. Note that the CE, which determines the composition of the solid species included in the BT-Settl model, does not give the same list. Among the most important species, forming in the BT-Settl model below Teff = 2900 K, are additionally ZrO2, CaTiO3, CaSiO3, Ca2SiO4, Ca2Al2SiO7, Ca2MgSi2O7, CaMgSi2O6, Ti2O3, Ti4O7, Fe, Ni, VO, V2O3, MgTiO3, MgTi2O5, MgAl2O4, Al2Si2O13. The DRIFT model includes, similarly to the BT-Settl model, mixing by convection and overshooting by assuming an exponential decrease in mass exchange frequency in the radiative zone (Woitke & Helling 2004). However it neglects the contribution of the gravity waves included in the BT-Settl model. The model code DRIFT-PHOENIX has been discussed in more detail by Witte et al. (2009).
We used a grid of DRIFT model atmosphere which spans the parameters as follows:
-
Teff from 2200 K to 3100 K with 100 K step;
-
log g = 4.5,5.0, and 5.5 dex;
-
[M/H] from −0.5 to 0.5 with 0.5 dex step.
4. Physical parameters determination and results
The first analysis of LHS 1070 by spectral synthesis was made by Leinert et al. (1998) using the FOS spectra and the pure gas phase NextGen model atmospheres (Allard et al. 1997; Hauschildt et al. 1999). But the quality of the fits, even for the A component was disappointing, especially below 0.72 μm, and the Teff of the B and C components were strongly overestimated (2700 K) mainly due to the absence of dust formation. Leinert et al. (2000) have therefore used the AMES-Dusty models (Allard et al. 2001) to re-analyze the LHS 1070 system. However if the quality of the fits and precision of the Teff for the B and C components were clearly improved, this was still clearly not the case of the M dwarf primary. The stellar parameters obtained with the assumption of a distance of 8.8 pc are summarized:
-
component A: Teff = 2950 K, log g = 5.3 ± 0.2, [M/H] = 0.0;
-
component B: Teff = 2400 K, log g = 5.5 ± 0.5, [M/H] = 0.0;
-
component C: Teff = 2300 K, log g = 5.5 ± 0.5, [M/H] = 0.0.
In the following, we derive the stellar parameters using more recent atmosphere models and spectroscopic informations covering both the optical and IR ranges. Metallicity and gravity are determined from peculiar spectral features, whereas effective temperature and radius are constrained from the overall shape of the spectra, following the different steps: (i) a first χ2 minimization is performed on the overall spectra considering effective temperature, radius, metallicity, and gravity as free parameters. It gives a first guess for the parameter space of each component; (ii) we looked for peculiar spectral features that are mainly sensitive to metallicity (see Sect. 4.2) or gravity (see Sect. 4.3) to refine these two parameters; (iii) we fixed these parameters to perform another χ2 minimization and derive effective temperature and radius (see Sect. 4.4). At each step we checked that the resulting value is not sensitive to changes on the value of the other parameters.
Age is estimated from kinematics and rotation. Before entering the details of our study, we also summarize our results in Table 2. Note that these values have been obtained by assuming a distance of 7.72 pc (Costa et al. 2005) whereas Leinert et al. (2000) used the higher value of 8.8 pc.
4.1. Spectral type
A well-defined spectral classification for the M dwarfs helps in the calibration of the temperature of the late type stars and for the definition of the end of the main sequence on the HR diagram. We have derived spectral indices and spectral types for all three components. For the early M-dwarf, i.e. the primary, we used the classification scheme based on the TiO and CaH band-strengths, as defined by Reid et al. (1995). For the late M-dwarfs, we also used the PC3 index defined by Lépine et al. (2003); Hawley et al. (2002); Martín et al. (1999). We have computed the spectral index H2O-K in the near-IR K-band defined by Covey et al. (2010) and used the spectral-type vs. index relation from Rojas-Ayala et al. (2010). The spectral indices and corresponding spectral types are given in Table 3. The obtained spectral classification for components B and C is one subclass higher as compared to Leinert et al. (2000). The spectral types obtained in the K-band differs from the optical indices by up to two subclasses showing inconsistency on the spectral type versus spectral index relations defined from the optical and near-IR spectra. Here we adopt the spectral type obtained from optical spectral indices.
4.2. Metallicity
In order to estimate the metallicity of the system, we looked for special features in the spectra that are mainly sensitive to the metallicity. The main indicator of metallicity is the VO absorption band at 7300–7600 Å. It is well reproduced at solar metallicity for all components, and shown in Fig. 5 for the primary with the BT-Settl model. We checked that the same metallicity is found when changing the other parameters. This solar metallicity can also be inferred from the NaI, CaI, and H2O features in the K-band of the primary using the calibration determined by Rojas-Ayala et al. (2010). In the following, we adopt this [M/H] = 0 dex value.
4.3. Gravity
The surface gravity can be estimated by analyzing the width of atomic lines such as the K I and Na I D doublets, as well as the relative strength of metal hydrides bands such as those of CaH. The K I doublet at 7665 Å and 7699 Å is a particular useful gravity discriminant for M stars. Figure 6 (left panel) shows the gravity effects on the strength and pressure broadening of the K I lines as modeled by the PHOENIX BT-atmospheres. The overall line strength (central depth and equivalent width) increases with gravity as the decreasing ionisation ratio due to the higher electron pressure leaves more neutral potassium in the deeper atmosphere. The width of the damping wings in addition increases due to the stronger pressure broadening, mainly by H2, He and H I collisions.
Spectral index values and derived spectral type computed from TiO and CaH band-strengths for component A and from the PC3 index for components B and C.
Figure 6 (right panel) shows the determination of gravity for the component A from the K I doublet using the BT-Settl, MARCS, and DRIFT models. The determined log g values are given in Table 2. The best agreement is obtained with log g = 5.0 dex for all the atmospheric models. This value is confirmed by the CaH molecular bands (Fig. 7). We checked that the same metallicity is found when changing the other parameters and adopt the value log g = 5.0 dex in the following. For comparison, the gravities inferred from the masses found from the orbits of the system (Seifahrt et al. 2008) are also listed, which are also in good agreement with the values found by fitting.
4.4. Effective temperature and radius
We performed a second χ2 minimization by adopting the metallicity and gravity derived in Sects. 4.2 and 4.3 and refined the effective temperature and the radius by comparing the overall shape of the observed and synthetic spectra. As opposed to the studies mentioned previously in which the best fit was found by trial and error, in this paper we derive the effective temperature and radius by performing a χ2 minimization technique. For this purpose, our approach was to first convolve the synthetic spectrum with a Gaussian kernel at the observed resolution and then rebin the outcome with the observation. For each of the observed spectra we have calculated the reduced χ2 value by comparing these spectra, taking into account their uncertainties estimated from the reduction procedures (see Sect. 2.2), with the grids of synthetic spectra in the wavelength range between 4500 Å to 2.4 μm. We have excluded the spectral region below 4500 Å due to the low signal-to-noise ratio of the observed spectra. The number of data points used for the χ2 computation is thus 1487 in the optical and 204 in the near-IR.
 |
Fig. 5 VO band observed in the primary (black) compared to the BT-Settl model at 2900 K, log g = 5.0, R = 0.134 R ⊙ for different metallicities. |
 |
Fig. 6 Right: BT-Settl and BT-Dusty models for an effective temperature of 2900 K and varying log g. The effect of gravity and the pressure broadening of the K I doublet is clearly visible. The details of the dust treatment only cause negligible differences at this Teff. Left: K I doublet as observed for the primary (black) compared to the BT-Dusty (red), BT-Settl (green), DRIFT (blue), and MARCS (brown) models with log g = 5.0. |
In a second step, a reduced χ2 map has been obtained for each component in the optical and in the near-IR as a function of temperature and radius. Such a map is shown in Fig. 8 for the primary using the BT-Dusty model. The χ2 minimum value is given on the left part of the color bar. The parameter space which gives an acceptable solution around the minimum χ2 valley is within the white contour, defined by visual inspection. The χ2 value at this significance level is indicated along the white contour. Error bars are derived from this contour.
We have identified on the contour maps the possible solutions in the optical and near-IR. The adopted values of effective temperature and radius are the common intersection between the solutions found in the optical and near-IR.
The solutions were finally inspected by comparing it with the observed spectra. The same procedure has been used with BT-Settl, MARCS and DRIFT model grids. Differences of 100 K to 200 K in the Teff determination (see Table 2) are found for the B and C components depending on the model used, whereas all models agree on the effective temperature of the primary.
4.5. Age and mass
With its high velocity component of W = 43 km s-1 perpendicular to the galactic plane based on Basri & Marcy (1995), LHS1070 has been considered as part of the old disk population with an age of several Gyrs. Reiners et al. (2007b) refined this estimate to about 1 Gyr based on measured rotation velocities of its components using a modified Skumanich braking law (Skumanich 1972). They do not exclude however that the braking law may also have to be changed in its absolute time scale, which could increase this estimate.
By an orbital fit, Leinert et al. (2001) have computed the combined mass of the components B and C and showed that their mass is very close to the hydrogen burning minimum mass, in good agreement with the masses of 0.080 to 0.083 M⊙ and 0.079 to 0.080 M⊙ derived by Leinert et al. (2000) from theoretical mass-luminosity relations (Baraffe et al. 1998; Chabrier et al. 2000). Seifahrt et al. (2008) constrained the combined mass of B and C to MB + MC = 0.157 ± 0.009 M⊙ which is higher than Leinert et al. (2001) because of the refined distance by Costa et al. (2005). Recently, an improved fit for the orbit of LHS 1070 B and C around each other, and an estimate for the orbit of B and C around A have been performed. The masses of the three components are found to be MA = 0.13 to 0.16 M⊙, MB = 0.077 ± 0.005 M⊙, and MC = 0.071 ± 0.004 M⊙ (Köhler et al. 2012). Here, the values for the primary are uncertain, because the wide orbit of this triple system has not yet been determined with sufficient accuracy. Finally, Seifahrt et al. (2008) have not measured individual masses for the B and C components, but using the mass ratio MC/MB = 0.923 from Köhler et al. (2012), their masses for A, B, C become 0.115 ± 0.01, 0.082 ± 0.01 and 0.075 ± 0.01 M⊙.
The interpolations of the NextGen (Baraffe et al. 1998) isochrone for the primary, and of the AMES-Dusty (Chabrier et al. 2000) isochrone for the B and C components, assuming an age of 1 Gyr for the dynamical masses of Seifahrt et al. (2008) are shown in Table 2. For masses above the hydrogen burning limit these values do not change much for larger ages, since in the stellar regime only show small evolution effects are seen after the age of 1 Gyr. No evolution models have yet been calculated using the BT-Settl models. However, only negligible changes are expected with the revision of the evolution calculations. Such revision of the interior and evolution models is currently being prepared (Baraffe, Exceter, priv. comm.).
 |
Fig. 7 CaH molecular bands in the spectrum of the primary (black) compared to the BT-Settl model at 2900 K, log g = 5.0 (red) and log g = 5.5 (green). |
4.6. Results
Figures 9 and 10 show the best fit model superimposed to the observed optical (FOS) and near-IR (NICMOS) spectra for all the three components using the BT-Settl, BT-Dusty, MARCS, and DRIFT models. Note that the observed NICMOS spectra of all three components plunge down away from the model predictions below 0.85 μm (see Fig. 10), whereas the observed FOS spectra are correctly represented by the models in the same wavelength range (see Fig. 9). This deviation is due to difficulties with the NICMOS data at the very edge of the wavelength range.
The FOS spectral distribution is better reproduced by the models for the primary than for the cooler components B and C. The revised opacities and oxygen abundance (among other elements) used in the current BT-Settl models allow a significant improvement compared to the AMES-Dusty and NextGen models used in previous analysis (Leinert et al. 1998, 2000). The slope of the spectra is now reproduced over the complete FOS spectral distribution, and the strength of molecular bands is reproduced on average quite well. However some problems remain which are probably due to uncertain and missing opacity sources. Hence, the MgH feature at around 5200 Å is too strong in all the models while the CaOH band at 5500 Å is missing in all models. The NaI doublet at around 5900 Å is far too strong in the models as well as the CaH band at 7000 Å. Largest discrepancies are found around 6000–6400 Å for all models. The TiO bands around 7055 Å as well as the CaH band around 6900 Å are too strong in all the models. The VO band around 7334 Å is also visible and is quite well matched by the BT-Settl model. The BT-Settl models also differ from the DRIFT models by the strength of atomic lines which are deeper in the DRIFT models.
In the near-IR NICMOS range, the BT-Settl models fit slightly better the primary than the DRIFT models. The MARCS model overestimates the flux over most of the spectral range above 1.3 μm while the DRIFT model shows a slightly different shape of the H band peak which is shared by the BT-Settl models in the case of the B and C components. But all the models appear over luminous in the J and H bands in the case of the B and C components for the selected radius and effective temperature. This is also apparent in Fig. 11 which shows the comparison of high resolution near-IR spectra (NACO) with the best fit of all the four models. The change in the NaI and CaI strength as the temperature decreases (K-band) is quite well reproduced by the BT-Settl, BT-Dusty and DRIFT models.
 |
Fig. 8 Left: χ2 map computed for component A using the optical spectrum and the BT-Dusty model. Right: same using the near-IR spectrum. All values inside the white contour give an acceptable fit (checked by eye). The adopted common solution to both χ2 maps is: Teff = 2900 K and a radius of 0.134 R ⊙ . |
 |
Fig. 9 Optical spectra of all three components. Comparison with model predictions. Black: observed FOS spectra. Green: best fit BT-Settl model. Blue: best fit DRIFT model. Brown: best fit MARCS model. The parameters that give the best fit are given in Table 2. |
 |
Fig. 11 Black: J (upper panel), H (middle panel), and K (lower panel) NACO spectra of all three components. Comparison with model predictions. Green: best fit BT-Settl model. Red: best fit BT-Dusty model. Blue: best fit DRIFT model. Brown: best fit MARCS model. The comparison of the BT-Dusty and BT-Settl models together with the observations are shown on the right panels. |
As an additional check on the effective temperature determination, we also compared the spectrum of the unresolved system in the 3−14 μm range with the BT-Dusty, BT-Settl and DRIFT models (MARCS models are not available in this wavelength range). The synthetic spectra of the unresolved system are computed by adding the individual best fit synthetic spectra. The comparison is shown in Fig. 12, where the ISOPHOT spectrum is in black, the BT-Dusty model in red, the BT-Settl model in green, and the DRIFT model in blue. Star symbols indicates the photometry obtained in the IR bands. The overall agreement is good except for the observed spectrum above 8.7 μm, where it gets quite noisy.
Relatively small differences distinguish the MARCS, DRIFT and BT models in the IR spectral range for the primary. In the case of the B and C components, the MARCS models suffer clearly of the lack of dust grain scattering which tends to flatten out or veil the spectral features in this spectra range. This effect is observed in the DRIFT, BT-Settl and BT-Dusty models which include dust formation. Differences in the cloud model approaches explain the differences between the DRIFT, BT-Dusty and BT-Settl models. The DRIFT models appear as dusty as the 2001 AMES-Dusty models with similar effective temperatures and surface gravities for B and C than derived by Leinert et al. (2000). The BT models tend to attribute slightly hotter effective temperatures (+100 K) and lower gravities (− 0.5 dex) to these objects, while the dust-free MARCS models would attribute them the highest values (+ 200 K). But judging from the overall fits obtained to the NICMOS spectra it appears that neither of the models are yet dusty enough to explain the IR spectral distribution of B and C. Indeed the over-luminosity of the models in the J band could be attributed to missing or to weak veiling by dust scattering.
 |
Fig. 12 Black: ISOPHOT thermal IR spectra of the unresolved system, with photometric measurements overplotted (stars). Red: best fit BT-Dusty model. Green: best fit BT-Settl model. Blue: best fit DRIFT model. |
The Köhler et al. (2012) mass estimate for the primary requires a 150 to 300 K higher effective temperature and up to 30% larger radius than using the revised Seifahrt et al. (2008) mass, resulting in an over-prediction of the luminosity of up to one magnitude. In the case of the B and C components, the Köhler et al. (2012) mass estimates correspond to effective temperatures which are 100 to 200 K cooler than obtained in this paper using the DRIFT models, and in correspondingly larger discrepancies with the BT-Settl fits. On the other hand, the results obtained in this paper for all three components are consistent with the isochrone interpolation for the revised Seifahrt et al. (2008) masses of the A, B and C components of LHS 1070 (see Table 2), and there is no evidence that the components may have been influenced by their binary nature.
5. Conclusions
This paper presents the results from spectral synthesis analysis for the LHS 1070 triple system. This system has been extensively observed from the optical to the IR, and dynamical masses have been determined (Leinert et al. 2001; Seifahrt et al. 2008). Therefore, it constitutes a testbed of model atmospheres of low-mass stars. Band strength indices are used to measure TiO, CaH and PC3 features to classify their spectral type. The components are classified as M5.5, M9.5, and L0 dwarfs, and their atmospheres lie in a temperature range where dust starts to form. We have determined the physical parameters Teff, log g, metallicity, and radius for the three components of the LHS 1070 system by comparing the observed spectra with the synthetic spectra computed with the most recent atmospheric models: BT-Dusty, BT-Settl, MARCS, and DRIFT. All the models agree for a solar metallicity for the system. The derived gravity is 5.0 dex and agrees within the uncertainties with the values derived from the dynamical mass (Seifahrt et al. 2008).
We found the same value for Teff for the primary from all models while differences of 100 K and 200 K are found for components B and C depending on the dust density content of the model atmosphere used. The revised oxygen abundance by Asplund et al. (2009) and Caffau et al. (2011) yield significant improvements of the BT-Settl fits to the primary compared to earlier studies based on the larger values of the solar oxygen abundance of Grevesse & Sauval (1998). These improvements are described in Allard & Homeier (2012). The even lower abundances of Grevesse et al. (2007) used in the MARCS models lead to an excess of near-IR flux due to weaker water vapor absorption.
The DRIFT and BT-Settl models differ mainly in their numerical approach in solving the equations for grain growth, sedimentation and opacities: the DRIFT model solves them from the top to the bottom of the atmosphere, while the BT-Settl model solves them from the bottom to the top of the atmosphere. This causes the BT-Settl model to tend to have a deficit of grains in the upper atmospheric layers compared to the DRIFT model despite an adequate account in both models of supersaturation effects. Despite these fundamental differences, the resulting grain sizes obtained by the models are quite similar. The over-luminosity shared by the models in the J bandpass could be indicative of grains of larger sizes and/or more numerous in the LHS1070 B and C component atmospheres. The results confirm the Allard & Homeier (2012) findings based on Teff-color constraints.
The Teff values found with the DRIFT atmospheres for components B and C agree with the Leinert et al. (2000) findings. Except for the MARCS models which do not include dust treatment, the models are able to reproduce the observations and describe the main features of the visible to IR spectra for all three components. This raises the confidence level in the dust-modeling approach.
However, the calculation of opacities for composite grains relies on relatively simple approximations and also does not account for possible distributions of grain shapes and structures such as porosity. Both models rely on results of radiation hydrodynamical simulations that provide the mixing and overshooting which compensates sedimentation effects. One problem is certainly that the translation of the resulting radial velocity field into a diffusion coefficient is currently uncertain. It is also possible that the mixing effects are being currently underestimated by local 2D simulations, and that additional mixing is provided by other phenomena on larger scales such as global rotation effects.
Acknowledgments
We thank Joris Blommaert for the calibration of the ISOCAM photometry, Chris Davis for obtaining the UIST data, Hongchi Wang for reducing the NACO spectra, Tom Herbst for the MAX data, and Thomas Müller for calibrating them. N.R. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. N.R. acknowledges support from the Swedish Research Council, VR and funds from Kungl. Fysiografiska Sällskapet i Lund. N.R. thanks Dr. Kjell Eriksson for valuable help and discussions concerning the running of the MARCS model-atmosphere program. We acknowledge financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. The research leading to these results has received funding from the “Agence Nationale de la Recherche” (ANR), the “Programme National de Physique Stellaire” (PNPS) of CNRS (INSU), the University of Franche-Comté, and the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement No. 247060). The computations were performed at the Pôle Scientifique de Modélisation Numérique (PSMN) at the École Normale Supérieure (ENS) in Lyon and at the Gesellschaft für Wissenschaftliche Datenverarbeitung Göttingen in collaboration with the Institut für Astrophysik Göttingen.
References
- Abel, M., Frommhold, L., Li, X., & Hunt, K. L. C. 2011, J. Phys. Chem. A, 115, 6805 [CrossRef] [Google Scholar]
- Allard, F. 1990, Ph.D. Thesis, Ruprecht Karls Univ. Heidelberg [Google Scholar]
- Allard, F., & Hauschildt, P. H. 1995, ApJ, 445, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., & Hauschildt, P. H. 1998, in Brown Dwarfs and Extrasolar Planets, eds. R. Rebolo, E. L. Martín, & M. R. Zapatero-Osorio, ASP Conf. Ser., 134, 370 [Google Scholar]
- Allard, F., Hauschildt, P. H., Alexander, D. R., & Starrfield, S. 1997, ARA&A, 35, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., & Homeier, D. 2012, Mem. Soc. Astron. It., submitted [arXiv:1206.1021] [Google Scholar]
- Allard, F., Alexander, D. R., & Hauschildt, P. H. 1998, in Cool Stars, Stellar Systems, and the Sun, eds. R. A. Donahue, & J. A. Bookbinder, ASP Conf. Ser., 154, 63 [Google Scholar]
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Guillot, T., Ludwig, H.-G., et al. 2003, in Brown Dwarfs, ed. E. Martín, IAU Symp., 211, 325 [Google Scholar]
- Allard, F., Allard, N. F., Homeier, D., et al. 2007, A&A, 474, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Basri, G., & Marcy, G. W. 1995, AJ, 109, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2012, A&A, accepted [arXiv:1111.5019] [Google Scholar]
- Borysow, A., Jørgensen, U. G., & Fu, Y. 2001, J. Quant. Spectr. Rad. Trans., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch, S., Ferre-Borrull, J., Leinfellner, N., & Canillas, A. 2000, Surf. Sci., 453, 9 [Google Scholar]
- Burrows, A., Ram, R. S., Bernath, P., Sharp, C. M., & Milsom, J. A. 2002, ApJ, 577, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Cesarsky, C. J., Abergel, A., Agnese, P., et al. 1996, A&A, 315, L32 [NASA ADS] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, A. M., Piotto, G., & King, I. R. 1996, ApJ, 468, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, E., Méndez, R. A., Jao, W.-C., et al. 2005, AJ, 130, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Covey, K. R., Lada, C. J., Román-Zúñiga, C., et al. 2010, ApJ, 722, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Dehn, M., Helling, C., Woitke, P., & Hauschildt, P. 2007, in Convection in Astrophysics, eds. T. Kuroda, H. Sugama, R. Kanno, & M. Okamoto, IAU Symp., 239, 227 [Google Scholar]
- Dulick, M., Bauschlicher, Jr., C. W.,Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Allard, F., Ludwig, H.-G., Homeier, D., & Steffen, M. 2010, A&A, 513, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabriel, C., Acosta-Pulido, J., Heinrichsen, I., Morris, H., & Tai, W.-M. 1997, in Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, ASP Conf. Ser., 125, 108 [Google Scholar]
- Gould, A., Bahcall, J. N., & Flynn, C. 1996, ApJ, 465, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammersley, P. L., Jourdain de Muizon, M., Kessler, M. F., et al. 1998, A&AS, 128, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Covey, K. R., Knapp, G. R., et al. 2002, AJ, 123, 3409 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Ackerman, A., Allard, F., et al. 2008a, MNRAS, 391, 1854 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Dehn, M., Woitke, P., & Hauschildt, P. H. 2008b, ApJ, 675, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Woitke, P., & Thi, W.-F. 2008c, A&A, 485, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, T. J. 1998, in Brown Dwarfs and Extrasolar Planets, eds. R. Rebolo, E. L. Martin, & M. R. Zapatero Osorio, ASP Conf. Ser., 134, 28 [Google Scholar]
- Henry, T. J., Franz, O. G., Wasserman, L. H., et al. 1999, ApJ, 512, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Homeier, D. 2005, Mem. Soc. Astron. Ital. Suppl., 7, 157 [NASA ADS] [Google Scholar]
- Homeier, D., Hauschildt, P., & Allard, F. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner (San Francisco: ASP), ASP Conf. Ser., 288, 357 [Google Scholar]
- Köhler, R., Ratzka, T., & Leinert, C. 2012, A&A, 541, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., & Ryabchikova, T. A. 1999, Publications de l’Observatoire Astronomique de Belgrad, 65, 223 [Google Scholar]
- Leggett, S. K., Harris, H. C., & Dahn, C. C. 1994, AJ, 108, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Allard, F., & Hauschildt, P. H. 1998, ApJ, 509, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Weitzel, N., Richichi, A., Eckart, A., & Tacconi-Garman, L. E. 1994, A&A, 291, L47 [NASA ADS] [Google Scholar]
- Leinert, C., Woitas, J., Allard, F., Richichi, A., & Jahreiss, H. 1998, in Brown Dwarfs and Extrasolar Planets, eds. R. Rebolo, E. L. Martin, & M. R. Zapatero Osorio, ASP Conf. Ser., 134, 203 [Google Scholar]
- Leinert, C., Allard, F., Richichi, A., & Hauschildt, P. H. 2000, A&A, 353, 691 [NASA ADS] [Google Scholar]
- Leinert, C., Jahreiß, H., Woitas, J., et al. 2001, A&A, 367, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemke, D., Klaas, U., Abolins, J., et al. 1996, A&A, 315, L64 [NASA ADS] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, Proc. SPIE, 4841, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., Rich, R. M., & Shara, M. M. 2003, AJ, 125, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Fegley, Jr., B. 2006, Chemistry of Low Mass Substellar Objects, ed. J. W. Mason (Springer Verlag), 1 [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2002, A&A, 395, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2006, A&A, 459, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Rieke, G. H., & Rieke, M. J. 1996, AJ, 111, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, E. L., Delfosse, X., Basri, G., et al. 1999, AJ, 118, 2466 [NASA ADS] [CrossRef] [Google Scholar]
- Mera, D., Chabrier, G., & Baraffe, I. 1996, ApJ, 459, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 1998, A&A, 337, 495 [NASA ADS] [Google Scholar]
- Reid, N. 1993, MNRAS, 265, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Homeier, D., Hauschildt, P. H., & Allard, F. 2007a, A&A, 473, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Seifahrt, A., Käufl, H. U., Siebenmorgen, R., & Smette, A. 2007b, A&A, 471, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A., Bragaglia, A., Ferraro, F. R., et al. 1996, ApJ, 465, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Robberto, M., & Herbst, T. M. 1998, Proc. SPIE, 3354, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2010, ApJ, 720, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Rossow, W. B. 1978, Icarus, 36, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, Proc. SPIE, 4839, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz, M. T., Leggett, S. K., & Allard, F. 1997, ApJ, 491, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Seifahrt, A., Röll, T., Neuhäuser, R., et al. 2008, A&A, 484, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skory, S., Weck, P. F., Stancil, P. C., & Kirby, K. 2003, ApJS, 148, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Tashkun, S. A., Perevalov, V. I., Teffo, J.-L., et al. 2004, Proc. SPIE, 5311, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T., Ohnaka, K., & Aoki, W. 1996a, A&A, 305, L1 [NASA ADS] [Google Scholar]
- Tsuji, T., Ohnaka, K., Aoki, W., & Nakajima, T. 1996b, A&A, 308, L29 [NASA ADS] [Google Scholar]
- Tsuji, T., Ohnaka, K., & Aoki, W. 1999, ApJ, 520, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Unsöld, A. 1968, Physik der Sternatmosphären, 2nd edn. (Heidelberg: Springer Verlag) [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., & Helling, C. 2004, A&A, 414, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Spectral index values and derived spectral type computed from TiO and CaH band-strengths for component A and from the PC3 index for components B and C.
All Figures
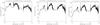 |
Fig. 1 Comparison between NICMOS and NACO spectra of the three components. |
| In the text | |
 |
Fig. 2 Optical spectra of the components of LHS 1070 obtained with the Faint Object Spectrograph (FOS) on HST. The atomic and molecular features visible in all three components are shown in the upper panel. |
| In the text | |
 |
Fig. 3 Near-IR spectra (solid line) and photometry (solid circles) obtained with NICMOS on HST for components A (upper left), B (upper right), and C (lower left). The ISOPHOT thermal IR spectra of the unresolved system is shown on the lower right panel, again with photometric measurements overplotted. |
| In the text | |
 |
Fig. 4 VLT (NACO) spectra of all the components in J, H and K bands with atomic and molecular lines indicated. |
| In the text | |
 |
Fig. 5 VO band observed in the primary (black) compared to the BT-Settl model at 2900 K, log g = 5.0, R = 0.134 R ⊙ for different metallicities. |
| In the text | |
 |
Fig. 6 Right: BT-Settl and BT-Dusty models for an effective temperature of 2900 K and varying log g. The effect of gravity and the pressure broadening of the K I doublet is clearly visible. The details of the dust treatment only cause negligible differences at this Teff. Left: K I doublet as observed for the primary (black) compared to the BT-Dusty (red), BT-Settl (green), DRIFT (blue), and MARCS (brown) models with log g = 5.0. |
| In the text | |
 |
Fig. 7 CaH molecular bands in the spectrum of the primary (black) compared to the BT-Settl model at 2900 K, log g = 5.0 (red) and log g = 5.5 (green). |
| In the text | |
 |
Fig. 8 Left: χ2 map computed for component A using the optical spectrum and the BT-Dusty model. Right: same using the near-IR spectrum. All values inside the white contour give an acceptable fit (checked by eye). The adopted common solution to both χ2 maps is: Teff = 2900 K and a radius of 0.134 R ⊙ . |
| In the text | |
 |
Fig. 9 Optical spectra of all three components. Comparison with model predictions. Black: observed FOS spectra. Green: best fit BT-Settl model. Blue: best fit DRIFT model. Brown: best fit MARCS model. The parameters that give the best fit are given in Table 2. |
| In the text | |
 |
Fig. 10 Same as Fig. 9 with NICMOS spectra in the near-IR. |
| In the text | |
 |
Fig. 11 Black: J (upper panel), H (middle panel), and K (lower panel) NACO spectra of all three components. Comparison with model predictions. Green: best fit BT-Settl model. Red: best fit BT-Dusty model. Blue: best fit DRIFT model. Brown: best fit MARCS model. The comparison of the BT-Dusty and BT-Settl models together with the observations are shown on the right panels. |
| In the text | |
 |
Fig. 12 Black: ISOPHOT thermal IR spectra of the unresolved system, with photometric measurements overplotted (stars). Red: best fit BT-Dusty model. Green: best fit BT-Settl model. Blue: best fit DRIFT model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


